Memory Approximate Message Passing

Approximate message passing (AMP) has attracted extensive research interest for this problem [4, 5]. AMP adopts a low-complexity matched filter (MF), so its complexity is as low as ${\cal O}(MN)$ per iteration. Remarkably, the asymptotic performance of AMP can be described by a scalar recursion called state evolution derived heuristically in [5] and proved rigorously in [4]. State evolution analysis in [4] implies that AMP is Bayes-optimal for zero-mean IID sub-Gaussian sensing matrices when the compression rate is larger than a certain threshold [7]. Spatial coupling [7, 8, 9, 10] is used for the optimality of AMP for any compression rate.

A basic assumption of AMP is that $\bm{A}$ has IID Gaussian entries [5, 4]. For matrices with correlated entries, AMP may perform poorly or even diverge [11, 12, 13]. It was discovered in [14, 15] that a variant of AMP based on a unitary transformation, called UTAMP, performs well for difficult (e.g. correlated) matrices $\bm{A}$. Independently, orthogonal AMP (OAMP) was proposed in [16] for unitarily invariant $\bm{A}$. OAMP is related to a variant of the expectation propagation algorithm [17] (called diagonally-restricted expectation consistent inference in [18] or scalar expectation propagation in [19]), as observed in [20, 21]. A closely related algorithm, an MMSE-based vector AMP (VAMP) [21], is equivalent to expectation propagation in its diagonally-restricted form [18]. The accuracy of state evolution for such expectation propagation type algorithms (including VAMP and OAMP) was conjectured in [16] and proved in [21, 20]. The Bayes optimality of OAMP is derived in [21, 20, 16] when the compression rate is larger than a certain threshold, and the advantages of AMP-type algorithms over conventional turbo receivers [23, 22] are demonstrated in [25, 24].

The main weakness of OAMP/VAMP is the high-complexity ${\cal O}(M^{3}+M^{2}N)$ incurred by linear MMSE (LMMSE) estimator. Singular-value decomposition (SVD) was used to avoid the high-complexity LMMSE in each iteration [21], but the complexity of the SVD itself is as high as that of the LMMSE estimator. The performance of OAMP/VAMP degrades significantly when the LMMSE estimator is replaced by the low-complexity MF [16] used in AMP. This limits the application of OAMP/VAMP to large-scale systems for which LMMSE is too complex.

In summary, the existing Bayes-optimal AMP-type algorithms are either limited to IID matrices (e.g. AMP) or need high-complexity LMMSE (e.g. OAMP/VAMP). Hence, a low-complexity Bayes-optimal message passing algorithm for unitarily invariant matrices is desired.

A long-memory AMP algorithm was originally constructed in [26] to solve the Thouless-Anderson-Palmer equations for Ising models with general invariant random matrices. The results in [26] were rigorously justified via SE in [27]. Recently, Takeuchi proposed convolutional AMP (CAMP), in which the AMP is modified by replacing the Onsager term with a convolution of all preceding messages [28]. The CAMP has low complexity and applies to unitarily invariant matrices. It is proved that the CAMP is Bayes-optimal if it converges to a unique fixed point [28]. However, it is found that the CAMP has a low convergence speed and may fail to converge, particularly for matrices with high condition numbers. In addition, a heuristic damping was used to improve the convergence of CAMP. However, the damping is performed on the a-posteriori outputs, which breaks orthogonality and the asymptotic Gaussianity of estimation errors [28].

To overcome the difficulties in AMP, OAMP/VAMP and CAMP, we propose a memory AMP (MAMP) using a low-complexity long-memory MF. Due to the correlated long memory, stricter orthogonality is required for MAMP to guarantee the asymptotic Gaussianity of estimation errors in MAMP [20, 28]. In detail, the step-by-step orthogonalization between current input and output estimation errors in OAMP/VAMP is not sufficient, and instead, the current output estimation error is required to be orthogonal to all preceding input estimation errors. A covariance-matrix state evolution is established for MAMP. Based on state evolution, relaxation parameters and a damping vector, preserving the orthogonality (e.g. the asymptotic Gaussianity of estimation errors), are analytically optimized to guarantee and improve the convergence of MAMP. The main properties of MAMP are summarized as follows.

• •

  MAMP has comparable complexity to AMP and much lower complexity than OAMP/VAMP.

• •

  MAMP converges to the same fixed point as that of OAMP/VAMP for all unitarily invariant matrices. As a result, it is Bayes-optimal if it has a unique fixed point.

Fig. 1(a) illustrates the system in (1) with two constraints:

$$\Gamma:\;\;\bm{y}=\bm{Ax}+\bm{n},\qquad\Phi:\;\;x_{i}\sim P_{x},\;\;\forall i.\vspace{-1mm}$$

(2)

Our aim is to use the AMP-type iterative approach in Fig. 1(b) to find an MMSE estimation of $\bm{x}$, i.e., its MSE converges to

$${\rm mmse}\{\bm{x}|\bm{y},\bm{A},{\Gamma},{\Phi}\}\equiv\tfrac{1}{N}{\mathrm{E}}\{\|\hat{\bm{x}}_{\rm post}-{\bm{x}}\|^{2}\},$$

(3)

where $\hat{\bm{x}}_{\rm post}\!=\!{\mathrm{E}}\{\bm{x}|\bm{y},\bm{A},{\Gamma},{\Phi}\}$ is the a-posteriori meas of $\bm{x}$.

Let the singular value decomposition of $\bm{A}$ be $\bm{A}\!=\!\bm{U}\bm{\Sigma}\bm{V}$, where $\bm{U}\!\in\!\mathbb{C}^{M\times M}$ and $\bm{V}\!\in\!\mathbb{C}^{N\times N}$ are orthogonal matrices, and $\bm{\Sigma}$ is a diagonal matrix. We assume that $\bm{A}$ is known and is right-unitarily-invariant, i.e., $\bm{U}$, $\bm{V}$ and $\bm{\Sigma}$ are independent, and $\bm{V}$ is Haar distributed. Let $\lambda_{t}=\tfrac{1}{N}{\rm E}\{{\rm tr}[(\bm{A}\bm{A}^{\rm H})^{t}]\}$ and ${\lambda}^{\dagger}\equiv[\lambda_{\max}+\lambda_{\min}]/2$, where $\lambda_{\min}$ and $\lambda_{\max}$ denote the minimal and maximal eigenvalues of $\bm{A}\bm{A}^{\rm H}$, respectively. We assume that $\lambda_{\min}$, $\lambda_{\max}$ and $\{\lambda_{t}\}$ are known. This assumption can be relaxed using specific approximations (see [1]).

Non-memory Iterative Process (NMIP): Fig. 1(b) illustrates an NMIP consisting of a linear estimator (LE) and a non-linear estimator (NLE): Starting with $t=1$,

$${\mathrm{LE:}}\quad\bm{r}_{t}=\gamma_{t}\left(\bm{x}_{t}\right),\qquad{\mathrm{NLE:}}\;\;\bm{x}_{t+1}=\phi_{t}\left(\bm{r}_{t}\right),\vspace{-1mm}$$

(4)

where $\gamma_{t}(\cdot)$ and $\phi_{t}(\cdot)$ process the two constraints $\Gamma$ and $\Phi$ separately, based only on their current inputs $\bm{x}_{t}$ and $\bm{r}_{t}$ respectively. Let

	$$\bm{r}_{t}=\bm{x}+\bm{g}_{t},\qquad\bm{x}_{t}=\bm{x}+\bm{f}_{t},\vspace{-1mm}$$		(5a)
where $\bm{g}_{t}$ and $\bm{f}_{t}$ indicate the estimation errors with zero means and variances:
	$\displaystyle v_{t}^{\gamma}=\tfrac{1}{N}{\rm E}\{\|\bm{g}_{t}\|^{2}\},\qquad v_{t}^{\phi}=\tfrac{1}{N}{\rm E}\{\|\bm{f}_{t}\|^{2}\}.$		(5b)

The asymptotic IID Gaussian property of an NMIP was conjectured in [16] and proved in [20, 21].

OAMP/VAMP [16, 21]: Let $\rho_{t}=\sigma^{2}/{v_{t}^{\phi}}$, $\hat{\phi}_{t}(\cdot)$ be an MMSE estimator, and $\hat{\gamma}_{t}(\cdot)$ be an estimator of $\bm{x}$ defined as

$$\hat{\gamma}_{t}\left(\bm{x}_{t}\right)\equiv\bm{A}^{\rm H}\big{(}\rho_{t}\bm{I}+\bm{A}\bm{A}^{\mathrm{H}}\big{)}^{-1}(\bm{y}-\bm{A}\bm{x}_{t}).$$

(8)

An OAMP/VAMP is then defined as: Starting with $t=1$, $v_{1}^{\phi}=1$ and $\bm{x}_{1}=\bm{0}$,

	$\displaystyle\!\!\!\!{\mathrm{LE:}}\quad\bm{r}_{t}=\gamma_{t}\left(\bm{x}_{t}\right)$	$\displaystyle\equiv\tfrac{1}{{\epsilon}^{\gamma}_{t}}\hat{\gamma}_{t}\left(\bm{x}_{t}\right)+\bm{x}_{t},$		(9a)
	$\displaystyle\!\!\!\!{\mathrm{NLE:}}\;\bm{x}_{t+1}\!=\!\phi_{t}\left(\bm{r}_{t}\right)$	$\displaystyle\!\equiv\!\tfrac{1}{\epsilon^{\phi}_{t+1}}\!\big{[}\hat{\phi}_{t}(\bm{r}_{t})\!+\!(\epsilon^{\phi}_{t+1}\!-\!1)\bm{r}_{t}\big{]},$		(9b)
where
	$\displaystyle{\epsilon}_{t}^{\gamma}$	$\displaystyle=\tfrac{1}{N}{\mathrm{tr}}\big{\{}\bm{A}^{\rm H}\big{(}\rho_{t}\bm{I}+\bm{A}\bm{A}^{\mathrm{H}}\big{)}^{\!-1}\!\!\bm{A}\big{\}},$		(9c)
	$\displaystyle v^{\gamma}_{t}$	$\displaystyle=\gamma_{\mathrm{SE}}(v_{t}^{\phi})\equiv{v}^{\phi}_{t}[({\epsilon}_{t}^{\gamma})^{-1}-1],$		(9d)
	$\displaystyle\epsilon^{\phi}_{t+1}$	$\displaystyle=1-\tfrac{1}{Nv^{\gamma}_{t}}\|\hat{\phi}_{t}(\bm{x}+\sqrt{v^{\gamma}_{t}}\bm{\eta})-\bm{x}\|^{2},$		(9e)
	$\displaystyle{v}^{\phi}_{t+1}$	$\displaystyle=\phi_{\mathrm{SE}}(v^{\gamma}_{t})\equiv v^{\gamma}_{t}[(\epsilon^{\phi}_{t+1})^{-1}-1],$		(9f)

and $\bm{\eta}\sim{\cal{CN}}(\bm{0},\bm{I})$ is independent of $\bm{x}$.

We assume that $\hat{\phi}_{t}(\cdot)$ is an MMSE estimator given by

$$\hat{\phi}_{t}(\bm{r}^{t})\equiv\mathrm{E}\{\bm{x}|\bm{r}^{t}\}.$$

(10)

It was proved in [20] that OAMP/VAMP satisfies the orthogonality in (6). Hence, the IID Gaussian property in (7) holds for OAMP/VAMP.

Complexity: The NLE in OAMP/VAMP is a symbol-by-symbol estimator, whose time complexity is as low as ${\cal O}(N)$. The complexity of OAMP/VAMP is dominated by LMMSE-LE, which costs $\mathcal{O}(M^{2}N\!+\!M^{3})$ time complexity per iteration for matrix multiplication and matrix inversion.

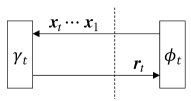
Memory Iterative Process (MIP): Fig. 2 illustrates an MIP based on a long-memory linear estimator (LMLE) and a non-linear estimator (NLE) defined as: Starting with $t=1$,

	$\displaystyle{\rm LMIE:}$	$\displaystyle\quad\quad\bm{r}_{t}$	$\displaystyle=\gamma_{t}\left(\bm{x}_{1},\cdots\bm{x}_{t}\right),$		(11a)
	$\displaystyle{\rm NLE:}$	$\displaystyle\quad\bm{x}_{t+1}$	$\displaystyle=\phi_{t}\left(\bm{r}_{t}\right).$		(11b)

We call (11) MIP since $\gamma_{t}(\cdot)$ contains long memory $\{\bm{x}_{i},i<t\}$. It should be emphasized that the step-by-step orthogonalization between current input and output estimation errors is not sufficient to guarantee the asymptotic IID Gaussianity for MIP. Thus, a stricter orthogonality is required, i.e., the estimation error of $\gamma_{t}(\cdot)$ is required to be orthogonal to all preceding estimation errors [28, 33].

Memory AMP: Let $\bm{B}=\lambda^{\dagger}\bm{I}-\bm{A}\bm{A}^{\mathrm{H}}$, and consider

$$\hat{\bm{r}}_{t}=\theta_{t}\bm{B}\hat{\bm{r}}_{t-1}+\xi_{t}(\bm{y}-\bm{A}\bm{x}_{t}).\vspace{-1mm}$$

(14)

An MAMP process is defined as: Starting with $t\!=\!\!1$ and ${\bm{x}}_{1}\!\!=\!\hat{\bm{r}}_{0}\!=\!\bm{0}$,

	$\displaystyle\bm{r}_{t}$	$\displaystyle=\gamma_{t}\left(\bm{x}_{1},\cdots\bm{x}_{t}\right)\equiv\tfrac{1}{{\varepsilon}_{t}}\big{(}\bm{A}^{\mathrm{H}}\hat{\bm{r}}_{t}+\textstyle\sum_{i=1}^{t}p_{ti}\bm{x}_{i}\big{)},$		(15a)
	$\displaystyle\bm{x}_{t+1}$

where $\phi_{t}(\cdot)$ is the same as that in OAMP/VAMP (see (9)).

The following are intuitions of MAMP.

• •

  In LMIE, all preceding messages are utilized in $\textstyle\sum_{i=1}^{t}p_{ti}\bm{x}_{i}$ to guarantee the orthogonality in (12). In NLE, at most $l_{t}-1$ preceding messages are utilized in $\textstyle\sum_{i=1}^{l_{t}-1}\scaleto{\zeta}{8pt}_{ti}\bm{x}_{t-l_{t}+1+i}$ (e.g. damping) to guarantee and improve the convergence of MAMP.

• •

  $\bm{B}=\lambda^{\dagger}\bm{I}-\bm{A}\bm{A}^{\mathrm{H}}$ ensures that MAMP has the same fixed point as OAMP/VAMP.

• •

  $\{{\varepsilon}_{t}\}$ and $\{p_{ti}\}$, given in Subsection IV-A (see (15q)), guarantee the orthogonality in (12) (see Theorem 1).

• •

  $\{\theta_{t}\}$ and $\{\xi_{t}\}$ improve the convergence speed of MAMP. The optimizations of $\theta_{t}$ and $\xi_{t}$ are given in Subsections V-A (see (15ag)) and V-B (see (15ae)), respectively.

• •

  $\scaleto{\bm{\zeta}}{8pt}_{t}=[{\scaleto{\zeta}{8pt}}_{t1},\cdots,{\scaleto{\zeta}{8pt}}_{tl_{t}}]^{\rm T}$, optimized in Subsection V-C (see (15ai)), is a damping vector with $\textstyle\sum_{i=1}^{l_{t}}{\scaleto{\zeta}{8pt}}_{ti}=1$. In particular, no damping is applied for $\scaleto{\bm{\zeta}}{8pt}_{t}=[0,\cdots,0,1]^{\rm T}$. We set $l_{t}=\min\{L,t\!+\!1\}$, where $L$ is the maximum damping length (in general, $L=3$). Damping guarantees and improves the convergence of MAMP.

We call (15) memory AMP as it involves a long memory $\{\bm{x}_{i},i<t\}$ at LMIE that is different from the non-memory LE in OAMP/VAMP. Matrix-vector multiplications instead of matrix inverse are involved. Thus, the complexity of MAMP is comparable to AMP, i.e., as low as ${\cal O}(MN)$ per iteration.

Let $\bm{W}_{t}=\bm{A}^{\rm H}\bm{B}^{t}\bm{A}$. For $t\geq 0$, we define

	$\displaystyle b_{t}$	$\displaystyle\equiv\tfrac{1}{N}{\rm tr}\{\bm{B}^{t}\}=\textstyle\sum_{i=0}^{t}\binom{t}{i}(-1)^{i}(\lambda^{\dagger})^{t-i}\lambda_{i},$		(15pa)
	$\displaystyle w_{t}$	$\displaystyle\equiv\tfrac{1}{N}{\rm tr}\{\bm{W}_{t}\}=\lambda^{\dagger}b_{t}-b_{t+1}.$		(15pb)

For $1\leq i\leq t$,

$\displaystyle\!\!\vartheta_{ti}\equiv\xi_{i}\!\textstyle\prod_{\tau=i+1}^{t}\!\theta_{\tau},\;\;\;p_{ti}\equiv\vartheta_{ti}w_{t-i},\;\;\;{\varepsilon}_{t}=\textstyle\sum_{i=1}^{t}p_{ti}.$

(15q)

Furthermore, $\vartheta_{ti}=1$ if $i>t$.

The following is based on Lemma 3 and Proposition 1.

Using the IID Gaussian property in Theorem 1, we establish a state evolution for the dynamics of the MSE of MAMP. The main challenge is the correlation between the long-memory inputs of LMIE. It requires a covariance-matrix state evolution to track the dynamics of MSE.

Define the covariance matrices as follows:

	$$\bm{V}_{t}^{\gamma}=[v^{\gamma}_{ij}]_{t\times t},\qquad\bm{V}_{t}^{\bar{\phi}}=[v^{\bar{\phi}}_{ij}]_{t\times t},\vspace{-1mm}$$		(15sa)
where
	$\displaystyle v^{\gamma}_{tt^{\prime}}\equiv\tfrac{1}{N}{\mathrm{E}}\{\bm{g}_{t}^{\mathrm{H}}\bm{g}_{t^{\prime}}\},\qquad v^{\bar{\phi}}_{tt^{\prime}}\equiv\tfrac{1}{N}{\mathrm{E}}\{\bm{f}_{t}^{\mathrm{H}}\bm{f}_{t^{\prime}}\}.$		(15sb)

The following theorem gives the convergence and Bayes optimality of the optimized MAMP. The proof is provided in Appendix F in [1].

Table I compares the time and space complexity of MAMP, CAMP, AMP and OAMP/VAMP, where $T$ is the number of iterations. MAMP and CAMP have the similar time and space complexity. OAMP/VAMP has higher complexity than AMP, CAMP and MAMP, while MAMP and CAMP have comparable complexity to AMP for $T\ll N$. For more details, refer to Section IV-D in [1].

The optimal $\theta_{t}$ is given by

$$\theta_{t}=(\lambda^{\dagger}+\sigma^{2}/v_{tt}^{\phi})^{-1},$$

(15ae)

which minimizes the spectral radius of $\theta_{t}\bm{B}$. From (15ae), the spectral radius of $\theta_{t}\bm{B}$ satisfies

$$\rho(\theta_{t}\bm{B})=\tfrac{\lambda_{\max}-\lambda_{\min}}{\lambda_{\max}+\lambda_{\min}+2\rho_{t}}<1.$$

(15af)

That is, the convergence condition is satisfied. In addition, (15ae) also optimizes the convergence speed of MAMP.

Let $\bm{\mathcal{V}}_{t+1}^{\phi}$ be the covariance matrix of the input errors of $\bar{\phi}_{t}$, i.e. $\{\bm{f}_{t-l_{t}+2},\cdots,\bm{f}_{t},\phi_{t}(\bm{r}_{t})-\bm{x}\}$.

It is easy to see that the MSE of current iteration with optimized damping is not worse than that of the previous iteration, which is a special case of $\scaleto{\bm{\zeta}}{8pt}_{t}=[0,\cdots,1,0]^{\rm T}$. That is, the MSE of MAMP with optimized damping is monotonically decreasing in the iterations.

Fig. VI-A shows the influence of the relaxation parameters $\{\lambda^{\dagger},\theta_{t},\xi_{t}\}$ and damping. Without damping (e.g. $L=1$) the convergence of MAMP is not guaranteed. In addition, the optimization of $\{\lambda^{\dagger},\theta_{t},\xi_{t}\}$ has significant improvement in the MSE of MAMP. That is

• (i)

  damping guarantees the convergence of MAMP, and

• (ii)

  the relaxation parameters $\{\lambda^{\dagger},\theta_{t},\xi_{t}\}$ do not change the fixed point of MAMP, but they can be optimized to improve the convergence speed.

Fig. 4 shows MSE versus the number of iterations for AMP, CAMP, OMAP/VAMP and MAMP. To improve the convergence, both AMP and CAMP are damped. As can be seen, for an ill-conditioned matrix with $\kappa=10$, the MSE performance of AMP is poor. CAMP converges to the same performance as that of OAMP/VAMP. However, the state evolution (SE) of CAMP is inaccurate since damping is made on the a-posteriori outputs, which breaks the Gaussianity of the estimation errors. MAMP converges faster than CAMP to OAMP/VAMP. Furthermore, the state evolution of MAMP is accurate since damping is made on the orthogonal outputs, which preserves the Gaussianity of the estimation errors.

Fig. 5 shows MSE versus the number of iterations for MAMP with different damping lengths. As can be seen, MAMP converges to OAMP/VAMP for the matrix with high condition number $\kappa=100$, and the state evolution (SE) of MAMP matches well with the simulated MSE. Note that CAMP diverges when $\kappa>15$ (see Fig. 4 in [28]). In addition, MAMP with $L=3$ (damping length) has significant improvement in convergence speed compared with $L=2$ when the condition number is large. It should be mentioned that $L=3$ is generally enough for MAMP, since the MSEs of MAMP are almost the same when $L\geq 3$.