Memory-only selection of dictionary PINs
Abstract
We estimate the security of dictionary-based PINs (Personal Identification Numbers) that a user selects from his/her memory without any additional aids. The estimates take into account the distribution of words in source language. We use established security metrics, such as entropy, guesswork, marginal guesswork and marginal success rate. The metrics are evaluated for various scenarios – aimed at improving the security of the produced PINs. In general, plain and straightforward construction of memory-only dictionary PINs yields unsatisfactory results and more involved methods must be used to produce secure PINs.
1 Introduction
A PIN is frequently used form of user authentication. The PIN is a fixed-length string of digits, usually of length 4, 5 or 6. There are recommendations on how to choose and work with the PINs in secure manner, e.g. [11, 15, 6]. Other proposals try to devise methods for producing sufficiently secure PIN [7, 8]. Even though the users are often informed and aware of PIN security, several studies showed that the significant portion of the users choose weak, easily guessable PINs [2, 4]. Weaknesses can also lie in other aspects of using authentication secrets, e.g. partial password/PIN verification [1].
One possibility of choosing and memorizing the PIN is to use so-called dictionary PIN. Dictionary PIN is derived from a word with the mapping offered by numpads of ATMs, mobile phones or Point-of-Sale terminals. The most commonly used letter to digit mapping is the standard mapping shown in Figure 1.
Certainly, other mappings are possible, covering also digits 0 and 1. Recent study of dictionary PINs [12] analyzed the security of dictionary PINs with respect to various languages and dictionaries. It also described and assessed several methods of improving dictionary PINs selection. The assessment assumed uniform distribution of dictionary words, see [12]:
“Let us stress that the experiments treat the words in a dictionary as equally probable. This is certainly not true if a user chooses the word from his/her memory. The uniform distribution can be easily achieved with the aid of an application that offers random sets of words for the user to choose from.”
Nevertheless, sometimes it can be impractical to use an external application and some users can hesitate to use or they would not even trust such application for PIN selection. Therefore we focus on dictionary PINs that user selects from his/her memory, without any external aid. We address the question of the security of such user-generated dictionary PINs in this paper. The main findings of our experiments are the following:
-
Considering uniform frequencies of dictionary words is inadequate for estimating the security of memory-only selection of dictionary PINs.
-
The straightforward word to PIN translation yields unacceptable marginal success rates when frequencies are taken into account.
-
Simple blacklisting, prefix, and two-dictionary methods offer only a moderate improvement in security metrics.
-
A more demanding methods, such as morphing or combination of multiple methods, are needed to obtain significantly better results.
1.1 Quantifying the predictability of PIN
Let be the size of an PIN space, for PIN length . Let be a random variable over the set . Let denotes the probability of choosing a particular PIN . Without loss of generality we assume that PINs are sorted in the descending order of their probabilities, i.e. .
Various measures for the PIN choices were proposed and studied, for details, discussions and relations among these metrics see [3, 4, 16]. The most important ones are defined in the following list.
-
Shannon entropy, expressed in bits, measures the uncertainty in a random variable:
-
The guesswork measures the expected number of guesses needed to find a PIN, trying in descending order according their probability:
-
The marginal guesswork measures the expected number of guesses needed to increase the success probability of finding the PIN to at least (usually ):
-
The marginal success rate measures the probability of guessing the PIN given attempts ( is usually or ):
Since the guesswork and the marginal guesswork are not directly comparable to Shannon entropy, the values of and are converted into bits using the following formulas [3]: , .
Since the standard mapping does not cover digits 0 and 1, the ideal security metrics have the following values for dictionary PINs (assuming uniform distribution of PINs) :
-
PIN length 4: bits, ,
-
PIN length 5: bits, .
2 Estimating metrics for dictionary PIN selection
In order to model frequency distribution of words in a language we use frequency lists based on subtitles. This is a respected method for analyzing contemporary languages [5]. We use two frequency lists for English – a carefully prepared SUBTLEXus [13] containing 60,384 words with a frequency higher than 1, and the list compiled from subtitles available from opensubtitles.org [10], containing more than 450,000 words (even words with frequency 1). We will denote the results obtained using the first/second list with label “SUBTLEXus”/“opensub”, respectively.
2.1 Basic statistics
We compare the metrics for straightforward translation of words to PINs using the standard mapping, see Figure 1, with results obtained in [12]. We consider only the words with the length equal to the PIN length . The translation starts with stripping the diacritical marks, if they are present. Then, the word is mapped to PIN using the standard mapping, e.g. “love” and “hate” yield 5683 and 4283, respectively. The frequency of particular word contributes to the probability of resulting PIN.
The results for the PIN lengths 4 and 5 are shown in Table 1. The columns labeled “uniform” contain results for PINs derived from a large (spell-checker) English dictionary assuming uniform frequencies of words [12]. The columns labeled “RockYou” contains results for PINs derived from RockYou password database where frequencies of words (passwords) were taken into account. It is easy to notice a striking difference between scenarios that consider the frequencies of words and those that do not.
| SUBTLEXus | opensub | uniform [12] | RockYou [12] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (bits) | |||||||||||
| (bits) | |||||||||||
| (bits) | |||||||||||
| (%) | |||||||||||
A closer look at the most frequent dictionary PINs from SUBTLEXus and opensub reveals the following observations:
-
PIN length 4: Top 7 PINs share the same spots in SUBTLEXus and opensub scenarios (the last three spots in top 10 are just permuted, i.e. the top 10 contains exactly the same set of PINs in both scenarios). The high marginal success rates are caused by the frequencies of the following PINs: 8428 (probability based on SUBTLEXus, e.g. produced from the word “that”), 9428 (, “what”), 8447 (, “this”), 4283 (, “have”), 9687 (, “your”), and 5669 (, “know”).
-
PIN length 5: The sets of top 10 PINs differ in just two PINs, while the first 5 spots are exactly the same in SUBTLEXus and opensub scenarios. For SUBTLEXus scenario the most frequent PINs are: 84373 (, e.g. produced from the word “there”), 74448 (, “right”), 22688 (, “about”), 84465 (, “think”), 46464 (, “going”), and 46662 (, “gonna”).
We can conclude that considering uniform frequencies of dictionary words is inadequate for estimating the security of memory-only selection of dictionary PIN. The results show the deficiency of such PINs clearly – the marginal success rates are unacceptable. Moreover, it seems that this strategy is worse (in average) than strategies currently employed by users. In order to compare memory-only dictionary PINs with “common” PIN selection strategies, we present estimates of PIN metrics based on RockYou password database and iPhone unlock codes [4] in Table 2. On the other hand, the lack of digits 0 and 1 in the standard mapping ensures that these digits do not appear in the resulting PIN. Therefore the PINs that are often blacklisted, e.g. 0000, 1111 or 1234, or those the users are warned not to use, e.g. birthday or anniversary years, cannot be selected this way.
| RockYou | iPhone | |
|---|---|---|
| (bits) | ||
| (bits) | ||
| (bits) | ||
| (%) |
We explore few possibilities for improving memory-only dictionary PINs in the following sections.
2.2 Blacklisting
Blacklisting is a common method for improving the security of user-selected PINs. Even if not strictly enforced (by forbidding the selection of some PINs), at least there are recommendations what PINs a user should not choose, e.g. see [15]:
“Select a PIN that cannot be easily guessed (i.e., do not use birth date, partial account numbers, sequential numbers like 1234, or repeated values such as 1111).”
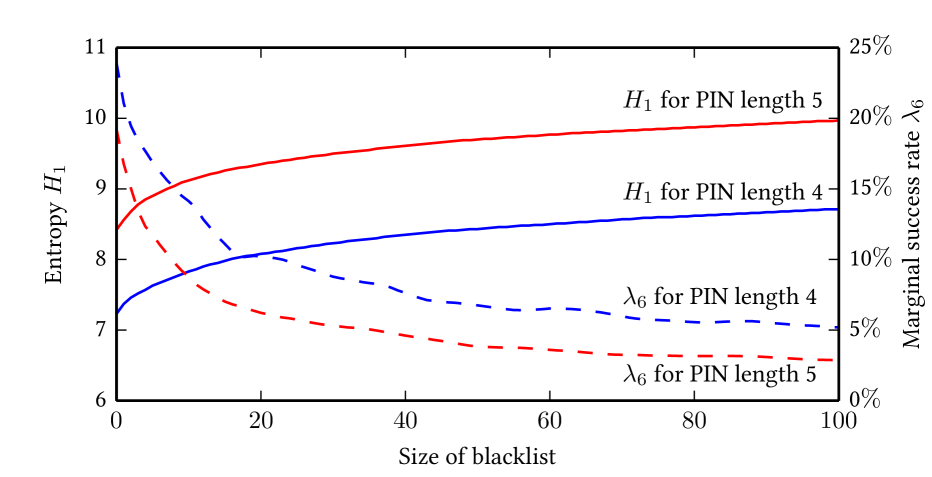
There are two possibilities for blacklisting in dictionary PIN scenario: first, blacklisting the most frequent words; and second, blacklisting the most frequent PINs. The PIN blacklisting is easier to enforce in practice, and the values of security metrics are comparable for both approaches. Figure 2 shows the entropy and the marginal success rate () for PIN blacklisting (based on SUBTLELXus) ranging from to blacklisted PINs. The results show only a moderate improvement in security metrics, therefore blacklisting alone is not a satisfactory method for improving memory-only dictionary PINs.
2.3 Modifications of PIN construction
In order to improve the security metrics of resulting PIN, some natural modifications to basic translation of dictionary word to PIN were proposed in [12]. We evaluate these modifications when applied to our “frequency-aware” experiments:
-
Stretched mapping – in order to cover digits and , we can stretch the standard mapping. Our estimates for this modification use the following mapping: a, b ; c, d ; e, f ; g, h, i ; j, k, l ; m, n ; o, p, q ; r, s, t ; u, v, w ; x, y, z .
-
Prefix – instead of taking just words with the desired PIN length, i.e. , we use any word with the length greater or equal to and we use its prefix for translation to PIN.
-
Morphing – the standard word to PIN translation is enriched by random change of one character. Assuming that user can choose a random position in a word/PIN and a random digit, the resulting PIN is formed by replacing this position by the chosen digit. For example “this” can be translated to “t1is”/8147, “0his”/0447, “thi9”/8449, etc. Certainly, this method is more demanding than the straightforward use of dictionary words. Our estimates assume uniform distribution of positions and digits for this method.
The results for all above methods are presented in Table 3. The stretched mapping yields no improvement at all – the most frequent PINs changed their values, but their frequencies remained almost unchanged. The prefix method offers a moderate improvement in security metrics. Obviously, the morphing is the most successful approach by a wide margin.
| Stretched map. | Prefix | Morphing | ||||||
|---|---|---|---|---|---|---|---|---|
| (bits) | ||||||||
| (bits) | ||||||||
| (bits) | ||||||||
| (%) | ||||||||
Comparing these results with the estimates from Table 2, we can notice that the prefix method for dictionary PINs offers slightly better marginal success rate but worse entropy, guesswork and marginal guesswork. An interesting observation is that the morphing offers much better marginal success rate while keeping other security metrics comparable to real-word estimates from Table 2.
Interestingly, the prefix method and the morphing yield better results than the estimates of PIN entropy by NIST [9]: 9 and 10 bits for PIN lengths 4 and 5, respectively. On the other hand, plain memory-only dictionary PINs offer less entropy than these estimates.
2.4 Blacklisting the prefix and the morphing methods
We expect that blacklisting of the most frequent PINs can further improve the security metrics of promising methods from the previous section (i.e. prefix and morphing methods). Indeed, our experiments confirm this expectation. Table 4 shows the values of the entropy and the marginal success rate for various sizes of the blacklist (, , and ).
| Prefix | Morphing | ||||||
|---|---|---|---|---|---|---|---|
| blacklist | |||||||
| (bits) | 0 | ||||||
| 10 | |||||||
| 20 | |||||||
| (%) | 0 | ||||||
| 10 | |||||||
| 20 | |||||||
The blacklisting substantially improves the marginal success rate, but offers only a moderate improvement of the entropy. A disadvantage of the blacklisting is that it complicates the implementation of authentication.
2.5 Two-dictionary PINs
Many people know more than one language. In such case, it is easy to adopt a strategy where a user randomly choses a language and then (s)he selects a word for PIN construction. We expect obviously an improvement in security metrics values. In order to assess the improvement we use English and Dutch frequency dictionaries SUBTLEXus and SUBTLEXnl [14]. We use words with frequency above 1 in both dictionaries, and we assume that the user selects the dictionary with probability . The results for this two-dictionary scenario are shown in Table 5, where “basic” denotes the construction using words with the length , “prefix” denotes the prefix method, and “prefix (BL)” denotes the combination of the prefix method with the blacklist of the length .
| Basic | Prefix | Prefix (BL 10) | ||||||
|---|---|---|---|---|---|---|---|---|
| (bits) | ||||||||
| (bits) | ||||||||
| (bits) | ||||||||
| (%) | ||||||||
As expected, the results are better than results for corresponding single-dictionary scenario methods. However, even with the blacklisting the results cannot match the morphing method results for single dictionary.
3 Conclusion
We analyzed the security of memory-only selection of dictionary PINs. The results show that plain construction of dictionary PINs is unsatisfactory and more involved methods should be used for improved security metrics.
Acknowledgment
The author acknowledges support by VEGA 1/0259/13.
References
- [1] Aspinall D, Just M. “Give Me Letters 2, 3 and 6!”: Partial Password Implementations and Attacks. In:Proceedings of 17th International Conference on Financial Cryptography and Data Security (FC 2013). LNCS 7859. Springer; 2013.
-
[2]
Berry N. PIN analysis. DataGenetics; 2012.
Available at www.datagenetics.com/blog/september32012/index.html [accessed 31 March 2014]. - [3] Bonneau J, Just M, Matthews G. What’s in name? Evaluating statistical attacks against personal knowledge questions. In: Proceedings of the 14th International Conference on Financial Cryptography and Data Security. LNCS 6052. Springer; 2010, pp. 98–113.
- [4] Bonneau J, Preibusch S, Anderson R. A birthday present every eleven wallets? The security of customer-chosen banking PINs. In: Proceedings of the 16th International Conference on Financial Cryptography and Data Security. LNCS 7397. Springer; 2012, pp. 25–40.
- [5] Brysbaert M, New B. Moving beyond Kučera and Francis: A critical evaluation of current word frequency norms and the introduction of a new and improved word frequency measure for American English. Behavior Research Methods, 41(1):977–990, Springer-Verlag; 2009.
- [6] International Organization for Standardization. Financial services – Personal Identification Number (PIN) management and security, Part 1: Basic principles and requirements for PINs in card-based systems, ISO 9564-1; 2011.
-
[7]
Jakobsson M, Liu D. Bootstrapping Mobile PINs Using Passwords.
W2SP 2011: Web 2.0 Security and Privacy; 2011.
Available at w2spconf.com/2011/papers/mobilePIN.pdf [accessed 31 March 2014]. - [8] Jakobsson M, Liu D. Your Password is Your New PIN. SpringerBriefs in Computer Science 2013, pp 25-36, Springer; 2013.
- [9] NIST. Electronic Authentication Guideline. Special Publication 800-63-1; 2011.
-
[10]
Frequency Word Lists. 2012.
Available at http://invokeit.wordpress.com/frequency-word-lists/ [accessed 31 March 2014]. -
[11]
PCI Security Standards Council. Payment Card Industry PIN Security Requirements.
Version 1.0; 2011.
Available at www.pcisecuritystandards.org/security_standards [accessed 31 March 2014]. -
[12]
Staneková L, Stanek M: Analysis of dictionary methods for PIN selection.
Computers & Security, Volume 39, Part B, Elsevier, 2013, pp. 289-298.
http://dx.doi.org/10.1016/j.cose.2013.08.006. -
[13]
SUBTLEXus, Word Frequency American English, Ghent University, 2009.
Available at http://expsy.ugent.be/subtlexus/ [accessed 31 March 2014] -
[14]
SUBTLEXnl, Database of Dutch Word Frequencies, 2010.
Available at http://crr.ugent.be/programs-data/subtitle-frequencies/subtlex-nl [accessed 31 March 2014] -
[15]
VISA. Issuer PIN Security Guidelines; 2010.
Available at https://usa.visa.com/download/merchants/visa-issuer-pin-security-guideline.pdf [accessed 31 March 2014]. - [16] Weir M, Aggarwal S, Collins M, Stern H. Testing Metrics for Password Creation Policies by Attacking Large Sets of Revealed Passwords. In: Proceedings of the 17th ACM conference on Computer and Communications Security, CCS’10, ACM; 2010. pp. 162–175.