Meridional almost normal surfaces in knot complements
Abstract.
Suppose is a knot in a closed 3-manifold such that is irreducible. We show that for any integer there exists a triangulation of such that any weakly incompressible bridge surface for of bridges or fewer is isotopic to an almost normal bridge surface.
Key words and phrases:
bridge surface, Heegaard splitting, almost normal surface1991 Mathematics Subject Classification:
Primary 57M1. Introduction
It was shown independently by M. Stocking [15] and J. H. Rubinstein [13] that any strongly irreducible Heegaard splitting for an irreducible 3-manifold is isotopic to an almost normal surface. Also see [11] for another proof of this result. The concept of a bridge surface for a knot complement is analogous to the idea of a Heegaard surface for a 3-manifold in that the bridge surface is a splitting surface that separates the knot complement into two equivalent and fairly elementary submanifolds. In addition, the fact that a bridge surface lifts to a Heegaard surface in the 2-fold branched cover of a knot complement gives another important connection between bridge surfaces for knot complements and Heegaard surfaces for 3-manifolds.
In the study of bridge surfaces for knots and links the idea of a weakly incompressible splitting surface is immediately analogous to the idea of a strongly irreducible Heegaard surface for a 3-manifold. In this paper we prove an analog to the main theorem of [15] and Theorem 3 in [13]. We show that any weakly incompressible bridge surface in a 3-manifold is isotopic to an almost normal bridge surface.
1 Main Theorem.
Let be a knot in a closed, orientable, irreducible 3-manifold . Let be a regular neighborhood of and suppose that the closure of the complement is irreducible. Then for any integer there is a triangulation of such that if is a bridge surface for of bridges or fewer that gives an irreducible Heegaard splitting of and is weakly incompressible, then is properly isotopic in to an almost normal surface with respect to .
The proof will be similar in spirit to that of [15] but the proof here fills in a few missing cases and simplifies the argument by making greater use of edge slides. A closely related result was proved by David Bachman in [1], however it requires additional hypotheses. In Section 2 we briefly introduce some definitions and notation. The proof of the main theorem is contained in Section 3.
This research was done while under the support of the UC President’s Postdoctoral Fellowship Program and the Department of Mathematics at UC Santa Barbara. I would like to thank Martin Scharlemann for all of the helpful conversations and many valuable comments, as well as Scott Taylor for his insightful comments about the proof of Lemma 23.
2. Preliminaries
Notation: If is a properly embedded 1-manifold in a 3-manifold then let . If is any surface in transverse to such that , then let . For a triangulation of a 3-manifold , let denote the restriction of to .
The following definition is from [18] and is based on the definition of a -compression body given in [2].
2 Definition ([18]).
A properly embedded arc in a 3-manifold is boundary parallel if there is a disk in the 3-manifold so that is the end point union of and an arc in . The disk is called a cancelling disk for . A -handlebody is a handlebody containing a finite collection of boundary parallel arcs . When there is little risk of confusion we will also refer to as a -handlebody. For our purposes, a -compression body (W,K) is a compression body containing a finite collection of arcs properly embedded in such that each arc has one end on each of and and each arc is vertical in the product region .
3 Remark.
Two sets and of boundary parallel arcs in a handlebody or vertical arcs in a compression body are properly isotopic in if they have the same cardinality, i.e., .
4 Definition.
A spine of a handlebody is a graph properly embedded in such that is a product . Let be a -handlebody and suppose that is a spine for handlebody and is a collection of boundary parallel arcs. Let be a collection of arcs, each connecting to a single arc of . Then a regular neighborhood is again a handlebody, and intersects it in a boundary parallel set of arcs . If the closure of the region between them is a product then is called a spine of the -handlebody . A spine of a compression body is the union of and a properly embedded graph such that is a product . If is a -compression body then a spine for will mean a spine for that is disjoint from .
5 Remark.
It is relatively easy to find such a spine for a -handlebody or -compression body . Choose a spine for of handlebody (compression body) and isotope so that in the product structure , each (boundary parallel) arc of has a single maximum. Let () be a collection of vertical arcs in this product structure, connecting each maximum of to .
6 Definition ([17]).
Let be a knot in a closed, orientable 3-manifold and let be a Heegaard surface for . That is, , where and are handlebodies in . If in addition, and are -handlebodies then we call a bridge surface for . (We will often abuse notation and call the punctured surface a bridge surface as well.) We call the decomposition a bridge splitting of the 3-manifold and we say that is in bridge position with respect to bridge surface .
7 Definition ([17]).
Let be a 1-manifold embedded in and suppose that is a properly embedded surface in so that is transverse to . A simple closed curve on is essential if it doesn’t bound a disk or a once punctured disk in . An embedded disk is a compressing disk for a surface if and is an essential curve in . A surface in is a splitting surface for if we can express as the union of two 3-manifolds along . If is a splitting surface for then we say that the surface is weakly incompressible if any pair of compressing disks on opposite sides of the surface intersect. If compresses on both sides but is not weakly incompressible then it is called strongly compressible.
The study of normal surfaces was first developed by Haken [6]. The concept of an almost normal surface that is used in this paper first appeared in [13].
8 Definition.
Let be a triangulated surface and let be a curve on . Assume that is transverse to the 1-skeleton of the triangulation. A curve in is called normal if the intersection of with any triangle of the triangulation contains no closed curves and no arcs with both endpoints on the same edge.
9 Definition ([6]).
Let be a triangulated 3-manifold. A normal triangle in a tetrahedron of the triangulation is an embedded disk that meets three edges and three faces of the tetrahedron. A normal quadrilateral is an embedded disk in a tetrahedron that meets four edges and four faces of the tetrahedron. Normal triangles and quadrilaterals are called normal disks. Normal disks meet the faces of the boundary of a tetrahedron in normal arcs.
10 Definition ([13]).
Let be a triangulated 3-manifold. An embedded surface is a normal surface if it meets each tetrahedron in a disjoint collection of normal disks. A surface is almost normal if meets each tetrahedron of the triangulation in a collection of normal disks, but in one tetrahedron there is exactly one exceptional piece. This exceptional piece is either a normal octagon, or it is an annulus consisting of two normal disks with a tube between them that is parallel to an edge of the 1-skeleton.
The proof of the main theorem relies heavily on the idea of thin position, first introduced by Gabai [5].
11 Definition ([15]).
Let denote a bridge splitting of . Given spines and for the -handlebodies and respectively, there is a diffeomorphism . For denote the surface corresponding to by . A standard singular foliation of extends this structure to all of by adding two singular leaves and , called the top and bottom leaves. All leaves meet the the torus in the standard foliation in meridian circles. The top and bottom singular leaves consist of the union of the spines of the -handlebodies and respectively, and the meridian circle of corresponding to each of the endpoints of and . There is a height function associated with the standard singular foliation given by the map that sends all points on a leaf together with the incident meridian disks of to the point in .
12 Definition ([16], [15]).
Assume that is a collection of arcs properly embedded in and is in general position with respect to , a standard singular foliation of . That is, all but a finite number of leaves of intersect transversally, every leaf in has at most one point of tangency with , and is disjoint from the singular subarcs of the singular leaf. If a leaf has a point of tangency with call it a tangent leaf and all other leaves transverse leaves. Between each two adjacent tangent leaves choose a transverse leaf . Define the width of a fixed embedding of with respect to to be the sum over of (the number of times intersects ). If has been properly isotoped to minimize its with with respect to then we say that is in thin position with respect to .
13 Definition ([16], [15]).
Let be in thin position with respect to standard singular foliation . Then as we move down the foliation from the top the arcs will form a sequence of maxima with respect to , then a sequence of minima, and so on. We will call a leaf in a region where the sequence shifts from maxima to minima a thick leaf and we will call such a region a thick region. An upper (lower) disk for a transverse leaf of is a disk in such that where is an arc embedded in , is a subarc of , , intersects transversely, and a small neighborhood of lies above (below) .
For the proof of the main theorem we will need the following Lemmas. The first theorem is proved by Stocking in [15].
14 Lemma (Lemma 1, [15]).
Let be an almost normal surface in an irreducible 3-manifold. Suppose that is incompressible to one side. Then is isotopic to a normal surface that does not intersect and that does not contain to the incompressible side.
A version of the following theorem was proved for strongly irreducible Heegaard surfaces by Casson and Gordon in [3] and has been adapted to the situation of weakly incompressible bridge surfaces by Tomova in [18].
15 Lemma (Corollary 6.3, [18]).
Let be a knot in a closed, orientable, irreducible 3-manifold . Let be a weakly incompressible splitting surface for and let be a surface that is obtained from by compressing to one side. Then is incompressible to the other side.
3. Almost normal bridge surfaces
The proof of the main theorem follows from an application of ideas from [15] where the Heegaard surface is replaced with a bridge surface. An important difference between the two arguments is that the leaves of the foliations in this case are surfaces with boundary as opposed to closed surfaces. The argument relies heavily on Lemmas 16, 23, and 24 whose statements are close to that of Lemmas 4 and 5 in [15]. The proofs of these two lemmas are similar in spirit to the originals, but differ in detail. Several cases missed in the original proof in [15] are included here, more extensive use is made of edgeslides, and the arguments have been adapted to our situation.
Proof of Main Theorem.
Let be a knot in a closed, orientable 3-manifold and assume that and are both irreducible. Suppose that the knot is in -bridge position with bridge surface so that is an irreducible Heegaard splitting of and the punctured surface is weakly incompressible. Suppose that separates into the two -handlebodies and . Let denote the bridge splitting of by . We can foliate with a standard singular foliation that intersects the torus in meridian circles. The top singular leaf of the foliation, , is a 1-complex given by the union of a spine of and one meridian circle of for each of the endpoints of on . Similarly, the bottom singular leaf of the foliation, , is a 1-complex given by the union of a spine of and one meridian circle of for each of the endpoints of on . Thus there is a symmetric picture near the top and bottom leaves of the foliation.
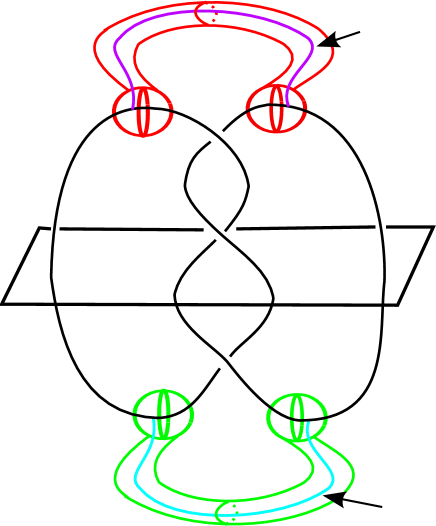
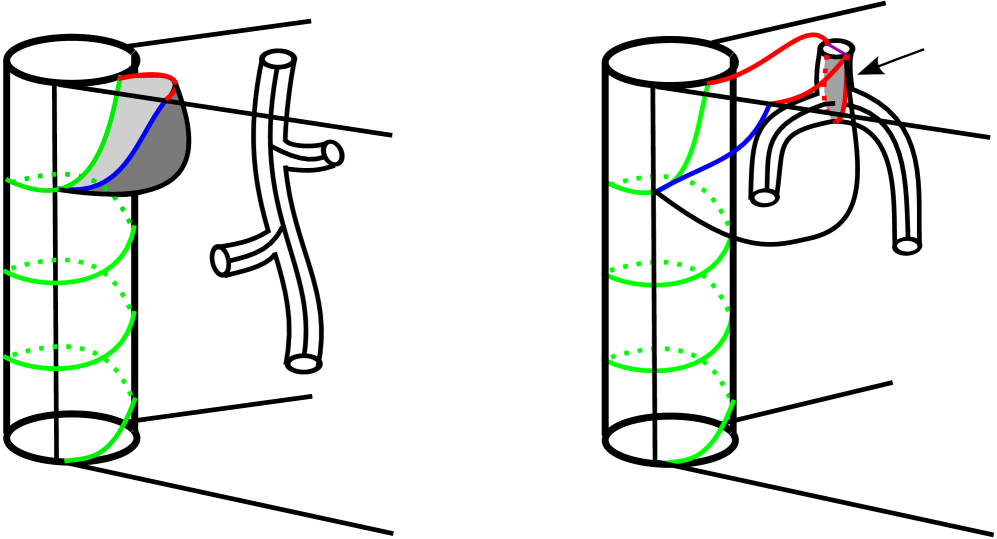
Consider a nearby leaf of the frontier of a regular neighborhood of (resp. ) in . It can be viewed as consisting of two parts. The first is a collection (resp. ) of boundary parallel annuli. Secondly, these annuli are tubed together via the boundary (resp. ) of a regular neighborhood of (resp. ). Topologically (resp. ) consists of once-punctured annuli and (resp. ) consists of an -punctured copy of . Since and arise as the boundary of a regular neighborhood of a 1-complex it is natural to refer to them as collections of “tubes”. We will refer to the pair of annuli and as . See Figure 1. Throughout the paper the foliation we refer to will always be the standard product foliation of on each component between the top and bottom annuli on .
Next we will describe how to triangulate so that the collection of annuli are normal with respect to the triangulation. Consider the collection of meridional annuli on parallel to . In each annulus choose a meridian circle and view it as the union of a vertex and an edge. This divides into rectangles. Now subdivide each rectangle by adding a diagonal edge connecting two adjacent vertices. This gives a triangulation of . See Figure 2.
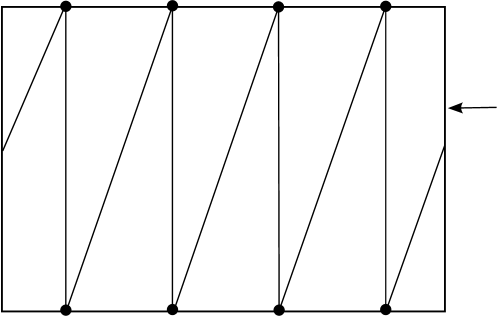
By [8] (also see [10] pg. 56) we can extend the triangulation of to a triangulation of all of without adding any vertices. Denote this triangulation of by . All of the vertices of this triangulation are contained in a neighborhood of the top and bottom leaves of the foliation. The collection of annuli are normal with respect to this triangulation and contains all of the vertices of the triangulation to one side, separating them from the rest of . Also note that has all of its vertices on , so it has no vertex-linking 2-spheres. However, may contain normal 2-spheres disjoint from that are not vertex-linking.
Let denote a maximal collection of non-parallel disjoint normal 2-spheres in disjoint from . Cutting open along results in several components, but only one component will contain the torus boundary of . Call this component . Note that may have multiple 2-sphere boundary components along with . Since is irreducible each 2-sphere in must bound a 3-ball to the opposite side of .
Since the annuli are normal and they contain the vertices of the triangulation to one side, each 2-sphere in is connected to via an edge of . If an edge of connects two 2-sphere boundary components of then by Lemma 2 of [16] it follows that must be a punctured 3-ball with a torus boundary component, which it clearly is not. Thus we can conclude each 2-sphere component of is connected to or by an edge of . Assume without loss of generality that an edge connects the 2-sphere to . Taking a tube parallel to this edge connecting to the normal 2-sphere gives an almost normal annulus isotopic to an annulus in . By Lemma 14 this surface is isotopic to a normal surface giving a new collection of normal annuli that we will call . We can isotope the tubes so that they lie in . We can do this for each normal 2-sphere in and then replace the original singular leaf with the singular leaf . Let be the side of that lies in .
Let . Isotoping the bridge surface to be disjoint from induces a splitting of into two -compression bodies and . Continue to call this splitting surfaces . The surface is a weakly incompressible splitting surface for . We can foliate with a standard foliation with leaves isotopic to . The top leaf of the foliation is and the bottom leaf is . Let denote the part of the 1-skeleton of that lies in the interior of . Put into thin position with respect to . Let denote the pair of spines and of the -compression bodies and respectively. Note that and . If intersects then isotope slightly off of . Let denote the pair and .
The triple is the first step in an iterative process. Each later step will consist of a triple with the following properties: will be a submanifold of for each . The surface will be a pair and of properly embedded normal surfaces with respect to the triangulation given above. Let . The submanifold has a weakly incompressible splitting surface that separates into two -compression bodies and . Let and denote the spines and of -compression bodies and respectively. Let denote the pair of spines and of and respectively. The spine (resp. ) can be extended to give a spine of (resp. ). As usual we define up to isotopy and slides of edges over other edges and over . The complement of a regular neighborhood (resp. )) in is foliated by copies of with singular leaf (resp. ). Thus can be foliated with a singular foliation by copies of with its top singular leaf consisting of and its bottom singular leaf consisting of . Now consider the edges of that do not lie on and let denote their intersection with . Put into thin position with respect to .
Denote by and the boundary of a regular neighborhood in which we continue to call “tubes”. A regular leaf near the top (resp. bottom) singular leaf is then obtained by attaching (resp. ) to a punctured copy of (resp. ).
Here is a sketch of the iterative process that we will describe in detail later. Start with . If, without loss of generality, and is isotopic to an almost normal surface then since is obtained by compressing a leaf of the foliation it follows that is isotopic to and we are done. Otherwise apply either Lemma 16 or Lemma 23 to obtain a new collection of normal and almost normal surfaces in . If there is an almost normal surface in the collection with then again because the almost normal surface comes from compressing a leaf of the foliation we know must be isotopic to and we are done. Otherwise use Lemma 14 to isotope the almost normal surfaces (if any) in the collection to be normal. Then, using this new collection of normal surfaces we can cut along this collection to obtain , which will also satisfy the above properties. It turns out that we only need to repeat the recursive step a finite number of times before obtaining an almost normal surface isotopic to . This completes the sketch.
Now, consider the arcs in in thin position with respect to . Recall that all ends of lie on or , part of the top or bottom singular leaves of . One possibility is that there is a maximum of that is above a minimum of which implies that there is a thick region of in . The other possibility is that all of the minima of are above all of the maxima of and so there is no thick region. In this situation we will consider separately the following two possibilities. The first is that there is no thick region and there is some arc of with both ends on or both ends on . The second possibility is that there is no thick region and each arc each arc of has one endpoint on and the other endpoint on . We will consider each of the three possibilities in turn.
The first possibility is that there a thick region of with respect to .
16 Lemma (cf. Lemma 5, [15]).
If there is a thick region for in , then there is a collection of normal and almost normal surfaces in obtained from a leaf of the foliation by compressing the leaf to one side. At most one surface can be almost normal. Not all of the surfaces are boundary parallel.
Proof.
The proofs of the following Claims 17, 18, 19, and 20 can be found in [16]. Let be as described above, where is in thin position with respect to the foliation of . Since there is a thick region of in we can apply Claim 4.5 of [16].
17 Claim (Claim 4.5, [16]).
There exists a transverse leaf in the first thick region of which intersects the 2-skeleton entirely in normal arcs and simple closed curves disjoint from the 1-skeleton.
Let be a leaf of in a thick region intersecting the 2-skeleton in normal arcs and simple closed curves disjoint from as is guaranteed by Claim 17. Then we can apply the following Claims 18, 19, and 20 to the leaf .
18 Claim (Claim 4.1, [16]).
Let be any tetrahedron in the triangulation of . Then contains no parallel curves of length greater than or equal to eight.
19 Claim (Claim 4.2, [16]).
Let be any tetrahedron in the triangulation of . Then contains no curve of length greater than eight.
20 Claim (Claim 4.3, [16]).
Let and be distinct tetrahedra in the triangulation of . Then and do not both contain curves of length eight.
The above claims together imply that this leaf of the foliation intersects the 2-skeleton only in simple closed curves disjoint from the 1-skeleton and normal curves of lengths three, four, and at most one of length eight. Compressing the simple closed curves in and the surfaces in the interior of the tetrahedra gives a collection of normal surfaces with at most one almost normal surface. The almost normal surface, if it exists, must be a normal octagon since we have compressed all annuli in the interior of the tetrahedra. We can think of the leaf as this collection of normal and almost normal surfaces with tubes attached. Since our triangulation has no normal 2-spheres we can conclude that this collection will contain no almost normal 2-spheres as well since any almost normal 2-sphere can be isotoped to give a normal one by Lemma 14. Also notice that in this collection we will not have a normal surface tubed to the opposite side of another normal surface or we get a contradiction to the leaf being weakly compressible. To see that all of the compressions of are to one side, observe that as long as there are no normal 2-spheres in the collection then we know that compressions of are compressions of for any tetrahedron of . Lemma 15 implies that after compressing to one side the remaining surface is incompressible to the opposite side, thus there cannot be compressions on opposite sides of . This completes the proof of Lemma 16. ∎
21 Remark.
There is no choice in the direction in which the tubes of compress, however Theorem 15 implies that after compressing , the remaining collection of normal and almost normal surfaces is incompressible in the direction opposite to which we have compressed.
For the proof of the Lemma 23 we will need the following:
22 Claim.
A properly embedded, orientable, normal surface is incompressible and boundary incompressible in the complement of the 1-skeleton .
Proof.
This claim follows from a standard innermost disk and outermost arc argument. ∎
The second possibility is that there is no thick region and some arc of has both endpoints on or both endpoints on .
23 Lemma (cf. Lemma 4, [15]).
If there is no thick region for in and some arc of has both endpoints on (resp. has both endpoints on ), then there is an almost normal surface in that is isotopic to a surface obtained from a leaf of by compressing the leaf above (resp. below).
Proof.
We will prove the Lemma for arcs of with both endpoints on . The argument for arcs of with both endpoints on is symmetric. Let be a leaf of the foliation near the top singular leaf, so that consists of the normal surface punctured and attached to the tubes . See Figure 1 for the case and . Choose an arc , a subarc of . Since there is no thick region for , has only a single minimum and it is parallel to an arc on , so there is a lower disk whose boundary is the union of and an arc in . We will show that after some edge slides and isotopies of , runs once over exactly one tube of , and that this tube connects two normal disks in a tetrahedron, therefore is part of an almost normal surface.
Define the complexity of to be , lexicographically ordered, where is the number of points of to which is also incident, and is the number of components in which meets the 2-skeleton of . We will assume that the complexity of has been minimized over all choices of .
Observe that the arc of can’t lie entirely in . Otherwise would be a boundary compressing disk in the complement of the 1-skeleton of the normal surface which contradicts Claim 22. Our strategy will be to show that there is a sequence of proper isotopies of and slides of ends of arcs of over each other and over (neither of which affect the isotopy class of ) so that afterwards is incident to a single edge in , runs along this arc once, and lies entirely inside a single tetrahedron. Then is the required almost normal surface obtained from by compressing all other tubes of . Now that we have established some notation, for the rest of the proof we will consider the intersections of the disk with the 2-skeleton of and we will show that any intersection violates the minimality of
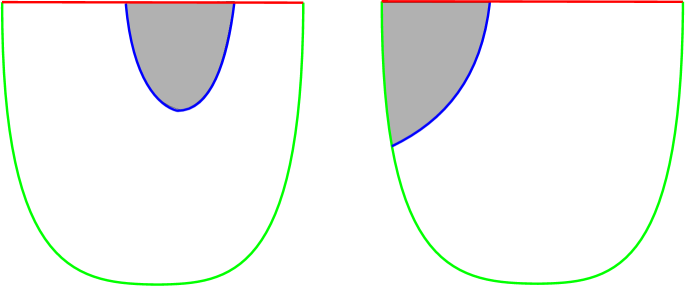
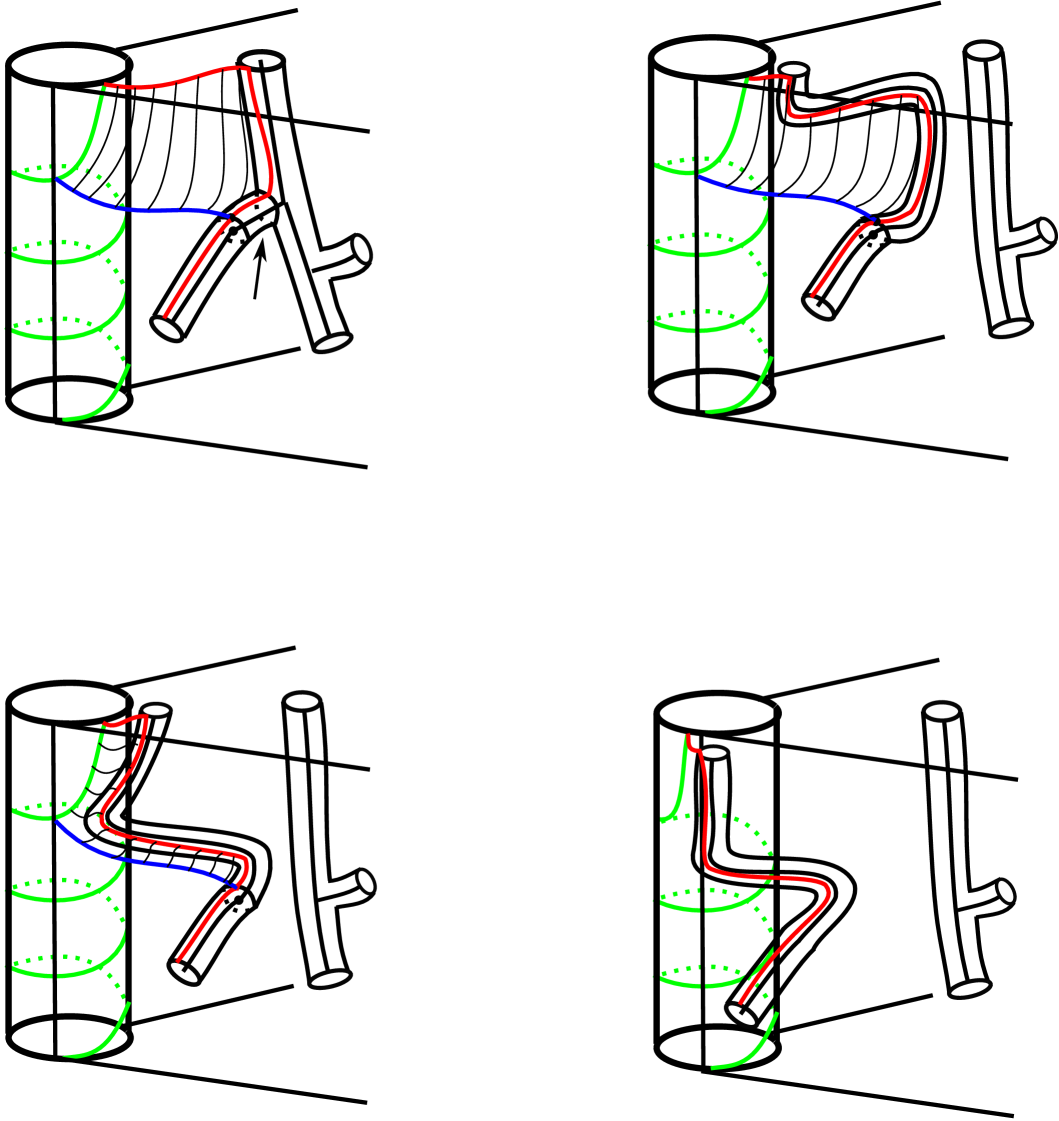
When we consider the arcs of intersection between and the 2-skeleton, we can get four types of components of in . Components of Type I are simple closed curves in . Components of Type II are arcs with both endpoints on . Components of Type III are arcs with both endpoints on , and components of Type IV are arcs with one endpoint on and the other endpoint on . See Figure 3. Next we will describe how each type of component of intersection of can be removed, violating minimality of .

Components of Type I are simple closed curves in . A component of Type I that is innermost in a 2-simplex of can be removed by substituting the disk it bounds in for the disk it bounds in . This reduces the number of times that meets the 2-skeleton, thus reducing and contradicting the minimality of .
A component of Type II corresponds to an arc in a face of some tetrahedron of that either 1) has both endpoints on distinct components of , or 2) has both endpoints on the same component of . Suppose is an arc of intersection between and that is outermost in and is of Type II. Let be a subarc of such that is the boundary of a disk in . See Figure 4b). Then the arc is either of type 1) or 2) above. In what follows we will use edge slides of to remove components of and . Recall that is the boundary of a neighborhood of , and we will abuse notation and consider as an arc on when we really mean that is an arc on .
Any two ends of edges of that meet the same normal disk in can be isotoped together so that there is at most one edge incident to each normal disk. Since can be extended to give a spine of , any cycle in gives a cycle in . Since is an irreducible Heegaard splitting of it follows from [4] (also see Proposition 2.5 of [14]) that no cycle of lies in a 3-ball. Hence for any tetrahedron of , cannot contain a cycle. Thus is a union of trees for each tetrahedron in . Each component of is a tree and each component of is a tree with disks attached and so is simply connected.
Arcs of type 1) fall into the following subcases:
Case a) Let be the tetrahedron in that contains and let denote the component of that contains . If is a single arc with both endpoints on the same face of then describes an isotopy that removes two points of intersection of with . This reduces the number of points of to which is incident, thus reducing , which is a contradiction.
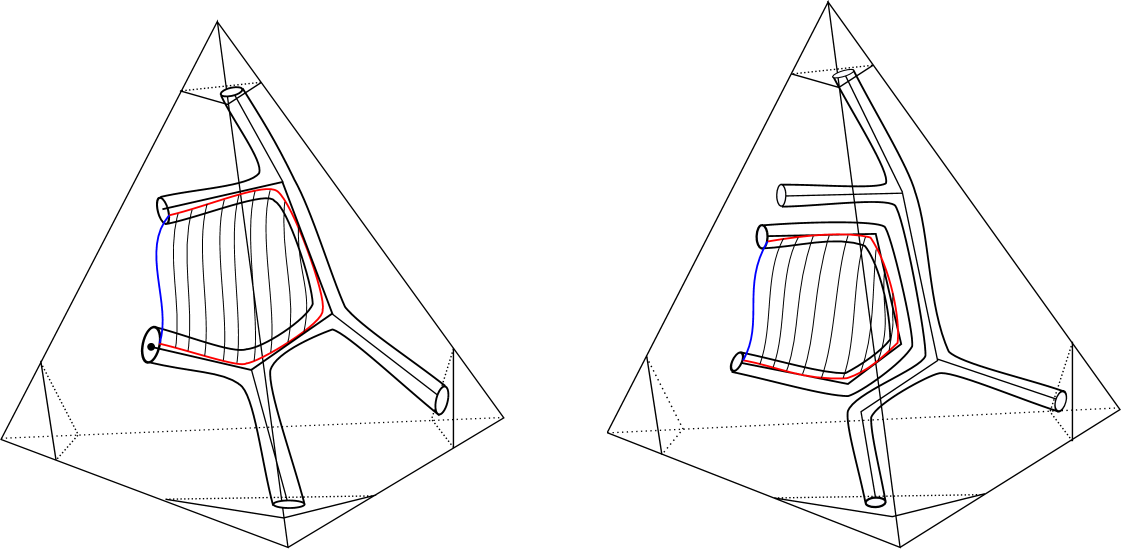
Case b) Now suppose that is not an arc and is a path in that begins at point in that is not in a normal disk but is in some face of . Let be the edge of containing . Then describes a series of edge slides of which culminate by introducing an extra point of intersection between and . However, after the edge slides the disk runs only over the edge . Hence we can reduce the number of intersections of edges of incident to that meet by two as in Case a) reducing by at least one and contradicting the minimality assumptions. See Figure 5.
Case c) If is an arc on that has both endpoints of on normal disks of , then either must run over some edges of or it lies in a normal disk. If lies in a normal disk then as an outermost arc of the normal disk it cuts off a subdisk in the normal disk. Together and bound a disk so that bounds a 3-ball that can be used to isotope into the next tetrahedron removing and thus reducing complexity.
So we can assume that runs over some edges of . Say that runs from normal disk to normal disk . Since is incident to in only a single point, is incident to in a single point. It follows that is an annulus and intersects the annulus in a single spanning arc. Thus runs precisely once along the edge that is incident to . Then, as above, describes a slide and isotopy of that carries it to the arc in a simplex of . But then a subdisk of that face describes a parallelism between and a subarc of . In particular, attaching a tube to along gives an almost normal surface.
Arcs of type 2) have endpoints on the same component of . Let denote the endpoint of in the face of tetrahedron . We assume that , so forms a loop based at in bounding a disk in ; the case where both ends of lie on a normal disk is similar:
Case a) If , then construct new disks and by cutting the disk along and attaching a copy of to each piece. One of the disks or will still be a lower disk and it will meet in fewer components than , contradicting the minimality of .
Case b) Now suppose that . Since is a union of trees in , we know that a neighborhood of each component of is a 3-ball. So there is a disk in whose boundary is the union of and a diameter of a small disk with which meets at .
Isotope the leaf by compressing to in , splitting the disk in two. The effect on the spine is a possibly complicated series of edge slides. The overall effect is that the number of components of increases by one when splits, and becomes a disk disjoint from and parallel to . The disk now contains at least two points of . Now push across to remove , thus reducing which is a contradiction. See Figure 6.

To see how to remove components of Types III and IV it will be helpful to view the arc that runs along the edge of as an arc that lies on . As an arc on , may wind around the edge . If the winding is not monotone a priori then we can reduce the number of components in which the disk meets the faces of , contradicting minimality. Thus we may assume that the curve winds monotonically around the edge . This implies that there are no curves of Type III since the existence a curve of Type III means that the arc must ‘double back’ as it winds around , contradicting monotonicity.
Let be an outermost arc component of Type IV, and let be the corresponding outermost sub-disk of . Let be the face of that contains . The disk is co-bounded by a sub-arc of , a sub-arc of , and . See Figure 4a). Let denote the tetrahedron containing in its interior and with as a face.
There are two cases that we will consider separately. The first case is when the arc of that runs from the edge to ends on a normal disk of . The second case is when ends on a tube (neighborhood of ) of .
Case a): Suppose first that ends on a normal disk . In this situation there are two subcases. Either or . See Figure 7a) and 7b).
Subcase 1): Suppose that . In this case the arc runs over only normal disks. Observe that there is a disk in that is bounded by , a copy of part of the edge that bounds the face , and a copy of a meridian of . In this case bounds a 3-ball in that we can use to isotope across and into the next tetrahedron, removing and reducing , thus reducing the complexity of , a contradiction. See Figure 7a).
Subcase 2): Suppose now that . Since is a union of trees, each component of is a 3-ball. In particular, there is a disk in whose boundary is the union of a sub-arc of and a diameter of the disk with which intersects the normal disk . Isotope by compressing to in , splitting the disk in two. The effect on is a series of edge slides that results in a new component of that is on the same side of as . Now proceed as in Subcase 1). See Figure 7b).
Case b): Now suppose that ends on a tube of . The core of this tube is an edge that may connect to other edges of in , and connects to a normal disk . See Figure 8. We will describe in two steps a slide of and an isotopy of that will remove a component of , reducing , and thereby reducing the complexity of .
First, since connects to other edges of in , describes an edge slide of that keeps fixed but slides the opposite end of the edge off of and onto the normal disk . We continue to slide along following until it almost meets . See Figure 8b). Now we can use the disk to isotope all of until it lies close to . At this point the entire disk and tube lie very close to in . See Figure 8c).
For the second step recall the disk in that is bounded by , a copy of part of the edge that bounds the face , and a copy of a meridian of . The disks and describe an isotopy of across the face and into the next tetrahedron, removing the component from and, in particular, removing the component of intersection between and , reducing , which is a contradiction. See Figure 8d). Thus there can be no arcs of Type IV. Therefore the arc of , the edges of that runs along, and the disk are all contained in one tetrahedron. The proof now follows as in Case 1c) above. ∎
The third possibility is that there is no thick region and each arc of has one endpoint on and the other endpoint on .
24 Lemma.
If there is no thick region for in and each arc of has one endpoint on and has the other endpoint on then is a product region.
Proof.
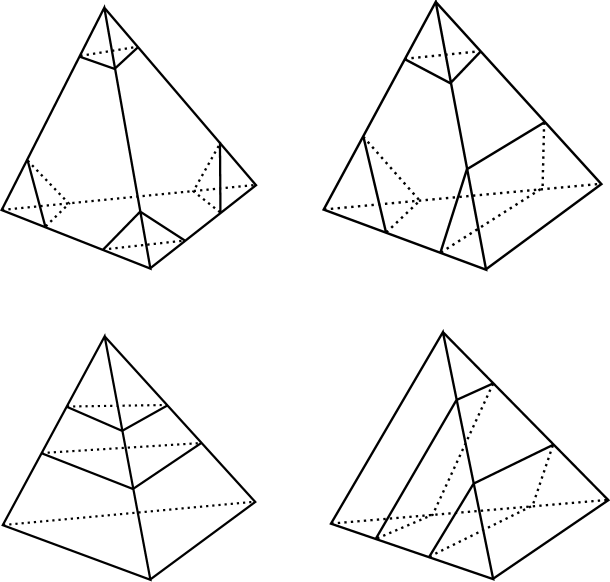
Recall that . Since and are normal with respect to it follows that there are two possibilities for how the region between and can intersect a face of the 2-skeleton. Either the region bounded by and is a trapezoid region or a hexagon region.
Suppose that there is a hexagon region of . Then three edges of the hexagon are arcs of and that the other three edges are arcs of connecting the three components of . But this implies that some arc of connects either to or to which is a contradiction. Therefore there cannot be any hexagonal components and all regions of intersection between and are trapezoids.
Because we know that there are no hexagonal components of intersection between and this implies that the only possibilities for components of intersection between and the tetrahedra of the 3-skeleton are triangular product regions and quadrilateral product regions. See Figure 9. Each triangular and quadrilateral product region is bounded on one side by a normal disk of and on the other by a normal disk of . Since each component of is a product region with one end on each of and for each tetrahedron in we can conclude that is itself such a product region.
∎
We can now complete the proof of Theorem 1. We will prove the theorem by describing a recursive process that will end when it produces an almost normal surface isotopic to the bridge surface . Recall that we began with a knot in a closed 3-manifold with the assumptions that and are irreducible. We foliated by copies of the bridge surface with two singular leaves and triangulated so that the annuli are normal and the vertices of are to one side of . Cutting along a maximal family of non-parallel normal 2-spheres tubed to the normal annuli we obtained the submanifold of . The surface induces a splitting of into -compression bodies and , and is foliated by copies of the bridge surface , and where the top (resp. bottom) leaf of the foliation is given by the union of the spine (resp. ) of (resp. ) and (resp. ). Here (resp. ) are the normal annuli in . The triple is the beginning of the recursive process. Each later step will produce a triple such that and for each the surface is a weakly incompressible splitting surface for separating it into two -compression bodies and , where . The spine (resp. ) of (resp. ) is contained in some spine for (resp. ), and is a pair of collections of normal surfaces and in .
The top (bottom) leaf of a singular foliation is given by the intersection with (resp. with ). It is a 1-complex in properly embedded in . Put , the part of lying in , in thin position with respect to . As mentioned earlier, either the arcs of all have one endpoint on and one endpoint on ; or there is some arc that either has both endpoints on or both endpoints on . If there is a thick region of in then we are in a position to apply Lemma 16. Otherwise we are in a position to apply either Lemma 23 or 24.
We will describe the step that takes us from to . First consider the initial step. If at the first step we encounter a thick region in , then start with a leaf in a thick region of intersecting in normal arcs and simple closed curves as is guaranteed by Claim 17. Applying Lemma 16 we obtain a collection of normal surfaces and at most one almost normal surface obtained by compressing to one side. If contains an almost normal surface and is incompressible above and below then is an almost normal surface isotopic to a leaf and we are done. If does not contain an almost normal surface then without loss of generality let and proceed as below.
Henceforth assume without loss of generality that compresses above to give . Otherwise we can invert the picture and declare to be the “top” leaf. Since has been obtained by compressing above, Lemma 15 implies that is incompressible below. By Lemma 14 we can isotope the almost normal surface to be normal. This gives a new collection of normal surfaces isotopic to . Cut along the collection and keep the component to the incompressible side below that contains part of . Call this submanifold . Observe that . The cores of the tubes of the thick leaf that were compressed to give the almost normal surface form the required 1-complex . Let denote the pair and , and let denote the pair and . This completes the first step.
The remainder of the proof falls into the following three cases:
Case 1): contains a thick region of with respect to .
In this case using Claim 17 start with a leaf in a thick region of the foliation intersecting in normal arcs and simple closed curves disjoint from the 1-skeleton. Applying Lemma 16 we obtain a collection of normal surfaces and at most one almost normal surface obtained by compressing to one side. Lemma 15 implies that is incompressible to the opposite side. If is incompressible then and since is isotopic to a leaf we are done. So suppose without loss of generality that is compressible above to give . The cores of the tubes of that are compressed above to give will make up the spine . Let denote the pair and . By Lemma 14 we can isotope the almost normal surface to give a new collection of normal surfaces. Cut along the collection and keep the component to the incompressible side below that contains part of . Call this new submanifold . Let denote the pair , .
If on the other hand is compressible below then the cores of the tubes of that are compressed below to give will make up the spine . By Lemma 14 we can isotope to be normal and call the new collection of normal surfaces . Let denote the pair , and . Cut along the collection of normal surfaces and keep the component to the incompressible side above . Call this new submanifolds . This completes the recursive step in this case.
Case 2): contains no thick region of and some arc of either has both endpoints on or has both endpoints on .
Without loss of generality suppose that there is an arc of with both endpoints on . Applying Lemma 23, starting with a leaf of near the top singular leaf above all of the minima we obtain an almost normal surface in by compressing the leaf above. If follows from Lemma 15 that is incompressible below. Moreover, . Using Lemma 15 isotope the almost normal surface to give a normal surface . Cut along and keep the component to the incompressible side below to obtain the submanifold . Denote by the pair and . The spine of consists of the cores of the tubes of that are compressed above to give . Denote by the pair and .
In both Cases 1) and 2) the new surface isotopic to (resp. ) in is not parallel as a normal surface to the normal surfaces (resp. ). The reason depends on whether Lemma 16 or Lemma 23 was applied. If the surface, without loss of generality say , comes from compressing a thick leaf via Lemma 16 then there is a subarc of lying between and with both ends on . Hence and are not parallel. If comes via Lemma 23 then so the surfaces are not parallel. If and are parallel then all leaves where are parallel as well. In particular, then is parallel to which cannot happen as we have just seen above. Therefore it follows that is non-parallel to for all .
Case 3): contains no thick region of and each arc of has one endpoint on and one endpoint on .
In this case by Lemma 24 is a product. Suppose . The submanifold is a product as well, and has the surface as a Heegaard surface that gives an irreducible Heegaard splitting of . By [14] it follows that the splitting surface is isotopic to and , one of which is in turn isotopic to the almost normal surface and so we are done.
If then the argument above shows that the surface consists of a collection of annuli. However the surface is a bridge surface for so it is connected. Therefore consists of one annulus and must be the unknot.
It follows from a well known result of Haken that there are only a finite number of non-parallel, disjoint, normal surfaces in . See [6]. Therefore we will only have to apply Lemmas 23 and Lemma 16 a finite number of times before we either reach a situation where we apply Lemma 24 and obtain an almost normal surface isotopic to the bridge surface or we exhaust all of the non-parallel, disjoint, normal surfaces in and we obtain an almost normal surface isotopic to .
∎
References
-
- [1] David Bachman, Heegaard splittings with boundary and almost normal surfaces, Top. and Appl. 116 (2001) 153–184.
- [2] David Bachman, Thin position with respect to a Heegaard surface, preprint.
- [3] A. Casson and C. Gordon, Reducing Heegaard splittings, Topology and its Applications. 27 (1997).
- [4] Charles Frohman, The topological uniqueness of triply periodic minimal surfaces in , J. Differential. Geom. 31 (1990) 277–283.
- [5] David Gabai, Foliations and the topology of 3-manifolds iii, J. Diff, Geom. 26 (1987) 479–536.
- [6] Wolfgang Haken, Teorie der Normalflaschen, Acta. Math. 105 (1961) 245–375.
- [7] Joel Hass, Algorithms for recognizing knots and 3-manifolds, preprint. arXiv:math.GT/9712269 v1 30 Dec 1997.
- [8] William Jaco, David Letscher, and Hyam Rubinstein, One vertex, ideal, and efficient triangulations of 3-manifolds, in preparation.
- [9] William Jaco and Ulrich Oertel, An algorithm to decide if a 3-Manifold is a Haken manifold, Topology. 23-2 (1984) 195–209.
- [10] William Jaco and Hyam Rubinstein, 0-efficient triangulations of 3-manifolds, J. Differential Geom. 65-1 (2003) 61–168.
- [11] Simon King, Almost normal Heegaard surfaces, preprint. arXiv:math.GT/0303377, 5 Oct 2003.
- [12] Yoav Moriah, Saul Schleimer, and Eric Sedgwick, Heegaard splittings of the form , Comm. Anal. Geom. 14-2 (2006) 215–247.
- [13] J. H. Rubinstein, Polyhedral Minimal Surfaces, Heegaard splittings and decision problems for 3-dimensional manifolds. Geometric Topology (Athens, GA, 1993), 1–20, AMS/IP Stud. Adv. Math., 2.1, Amer. Math. Soc., Prov. RI, 1997.
- [14] Martin Scharlemann and Abigail Thompson, Heegaard splittings of are standard, Math. Ann. 295 (1993) 594–564.
- [15] Michelle Stocking, Almost normal surfaces in 3-Manifolds. Trans. of the American Mathematical Society, 352-1 (1999) 171–207.
- [16] Abigail Thompson, Thin position and the recognition problem for . Mathematical Research Letters, 1 (1994) 613–630.
- [17] Marty Scharlemann and Maggy Tomova, Uniqueness of bridge surfaces for 2-bridge links, preprint. arXiv: math.GT/0609567 v1 20 Sep 2006.
- [18] Maggy Tomova, Multiple bridge surfaces restrict knot distance, preprint. arXiv:math.GT/70511139 v3, 16 Nov 2006.
- [19] Robin Wilson, Knots with infinitely many incompressible Seifert Surfaces, preprint. arXiv: math.GT/0604001 26 May 2006.