Microcanonical Truncations of Observables in Quantum Chaotic Systems
Abstract
We consider the properties of an observable (such as a single spin component that squares to the identity) when expressed as a matrix in the basis of energy eigenstates, and then truncated to a microcanonical slice of energies of varying width. For a quantum chaotic system, we model the unitary or orthogonal matrix that relates the spin basis to the energy basis as a random matrix selected from the appropriate Haar measure. We find that the spectrum of eigenvalues is given by a centered Jacobi distribution that approaches the Wigner semicircle of a random hermitian matrix for small slices. For slices that contain more than half the states, there is a set of eigenvalues of exactly . The transition to this qualitatively different behavior at half size is similar to that seen in other quantities such as entanglement entropy. Our results serve as a benchmark model for numerical calculations in realistic physical systems.
I Introduction
The eigenstate thermalization hypothesis (ETH) [1, 2, 3, 4, 5, 6, 7] is now widely accepted as a microscopic mechanism that is able to explain how an isolated quantum many-body system can come to thermal equilibrium when starting from an initial pure state that appears to be far from equilibrium. ETH is expected to hold for a “chaotic” quantum system that is sufficiently far (in a parameter space of possible hamiltonians) from any point of integrability and which also does not exhibit many-body localization due to strong disorder. ETH then takes the form of an ansatz for the matrix elements (in the energy-eigenstate basis) of each observable that would be measured in order to determine whether or not the system is in thermal equilibrium. This ansatz is
| (1) |
where is the average energy of the two eigenstates, is their energy difference, is the thermodynamic entropy (logarithm of the density of states) at energy , and are smooth, real functions of their arguments, with , and varies erratically, with overall zero mean and unit variance in local ranges of and .
A question of interest is whether more can be said about the statistical properties of the ’s. An argument based on the central limit theorem would indicate that they can be treated as independent gaussian random variables, and numerical investigations in specific systems have generally been consistent with this. However, as has been pointed out before [8, 9], this gaussianity cannot be an exact property, as it would yield various unphysical predictions, including an expression of any -point time correlation function of in terms of the 2-point function. Furthermore, the operator has a spectrum of eigenvalues, and this spectrum must somehow be encoded in the energy-basis matrix elements . Because of this, as noted in [8], it is more useful to think of the unitary matrix that transforms basis states in which is diagonal to the energy-eigenstate basis as a statistically random matrix.
In [9] (see also [10]), the observable was taken to be a component of a single spin in a lattice spin system, and the eigenvalues of computed when and were restricted to particular ranges of energies. If this submatrix had the statistical properties of a gaussian random matrix, then a Wigner semi-circular distribution of eigenvalues would be expected. This was found for small energy ranges, but significant deviations appeared at larger ranges.
Our goal here is to provide a theoretical benchmark for these calculations, computing the expected eigenvalue spectrum for a single-spin-component operator (which obeys ) when its matrix in the energy-eigenstate basis is truncated, with the energies and each in the same finite range. We refer to this as a microcanonical slicing. We specialize to the case where the function in Eq. (1) is zero; this is equivalent to
| (2) |
for all inverse temperatures . This corresponds to a system in which the hamiltonian is invariant under . We then treat the diagonalizing matrix as either a unitary or orthogonal Haar-random matrix. (The result is the same in both cases.) This is the strongest possible assumption of random-matrix behavior; for an actual physical system, we expect correlations that result in having an approximately banded structure. We hope that our benchmark results can be used in the future to help elucidate this structure in different physical systems of interest.
II Setup
We consider an operator that obeys and . We take the dimension of the full Hilbert space to be ; for a system of two-component spins, we would have . The eigenvalues of are hence , with eigenvalues of each sign.
We then write
| (3) |
where is a diagonal matrix,
| (4) |
and is a unitary (or orthogonal) matrix that transforms from the computational basis (in which a component of each spin is diagonal) to the energy basis (in which the hamiltonian is diagonal).
We are now interested in a microcanonical slicing of , defined as
| (5) |
where is a projection operator onto an energy window that spans energy eigenstates.
We first specialize to the case . We treat as either a unitary or orthogonal matrix that is selected at random from the corresponding Haar measure, and consider the expected distribution of the eigenvalues of in the limit of large .
This problem has been solved in a different context [11], and the result (for either unitary or orthogonal ) is a special case of the centered Jacobi distribution,
| (6) |
where we have defined
| (7) |
and where vanishes for values of for which the argument of the square-root is negative. We have normalized to integrate to one.
For a thin microcanonical slice, and hence , the maximum value of is , and then we can replace in the denominator of Eq. (6) with . We then have
| (8) |
We can compare this result with the Wigner semicircle for an hermitian random matrix with matrix elements drawn from a gaussian distribution with the expected value of , , given by ; this is [12]
| (9) |
Our matrix obeys , and hence
| (10) |
This implies that the expected value of each is . If we set in Eq. (9), we find that Eq. (8) matches it. This result agrees with the expectation from ETH that, for small energy differences, the energy-basis matrix elements of a local observable should have the statistics of independent gaussian random variables.
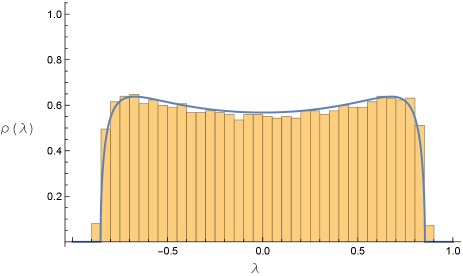
For larger values of , Eq. (6) begins to differ from the Wigner semicircle. The curvature at the origin is one diagnostic; it is negative for but turns positive for . At , , we find an arcsine distribution with integrable singularities at ,
| (11) |
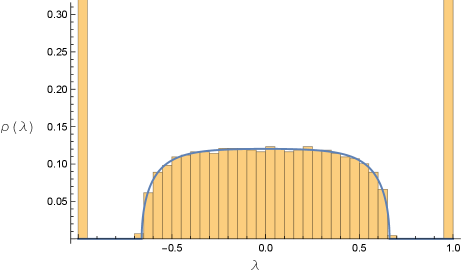
In Fig. 1(a,b,c), we show the eigenvalue distribution for a matrix with and with a particular orthogonal matrix selected at random from the Haar measure, and with , along with the predicted distribution of Eq. (6). We find very good agreement.
Next we consider the case . This can be related to the case by considering the complementary microcanonical projection operator,
| (12) |
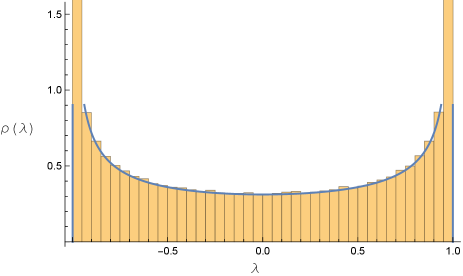
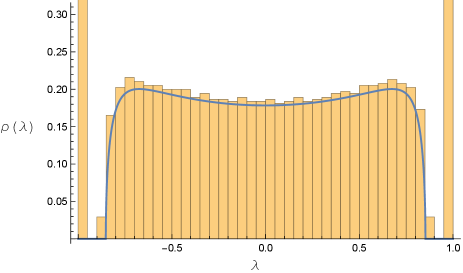
We show in the Appendix that for the eigenvalues of are minus those of , plus extra pairs of eigenvalues of exactly . This is true for any specific individual . Hence, after averaging over a Haar measure, the result will be a continuous spectrum given by Eq. (6) (though with the normalizing factor of in the denominator replaced by ), plus a discrete spectrum of eigenvalues and eigenvalues .
In Fig. 1(d,e), we show the eigenvalue distribution for . We find, as predicted, a continuous distribution that matches that of the matrix with , with all remaining eigenvalues exactly equal to .
These results for are contrary to our initial expectations. We expected to find the Wigner semicircle for , and for this to gradually morph into a set of only at . Our expectations are met by the results for , but the sudden appearance of some exact eigenvalues for every , along with an additional continuous distribution that mirrors the distribution for and eventually becomes a Wigner semicircle for small , came as a surprise to us. We will discuss this further in our conclusions.
III Conclusions
Motivated by the investigations of [9], we have considered the properties of a single spin-component operator (with eigenvalues that are an equal number of plus ones and minus ones) in a many-body quantum-chaotic system. We are interested in the statistical properties of the matrix elements of such an operator in the energy-eigenstate basis. We model this by treating the unitary (or orthogonal) matrix that relates the spin-eigenstate basis to the energy-eigenstate basis as a random matrix selected from the Haar measure. We then consider microcanonical truncations of this matrix in the energy basis, and study their eigenvalues. For truncations to a much smaller matrix, we find the distribution agrees with the Wigner semicircle expected for a hermitian random matrix. For larger truncations, we find that the truncated matrix begins to “remember” that the eigenvalues of the full matrix are .
Once the truncation is to a matrix larger than half the size of the original, we find that there are now a set of eigenvalues of exactly , along with a continuous distribution that matches that of the complementary truncation. This result was counter to what we initially expected, and shows a kind of phase transition at half system size. This is reminiscent of a similar transition in the behavior of entanglement and Rényi entropies [13], which also exhibit sudden changes of behavior at half system size. Similar transitions have also been discussed in [14] for operators that include more than half the degrees of freedom of the system.
Our results are based on the most chaotic possible behavior of a physical system, in which the energy eigenstates are completely random superpositions of basis states, without any additional structure. Though this is unlikely to be true for any realistic physical system, our results serve as a useful benchmark of comparison for numerical calculations in these systems.
Acknowledgements.
The work of F.I. was supported by an NSF Graduate Research Fellowship under Grant No. 2139319 and funds from the University of California. M.S. thanks Lauri Foini, Jorge Kurchan, and Silvia Pappalardi for helpful discussions.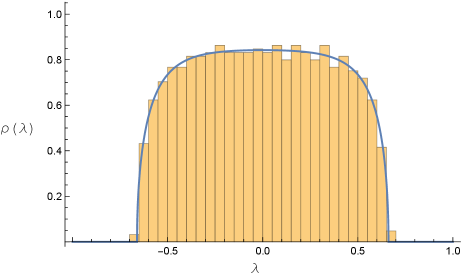 |
 |
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
|
| (e) | |
Appendix A Truncations Greater than Half
We write in block-diagonal form,
| (13) |
We take . Since the eigenvalues of are , we have
| (14) |
This yields the three equations
| (15) | ||||
| (16) | ||||
| (17) |
We can make independent unitary transformations on the upper block and on the lower block that render and diagonal. We then write
| (18) |
where and . Taking the matrix element of Eq. (16), we get
| (19) |
This shows that a nonvanishing matrix element of is possible if and only if there is an eigenvalue of that is the negative of an eigenvalue of . For , there are more eigenvalues of than there are of , and Eq. (17) then implies that these extra eigenvalues must be . Since , these extra eigenvalues must come in pairs.
We conclude that, for , the eigenvalues of consist of eigenvalues that are equal in magnitude and opposite in sign to the eigenvalues of , eigenvalues , and eigenvalues .
References
- [1] J. M. Deutsch. Quantum statistical mechanics in a closed system. Phys. Rev. A, 43:2046–2049, Feb 1991.
- [2] Mark Srednicki. Chaos and quantum thermalization. Phys. Rev. E, 50:888–901, Aug 1994.
- [3] Mark Srednicki. Thermal fluctuations in quantized chaotic systems. J. Phys. A: Math. Gen., 29(4):L75–L79, feb 1996.
- [4] Mark Srednicki. The approach to thermal equilibrium in quantized chaotic systems. J. Phys. A: Math. Gen., 32(7):1163, 1999.
- [5] Marcos Rigol, Vanja Dunjko, and Maxim Olshanii. Thermalization and its mechanism for generic isolated quantum systems. Nature, 452:854, Apr 2008.
- [6] Luca D’Alessio, Yariv Kafri, Anatoli Polkovnikov, and Marcos Rigol. From quantum chaos and eigenstate thermalization to statistical mechanics and thermodynamics. Adv. Phys., 65(3):239–362, 2016.
- [7] Joshua M Deutsch. Eigenstate thermalization hypothesis. Rep. Prog. Phys., 81(8):082001, jul 2018.
- [8] Laura Foini and Jorge Kurchan. Eigenstate thermalization hypothesis and out of time order correlators. Phys. Rev. E, 99(4):042139, 2019.
- [9] Jonas Richter, Anatoly Dymarsky, Robin Steinigeweg, and Jochen Gemmer. Eigenstate thermalization hypothesis beyond standard indicators: Emergence of random-matrix behavior at small frequencies. Phys. Rev. E, 102:042127, Oct 2020.
- [10] Silvia Pappalardi, Laura Foini, and Jorge Kurchan. Microcanonical windows on quantum operators, 2023.
- [11] Benoît Collins. Product of random projections, jacobi ensembles and universality problems arising from free probability. Probability Theory and Related Fields, 133(3):315–344, 2005.
- [12] Madan Lal Mehta. Random Matrices. Elsevier, Amsterdam, 3rd edition, 2004.
- [13] Tsung Cheng Lu and Tarun Grover. Renyi entropy of chaotic eigenstates. Physical Review E, 99(3):032111, 2019.
- [14] James R. Garrison and Tarun Grover. Does a single eigenstate encode the full hamiltonian? Phys. Rev. X, 8:021026, Apr 2018.