Mini-Batch Optimization of Contrastive Loss
Abstract
Contrastive learning has gained significant attention as a method for self-supervised learning. The contrastive loss function ensures that embeddings of positive sample pairs (e.g., different samples from the same class or different views of the same object) are similar, while embeddings of negative pairs are dissimilar. Practical constraints such as large memory requirements make it challenging to consider all possible positive and negative pairs, leading to the use of mini-batch optimization. In this paper, we investigate the theoretical aspects of mini-batch optimization in contrastive learning. We show that mini-batch optimization is equivalent to full-batch optimization if and only if all mini-batches are selected, while sub-optimality may arise when examining only a subset. We then demonstrate that utilizing high-loss mini-batches can speed up SGD convergence and propose a spectral clustering-based approach for identifying these high-loss mini-batches. Our experimental results validate our theoretical findings and demonstrate that our proposed algorithm outperforms vanilla SGD in practically relevant settings, providing a better understanding of mini-batch optimization in contrastive learning.
1 Introduction
Contrastive learning has been widely employed in various domains as a prominent method for self-supervised learning [25]. The contrastive loss function is designed to ensure that the embeddings of two samples are similar if they are considered a “positive” pair, in cases such as coming from the same class [30], being an augmented version of one another [9], or being two different modalities of the same data [48]. Conversely, if two samples do not form a positive pair, they are considered a “negative” pair, and the contrastive loss encourages their embeddings to be dissimilar.
In practice, it is not feasible to consider all possible positive and negative pairs when implementing a contrastive learning algorithm due to the quadratic memory requirement when working with samples. To mitigate this issue of full-batch training, practitioners typically choose a set of mini-batches, each of size , and consider the loss computed for positive and negative pairs within each of the batches [7, 9, 24, 69, 8, 72, 17]. For instance, Gadre et al. [17] train a model on a dataset where and . This approach results in a memory requirement of for each mini-batch, and a total computational complexity linear in the number of chosen mini-batches. Despite the widespread practical use of mini-batch optimization in contrastive learning, there remains a lack of theoretical understanding as to whether this approach is truly reflective of the original goal of minimizing full-batch contrastive loss. This paper examines the theoretical aspects of optimizing mini-batches loaded for the contrastive learning.
Main Contributions.
The primary contributions of this paper are twofold. First, we show that under certain parameter settings, mini-batch optimization is equivalent to full-batch optimization if and only if all mini-batches are selected. These results are based on an interesting connection between contrastive learning and the neural collapse phenomenon [36]. From a computational complexity perspective, the identified equivalence condition may be seen as somewhat prohibitive, as it implies that all mini-batches must be considered.
Our second contribution is to show that Ordered SGD (OSGD) [29] can be effective in finding mini-batches that contain the most informative pairs and thereby speeding up convergence. OSGD, proposed in a work by Kawaguchi & Lu [29], is a variant of SGD that modifies the model parameter updates. Instead of using the gradient of the average loss of all samples in a mini-batch, it uses the gradient of the average loss over the top- samples in terms of individual loss values. We show that the convergence result from Kawaguchi & Lu [29] can be applied directly to contrastive learning. We also show that OSGD can improve the convergence rate of SGD by a constant factor in certain scenarios. Furthermore, in a novel approach to address the challenge of applying OSGD to the mini-batch optimization (which involves examining batches to select high-loss ones), we reinterpret the batch selection as a min-cut problem in graph theory [13]. This novel interpretation allows us to select high-loss batches efficiently via a spectral clustering algorithm [43]. The following informal theorems summarize our main findings.
Theorem 1 (informal).
Under certain parameter settings, the mini-batch optimization of contrastive loss is equivalent to full-batch optimization of contrastive loss if and only if all mini-batches are selected. Although mini-batch contrastive loss and full-batch loss are neither identical nor differ by a constant factor, the optimal solutions for both mini-batch and full-batch are identical (see Sec. 4).
Theorem 2 (informal).
In a demonstrative toy example, OSGD operating on the principle of selecting high-loss batches, can potentially converge to the optimal solution of mini-batch contrastive loss optimization faster by a constant factor compared to SGD (see Sec. 5.1).
We validate our theoretical findings and the efficacy of the proposed spectral clustering-based batch selection method by conducting experiments on both synthetic and real data. On synthetic data, we show that our proposed batch-selection algorithms do indeed converge to the optimal solution of full-batch optimization significantly faster than the baselines. We also apply our proposed method to ResNet pre-training with CIFAR-100 [31] and Tiny ImageNet [33]. We evaluate the performance on downstream retrieval tasks, demonstrating that our batch selection method outperforms vanilla SGD in practically relevant settings.
2 Related Work
Contrastive losses.
Contrastive learning has been used for several decades to learn a similarity metric to be used later for applications such as object detection and recognition [41, 1]. Chopra et al. [12] proposed one of the early versions of contrastive loss which has been updated and improved over the years [60, 61, 59, 30, 45]. More recently, contrastive learning has been shown to rival and even surpass traditional supervised learning methods, particularly on image classification tasks [10, 3]. Further, its multi-modal adaptation leverages vast unstructured data, extending its effectiveness beyond image and text modalities [48, 27, 47, 39, 56, 16, 18, 34, 51, 52]. Unfortunately, these methods require extremely large batch sizes in order to perform effectively. Follow-up works showed that using momentum or carefully modifying the augmentation schemes can alleviate this issue to some extent [22, 10, 19, 64].
Effect of batch size.
While most successful applications of contrastive learning use large batch sizes (e.g., 32,768 for CLIP and 8,192 for SimCLR), recent efforts have focused on reducing batch sizes and improving convergence rates [65, 7]. Yuan et al. [68] carefully study the effect of the requirements on the convergence rate when a model is trained for minimizing SimCLR loss, and prove that the gradient of the solution is bounded by . They also propose SogCLR, an algorithm with a modified gradient update where the correction term allows for an improved convergence rate with better dependence on . It is shown that the performance for small batch size can be improved with the technique called hard negative mining [55, 28, 70].
Neural collapse.
Neural collapse is a phenomenon observed in [46] where the final classification layer of deep neural nets collapses to the simplex Equiangular Tight Frame (ETF) when trained well past the point of zero training error [26, 71]. Lu & Steinerberger [36] prove that this occurs when minimizing cross-entropy loss over the unit ball. We extend their proof techniques and show that the optimal solution for minimizing contrastive loss under certain conditions is also the simplex ETF.
Optimal permutations for SGD.
The performance of SGD without replacement under different permutations of samples has been well studied in the literature [5, 53, 54, 42, 66, 2, 49, 40, 58, 57, 20, 44, 37, 50, 63, 38, 6, 11]. One can view batch selection in contrastive learning as a method to choose a specific permutation among the possible mini-batches of size . However, it is important to note that these bounds do not indicate an improved convergence rate for general non-convex functions and thus would not apply to the contrastive loss, particularly in the setting where the embeddings come from a shared embedding network. We show that in the case of OSGD [29], we can indeed prove that contrastive loss satisfies the necessary conditions in order to guarantee convergence.
3 Problem Setting
Suppose we are given a dataset of positive pairs (data sample pairs that are conceptually similar or related), where and are two different views of the same object. Note that this setup includes both the multi-modal setting (e.g., CLIP [48]) and the uni-modal setting (e.g., SimCLR [9]) as follows. For the multi-modal case, one can view as two different modalities of the same data, e.g., is the image of a scene while is the text description of the scene. For the uni-modal case, one can consider and as different augmented images from the same image.
We consider the contrastive learning problem where the goal is to find embedding vectors for and , such that the embedding vectors of positive pairs are similar, while ensuring that the embedding vectors of other (negative) pairs are well separated. Let be the embedding vector of , and be the embedding vector of . In practical settings, one typically considers parameterized encoders so that and . We define embedding matrices and which are the collections of embedding vectors. Now, we focus on the simpler setting of directly optimizing the embedding vectors instead of model parameters and in order to gain theoretical insights into the learning embeddings. This approach enables us to develop a deeper understanding of the underlying principles and mechanisms. Consider the problem of directly optimizing the embedding vectors for pairs which is given by
| (1) |
where denotes the norm, the set denotes the set of integers from to , and the contrastive loss (the standard InfoNCE loss [45]) is defined as
| (2) |
Note that is the full-batch version of the loss which contrasts all embeddings with each other. However, due to the large computational complexity and memory requirements during optimization, practitioners often consider the following mini-batch version instead. Note that there exist different mini-batches, each of which having samples. For , let be the -th mini-batch satisfying and . Let and . Then, the contrastive loss for the -th mini-batch is .
4 Relationship Between the Optimization for Full-Batch and Mini-Batch
Recall that we focus on finding the optimal embedding matrices (, ) that minimize the contrastive loss. In this section, we investigate the relationship between the problem of optimizing the full-batch loss and the problem of optimizing the mini-batch loss . Towards this goal, we prove three main results, the proof of which are in Appendix B.1.
- •
- •
-
•
We show that minimizing the mini-batch loss summed over only a strict subset of mini-batches can lead to a sub-optimal solution that does not minimize the full-batch loss (Thm. 5).
4.1 Full-batch Contrastive Loss Optimzation
In this section, we characterize the optimal solution for the full-batch loss minimization in Eq. (1). We start by providing the definition of the simplex equiangular tight frame (ETF) which turns out to be the optimal solution in certain cases. The original definition of ETF [62] is for vectors in a -dimensional space where 111See Def. 4 in Appendix A for the full definition. Papyan et al. [46] defines the ETF for the case where to characterize the phenomenon of neural collapse. In our work, we use the latter definition of simplex ETFs which is stated below.
Definition 1 (Simplex ETF).
We call a set of vectors form a simplex Equiangular Tight Frame (ETF) if and .
In the following Lemma, we first prove that the optimal solution of full-batch contrastive learning is the simplex ETF for which follows almost directly from Lu & Steinerberger [36].
Lemma 1 (Optimal solution when ).
Suppose . Then, the optimal solution of the full-batch contrastive learning problem in Eq. (1) satisfies two properties: (i) , and (ii) the columns of form a simplex ETF.
Actually, many practical scenarios satisfy . However, the approach used in Lu & Steinerberger [36] cannot be directly applied for , leaving it as an open problem. While solving the open problem for the general case seems difficult, we characterize the optimal solution for the specific case of , subject to the conditions stated below.
Definition 2 (Symmetric and Antipodal).
Embedding matrices and are called symmetric and antipodal if satisfies two properties: (i) Symmetric i.e., ; (ii) Antipodal i.e., for each , there exists such that .
We conjecture that the optimal solutions for are symmetric and antipodal. Note that the symmetric property holds for case, and the antipodality is frequently assumed in geometric problems such as the sphere covering problem in [4].
Thm. 3 shows that when , the optimal solution for the full-batch loss minimization, under a symmetric and antipodal configuration, form a cross-polytope which is defined as the following.
Definition 3 (Simplex cross-polytope).
We call a set of vectors form a simplex cross-polytope if, for all , the following three conditions hold: ; there exists a unique such that ; and for all .
Theorem 3 (Optimal solution when ).
Let
| (3) |
where . Then, the columns of form a simplex cross-polytope for .
Proof Outline. By the antipodality assumption, we can apply Jensen’s inequality to indices without itself and antipodal point for a given . Then we show that the simplex cross-polytope also minimizes this lower bound while satisfying the conditions that make the applications of Jensen’s inequality tight.
For the general case of , excluding we still leave it as an open problem.
4.2 Mini-batch Contrastive Loss Optimization
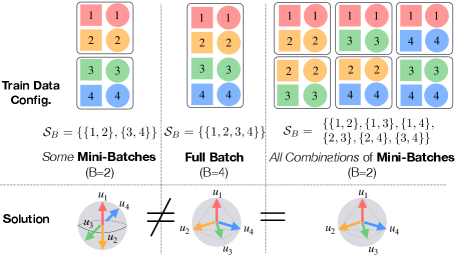
Here we consider the mini-batch contrastive loss optimization problem, where we first choose multiple mini-batches of size and then find that minimize the sum of contrastive losses computed for the chosen mini-batches. Note that this is the loss that is typically considered in the contrastive learning since computing the full-batch loss is intractable in practice. Let us consider a subset of all possible mini-batches and denote their indices by . For a fixed , the mini-batch loss optimization problem is formulated as:
| (4) |
where the loss of given mini-batches is To analyze the relationship between the full-batch loss minimization in Eq. (1) and the mini-batch loss minimization in Eq. (4), we first compare the objective functions of two problems as below.
Proposition 1.
The mini-batch loss and full-batch loss are not identical, nor is one a simple scaling of the other by a constant factor. In other words, when , for all , there exists no constant such that .
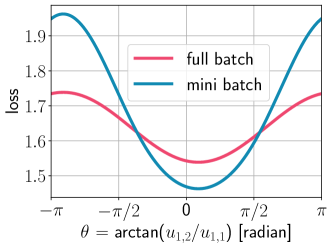
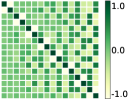
We illustrate this proposition by visualizing the two loss functions in Fig. 1 when , and . We visualize it along a single embedding vector by freezing all other embeddings ( and ) at the optimal solution and varying as for . One can confirm that two losses are not identical (even up to scaling).
Interestingly, the following result shows that the optimal solutions of both problems are identical.
Theorem 4 (Optimization with all possible mini-batches).
Suppose . The set of minimizers of the mini-batch problem in Eq. (4) is the same as that of the full-batch problem in Eq. (1) for two cases: (i) , and (ii) and the pairs (, ) are restricted to those satisfying the conditions stated in Def. 2. In such cases, the solutions for the mini-batch optimization problem satisfies the following: Case (i) forms a simplex ETF and for all ; Case (ii): forms a simplex cross-polytope.
Proof Outline. Similar to the proof of Lem. 1, we bound the objective function from below using Jensen’s inequality. Then, we show that this lower bound is equivalent to a scaling of the bound from the proof of Lem. 1, by using careful counting arguments. Then, we can simply repeat the rest of the proof to show that the simplex ETF also minimizes this lower bound while satisfying the conditions that make the applications of Jensen’s inequality tight.
Now, we present mathematical results specifying the cases when the solutions of mini-batch optimization and full-batch optimization differ. First, we show that when , minimizing the mini-batch loss over any strict subset of batches, is not equivalent to minimizing the full-batch loss.
Theorem 5 (Optimization with fewer than mini-batches).
Proof Outline. We show that there exist embedding vectors that are not the simplex ETF, and have a strictly lower objective value. This implies that the optimal solution of any set of mini-batches that does not contain all mini-batches is not the same as that of the full-batch problem.
5 Ordered Stochastic Gradient Descent for Mini-Batch Contrastive Learning
Recall that the optimal embeddings for the full-batch optimization problem in Eq. (1) can be obtained by minimizing the sum of mini-batch losses, according to Thm. 4. An easy way of approximating the optimal embeddings is using gradient descent (GD) on the sum of losses for mini-batches, or to use a stochastic approach which applies GD on the loss for a randomly chosen mini-batch. Recent works found that applying GD on selective batches outperforms SGD in some cases [29, 37, 35]. A natural question arises: does this hold for mini-batch contrastive learning? Specifically, (i) Is SGD enough to guarantee good convergence on mini-batch contrastive learning?, and (ii) Can we come up with a batch selection method that outperforms vanilla SGD? To answer this question:
- •
-
•
We reformulate the batch selection problem into a min-cut problem in graph theory [13], by considering a graph with nodes where each node is each positive pair and each edge represents a proxy to the contrastive loss between two nodes. This allows us to devise an efficient batch selection algorithm by leveraging spectral clustering [43] (Sec. 5.3).
5.1 Convergence Comparison in a Toy Example: OSGD vs. SGD
This section investigates the convergence of two gradient-descent-based methods, OSGD and SGD. The below lemma shows that the contrastive loss is geodesic non-quasi-convex, which implies the hardness of proving the convergence of gradient-based methods for contrastive learning in Eq. (1).
Lemma 2.
Contrastive loss is a geodesic non-quasi-convex function of on .
We provide the proof in Appendix B.2.
In order to compare the convergence of OSGD and SGD, we focus on a toy example where convergence to the optimal solution is achievable with appropriate initialization. Consider a scenario where we have embedding vectors with . Each embedding vector is defined as for parameters . Over time step , we consider updating the parameters using gradient descent based methods. For all , the initial parameters are set as , and the other embedding vectors are initialized as . This setting is illustrated in Fig. 2.
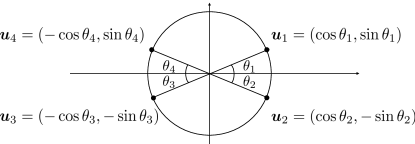
At each time step , each learning algorithm begins by selecting a mini-batch with batch size . SGD randomly selects a mini-batch, while OSGD selects a mini-batch as follows: . Then, the algorithms update using gradient descent on with a learning rate : . For a sufficiently small margin , let be the minimal time required for the algorithms to reach the condition . Under this setting, the following theorem compares OSGD and SGD, in terms of the lower bound on the time required for the convergence to the optimal solution.
Theorem 6.
Consider the described setting where the parameters of embedding vectors are updated, as shown in Fig. 2. Suppose there exist , such that for all satisfying or , , and Then, we have the following inequalities:
Corollary 1.
Suppose lower bounds of , in Thm. 6 are tight, and the learning rate is small enough. Then, .
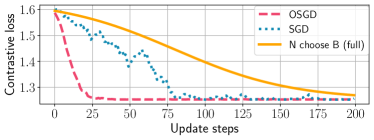
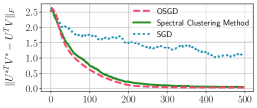
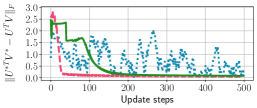
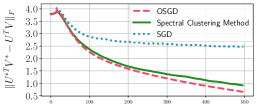
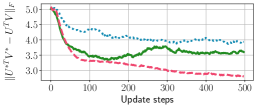
In Fig. 2, we present training loss curves of the full-batch contrastive loss in Eq. (2) for various algorithms implemented on the toy example. One can observe that the losses of all algorithms eventually converge to 1.253, the optimal loss achievable when the solution satisfies and form simplex cross-polytope. As shown in the figure, OSGD converges faster than SGD to the optimal loss. This empirical evidence corroborates our theoretical findings in Corollary 1.
5.2 Convergence of OSGD in Mini-batch Contrastive Learning Setting
Recall that it is challenging to prove the convergence of gradient-descent-based methods for contrastive learning problem in Eq. (1) due to the non-quasi-convexity of the contrastive loss . Instead of focusing on the contrastive loss, we consider a proxy, the weighted contrastive loss defined as with for two arbitrary natural numbers where is a mini-batch with -th largest loss among batches of size . Indeed, this is a natural objective obtained by applying OSGD to our problem, and we show the convergence of such an algorithm by extending the results in Kawaguchi & Lu [29]. OSGD updates the embedding vectors using the gradient averaged over batches that have the largest losses among randomly chosen batches (see Algo. 2 in Appendix B.2). Let , be the updated embedding matrices when applying OSGD for steps starting from , , using the learning rate . Then the following theorem, proven in Appendix B.2, holds.
Theorem 7 (Convergence results).
Consider sampling from with probability proportional to , that is, . Then , we have
where denotes the minimized value of .
Given sufficiently small learning rate decays at the rate of Therefore, this theorem guarantees the convergence of OSGD for mini-batch contrastive learning.
5.3 Suggestion: Spectral Clustering-based Approach

Applying OSGD to mini-batch contrastive learning has a potential benefit as shown in Sec. 5.1, but it also has some challenges. Choosing the best batches with high loss in OSGD is only doable after we evaluate losses of all combinations, which is computationally infeasible for large . A naive solution to tackle this challenge is to first randomly choose batches and then select high-loss batches among batches. However, this naive random batch selection method does not guarantee that the chosen batches are having the highest loss among all candidates. Motivated by these issues of OSGD, we suggest an alternative batch selection method inspired by graph theory. Note that the contrastive loss for a given batch is lower bounded as follows:
| (5) |
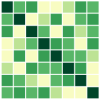
This lower bound is derived using Jensen’s inequality. Detailed derivation is provided in Appendix C.1. A nice property of this lower bound is that it can be expressed as a summation of terms over a pair of samples within batch . Consider a graph with nodes, where the weight between node and is defined as . Recall that our goal is to choose batches having the highest contrastive loss among batches. We relax this problem by reducing our search space such that the chosen batches form a partition of samples, i.e., and . In such scenario, our target problem is equivalent to the problem of clustering nodes in graph into clusters with equal size, where the objective is to minimize the sum of weights of inter-cluster edges. This problem is nothing but the min-cut problem [13], and we can employ even-sized spectral clustering algorithm which solves it efficiently. The pseudo-code of our batch selection method222Our algorithm finds good clusters at once, instead of only finding a single best cluster. Compared with such alternative approach, our method is (i) more efficient when we update models for multiple iterations, and (ii) guaranteed to load all samples with batches, thus expected to have better convergence [5, 21, 20]. is provided in Algo. 1, and further details of the algorithm are provided in Appendix C. Fig. 3 shows the histogram of contrastive loss for batches chosen by the random batch selection method and the proposed spectral clustering (SC) method. One can observe that the SC method favors batches with larger loss values.
6 Experiments
We validate our theoretical findings and the effectiveness of our proposed batch selection method by providing experimental results on synthetic and real datasets. We first show that our experimental results on synthetic dataset coincide with two main theoretical results: (i) the relationship between the full-batch contrastive loss and the mini-batch contrastive loss given in Sec. 4, (ii) the analysis on the convergence of OSGD and the proposed SC method given in Sec. 5. To demonstrate the practicality of our batch selection method, we provide experimental results on CIFAR-100 [31] and Tiny ImageNet [33]. Details of the experimental setting can be found in Appendix D, and our code is available at https://github.com/krafton-ai/mini-batch-cl.
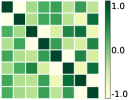
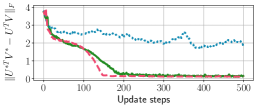
6.1 Synthetic Dataset
Consider the problem of optimizing the embedding matrices using GD, where each column of is initialized as a multivariate normal vector and then normalized as , . We use learning rate , and apply the normalization step at every iteration.
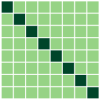
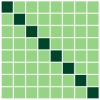
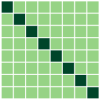
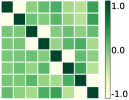
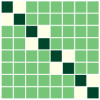
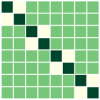
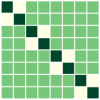
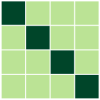
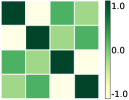
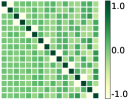
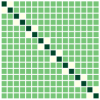
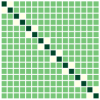
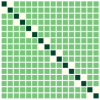
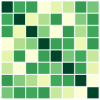
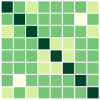
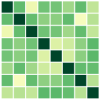
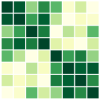
First, we compare the minimizers of three optimization problems: (i) full-batch optimization in Eq.(1); (ii) mini-batch optimization in Eq. (4) with ; (iii) mini-batch optimization with . We apply GD algorithm to each problem for and , obtain the updated embedding matrices, and then show the heatmap plot of gram matrix containing all the pairwise inner products in Fig. 4(b)-(d). Here, we plot for two regimes: for the top row, and for the bottom row. In Fig. 4(a), we plot the gram matrix for the optimal solution obtained in Sec. 4.2. One can observe that when either full-batch or all mini-batches are used for training, the trained embedding vectors reach a simplex ETF and simplex cross-polytope solutions for and , respectively, as proved in Thm 4. In contrast, when a strict subset of mini-batches are used for training, these solutions are not achieved.
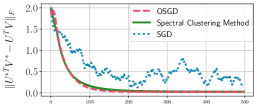
Second, we compare the convergence speed of three algorithms in mini-batch optimization: (i) OSGD; (ii) the proposed SC method; and (iii) SGD (see details of the algorithms in Appendix C). Fig. 4(e) shows the which is the Frobenius norm of the difference between heatmaps of the ground-truth solution () and the embeddings at each step . We restrict the number of updates for all algorithms, specifically 500 steps. We observe that both OSGD and the proposed method nearly converge to the ground-truth solutions proved in Thm. 4 within 500 steps, while SGD does not. We obtain similar results for other values of and , given in Appendix D.2.
| CIFAR-100 | Tiny ImageNet | |||
|---|---|---|---|---|
| SimCLR | SogCLR | SimCLR | SogCLR | |
| OSGD | 31.4 0.03 | 23.8 0.02 | 33.6 0.04 | 29.7 0.04 |
| SGD | 31.3 0.02 | 23.6 0.05 | 33.2 0.03 | 28.6 0.03 |
| SC | 0.05 | 0.04 | 0.04 | 0.03 |
6.2 Real Datasets
Here we show that the proposed SC method is effective in more practical settings where the embedding is learned by a parameterized encoder, and can be easily applied to existing uni-modal frameworks, such as SimCLR [9] and SogCLR [68]. We conduct mini-batch contrastive learning on CIFAR-100 and Tiny ImageNet datasets and report the performances in the image retrieval downstream task on corrupted datasets, the results of which are in Table 1. Due to the page limit, we provide detailed experimental information in the Appendix D.3.
7 Conclusion
We provided a thorough theoretical analysis of mini-batch contrastive learning. First, we showed that the solution of mini-batch optimization and that of full-batch optimization are identical if and only if all mini-batches are considered. Second, we analyzed the convergence of OSGD and devised spectral clustering (SC) method, a new batch selection method which handles the complexity issue of OSGD in mini-batch contrastive learning. Experimental results support our theoretical findings and the efficacy of SC.
Limitations
We note that our theoretical results have two major limitations:
-
1.
While we would like to extend our results to the general case of , we were only able to characterize the optimal solution for the specific case of . Furthermore, our result for the case of in Thm. 4 requires the use of the conjecture that the optimal solution is symmetric and antipodal. However, as mentioned by Lu & Steinerberger [36], the general case of seems quite challenging in the non-asymptotic regime.
-
2.
In practice, the embeddings are usually the output of a shared neural network encoder. However, our results are for the case when the embeddings only have a norm constraint. Thus, our results do not readily indicate any generalization to unseen data. We expect however, that it is possible to extend our results to the shared encoder setting by assuming sufficient overparameterization.
References
- Aberdam et al. [2021] Aberdam, A., Litman, R., Tsiper, S., Anschel, O., Slossberg, R., Mazor, S., Manmatha, R., and Perona, P. Sequence-to-sequence contrastive learning for text recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 15302–15312, 2021.
- Ahn et al. [2020] Ahn, K., Yun, C., and Sra, S. Sgd with shuffling: optimal rates without component convexity and large epoch requirements. Advances in Neural Information Processing Systems, 33:17526–17535, 2020.
- Bachman et al. [2019] Bachman, P., Hjelm, R. D., and Buchwalter, W. Learning representations by maximizing mutual information across views. Advances in neural information processing systems, 32, 2019.
- Borodachov [2022] Borodachov, S. Optimal antipodal configuration of points on a sphere in for covering. arXiv preprint arXiv:2210.12472, 2022.
- Bottou [2009] Bottou, L. Curiously fast convergence of some stochastic gradient descent algorithms. In Proceedings of the symposium on learning and data science, Paris, volume 8, pp. 2624–2633, 2009.
- Cha et al. [2023] Cha, J., Lee, J., and Yun, C. Tighter lower bounds for shuffling sgd: Random permutations and beyond, 2023.
- Chen et al. [2022] Chen, C., Zhang, J., Xu, Y., Chen, L., Duan, J., Chen, Y., Tran, S. D., Zeng, B., and Chilimbi, T. Why do we need large batchsizes in contrastive learning? a gradient-bias perspective. In Oh, A. H., Agarwal, A., Belgrave, D., and Cho, K. (eds.), Advances in Neural Information Processing Systems, 2022.
- Chen et al. [2021] Chen, H., Lagadec, B., and Bremond, F. Ice: Inter-instance contrastive encoding for unsupervised person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 14960–14969, 2021.
- Chen et al. [2020a] Chen, T., Kornblith, S., Norouzi, M., and Hinton, G. A simple framework for contrastive learning of visual representations. In International conference on machine learning, pp. 1597–1607. PMLR, 2020a.
- Chen et al. [2020b] Chen, X., Fan, H., Girshick, R., and He, K. Improved baselines with momentum contrastive learning. arXiv preprint arXiv:2003.04297, 2020b.
- Cho & Yun [2023] Cho, H. and Yun, C. Sgda with shuffling: faster convergence for nonconvex-pł minimax optimization, 2023.
- Chopra et al. [2005] Chopra, S., Hadsell, R., and LeCun, Y. Learning a similarity metric discriminatively, with application to face verification. In 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), volume 1, pp. 539–546. IEEE, 2005.
- Cormen et al. [2022] Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein, C. Introduction to algorithms. MIT press, 2022.
- Crouse [2016] Crouse, D. F. On implementing 2d rectangular assignment algorithms. IEEE Transactions on Aerospace and Electronic Systems, 52(4):1679–1696, 2016.
- Davis & Drusvyatskiy [2019] Davis, D. and Drusvyatskiy, D. Stochastic model-based minimization of weakly convex functions. SIAM Journal on Optimization, 29(1):207–239, 2019.
- Elizalde et al. [2023] Elizalde, B., Deshmukh, S., Ismail, M. A., and Wang, H. Clap learning audio concepts from natural language supervision. In ICASSP 2023 - 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1–5, 2023.
- Gadre et al. [2023] Gadre, S. Y., Ilharco, G., Fang, A., Hayase, J., Smyrnis, G., Nguyen, T., Marten, R., Wortsman, M., Ghosh, D., Zhang, J., et al. Datacomp: In search of the next generation of multimodal datasets. arXiv preprint arXiv:2304.14108, 2023.
- Goel et al. [2022] Goel, S., Bansal, H., Bhatia, S., Rossi, R., Vinay, V., and Grover, A. Cyclip: Cyclic contrastive language-image pretraining. In Advances in Neural Information Processing Systems, volume 35, pp. 6704–6719. Curran Associates, Inc., 2022.
- Grill et al. [2020] Grill, J.-B., Strub, F., Altché, F., Tallec, C., Richemond, P., Buchatskaya, E., Doersch, C., Avila Pires, B., Guo, Z., Gheshlaghi Azar, M., et al. Bootstrap your own latent-a new approach to self-supervised learning. Advances in neural information processing systems, 33:21271–21284, 2020.
- Gürbüzbalaban et al. [2021] Gürbüzbalaban, M., Ozdaglar, A., and Parrilo, P. A. Why random reshuffling beats stochastic gradient descent. Mathematical Programming, 186(1):49–84, 2021.
- Haochen & Sra [2019] Haochen, J. and Sra, S. Random shuffling beats sgd after finite epochs. In International Conference on Machine Learning, pp. 2624–2633. PMLR, 2019.
- He et al. [2020] He, K., Fan, H., Wu, Y., Xie, S., and Girshick, R. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 9729–9738, 2020.
- Hendrycks & Dietterich [2019] Hendrycks, D. and Dietterich, T. G. Benchmarking neural network robustness to common corruptions and perturbations. In 7th International Conference on Learning Representations, ICLR 2019, 2019.
- Hu et al. [2021] Hu, Q., Wang, X., Hu, W., and Qi, G.-J. Adco: Adversarial contrast for efficient learning of unsupervised representations from self-trained negative adversaries. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 1074–1083, 2021.
- Jaiswal et al. [2020] Jaiswal, A., Babu, A. R., Zadeh, M. Z., Banerjee, D., and Makedon, F. A survey on contrastive self-supervised learning. Technologies, 9(1):2, 2020.
- Ji et al. [2022] Ji, W., Lu, Y., Zhang, Y., Deng, Z., and Su, W. J. An unconstrained layer-peeled perspective on neural collapse. In International Conference on Learning Representations, 2022.
- Jia et al. [2021] Jia, C., Yang, Y., Xia, Y., Chen, Y.-T., Parekh, Z., Pham, H., Le, Q., Sung, Y.-H., Li, Z., and Duerig, T. Scaling up visual and vision-language representation learning with noisy text supervision. In International Conference on Machine Learning, pp. 4904–4916. PMLR, 2021.
- Kalantidis et al. [2020] Kalantidis, Y., Sariyildiz, M. B., Pion, N., Weinzaepfel, P., and Larlus, D. Hard negative mixing for contrastive learning. Advances in Neural Information Processing Systems, 33:21798–21809, 2020.
- Kawaguchi & Lu [2020] Kawaguchi, K. and Lu, H. Ordered sgd: A new stochastic optimization framework for empirical risk minimization. In International Conference on Artificial Intelligence and Statistics, pp. 669–679. PMLR, 2020.
- Khosla et al. [2020] Khosla, P., Teterwak, P., Wang, C., Sarna, A., Tian, Y., Isola, P., Maschinot, A., Liu, C., and Krishnan, D. Supervised contrastive learning. Advances in Neural Information Processing Systems, 33:18661–18673, 2020.
- Krizhevsky et al. [2009] Krizhevsky, A., Hinton, G., et al. Learning multiple layers of features from tiny images. 2009.
- Kuhn [1955] Kuhn, H. W. The hungarian method for the assignment problem. Naval research logistics quarterly, 2(1-2):83–97, 1955.
- Le & Yang [2015] Le, Y. and Yang, X. Tiny imagenet visual recognition challenge. CS 231N, 7(7):3, 2015.
- Lee et al. [2022] Lee, J., Kim, J., Shon, H., Kim, B., Kim, S. H., Lee, H., and Kim, J. UniCLIP: Unified framework for contrastive language-image pre-training. In Advances in Neural Information Processing Systems, 2022.
- Loshchilov & Hutter [2015] Loshchilov, I. and Hutter, F. Online batch selection for faster training of neural networks. arXiv preprint arXiv:1511.06343, 2015.
- Lu & Steinerberger [2022] Lu, J. and Steinerberger, S. Neural collapse under cross-entropy loss. Applied and Computational Harmonic Analysis, 59:224–241, 2022. ISSN 1063-5203. Special Issue on Harmonic Analysis and Machine Learning.
- Lu et al. [2021] Lu, Y., Meng, S. Y., and De Sa, C. A general analysis of example-selection for stochastic gradient descent. In International Conference on Learning Representations, 2021.
- Lu et al. [2022] Lu, Y., Guo, W., and Sa, C. D. Grab: Finding provably better data permutations than random reshuffling. In Advances in Neural Information Processing Systems, 2022.
- Ma et al. [2021] Ma, S., Zeng, Z., McDuff, D., and Song, Y. Active contrastive learning of audio-visual video representations. In International Conference on Learning Representations, 2021.
- Mishchenko et al. [2020] Mishchenko, K., Khaled, A., and Richtárik, P. Random reshuffling: Simple analysis with vast improvements. Advances in Neural Information Processing Systems, 33:17309–17320, 2020.
- Misra & Maaten [2020] Misra, I. and Maaten, L. v. d. Self-supervised learning of pretext-invariant representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 6707–6717, 2020.
- Nagaraj et al. [2019] Nagaraj, D., Jain, P., and Netrapalli, P. Sgd without replacement: Sharper rates for general smooth convex functions. In International Conference on Machine Learning, pp. 4703–4711. PMLR, 2019.
- Ng et al. [2001] Ng, A., Jordan, M., and Weiss, Y. On spectral clustering: Analysis and an algorithm. Advances in neural information processing systems, 14, 2001.
- Nguyen et al. [2021] Nguyen, L. M., Tran-Dinh, Q., Phan, D. T., Nguyen, P. H., and Van Dijk, M. A unified convergence analysis for shuffling-type gradient methods. The Journal of Machine Learning Research, 22(1):9397–9440, 2021.
- Oord et al. [2018] Oord, A. v. d., Li, Y., and Vinyals, O. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748, 2018.
- Papyan et al. [2020] Papyan, V., Han, X., and Donoho, D. L. Prevalence of neural collapse during the terminal phase of deep learning training. Proceedings of the National Academy of Sciences, 117(40):24652–24663, 2020.
- Pham et al. [2021] Pham, H., Dai, Z., Ghiasi, G., Liu, H., Yu, A. W., Luong, M.-T., Tan, M., and Le, Q. V. Combined scaling for zero-shot transfer learning. arXiv preprint arXiv:2111.10050, 2021.
- Radford et al. [2021] Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh, G., Agarwal, S., Sastry, G., Askell, A., Mishkin, P., Clark, J., et al. Learning transferable visual models from natural language supervision. In International Conference on Machine Learning, pp. 8748–8763. PMLR, 2021.
- Rajput et al. [2020] Rajput, S., Gupta, A., and Papailiopoulos, D. Closing the convergence gap of sgd without replacement. In International Conference on Machine Learning, pp. 7964–7973. PMLR, 2020.
- Rajput et al. [2022] Rajput, S., Lee, K., and Papailiopoulos, D. Permutation-based SGD: Is random optimal? In International Conference on Learning Representations, 2022.
- Ramesh et al. [2021] Ramesh, A., Pavlov, M., Goh, G., Gray, S., Voss, C., Radford, A., Chen, M., and Sutskever, I. Zero-shot text-to-image generation. In International Conference on Machine Learning, pp. 8821–8831. PMLR, 2021.
- Ramesh et al. [2022] Ramesh, A., Dhariwal, P., Nichol, A., Chu, C., and Chen, M. Hierarchical text-conditional image generation with clip latents. arXiv preprint arXiv:2204.06125, 2022.
- Recht & Re [2012] Recht, B. and Re, C. Toward a noncommutative arithmetic-geometric mean inequality: Conjectures, case-studies, and consequences. In Proceedings of the 25th Annual Conference on Learning Theory, volume 23 of Proceedings of Machine Learning Research, pp. 11.1–11.24. PMLR, 2012.
- Recht & Ré [2013] Recht, B. and Ré, C. Parallel stochastic gradient algorithms for large-scale matrix completion. Mathematical Programming Computation, 5(2):201–226, 2013.
- Robinson et al. [2021] Robinson, J. D., Chuang, C.-Y., Sra, S., and Jegelka, S. Contrastive learning with hard negative samples. In International Conference on Learning Representations, 2021.
- Sachidananda et al. [2022] Sachidananda, V., Tseng, S.-Y., Marchi, E., Kajarekar, S., and Georgiou, P. Calm: Contrastive aligned audio-language multirate and multimodal representations. arXiv preprint arXiv:2202.03587, 2022.
- Safran & Shamir [2021a] Safran, I. and Shamir, O. How good is sgd with random shuffling?, 2021a.
- Safran & Shamir [2021b] Safran, I. and Shamir, O. Random shuffling beats sgd only after many epochs on ill-conditioned problems. Advances in Neural Information Processing Systems, 34:15151–15161, 2021b.
- Schroff et al. [2015] Schroff, F., Kalenichenko, D., and Philbin, J. Facenet: A unified embedding for face recognition and clustering. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 815–823, 2015.
- Sohn [2016] Sohn, K. Improved deep metric learning with multi-class n-pair loss objective. Advances in neural information processing systems, 29, 2016.
- Song & Ermon [2020] Song, J. and Ermon, S. Understanding the limitations of variational mutual information estimators. In International Conference on Learning Representations, 2020.
- Sustik et al. [2007] Sustik, M. A., Tropp, J. A., Dhillon, I. S., and Heath Jr, R. W. On the existence of equiangular tight frames. Linear Algebra and its applications, 426(2-3):619–635, 2007.
- Tran et al. [2021] Tran, T. H., Nguyen, L. M., and Tran-Dinh, Q. Smg: A shuffling gradient-based method with momentum. In Meila, M. and Zhang, T. (eds.), Proceedings of the 38th International Conference on Machine Learning, volume 139 of Proceedings of Machine Learning Research, pp. 10379–10389. PMLR, 2021.
- Wang & Qi [2022] Wang, X. and Qi, G.-J. Contrastive learning with stronger augmentations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022.
- Yeh et al. [2022] Yeh, C.-H., Hong, C.-Y., Hsu, Y.-C., Liu, T.-L., Chen, Y., and LeCun, Y. Decoupled contrastive learning. In European Conference on Computer Vision, pp. 668–684. Springer, 2022.
- Ying et al. [2020] Ying, B., Yuan, K., and Sayed, A. H. Variance-reduced stochastic learning under random reshuffling. IEEE Transactions on Signal Processing, 68:1390–1408, 2020. doi: 10.1109/TSP.2020.2968280.
- You et al. [2017] You, Y., Gitman, I., and Ginsburg, B. Large batch training of convolutional networks. arXiv preprint arXiv:1708.03888, 2017.
- Yuan et al. [2022] Yuan, Z., Wu, Y., Qiu, Z.-H., Du, X., Zhang, L., Zhou, D., and Yang, T. Provable stochastic optimization for global contrastive learning: Small batch does not harm performance. In International Conference on Machine Learning, pp. 25760–25782. PMLR, 2022.
- Zeng et al. [2021] Zeng, D., Wu, Y., Hu, X., Xu, X., Yuan, H., Huang, M., Zhuang, J., Hu, J., and Shi, Y. Positional contrastive learning for volumetric medical image segmentation. In Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, September 27–October 1, 2021, Proceedings, Part II 24, pp. 221–230. Springer, 2021.
- Zhang & Stratos [2021] Zhang, W. and Stratos, K. Understanding hard negatives in noise contrastive estimation. In North American Chapter of the Association for Computational Linguistics, 2021.
- Zhou et al. [2022] Zhou, J., Li, X., Ding, T., You, C., Qu, Q., and Zhu, Z. On the optimization landscape of neural collapse under mse loss: Global optimality with unconstrained features. In International Conference on Machine Learning, pp. 27179–27202. PMLR, 2022.
- Zolfaghari et al. [2021] Zolfaghari, M., Zhu, Y., Gehler, P., and Brox, T. Crossclr: Cross-modal contrastive learning for multi-modal video representations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pp. 1450–1459, 2021.
Organization of the Appendix
-
1.
In Appendix A, we introduce an additional definition for posterity.
-
2.
In Appendix B, we provide detailed proofs of the theoretical results as well as any intermediate results/lemmas that we found useful.
- (a)
- (b)
- (c)
-
3.
Appendix C specifies the pseudo-code and details for the three algorithms: (i) Spectral Clustering; (ii) Stochastic Gradient Descent (SGD) and (iii) Ordered SGD (OSGD).
- 4.
Appendix A Additional Definition
Definition 4 (Sustik et al. [62]).
A set of vectors in the form an equiangular tight frame (ETF) if (i) they are all unit norm: for every , (ii) they are equiangular: for all and some , and (iii) they form a tight frame: where is a matrix whose columns are , and is the identity matrix.
Appendix B Proofs
B.1 Proofs of Results From Section 4
See 1
Proof.
First, we define the contrastive loss as the sum of two symmetric one-sided contrastive loss terms to simplify the notation. We denote the following term as the one-sided contrastive loss
| (6) |
Then, the overall contrastive loss is given by the sum of the two one-sided contrastive losses:
| (7) |
Since is symmetric in its arguments, results pertaining to the optimum of readily extend to . Now, let us consider the simpler problem of minimizing the one-sided contrastive loss from Eq. (6) which reduces the problem to exactly the same setting as Lu & Steinerberger [36]:
Note that, we have for any fixed
| (8) |
where follows by applying Jensen inequality for and follows from . Since is monotonic, we have that and therefore,
| (9) |
where follows by applying Jensen inequality to the convex function for , and follow from .
Note that for equalities to hold in Eq. (8) and (9), we need constants such that
| (10) | |||
| (11) |
Since and are both monotonic, minimizing the lower bound in Eq. (8) is equivalent to
| (12) |
All that remains is to show that the solution that maximizes Eq 12 also satisfies the conditions in Eq. (10) and (11). To see this, first note that the maximization problem can be written as
where is a vector in formed by stacking the vectors together. is similarly defined. denotes the identity matrix, denotes the all-one vector in , and denotes the Kronecker product. It is easy to see that since each . Since the eigenvalues of are the product of the eigenvalues of and , in order to analyze the spectrum of the middle term in the above maximization problem, it suffices to just consider the eigenvalues of . As shown by the elegant analysis in Lu & Steinerberger [36], for any such that and for any such that for some . Therefore it follows that its eigenvalues are with multiplicity and . Since its largest eigenvalue is and since , applying cauchy schwarz inequality, we have that
Moreover, we see that setting and setting to be the simplex ETF attains the maximum above while also satisfying the conditions in Eq. (10) and (11) with and . Therefore, the inequalities in Eq. (8) and (9) are actually equalities for when they are chosen to be the simplex ETF in which is attainable since . Therefore, we have shown that if is the simplex ETF and , then over the unit sphere in . All that remains is to show that this is also the minimizer for .
First note that is also the minimizer for through symmetry. One can repeat the proof exactly by simply exchanging and to see that this is indeed true. Now recalling Eq. (7), we have
| (13) | ||||
However, since the minimizer of both terms in Eq. (13) is the same, the inequality becomes an equality. Therefore, we have shown that ( is the minimizer of completing the proof. ∎
Remark 1.
See 3
Proof.
By applying the logarithmic property that allows division to be represented as subtraction,
Since (symmetric property), the contrastive loss satisfies
| (14) |
Since for any , we can derive the following relations:
We incorporate these relations into Eq. (23) as follows:
The antipodal property of indicates that for each , there exists a such that . By applying this property, we can manipulate the summation of over as the following:
Therefore,
where (a) follows by applying Jensen’s inequality to the concave function ; and (b) follows by Lem. 3, and the fact that function is convex and monotonically decreasing. denotes a set of vectors which forms a cross-polytope.
Both inequalities in and are equalities only when the columns of form a cross-polytope. Therefore, the columns of form a cross-polytope. ∎
Lemma 3.
Given a function is convex and monotonically decreasing, let
| (15) |
where . Then, the columns of form a simplex cross-polytope for .
Proof.
Suppose and . Given a function is convex and monotonically decreasing. denotes the corresponding index for such that , and . Under these conditions, we derive the following:
where follows by Jensen’s inequality; and (b) follows from the fact that and the function is monotonically decreasing. The equality conditions for and only hold when the columns of form a cross-polytope. We can conclude that the columns of form a cross polytope. ∎
See 1
Proof.
Consider defined such that where is -th unit vector in First note that and . Then,
| (16) | |||
| (17) |
We now consider the second part of the statement. For contradiction, assume that there exists some such that . Let be defined such that , where Note that . Then,
| (18) | |||
| (19) |
See 4
Proof.
Case (i): Suppose
For simplicity, first consider just one of the two terms in the two-sided loss. Therefore, the optimization problem becomes
Similar to the proof of Lem. 1, we have that
where and follows by applying Jensen’s inequality to and for , respectively. Note that for equalities to hold in Jensen’s inequalities, we need constants such that
| (20) | |||
| (21) |
Now, we carefully consider the two terms in the numerator:
To simplify , first note that for any fixed such that , there are batches that contain and . And for , there are batches that contain that pair. Since these terms all occur in , we have that
Similarly, we have that
Plugging these back into the above inequality, we have that
Observe that the term inside the exponential is identical to Eq. (9) and therefore, we can reuse the same spectral analysis argument to show that the simplex ETF also minimizes . Once again, since the proof is symmetric the simplex ETF also minimizes .
Case (ii): Suppose and , are symmetric and antipodal. Next, we consider the following optimization problem
| (22) |
where . Since (symmetric property) the contrastive loss satisfies
| (23) |
Therefore, the solution of the optimization problem in Eq. (22) is identical to the minimizer of the following optimization problem:
The objective of the optimization problem can be rewritten by reorganizing summations as
| (24) |
where represents the set of batch indices containing . We then divide the summation term in Eq. (24) into two terms:
| (25) |
by partitioning the set for each into as the following with being the index for which :
We will prove that the columns of form a cross-polytope by showing that the minimizer of each term of the RHS in Eq. (25) also forms a cross-polytope. Let us start with the first term of the RHS in Eq. (25). Starting with applying Jensen’s inequality to the concave function , we get:
where follows by Lem. 3 and the fact that for is convex and monotonically decreasing. denotes a set of vectors which forms a cross-polytope. All equalities hold only when the columns of form a cross-polytope.
Next consider the second term of the RHS in Eq. (25). By following a similar procedure above, we get:
where denotes a set of vectors which forms a cross-polytope.
Both terms of RHS in Eq. (25) have the minimum value when forms a cross-polytope. Therefore, we can conclude that the columns of form a cross-polytope. ∎
See 5
Proof.
Consider a set of batches with the batch size . Without loss of generality, assume that . For contradiction, assume that the simplex ETF - is indeed the optimal solution of the loss over these batches. Then, by definition, we have that for any
| (26) |
where is defined such that for all and for all . Also recall that for all . Therefore, we also have
| (27) |
where the last equality is due to the fact that .
Now, let us consider defined such that for all , and for all . Intuitively, this is equivalent to placing on a simplex ETF of points and setting . This is clearly possible because which is the condition required to place points on a simplex ETF in . Therefore,
| (28) |
where the last equality follows since . It is easy to see from Eq. (27) and (28) that which contradicts Eq. (26). Therefore, the optimal solution of minimizing the contrastive loss over any batches is not the simplex ETF completing the proof. ∎
Proposition 2.
Proof.
The proof follows in a fairly similar manner to that of Thm. 5. Consider a set of batches of size , . Without loss of generality, assume that for any . For contradiction, assume that the simplex ETF - is the optimal solution of the loss over these batches. Then, by definition, we have that for any
Once again, for contradiction assume that the simplex ETF - is indeed the optimal solution of the loss over these batches. Then, by definition for any
| (29) |
where is defined such that for all and for all . Also recall that for all . Therefore, we also have
| (30) |
Now, let us consider defined such that for all , and for all . Once again, note that this is equivalent to placing on a simplex ETF of points and setting . Hence,
| (31) |
where for the final equality note that following. The only pair for which is . Since there is no such that , this term never appears in our loss. From Eq. (30) and Eq. (31), we have that which contradicts Eq. (29). Therefore, we conclude that the optimal solution of the contrastive loss over any batches is not the simplex ETF. ∎
Proposition 3.
Proof.
Applying Lem. 1 specifically to a single batch gives us that the optimal solution for just the loss over this batch is the simplex ETF over points. In the case of non-overlapping batches, the objective function can be separated across batches and therefore the optimal solution for the sum of the losses is equal to the solution of minimizing each term independently. More precisely, we have
where and , respectively, and the equality follows from the fact that ’s are disjoint. ∎
B.2 Proofs of Results From Section 5
See 2
Proof.
The contrastive loss function is geodesic quasi-convex if for any two points and in the domain and for all in :
We provide a counter-example for geodesic quasi-convexity, which is a triplet of points , , where is on the geodesic between other two points and satisfies . Let and
Now, define and , which is the “midpoint” of the geodesic between and . By direct calculation, we obtain , which indicates is geodesic non-quasi-convex. ∎
Theorem 8 (Theorem 6 restated).
Consider samples and their embedding vectors , with dimension . Suppose ’s are parametrized by as in the setting described in Sec. 5.1 (see Fig. 2). Consider initializing and for all , then updating via OSGD and SGD with the batch size as described in Sec. 5.1. Let , be the minimal time required for OSGD, SGD algorithm to have . Suppose there exist , such that for all satisfying or , , and Then,
Proof.
We begin with the proof of
Assume that the parameters are initialized at . Then, there are six batches with the batch size , and we can categorize the batches according to the mini-batch contrastive loss:
-
1.
:
-
2.
:
-
3.
:
Without loss of generality, we assume that OSGD algorithm described in Algo. 6 chooses the mini-batch corresponding to the highest loss at time and updates the parameter as
Then, for the next update, OSGD choose which is now closer than updated . And would be updated as same as what previously have changed. Thus, updates only at the even time, and stays at the odd time, i.e.
Iterating this procedure, we can view OSGD algorithm as one-parameterized algorithm of parameter as:
where , and In the procedure of updates, we may assume that for all . To analyze the drift of , we firstly study smoothness of ;
We can observe that , hence has Lipschitz constant i.e.
Therefore,
where the first inequality is from Lipschitz-continuity of , and the second equality is from Taylor expansion of at as;
Hence, indicates that
for some constant Moreover implies that
So, we obtain the lower bound of by doubling
We estimate of
Now, we study convergence rate of SGD algorithm. We claim that
Without loss of generality, we firstly focus on the drift of . Since batch selection is random, given :
-
1.
with probability . Then, implies
-
2.
with probability . At , the initial batch selection can be primarily categorized into three distinct sets; closely positioned vectors or , vectors that form obtuse angles or , and vectors diametrically opposed at or . Given that is substantially small, the possibility of consistently selecting batches from the same category for subsequent updates is relatively low. As such, it is reasonable to infer that each batch is likely to maintain its position within the initially assigned categories. From this, one can deduce that vector sets such as or continue to sustain an angle close to . Given these conditions, it is feasible to postulate that if the selected batch encompasses either or , the magnitude of the gradient of the loss function , denoted by , would be less than a particular threshold i.e.
Then,
-
3.
with probability . Then, implies
Since there is no update on for the other cases, taking expectation yields
where is defined as:
We study smoothness of by setting , where
Note that
for some constant Then for ,
In the same way, we can define the functions all having Lipschitz constant . As we define , it has Lipschitz constant satisfying that
where Big is applied elementwise to the vector, denoting that each element follows independently. From Lipschitzness of , for any
By taking expecations for both sides,
Applying the triangle inequality, , we further deduce that
Setting we can write
Thus, with constant
By Taylor expansion of near :
we get
Since ,
Therefore,
∎
Remark 2.
To simply compare the convergence rates of two algorithms, we assumed that there is some constant such that , in Theorem 8. However, without this assumption, we could still obtain lower bounds of both algorithms as;
where , and their approximations are For small enough we can observe OSGD algorithm converges faster than SGD algorithm, if the inequalities are tight.
Direct Application of OSGD and its Convergence
We now focus exclusively on the convergence of OSGD. We prove Theorem 7, which establishes the convergence of an application of OSGD to the mini-batch contrastive learning problem, with respect to the loss function .
For ease of reference, we repeat the following definition:
| (32) |
where represents the batch with the -th largest loss among all possible batches, and , are parameters for the OSGD.
See 7
Proof.
Define . We begin by reffering to Lemma 2.2. in [15], which provides the following equations:
Furthermore, we have that is -Lipschitz in by Thm. 11. This gives
Therefore,
As a consequence of Thm 9,
Note that is the minimized value of , and the last inequality is due to , because
| by putting , and | ||||
for any , , implying that . ∎
We provide details, including proof of theorems and lemmas in the sequel.
Theorem 9.
Consider sampling from with probability . Then , we have
where , and denotes the minimized value of .
Proof.
is -Lipschitz in by Thm. 11. Hence, it is -weakly convex by Lem. 5. Furthermore, the gradient norm of a mini-batch loss, or is bounded by . Finally, [29, Theorem 1] states that the expected value of gradients of the OSGD algorithm is at each iteration . Therefore, we can apply [15, Thm. 3.1] to the OSGD algorithm to obtain the desired result. ∎
Roughly speaking, Theorem 7 shows that are close to a stationary point of . We refer readers to Davis & Drusvyatskiy [15] which illustrates the role of the norm of the gradient of the Moreau envelope, , being small in the context of stochastic optimization.
We leave the results of some auxiliary theorems and lemmas to Subsection B.3.
B.3 Auxiliaries for the Proof of Theorem 7
For a square matrix , we denote its trace by . If matrices and are of the same shape, we define the canonical inner product by
Following a pythonic notation, we write and for the -th row and -th column of a matrix , respectively. The Cauchy–Schwarz inequality for matrices is given by
where a norm is a Frobenius norm in matrix i.e.
Lemma 4.
Let , . Then, .
Proof.
By a basic calculation, we have
Meanwhile, for any positive semidefinite matrix , let be a spectral decomposition of . Then, we have
where denotes the -th eigenvalue of a matrix . Invoking this fact, we have
or equivalently, . Similarly, we have . Therefore, we obtain
which means . ∎
If is a function of a matrix , we write a gradient of with respect to as a matrix-valued function defined by
Then, the chain rule gives
for a scalar variable . If is a function of two matrices , , we define as a horizontal stack of two gradient matrices, i.e., .
Now, we briefly review some necessary facts about Lipschitz functions.
Lemma 5 (Rendering of weak convexity by a Lipschitz gradient).
Let be a -smooth function, i.e., is a -Lipschitz function. Then, is -weakly convex.
Proof.
For the sake of simplicity, assume is twice differentiable. We claim that , where is the identity matrix and means is a positive semidefinite matrix. It is clear that this claim renders to be convex.
Let us assume, contrary to our claim, that there exists with . Therefore, has an eigenvalue . Denote corresponding eigenvector by , so we have , and consider ; the (elementwise) Taylor expansion of at gives
which gives
Taking , we obtain , which is contradictory to -Lipschitzness of . ∎
For , let us define
Using this function, we can write the loss corresponding to a mini-batch of size by
We now claim the following:
Lemma 6.
Consider , where for all . Then, is bounded by and -Lipschitz.
Proof.
With basic calculus rules, we obtain
| (33) |
where is the identity matrix and
From for all , it is easy to see that . This gives , and similarly . Therefore, we have
| (34) |
or equivalently
| (35) |
We now show that is -Lipschitz. Define by
Then, we have
For , we have for any . Thus,
which means is -Lipschitz, i.e., for any , . Using this fact, we can bound for , as follows:
Similarly, we have . Summing up,
which renders
∎
Recall that for , (They correspond to embeddings corresponding to a mini-batch ). Using this relation, we can calculate the gradient of with respect to . Denote a one-hot matrix, which is a matrix of zero entries except for indices being , and write . Then,
This elementwise relation means
| (36) | ||||
| and similarly, | ||||
| (37) | ||||
We introduce a simple lemma for bounding the difference between two multiplication of matrices.
Lemma 7.
For , and , , we have
Proof.
Theorem 10.
For any , and any batch of size , we have .
Proof.
Suppose , , we have
from Eq. (36) and (37). By following the fact that , and (see Lem. 6), we get
| and | ||||
Then,
Since is independent of and , we have
∎
Theorem 11.
is -Lipschitz for , , or to clarify,
for any , , , , where .
Proof.
Denoting , as parts of , that correspond to a mini-batch , we first show holds. For any , , we have
from Eq. 36 and Eq. 37. Recall Lemma 6; for any , (), we have
| and | ||||
We invoke Lemma 7 and obtain
| and similarly | ||||
Using the fact that
holds for any , and , , we obtain
Restating this with , we have
| (38) |
Recall the definition of :
where and . For any , , we can find a neighborhood of so that value rank of over does not change, since is -Lipschitz. More precisely speaking, we can find a rank that can be accepted by all points in the neighborhood. Therefore, we have
and since , is locally -Lipschitz. Since is smooth, such property is equivalent to , where is the identity matrix. Therefore, is -Lipschitz on . ∎
Appendix C Algorithm Details
C.1 Spectral Clustering Method
Here, we provide a detailed description of the proposed spectral clustering method (see Sec. 5.3) from Algo. 1. Recall that the contrastive loss for a given mini-batch is lower bounded as the following by Jensen’s inequality:
and we consider the graph with nodes, where the weight between node and is defined as
The proposed method employs the spectral clustering algorithm from [43], which bundles nodes into clusters. We aim to assign an equal number of nodes to each cluster, but we encounter a problem where varying numbers of nodes are assigned to different clusters. To address this issue, we incorporate an additional step to ensure that each cluster (batch) has the equal number of positive pairs. This step is to solve an assignment problem [32, 14]. We consider a minimum weight matching problem in a bipartite graph [14], where the first partite set is the collection of data points and the second set represents copies of each cluster center obtained after the spectral clustering. The edges in this graph are weighted by the distances between data points and centers. The goal of the minimum weight matching problem is to assign exactly data points to each center, minimizing the total cost of the assignment, where cost is the sum of the distances from each data point to its assigned center. This guarantees an equal number of data points for each cluster while minimizing the total assignment cost. A annotated procedure of the method is provided in Algo. 3.
C.2 Stochastic Gradient Descent (SGD)
We consider two SGD algorithms:
- 1.
- 2.
In the more practical setting where and , SGD updates the model parameters using the gradients instead of explicitly updating and .
C.3 Ordered SGD (OSGD)
We consider two OSGD algorithms:
- 1.
- 2.
In the more practical setting where and , OSGD updates the model parameters using the gradients instead of explicitly updating and .
Appendix D Experiment Details
In this section, we describe the details of the experiments in Sec. 6 and provide additional experimental results. First, we present histograms of mini-batch counts for different loss values from models trained with different batch selection methods. Next, we provide the results for on the synthetic dataset. Lastly, we explain the details of the experimental settings on real dataset, and provide the results of the retrieval downstream tasks.
D.1 Batch Counts: SC method vs. Random Batch Selection
We provide additional results comparing the mini-batch counts of two batch selection algorithms: the proposed SC method and random batch selection. The mini-batch counts are based on the mini-batch contrastive loss . We measure mini-batch losses from ResNet-18 models trained on CIFAR-100 using the gradient descent algorithm with different batch selection methods: (i) SGD (Algo. 5), (ii) OSGD (Algo. 7), and (iii) the SC method (Algo. 3). Fig. 5 illustrates histograms of mini-batch counts for mini-batches, where and . The results show that mini-batches generated through the proposed spectral clustering method tend to contain a higher proportion of large loss values when compared to the random batch selection, regardless of the pre-trained models used.



D.2 Synthetic Dataset
With the settings from Sec. 6.1, where each column of embedding matrices is initialized as a multivariate normal vector and then normalized as , for all , we provide the results for and or . Fig. 6 and 7 show the results for and , respectively. We additionally present the results for theoretically unproven cases, specifically for and (see Fig. 8). The results provide empirical evidence that all combinations of mini-batches leads to the optimal solution of full-batch minimization for the theoretically unproven cases.
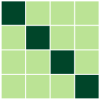
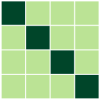








D.3 Real Datasets
To demonstrate the practical effectiveness of the proposed SC method, we consider a setting where embeddings are learned by a parameterized encoder. We employ two widely recognized uni-modal mini-batch contrastive learning algorithms: SimCLR [9] and SogCLR [68], and integrate different batch selection methods from: (i) SGD (algo. 5), (ii) OSGD (algo. 7), (iii) SC (algo. 3) into these frameworks. We compare the pre-trained models’ performances in the retrieval downstream tasks on the corrupted and the original datasets.
We conduct the mini-batch contrastive learning with the mini-batch size using ResNet18-based encoders on CIFAR-100 and Tiny ImageNet datasets. All learning is executed on a single NVIDIA A100 GPU. The training code and hyperparameters are based on the official codebase of SogCLR333https://github.com/Optimization-AI/SogCLR [68]. We use LARS optimizer[67] with the momentum of and the weight decay of . We utilize the learning rate scheduler which starts with a warm-up phase in the initial 10 epochs, during which the learning rate increases linearly to the maximum value . After this warm-up stage, we employ a cosine annealing (half-cycle) schedule for the remaining epochs. For OSGD, we employ , . To expedite batch selection in the proposed SC, we begin by randomly partitioning positive pairs into -sized clusters, using . We then apply the SC method to each cluster to generate mini-batches, resulting in a total of mini-batches. We train models for a total of 100 epochs.
Table 2 presents the top-1 retrieval accuracy on CIFAR-100 and Tiny ImageNet. We measure validation retrieval performance on the true as well as corrupted datasets. The retrieval task is defined to be finding the positive pair image of a given image among all pairs (the number of images of the validation dataset).
| Image Retrieval | ||||
| CIFAR-100 | Tiny ImageNet | |||
| SimCLR | SogCLR | SimCLR | SogCLR | |
| SGD | 46.91% | 12.34% | 57.88% | 16.70% |
| OSGD | 47.55% | 13.88% | 59.34% | 20.43% |
| SC | ||||
We also consider the retrieval task under a harder setting, where the various corruptions are applied per image so that we can consider a set of corrupted images as a hard negative samples. Table 1 presents the top-1 retrieval accuracy results on CIFAR-100-C and Tiny ImageNet-C, the corrupted datasets [23] designed for robustness evaluation. CIFAR-100-C (Tiny ImageNet-C) has the same images as CIFAR-100 (Tiny ImageNet), but these images have been altered by 19 (15) different types of corruption (e.g., image noise, blur, etc.). Each type of corruption has five severity levels. We utilize images corrupted at severity level 1. These images tend to be more similar to each other than those corrupted at higher severity levels, which consequently makes it more challenging to retrieve positive pairs among other images. To perform the retrieval task, we follow the following procedures: (i) We apply two distinct augmentations to each image to generate positive pairs; (ii) We extract embedding features from the augmented images by employing the pre-trained models; (iii) we identify the pair image of the given augmented image among augmentations of 19 (15) corrupted images with the cosine similarity of embedding vectors. This process is iterated across K CIFAR-100 images (K Tiny-ImageNet images). The top-1 accuracy measures a percentage of retrieved images that match its positive pair image, where each pair contains two different modality stemming from a single image.