Minimizing Instability in Strategy-Proof Matching Mechanism Using A Linear Programming Approach

Tohya Sugano
The University of Tokyo, Japan Graduate School of Economics, The University of Tokyo. Email: sugano-tohya1011@g.ecc.u-tokyo.ac.jp

Abstract

In this paper we address the design of matching mechanisms that are strategy-proof and simultaneously as stable as possible. Building on the impossibility result by Roth [1982] for one-to-one matching problems, we formulate an optimization problem that maximizes stability under the constraint of strategy-proofness. In our model the objective is to minimize the degree of instability measured as the sum (or worst-case maximum) of stability violations over all preference profiles. We further introduce the socially important properties of anonymity and symmetry into the formulation.

Our computational results show that, for small markets, our optimization approach leads to mechanisms with substantially lower stability violations than RSD. In particular, the optimal mechanism under our formulation exhibits roughly one-third the stability violation of RSD.

For deterministic mechanisms in the three-agent case, we also find that any strategy-proof mechanism hvae at least two blocking pairs at the worst case, and we propose an algorithm that attains this lower bound. Finally, we discuss extensions to larger markets and present simulation evidence that our mechanism yields a reduction of approximately $0.25$ blocking pairs on average compared to SD mechanism.

1 Introduction

Matching theory is a central research area in economics, computer science, and mathematics with numerous real-world applications, such as kidney exchange and residency matching. In particular, the one-to-one matching problem (exemplified by the marriage problem) has received extensive attention. Gale and Shapley [1962] demonstrated that a stable matching always exists in one-to-one matching markets and that the deferred acceptance (DA) algorithm (which is strategy-proof for one side) produces a stable matching. On the other hand, Roth [1982] established an impossibility result showing that no mechanism can simultaneously guarantee stability and strategy-proofness for both sides.

While there is a growing literature on strategy-proof mechanisms, the design of matching mechanisms that achieve the highest possible stability subject to strategy-proofness has not been thoroughly explored. Moreover, aside from SD, little is known about the design of two-sided strategy-proof matching mechanisms.

In this study, we search for the most stable matching mechanism among those that are strategy-proof by formulating an optimization problem that is solved computationally. Strategy-proofness is a critical property: mechanisms that are not strategy-proof may incentivize agents to misreport their preferences, thereby generating inefficient matchings and perceptions of unfairness. Our main contributions are twofold. First, we propose a mechanism for small matching markets that, while satisfying strategy-proofness, substantially reduces instability. Second, we provide a deterministic mechanism for the general case that always yields no more blocking pairs than SD.

Our optimization approach can be applied to many small-market problems, offering a novel perspective on impossibility theorems.

2 Related Work

The one-to-one matching problem was first formalized by Gale and Shapley [1962], who showed the existence of a stable matching. Roth [1982] later demonstrated the impossibility of achieving both stability and two-sided strategy-proofness.

Among prominent matching algorithms, the deferred acceptance algorithm is known to produce stable matchings but is not strategy-proof for both sides. AbdulkadiroÄlu and SÃ¶nmez [2003] introduced the top trading cycle (TTC) algorithm for school choice, which is Pareto efficient but not strategy-proof for both-sides. The Boston mechanism, discussed by Kumano [2013], is neither stable nor fully strategy-proof, although it may be strategy-proof and stable under strong non-cyclic preferences—a condition often deemed unrealistic.

Other studies have modeled stable matchings as solutions to linear programming formulations [Roth et al. [1993]] and characterized them as vertices of a polytope. Recent work by Ravindranath et al. [2021] considered the trade-off between stability violations and deviations from strategy-proofness using a neural network approach. However, minimizing a loss function by neural network methods does not yield mechanisms that are exactly strategy-proof or optimally stable. In contrast, our work formulates the design problem as a linear program that explicitly minimizes stability violations under strategy-proofness constraints.

3 Preliminaries

Let $S=\{1,\dots,n\}$ denote the set of students and $C=\{1,\dots,m\}$ the set of schools. Let $P_{S}$ be the set of all linear orders on $C\cup\{\emptyset\}$ , and let $P_{C}$ be the set of all linear orders on $S\cup\{\emptyset\}$ . Each student $s\in S$ has a strict preference $\succ_{s}\in P_{S}$ over $C\cup\{\emptyset\}$ and each school $c\in C$ has a strict preference $\succ_{c}\in P_{C}$ over $S\cup\{\emptyset\}$ . We denote the profile of student preferences by $\succ_{S}=(\succ_{s})_{s\in S}$ , the profile of school preferences by $\succ_{C}=(\succ_{c})_{c\in C}$ , and the entire preference profile by $\succ=(\succ_{i})_{i\in S\cup C}$ . The set of all possible preference profiles is denoted by $P$ . For any agent $i\in S\cup C$ , we denote by $\succ_{-i}$ the preferences of all agents except $i$ .

A randomized matching is given by a matrix

[r(s,c)]_{s\in S\cup\{\emptyset\},\,c\in C\cup\{\emptyset\}}

satisfying:

(i)

$r(s,c)\geq 0$ for all $s\in S\cup\{\emptyset\}$ and $c\in C\cup\{\emptyset\}$ ;
(ii)

$\sum_{c\in C\cup\{\emptyset\}}r(s,c)=1$ for all $s\in S$ ;
(iii)

$\sum_{s\in S\cup\{\emptyset\}}r(s,c)=1$ for all $c\in C$ .

We denote the set of all randomized matchings by $M$ . When for every $(s,c)\in S\times C$ the entry $r(s,c)$ is either 0 or 1, we say that $r$ is deterministic.

By the Birkhoff-von Neumann theorem [Birkhoff, 1946, Von Neumann, 1953], every randomized matching can be represented as a convex combination of deterministic matchings.

A function

g:P_{S}^{n}\times P_{C}^{m}\to M

is called a randomized matching mechanism. If $g$ always returns a deterministic matching, we call it a deterministic matching mechanism.

3.1 Stability

A randomized matching $r$ is said to be ex-ante stable if there does not exist a pair $(s,s^{\prime},c,c^{\prime})$ such that student $s$ prefers school $c$ to some school $c^{\prime}$ that he is matched with positive probability and school $c$ prefers student $s$ to some student $s^{\prime}$ who is matched with positive probability. In other words, no pair $(s,s^{\prime},c,c^{\prime})$ exists such that

c^{\prime}\succ_{s}c,\quad s^{\prime}\succ_{c}s,\quad r(s,c^{\prime})>0,\quad r(s^{\prime},c)>0.

We refer to such a pair $(s,c)$ as a blocking pair.

A randomized matching $r$ is said to be ex-post stable if it can be decomposed into stable deterministic matchings. Moreover, $r$ is fractionally stable if for every $(s,c)\in S\times C$ it holds that

r(s,c)+\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}r(s,c^{\prime})+\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}r(s^{\prime},c)\geq 1.

(1)

For deterministic matchings, ex-ante stability and ex-post stability coincide, and we simply say that $r$ is stable. In fact, it is known that ex-post stability and fractional stability are equivalent for randomized matchings (see, e.g., Aziz and Klaus [2019]).

A deterministic matching mechanism $g$ is called stable if for every $\succ\in P$ , the matching $g(\succ)$ is stable. Similarly, a randomized matching mechanism is said to be fractionally stable if $g(\succ)$ satisfies (1) for every $\succ\in P$ .

For a given randomized matching $r$ , we define the stability violation for a pair $(s,c)$ as

\max\Bigl{\{}1-r(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}r(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}r(s^{\prime},c),\,0\Bigr{\}},

(2)

and the stability violation for a matching as

\sum_{(s,c)\in S\times C}\max\Bigl{\{}1-r(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}r(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}r(s^{\prime},c),\,0\Bigr{\}},

(3)

In the deterministic case, this coincide with the number of blocking pairs.

3.2 Strategy-Proofness

A randomized matching mechanism $g$ is said to be strategy-proof if for every student $s\in S$ , for every preference profile $\succ\in P$ , for every alternative preference $\succ^{\prime}_{s}\in P_{S}$ , and for every school $c\in C$ with $c\succ_{s}\emptyset$ , it holds that

\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g(\succ)(s,c^{\prime})\geq\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g\bigl{(}\succ^{\prime}_{s},\succ_{-s}\bigr{)}(s,c^{\prime}).

(4)

An analogous condition is imposed when the roles of students and schools are interchanged.

3.3 Anonymity

Let $\pi_{S}:S\to S$ and $\pi_{C}:C\to C$ be a permutation of students and permutation of schools respectively. Denote by $\Pi_{S}$ and $\Pi_{C}$ the sets of all permutations. Given a school preference $\succ_{c}$ and a permutation $\pi_{S}$ , define $\rho_{C}(\succ_{c},\pi_{S})$ as the preference order obtained by renaming according to $\pi_{S}$ ; similarly, define $\rho_{S}(\succ_{s},\pi_{C})$ for student preferences.

For example, if $n=3$ , $(\pi_{S}(s))_{s\in S}=(3,1,2)$ and $3\succ_{c}2\succ_{c}1$ , then writing $\succ^{\prime}_{c}=\rho_{C}(\succ_{c},\pi_{S})$ yields $2\succ^{\prime}_{c}1\succ^{\prime}_{c}3$ . (Here, the permutation $(3,1,2)$ indicates that the name of student $1$ is replaced by $3$ , student $2$ by $1$ , and student $3$ by $2$ .)

We denote by $\rho_{C}(\succ_{C},\pi_{S})$ the profile obtained by applying $\rho_{C}$ to each school’s preference.

A randomized matching mechanism $g$ is said to be anonymous if for every $\succ\in P$ , for every $\pi_{S}\in\Pi_{S}$ , $\pi_{C}\in\Pi_{C}$ , and for every $s\in S$ , $c\in C$ , letting

\succ^{\prime}_{S}=\rho_{S}(\succ_{S},\pi_{C})\quad\text{and}\quad\succ^{\prime}_{C}=\rho_{C}(\succ_{C},\pi_{S}),

we have

g(\succ)(s,c)=g\Bigl{(}(\succ^{\prime}_{\pi_{S}(s)})_{s\in S},\,(\succ^{\prime}_{\pi_{C}(c)})_{c\in C}\Bigr{)}\bigl{(}\pi_{S}(s),\pi_{C}(c)\bigr{)}.

(5)

That is, permuting the names of agents does not affect the outcome.

3.4 Symmetry

When the number of students equals the number of schools (i.e., $n=m$ ), we say that a randomized matching mechanism $g$ is symmetric if for every $\succ\in P$ the following holds. For each student $i\in\{1,\dots,n\}$ , let $\succ^{\prime}$ be the profile obtained from $\succ$ by interchanging the roles of students and schools: whenever, in $\succ$ , student $i$ prefers school $j$ to school $j^{\prime}$ , in $\succ^{\prime}$ school $i$ prefers student $j$ to student $j^{\prime}$ (and similarly when swapping the roles). Then for every $(i,j)\in\{1,\dots,n\}^{2}$ , we require that

g(\succ)(i,j)=g(\succ^{\prime})(j,i).

(6)

This property ensures that the mechanism treats both sides of the market equally.

3.5 Nonwastefullness

A randomized matching mechanism $g$ is said to be nonwasteful if for every $\succ\in P$ and for every pair $(s,c)\in S\times C$ satisfying $s\succ_{c}\emptyset$ and $c\succ_{s}\emptyset$ , it holds that either

\sum_{c^{\prime}\in C}g(\succ)(s,c^{\prime})=1\quad\text{or}\quad\sum_{s^{\prime}\in S}g(\succ)(s^{\prime},c)=1.

3.6 Individual Rationality

A randomized matching mechanism $g$ is called individually rational if for every $\succ\in P$ and every $(s,c)\in S\times C$ , whenever $g(\succ)(s,c)>0$ , it follows that $s\succ_{c}\emptyset$ and $c\succ_{s}\emptyset$ .

4 The Optimization Problem for Matching Problems

In the following, we assume that every agent strictly prefers being matched with someone rather than remaining unmatched; that is, we assume

\forall s\in S,\;\forall c\in C:\quad c\succ_{s}\emptyset,\quad s\succ_{c}\emptyset.

Our objective is to design a strategy-proof matching mechanism that maximizes stability. We define the ”most stable” mechanism as the one that minimizes the average (or worst-case) stability violation as measured by (3). Hence, we consider the following optimization problem: {equationarray}llr gminimize & ∑≻∈P ∑(s,c)∈S×C max{ 1 - g(≻)(s, c) - ∑c’ ∈C : c’ ≻sc g(≻)(s, c’) - ∑s’ ∈S : s’ ≻cs g(≻)(s’, c), 0 }

subject to 0 ≤g(≻)(s, c) ≤1 ∀≻∈P, ∀s ∈S, ∀c ∈C

∑s ∈S g(≻)(s, c) ≤1 ∀≻∈P, ∀c ∈C

∑c ∈C g(≻)(s, c) ≤1 ∀≻∈P, ∀s ∈S

∑c’ ∈C : c’ ⪰sc g(≻)(s, c’) ≥∑c’ ∈C : c’ ⪰sc g(≻’s, ≻-s)(s, c’) ∀≻∈P, ∀≻’s ∈PS, ∀c ∈C

∑s’ ∈S : s’ ⪰cs g(≻)(s’, c) ≥∑s’ ∈S : s’ ⪰cs g(≻’c, ≻-c)(s’, c) ∀≻∈P, ∀≻’c ∈PC, ∀s ∈S Constraints (4) $\sim$ (4) ensure that $g$ is a valid matching mechanism, while (4) and (4) impose strategy-proofness. (If one replaces (4) by $g(\succ)(s,c)\in\{0,1\}$ , the mechanism is forced to be deterministic.) Since the feasible region is compact and the objective is linear (after suitable linearization of the maximum function), an optimal solution exists.

In this formulation the objective function represents the average stability violation (denoted by objective function $A$ ). Alternatively, one may change the objective to minimize

\max_{\succ\in P}\;\sum_{(s,c)\in S\times C}\max\Biggl{\{}1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c),\;0\Biggr{\}},

(7)

which corresponds to minimizing the worst-case stability violation (denoted by objective function $B$ ). In the latter case the mechanism is evaluated independently of the distribution over preference profiles.

Directly solving this optimization problem is extremely time-consuming and leads to results that are complex and difficult to interpret, since the number of variables is as large as $(3!)^{6}\cdot 3^{2}=419,904$ even in the case where $n=m=3$ . Therefore, to both accelerate the computation and facilitate interpretation, we now present two theorems.

The following two theorems show that, without loss of optimality, one may restrict attention to mechanisms that are anonymous and (when $n=m$ ) symmetric.

Theorem 1.

Any value of the objective function that is achievable by a strategy-proof randomized matching mechanism is also achievable by a strategy-proof and anonymous randomized matching mechanism. This holds for both objective functions $A$ and $B$ .

Proof.

Let $\succ\in P$ be given. Define $A(\succ)$ to be the set of all outcomes resulting from every possible permutation, that is,

A(\succ)=\Bigl{\{}\succ^{\prime}\in P:\succ^{\prime}=\Bigl{(}\bigl{(}\succ_{\pi_{S}(s)}\bigr{)}_{s\in S},\,\bigl{(}\succ_{\pi_{C}(c)}\bigr{)}_{c\in C}\Bigr{)}\Bigr{\}}.

Then, for any $\succ,\succ^{\prime}\in P$ , we have that $\succ^{\prime}\in A(\succ)$ if and only if $\succ\in A(\succ^{\prime})$ . Moreover, if $\succ^{\prime}$ does not belong to $A(\succ)$ then

A(\succ)\cap A(\succ^{\prime})=\emptyset.

Thus, there exist profiles $\succ^{1},\dots,\succ^{k}$ such that for any $i,j\in\{1,\dots,k\}$ with $i\neq j$ , we have

A(\succ^{i})\cap A(\succ^{j})=\emptyset,

and

\bigcup_{i=1}^{k}A(\succ^{i})=P.

Let $f$ be a strategy-proof probabilistic matching mechanism. We now define a mechanism $g$ as follows: For every $\succ\in P$ , every $s\in S$ , and every $c\in C$ , let

g(\succ)(s,c)=\frac{1}{|A(\succ)|}\sum_{\pi_{S}\in\Pi_{S},\,\pi_{C}\in\Pi_{C}}f\Bigl{(}\bigl{(}\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\bigr{)}_{s\in S},\,\bigl{(}\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\bigr{)}_{c\in C}\Bigr{)}\Bigl{(}\pi_{S}(s),\pi_{C}(c)\Bigr{)}.

(8)

In other words, $g$ returns the average matching probability over all permutations of the agents. We now show that $g$ is a strategy-proof and anonymous probabilistic matching mechanism that achieves the same objective value as $f$ .

(Anonymity) Let $\pi_{S},\pi^{\prime}_{S}\in\Pi_{S}$ be given. Then there exists a unique $\pi^{\prime\prime}_{S}\in\Pi_{S}$ such that

\pi^{\prime}_{S}\bigl{(}\pi_{S}(s)\bigr{)}=\pi^{\prime\prime}_{S}(s).

Similarly, for any $\pi_{C},\pi^{\prime}_{C}\in\Pi_{C}$ , there exists a unique $\pi^{\prime\prime}_{C}\in\Pi_{C}$ satisfying

\pi^{\prime}_{C}\bigl{(}\pi_{C}(c)\bigr{)}=\pi^{\prime\prime}_{C}(c).

For such $\pi_{S},\pi^{\prime}_{S},\pi^{\prime\prime}_{S},\pi_{C},\pi^{\prime}_{C},$ and $\pi^{\prime\prime}_{C}$ , we have

\rho_{S}\Bigl{(}\rho_{S}\bigl{(}\succ_{\pi^{\prime}_{S}(\pi_{S}(s))},\pi_{C}\bigr{)},\pi^{\prime}_{C}\Bigr{)}=\rho_{S}\bigl{(}\succ_{\pi^{\prime\prime}_{S}(s)},\pi^{\prime\prime}_{C}\bigr{)}.

An analogous property holds when the roles of $S$ and $C$ are interchanged. Therefore, for any $\pi_{S},\pi^{\prime}_{S}\in\Pi_{S}$ and $\pi_{C},\pi^{\prime}_{C}\in\Pi_{C}$ , there exists a unique pair $\pi^{\prime\prime}_{S},\pi^{\prime\prime}_{C}$ such that

	$\displaystyle f\left((\rho_{S}(\rho_{S}(\succ_{\pi^{\prime}(\pi(s))},\pi_{C}),\pi^{\prime}_{C}))_{s\in S},(\rho_{C}(\rho_{C}(\succ_{\pi^{\prime}(\pi(c))},\pi_{S}),\pi^{\prime}_{S}))_{c\in C}\right)(\pi^{\prime}_{S}(\pi_{S}(s)),\pi^{\prime}_{C}(\pi_{C}(c)))$
	$\displaystyle=f\left(\left(\rho_{S}(\succ_{\pi^{\prime\prime}_{S}(s)},\pi^{\prime\prime}_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi^{\prime\prime}_{C}(c)},\pi^{\prime\prime}_{S})\right)_{c\in C}\right)\left(\pi^{\prime\prime}_{S}(s),\pi^{\prime\prime}_{C}(c)\right)$

Thus, for any $\pi_{S},\pi_{C}$ , we have

	$\displaystyle g\left((\rho(\succ_{\pi_{S}(s)},\pi_{C}))_{s\in S},(\rho(\succ_{\pi_{C}(c)},\pi_{S}))_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{\pi^{\prime}_{S}\in\Pi_{S},\pi^{\prime}_{C}\in\Pi_{C}}f\left((\rho_{S}(\rho_{S}(\succ_{\pi^{\prime}(\pi(s))},\pi_{C}),\pi^{\prime}_{C}))_{s\in S},(\rho_{C}(\rho_{C}(\succ_{\pi^{\prime}(\pi(c))},\pi_{S}),\pi^{\prime}_{S}))_{c\in C}\right)(\pi^{\prime}_{S}(\pi_{S}(s)),\pi^{\prime}_{C}(\pi_{C}(c)))$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{\pi^{\prime\prime}_{S}\in\Pi_{S},\pi^{\prime\prime}_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi^{\prime\prime}_{S}(s)},\pi^{\prime\prime}_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi^{\prime\prime}_{C}(c)},\pi^{\prime\prime}_{S})\right)_{c\in C}\right)\left(\pi^{\prime\prime}_{S}(s),\pi^{\prime\prime}_{C}(c)\right)$
	$\displaystyle=g(\succ)(s,c)$

(Strategy-Proofness) Let $\succ^{\prime}_{s}\in P_{S}$ be an alternative preference for student $s$ , and denote by $\succ^{\prime}=(\succ^{\prime}_{s},\succ_{-s})$ . Since $f$ is strategy-proof, for every $\succ^{\prime}_{s}\in P_{S}$ and every $c\in C$ we have

\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}f(\succ)(s,c^{\prime})\geq\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}f(\succ^{\prime})(s,c^{\prime}).

Since this inequality remains valid under any permutation of the agents, it follows that for any $\pi_{S},\pi_{C}$ ,

	$\displaystyle\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)$
	$\displaystyle\geq\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq^{\prime}_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ^{\prime}_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ^{\prime}_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)(\pi_{S}(s),c^{\prime})$

Since $|A(\succ)|=|A(\succ^{\prime})|$ , it follows that for every $\succ\in P$ , every $s\in S$ , and every $\succ^{\prime}_{s}\in P_{S}$ , we have

	$\displaystyle\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g(\succ)(s,c^{\prime})$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f((\rho(\succ_{s},\pi_{C}))_{s\in S},(\rho(\succ_{c},\pi_{S})))_{c\in C}(\pi_{S}(s),c^{\prime})$
	$\displaystyle\geq\frac{1}{\|A(\succ^{\prime})\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f((\rho(\succ^{\prime}_{s},\pi_{C}))_{s\in S},(\rho(\succ^{\prime}_{c},\pi_{S})))_{c\in C}(\pi_{S}(s),c^{\prime})$
	$\displaystyle=\frac{1}{\|A(\succ^{\prime})\|}\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ^{\prime}_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ^{\prime}_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle=\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g(\succ^{\prime})(s,c^{\prime})$

A similar argument holds when interchanging the roles of $s$ and $c$ .

(Achievablity) We now show that the objective function value achievable by $f$ (with respect to objective function $A$ ) is also achievable by $g$ . First, observe that

	$\displaystyle 1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c)$
	$\displaystyle=1-\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s^{\prime}),\pi_{C}(c)\right)$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\Biggl{[}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right)\biggr{\}}\Biggr{]}$

Thus,

	$\displaystyle\max\left\{1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c),0\right\}$
	$\displaystyle=\max\Biggl{\{}\frac{1}{\|A(\succ)\|}\Biggl{[}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right)\biggr{\}}\Biggr{]},0\Biggr{\}}$
	$\displaystyle\leq\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\max\Biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right),0\Biggr{\}}$

Moreover, for every $\succ\in P$ , there is exactly one pair $\pi_{S},\pi_{C}$ such that

\succ=\Bigl{(}\bigl{(}\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\bigr{)}_{s\in S},\,\bigl{(}\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\bigr{)}_{c\in C}\Bigr{)}.

Therefore,

	$\displaystyle\sum_{\succ\in P}\max\left\{1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c),0\right\}$
	$\displaystyle=\sum_{\succ\in P}\max\Biggl{\{}\frac{1}{\|A(\succ)\|}\Biggl{[}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right)\biggr{\}}\Biggr{]},0\Biggr{\}}$
	$\displaystyle\leq\frac{1}{\|A(\succ)\|}\sum_{\succ\in P}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\max\Biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right),0\Biggr{\}}$
	$\displaystyle=\sum_{\succ\in P}\max\left\{1-f(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}f(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}f(\succ)(s^{\prime},c),0\right\}$

Hence,

	$\displaystyle\sum_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\left\{1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c),0\right\}$
	$\displaystyle\leq\sum_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\left\{1-f(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}f(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}f(\succ)(s^{\prime},c),0\right\}$

Next, we show that the worst-case value of the objective function $B$ achievable by $f$ is also achievable by $g$ . That is,

	$\displaystyle\max_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\left\{1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c),0\right\}$
	$\displaystyle=\max_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\Biggl{\{}\frac{1}{\|A(\succ)\|}\Biggl{[}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right)\biggr{\}}\Biggr{]},0\Biggr{\}}$
	$\displaystyle\leq\frac{1}{\|A(\succ)\|}\max_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\max\Biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right),0\Biggr{\}}$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\max_{\succ\in P}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\sum_{s\in S}\sum_{c\in C}\max\Biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right),0\Biggr{\}}$
	$\displaystyle\leq\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\max_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\Biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right),0\Biggr{\}}$
	$\displaystyle=\max_{\succ\in P}\sum_{s\in S}\sum_{c\in C}\max\left\{1-f(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}f(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}f(\succ)(s^{\prime},c),0\right\}$

∎

Theorem 2.

Suppose that $n=m$ . Then any objective value achievable by a strategy-proof randomized matching mechanism is also achievable by a strategy-proof and symmetric randomized matching mechanism. This holds for both objective functions $A$ and $B$ .

Proof.

Let $\succ\in P$ be given. Define a new preference profile $\succ^{\prime}$ as follows. For each student $i\in\{1,\dots,n\}$ and for any two schools $j,j^{\prime}\in\{1,\dots,n\}$ , if in $\succ$ student $i$ prefers school $j^{\prime}$ to school $j$ , then in $\succ^{\prime}$ we define that school $i$ prefers student $j^{\prime}$ to student $j$ . (A similar definition is applied when interchanging the roles of students and schools.)

Let $f$ be a strategy-proof probabilistic matching mechanism. For any $\succ\in P$ and for any $i,j\in\{1,\dots,n\}$ , define the mechanism $g$ by

g(\succ)(i,j)=\frac{1}{2}\Bigl{(}f(\succ)(i,j)+f(\succ^{\prime})(j,i)\Bigr{)}.

(9)

That is, $g$ outputs the average matching probability over the two assignments given by $f(\succ)$ and by $f(\succ^{\prime})$ , where in the latter the roles of students and schools are interchanged. We now show that $g$ is both strategy-proof and symmetric, and that it attains the same objective function value as $f$ .

(Symmetry)
We verify that $g$ satisfies symmetry. Observe that

	$\displaystyle g(\succ^{\prime})(j,i)$	$\displaystyle=\frac{1}{2}\left(f(\succ^{\prime})(j,i)+f(\succ)(i,j)\right)$
		$\displaystyle=g(\succ)(i,j)$

Thus, $g$ is symmetric.

(Strategy-Proofness)
Suppose that under the true preference profile $\succ$ student $i$ submits a false preference $\triangleright_{i}$ , and let $\triangleright$ denote the resulting profile. Next, define $\triangleright^{\prime}$ in an analogous manner as follows: in $\triangleright$ , for each student $i\in\{1,\dots,n\}$ , if student $i$ prefers school $j^{\prime}$ to school $j$ , then in $\triangleright^{\prime}$ we define that school $i$ prefers student $j^{\prime}$ to student $j$ (and the same rule applies when interchanging the roles of students and schools). Then, under $\succ^{\prime}$ if school $i$ receives the false preference $\triangleright_{i}$ , the resulting profile coincides with $\triangleright$ . Consequently, we have

	$\displaystyle 2\sum_{j^{\prime}\succ_{i}j}\left(g(\succ)(i,j)-g(\triangleright)(i,j)\right)$
	$\displaystyle=\sum_{j^{\prime}\succ_{i}j}\left(f(\succ)(i,j)+f(\succ^{\prime})(j,i)-f(\triangleright)(i,j)-f(\triangleright^{\prime})(j,i)\right)$
	$\displaystyle=\sum_{j^{\prime}\succ_{i}j}\left(f(\succ)(i,j)-f(\triangleright)(i,j)\right)+\sum_{j^{\prime}\succ_{i}j}\left(f(\succ^{\prime})(j,i)-f(\triangleright^{\prime})(j,i)\right)$
	$\displaystyle\geq 0$

Thus, $g$ is strategy-proof.

(Achievablity)
We now show that the objective function value (with respect to both objective functions $A$ and $B$ ) achieved by $f$ is also achievable by $g$ .

First, consider objective function $A$ . We have

	$\displaystyle 2\sum_{\succ\in P}\sum_{i}\sum_{j}\max\left\{1-g(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}g(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}g(\succ)(i^{\prime},j),0\right\}$
	$\displaystyle=\sum_{\succ\in P}\sum_{i}\sum_{j}\max\Biggl{\{}1-\left(f(\succ)(i,j)+f(\succ^{\prime})(j,i)\right)$
	$\displaystyle\quad-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}\left(f(\succ)(i,j^{\prime})+f(\succ^{\prime})(j^{\prime},i)\right)-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}\left(f(\succ)(i^{\prime},j)+f(\succ^{\prime})(j,i^{\prime})\right),0\Biggr{\}}$
	$\displaystyle\leq\sum_{\succ\in P}\sum_{i}\sum_{j}\Biggl{[}\max\Bigl{\{}1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\Bigr{\}}$
	$\displaystyle\quad+\max\Bigl{\{}1-f(\succ^{\prime})(j,i)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ^{\prime})(j^{\prime},i)-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ^{\prime})(j,i^{\prime}),0\Bigr{\}}\Biggr{]}$
	$\displaystyle=\sum_{\succ\in P}\sum_{i}\sum_{j}\Biggl{[}\max\Bigl{\{}1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\Bigr{\}}$
	$\displaystyle\quad+\max\Bigl{\{}1-f(\succ^{\prime})(j,i)-\sum_{j^{\prime}:j^{\prime}\succ^{\prime}_{i}j}f(\succ^{\prime})(j^{\prime},i)-\sum_{i^{\prime}:i^{\prime}\succ^{\prime}_{j}i}f(\succ^{\prime})(j,i^{\prime}),0\Bigr{\}}\Biggr{]}$
	$\displaystyle=2\sum_{\succ\in P}\sum_{i}\sum_{j}\max\left\{1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\right\}$

The last equality follows from the fact that $\succ^{\prime}$ corresponds one-to-one with $\succ$ . Hence, the objective function value of $f$ is achievable by $g$ .

Next, we show that the worst-case objective function value corresponding to objective function $B$ that is achievable by $f$ is also achievable by $g$ . In particular, we have

	$\displaystyle 2\max_{\succ\in P}\sum_{i}\sum_{j}\max\left\{1-g(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}g(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}g(\succ)(i^{\prime},j),0\right\}$
	$\displaystyle=\sum_{\succ\in P}\sum_{i}\sum_{j}\max\Biggl{\{}1-\left(f(\succ)(i,j)+f(\succ^{\prime})(j,i)\right)$
	$\displaystyle\quad-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}\left(f(\succ)(i,j^{\prime})+f(\succ^{\prime})(j^{\prime},i)\right)-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}\left(f(\succ)(i^{\prime},j)+f(\succ^{\prime})(j,i^{\prime})\right),0\Biggr{\}}$
	$\displaystyle\leq\max{\succ\in P}\sum_{i}\sum_{j}\Biggl{[}\max\Bigl{\{}1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\Bigr{\}}$
	$\displaystyle\quad+\max\Bigl{\{}1-f(\succ^{\prime})(j,i)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ^{\prime})(j^{\prime},i)-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ^{\prime})(j,i^{\prime}),0\Bigr{\}}\Biggr{]}$
	$\displaystyle=\max_{\succ\in P}\sum_{i}\sum_{j}\Biggl{[}\max\Bigl{\{}1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\Bigr{\}}$
	$\displaystyle\quad+\max\Bigl{\{}1-f(\succ^{\prime})(j,i)-\sum_{j^{\prime}:j^{\prime}\succ^{\prime}_{i}j}f(\succ^{\prime})(j^{\prime},i)-\sum_{i^{\prime}:i^{\prime}\succ^{\prime}_{j}i}f(\succ^{\prime})(j,i^{\prime}),0\Bigr{\}}\Biggr{]}$
	$\displaystyle\leq 2\max_{\succ\in P}\sum_{i}\sum_{j}\max\left\{1-f(\succ)(i,j)-\sum_{j^{\prime}:j^{\prime}\succ_{i}j}f(\succ)(i,j^{\prime})-\sum_{i^{\prime}:i^{\prime}\succ_{j}i}f(\succ)(i^{\prime},j),0\right\}$

Thus, the worst-case objective function value (i.e., the value of objective function $B$ ) achieved by $f$ is also achievable by $g$ . ∎

After taking a strategy-proof probabilistic matching mechanism and rendering it anonymous using the method described in the proof of Theorem 1, and subsequently making it symmetric according to the procedure in the proof of Theorem 2, the resulting mechanism is a convex combination of anonymous mechanisms. Hence, its anonymity is easily shown. Thus, by6 Theorems 1 and 2 we can restrict our search to anonymous and symmetric mechanisms (when $n=m$ ) without loss of optimality. This not only reduces computational time and memory requirements but also improves interpretability. In the subsequent optimization we include anonymity and symmetry as constraints.

5 Results

In the following we report computational results for the cases $n=m=2$ and $n=m=3$ .

5.1 The Case $n=m=2$

When there are two students and two schools, we find that there exists a deterministic matching mechanism that is both strategy-proof and stable.

⬇

1Input: Preference profile

\succ

2Output: Matching

r

4Set

r(s,c)=0

for each

(s,c)\in S\times C

5If there exists

(s,c)\in S\times C

satisfying

6 "student

s

and school

c

are each other’s top choice"

7then

8 set

r(s,c)\leftarrow 1

and

r(s^{\prime},c^{\prime})\leftarrow 1

, where

s^{\prime}

and

c^{\prime}

are the remaining agents.

9Else,

10 Let

c\in C

be the school most preferred by student 1.

11 Set

r(1,c)\leftarrow 1

, and assign the remaining student and school accordingly.

12End if.

13Return

r

Algorithm 1: Deterministic Matching for

n=m=2

That is, Algorithm 1 matches mutually top-preferred pairs if they exist; otherwise, it assigns the best available school to student 1 and matches the remaining pair. In fact, for $n=m=2$ , Algorithm 1 produces the same outcome as the student-proposing DA algorithm.

Lemma 1.

Algorithm 1 is strategy-proof and stable.

Proof.

First, note that if an agent is matched to his second-choice partner, misreporting his preferences cannot yield a match with his top choice. In Algorithm 1, if agent $i$ is matched with his second-choice, then either the top-choice pair exists (in which case misreporting is futile) or the top-choice is already assigned to another agent. Hence, truthful reporting is a dominant strategy.

Stability follows directly from the fact that mutually top-preferred pairs are always matched. ∎

5.2 The Case $n=m=3$

5.2.1 Deterministic Matching Mechanisms

When restricting attention to deterministic mechanisms, our computational search shows that a strategy-proof, non-wasteful, and anonymous deterministic matching mechanism does not exist when $n=m=3$ .

Result 1.

For $n=m=3$ , there is no deterministic matching mechanism that is simultaneously strategy-proof, non-wasteful, and anonymous.

Results 1 shows that if one demands strategy-proofness for deterministic mechanisms, then one must sacrifice anonymity, which is socially undesirable.

Result 2.

For $n=m=3$ , no deterministic matching mechanism that is strategy-proof can achieve a worst-case stability violation (objective function $B$ ) of at most $1$ .

In other words, every strategy-proof deterministic mechanism must have at least two blocking pairs in the worst case. The following Algorithm 2 is strategy-proof and achieves a worst-case violation of $2$ , thereby being optimal among deterministic mechanisms.

⬇

1Input: Preference profile

\succ

2Output: Matching

r

4Set

r(s,c)=0

for each

(s,c)\in S\times C

5Let

c\in C

be the school most preferred by student 1.

6Assign

r(1,c)\leftarrow 1

; remove student 1 and school

c

7If there exists

(s,c)

in the remaining set satisfying

8 "

c\succ_{s}c^{\prime}

and

s\succ_{c}s^{\prime}

" (with

s\neq s^{\prime}

and

c\neq c^{\prime}

)

9then

10 set

r(s,c)\leftarrow 1

and

r(s^{\prime},c^{\prime})\leftarrow 1

11Else,

12 Let

c\in C

be the school most preferred by student 2.

13 Set

r(2,c)\leftarrow 1

and assign

r(3,c^{\prime})\leftarrow 1

for the remaining school

c^{\prime}\neq c

14End if.

15Return

r

Algorithm 2: Optimal Deterministic Matching for

n=m=3

Lemma 2.

Algorithm 2 is strategy-proof, non-wasteful, and the number of blocking pairs at the worst-case is $2$ .

Proof.

The strategy-proofness is verified by noting that student 1 is always assigned his top choice, and for the remaining two students, the procedure reduces to Algorithm 1, which is strategy-proof. Non-wastefulness is immediate by construction.

Regarding stability, observe that student 1, being matched with his top choice, cannot form any blocking pair. Moreover, in the remaining assignment, only the pair involving the school chosen by student 1 may possibly form a blocking pair, and at most two such blocking pairs can occur. ∎

It is worth noting that while Algorithm 2 limits the number of blocking pairs to two, SD may yield up to four blocking pairs in the worst case. Moreover, Algorithm 2 extends naturally to cases where $n\geq 4$ (see Section 5.3). In our numerical comparison (see Table 1), Algorithm 2 consistently outperforms SD.

Mechanism	Average STV(stavility violation)	Worst-case STV	Average Waste
SD	0.6666	3.0000	0.0000
Algorithm 2	0.4166	2.0000	0.0000

Table 1: Comparison of SD and Algorithm 2

5.2.2 Randomized Matching Mechanisms

We also solve the optimization problem for randomized matching mechanisms under four settings: using objective function $A$ or $B$ , and with or without the non-wastefulness constraint. We compare the results with RSDs (RSD) as well as a symmetrized version of Algorithm 2 (denoted by Algorithm 2’). Here RSD is implemented in two variants: (1) by assigning random orderings to both students and schools (denoted RSD1) and (2) by assigning an ordering to one side only (denoted RSD2). Both RSD1 and RSD2 satisfy strategy-proofness, non-wastefulness, anonymity, and symmetry. Table 2 reports the average stability violation, worst-case stability violation, and average waste (computed as $3-\sum_{s\in S}\sum_{c\in C}r(s,c)$ ) for the various mechanisms.

Mechanism	Average STV	Worst-case STV	Average Waste
RSD1 (full ordering)	0.6478	1.3333	0.0000
RSD2 (one-side ordering)	0.6229	1.3333	0.0000
Obj. $A$ , no waste constraint	0.2286	0.6224	0.0249
Obj. $A$ , with waste constraint	0.2348	0.6455	0.0000
Obj. $B$ , no waste constraint	0.4218	0.5000	0.0505
Obj. $B$ , with waste constraint	0.3730	0.5000	0.0000
Algorithm 2’	0.4063	1.6666	0.0000

Table 2: Comparison of Optimal Mechanisms

5.3 Generalization to $n\geq 4$

Algorithm 2 may be extended to the general case by employing the following procedure.

⬇

1Input: Preference profile

\succ

and a fixed ordering

(i_{k})_{k=1}^{2n}

of the agents in

S\cup C

2Output: Matching

r

4Initialize

r(s,c)=0

for every

(s,c)\in S\times C

5Set

k=1

6While

|S|>2

do:

7 Let

i=i_{k}

8 If

i\notin S\cup C

, then set

k\leftarrow k+1

9 Else if

i\in S

, then

10 Let

j\in C

be the school most preferred by

i

11 Set

r(i,j)\leftarrow 1

, remove

i

from

S

and

j

from

C

12 Else if

i\in C

, then

13 Let

j\in S

be the student most preferred by

i

14 Set

r(j,i)\leftarrow 1

, remove

i

from

C

and

j

from

S

15 End if.

16 Set

k\leftarrow k+1

17End while.

18If there exists

(s,c)\in S\times C

satisfying

19 "

c\succ_{s}c^{\prime}

and

s\succ_{c}s^{\prime}

" (with

s\neq s^{\prime}

and

c\neq c^{\prime}

)

20then

21 set

r(s,c)\leftarrow 1

and

r(s^{\prime},c^{\prime})\leftarrow 1

22Else,

23 Let

i\in S\cup C

be the agent highest in the fixed ordering.

24 If

i\in S

, then

25 Let

j\in C

be the school most preferred by

i

26 Let

i^{\prime}\neq i

and

j^{\prime}\neq j

be the remaining agents.

27 Set

r(i,j)\leftarrow 1

and

r(i^{\prime},j^{\prime})\leftarrow 1

28 Else,

29 (Symmetric assignment.)

30 End if.

31End if.

32Return

r

Algorithm 3: Generalization of Algorithm 2

When the same ordering is used, the number of blocking pairs in the matching produced by Algorithm 3 is no larger than that in SD. This is because in Algorithm 3 the final four agents and those previously matched do not form blocking pairs, whereas under sequential dictatorship blocking pairs may arise. However, when one symmetrizes the mechanism (to enforce anonymity and symmetry) SD may sometimes yield lower stability violations, as evidenced by Table 2.

5.4 Simulation

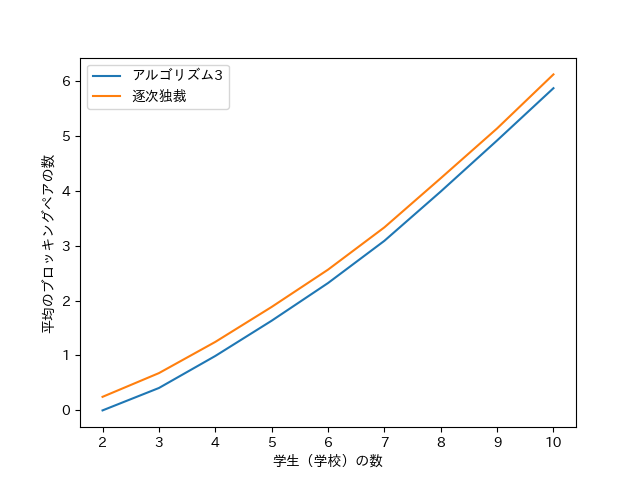
We conducted simulations to evaluate the performance of Algorithm 3 and SD as the number of agents increases. For each $n=m$ between 2 and 10, 1000 random preference profiles were generated and the average stability violation (computed as in (3)) was recorded.

In our implementation both Algorithm 3 and SD used the natural ordering of students 1, 2, $\dots$ , $n$ . Figure 2 shows that for all values of $n$ , Algorithm 3 produces approximately $0.25$ fewer blocking pairs on average than SD. (In each instance the difference is either $0$ or $1$ , with a probability of $0.25$ for a difference of $1$ .)

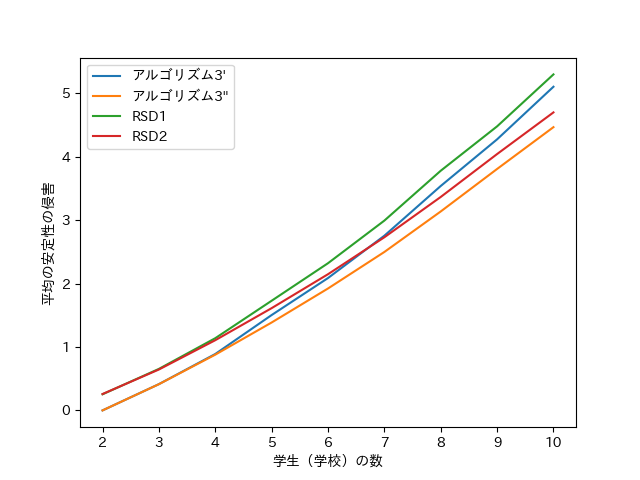
We further compared anonymized and symmetric randomized matching mechanisms. Two methods of symmetrization were considered: (1) assigning a random ordering independently to students and schools, and (2) assigning a random ordering to the union $S\cup C$ . Denote by Algorithm 3’ the version of Algorithm 3 symmetrized by (1) and by Algorithm 3” the version symmetrized by (2). Similarly, denote by RSD1 and RSD2 the corresponding variants of RSD. Figure 2 displays the simulation results. In both cases the (2) method produces lower average stability violation, and for every $n$ Algorithm 3 yields approximately $0.25$ less stability violation on average compared to SD.

Refer to caption — Figure 1: Comparison of Algorithm 3 and SD

6 Conclusion

In this paper we formulated the problem of designing a strategy-proof matching mechanism as an optimization problem, where the goal is to maximize stability (minimize the degree of stability violation) subject to strategy-proofness constraints. By incorporating anonymity and symmetry into our formulation, we are able to reduce the computational complexity and improve interpretability without loss of optimality.

For the case $n=m=2$ , we presented a deterministic algorithm that is both strategy-proof and stable. In the case $n=m=3$ , we demonstrated by computational means that no deterministic mechanism can guarantee fewer than two blocking pairs under strategy-proofness, and we proposed an optimal deterministic mechanism accordingly. For randomized matching mechanisms we provided computational evidence that mechanisms exist which reduce both the average and worst-case stability violations by roughly one-third compared to RSD. We also extended our approach to larger markets via a generalization of our algorithm and confirmed by simulation that our method consistently yields fewer blocking pairs.

The optimization techniques developed in this work are applicable to a wide range of small-scale matching problems (for instance, many-to-one matchings with capacity constraints or the roommates problem) and offer a new perspective on circumventing impossibility results by focusing on optimality in small markets.

Acknowledgements

I would like to express my sincere gratitude to Professor Michihiro Kandori for his continuous guidance and advice throughout this research. I am also very grateful to Professor Fuhito Kojima for his thoughtful suggestions that greatly contributed to the progress of this work. My thanks also go to Professors Hitoshi Matsushima and Satoru Takahashi for the many academic insights they shared during seminars and small-group discussions. Finally, I wish to thank all my colleagues and friends for their warm support and invaluable feedback, with special thanks to Keita Kuwahara and Kento Hashimoto.

References

AbdulkadiroÄlu and SÃ¶nmez [2003] Atila AbdulkadiroÄlu and Tayfun SÃ¶nmez. School choice: A mechanism design approach. Am. Econ. Rev., 93(3):729–747, May 2003.
Abdulkadiroglu and Sonmez [1998] Atila Abdulkadiroglu and Tayfun Sonmez. Random serial dictatorship and the core from random endowments in house allocation problems. Econometrica, 66(3):689, May 1998.
Ashlagi and Gonczarowski [2018] Itai Ashlagi and Yannai A Gonczarowski. Stable matching mechanisms are not obviously strategy-proof. J. Econ. Theory, 177:405–425, September 2018.
Aziz and Klaus [2019] Haris Aziz and Bettina Klaus. Random matching under priorities: stability and no envy concepts. Social Choice and Welfare, 53(2):213–259, 2019.
Bade and Root [2023] Sophie Bade and Joseph Root. Royal processions: Incentives, efficiency and fairness in two-sided matching. arXiv [econ.TH], January 2023.
Birkhoff [1946] Garrett Birkhoff. Three observations on linear algebra. Univ. Nac. Tacuman, Rev. Ser. A, 5:147–151, 1946.
Gale and Shapley [1962] D Gale and L S Shapley. College admissions and the stability of marriage. Am. Math. Mon., 69(1):9, January 1962.
Gale and Shapley [2014] David Gale and Lloyd S Shapley. College admissions and the stability of marriage. In Mircea Pitici, editor, The Best Writing on Mathematics 2014, pages 299–307. Princeton University Press, Princeton, December 2014.
Kumano [2013] Taro Kumano. Strategy-proofness and stability of the boston mechanism: An almost impossibility result. J. Public Econ., 105:23–29, September 2013.
Li [2019] S Li. Deep learning for two-sided matching markets. 2019.
Ravindranath et al. [2021] Sai Srivatsa Ravindranath, Zhe Feng, Shira Li, Jonathan Ma, Scott D Kominers, and David C Parkes. Deep learning for two-sided matching. arXiv [cs.GT], July 2021.
Roth [1982] Alvin E Roth. The economics of matching: Stability and incentives. Math. Oper. Res., 7(4):617–628, November 1982.
Roth et al. [1993] Alvin E Roth, Uriel G Rothblum, and John H Vande Vate. Stable matchings, optimal assignments, and linear programming. Math. Oper. Res., 18(4):803–828, November 1993.
Von Neumann [1953] John Von Neumann. A certain zero-sum two-person game equivalent to the optimal assignment problem. Contributions to the Theory of Games, 2(0):5–12, 1953.

	$\displaystyle\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g(\succ)(s,c^{\prime})$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f((\rho(\succ_{s},\pi_{C}))_{s\in S},(\rho(\succ_{c},\pi_{S})))_{c\in C}(\pi_{S}(s),c^{\prime})$
	$\displaystyle\geq\frac{1}{\|A(\succ^{\prime})\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\sum_{c^{\prime}\in C:c^{\prime}\rho(\succeq_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f((\rho(\succ^{\prime}_{s},\pi_{C}))_{s\in S},(\rho(\succ^{\prime}_{c},\pi_{S})))_{c\in C}(\pi_{S}(s),c^{\prime})$
	$\displaystyle=\frac{1}{\|A(\succ^{\prime})\|}\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ^{\prime}_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ^{\prime}_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle=\sum_{c^{\prime}\in C:c^{\prime}\succeq_{s}c}g(\succ^{\prime})(s,c^{\prime})$

	$\displaystyle 1-g(\succ)(s,c)-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}g(\succ)(s,c^{\prime})-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}g(\succ)(s^{\prime},c)$
	$\displaystyle=1-\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\succ_{s}c}\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c^{\prime})\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\succ_{c}s}\frac{1}{\|A(\succ)\|}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s^{\prime}),\pi_{C}(c)\right)$
	$\displaystyle=\frac{1}{\|A(\succ)\|}\Biggl{[}\sum_{\pi_{S}\in\Pi_{S},\pi_{C}\in\Pi_{C}}\biggl{\{}1-f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),\pi_{C}(c)\right)$
	$\displaystyle\quad-\sum_{c^{\prime}\in C:c^{\prime}\rho(\succ_{\pi_{S}(s)},\pi_{C})\pi_{C}(c)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(\pi_{S}(s),c^{\prime}\right)$
	$\displaystyle\quad-\sum_{s^{\prime}\in S:s^{\prime}\rho(\succ_{\pi_{C}(c)},\pi_{S})\pi_{S}(s)}f\left(\left(\rho_{S}(\succ_{\pi_{S}(s)},\pi_{C})\right)_{s\in S},\left(\rho_{C}(\succ_{\pi_{C}(c)},\pi_{S})\right)_{c\in C}\right)\left(s^{\prime},\pi_{C}(c)\right)\biggr{\}}\Biggr{]}$

Minimizing Instability in Strategy-Proof Matching Mechanism Using A Linear Programming Approach

Abstract

1 Introduction

2 Related Work

3 Preliminaries

3.1 Stability

3.2 Strategy-Proofness

3.3 Anonymity

3.4 Symmetry

3.5 Nonwastefullness

3.6 Individual Rationality

4 The Optimization Problem for Matching Problems

Theorem 1.

Proof.

Theorem 2.

Proof.

5 Results

5.1 The Case n=m=2n=m=2

Lemma 1.

Proof.

5.2 The Case n=m=3n=m=3

5.2.1 Deterministic Matching Mechanisms

Result 1.

Result 2.

Lemma 2.

Proof.

5.2.2 Randomized Matching Mechanisms

5.3 Generalization to n≥4n\geq 4

5.4 Simulation

6 Conclusion

Acknowledgements

References

5.1 The Case $n=m=2$

5.2 The Case $n=m=3$

5.3 Generalization to $n\geq 4$