Minimum numbers of Dehn colors of knots and -palette graphs
Abstract.
In this paper, we consider minimum numbers of colors of knots for Dehn colorings. In particular, we will show that for any odd prime number and any Dehn -colorable knot , the minimum number of colors for is at least . Moreover, we will define the -palette graph for a set of colors. The -palette graphs are quite useful to give candidates of sets of colors which might realize a nontrivially Dehn -colored diagram. In Appendix, we also prove that for Dehn -colorable knot, the minimum number of colors is .
Key words and phrases:
Knots, Dehn colorings, Minimum numbers of colors, -palette graphs2020 Mathematics Subject Classification:
57K10, 57K12Introduction
In knot theory, minimum numbers of colors for arc colorings have been studied in many papers (see [1, 2, 4, 5, 9, 10, 11] for example). We denote by the number for a Fox -colorable knot . As one of properties for , the following result is obtained in [8].
-
•
For any odd prime number and any Fox -colorable knot ,
Note that for the cases when is a composite number or is a link with multiple components, the similar results are known under some condition (see [6]).
On the other hand, a Dehn -coloring is well-known as one of region colorings of knot diagrams which is corresponding to a Fox -coloring. However, minimum numbers of colors for Dehn -colorings almost have not been studied yet.
In this paper, we will consider minimum numbers of colors of Dehn -colorable knots for an odd prime number . The number for a Dehn -colorable knot is denoted by . We show in Theorem 1.5 that
-
•
for any odd prime number and any Dehn -colorable knot ,
Moreover, we will define the -palette graph for a set of colors. The -palette graphs are quite useful to give candidates of sets of colors which might realize a nontrivially Dehn -colored diagram (see Theorem 5.1). In particular, in Theorem 5.3, we give the sets of colors which might realize a nontrivially Dehn -colored diagram for an odd prime number with . Furthermore, we show in Proposition 5.4 that there exists a knot with for some .
This paper is organized as follows: In Section 1, we review the definitions and some basic properties of Dehn colorings and minimum numbers of colors for Dehn colorings. Besides, our main result (Theorem 1.5) is stated in this section. Section 2 is devoted to setting up some extended coloring matrices which are used in Section 3. Theorem 1.5 is proven in Section 3. In Section 4, the -palette graph of a set of colors and that of a Dehn -colored diagram are defined. In Section 5, we give candidates of sets of colors each of which might realize a nontrivially Dehn -colored diagram by using the -palette graphs. Moreover in Appendix A, we show that for any Dehn -colorable knot .
1. Dehn colorings and minimum numbers of colors
In this paper, for a prime number , we denote by the cyclic group . When , read all the parts of this paper by replacing all and with .
Let be an odd prime number or . Let be a diagram of a knot and the set of regions of . A Dehn -coloring of is a map satisfying the following condition:
-
•
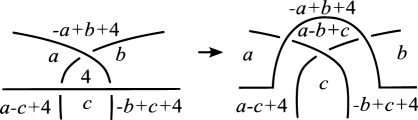
for each crossing with regions , and as depicted in Figure 1,
holds, where the region is adjacent to by an under-arc and is adjacent to by the over-arc.
We call the color of a region by . In this paper, as shown in the right of Figure 1, we represent a Dehn -coloring of a knot diagram by assigning the color to each region . We mean by a diagram given a Dehn -coloring , and call it a Dehn -colored diagram. We denote by the set of colors assigned to a region of by , that is . The set of Dehn -colorings of is denoted by . We remark that the number is an invariant of the knot .
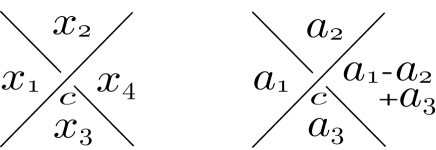
Let be a crossing of with regions , and as depicted in Figure 1. We say that of is trivially colored if
hold, and nontrivially colored otherwise. A Dehn -coloring of is trivial if each crossing of is trivially colored and nontrivial otherwise. We note that trivial -colorings are separated into two types: monochromatic colorings and checkerboard colorings with two colors. We call the former -trivial colorings and denote them by . We call the latter -trivial colorings and denote them by .
A knot is Dehn -colorable if has a Dehn -colored diagram such that is nontrivial.
For a semiarc of a Dehn -colored diagram , when the two regions and which are on the both side of have and for some , we call an -semiarc, where is regarded as a multiset when . Moreover, we call an arc including an -semiarc an -arc, where we note that the value does not depend on the choice of a semiarc included in .
Remark 1.1.
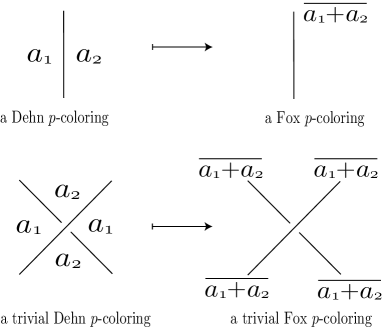
Fox colorings of knot diagrams have been well-studied for a long time. There is the -to- correspondence, given in the upper picture of Figure 2, from Dehn colorings to Fox colorings, where represent the colors of regions of a Dehn -colored diagram, represents the colors of arcs of the corresponding Fox -colored diagram, and we distinguish colors of regions for Dehn -colorings and those of arcs for Fox -colorings by putting a bar over a color of an arc as in Figure 2. Then a trivial (resp. nontrivial) Dehn -coloring corresponds to a trivial (resp. nontrivial) Fox -coloring as depicted in the lower picture of Figure 2. We also note that a knot is Dehn -colorable if and only if is Fox -colorable.
The set can be regarded as a -module with the scalar product and the addition with
Moreover, since for any , the constant map is a kind of Dehn -coloring, the map
is also a Dehn -coloring, and thus, the transformations are closed in . In particular, a transformation with is called a regular affine transformation on . Two Dehn -colorings are affine equivalent (written ) if they are related by a regular affine transformation on , that is, for some and .
A regular affine transformation on the -module is defined by for some and . Two subsets are affine equivalent (written ) if they are related by a regular affine transformation on , that is, for some and . We note that since any regular affine transformation is a bijection, holds if .
Lemma 1.2.
-
(1)
Let . Then we have
Hence we have
-
(2)
Let , and we assume that . Then there exists such that if and only if there exists such that .
Proof.
(1) A regular affine transformation on induces the regular affine transformation on with .
(2) Assume that holds for some regular affine transformation on . When there exists such that , we have the Dehn -coloring . Then holds.
∎
Remark 1.3.
(1) of Lemma 1.2 implies that when we focus on the number of colors used for each nontrivial Dehn -coloring of a diagram , we may consider only the number of colors used for a representative of each affine equivalence class for nontrivial Dehn -colorings of .
(2) of Lemma 1.2 implies that when we focus on the sets of colors each of which might be used for a nontrivial Dehn -coloring of a diagram, we may consider only representatives of the affine equivalence classes on the subsets of .
In this paper, we focus on the minimum number of colors.
Definition 1.4.
The minimum number of colors of a knot for Dehn -colorings is the minimum number of distinct elements of which produce a nontrivially Dehn -colored diagram of , that is,
We denote it by .
The next theorem is our main result, which will be proven in Section 3.
Theorem 1.5.
Let be an odd prime number. For any Dehn -colorable knot , we have
that is,
2. Extended coloring matrices
From now on, for an integer matrix , means the rank of regarded as a matrix on . Note again that is replaced with .
Let be a diagram of a knot . Let be the regions, and the crossings of . We set an arbitrary orientation for .
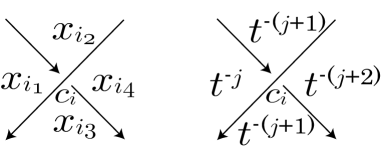
For each crossing , we set the equation
where are the regions around such that is in the right side of both of over- and under-arcs, is adjacent to by an under-arc and is adjacent to by the over-arc (see the left of Figure 3), and where we regard as variables of the equation. We then have the simultaneous equations
that is
| (2.1) |
The coefficient matrix is called the Dehn coloring matrix of as an unoriented diagram since the -module of solutions of (2.1) for an odd prime or is isomorphic to the -module by the isomorphism which sends a solution to the Dehn coloring such that for each .
It is known that the knot group of , which is the fundamental group of , has the presentation
| (2.2) |
where for each crossing as in the left of Figure 3, we set the relator by
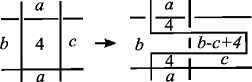
Let denote the Alexander matrix of obtained from the above presentation (2.2) by using the Fox calculus (see [3]), that is , where is the Fox derivative with , is the projection , and is the abelianization such that a meridian element is sent to . For the th row vector of , the th entry is if or , if or , and otherwise, which follows from
(refer to the right of Figure 3), where we here suppose that differ from each other. Thus we have
The greatest common divisor of all the ()-minors of is called the determinant of , which is denoted by .
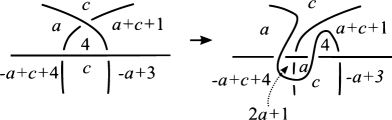
For an odd prime number , we suppose that there exists a nontrivial Dehn -coloring, say , satisfying that for some such that , , holds. Then we set
where for the last row vector, the th and th entries are and , respectively, and the other entries are .
Let us consider the ranks of the matrices , and .
For an odd prime or , we have at least two linearly independent solutions of (2.1) on : one, denoted by , is corresponding to the 1-trivial Dehn -coloring with , and the other, denoted by , is corresponding to a 2-trivial Dehn -coloring with and . Thus we can see that .
Besides, it is well-known that , which gives , and hence, . Considering this property together with the fact that , we have , and indeed, the -module of solutions of (2.1) on is spanned by two vectors and .
On the other hand, for an odd prime , if admits a nontrivial Dehn -coloring , then there exists a solution of (2.1) on such that , and are linearly independent. Hence, for this case, .
For the matrix , as mentioned above. For an odd prime or , note that the -module of solutions of the simultaneous equations
| (2.3) |
on is a submodule of that of (2.1) on . Any vector (, ) can not be a solution of (2.3) on since any solution of (2.3) needs to satisfy , while is a linearly independent solution of (2.3) on . This implies that the -module of solutions of (2.3) on is spanned by .
On the other hand, for an odd prime , if admits a nontrivial Dehn -coloring such that , then there exists a solution of (2.3) on such that and are linearly independent. Hence, for this case, .
For the matrix , we note that it is defined for a given odd prime , a Dehn -coloring , and . Note that the - (resp. -)module of solutions of the simultaneous equations
| (2.4) |
on (resp. ) is a submodule of that of (2.1) on (resp. ).
Any vector (, ) can not be a solution of (2.4) on (resp. ) since any solution of (2.4) needs to satisfy , while is a linearly independent solution of (2.4) on (resp. ). Hence the -module of solutions of (2.4) on is spanned by , which implies that .
On the other hand, since is a nontrivial -coloring, there exists a solution of (2.4) on , and and are linearly independent. Hence, .
As a summary, we have the following properties:
Lemma 2.1.
Let be an odd prime number.
-
(1)
Suppose that admits a nontrivial Dehn -coloring . Then we have
In particular, the module of solutions of (2.1) on is spanned by and , and that on is spanned by at least three linearly independent solutions: , and .
-
(2)
Suppose that admits a nontrivial Dehn -coloring with . Then we have
In particular, the module of solutions of (2.3) on is spanned by , and that on is spanned by at least two linearly independent solutions: and .
-
(3)
Suppose that admits a nontrivial Dehn -coloring satisfying that , for some with . Then we have
In particular, the module of solutions of (2.4) on is spanned by , and that on is spanned by at least two linearly independent solutions: and .
3. Proof of Theorem 1.5
Lemma 3.1.
Let be an integer square matrix of order which satisfies the following condition:
-
()
for each , the multiset of nonzero entries of the th row vector of is , , , , , , , , , , , , , or .
Then we have
Proof.
We prove this lemma by the induction of and the cofactar expantion of a matrix. In the case that , since or , it holds that .
Let . We assume that any square matrix , of order , satisfying the condition has .
We first note that the following transformations of matrices do not affect whether the condition is satisfied.
-
•
Compose a matrix from a matrix satisfying the condition ().
-
•
Remove a row and a column from a matrix satisfying the condition ().
Put . We will show by cases.
(i) In the case that has a row whose multiset of nonzero entries is or , the cofactor expantion of the row induces .
(ii) In the case that has a row whose multiset of nonzero entries is or , the cofactor expantion of the row induces .
(iii) In the case that has a row whose multiset of nonzero entries is , or , the cofactor expansion of the row induces .
(iv) In the case that has a row whose multiset of nonzero entries is , , or , assume that the -entry is or for some . Then we can see the determinant as follows.
Thus, this case comes down to the case (iii), and hence, we have .
(v) In the case that has a row whose multiset of nonzero entries is , assume that the -entry is or for some . Then we can see the determinant as follows.
Thus, this case comes down to the case (ii), and hence, we have .
(vi) In the case that has a row whose multiset of nonzero entries is or , we can see the determinant as follows.
Since the matrices and satisfy the condition , we obtain .
(vii) Lastly we consider the case that has a row whose multiset of nonzero entries is . We then have
This case comes down to the case (vi), and hence, we have .
This completes the proof. ∎
Let be an odd prime integer. Let be a diagram of a knot . Let be the regions, and the crossings of . Let and be the - and -trivial Dehn -coloring, respectively, such that , and . Let be a nontrivial Dehn -coloring of .
Lemma 3.2.
Suppose that for any such that , holds. Then we have
Proof.
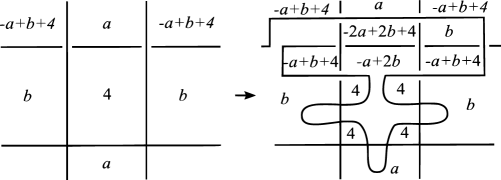
Put and , where is the matrix constructed in Section 2 by setting an arbitrary orientation for . By Lemma 1.2 and Remark 1.3, we may assume that by replacing the Dehn -coloring by a regular affine transformation if necessary. Put and . Then by (2) of Lemma 2.1,
and the simultaneous equations have the linearly independent solution on , and two linearly independent solutions and on .
We put and . We transform , , and as follows. Suppose that satisfy and . For , we add to and delete . For , and , we delete , and , respectively. We then have the new equation
and the solutions
on , and
on and , where means that the entry is removed. For the resultant matrix obtained from and the resultant column vectors obtained from , and , we repeat the same transformations unless the number of column vectors for the resultant matrix originally from is . Then, as a consequence, we have the -matrix , the column vectors , and , where is the column vector originally from .
Remark that . We can easily see that and , and is a linearly independent solution of on , and and are linearly independent solutions on . Hence, there exists an -submatrix of such that and , which implies that .
Furthermore, since we have by Lemma 3.1, it holds that . This gives the conclusion . ∎
Lemma 3.3.
Suppose that there exists with such that and . Then we have
Proof.
We prove this lemma in much the same way as Lemma 3.2. Put and , where is the matrix constructed in Section 2 by setting an arbitrary orientation for . Put and . Then by (3) of Lemma 2.1,
and the simultaneous equations have the linearly independent solution on , and two linearly independent solutions and on .
We put and . We transform , , and as follows. Suppose that satisfy and . For , we add to and delete . For , and , we delete , and , respectively. We then have the new equation
and the solutions
on , and
on and . For the resultant matrix obtained from and the resultant column vectors obtained from , and , we repeat the same transformations unless the number of column vectors for the resultant matrix originally from is . Then, as a consequence, we have the -matrix , the column vectors , and , where is the column vector originally from .
We can easily see that , and is a linearly independent solution of on , and and are linearly independent solutions on .
Hence, there exists an -submatrix of such that and , which implies that . Furthermore, since we have by Lemma 3.1, it holds that . This gives the conclusion .
∎
4. -palette graphs
Let be an odd prime number, and let with . Set , where is regarded as the multiset when .
For , we set
We note that this relation on is an equivalence relation. We denote by the equivalence class of .
Definition 4.1.
The -palette graph of is the simple graph composed of the vertex set
and the edge set satisfying that
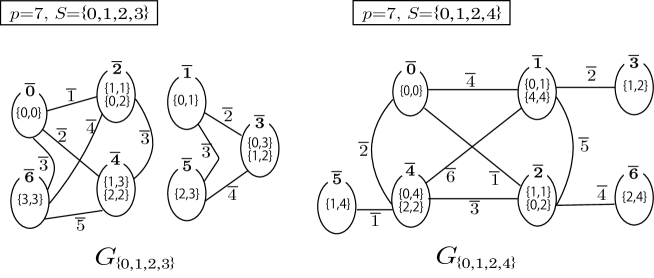
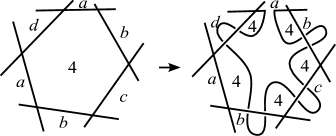
where means that is an edge connecting the vertices and . We attach the label to the edge between and (see Figure 4 for example).
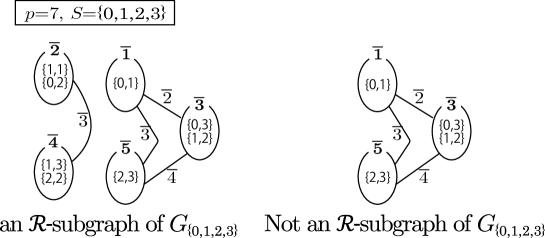
Let be the -palette graph of . A graph is an -subgraph of if is a subgraph of , and
holds, where is the label of (see Figure 5 for example).
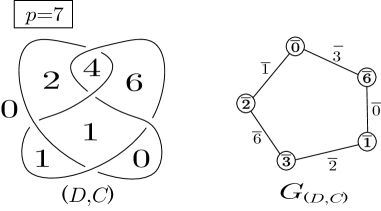
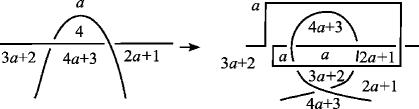
Let be a nontrivially Dehn -colored diagram of a knot. The -palette graph of is an -subgraph of composed of the vertex set
and the edge set satisfying that
As in the case of , we attach the label to the edge between and (see Figure 6 for example).
We remark that for a -arc was defined just a symbol, but is regarded as an equivalence class as in Definition 4.1 when it represents a vertex.
We also remark that this -palette graph of is isomorphic to the palette graph of defined in [8], where is the Fox -coloring corresponding to as shown in Remark 1.1. Furthermore, it was shown in [8] that the palette graph of is connected and has at least vertices.
5. Evaluations of by -palette graphs
Let be an odd prime number.
The next theorem can be used to evaluate the minimum number of colors of knots or select some sets of colors, as candidates, each of which might be the set of colors for a nontrivial Dehn -coloring of a knot diagram.
Theorem 5.1.
Let . If for some nontrivially Dehn -colored diagram of a knot, the -palette graph includes a connected -subgraph with at least vertices.
Proof.
This is evident because includes and as remarked in the previous section, is connected and has at least vertices. ∎
Example 5.2.
For any subset such that , the -palette graph includes no connected -subgraph with at least vertices. This and Theorem 5.1 imply that for any Dehn -colorable knot .
Any subset of with four elements is affine equivalent to either or . We note that by Lemma 1.2 and Remark 1.3, when we select candidates of sets of four colors each of which might be the set of colors for a nontrivially Dehn -colored diagram of a knot, it suffices to discuss only the representatives of the affine equivalence classes, that is and . As shown in the right of Figure 4, the -palette graph clearly has a connected -subgraph with at least vertices, which is itself for example. On the other hand, the -palette graph depicted in the left of Figure 4 does not include a connected -subgraph with at least vertices. Therefore, if there exists a nontrivially Dehn -colored diagram for a knot with , then is affine equivalent to , and moreover, there exists a Dehn -coloring of with and .
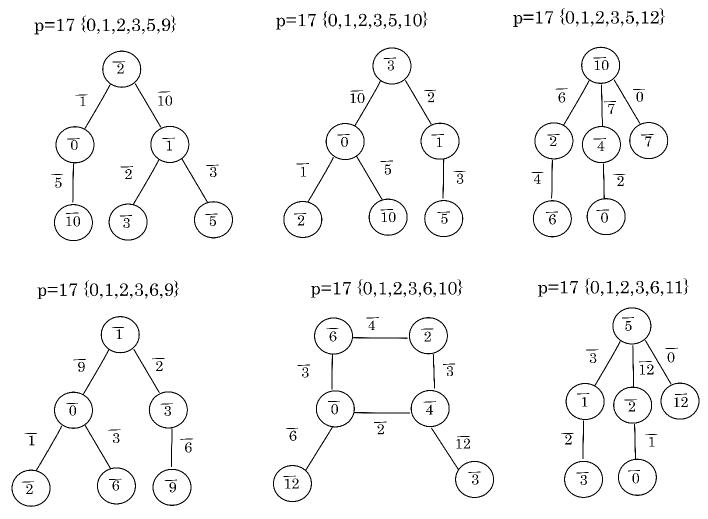
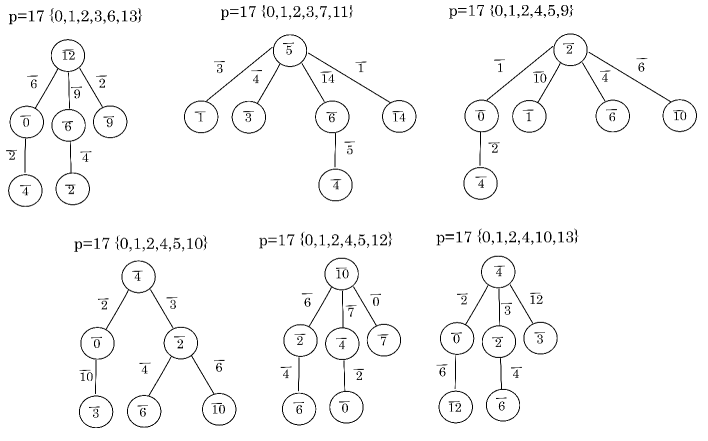
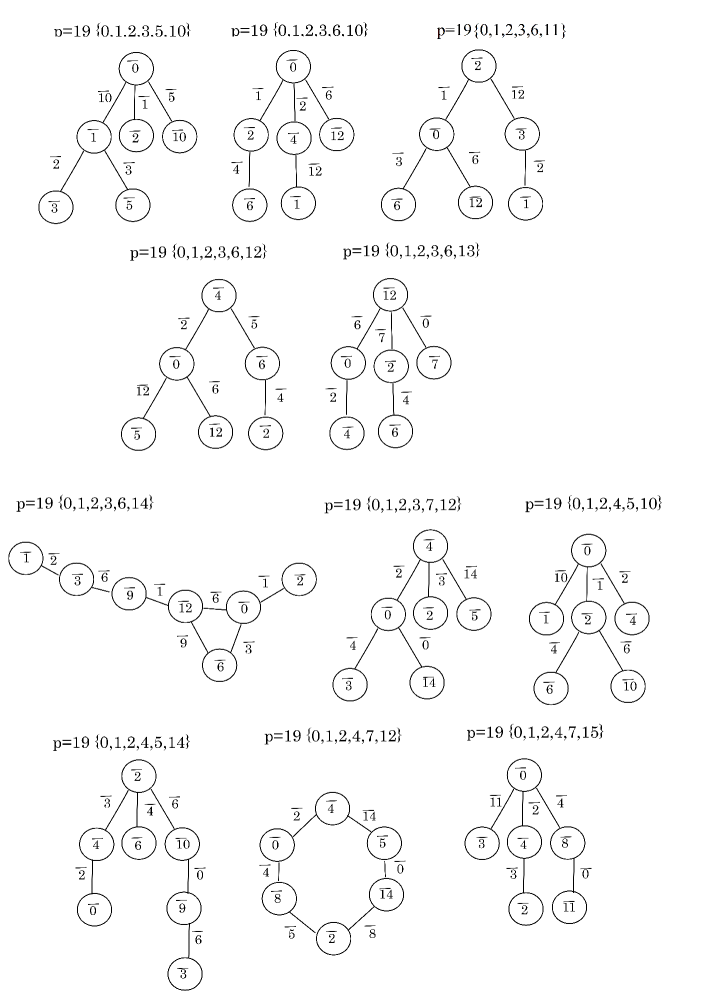
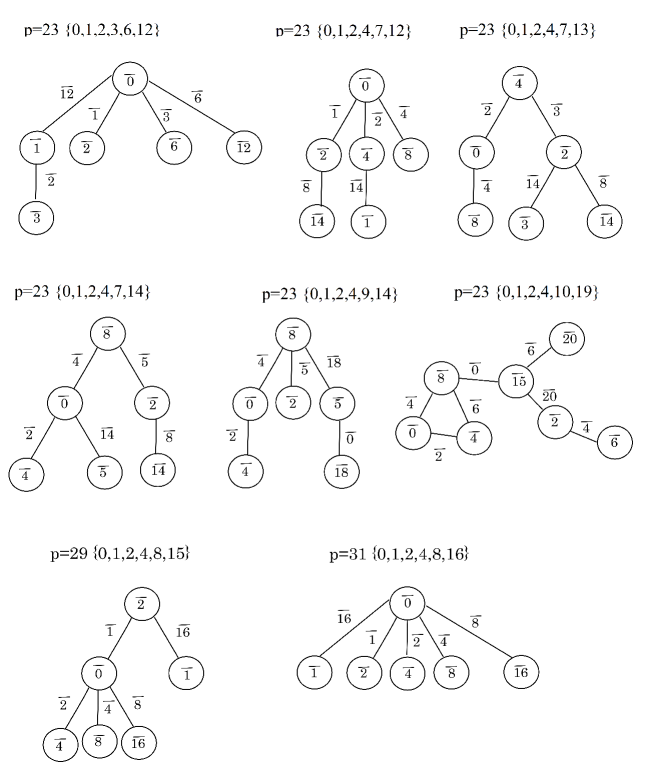
Similarly as Example 5.2, for each odd prime with , we can give the candidates of colors by using -palette graphs, where is the lower bound of the evaluation formula of Theorem 1.5. The next theorem gives the results.
Theorem 5.3.
Let be an odd prime number with .
-
(1)
There is no subset with at most elements such that the -palette graph includes a connected -subgraph with at least vertices. This implies that
for any Dehn -colorable knot .
-
(2)
If there exists a nontrivially Dehn -colored diagram of a knot such that , then
-
(i)
when ,
-
(ii)
when ,
-
(iii)
when ,
-
(iv)
or when ,
-
(v)
when ,
-
(vi)
, , , , , , , , , , , or when ,
-
(vii)
, , , , , , , , , , or when ,
-
(viii)
, , , , , or when ,
-
(ix)
when , and
-
(x)
when .
-
(i)
Proof.

We have the following proposition.
Proposition 5.4.
For each odd prime number with and , there exists a Dehn -colorable knot with .
Proof.
For (resp. ), the diagram illustrated in Figure 13 (resp. 13, 15, 15, 17, 17, 19, 19) admits the Dehn -coloring with colors. Hence, from these properties and Theorem 1.5, we can see that there exists a knot with for each .
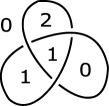
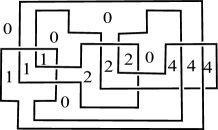
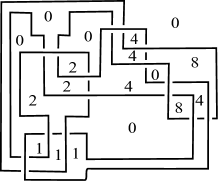
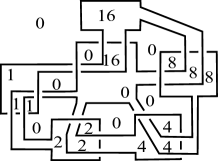
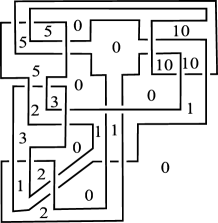
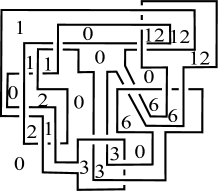
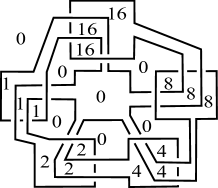
∎
Remark 5.5.
For or , there is no Dehn -colorable knot with . This result will be shown in our next paper [7].
Remark 5.6.
The following properties hold.
-
(1)
When , any -colorable knot has .
-
(2)
When , any -colorable knot has .
The proof of (1) is left as an exercise to the reader. We give the proof of (2) in Appendix A.
Appendix A
Proof of Remark 5.6 (2).
In this proof, an -gon means a region bounded by semiarcs.
Let be any nontrivially Dehn -colored diagram of a knot. We may construct a Dehn -colored diagram with four colors by removing regions with the color from in the following steps.
-
•
(Step 1) Remove crossings that have four or two regions colored by .
-
•
(Step 2) Remove -gons colored by for .
-
•
(Step 3) Remove -, and -gons colored by .
In this proof, suppose that are colors with , , .
(Step 1) First, we remove crossings that have only the color by the move depicted by Figure 20, where we note that there exists a region colored by some .
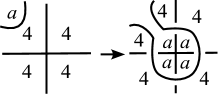
Next, we remove -semiarcs by the moves as depicted in Figures 22–25, where the situation around each -semiarc is represented by one of Figures 22–25.
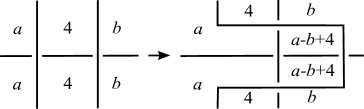
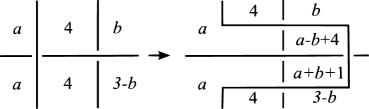
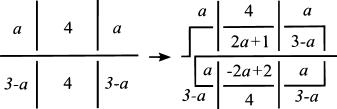
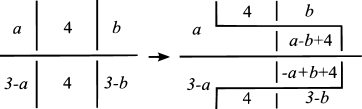
Here, we note that
| for Figure 22, | ||
| for Figure 22, | ||
| for Figure 24, | ||
| for Figure 24, | ||
| for Figure 25 |
from and .
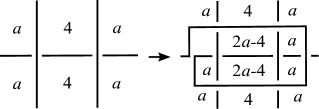
Next we delete crossings that have two regions colored by s diagonally as the following move depicted in Figure 26. Here we note that there exists a crossing which has four regions colored by and near an -semiarc.

Here we obtain the color that is not equal to from .
Thus, for the resultant Dehn -colored diagram, there exist no crossings that have four or two regions colored by .
(Step 2) For any -gon, say , colored by with , we focus on an -semiarc for some , say , on the boundary of . As in Figure 27, we move the semiarc by RII-moves with each semiarc on the boundary of which is not an -semiarc, where we perform the RII-moves as goes under each semiarc. Here, the 2-gons with no label in the right of Figure 27 are not colored by . Thus, we can delete the -gon with the color .
We note that the obtained new regions colored by are -, -, -gons such that the color is not appeared in the neighborhood of the regions. We also note that each -gon colored by is as depicted in the left of Figure 28.
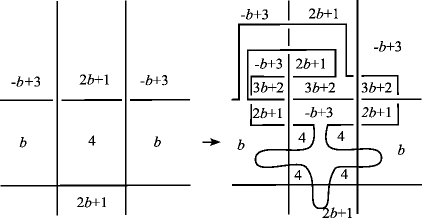
Here, we note that
from , ; , and , respectively, and the 2-gons with no label in the right of Figures 29 and 30 are not colored by .
Thus, for the resultant Dehn -colored diagram, each region colored by is a - or -gon around which the color is not appeared.
(Step 3) Now we consider -gons colored by , where we note that such -gons are as depicted in the left of Figure 31, the left of Figure 32 or the mirror images for some distinct .
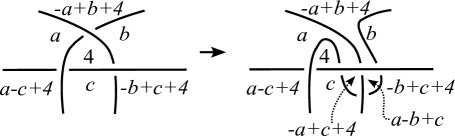
Here, we note that
because are distinct. Although the new -gon labeled by might be colored by , by considering the case of 3-gons in the left of Figure 32 or the mirror image, the -gon with the color can be removed. As for the mirror images of the -gons in the left of Figure 31, they are also removed by taking the mirror of the same move.
Next we remove -gons as depicted in the left of Figure 32 by the move shown in Figure 32 if and Figure 33 if .
Here, we note
because are distinct and . As for the mirror images of the -gons in the left of Figure 32, they are also removed by taking the mirror of the same moves.
Next let us consider the case of -gons colored by , where we note that such -gons are as depicted in the left of Figure 34, the left of Figure 35 or the mirror image for some .
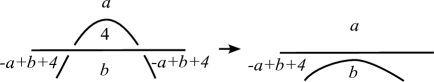
Here, note that
from . As for the -gons as depicted in the left of Figure 35, we remove them by the move as shown in Figure 35 if and , Figure 36 if (and ), and Figure 37 if (and ).
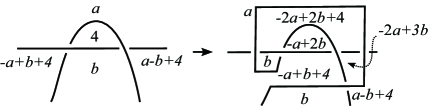
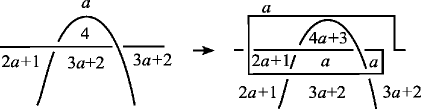
Here, we note that
because are distinct and . As for the mirror images of the -gons in the left of Figure 35, they are also removed by taking the mirror of the same moves.
The resultant diagram has no region colored by . This completes the proof. ∎
Acknowledgments
The authors wish to express their thanks to Professor Shin Satoh for several helpful comments on Theorem 5.1 and the property . The second author was supported by JSPS KAKENHI Grant Number 21K03233.
References
- [1] H. Abchir, M. Elhamdadi and S. Lamsifer, On the minimum number of Fox colorings of knots, Grad. J. Math. 5 (2020), no. 2, 122–137.
- [2] F. Bento and P. Lopes, The minimum number of Fox colors modulo 13 is 5, Topology Appl. 216 (2017), 85–115.
- [3] R. H. Crowell and R. H. Fox, Introduction to knot theory, Graduate Texts in Mathematics, No. 57. Springer-Verlag, New York-Heidelberg, 1977. x+182 pp.
- [4] Y. Han and B. Zhou, The minimum number of coloring of knots, J. Knot Theory Ramifications 31 (2022), no. 2, Paper No. 2250013, 55 pp.
- [5] F. Harary and L. H. Kauffman, Knots and graphs. I. Arc graphs and colorings, Adv. Appl. Math. 22(3) (1999), 312–337.
- [6] K. Ichihara and E. Matsudo, A lower bound on minimal number of colors for links, Kobe J. Math. 33 (2016), no. 1-2, 53–60.
- [7] E. Matsudo, K. Oshiro and G. Yamagishi, Minimum numbers of Dehn colors of knots and symmetric local biquandle cocycle invariants, preprint.
- [8] T. Nakamura, Y. Nakanishi, and S. Satoh, The pallet graph of a Fox coloring, Yokohama Math. J. 59 (2013), 91–97.
- [9] T. Nakamura, Y. Nakanishi, and S. Satoh, 11-colored knot diagram with five colors, J. Knot Theory Ramifications 25 (2016), no. 4, Paper No. 1650017, 22 pp.
- [10] K. Oshiro, Any 7-colorable knot can be colored by four colors, J. Math. Soc. Japan 62(3) (2010) 963–973.
- [11] S. Satoh, 5-colored knot diagram with four colors, Osaka J. Math. 46 (2009), no. 4, 939–948.