Mixed Nash Equilibria in the Adversarial Examples Game
Abstract
This paper tackles the problem of adversarial examples from a game theoretic point of view. We study the open question of the existence of mixed Nash equilibria in the zero-sum game formed by the attacker and the classifier. While previous works usually allow only one player to use randomized strategies, we show the necessity of considering randomization for both the classifier and the attacker. We demonstrate that this game has no duality gap, meaning that it always admits approximate Nash equilibria. We also provide the first optimization algorithms to learn a mixture of classifiers that approximately realizes the value of this game, i.e. procedures to build an optimally robust randomized classifier.
1 Introduction
Adversarial examples [6, 34] are one of the most dizzling problems in machine learning: state of the art classifiers are sensitive to imperceptible perturbations of their inputs that make them fail. Last years, research have concentrated on proposing new defense methods [24, 25, 13] and building more and more sophisticated attacks [18, 22, 11, 15]. So far, most defense strategies proved to be vulnerable to these new attacks or are computationally intractable. This asks the following question: can we build classifiers that are robust against any adversarial attack?
A recent line of research argued that randomized classifiers could help countering adversarial attacks [17, 40, 28, 39]. Along this line, [27] demonstrated, using game theory, that randomized classifiers are indeed more robust than deterministic ones against regularized adversaries. However, the findings of these previous works are dependent on the definition of adversary they consider. In particular, they did not investigate scenarios where the adversary also uses randomized strategies, which is essential to account for if we want to give a principled answer to the above question. Previous works studying adversarial examples from the scope of game theory investigated the randomized framework (for both the classifier and the adversary) in restricted settings where the adversary is either parametric or has a finite number of strategies [31, 26, 8]. Our framework does not assume any constraint on the definition of the adversary, making our conclusions independent on the adversary the classifiers are facing. More precisely, we answer the following questions.
Q1: Is it always possible to reach a Mixed Nash equilibrium in the adversarial example game when both the adversary and the classifier can use randomized strategies?
A1: We answer positively to this question. First we motivate in Section 2 the necessity for using randomized strategies both with the attacker and the classifier. Then, we extend the work of [29], by rigorously reformulating the adversarial risk as a linear optimization problem over distributions. In fact, we cast the adversarial risk minimization problem as a Distributionally Robust Optimization (DRO) [7] problem for a well suited cost function. This formulation naturally leads us, in Section 3, to analyze adversarial risk minimization as a zero-sum game. We demonstrate that, in this game, the duality gap always equals , meaning that it always admits approximate mixed Nash equilibria.
Q2: Can we design efficient algorithms to learn an optimally robust randomized classifier?
A2: To answer this question, we focus on learning a finite mixture of classifiers. Taking inspiration from robust optimization [33] and subgradient methods [9], we derive in Section 4 a first oracle algorithm to optimize over a finite mixture. Then, following the line of work of [16], we introduce an entropic reguralization which allows to effectively compute an approximation of the optimal mixture. We validate our findings with experiments on a simulated and a real image dataset, namely CIFAR-10 [21].
2 The Adversarial Attack Problem
2.1 A Motivating Example
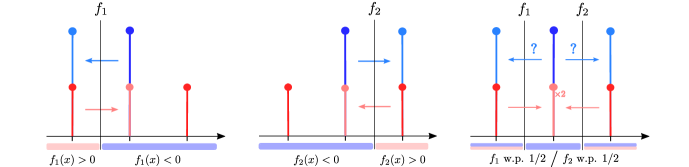
Consider the binary classification task illustrated in Figure 1. We assume that all input-output pairs are sampled from a distribution defined as follows
Given access to , the adversary aims to maximize the expected risk, but can only move each point by at most on the real line. In this context, we study two classifiers: and 111 is misclassified by if and only if . Both and have a standard risk of . In the presence of an adversary, the risk (a.k.a. the adversarial risk) increases to . Here, using a randomized classifier can make the system more robust. Consider where w.p. and otherwise. The standard risk of remains but its adversarial risk is . Indeed, when attacking , any adversary will have to choose between moving points from to or to . Either way, the attack only works half of the time; hence an overall adversarial risk of . Furthermore, if knows the strategy the adversary uses, it can always update the probability it gives to and to get a better (possibly deterministic) defense. For example, if the adversary chooses to always move to , the classifier can set w.p. to retrieve an adversarial risk of instead of .
Now, what happens if the adversary can use randomized strategies, meaning that for each point it can flip a coin before deciding where to move? In this case, the adversary could decide to move points from to w.p. and to otherwise. This strategy is still optimal with an adversarial risk of but now the classifier cannot use its knowledge of the adversary’s strategy to lower the risk. We are in a state where neither the adversary nor the classifier can benefit from unilaterally changing its strategy. In the game theory terminology, this state is called a Mixed Nash equilibrium.
2.2 General setting
Let us consider a classification task with input space and output space . Let be a proper (i.e. closed balls are compact) Polish (i.e. completely separable) metric space representing the inputs space222For instance, for any norm , is a proper Polish metric space.. Let be the labels set, endowed with the trivial metric . Then the space is a proper Polish space. For any Polish space , we denote the Polish space of Borel probability measures on . Let us assume the data is drawn from . Let be a Polish space (not necessarily proper) representing the set of classifier parameters (for instance neural networks). We also define a loss function: satisfying the following set of assumptions.
Assumption 1 (Loss function).
1) The loss function is a non negative Borel measurable function. 2) For all , is upper-semi continuous. 3) There exists such that for all , , .
It is usual to assume upper-semi continuity when studying optimization over distributions [38, 7]. Furthermore, considering bounded (and positive) loss functions is also very common in learning theory [2] and is not restrictive.
In the adversarial examples framework, the loss of interest is the loss, for whose surrogates are misunderstood [14, 1]; hence it is essential that the loss satisfies Assumption 1. In the binary classification setting (i.e. ) the loss writes . Then, assuming that for all , is continuous and for all , is continuous, the loss satisfies Assumption 1. In particular, it is the case for neural networks with continuous activation functions.
2.3 Adversarial Risk Minimization
The standard risk for a single classifier associated with the loss satisfying Assumption 1 writes: . Similarly, the adversarial risk of at level associated with the loss is defined as333For the well-posedness, see Lemma 4 in Appendix.
It is clear that for all . We can generalize these notions with distributions of classifiers. In other terms the classifier is then randomized according to some distribution . A classifier is randomized if for a given input, the output of the classifier is a probability distribution. The standard risk of a randomized classifier writes . Similarly, the adversarial risk of the randomized classifier at level is444This risk is also well posed (see Lemma 4 in the Appendix).
For instance, for the loss, the inner maximization problem, consists in maximizing the probability of misclassification for a given couple . Note that and . In the remainder of the paper, we study the adversarial risk minimization problems with randomized and deterministic classifiers and denote
| (1) |
Remark 1.
We can show (see Appendix E) that the standard risk infima are equal : . Hence, no randomization is needed for minimizing the standard risk. Denoting this common value, we also have the following inequalities for any , .
2.4 Distributional Formulation of the Adversarial Risk
To account for the possible randomness of the adversary, we rewrite the adversarial attack problem as a convex optimization problem on distributions. Let us first introduce the set of adversarial distributions.
Definition 1 (Set of adversarial distributions).
Let be a Borel probability distribution on and . We define the set of adversarial distributions as
where denotes the projection on the -th component, and the push-forward measure by a measurable function .
For an attacker that can move the initial distribution in , the attack would not be a transport map as considered in the standard adversarial risk. For every point in the support of , the attacker is allowed to move randomly in the ball of radius , and not to a single other point like the usual attacker in adversarial attacks. In this sense, we say the attacker is allowed to be randomized.
Link with DRO. Adversarial examples have been studied in the light of DRO by former works [33, 37], but an exact reformulation of the adversarial risk as a DRO problem has not been made yet. When is a Polish space and is a lower semi-continuous function, for , the primal Optimal Transport problem is defined as
with . When and for , the associated Wasserstein uncertainty set is defined as:
A DRO problem is a linear optimization problem over Wasserstein uncertainty sets for some upper semi-continuous function [41]. For an arbitrary , we define the cost as follows
This cost is lower semi-continuous and penalizes to infinity perturbations that change the label or move the input by a distance greater than . As Proposition 1 shows, the Wasserstein ball associated with is equal to .
Proposition 1.
Let be a Borel probability distribution on and and , then . Moreover, is convex and compact for the weak topology of .
Thanks to this result, we can reformulate the adversarial risk as the value of a convex problem over .
Proposition 2.
The adversarial attack problem is a DRO problem for the cost . Proposition 2 means that, against a fixed classifier , the randomized attacker that can move the distribution in has exactly the same power as an attacker that moves every single point in the ball of radius . By Proposition 2, we also deduce that the adversarial risk can be casted as a linear optimization problem over distributions.
Remark 2.
In a recent work, [29] proposed a similar adversary using Markov kernels but left as an open question the link with the classical adversarial risk, due to measurability issues. Proposition 2 solves these issues. The result is similar to [7]. Although we believe its proof might be extended for infinite valued costs, [7] did not treat that case. We provide an alternative proof in this special case.
3 Nash Equilibria in the Adversarial Game
3.1 Adversarial Attacks as a Zero-Sum Game
Thanks to Proposition 2, the adversarial risk minimization problem can be seen as a two-player zero-sum game that writes as follows,
| (3) |
In this game the classifier objective is to find the best distribution while the adversary is manipulating the data distribution. For the classifier, solving the infimum problem in Equation (3) simply amounts to solving the adversarial risk minimization problem – Problem (1), whether the classifier is randomized or not. Then, given a randomized classifier , the goal of the attacker is to find a new data-set distribution in the set of adversarial distributions that maximizes the risk of . More formally, the adversary looks for
In the game theoretic terminology, is also called the best response of the attacker to the classifier .
Remark 3.
Note that for a given classifier there always exists a “deterministic” best response, i.e. every single point is mapped to another single point . Let be defined such that for all , . Thanks to [4, Proposition 7.50], is -measurable. Then belongs to . Therefore, is the optimal “deterministic” attack against the classifier .
3.2 Dual Formulation of the Game
Every zero sum game has a dual formulation that allows for a deeper understanding of the framework. Here, from Proposition 2, we can define the dual problem of adversarial risk minimization for randomized classifiers. This dual problem also characterizes a two-player zero-sum game that writes as follows,
| (4) |
In this dual game problem, the adversary plays first and seeks an adversarial distribution that has the highest possible risk when faced with an arbitrary classifier. This means that it has to select an adversarial perturbation for every input , without seeing the classifier first. In this case, as pointed out by the motivating example in Section 2.1, the attack can (and should) be randomized to ensure maximal harm against several classifiers. Then, given an adversarial distribution, the classifier objective is to find the best possible classifier on this distribution. Let us denote the value of the dual problem. Since the weak duality is always satisfied, we get
| (5) |
Inequalities in Equation (5) mean that the lowest risk the classifier can get (regardless of the game we look at) is . In particular, this means that the primal version of the game, i.e. the adversarial risk minimization problem, will always have a value greater or equal to . As we discussed in Section 2.1, this lower bound may not be attained by a deterministic classifier. As we will demonstrate in the next section, optimizing over randomized classifiers allows to approach arbitrary closely.
3.3 Nash Equilibria for Randomized Strategies
In the adversarial examples game, a Nash equilibrium is a couple where both the classifier and the attacker have no incentive to deviate unilaterally from their strategies and . More formally, is a Nash equilibrium of the adversarial examples game if is a saddle point of the objective function
Alternatively, we can say that is a Nash equilibrium if and only if solves the adversarial risk minimization problem – Problem (1), the dual problem – Problem (6), and . In our problem, always exists but it might not be the case for . Then for any , we say that is a -approximate Nash equilibrium if solves the dual problem and satisfies .
We now state our main result: the existence of approximate Nash equilibria in the adversarial examples game when both the classifier and the adversary can use randomized strategies. More precisely, we demonstrate that the duality gap between the adversary and the classifier problems is zero, which gives as a corollary the existence of Nash equilibria.
Theorem 1.
Let . Let . Let satisfying Assumption 1. Then strong duality always holds in the randomized setting:
| (6) | |||
The supremum is always attained. If is a compact set, and for all , is lower semi-continuous, the infimum is also attained.
Corollary 1.
Under Assumption 1, for any , there exists a -approximate Nash-Equibilrium . Moreover, if the infimum is attained, there exists a Nash equilibrium to the adversarial examples game.
Theorem 1 shows that . From a game theoretic perspective, this means that the minimal adversarial risk for a randomized classifier against any attack (primal problem) is the same as the maximal risk an adversary can get by using an attack strategy that is oblivious to the classifier it faces (dual problem). This suggests that playing randomized strategies for the classifier could substantially improve robustness to adversarial examples. In the next section, we will design an algorithm that efficiently learn this classifier, we will get improve adversarial robustness over classical deterministic defenses.
4 Finding the Optimal Classifiers
4.1 An Entropic Regularization
Let samples independently drawn from and denote the associated empirical distribution. One can show the adversarial empirical risk minimization can be casted as:
where is defined as :
More details on this decomposition are given in Appendix E. In the following, we regularize the above objective by adding an entropic term to each inner supremum problem. Let such that for all , and let us consider the following optimization problem:
where is an arbitrary distribution of support equal to:
and for all ,
Note that when , we recover the problem of interest . Moreover, we show the regularized supremum tends to the standard supremum when .
Proposition 3.
For , one has
By adding an entropic term to the objective, we obtain an explicit formulation of the supremum involved in the sum: as soon as (which means that each ), each sub-problem becomes just the Fenchel-Legendre transform of which has the following closed form:
Finally, we end up with the following problem:
In order to solve the above problem, one needs to compute the integral involved in the objective. To do so, we estimate it by randomly sampling samples from for all which leads to the following optimization problem
| (7) |
denoted where in the following. Now we aim at controlling the error made with our approximations. We decompose the error into two terms
where the first one corresponds to the statistical error made by our estimation of the integral, and the second to the approximation error made by the entropic regularization of the objective. First, we show a control of the statistical error using Rademacher complexities [2].
Proposition 4.
Let and and denote and . Then by denoting , we have with a probability of at least
where and with i.i.d. sampled as .
We deduce from the above Proposition that in the particular case where is finite such that , with probability of at least
This case is of particular interest when one wants to learn the optimal mixture of some given classifiers in order to minimize the adversarial risk. In the following proposition, we control the approximation error made by adding an entropic term to the objective.
Proposition 5.
Denote for , and , . If there exists such that for all and , then we have
The assumption made in the above Proposition states that for any given random classifier , and any given point , the set of -optimal attacks at this point has at least a certain amount of mass depending on the chosen. This assumption is always met when is sufficiently large. However in order to obtain a tight control of the error, a trade-off exists between and the smallest amount of mass of -optimal attacks.
Now that we have shown that solving (7) allows to obtain an approximation of the true solution , we next aim at deriving an algorithm to compute it.
4.2 Proposed Algorithms
From now on, we focus on finite class of classifiers. Let , we aim to learn the optimal mixture of classifiers in this case. The adversarial empirical risk is therefore defined as:
for , the probability simplex of . One can notice that is a continuous convex function, hence is attained for a certain . Then there exists a non-approximate Nash equilibrium in the adversarial game when is finite. Here, we present two algorithms to learn the optimal mixture of the adversarial risk minimization problem.
for do
A First Oracle Algorithm. The first algorithm we present is inspired from [33] and the convergence of projected sub-gradient methods [9]. The computation of the inner supremum problem is usually NP-hard 666See Appendix E for details., but one may assume the existence of an approximate oracle to this supremum. The algorithm is presented in Algorithm 1. We get the following guarantee for this algorithm.
The main drawback of the above algorithm is that one needs to have access to an oracle to guarantee the convergence of the proposed algorithm. In the following we present its regularized version in order to approximate the solution and propose a simple algorithm to solve it.
An Entropic Relaxation. Adding an entropic term to the objective allows to have a simple reformulation of the problem, as follows:
Note that in , the objective is convex and smooth. One can apply the accelerated PGD [3, 36] which enjoys an optimal convergence rate for first order methods of for iterations.
5 Experiments
5.1 Synthetic Dataset
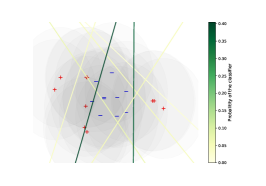
To illustrate our theoretical findings, we start by testing our learning algorithm on the following synthetic two-dimensional problem. Let us consider the distribution defined as , and . We sample training points from this distribution and randomly generate linear classifiers that achieves a standard training risk lower than . To simulate an adversary with budget in norm, we proceed as follows. For every sample we generate points uniformly at random in the ball of radius and select the one maximizing the risk for the loss. Figure 2 (left) illustrates the type of mixture we get after convergence of our algorithms. Note that in this toy problem, we are likely to find the optimal adversary with this sampling strategy if we sample enough attack points.
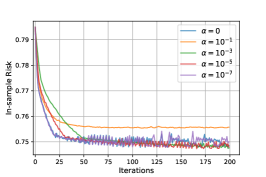
To evaluate the convergence of our algorithms, we compute the adversarial risk of our mixture for each iteration of both the oracle and regularized algorithms. Figure 2 illustrates the convergence of the algorithms w.r.t the regularization parameter. We observe that the risk for both algorithms converge. Moreover, they converge towards the oracle minimizer when the regularization parameter goes to .
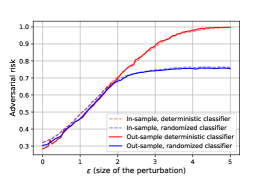
Finally, to demonstrate the improvement randomized techniques offer against deterministic defenses, we plot in Figure 2 (right) the minimum adversarial risk for both randomized and deterministic classifiers w.r.t. . The adversarial risk is strictly better for randomized classifier whenever the adversarial budget is bigger than . This illustration validates our analysis of Theorem 1, and motivates a in depth study of a more challenging framework, namely image classification with neural networks.
5.2 CIFAR-10 Dataset
| Models | Acc. | Rob. Acc. | ||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 |
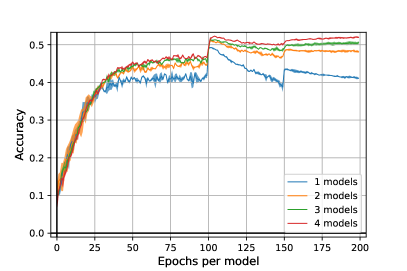
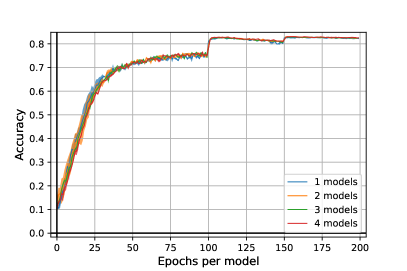
Adversarial examples are known to be easily transferrable from one model to another [35]. To counter this and support our theoretical claims, we propose an heuristic algorithm (see Algorithm 2) to train a robust mixture of classifiers. We alternatively train these classifiers with adversarial examples against the current mixture and update the probabilities of the mixture according to the algorithms we proposed in Section 4.2. More details on the heuristic algorithm are available in Appendix D.
: number of models, : number of iterations,
: number of updates for the models ,
: number of updates for the mixture ,
for do
if then
Attack of images in for the model
Update with for fixed with a SGD step
Experimental Setup. To evaluate the performance of Algorithm 2, we trained from to ResNet18 [20] models on epochs per model777 epochs in total, where is the number of models.. We study the robustness with regards to norm and fixed adversarial budget . The attack we used in the inner maximization of the training is an adapted (adaptative) version of PGD for mixtures of classifiers with steps. Note that for one single model, Algorithm 2 exactly corresponds to adversarial training [24]. For each of our setups, we made two independent runs and select the best one. The training time of our algorithm is around four times longer than a standard Adversarial Training (with PGD 10 iter.) with two models, eight times with three models and twelve times with four models. We trained our models with a batch of size on Nvidia V100 GPUs. We give more details on implementation in Appendix D.
Evaluation Protocol. At each epoch, we evaluate the current mixture on test data against PGD attack with iterations. To select our model and avoid overfitting [30], we kept the most robust against this PGD attack. To make a final evaluation of our mixture of models, we used an adapted version of AutoPGD untargeted attacks [15] for randomized classifiers with both Cross-Entropy (CE) and Difference of Logits Ratio (DLR) loss. For both attacks, we made iterations and restarts.
Results. The results are presented in Figure 3. We remark our algorithm outperforms a standard adversarial training in all the cases by more , without additional loss of standard accuracy as it is attested by the left figure. Moreover, it seems our algorithm, by adding more and more models, reduces the overfitting of adversarial training. So far, experiments are computationally very costful and it is difficult to raise precise conclusions. Further, hyperparameter tuning [19] such as architecture, unlabeled data [12], activation function, or the use of TRADES [43] may still increase the results.
6 Related Work and Discussions
Distributionally Robust Optimization. Several recent works [33, 23, 37] studied the problem of adversarial examples through the scope of distributionally robust optimization. In these frameworks, the set of adversarial distributions is defined using an Wasserstein ball (the adversary is allowed to have an average perturbation of at most in norm). This however does not match the usual adversarial attack problem, where the adversary cannot move any point by more than . In the present work, we introduce a cost function allowing us to cast the adversarial example problem as a DRO one, without changing the adversary constraints.
Optimal Transport (OT). [5] and [29] investigated classifier-agnostic lower bounds on the adversarial risk of any deterministic classifier using OT. These works only evaluate lower bounds on the primal deterministic formulation of the problem, while we study the existence of mixed Nash equilibria. Note that [29] started to investigate a way to formalize the adversary using Markov kernels, but did not investigate the impact of randomized strategies on the game. We extended this work by rigorously reformulating the adversarial risk as a linear optimization problem over distributions and we study this problem from a game theoretic point of view.
Game Theory. Adversarial examples have been studied under the notions of Stackelberg game in [10], and zero-sum game in [31, 26, 8]. These works considered restricted settings (convex loss, parametric adversaries, etc.) that do not comply with the nature of the problem. Indeed, we prove in Appendix C.3 that when the loss is convex and the set is convex, the duality gap is zero for deterministic classifiers. However, it has been proven that no convex loss can be a good surrogate for the loss in the adversarial setting [1, 14], narrowing the scope of this result. If one can show that for sufficiently separated conditional distributions, an optimal deterministic classifier always exists (see Appendix E for a clear statement), necessary and sufficient conditions for the need of randomization are still to be established. [27] studied partly this question for regularized deterministic adversaries, leaving the general setting of randomized adversaries and mixed equilibria unanswered, which is the very scope of this paper.
References
- [1] H. Bao, C. Scott, and M. Sugiyama. Calibrated surrogate losses for adversarially robust classification. In J. Abernethy and S. Agarwal, editors, Proceedings of Thirty Third Conference on Learning Theory, volume 125 of Proceedings of Machine Learning Research, pages 408–451. PMLR, 09–12 Jul 2020.
- [2] P. L. Bartlett and S. Mendelson. Rademacher and gaussian complexities: Risk bounds and structural results. Journal of Machine Learning Research, 3:463–482, 2002.
- [3] A. Beck and M. Teboulle. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM journal on imaging sciences, 2(1):183–202, 2009.
- [4] D. P. Bertsekas and S. Shreve. Stochastic optimal control: the discrete-time case. 2004.
- [5] A. N. Bhagoji, D. Cullina, and P. Mittal. Lower bounds on adversarial robustness from optimal transport. In Advances in Neural Information Processing Systems 32, pages 7496–7508. Curran Associates, Inc., 2019.
- [6] B. Biggio, I. Corona, D. Maiorca, B. Nelson, N. Šrndić, P. Laskov, G. Giacinto, and F. Roli. Evasion attacks against machine learning at test time. In Joint European conference on machine learning and knowledge discovery in databases, pages 387–402. Springer, 2013.
- [7] J. Blanchet and K. Murthy. Quantifying distributional model risk via optimal transport. Mathematics of Operations Research, 44(2):565–600, 2019.
- [8] A. J. Bose, G. Gidel, H. Berard, A. Cianflone, P. Vincent, S. Lacoste-Julien, and W. L. Hamilton. Adversarial example games, 2021.
- [9] S. Boyd. Subgradient methods. 2003.
- [10] M. Brückner and T. Scheffer. Stackelberg games for adversarial prediction problems. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD ’11, page 547–555, New York, NY, USA, 2011. Association for Computing Machinery.
- [11] N. Carlini and D. Wagner. Adversarial examples are not easily detected: Bypassing ten detection methods. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, pages 3–14, 2017.
- [12] Y. Carmon, A. Raghunathan, L. Schmidt, P. Liang, and J. C. Duchi. Unlabeled data improves adversarial robustness. arXiv preprint arXiv:1905.13736, 2019.
- [13] J. M. Cohen, E. Rosenfeld, and J. Z. Kolter. Certified adversarial robustness via randomized smoothing. arXiv preprint arXiv:1902.02918.
- [14] Z. Cranko, A. Menon, R. Nock, C. S. Ong, Z. Shi, and C. Walder. Monge blunts bayes: Hardness results for adversarial training. In K. Chaudhuri and R. Salakhutdinov, editors, Proceedings of the 36th International Conference on Machine Learning, volume 97 of Proceedings of Machine Learning Research, pages 1406–1415. PMLR, 09–15 Jun 2019.
- [15] F. Croce and M. Hein. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In International Conference on Machine Learning, 2020.
- [16] M. Cuturi. Sinkhorn distances: Lightspeed computation of optimal transport. Advances in neural information processing systems, 26:2292–2300, 2013.
- [17] G. S. Dhillon, K. Azizzadenesheli, J. D. Bernstein, J. Kossaifi, A. Khanna, Z. C. Lipton, and A. Anandkumar. Stochastic activation pruning for robust adversarial defense. In International Conference on Learning Representations, 2018.
- [18] I. Goodfellow, J. Shlens, and C. Szegedy. Explaining and harnessing adversarial examples. In International Conference on Learning Representations, 2015.
- [19] S. Gowal, C. Qin, J. Uesato, T. Mann, and P. Kohli. Uncovering the limits of adversarial training against norm-bounded adversarial examples. arXiv preprint arXiv:2010.03593, 2020.
- [20] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016.
- [21] A. Krizhevsky and G. Hinton. Learning multiple layers of features from tiny images. Technical report, Citeseer, 2009.
- [22] A. Kurakin, I. Goodfellow, and S. Bengio. Adversarial examples in the physical world. arXiv preprint arXiv:1607.02533, 2016.
- [23] J. Lee and M. Raginsky. Minimax statistical learning with wasserstein distances. In Advances in Neural Information Processing Systems 31, pages 2687–2696. Curran Associates, Inc., 2018.
- [24] A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu. Towards deep learning models resistant to adversarial attacks. In International Conference on Learning Representations, 2018.
- [25] S.-M. Moosavi-Dezfooli, A. Fawzi, J. Uesato, and P. Frossard. Robustness via curvature regularization, and vice versa. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 9078–9086, 2019.
- [26] J. C. Perdomo and Y. Singer. Robust attacks against multiple classifiers. arXiv preprint arXiv:1906.02816, 2019.
- [27] R. Pinot, R. Ettedgui, G. Rizk, Y. Chevaleyre, and J. Atif. Randomization matters. how to defend against strong adversarial attacks. International Conference on Machine Learning, 2020.
- [28] R. Pinot, L. Meunier, A. Araujo, H. Kashima, F. Yger, C. Gouy-Pailler, and J. Atif. Theoretical evidence for adversarial robustness through randomization. In Advances in Neural Information Processing Systems, pages 11838–11848, 2019.
- [29] M. S. Pydi and V. Jog. Adversarial risk via optimal transport and optimal couplings. In International Conference on Machine Learning. 2020.
- [30] L. Rice, E. Wong, and Z. Kolter. Overfitting in adversarially robust deep learning. In International Conference on Machine Learning, pages 8093–8104. PMLR, 2020.
- [31] S. Rota Bulò, B. Biggio, I. Pillai, M. Pelillo, and F. Roli. Randomized prediction games for adversarial machine learning. IEEE Transactions on Neural Networks and Learning Systems, 28(11):2466–2478, 2017.
- [32] S. Shalev-Shwartz and S. Ben-David. Understanding machine learning: From theory to algorithms. Cambridge university press, 2014.
- [33] A. Sinha, H. Namkoong, and J. Duchi. Certifying some distributional robustness with principled adversarial training. arXiv preprint arXiv:1710.10571, 2017.
- [34] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus. Intriguing properties of neural networks. In International Conference on Learning Representations, 2014.
- [35] F. Tramèr, N. Papernot, I. Goodfellow, D. Boneh, and P. McDaniel. The space of transferable adversarial examples. arXiv preprint arXiv:1704.03453, 2017.
- [36] P. Tseng. On accelerated proximal gradient methods for convex-concave optimization. submitted to SIAM Journal on Optimization, 1, 2008.
- [37] Z. Tu, J. Zhang, and D. Tao. Theoretical analysis of adversarial learning: A minimax approach. arXiv preprint arXiv:1811.05232, 2018.
- [38] C. Villani. Topics in optimal transportation. Number 58. American Mathematical Soc., 2003.
- [39] B. Wang, Z. Shi, and S. Osher. Resnets ensemble via the feynman-kac formalism to improve natural and robust accuracies. In Advances in Neural Information Processing Systems 32, pages 1655–1665. Curran Associates, Inc., 2019.
- [40] C. Xie, J. Wang, Z. Zhang, Z. Ren, and A. Yuille. Mitigating adversarial effects through randomization. In International Conference on Learning Representations, 2018.
- [41] M.-C. Yue, D. Kuhn, and W. Wiesemann. On linear optimization over wasserstein balls. arXiv preprint arXiv:2004.07162, 2020.
- [42] S. Zagoruyko and N. Komodakis. Wide residual networks. In Proceedings of the British Machine Vision Conference (BMVC), pages 87.1–87.12. BMVA Press, 2016.
- [43] H. Zhang, Y. Yu, J. Jiao, E. P. Xing, L. E. Ghaoui, and M. I. Jordan. Theoretically principled trade-off between robustness and accuracy. International conference on Machine Learning, 2019.
Supplementary material
Appendix A Notations
Let be a Polish metric space (i.e. complete and separable). We say that is proper if for all and , is compact. For a Polish space, we denote the set of Borel probability measures on endowed with strong topology. We recall the notion of weak topology: we say that a sequence of converges weakly to if and only if for every continuous function on , . Endowed with its weak topology, is a Polish space. For , we define the set of integrable functions with respect to . We denote and respectively the projections on the first and second component, which are continuous applications. For a measure and a measurable mapping , we denote the pushforward measure of by . Let be an integer and denote , the probability simplex of .
Appendix B Useful Lemmas
Lemma 1 (Fubini’s theorem).
Let satisfying Assumption 1. Then for all , is Borel measurable; for , is Borel measurable. Moreover:
Lemma 2.
Let satisfying Assumption 1. Then for all , is upper semi-continuous and hence Borel measurable.
Proof.
Let be a sequence of converging to . For all , is non negative and lower semi-continuous. Then by Fatou’s Lemma applied:
Then we deduce that: is lower semi-continuous and then is upper-semi continuous. ∎
Lemma 3.
Let satisfying Assumption 1 Then for all , is upper semi-continuous for weak topology of measures.
Proof.
is lower semi-continuous from Lemma 2. Then is lower semi-continuous and non negative. Let denote this function. Let be a non-decreasing sequence of continuous bounded functions such that . Let converging weakly towards . Then by monotone convergence:
Then is lower semi-continuous and then is upper semi-continuous for weak topology of measures. ∎
Lemma 4.
Let satisfying Assumption 1. Then for all , is universally measurable (i.e. measurable for all Borel probability measures). And hence the adversarial risk is well defined.
Appendix C Proofs
C.1 Proof of Proposition 1
Proof.
Let . Let . There exists such that, , -almost surely, and , and . Then . Then, we deduce that , and . Reciprocally, let . Then, since the infimum is attained in the Wasserstein definition, there exists such that . Since when and , we deduce that, and , -almost surely. Then . We have then shown that: .
The convexity of is then immediate from the relation with the Wasserstein uncertainty set.
Let us show first that is relatively compact for weak topology. To do so we will show that is tight and apply Prokhorov’s theorem. Let , being a Polish space, is tight then there exists compact such that . Let . Recalling that is proper (i.e. the closed balls are compact), so is compact. Moreover for , . And then, Prokhorov’s theorem holds, and is relatively compact for weak topology.
Let us now prove that is closed to conclude. Let be a sequence of converging towards some for weak topology. For each , there exists such that and -almost surely and , . is relatively compact, then tight, then is tight, then relatively compact by Prokhorov’s theorem. , then up to an extraction, . Then and -almost surely, and by continuity, and by continuity, . And hence is closed.
Finally is a convex compact set for the weak topology. ∎
C.2 Proof of Proposition 2
Proof.
Let . Let . is upper-semi continuous, hence upper semi-analytic. Then, by upper semi continuity of on the compact and [4, Proposition 7.50], there exists a universally measurable mapping such that . Let , then . And then .
Reciprocally, let . There exists , such that and -almost surely, and, and . Then: -almost surely. Then, we deduce that:
Then we deduce the expected result:
Let us show that the optimum is attained. is upper semi continuous by Lemma 3 for the weak topology of measures, and is compact by Proposition 1, then by [4, Proposition 7.32], the supremum is attained for a certain .
∎
C.3 Proof of Theorem 1
Let us first recall the Fan’s Theorem.
Theorem 2.
Let be a compact convex Haussdorff space and be convex space (not necessarily topological). Let be a concave-convex function such that for all , is upper semi-continuous then:
We are now set to prove Theorem 1.
Proof.
In the related work (Section 6), we mentioned a particular form of Theorem 1 for convex cases. As mentioned, this result has limited impact in the adversarial classification setting. It is still a direct corollary of Fan’s theorem. This theorem can be stated as follows:
Theorem 3.
Let , and a convex set. Let be a loss satisfying Assumption 1, and also, , is a convex function, then we have the following:
The supremum is always attained. If is a compact set then, the infimum is also attained.
C.4 Proof of Proposition 3
Proof.
Let us first show that for , admits a solution. Let , a sequence such that
As is tight ( is a proper metric space therefore all the closed ball are compact) and by Prokhorov’s theorem, we can extract a subsequence which converges toward . Moreover, is upper semi-continuous (u.s.c), thus is also u.s.c.888Indeed by considering a decreasing sequence of continuous and bounded functions which converge towards and by definition of the weak convergence the result follows. Moreover is also u.s.c. 999for the result is clear, and if , note that is lower semi-continuous, therefore, by considering the limit superior as goes to infinity we obtain that
from which we deduce that is optimal.
Let us now show the result. We consider a positive sequence of such that . Let us denote and the solutions of and respectively. Since is tight, is also tight and we can extract by Prokhorov’s theorem a subsequence which converges towards . Moreover we have
from which follows that
Then by considering the limit superior we obtain that
from which follows that
and by optimality of we obtain the desired result. ∎
C.5 Proof of Proposition 4
Proof.
Let us denote for all ,
Let also consider and two sequences such that
We first remarks that
and by considering the limit, we obtain that
Simarly we have that
from which follows that
Therefore we obtain that
Observe that , therefore because the function is 1-Lipschitz on , we obtain that
Let us now denote for all ,
and let us define
where . By denoting , we have that
where the last inequality comes from the fact that the loss is upper bounded by . Then by appling the McDiarmid’s Inequality, we obtain that with a probability of at least ,
Thanks to [32, Lemma 26.2], we have for all
where for any class of function defined on and point
Moreover as is -Lipstchitz on , by [32, Lemma 26.9], we have
where
Let us now define
We observe that
By Applying the McDiarmid’s Inequality, we have that with a probability of at least
Remarks also that
Finally, applying a union bound leads to the desired result.
∎
C.6 Proof of Proposition 5
Proof.
Following the same steps than the proof of Proposition 4, let and two sequences such that
Remarks that
Then by considering the limit we obtain that
Similarly, we obtain that
from which follows that
Let and , then we have
∎
C.7 Proof of Proposition 6
Proof.
Thanks to Danskin theorem, if is a best response to , then is a subgradient of . Let be the learning rate. Then we have for all :
We then deduce by summing:
Then we have:
The left-hand term is minimal for , and for this value:
∎
.
Appendix D Additional Experimental Results
D.1 Experimental setting.
Optimizer.
For each of our models, The optimizer we used in all our implementations is SGD with learning rate set to at epoch and is divided by at half training then by at the three quarters of training. The momentum is set to and the weight decay to . The batch size is set to .
Adaptation of Attacks.
Since our classifier is randomized, we need to adapt the attack accordingly. To do so we used the expected loss:
to compute the gradient in the attacks, regardless the loss (DLR or cross-entropy). For the inner maximization at training time, we used a PGD attack on the cross-entropy loss with . For the final evaluation, we used the untargeted attack with default parameters.
Regularization in Practice.
The entropic regularization in higher dimensional setting need to be adapted to be more likely to find adversaries. To do so, we computed PGD attacks with only iterations with different restarts instead of sampling uniformly points in the -ball. In our experiments in the main paper, we use a regularization parameter . The learning rate for the minimization on is always fixed to .
Alternate Minimization Parameters.
Algorithm 2 implies an alternate minimization algorithm. We set the number of updates of to and, the update of to .
D.2 Effect of the Regularization
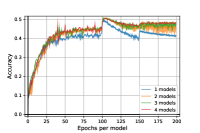
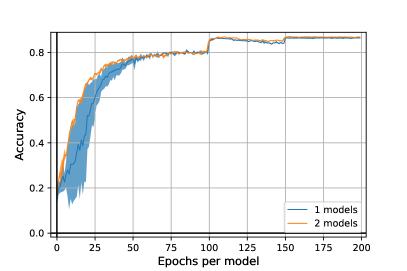
In this subsection, we experimentally investigate the effect of the regularization. In Figure 4, we notice, that the regularization has the effect of stabilizing, reducing the variance and improving the level of the robust accuracy for adversarial training for mixtures (Algorithm 2). The standard accuracy curves are very similar in both cases.



D.3 Additional Experiments on WideResNet28x10
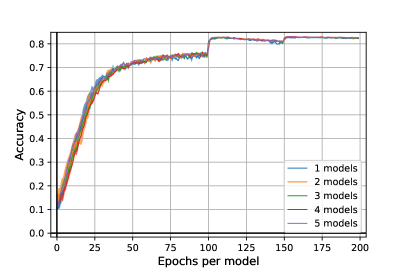
We now evaluate our algorithm on WideResNet28x10 [42] architecture. Due to computation costs, we limit ourselves to and models, with regularization parameter set to as in the paper experiments section. Results are reported in Figure 5. We remark this architecture can lead to more robust models, corroborating the results from [19].
| Models | Acc. | Rob. Acc. | ||
|---|---|---|---|---|
| 1 | ||||
| 2 |
D.4 Overfitting in Adversarial Robustness
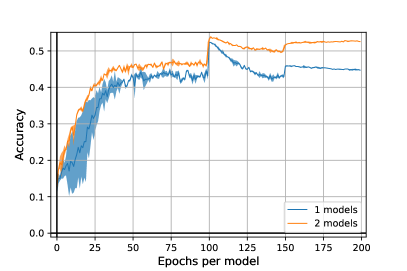
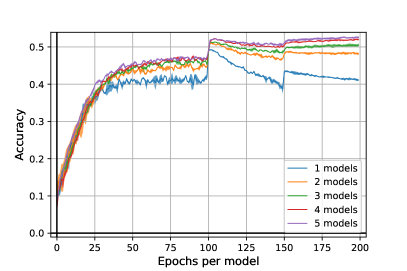
We further investigate the overfitting of our heuristic algorithm. We plotted in Figure 6 the robust accuracy on ResNet18 with to models. The most robust mixture of models against PGD with iterations arrives at epoch , i.e. at the end of the training, contrary to to models, where the most robust mixture occurs around epoch . However, the accuracy against AGPD with 100 iterations in lower than the one at epoch with global robust accuracy of at epoch and at epoch 198. This strange phenomenon would suggest that the more powerful the attacks are, the more the models are subject to overfitting. We leave this question to further works.
Appendix E Additional Results
E.1 Equality of Standard Randomized and Deterministic Minimal Risks
Proposition 7.
Let be a Borel probability distribution on , and a loss satisfying Assumption 1, then:
Proof.
It is clear that: . Now, let , then:
where denotes the essential infimum. ∎
We can deduce an immediate corollary.
Corollary 2.
Under Assumption 1, the dual for randomized and deterministic classifiers are equal.
E.2 Decomposition of the Empirical Risk for Entropic Regularization
Proposition 8.
Proof.
This proposition is a direct application of Proposition 2 for diracs . ∎
E.3 On the NP-Hardness of Attacking a Mixture of Classifiers
In general, the problem of finding a best response to a mixture of classifiers is in general NP-hard. Let us justify it on a mixture of linear classifiers in binary classification: for and . Let us consider the norm and and . Then the problem of attacking is the following:
This problem is equivalent to a linear binary classification problem on , which is known to be NP-hard.
E.4 Case of Separated Conditional Distribtions
Proposition 9.
Let . Let . Let . For , let us denote the distribution of conditionally to . Let us assume that . Let us consider the nearest neighbor deterministic classifier : and the loss . Then satisfies both optimal standard and adversarial risks: and .
Proof.
Let Let denote . Then we have
For , we have, for all such that , , then: . Similarly, we have . We then deduce the result. ∎