Mixed-permutation channel with its application to estimate quantum coherence
Abstract
Quantum channel, as the information transmitter, is an indispensable tool in quantum information theory. In this paper, we study a class of special quantum channels named the mixed-permutation channels. The properties of these channels are characterized. The mixed-permutation channels can be applied to give a lower bound of quantum coherence with respect to any coherence measure. In particular, the analytical lower bounds for -norm coherence and the relative entropy of coherence are shown respectively. The extension to bipartite systems is presented for the actions of the mixed-permutation channels.
1 Introduction
Quantum channel is a deterministic quantum operation and it transmits the information from the input to the output. It is indispensable in various information processing tasks, such as quantum communication [1], quantum computation [2, 3] and quantum cryptography [4, 5]. So the study about quantum channel is an interesting and attractive topic. Explicitly, the resource theory of quantum channels deals with understanding the properties and capabilities of quantum channels in terms of the resources they consume and produce [6, 7, 8, 9, 10, 11]. It also has important implications for the design of quantum protocols, as it provides a unified framework [12] for characterizing the capabilities and limitations of different types of quantum channels. For quantum channels, the uncertainty relations, a fundamental topic in quantum mechanics, are also established recently. They describe the theoretical restrictions about two or more quantum channels [13, 14, 15], just like that about two or more observables. In addition, quantum channels are also intimately related to the dynamical behavior of quantum states and the investigation of open quantum system [16, 17, 18].
One special kind of the most commonly-used quantum channels is the projective measurement. Within the framework of the projective measurement, many quantum features are manifested. For instance, quantum coherence is such a quantum feature and it is of practical significance in quantum computation and quantum communication [19, 20, 21]. The quantum coherence is further quantified by coherence measures such as the -norm coherence [22], the relative entropy of coherence [22], the coherence concurrence [23], the geometric coherence [24] and the robustness of coherence [25] and so on. However, the evaluation of the coherence measure is not always easy for arbitrary quantum states, especially for mixed states.
In this paper, we investigate an interesting quantum channel called the mixed-permutation channel, which maps an input state to an average of their permutation conjugations. This mixed-permutation channel can be viewed as a special mixed-unitary channels with equal weights [26]. More than that, it is also an example of a covariant quantum channel [27], meaning that it commutes with certain symmetry operations on the input states. In this case, this mixed-permutation channel is covariant with respect to the conjugated action of the symmetric group .
This work is factually a follow-up study of [28], which investigates the application of the mixed-permutation channel in quantifying quantum coherence. Here we aim to explore the mixed-permutation channel further and characterize it systematically. Moreover, we find the application of the mixed-permutation channel to evaluate the quantum coherence. This evaluation is applicable to all coherence measures and is tight for some special quantum states.
The paper is organized as follows. In Sect. 2, we give the definition of the mixed-permutation channels and list their basic properties. We also present the specific form of the mixed-permutation channels, and characterize the image states. The applications of the mixed-permutation channel in estimating quantum coherence is also presented. Subsequently, in Sect. 3, we extend the action of the mixed-permutation channels to bipartite systems. We conclude this paper in Sect. 4.
2 Mixed-permutation channel and its application in estimating quantum coherence
In this section, we consider the -dimensional quantum system with its Hilbert space and fix the reference basis as . The so-called quantum state is represented by the density matrices/operators acting on the Hilbert space . We denote the set of all density matrices by
Any quantum channel acting on the density matrices/operators in can be expressed with Kraus representation where , the identity operator on . Next we shall introduce the mixed-permutation channels and characterize it both analytically and geometrically. Then we explain its application in estimating quantum coherence.
2.1 Mixed-permutation channels
Definition 1.
For any matrix acting on , we define the mixed-permutation channel as
| (1) |
where is the symmetric group of permutations of elements, and the permutation matrix is
| (2) |
induced by .
By this definition we see for any matrix acting on , the action of the mixed-permutation channel is the average action over all possible permutation matrices. It is easily seen that and for any and in . Moreover, . The properties of the mixed-permutation channel can be listed below:
-
(i)
, that is for any matrix acting on .
-
(ii)
is unital, that is , where is the identity matrix on .
-
(iii)
is self-adjoint with respect to Hilbert-Schmidt inner product, i.e., in the sense of for all matrices acting on , that is, .
-
(iv)
, that is .
-
(v)
is invariant under any permutation matrices, that is, for any permutation matrix , induced by the permutation .
Furthermore, the explicit form of the mixed-permutation channel on the can be obtained analytically.
Theorem 1.
For any matrix , the mixed-permutation channel can be characterized as
| (3) |
where for -dimensional vector with all entries being one.
Proof.
In fact, this result will be established by linearity once we show it holds for any Hermitian matrix because every complex square matrix can be represented as a complex linear combination of two Hermitian matrices, i.e., , where and . In what follows, it suffices to consider Hermitian case.
Let us assume that is Hermitian. If , then
Now there exists a permutation such that and due to the assumption . Then
implying that, whenever , then
Similarly, if , then
Note that , which means that
From the above discussion, let , where . We see that
Then, via ,
Because , we get that . From these, we see that
from which we get
Therefore
After simplifying it then we get the desired expression. This completes the proof. ∎
In Theorem 1, when is taken as a quantum state , i.e., if a quantum state goes through the mixed-permutation channel , then the output state can be characterized analytically.
Corollary 1.
For any quantum state , the corresponding output state from the mixed-permutation channel is given by
| (8) |
where
| (9) |
for the given reference basis .
Remark 1.
We remark here that . Indeed,
Therefore, combining , where and are the minimum and maximum eigenvalues of the quantum state respectively, we have,
| (10) |
In order to see clearly what is the image states of the channel when input state is , let us focus on qubit systems. In fact, any qubit state can be represented as
| (13) |
where , , and , is the vector of the Pauli matrices, given by
| (20) |
It is easily seen that the action of is
| (23) |
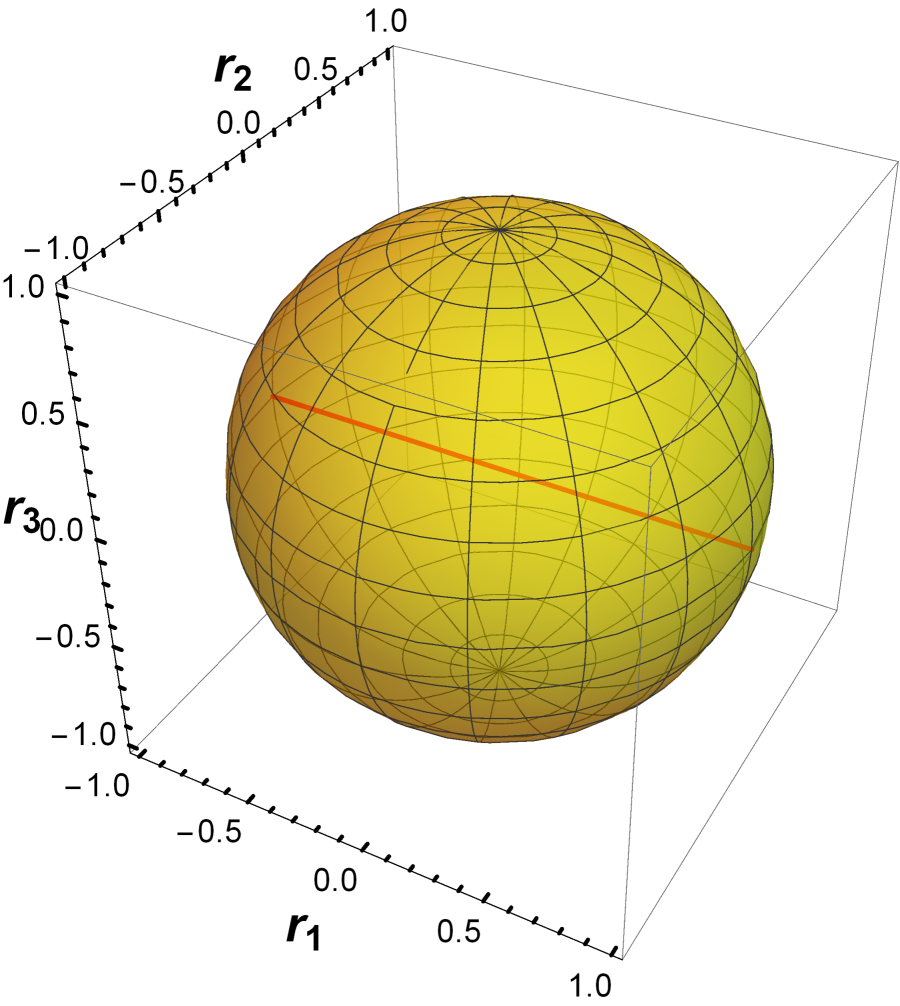
So the action of the mixed-permutation channel on the set of quantum states can be simulated by the transformation on the Bloch ball, i.e.,
| (24) |
From Figure 1, we see that the Bloch ball is mapped into a red line segment by the action of the mixed-permutation channel.
2.2 Applying the mixed-permutation channel to estimate quantum coherence
In order to estimate quantum coherence using the mixed-permutation channel, we need recall some notions about quantum coherence. Given the reference basis , a diagonal quantum state is called the incoherent state. The set of incoherent states is denoted as . The so-called incoherent operation is a completely positive linear mapping such that its Kraus decomposition with fulfills for all and for all .
The quantum coherence is quantified by a nonnegative function named the coherence measure. A coherence measure is required to satisfy the following conditions [22]:
-
(A1)
Nonnegativity: for , and moreover for all ;
-
(A2)
Monotonicity: for any incoherent operation ;
-
(A3)
Strong monotonicity: for any incoherent operation with and ;
-
(A4)
Convexity: for any quantum state with and .
Two commonly used coherence measures are the -norm coherence and the relative entropy of coherence [22]. The -norm coherence of the quantum state is the sum of the magnitudes of all the off-diagonal entries
| (25) |
The relative entropy of coherence is the difference of von Neumann entropy between the density matrix and the diagonal matrix given by its diagonal entries,
| (26) |
where is the diagonal matrix obtained by the diagonal entries of and is the von Neumann entropy of the state .
Now we come back to the mixed-permutation channel. It is obvious that is incoherent for any incoherent state . So the mixed-permutation channel is an incoherent operation. By the monotonicity of the coherence measures, we know the coherence of input state is nonincreasing under this channel. Since the output states of the mixed-permutation channel have an analytical form in Eq. (8), we can utilize it to estimate the coherence of the input state .
Theorem 2.
For any coherence measure and any quantum state , the quantum coherence of is bounded from below by the quantum coherence of , namely,
| (27) |
Proof.
First, since any permutation matrices and are incoherent operations, so
Therefore for any permutation matrcix . Then by the convexity of coherence measure, we have further that
which completes the proof. ∎
From the proof above, we see that Theorem 2 is universal in the sense that Eq. (30) is independent of the coherence measures. So Theorem 2 can be applied to all coherence measures. Additionally, the output states is of one parameter, so its coherence is much easy to calculate compared with the input state. In fact, for any quantum state , the output state in Corollary 1 can be decomposed as
| (28) |
where the weight is relevant to the quantum state as
| (29) |
and is the maximally coherent state [29]. This state is also called the maximally coherent mixed state in [30]. By this decomposition in Eq. (28), we get the eigenvalues of is and with multiplicity . In view of this, we get the following result:
Corollary 2.
For norm coherence, the lower bound in Eq. (30) is tight for real quantum states, that is,
| (32) |
for any real quantum state . Now we consider the -norm coherence and the relative entropy of coherence in qubit system.
Example 1.
In qubit systems, any qubit state can be represented as in Eq. (13) with the spectral decomposition as
with the eigenvalues , and the corresponding eigenvectors
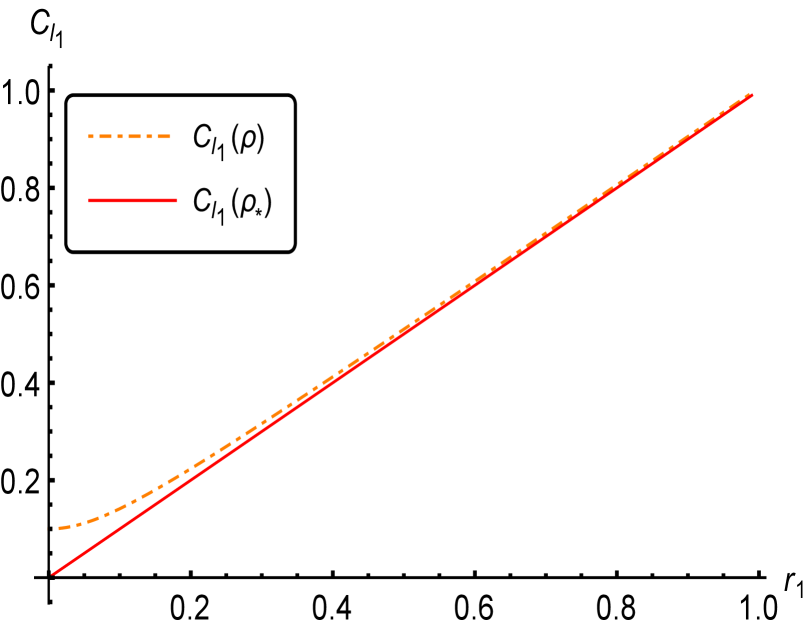
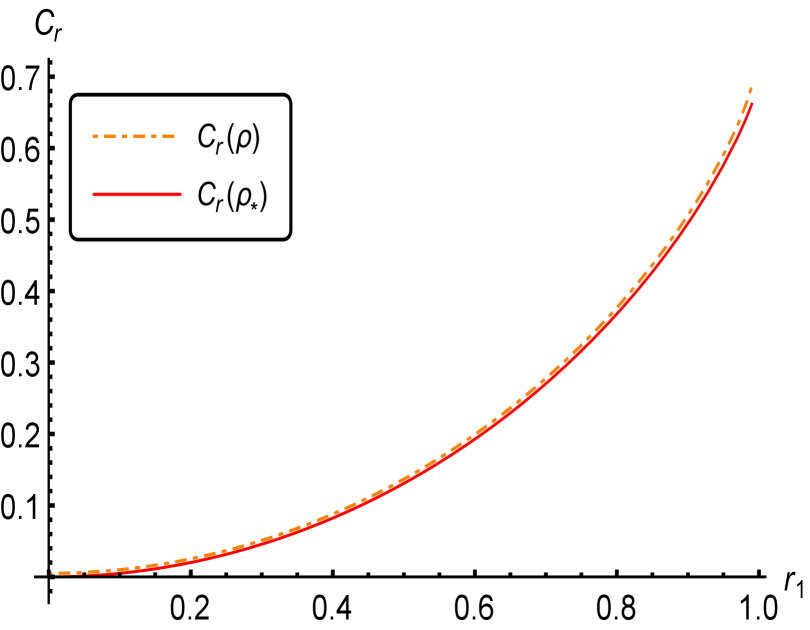
Let , we calculate the -norm coherence and the relative entropy coherence as well as the lower bound the -norm coherence and the relative entropy coherence and make a comparison in Figures 2 and 2.
From another point of view, it is interesting to estimate quantum coherence from above. Let us turn to another quantity called the coherence of assistance, induced by any coherence measure , which is defined in the form of concave bottom extension,
| (33) |
where the maximization is taken over all pure state decompositions of . Coherence of assistance quantifies the coherence that can be extracted assisted by another party under local measurements and classical communication [31]. Suppose Alice holds a state with coherence . Bob holds another part of the purified state of . The joint state between Alice and Bob is . Bob performs local projective measurements along the given basis and informs Alice the measurement outcomes by classical communication. Alice’s system will be in a pure state ensemble with average coherence . The process is called assisted coherence distillation. The maximum average coherence is called the coherence of assistance which quantifies the one-way coherence distillation rate [31].
The coherence of assistance of any quantum state can be estimated by the output state .
Theorem 3.
For any coherence measure and any quantum state , the coherence of assistance of is bounded from above by the coherence of assistance of ,
| (34) |
Proof.
Note that
Here the inequality is the concavity of the coherence of assistance. The last equality is due to the equality for any permutation . ∎
3 Mixed-permutation channel on bipartite systems
In this section we study the mixed-permutation channel on bipartite systems . Without loss of generality, we suppose . Suppose that and are rothonormal bases of the subsystems and , respectively, we denote by
the set of density operators acting on . The identical channel on operator spaces are denoted by . By Theorem 1, we derive the explicit form of the mixed-permutation channel on bipartite systems .
Theorem 4.
For any bipartite operator acting on , denote where is a -dimensional column vector with all entries being one, we have
| (35) |
and thus
| (36) | |||||
where
| (37) |
Proof.
The result can be also established by linearity once we show it holds for any Hermitian matrix . So it suffices to consider the Hermitian case.
-
(i)
In fact, for where , we suppose its Schmidt decomposition is
with and the orthnormal bases of the subsystems and respectively, then the density operator of can be expressed as
In the following reasoning, we omit the subindexes and when no confusing arises. The action of the mixed-permutation channel on the first subsystem is then
By the linearity of both sides, this equality holds for any positive semi-definite bipartite operator, and thus for a general bipartite operator.
-
(ii)
The proof goes similarly.
We have done the proof. ∎
If we focus on the bipartite quantum states, then we get an output state of the one-sided and two-sided mixed-permutation channels as follows.
Corollary 3.
For any quantum state , if the first subsystem goes through the mixed-permutation channel, then the output state is
| (38) |
where . If both subsystems go through the separate mixed-permutation channels, the output state is
Here and . Moreover,
By the form of the output states and in the above Corollary 3, we get both and are positive under partial transpositions (PPT) for all states . Since PPT states in qubit-qubit systems and qubit-qutrit systems are all separable, so the action of the local mixed-permutation channel(s) on two-qubit systems will completely erase the entanglement between two subsystems.
Example 2.
For any quantum state in ,
if the first qubit goes through the mixed-permutation channel, then the output state is
| (39) |
with
More explicitly,
| (44) |
with . Furthermore, if both two qubits go through the mixed-permutation channel, then the output state is
where
implying that must be separable. Moreover, the eigenvalues are given by
From the above, we see that and are PPT states. Thus by Peres-Horodecki criterion [32, 33], the output states and are separable ones for all two-qubit states .
In what follows, let us recall the notion of the entanglement-breaking channel [34]. The so-called entanglement-breaking channel means that is separable for every bipartite state . As already known in [35], in qubit systems, any quantum channel is entanglement breaking if and only if its Choi representation is separable. Because is separable for any two-qubit state , a fortiori for maximally entangled two-qubit state. Thus is entanglement breaking in qubit systems. In fact, the mixed-permutation channel is entanglement-breaking channel in qudit systems, which can be summarized into the following result:
Corollary 4.
The mixed-permutation channel characterized in Theorem 1 is entanglement-breaking channel in qudit systems.
Proof.
Example 3 (The family of Bell-diagonal states).
The Bell-diagonal states [36] in two-qubit system can be written as
| (46) |
with three Pauli operators in Eq. (20). So a Bell-diagonal state is specified by three real variables , and such that
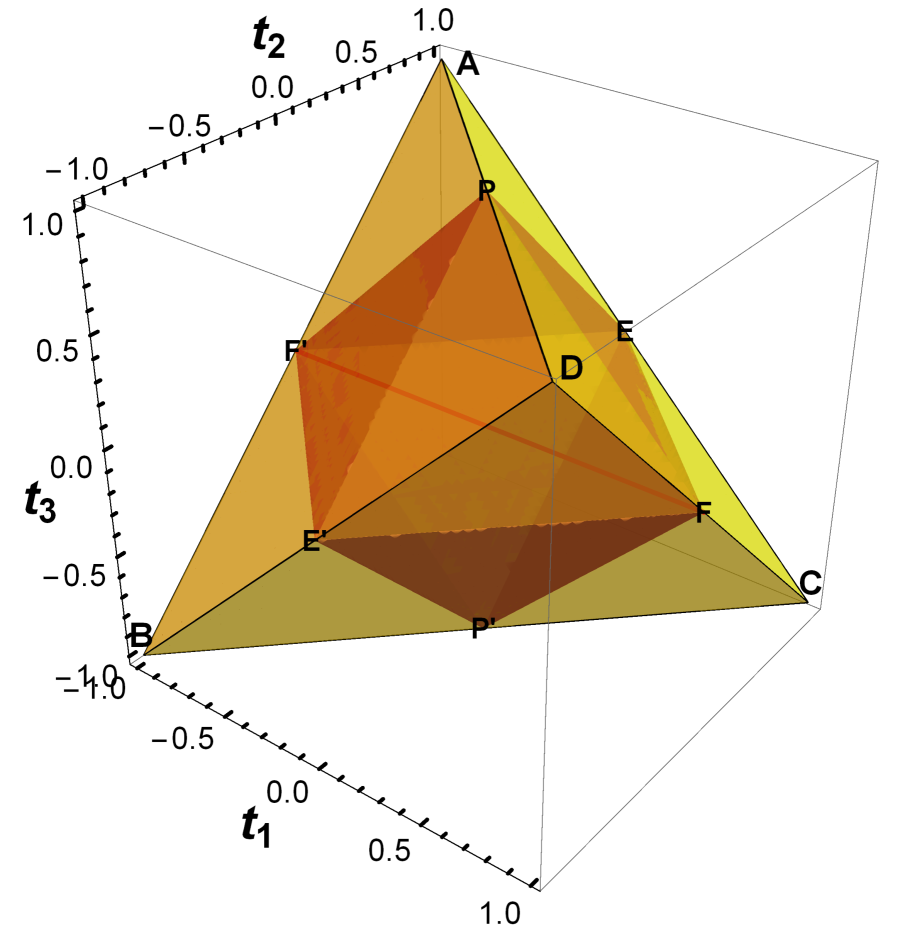
Denote the set of all above such tuples by . Because the four eigenvalues of are in , we see that . That is, . The Bell-diagonal states can be geometrically described by a tetrahedron. One can show that a Bell-diagonal state is separable if and only if holds. Geometrically, the set of Bell-diagonal states is a tetrahedron and the set of separable Bell-diagonal states is an octahedron [36], which is denoted by . That is, . We find that
| (47) |
We make a plot in arguments about the image states in (47) of the one-sided action of the mixed-permutation channel on the family (46) of Bell diagonal states in the following Figure 3.
4 Conclusions and discussions
In summary, we studied one kind of special channels, i.e., the mixed-permutation channels. The properties of this channel was characterized. The mixed-permutation channel can be used in bounding quantum coherence with respect to all coherence measures. The action of the mixed-permutation channel on bipartite systems is also discussed and can be generalized to multipartite systems. Beyond that, there are some interesting problems which can be further considered in the future:
-
•
The first question is what is the average collective action of the permutations on the bipartite quantum states,
We are expecting a closed-form formula of the above expression. With this potential formula, we can extend symmetrized variance for pure states in [28] to mixed states.
- •
In light of the special properties and the closed form of the output state of the mixed-permutation channel, we expect the corresponding correlation measure and coherence measure could characterize the quantum features of quantum states from a permutation-invariant way.
Acknowledgments
This research is supported by Zhejiang Provincial Natural Science Foundation of China under Grant No. LZ23A010005 and by NSFC under Grant Nos.11971140 and 12171044.
Data Availability Statement
No Data associated in the manuscript.
References
- [1] R. Takagi, K. Wang, and M. Hayashi, Application of the resource theory of channels to communication scenarios, Phys. Rev. Lett. 124, 120502 (2020).
- [2] D.P. Divincenzo, Quantum computation, Science 270(5234), 255-261(1995).
- [3] A. Ekert and R. Jozsa, Quantum computation and Shor’s factoring algorithm, Rev. Math. Phys. 68, 733 (1996).
- [4] N. Gisin, G. Ribordy, W. Tittel, and H. Zbinden, Quantum cryptography, Rev. Math. Phys. 74, 145 (2002).
- [5] S. Pirandola et al., Advances in quantum cryptography, Advances in Optics and Photonics 12(4), 1012-1236 (2020).
- [6] E. Chitambar and G. Gour, Quantum resource theories, Rev. Math. Phys. 91, 025001 (2019).
- [7] X. Wang and M.M. Wilde, Resource theory of asymmetric distinguishability for quantum channels, Phys. Rev. Research 1, 033169 (2019).
- [8] X. Wang, M.M. Wilde, and Y. Su, Quantifying the magic of quantum channels, New. J. Phys. 21, 103002 (2019).
- [9] F.H. Kamin, F.T. Tabesh, S. Salimi, and F. Kheirandish, The resource theory of coherence for quantum channels, Quant Inf Process 19, 210 (2020).
- [10] Y. Liu and X. Yuan, Operational resource theory of quantum channels, Phys. Rev. Research 2, 012035(R) (2020).
- [11] H. Zhou, T. Gao, F. Yan, Entanglement resource theory of quantum channel, Phys. Rev. Research 4, 013200 (2022).
- [12] R. Takagi, Operational Quantum Resource Theories: Unified Framework and Applications, PhD Thesis (2020).
- [13] S. Fu, Y. Sun, S. Luo, Skew information-based uncertainty relations for quantum channels, Quantum Inf. Process. 18, 258 (2019).
- [14] N. Zhou, M. J. Zhao, Z. Wang, T. Li, The uncertainty relation for quantum channels based on skew information, Quantum Inf. Process. 22, 6 (2023).
- [15] Q-H. Zhang, J.F. Wu, S-M. Fei, A note on uncertainty relations of arbitrary N quantum channels, Laser Phys. Lett. 18, 095204(2021).
- [16] T.R. Bromley, M. Cianciaruso, and G. Adesso, Frozen quantum coherence, Phys. Rev. Lett. 114, 210401 (2015).
- [17] X.D. Yu, D.J. Zhang, C.L. Liu, and D.M. Tong, Measure-independent freezing of quantum coherence, Phys. Rev. A 93, 060303 (2016).
- [18] M.L. Hu, and H. Fan, Evolution equation for quantum coherence, Sci. Rep. 6, 29260 (2016).
- [19] A. Streltsov, G. Adesso, and M. B. Plenio, Colloquium: Quantum coherence as a resource, Rev. Math. Phys. 89, 041003 (2017).
- [20] E. Chitambar and G. Gour, Quantum resource theories, Rev. Math. Phys. 91, 025001 (2019).
- [21] M.L. Hu, X. Hu, J. Wang, Y. Peng, Y.R. Zhang, H. Fan, Quantum coherence and geometric quantum discord, Phys. Rep. 762-764, 1-100 (2018).
- [22] T. Baumgratz, M. Cramer, and M. B. Plenio, Quantifying coherence, Phys. Rev. Lett. 113, 140401 (2014).
- [23] X. Qi, T. Gao, and F.L. Yan, Measuring coherence with entanglement concurrence, J. Phys. A 50, 285301 (2017).
- [24] A. Streltsov, U. Singh, H. S. Dhar, M. N. Bera, and G. Adesso, Measuring Quantum Coherence with Entanglement, Phys. Rev. Lett. 115, 020403 (2015).
- [25] C. Napoli, T. R. Bromley, M. Cianciaruso, M. Piani, N. Johnston, and G. Adesso, Robustness of coherence: an operational and observable measure of quantum coherence, Phys. Rev. Lett. 116, 150502 (2016).
- [26] J. I de Vicente and A. Streltsov, Genuine quantum coherence, J. Phys. A: Math. Theor. 50, 045301 (2017).
- [27] A.S. Holevo, Additive conjecture and covariant channels, Int. J. Quantum Information, 3(1),41-47 (2005).
- [28] M. J. Zhao, L. Zhang, and S. M. Fei, Standard symmetrized variance with applications to coherence, uncertainty, and entanglement, Phys. Rev. A 106, 012417 (2022).
- [29] Y. Peng, Y. Jiang, and H. Fan, Maximally coherent states and coherence-preserving operations, Phys. Rev. A 93, 032326 (2016).
- [30] U. Singh, M. N. Bera, H. S. Dhar, and A. K. Pati, Maximally coherent mixed states: Complementarity between maximal coherence and mixedness, Phys. Rev. A 91, 052115 (2015).
- [31] E. Chitambar, A. Streltsov, S. Rana, M.N. Bera, G. Adesso, and M. Lewenstein, Assisted Distillation of Quantum Coherence, Phys. Rev. Lett. 116, 070402 (2016).
- [32] A. Peres, Separability Criterion for Density Matrices, Phys. Rev. Lett. 77, 1413 (1996).
- [33] M. Horodecki and P. Horodecki, Reduction criterion of separability and limits for a class of distillation protocols, Phys. Rev. A 59, 4206 (1999).
- [34] M. Horodecki, P.W. Shor, and M.B. Ruskai, Entanglement breaking channels, Rev. Math. Phys. 15(6), 629-641 (2003).
- [35] M.B. Ruskai, Qubit entanglement breaking channels, Rev. Math. Phys. 15(6), 643(2003).
- [36] R. Horodecki, M. Horodecki, Information-theoretic aspects of inseparability of mixed states, Phys. Rev. A 54(3), 1838 (1996).
- [37] N. Li, S. Luo, Y. Sun, Quantifying correlations via local channels, Phys. Rev. A 105, 032436 (2022).
- [38] Y. Sun, N. Li, S. Luo, Quantifying coherence relative to channels via metric-adjusted skew information, Phys. Rev. A 106, 012436 (2022).