Present address: ]Department of Physics, University of Notre Dame, Notre Dame, Indiana 46556, USA.

Introduction. Protons and neutrons are the building blocks of atomic nuclei, which feature collective excitations which are symmetric or not symmetric with respect to the proton-neutron degree of freedom Heyde and Sau (1986). Excitations resulting from the antisymmetric coupling of proton and neutron eigenstates are usually referred to as mixed-symmetry states (MSS), whereas the symmetric coupling results in fully-symmetric states (FSS) Iachello (1984). Mixed-symmetry quadrupole excitations are predicted within the $sd$ proton-neutron version of the interacting boson model ($sd$-IBM-2) Arima and Iachello (1975); Arima et al. (1977); Otsuka et al. (1978); van Isacker et al. (1986), where $s$- and $d$-bosons are obtained by coupling protons and neutrons to pairs with angular momentum $L=0$ and $L=2$, respectively. In the IBM-2, MSS and FSS can be distinguished by their $F$-spin quantum number Arima et al. (1977); Otsuka et al. (1978), which is the bosonic analog of isospin for fermions. Strong $F$-vector ($\Delta F=1$) $M1$ transitions from MSS to their symmetric counterparts are predicted by the model. In the IBM-1, where proton and neutron bosons are not distinguished, $M1$ transitions with a one-body $M1$ transition operator are forbidden. Thus, $M1$ transitions serve as a key signature for MSS Heyde et al. (2010); Pietralla et al. (2008).

Mixed-symmetry quadrupole excitations are well established in the stable $N=52$ isotones Pietralla et al. (1999, 2000, 2001); Werner et al. (2002); Klein et al. (2002); Fransen et al. (2003, 2005); Linnemann et al. (2005); Orce et al. (2006); Pietralla et al. (2008), see Ref. Pietralla et al. (2008) for a review. In addition, the existence of higher-order multipolarity mixed-symmetry states has been recently proposed for the $N=52$ isotones ⁹²Zr and ⁹⁴Mo, namely, of octupole ($L=3$) Fransen et al. (2003); Smirnova et al. (2000); Scheck et al. (2010) and hexadecapole ($L=4$) character Fransen et al. (2003, 2005); Casperson et al. (2013). As for the quadrupole MSS, experimental evidence came from the observation of remarkably strong $M1$ transition strengths in the order of $\sim 1~\mu_{N}^{2}$ between the lowest-lying $3^{-}$ and $4^{+}$ states, respectively.

Candidates for octupole excitations with mixed-symmetry character have been proposed in various nuclei in the $A\approx 100$ mass region Scheck et al. (2010), among others also in the $N=52$ isotones ⁹²Zr and ⁹⁴Mo Fransen et al. (2005, 2003). MS octupole excitations were predicted in $sdf$-IBM-2 calculations Smirnova et al. (2000). Along with the $M1$ fingerprint, a sizable $E1$ transition to the FS one-phonon quadrupole state $2^{+}_{\mathrm{s}}$ is expected in the $U_{\pi\nu}(1)\otimes U_{\pi\nu}(5)\otimes U_{\pi\nu}(7)$ limit, according to the two-body nature of the $E1$ operator Pietralla et al. (2003); Scheck et al. (2010). In addition, a strong $E1$ transition to the MS one-phonon quadrupole state $2^{+}_{\mathrm{ms}}$ has been observed in the case of ⁹⁴Mo.

Recently, the strong $M1$ transition between the lowest-lying $4^{+}$ states of ⁹⁴Mo was successfully reproduced within the $sdg$-IBM-2 without abandoning the description of quadrupole MSS Casperson et al. (2013), suggesting the strong $M1$ transition to result from MS and FS one-phonon hexadecapole components in the $4^{+}_{2}$ and $4^{+}_{1}$ states, respectively. Additional evidence for this interpretation is provided by shell-model calculations for ⁹²Zr and ⁹⁴Mo Werner et al. (2002); Lisetskiy et al. (2000); Fransen et al. (2003), indicating dominant $\nu=2$, $j=4$ configurations for the lowest-lying $4^{+}$ states. These are by definition identified with $g$-bosons in the IBM; here, $\nu$ denotes the seniority.

The study in Ref. Casperson et al. (2013) was based on the only experimentally known case at that time. The intention of the present work is to show, that the case of ⁹⁴Mo is not exceptional, but that the presence of hexadecapole components in the wave functions of low-lying $4^{+}$ states in near-spherical nuclei is a general phenomenon. For this purpose, we have studied the heaviest stable $N=52$ isotone ⁹⁶Ru in two proton-scattering experiments. In addition, the structure of the low-lying $4^{+}$ states was investigated in the framework of $sdg$-IBM-2 calculations. Details on the experimental aspects will be given in a more extensive article.

Experiments. To identify MSS based on absolute transition strength, two inelastic proton scattering experiments were performed. The first one at the Wright Nuclear Structure Laboratory (WNSL) at Yale University, USA, the second one at the Institute for Nuclear Physics at the University of Cologne, Germany.

In the former, an $8.4~\mathrm{MeV}$ proton beam, provided by the ESTU Tandem Accelerator, impinged on a $106~\mathrm{\mu g/cm^{2}}$ enriched ⁹⁶Ru target, supported by a ¹²C backing with a thickness of $14~\mathrm{\mu g/cm^{2}}$. The scattered protons were detected using five silicon surface-barrier detectors, positioned predominantly at backward angles. For the $\gamma$-ray detection, eight BGO-shielded Clover-type HPGe detectors of the YRAST Ball spectrometer Beausang et al. (2000) were used. Further information on the experimental setup can be found in Ref. Elvers et al. (2011). From the energy information of scattered protons, the excitation energy $E_{x}$ was deduced on an event-by-event basis. Thus, $\gamma$-decay branching ratios were extracted with high sensitivity from the acquired $p\gamma$ coincidence data by gating on a specific excitation energy Wilhelm et al. (1996). Spin quantum numbers and multipole mixing ratios were obtained by means of the $\gamma\gamma$ angular-correlation technique Krane et al. (1973).

For the extraction of level lifetimes, a second proton-scattering experiment was performed at the Institute for Nuclear Physics at the University of Cologne. The same target was bombarded with a $7.0~\mathrm{MeV}$ proton beam, provided by the 10 MV FN Tandem accelerator. For the coincident detection of the scattered protons and de-exciting $\gamma$-rays, the particle-detector array SONIC, equipped with six passivated implanted planar silicon (PIPS) detectors, was embedded within the $\gamma$-ray spectrometer HORUS. Nuclear level lifetimes were measured by means of the Doppler-shift attenuation method (DSAM) Alexander and Forster (1978); Petkov et al. (1998) using $p\gamma$ coincidence data Seaman et al. (1969). Peak centroids were extracted from $\gamma$-ray spectra that were gated on the excitation energy of the level of interest. This way, feeding from higher-lying states is eliminated. The stopping process of the recoil nuclei in the target and stopper material was modeled by means of a Monte-Carlo simulation Currie (1969) using the computer code dstop96 Petkov et al. (1998) which is based on the code desastop Winter (1983). More detailed information on the experimental technique and the data analysis will be the subject of an upcoming publication. Absolute transition strengths were finally calculated from the combined experimental data of both experiments.

Mixed-symmetry octupole excitations. For the $J=3$ state of ⁹⁶Ru at $3076~\mathrm{keV}$, a negative parity has been previously assigned based on the observation of a $\gamma$ decay to the $5^{-}$ state at $2588~\mathrm{keV}$ Adamides et al. (1986). As in Klein et al. (2002), this $\gamma$ decay was not confirmed in the present experiments. However, since the $3^{-}_{\mathrm{ms}}$ candidates of ⁹⁴Mo ($3011~\mathrm{keV}$) and ⁹²Zr ($3040~\mathrm{keV}$) have been observed at similar excitation energies, a negative parity was assigned tentatively. With this assumption, an $M1$ transition strength of $B(M1)=0.14(4)~\mathrm{\mu_{N}^{2}}$ was obtained for the $3^{(-)}_{2}\rightarrow~3^{-}_{1}$ transition. Therewith, the $3^{(-)}_{2}$ state is a likely candidate for the one-phonon MS octupole state. As for the case of ⁹⁴Mo, an $E1$ strength of $B(E1)=0.14(3)~\mathrm{mW.u.}$ to the known $2^{+}_{\mathrm{ms}}$ state at $E_{x}=2283~\mathrm{keV}$ was obtained. However, only a weak $E1$ strength of $B(E1)=0.0017(3)~\mathrm{mW.u.}$ was extracted for the $3^{(-)}_{2}\rightarrow~2^{+}_{\mathrm{s}}$ transition.

As expected for collective excitations, the $3^{-}_{2}\rightarrow~3^{-}_{1}$ $M1$ matrix element scales with the one for the $2^{+}_{\mathrm{ms}}\rightarrow~2^{+}_{\mathrm{s}}$ transition for several nuclei in the $A\approx 100$ mass region Scheck et al. (2010), in particular also for the $N=52$ isotones ⁹²Zr and ⁹⁴Mo. With the bare $g$ factors ($g_{\pi}=1$ and $g_{\nu}=0$), a value of $\sqrt{14/5}\approx 1.67$ is predicted in the $U_{\pi\nu}(1)\otimes U_{\pi\nu}(5)\otimes U_{\pi\nu}(7)$ limit of the $sdf$-IBM-2 for the ratio of the matrix elements Smirnova et al. (2000). The experimental ratios are close to unity but stay rather constant Scheck et al. (2010). Only the value for ⁹⁶Mo deviates from the others by a factor of 2. From our new data, we calculated a ratio of $\frac{\left<3^{-}_{1}\left||M1\right||3^{(-)}_{2}\right>}{\left<2^{+}_{\mathrm{s}}\left||M1\right||2^{+}_{\mathrm{ms}}\right>}=0.53(9)$ for ⁹⁶Ru, close to the value for ⁹⁶Mo. The deviation of the ratio for ⁹⁶Ru compared to the values for the other $N=52$ isotones might result from the more $O(6)$-like structure of ⁹⁶Ru compared to, e.g., ⁹⁴Mo (see below).

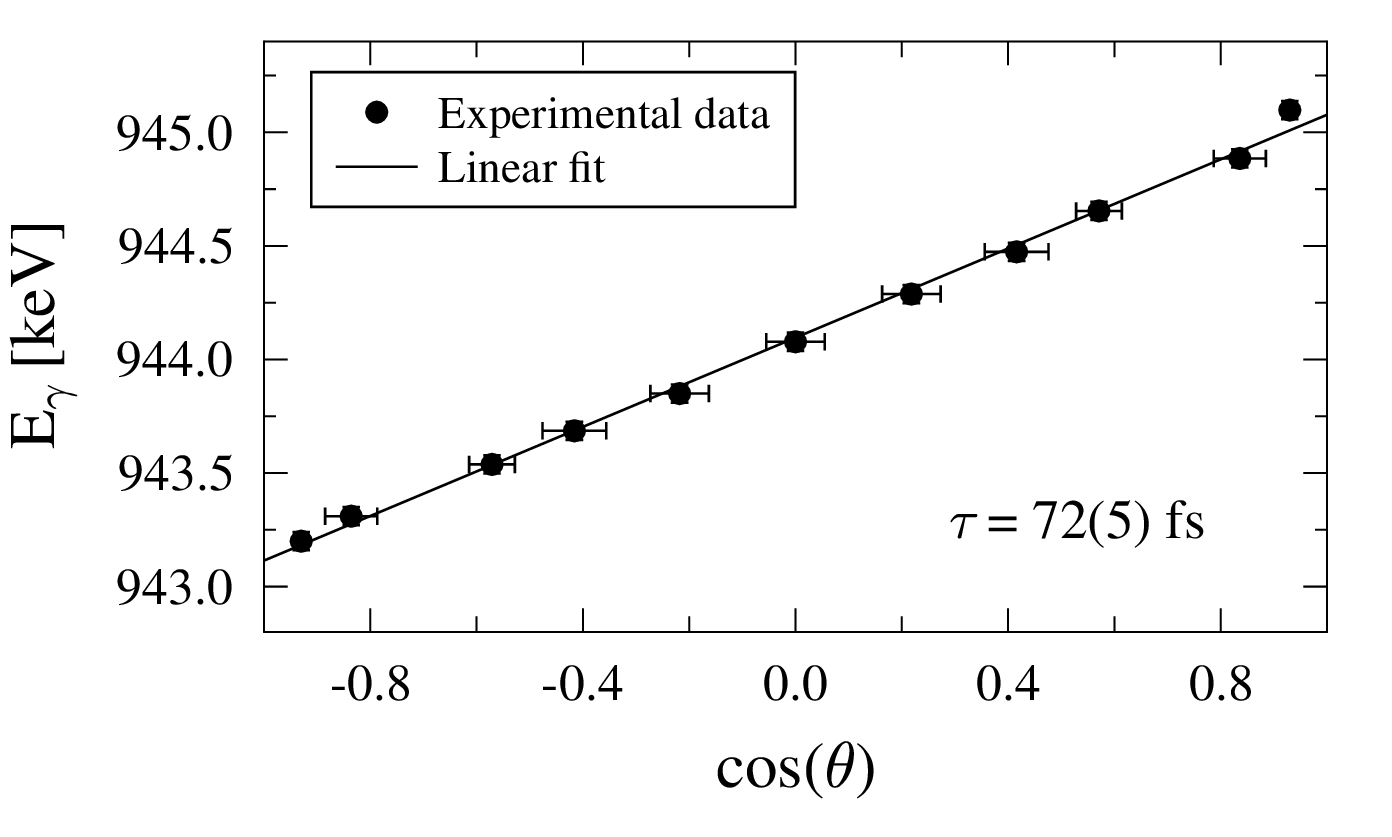
Hexadecapole excitations. For the $J=4$ state of ⁹⁶Ru at $E_{x}=2462~\mathrm{keV}$, a positive parity was assigned because of a newly observed $\gamma$-decay to the $2^{+}_{1}$ state. A lifetime of $\tau=140^{+70}_{-40}~\mathrm{fs}$ has been previously reported for this state Adamides et al. (1986), characterized by large uncertainties in the determination of the Doppler-shift attenuation factor. From our present analysis a lifetime of $\tau=72(5)~\mathrm{fs}$ was extracted. Figure 1 shows the centroid energy of the $E_{\gamma}^{0}=944~\mathrm{keV}$ $4^{+}_{2}\rightarrow~4^{+}_{1}$ $\gamma$-transition as a function of $\cos(\theta)$, where $\theta$ is the angle between the initial direction of motion of the recoil nucleus and the direction of the $\gamma$-ray emission. For the transition to the $4^{+}_{1}$ state, an $M1$ transition strength of $0.90(18)~\mathrm{\mu_{N}^{2}}$ was derived, which is even stronger than the $M1$ strength of the $2^{+}_{\mathrm{ms}}\rightarrow~2^{+}_{\mathrm{s}}$ transition Pietralla et al. (2001). The $M1$ strength between the lowest-lying $4^{+}$ states of ⁹⁴Mo is of comparable size Fransen et al. (2003). Hence, the $4^{+}_{2}$ state is a likely candidate to show one-phonon hexadecapole MS contributions.

$sdg$-IBM-2 calculations. The first $sdg$-IBM-2 calculations on the $N=52$ isotones were performed by Casperson et al. for the nucleus ⁹⁴Mo Casperson et al. (2013). For the first time, the strong $M1$ transition between the lowest-lying $4^{+}$ states in ⁹⁴Mo was reproduced without deteriorating the description of the well established quadrupole mixed-symmetry features. Motivated by this work, we chose the same Hamiltonian and transition operators for the description of ⁹⁶Ru:

with

and $\rho=\pi,\nu$. The $M1$ and $E2$ transition operators are defined as

and

respectively. For detailed information on the Hamiltonian and the transition operators, see Casperson et al. (2013). The calculations were performed with the computer code ArbModel Heinze (2008). The number of valence bosons was chosen with respect to ¹⁰⁰Sn as inert core, resulting in $N_{\pi}=3$ and $N_{\nu}=1$.

To reduce the number of parameters, the proton $g$-factors $g_{d_{\pi}}$ and $g_{g_{\pi}}$ were set equal and the neutron effective charges $e_{B_{\nu}}$ and $g$ factors $g_{d_{\nu}}$ and $g_{g_{\nu}}$ were set to zero, as were the parameters $\chi_{d}$ and $\chi_{g}$. To fix the remaining five free parameters of the Hamiltonian, a parameter scan was performed to optimize the calculation to reproduce the energy of the $2^{+}_{1}$ state, the $R_{4/2}$ ratio, the $B(E2;4^{+}_{1}\rightarrow~2^{+}_{1})/B(E2;2^{+}_{1}\rightarrow~0^{+}_{1})$ ratio, the energy of the known one-phonon quadrupole MSS, which is the $2^{+}_{3}$ state of ⁹⁶Ru Pietralla et al. (2001), and the $B(M1;4^{+}_{2}\rightarrow~4^{+}_{1})/B(M1;2^{+}_{3}\rightarrow~2^{+}_{1})$ ratio.

The effective charges $e_{B_{\rho}}$ set the scale for $E2$ transitions and were fixed to reproduce the $B(E2;2^{+}_{1}\rightarrow~0^{+}_{1})$ value. The $g$ factor $g_{\pi}=g_{d_{\pi}}=g_{g_{\pi}}$ was fixed to describe the $B(M1;2^{+}_{3}\rightarrow~2^{+}_{1})$ value. The obtained parameters are quoted in Table 1 and are similar to those obtained for ⁹⁴Mo Casperson et al. (2013). The larger value of $\zeta=0.78$ for ⁹⁶Ru indicates a more $O(6)$-like structure compared to ⁹⁴Mo. Only little difference is found for the excitation energies of the $d$ and $g$ bosons for ⁹⁶Ru, governed by the parameter $\alpha$.

The $sdg$-IBM-2 with the chosen Hamiltonian and parameters is a simplified approach. A more sophisticated description has to include for example non-vanishing parameters $\chi_{d,g}^{\rho}$ to allow $SU(3)$ contributions. However, the choice of $\chi^{\pi}_{d,g}\neq\chi^{\nu}_{d,g}$ would result in a breaking of $F$-spin symmetry, which was avoided to maintain a clear distinction between MSS and FSS. In addition, the chosen Hamiltonian conserves $d$-parity Pietralla et al. (1998).

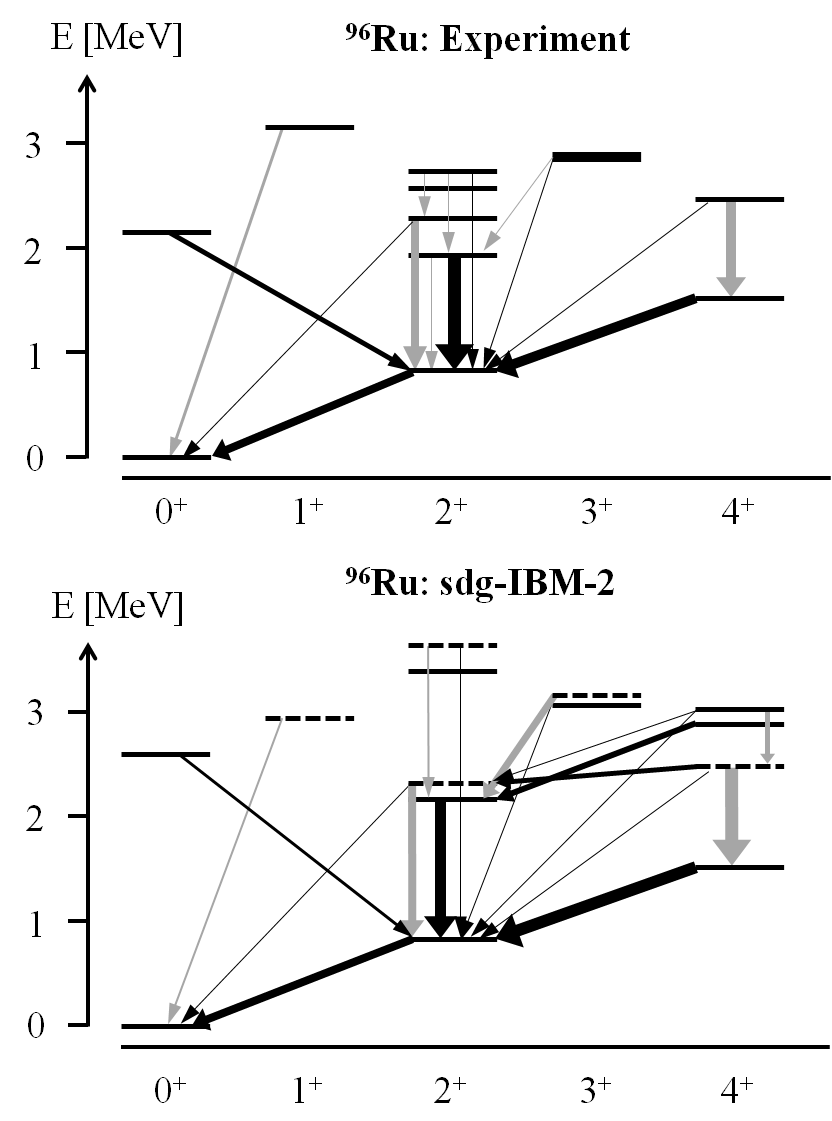
The calculated level scheme is in good agreement with the data, as shown in Fig. 2. In particular, the excitation energies of the $4^{+}_{1,2}$ states are well reproduced. Only for the excitation energies of the $2^{+}_{4}$ and $2^{+}_{5}$ states significant deviations from the experimental values were obtained.

The experimental and calculated level energies as well as the $M1$ and $E2$ transition strengths are compiled in Table 2. As for the level scheme, the transition strengths are in overall agreement. Only the transitions depopulating the $3^{+}$ states are predicted too strong by about one order of magnitude. For transitions which are forbidden for the applied Hamiltonian, only small transition strengths are observed experimentally. Of particular interest for the investigation of hexadecapole components in the $4^{+}_{1,2}$ states is the $4^{+}_{2}\rightarrow~4^{+}_{1}$ $M1$ transition. The IBM predicts a transition strength of $1.13~\mu_{N}^{2}$ which is close to the experimental value of $0.90(18)~\mu_{N}^{2}$. No other $4^{+}$ state is found to show enhanced $M1$ transitions to the $4^{+}_{1}$ state in the calculations. Also the $4^{+}_{2}\rightarrow~2^{+}_{1}$ $E2$ transition strength is reproduced by the model. The predicted $E2$ branching with sizable strength of $10.5~\mathrm{W.u.}$ to the $2^{+}_{3}$ state is way below the experimental sensitivity limit.

The predicted $F$-spin quantum numbers are shown in Table 2 as well. $F$-spin quantum numbers of $F_{\mathrm{max}}-1$ are obtained for the $2^{+}_{3}$, $1^{+}_{1}$, $3^{+}_{2}$, and $4^{+}_{2}$ states. From their decay properties, the $2^{+}_{3}$ state and the $1^{+}_{1}$ and $3^{+}_{2}$ states can be identified as the experimentally known one- and two-phonon quadrupole MSS, respectively Pietralla et al. (2001); Klein et al. (2002). They will be discussed in an upcoming publication. A mixed-symmetry character is also predicted for the $4^{+}_{2}$ state. A variation of the strength parameters $\lambda_{\mathrm{sd}}$ and $\lambda_{\mathrm{sg}}$ revealed, that the $4^{+}_{2}$ state is most sensitive to the $\hat{M}_{sg}$ operator. Thus a one-phonon mixed-symmetry hexadecapole character is obtained for the $4^{+}_{2}$ state. In contrast, a fully-symmetric character is predicted for the $4^{+}_{1}$ state based on the calculated $F$-spin quantum number.

To quantify the amount of $M1$ strength of the $4^{+}_{2}\rightarrow~4^{+}_{1}$ transition related to the $g$- and $d$-boson parts of the $M1$ operator, the $\left<4^{+}_{1}\left||M1\right||4^{+}_{2}\right>$ matrix element was recalculated with the values $g_{d_{\pi}}=0$ and $g_{g_{\pi}}=0$, respectively. The respective other value was kept at the value obtained from the parameter scan. With a contribution of $83\mathrm{\%}$ the $\left<4^{+}_{1}\left||M1\right||4^{+}_{2}\right>$ matrix element is dominated by the $g$-boson part of the $M1$ operator, while only $17\mathrm{\%}$ is related to the $d$-boson part.

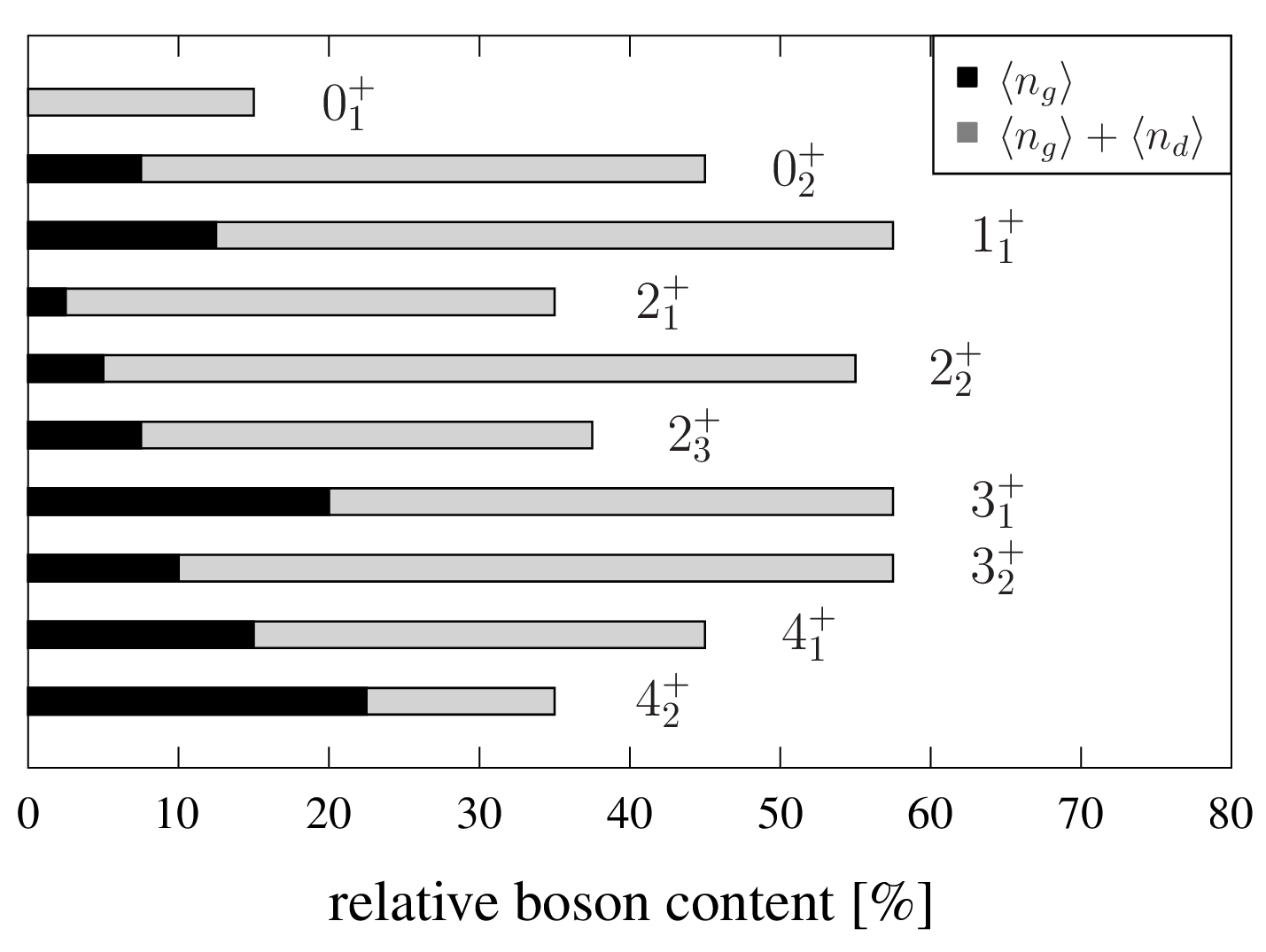
The $d$- and $g$-boson contents of the low-lying, positive-parity low-spin states are shown in Fig. 3. With a value of $23~\mathrm{\%}$, the largest $g$-boson content is obtained for the $4^{+}_{2}$ state, supporting the one-phonon hexadecapole assignment. A similar $g$-boson contribution is predicted for the $3^{+}_{1}$ state. This can be explained assuming a dominant $(g^{\dagger}d^{\dagger})^{(3)}$ structure. In this case the $E2$ transition to the $2^{+}_{1}$ state would be forbidden by $d$-parity selection rules. This is supported by the calculation and is in remarkable agreement with the data (see Table 2). Also for the $4^{+}_{1}$ state a large $g$-boson content is obtained which is considerably enhanced compared to, e.g., the $2^{+}_{2}$ state, which is known to be the $2^{+}$ member of the ($2^{+}_{\mathrm{s}}\otimes 2^{+}_{\mathrm{s}}$) triplet. In addition to the $g$-boson content, a $d$-boson contribution of about $30~\mathrm{\%}$ is predicted by the IBM for the $4^{+}_{1}$ state. For the chosen parameter of $\beta$, a mixing of the one-phonon $g$-boson excitation with two-phonon $d$-boson excitations is allowed, which are at similar energies. This is also reflected by the collective $B(E2;4^{+}_{1}\rightarrow~2^{+}_{1})$ transition strength. In contrast, the $d$-boson content of the $4^{+}_{2}$ state is a factor of 2 less compared to the $4^{+}_{1}$ state.

If the enhanced $g$-boson contributions can be attributed to one-phonon hexadecapole contents in the wave functions, this should lead to sizable $E4$ strengths. The $E4$ transition operator was defined in the same way as in Casperson et al. (2013), namely

Since no $B(E4)$ strengths are known for ⁹⁶Ru so far, the $e_{\pi 1}$ value was arbitrarily set to $1~\sqrt{\mathrm{W.u.}}$. With this, $E4$ transition strengths of $1.09$ and $0.55~\mathrm{W.u.}$ are predicted for the $4^{+}_{1}$ and $4^{+}_{2}$ states, respectively. Their $E4$ strengths are enhanced compared to, e.g., that of the $4^{+}_{3}$ state. However, a similar $E4$ transition to the ground state is predicted for the $4^{+}_{4}$ state as well. Further constraints for the $E4$ transition operator might be obtained from a measurement of $E4$ strengths, e.g., in $(e,e^{\prime})$ experiments.

To conclude, the $sdg$-IBM-2 calculations provide strong evidences for MS and FS one-phonon hexadecapole contributions to the lowest-lying $4^{+}$ states of ⁹⁶Ru. However, other mechanisms, such as the $g$ factors of the individual microscopic configurations in their wave functions have to be considered as well as being responsible for the generation of $M1$ strengths between low-lying $4^{+}$ states. They might be studied within the scope of shell-model calculations with realistic interactions or the quasiparticle phonon model (QPM).

Comparison to ⁹²Zr and ⁹⁴Mo. With the new experimental data obtained in this work, one-phonon MSS of quadrupole and possible octupole and hexadecapole character were studied in the $N=52$ isotones as a function of proton number. Figure 4 shows the $M1$ transition strengths of the one-phonon MS to FS states for the different multipolarities for the nuclei ⁹²Zr, ⁹⁴Mo, and ⁹⁶Ru. While for the quadrupole states an increase of $M1$ strength is observed with increasing proton number, the $M1$ strength decreases from ⁹⁴Mo to ⁹⁶Ru for higher multipolarities. It has to be mentioned, that the decrease might be related to a possible fragmentation of the one-phonon octupole and hexadecapole mixed-symmetry states which can not be excluded on the basis of the present experimental data.

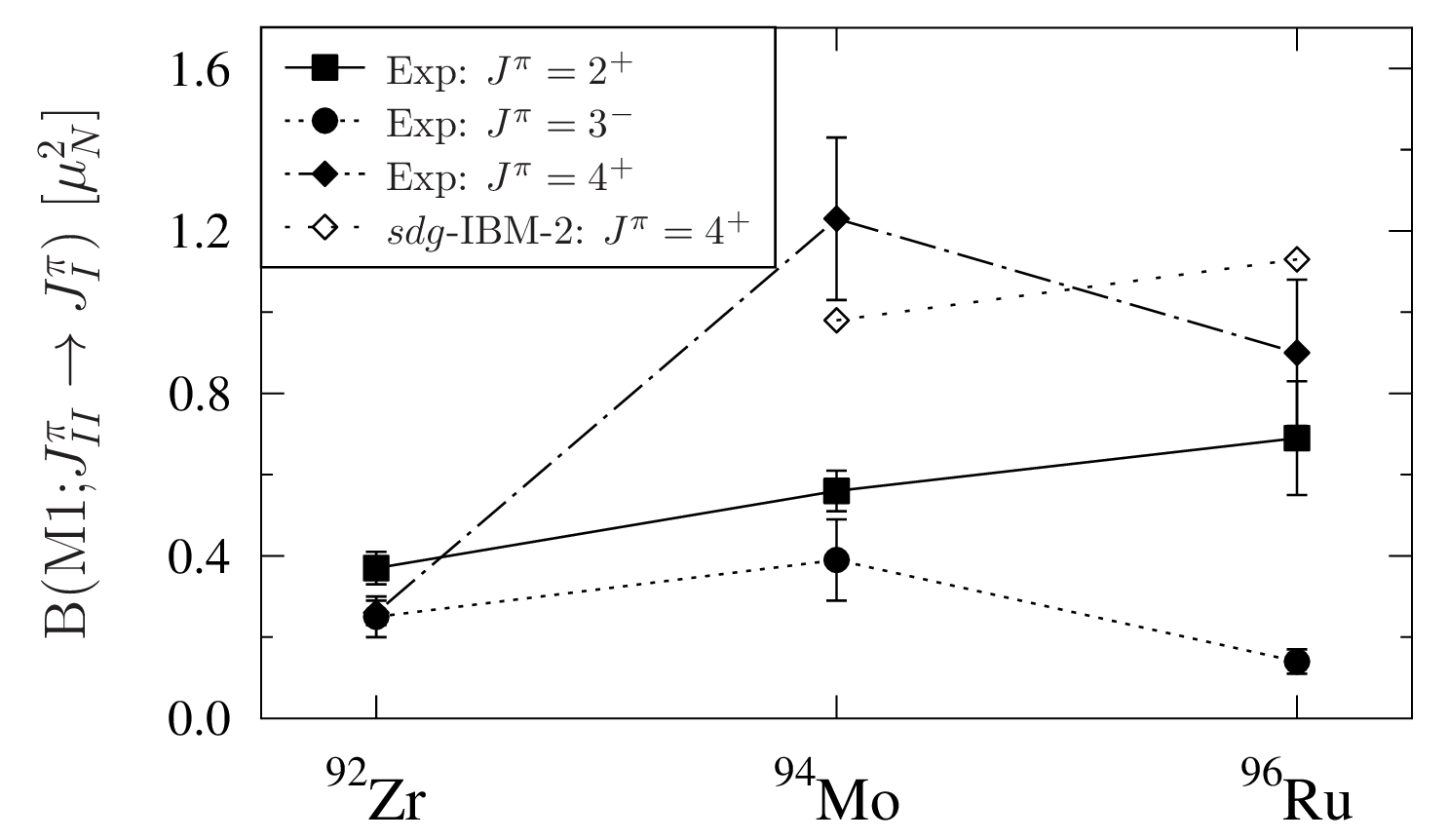
The trend for the quadrupole states agrees with shell-model calculations, predicting a maximum $M1$ strength for ⁹⁶Ru, based on the concept of configuration isospin polarization (CIP) Holt et al. (2007). Unfortunately, no results on $4^{+}$ states were reported in Ref. Holt et al. (2007). The decrease of the $M1$ strengths for the $4^{+}$ states with increasing proton number is not reproduced by the IBM, which predicts a similar trend as for the quadrupole states.

Summary. The observation of strong $M1$ transitions in ⁹⁶Ru between the lowest-lying $3^{-}$ and $4^{+}$ states provides experimental evidence for one-phonon mixed-symmetry octupole and hexadecapole components in the wavefunctions of the $3^{(-)}_{2}$ and $4^{+}_{2}$ states, respectively. The interpretation on the latter is supported by $sdg$-IBM-2 calculations. Together with the results of Ref. Casperson et al. (2013), the new data on ⁹⁶Ru suggest that the presence of hexadecapole components in the wave functions of low-lying $4^{+}$ states is a general phenomenon in near spherical nuclei.

Acknowledgments. The authors thank R. Casperson and S. Heinze for support with the IBM calculations and A. Poves for useful discussions. Furthermore, we highly acknowledge the support of the accelerator staff at WNSL, Yale and IKP, Cologne during the beam times. This work is supported by the DFG under grant No. ZI 510/4-2 and grant No. SFB 634, the U.S. Department of Energy grant No. DE-FG02-01ER40609, and the BMBF grant No. 05P12RDFN8. P.P. is grateful for the financial support of the Bulgarian Science Fund under contract DFNI-E 01/2. D.R. and D.S. acknowledge the German Academic Exchange Service (DAAD) for financial support. S.G.P. and M.S. are supported by the Bonn-Cologne Graduate School of Physics and Astronomy.