MMHMR: Generative Masked Modeling for Hand Mesh Recovery

Muhammad Usama Saleem, Ekkasit Pinyoanuntapong, Mayur Jagdishbhai Patel, Hongfei Xue,
Ahmed Helmy, Srijan Das, Pu Wang
University of North Carolina at Charlotte, Charlotte, NC, USA
{msaleem2, epinyoan, mpate169, hxue2, ahelmy1, sdas24, pwang13}@charlotte.edu

Abstract

Reconstructing a 3D hand mesh from a single RGB image is challenging due to complex articulations, self-occlusions, and depth ambiguities. Traditional discriminative methods, which learn a deterministic mapping from a 2D image to a single 3D mesh, often struggle with the inherent ambiguities in 2D-to-3D mapping. To address this challenge, we propose MMHMR, a novel generative masked model for hand mesh recovery that synthesizes plausible 3D hand meshes by learning and sampling from the probabilistic distribution of the ambiguous 2D-to-3D mapping process. MMHMR consists of two key components: (1) a VQ-MANO, which encodes 3D hand articulations as discrete pose tokens in a latent space, and (2) a Context-Guided Masked Transformer that randomly masks out pose tokens and learns their joint distribution, conditioned on corrupted token sequence, image context, and 2D pose cues. This learned distribution facilitates confidence-guided sampling during inference, producing mesh reconstructions with low uncertainty and high precision. Extensive evaluations on benchmark and real-world datasets demonstrate that MMHMR achieves state-of-the-art accuracy, robustness, and realism in 3D hand mesh reconstruction. Project website: https://m-usamasaleem.github.io/publication/MMHMR/mmhmr.html.

1 Introduction

Hand mesh recovery has gained significant interest in computer vision due to its broad applications in fields such as robotics, human-computer interaction [41, 53], animation, and AR/VR [10, 30]. While previous methods have explored markerless, image-based hand understanding, most depend on depth cameras [3, 22, 42, 47, 54] or multi-view images [5, 23, 51, 52]. Consequently, most of these methods are not feasible for real-world applications where only monocular RGB images are accessible. On the other hand, monocular hand mesh recovery from a single RGB image, especially without body context or explicit camera parameters, is highly challenging due to substantial variations in hand appearance in 3D space, frequent self-occlusions, and complex articulations.

Recent advances, especially in transformer-based methods, have shown significant promise in monocular hand mesh recovery (HMR) by capturing intricate hand structures and spatial relationships. For instance, METRO [13] and MeshGraphormer [39] utilize multi-layer attention mechanisms to model both vertex-vertex and vertex-joint interactions, thereby enhancing mesh fidelity. Later, HaMeR [46] illustrated the scaling benefits of large vision transformers and extensive datasets for HMR, achieving improved reconstruction accuracy. However, these methods are inherently discriminative, producing deterministic outputs for each image. Consequently, they face limitations in complex, real-world scenes where ambiguities arise due to occlusions, hand-object interactions, and challenging viewpoints are prevalent.

To overcome these limitations, we introduce MMHMR, a novel generative masked model designed for accurate 3D hand mesh recovery. By learning and sampling from the underlying joint distribution of hand articulations and image features, our model synthesizes most probable 3D hand meshes, mitigating ambiguities inherent in single-view reconstruction. MMHMR consists of two main components: a VQ-MANO and a context-guided masked transformer, which are trained in two consecutive stages. In the first stage, VQ-MANO is trained with Vector Quantized Variational Autoencoders (VQ-VAE) [56] to encode continuous hand poses (e.g., joint rotations) of the MONO parametric hand model into a sequence of discrete pose tokens. In the second stage, the token sequence is partially masked and the context-guided masked transformer is trained to reconstruct the masked tokens by learning token conditional distribution, based on multiple contextual clues, including corrupted token sequence, image features, and 2D pose structures.

This generative masked training allows MMHMR to learn an explicit probabilistic mapping from 2D images to plausible 3D hand meshes. Such probabilistic mapping enables confidence-guided sampling during inference, where only pose tokens with high prediction confidence are retained. This sampling process enables MMHMR to leverage measurable uncertainty to mitigate ambiguities in the 2D-to-3D mapping, resulting in enhanced mesh reconstruction accuracy. Our contributions are summarized as follows

•

MMHMR is the first to leverage generative masked modeling for reconstructing robust 3D hand mesh. The main idea is to explicitly learn the 2D-to-3D probabilistic mapping and synthesize high-confidence, plausible 3D meshes by sampling from learned probabilistic distribution.
•

We design context-guided masked transformer that effectively fuses multiple contextual clues, including 2D pose, image features, and unmasked 3D pose tokens.
•

We propose differential masked training to learn hand pose token distribution, conditioned on all contextual clues. This learned distribution facilitates confidence-guided sampling during inference, producing mesh reconstructions with low uncertainty and high precision.
•

We demonstrate through extensive experiments that MMHMR outperforms SOTA methods on standard datasets.

2 Related Work

2.1 Discriminative Methods

Human hand recovery has been developed in recent years, with early approaches [21, 28, 55, 58, 68, 70] leveraging optimization techniques to estimate hand poses based on 2D skeleton detections. Later, MANO [49] introduced a differentiable parametric mesh model that capture hand shape and articulation, allowing the model to provide a plausible mesh with end-to-end estimation of model parameters directly from a single-view image. Boukhayma et al. [6] presented the first fully learnable framework to directly predict the MANO hand model parameters [49] from RGB images. Similarly, several subsequent methods have leveraged heatmaps [67] and iterative refinement techniques [4] to ensure 2D alignment. Kulon et al. [34, 35] proposed a different regression approach that predicts 3D vertices instead of MANO pose parameters, achieving notable improvements over prior methods. Recent methods, such as METRO [13], MeshGraphormer [39], HaMeR [46] achieve the SOTA performance by modeling both vertex-vertex and vertex-joint interactions. These existing methods, based on discriminative regression, learn a deterministic mapping from the input image to the output mesh. This deterministic approach struggles to capture the uncertainties and ambiguities caused by hand self-occlusions, interactions with objects, and extreme poses or camera angles, resulting in unrealistic hand mesh reconstructions.

2.2 Generative Methods

Our MMHMR employs a generative method that learns a probabilistic mapping from the input image to the output mesh. It utilizes this learned distribution to synthesize high-confidence, plausible 3D hand meshes based on 2D visual contexts. HHMR [37] is the only other generative hand mesh recovery method in the literature. Unlike HHMR [37] that utilizes diffusion models, MMHMR is inspired by the success of masked image and language models for image and text generation tasks [16, 69, 7, 17, 8]. This fundamental difference allows MMHMR to explicitly and quantitatively estimate confidence levels or prediction probabilities for all mesh reconstruction hypotheses, enabling confidence-guided hypothesis selection for accurate reconstruction. In contrast, HHMR’s denoising diffusion process synthesizes multiple mesh hypotheses without associating a confidence level with each hypothesis. Thus, it only reports the theoretically best mesh reconstruction by finding the hypothesis with minimal reconstruction errors under the assumption that ground-truth meshes are available.

3 Proposed Method: MMHMR

Problem Formulation. Given a single-hand image $I$ , we aim to learn a mapping function $f(I)=\{\theta,\beta,\pi\}$ that regresses the MANO [49] model parameters from the input image. This mapping function encompasses three key components: the hand pose parameters $\theta\in\mathbb{R}^{48}$ , shape parameters $\beta\in\mathbb{R}^{10}$ , and camera parameters $\pi\in\mathbb{R}^{3}$ , enabling comprehensive 3D hand reconstruction.

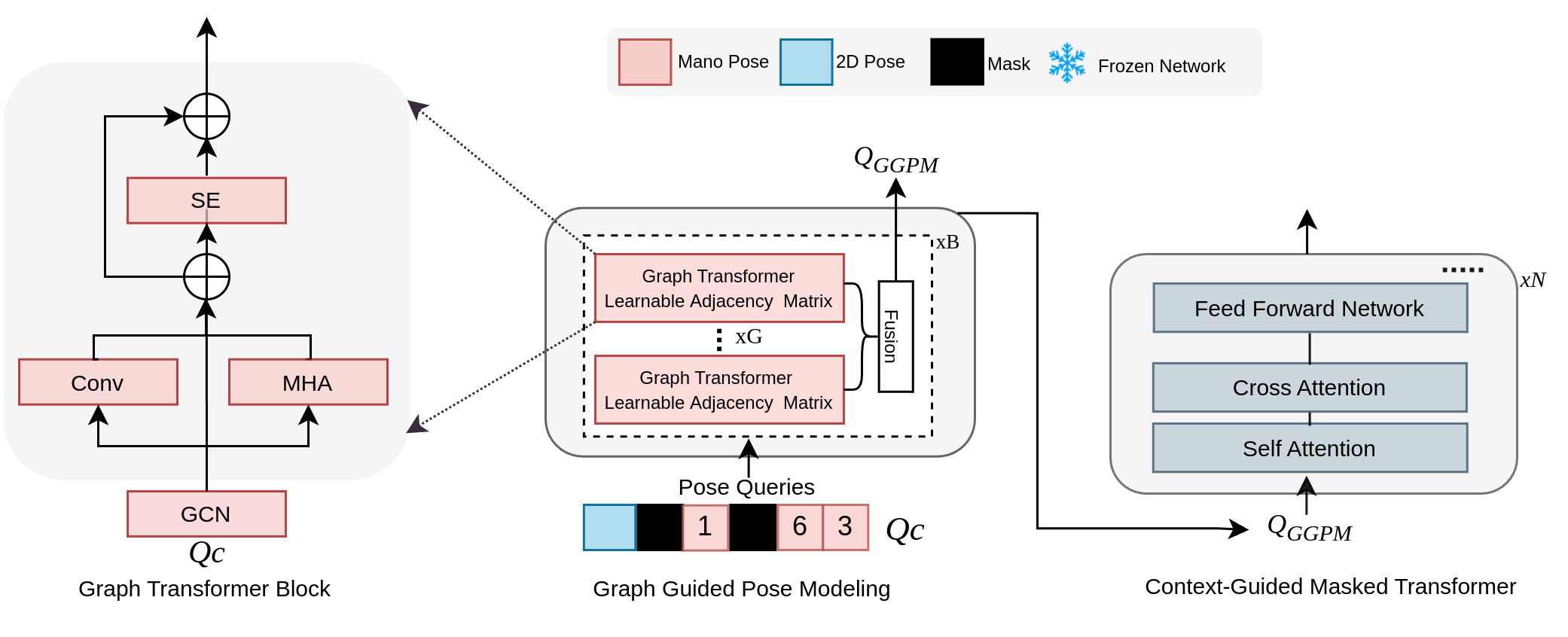
Overview of Proposed Method. As depicted in Figure 1, the MMHMR architecture comprises two main modules: VQ-MANO and the Context-Guided Masked Transformer. The process initiates with VQ-MANO, which converts 3D MANO pose parameters ( $\theta$ ) into discrete pose tokens. These tokens are then processed by the Context-Guided Masked Transformer, which includes a image encoder and masked decoder. The encoder extracts multi-scale image features, which, along with 2D pose guidance and unmasked pose tokens, are fused by masked graph transformer decoder. Within the decoder, Graph-Guided Pose Modeling ensures anatomical coherence by modeling joint dependencies, while the Context-Infused Masked Synthesizer fuses image features and token dependencies to learn the probabilistic reconstruction of pose tokens via differential masked modeling. During inference, the model iteratively refines pose predictions, retaining high-confidence tokens and re-masking those with low confidence, leveraging image semantics, inter-token relationships, and 2D pose guidance to progressively improve accuracy. Finally, the reconstruction is completed as the predicted pose ( $\theta$ ) , shape ( $\beta$ ) and camera parameters ( $\pi$ ) are feed into the MANO hand model.

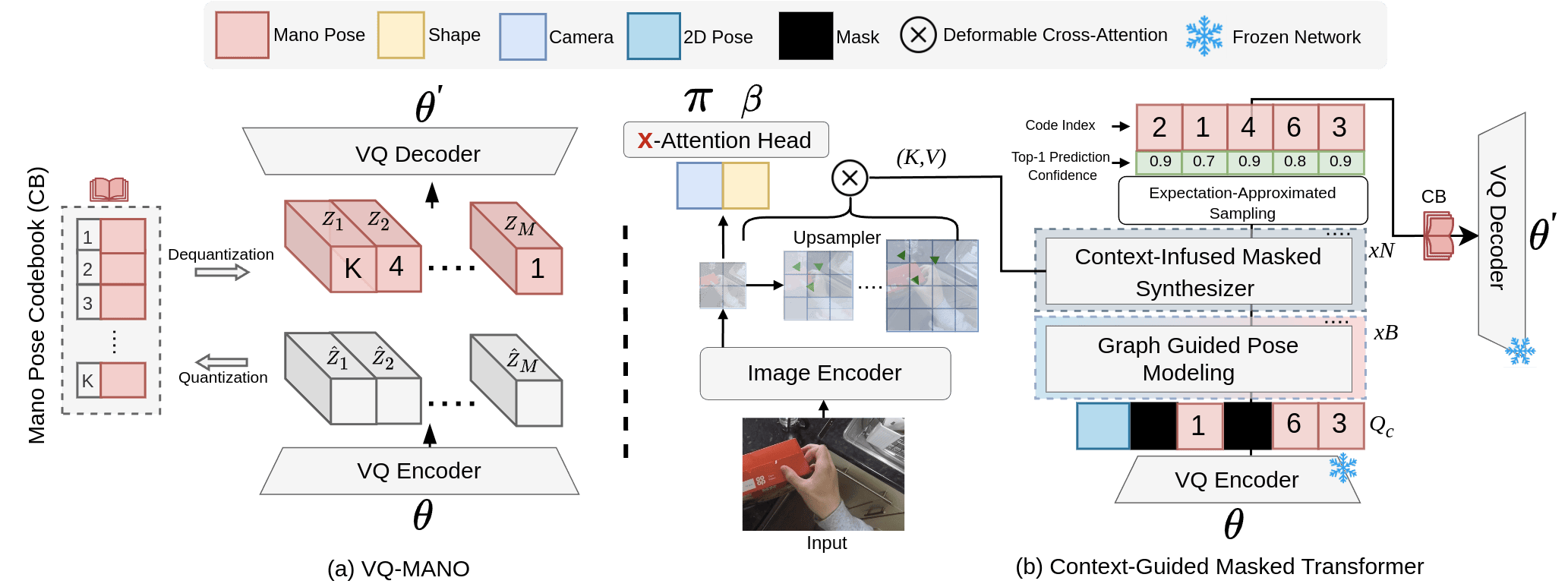
Refer to caption — Figure 1: MMHMR Training Phase. MMHMR consists of two key components: (1) VQ-MANO, which encodes 3D hand poses into a sequence of discrete tokens within a latent space, and (2) a Context-Guided Masked Transformer that models the probabilistic distributions of these tokens, conditioned on the input image, 2D pose cues, and a partially masked token sequence.

3.1 Hand Model and VQ-MANO

Our approach utilizes the MANO hand model [49], which takes pose parameters $\theta\in\mathbb{R}^{48}$ and shape parameters $\beta\in\mathbb{R}^{10}$ as input. The function $M(\theta,\beta)$ outputs a 3D hand mesh $M\in\mathbb{R}^{V\times 3}$ with $V=778$ vertices and joint locations $X\in\mathbb{R}^{K\times 3}$ with $K=21$ joints, enabling both surface and pose representation.

The VQ-MANO is a MANO hand tokenizer that learn a discrete latent space for 3D pose parameters $\theta\in\mathbb{R}^{48}$ by quantizing the continuous pose embeddings into a learned codebook $C$ with discrete code entries, as depicted in Figure 1(a). To this end, we employ a Vector Quantized Variational Autoencoder (VQ-VAE) [56] for pretraining the tokenizer. Specifically, we input the MANO pose parameters $\theta$ into a convolutional encoder $E$ , which maps them to a latent embedding $z$ . Each embedding $z_{i}$ is then quantized to its nearest codebook entry $c_{k}\in C$ based on Euclidean distance, defined as

\hat{z}_{i}=\arg\min_{c_{k}\in C}\|z_{i}-c_{k}\|_{2}.

The total loss function of VQ-MANO is formulated as:

\mathcal{L}_{\text{vq-mano}}=\lambda_{\text{re}}\mathcal{L}_{\text{recon}}+\lambda_{\text{E}}\|\operatorname{sg}[z]-c\|_{2}+\lambda_{\alpha}\|z-\operatorname{sg}[c]\|_{2},

where $\mathcal{L}_{\text{vq-mano}}$ consists of a MANO reconstruction loss $\mathcal{L}_{\text{recon}}$ , a latent embedding loss, and a commitment loss, weighted by hyperparameters $\lambda_{\text{re}}$ , $\lambda_{\text{E}}$ , and $\lambda_{\alpha}$ , respectively. Here, $\operatorname{sg}[\cdot]$ denotes the stop-gradient operator, which prevents gradients from flowing through its argument during backpropagation. To further enhance reconstruction quality, we incorporate an additional L1 loss:

\mathcal{L}_{\text{recon}}=\lambda_{\theta}\mathcal{L}_{\theta}+\lambda_{\text{V}}\mathcal{L}_{\text{V}}+\lambda_{\text{J}}\mathcal{L}_{\text{J}},

which aims to minimize the discrepancies between the predicted and ground-truth MANO parameters, including the pose parameters $\theta$ , mesh vertices $V$ , and hand joints $J$ . The tokenizer is optimized using a straight-through gradient estimator to facilitate gradient propagation through the non-differentiable quantization step. Additionally, the codebook entries $C$ are updated via exponential moving averages and periodic codebook resets, as described in [19, 60].

3.2 Context-Guided Masked Transformer

The context-guided masked transformer comprises two main components: the multi-scale image encoder and the masked graph transformer decoder.

3.2.1 Multi-scale Image Encoder

Our encoder uses a vision transformer (ViT-H/16) to extract image features [46], processing 16x16 pixel patches into feature tokens. Following ViTDet [2], we adopt a multi-scale feature approach by upsampling the initial feature map to produce feature maps at varying resolutions. This multi-scale representation is critical for handling complex articulations and self-occlusions in hand poses. High-resolution maps provide fine-grained joint details, while low-resolution maps capture global hand structure, balancing precision in joint positioning with overall anatomical coherence. Moreover, we utilize cross-attention with low-resolution feature maps in the x-Attention head to regress stable shape parameters ( $\beta$ ) and camera orientation ( $\pi$ ), making the process computationally efficient. This approach decouples shape estimation from pose modeling, preserving morphological stability and spatial alignment, and enhancing robustness and anatomical accuracy in 3D hand reconstruction.

3.2.2 Masked Graph Transformer Decoder

The Masked Transformer Decoder is composed of two key components: Graph-Guided Pose Modeling (GGPM) and the Context-Infused Masked Synthesizer Module.

Graph-Guided Pose Modeling (GGPM). Our decoder employs 2 blocks of lightweight graph transformer that processes pose tokens generated by VQ-MANO, enriched with 2D pose guidance, where hand pose tokens are represented as graph nodes linked by learnable adjacency matrices to capture joint relationships effectively. To enhance stability and anatomical accuracy, we integrate a transformer encoder with a Squeeze-and-Excitation (SE) block [29], which emphasizes joint orientations and angles and ensures spatial alignment through a 1x1 convolution layer. Within the transformer encoder, Multi-Head Attention (MHA) and pointwise convolution layers refine high-resolution dependencies between joints, producing a cohesive and anatomically aligned 3D pose representation, denoted as $Q_{\text{GGPM}}$ . The output $Q_{\text{GGPM}}$ is formulated as:

Q^{\prime}=\text{MHA}(\text{Norm}(Q_{\text{C}}))+\text{Conv}(\text{Norm}(Q_{\text{C}}))+Q_{\text{C}}

(1)

Q_{\text{GGPM}}=\text{SE}(\text{Norm}(Q^{\prime}))

(2)

where $Q_{\text{C}}\in\mathbb{R}^{K\times D}$ represents refined MANO pose tokens and 2D pose guidance queries, and $Q_{\text{GGPM}}$ is the stabilized, anatomically consistent pose representation. The refined pose token queries $Q_{\text{GGPM}}$ are then passed to the Context-Infused Masked Synthesize to synthesize a precise 3D hand mesh that integrates global and local anatomical features.

Context-Infused Masked Synthesizer. We leverage a multi-layer transformer whose inputs are refined pose tokens $Q_{\text{GGPM}}$ and cross-attends them with multi-scale feature maps generated by the image encoder. To enhance computational efficiency with high-resolution feature maps, a deformable cross-attention mechanism is employed [72]. This allows each pose token to focus on a selected set of sampling points around a learnable reference point, rather than the entire feature map. By concentrating attention on relevant areas, the model achieves a balance between computational efficiency and spatial precision, preserving essential information for accurate 3D hand modeling. The deformable cross-attention is defined as:

\text{MCDA}(Q_{\text{GGPM}},\hat{p}_{y},\{x^{l}\})=\sum_{l,k}A_{lyk}\cdot\mathbf{W}x^{l}(\hat{p}_{y}+\Delta p_{lyk})

where $Q_{\text{GGPM}}$ are refined manopose token queries, $\hat{p}_{y}$ are learnable reference points, $\Delta p_{lyk}$ are sampling offsets, $\{x^{l}\}$ are multi-scale features, $A_{lyk}$ are attention weights, and $\mathbf{W}$ is a learnable weight matrix. With the inclusion of a [MASK] token in the masked transformer decoder, the module can predict masked pose tokens during training, while also facilitating token generation during inference. This approach allows the [MASK] token to serve as a placeholder for final pose token predictions, supporting robust synthesis of occluded or unobserved hand parts for a coherent 3D hand reconstruction.

3.3 Training: Differential Masked Modeling

Context-conditioned Masked Modeling. We employ masked modeling to train our model that learns the probabilistic distribution of 3D hand poses, conditioned on multiple contextual cues. Given a sequence of discrete pose tokens $Y=[y_{i}]_{i=1}^{L}$ from the pose tokenizer, where $L$ is the sequence length, we randomly mask out a subset of $m$ tokens with $m=\lceil\gamma(\tau)\cdot L\rceil$ , where $\gamma(\tau)$ is a cosine-based masking ratio function. Here, $\tau$ is drawn from a uniform distribution $U(0,1)$ , and we adopt the masking function $\gamma(\tau)=\cos\left(\frac{\pi\tau}{2}\right)$ , inspired by generative text-to-image modeling strategies [7].

Masked tokens are replaced with learnable [MASK] tokens, forming a corrupted sequence $Y_{\overline{\mathbf{M}}}$ that the model must reconstruct. Each token $y_{i}$ is predicted based on the probabilistic distribution $p(y_{i}|Y_{\overline{\mathbf{M}}},X_{2D},X_{img})$ , conditioned on corrupted token sequence $Y_{\overline{\mathbf{M}}}$ , 2D pose embedding $X_{2D}$ , and image prompt $X_{img}$ . This approach enables the model to explicitly account for the uncertainty inherent in mapping 2D observations to a coherent 3D hand mesh. The training objective is to minimize the negative log-likelihood of correctly predicting each pose token in the sequence, formulated as follows:

\mathcal{L}_{\text{mask}}=-\mathbb{E}_{Y\in\mathcal{D}}\left[\sum_{\forall i\in[1,L]}\log p(y_{i}|Y_{\overline{\mathbf{M}}},X_{2D},X_{img})\right].

Expectation-Approximated Differential Sampling. The training objective, $\mathcal{L}_{\text{mask}}$ , captures stochastic uncertainty in hand mesh reconstruction, enabling precise estimation of the pose parameter $\theta$ within a structured discrete latent space. Recent studies [46] demonstrate that applying auxiliary 3D and 2D joint losses—measuring alignment between predicted and ground-truth joints in both 3D coordinates and their 2D projections—further refines pose recovery. In generative masked model training, integrating these auxiliary losses requires transforming latent pose tokens into the MANO pose parameter $\theta$ , a process that involves non-differentiable probabilistic sampling. To address this, instead of sampling the distribution $p(y_{i}|Y_{\overline{\mathbf{M}}},X_{2D},X_{img})$ to obtain the most probable token from codebook, we implement an expectation-based differential relaxation: instead of directly estimating discrete code indices, the model outputs logits $L$ for each token. These logits undergo a softmax operation, producing the token distribution, which are multiplied by the pretrained codebook, resulting in the mean quantized feature representations $\bar{z}=[\bar{z}_{1},\bar{z}_{2},\dots,\bar{z}_{M}]$ :

\bar{z}=\textnormal{softmax}(L_{M\times K})\times\text{CB}_{K\times D}

where $L$ represents the logits matrix, CB denotes the codebook, $M$ is the token count, $K$ specifies the codebook size, and $D$ defines the dimensionality of each codebook entry. This mean token embeddings $\bar{z}$ are feed into the decoder to reconstruct the pose parameter $\theta^{\prime}$ . Combined with shape parameters $\beta$ and camera parameters $\pi$ , this process reconstructs the 3D hand mesh, enabling the computation of both 3D joint loss and 2D projection loss. Since obtaining $\bar{z}$ is differential, the model can be trained end-to-end using the overall loss function

\mathcal{L}_{\text{total}}=\mathcal{L}_{\text{mask}}+\mathcal{L}_{\text{MANO}}+\mathcal{L}_{\text{3D}}+\mathcal{L}_{\text{2D}}

which combines the masked token prediction loss ( $\mathcal{L}_{\text{mask}}$ ), 3D joint loss ( $\mathcal{L}_{\text{3D}}$ ), 2D projection loss ( $\mathcal{L}_{\text{2D}}$ ), and MANO parameter loss $\mathcal{L}_{\text{MANO}}$ . Together, these terms collectively minimize discrepancies in the shape and pose parameters within the MANO space, leading to a precise reconstruction of the 3D hand mesh.

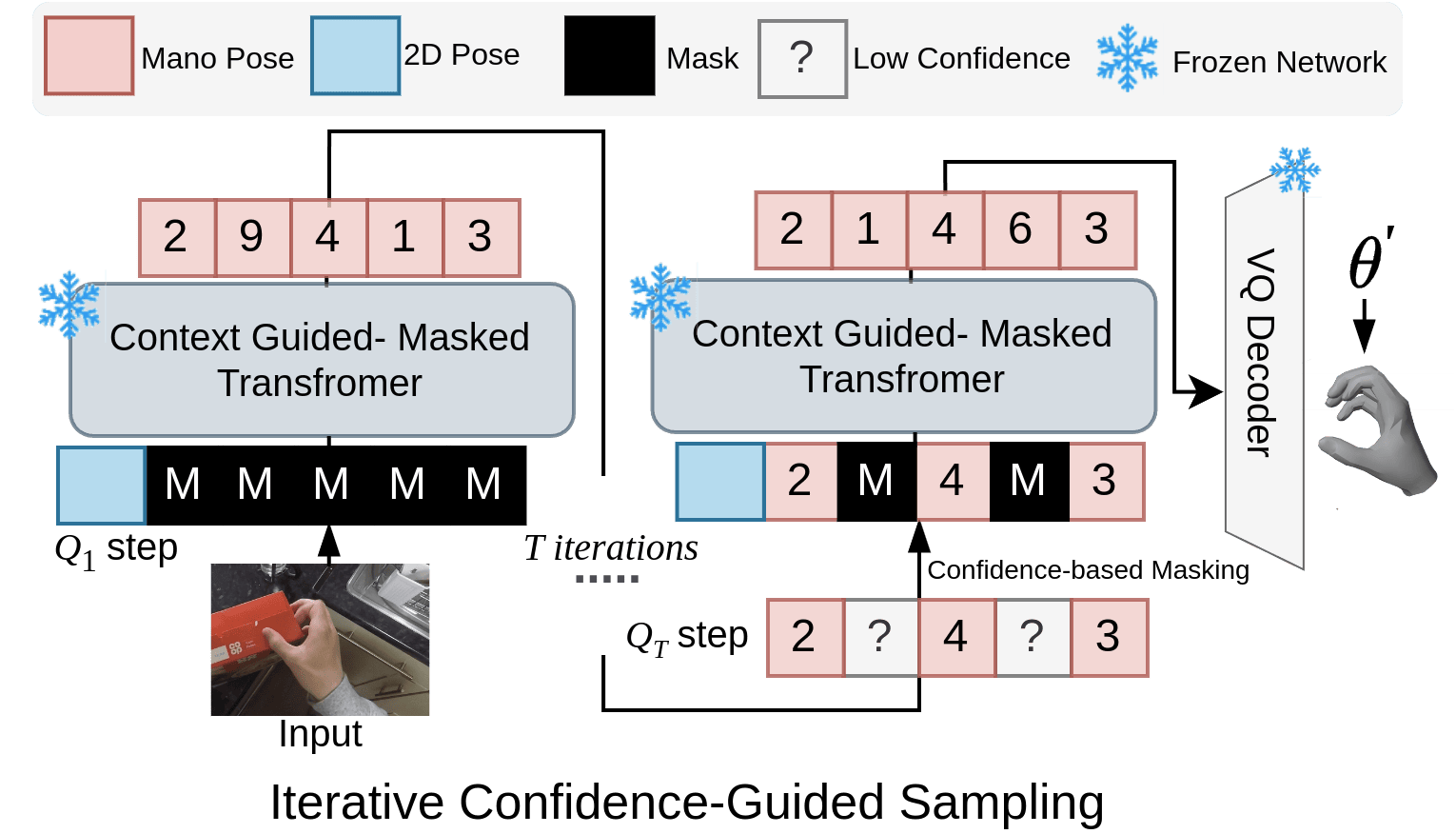
3.4 Inference: Confidence-Guided Sampling

Our model leverages confidence-guided sampling to achieve precise and stable 3D hand pose predictions. This process begins with a fully masked sequence $Y_{1}$ of length $L$ , with each token initialized as [MASK]. Over $T$ decoding iterations, each iteration $t$ applies stochastic sampling to predict masked tokens based on their distributions $p(y_{i}|Y_{\overline{\mathbf{M}}},X_{2D},X_{img})$ . Following each sampling step, tokens with the lowest prediction confidences are re-masked to be re-predicted in subsequent iterations. The number of tokens re-masked is determined by a masking schedule $\lceil\gamma\left(\frac{t}{T}\right)\cdot L\rceil$ , where $\gamma$ is a decaying function of $t$ . This schedule dynamically adjusts masking intensity based on confidence, using a higher masking ratio in earlier iterations when prediction confidence is lower. Consequently, the model iteratively refines ambiguous regions, progressively improving prediction confidence as context builds. The masking ratio decreases with each step, stabilized by the cosine decay function $\gamma$ ; alternative decay functions are discussed in the supplementary material.

4 Experiments

Table 1: 3D Reconstruction Accuracy Evaluation on the HO3Dv3 [26] Benchmark: Comparison with SOTA Methods. ”-” indicates metrics not reported by the model.

Method	Venue	PA-MPJPE (↓)	PA-MPVPE (↓)	F@5mm (↑)	F@15mm (↑)	AUC_J (↑)	AUC_V (↑)
S²HAND [11]	CVPR 2021	11.5	11.1	0.448	0.932	0.769	0.778
KPT-Transf. [26]	CVPR 2022	10.9	-	-	-	0.785	-
ArtiBoost [62]	CVPR 2022	10.8	10.4	0.507	0.946	0.785	0.792
Yu et al. [64]	BMVC 2022	10.8	10.4	-	-	-	-
HandGCAT [59]	ICME 2022	9.3	9.1	0.552	0.956	0.814	0.818
AMVUR [31]	CVPR 2023	8.7	8.3	0.593	0.964	0.826	0.834
HMP [18]	WACV 2024	10.1	-	-	-	-	-
SPMHand [40]	TMM 2024	8.8	8.6	0.574	0.962	-	-
MMHMR	Ours	7.0	7.0	0.663	0.984	0.860	0.860

Table 2: 3D Reconstruction Accuracy on the FreiHAND [74] Benchmark: Comparison with State-of-the-Art Methods. ^†Indicates use of Test-Time Augmentation (TTA). PA-MPJPE and PA-MPVPE are reported in millimeters (mm). ”-” indicates metrics not reported by the model.

Methods	Venue	PA-MPJPE (↓)	PA-MPVPE (↓)	F@5mm (↑)	F@15mm (↑)
MeshGraphormer^† [39]	ICCV 2021	5.9	6.0	0.764	0.986
FastMETRO [14]	ECCV 2022	6.5	7.1	0.687	0.983
FastViT [57]	ICCV 2023	6.6	6.7	0.722	0.981
AMVUR [31]	CVPR 2023	6.2	6.1	0.767	0.987
Deformer [63]	CVPR 2023	6.2	6.4	0.743	0.984
PointHMR [33]	CVPR 2023	6.1	6.6	0.720	0.984
Zhou et al. [71]	CVPR 2024	5.7	6.0	0.772	0.986
HaMeR [46]	CVPR 2024	6.0	5.7	0.785	0.990
HHMR $\mathsection$ [37]	CVPR 2024	5.8	5.8	-	-
MMHMR $\ddagger$	Ours	5.7	5.5	0.793	0.991

$\ddagger$ MMHMR reports most confident mesh reconstruction, guided by the learned 2D-to-3D distribution without assumption of available GT meshes.

$\mathsection$ HHMR reports best hypothesis mesh reconstruction with minimum MPJPE and MPVPE, with the assumption of available GT meshes.

Table 3: Real-World Robustness Evaluation on the HInt Benchmark [46] using the PCK Metric: Comparison with SOTA Methods. None of the models were trained on or have previously seen the HInt dataset.

Method	Venue	NewDays			VISOR			Ego4D
		@0.05 (↑)	@0.1 (↑)	@0.15 (↑)	@0.05 (↑)	@0.1 (↑)	@0.15 (↑)	@0.05 (↑)	@0.1 (↑)	@0.15 (↑)
All Joints
FrankMocap [50]	ICCVW 2021	16.1	41.4	60.2	16.8	45.6	66.2	13.1	36.9	55.8
METRO [38]	CVPR 2021	14.7	38.8	57.3	16.8	45.4	65.7	13.2	35.7	54.3
MeshGraphormer [39]	ICCV 2021	16.8	42.0	59.7	19.1	48.5	67.4	14.6	38.2	56.0
HandOccNet (param) [45]	CVPR 2022	9.1	28.4	47.8	8.1	27.7	49.3	7.7	26.5	47.7
HandOccNet (no param) [45]	CVPR 2022	13.7	39.1	59.3	12.4	38.7	61.8	10.9	35.1	58.9
HaMeR [46]	CVPR 2024	48.0	78.0	88.8	43.0	76.9	89.3	38.9	71.3	84.4
MMHMR	Ours	48.7	79.2	90.0	46.1	81.4	92.1	46.4	77.5	90.1
Visible Joints
FrankMocap [50]	ICCVW 2021	20.1	49.2	67.6	20.4	52.3	71.6	16.3	43.2	62.0
METRO [38]	CVPR 2021	19.2	47.6	66.0	19.7	51.9	72.0	15.8	41.7	60.3
MeshGraphormer [39]	ICCV 2021	22.3	51.6	68.8	23.6	56.4	74.7	18.4	45.6	63.2
HandOccNet (param) [45]	CVPR 2022	10.2	31.4	51.2	8.5	27.9	49.8	7.3	26.1	48.0
HandOccNet (no param) [45]	CVPR 2022	15.7	43.4	64.0	13.1	39.9	63.2	11.2	36.2	56.0
HaMeR [46]	CVPR 2024	60.8	87.9	94.4	56.6	88.0	94.7	52.0	83.2	91.3
MMHMR	Ours	61.0	87.1	94.8	62.1	90.2	95.0	59.3	88.3	94.4
Occluded Joints
FrankMocap [50]	ICCVW 2021	9.2	28.0	46.9	11.0	33.0	55.0	8.4	26.9	45.1
METRO [38]	CVPR 2021	7.0	23.6	42.4	10.2	32.4	53.9	8.0	26.2	44.7
MeshGraphormer [39]	ICCV 2021	7.9	25.7	44.3	10.9	33.3	54.1	9.3	32.6	51.7
HandOccNet (param) [45]	CVPR 2022	7.2	23.5	42.4	7.4	26.1	46.7	7.2	26.1	45.7
HandOccNet (no param) [45]	CVPR 2022	9.8	31.2	50.8	9.9	33.7	55.4	9.6	31.1	52.7
HaMeR [46]	CVPR 2024	27.2	60.8	78.9	25.9	60.8	80.7	23.0	56.9	76.3
MMHMR	Ours	29.4	64.1	80.3	31.4	64.2	83.6	29.4	65.3	80.1

Datasets.To train the hand pose tokenizer, we employed a diverse set of datasets to capture a wide range of hand poses and interactions. This includes DexYCB [9], InterHand2.6M [43], MTC [61], and RHD [73]. For training MMHMR, we utilized a diverse dataset, following a similar setup as in [46] to ensure a fair comparison. Specifically, the training data was drawn from FreiHAND [74], HODv2 [25], MTC [61], RHD [73], InterHand2.6M [43], H2O3D [25], DexYCB [9], COCO-Wholebody [32], Halpe [20], and MPII NZSL [51].

Evaluation Metrics. Following standard protocols [46, 37, 71], MMHMR evaluated on reconstructed 3D joints using PA-MPJPE and AUC_J, while 3D mesh vertices were evaluated with PA-MPVPE, AUC_V, F@5mm, and F@15mm. Additionally, to examine MMHMR’s generalization and accuracy in diverse real-world settings, we employed the Percentage of Correct Keypoints (PCK) [46] metric at multiple thresholds, ensuring a robust evaluation of its performance across varied conditions. To evaluate hand image generation with mesh-guided control, we compute FID-H and KID-H on cropped hand regions, following previous works [44] and use MediaPipe [65] as a hand detector to measure confidence.

3D Reconstruction Accuracy Evaluation.To comprehensively evaluate MMHMR’s 3D joints and mesh reconstruction capabilities, we used the HO3Dv3 [26] and FreiHAND datasets. HO3Dv3 [26], the largest 3D hand pose test dataset with 20K annotated images, serves as a rigorous test ground with diverse hand poses and complex scenarios. MMHMR was directly tested on HO3Dv3 without prior training on this dataset, assessing its ability to generalize to new data and confirming the model’s robustness in challenging settings. This evaluation underscores MMHMR’s resilience to dataset-specific biases, proving its adaptability across varied scenarios. Additionally, we evaluated MMHMR on the FreiHAND dataset [74], which includes 4K images spanning controlled environments. For fair comparison, as previous methods like MeshGraphormer [39] and HHMR [37] were evaluated on FreiHAND, we evaluated MMHMR trained solely on the FreiHAND [74].

Real-World Robustness Evaluation. To validate MMHMR’s adaptability, we tested it on the HInt benchmark [46] without prior training. HInt introduces diverse real-world conditions, including varied lighting, angles, and hand-object interactions, offering a realistic evaluation framework. Using the Percentage of Correct Keypoints (PCK) metric, we assessed MMHMR on HInt-NewDays [12], HInt-EpicKitchensVISOR [15], and HInt-Ego4D [24], highlighting its robust generalization and effectiveness in complex environments.

4.1 Comparison to State-of-the-art Approaches

We evaluate MMHMR against a range of state-of-the-art methods (SOTA) on the HO3Dv3 [26], FreiHAND [74], and HInt [46] benchmarks, as detailed in Table 1, Table 2, and Table 3. MMHMR consistently outperforms competing methods across key evaluation metrics, demonstrating robust accuracy in 3D hand reconstruction. Notably, we perform zero-shot evaluations on both the HO3Dv3 and HInt benchmarks to assess MMHMR’s generalizability. A core contributor to MMHMR’s success is its capability to model and refine uncertainty, making it highly effective in scenarios with complex hand poses and significant occlusions. On the HO3Dv3 dataset (Table 1), MMHMR achieves a PA-MPJPE reduction of approximately 19.5% and a PA-MPVPE reduction of 15.7% compared to the existing SOTA method. This improvement underscores MMHMR’s precision in handling challenging hand poses and occlusions. Similarly, on the HInt benchmark (Table 3), MMHMR achieves notable improvements in occluded joint reconstruction at the PCK@0.05 threshold on the HInt benchmark. Specifically, MMHMR shows an 8.1% increase on HInt-NewDays, a 21.2% increase on HInt-VISOR, and a 27.8% increase on HInt-Ego4D compared to the closest SOTA methods. These gains underscore MMHMR’s effectiveness in synthesizing unobserved parts and handling real-world occlusions with high accuracy. This highlights MMHMR’s strength in synthesizing unobserved parts, enabling accurate reconstruction of occluded regions.

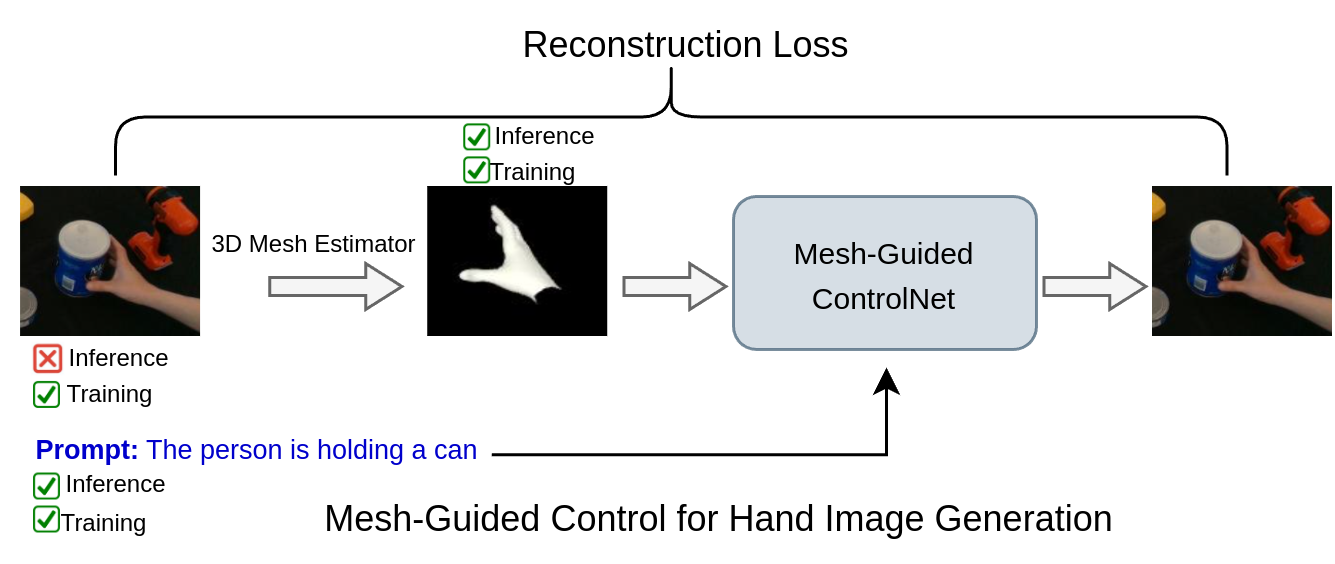
Mesh-Guided Control for Hand Image Generation. As shown in the Generation Pipeline (Figure 4) and Table 13, MMHMR demonstrates adaptability in generating realistic hand images under diverse conditions. We train ControlNet [66]on DexYCB [9] and test it on HO3Dv3 [26]. MMHMR processes input images through a mesh estimator i.e. (MMHMR) to extract 3D hand meshes, which serve as control signals in ControlNet [66] alongside text prompts. Compared to HaMer [46] as a mesh estimator method [46], MMHMR achieves lower FID-H and KID-H scores, indicating better image quality, and a higher hand detection confidence score, reflecting improved anatomical accuracy. Accurate mesh estimation ensures precise control signals for consistent, high-quality hand generation. More details are in the supplementary material.

Table 4: Mesh-Guided Control for Hand Image Generation

Mesh Estimator	FID-H $\downarrow$	KID-H $\downarrow$	Hand Det Conf. $\uparrow$
HaMer [46]	45.65	0.035	0.865
MMHMR (Ours)	40.23	0.027	0.912

4.2 Ablation Study

The effectiveness of MMHMR is grounded in its mask modeling and iterative decoding techniques. This ablation study examines how iterative refinement and mask-scheduling strategies impact model performance. Additional experimental results and visualizations in the Supplementary Material provide in-depth analyses of the key factors driving MMHMR’s performance. These include (1) architectural components, such as the VQ-MANO tokenizer, GGPM design, Context-Infused Masked Synthesizer, and feature resolution choices, (2) training strategies, including mask scheduling and regularization via keypoint and MANO losses, and (3) the model’s limitations.

Effectiveness of Proposed Components. Our ablation study on the HO3Dv3 dataset [26] (Table 5) underscores the importance of MMHMR’s components. The Upsampler plays a key role in enhancing fine-grained details and resolution, while the 2D OpenPose Context provides essential spatial cues; their absence leads to reduced accuracy. The x-Attention Head is crucial for maintaining hand shape stability by integrating shape and camera parameters, with its removal resulting in a decline in 3D accuracy. Iterative Decoding is vital for refining predictions by leveraging contextual cues, with its absence causing significant performance degradation. The largest performance drop is observed when Graph-Guided Pose Modeling (GGPM) is removed, emphasizing its critical role in capturing joint dependencies and ensuring anatomical coherence.

Table 5: Ablation study of testing results on the HO3Dv3 dataset [26] to evaluate the impact of proposed components. ’w/o’ denotes ’without’.

Method	PA-MPJPE (↓)	PA-MPVPE (↓)	F@5mm (↑)	AUC_J (↑)	AUC_V (↑)
w/o. Upsampler	7.2	7.2	0.654	0.857	0.857
w/o. 2D Pose Context	7.1	7.1	0.656	0.857	0.858
w/o. x-Attention Head	7.3	7.1	0.655	0.855	0.858
w/o. GGPM	7.3	7.3	0.645	0.853	0.854
w/o. Iterative Decoding	7.2	7.2	0.654	0.857	0.857
MMHMR (Full)	7.0	7.0	0.663	0.860	0.860

Impact of Iterative Confidence-Guided Sampling. The number of iterations in confidence-guided sampling impacts both accuracy and efficiency in 3D hand pose estimation. As shown in Table 6, increasing iterations from 1 to 5 improves accuracy, with PA-MPVPE dropping from 7.2 to 7.0 on HO3Dv3 and from 5.8 to 5.5 on FreiHAND. This refinement enhances precision by leveraging contextual cues and 2D pose guidance. However, increasing to 10 iterations shows minimal benefit, making 5 iterations optimal for balancing accuracy and computational cost.

Table 6: Iterations in Iterative Confidence-Guided Sampling

	HO3Dv3		FreiHAND
# of iter.	PA-MPJPE	PA-MPVPE	PA-MPJPE	PA-MPVPE
1	7.2	7.2	5.9	5.8
3	7.1	7.1	5.8	5.7
5	7.0	7.0	5.7	5.5
10	7.1	7.0	5.7	5.5

Masking Ratio during Training. The ablation study in Table 7 shows that a broader masking range $\gamma(\tau\in\mathcal{U}(0,0.7))$ achieves optimal results on HO3Dv3 and FreiHAND, with the lowest PA-MPVPE values of 7.0 and 5.5, respectively. This cosine-based masking strategy, where the model learns to reconstruct from partially masked sequences, enhances robustness in 3D hand reconstruction. Narrower masking ranges, such as $\gamma(\tau\in\mathcal{U}(0,0.3))$ , increase error, highlighting the importance of challenging the model with broader masking for better generalization.

Table 7: Impact of masking ratio during training on HO3Dv3 [26] and FreiHAND [74] datasets.

Masking Ratio $\gamma(\tau)$	HO3Dv3		FreiHAND
	PA-MPJPE	PA-MPVPE	PA-MPJPE	PA-MPVPE
$\gamma(\tau\in\mathcal{U}(0,0.3))$	7.2	7.2	6.0	6.1
$\gamma(\tau\in\mathcal{U}(0,0.5))$	7.1	7.1	5.8	5.7
$\gamma(\tau\in\mathcal{U}(0,0.7))$	7.0	7.0	5.7	5.5
$\gamma(\tau\in\mathcal{U}(0,1.0))$	7.2	7.3	6.0	6.0

5 Conclusion

In this paper, we introduced MMHMR, a novel generative masked model designed for accurate and robust 3D hand mesh reconstruction from single RGB images. MMHMR addresses the longstanding challenges posed by complex hand articulations, self-occlusions, and depth ambiguities by leveraging a generative framework that captures and refines hand pose distributions. Central to our approach are two key components: VQ-MANO, which encodes 3D hand articulations as discrete pose tokens in a learned latent space, and the Context-Guided Masked Transformer, which models token dependencies conditioned on both image features and 2D pose cues. This framework uses confidence-guided iterative sampling to refine reconstructions, producing realistic hand meshes under challenging conditions. MMHMR outperforms state-of-the-art methods, setting a new benchmark for 3D hand modeling in human-computer interaction, AR, and VR.

References

[1] Kaggle asl alphabet. Available online: https://www.kaggle.com/grassknoted/asl-alphabet (accessed on 19 July 2021).
Alexey [2020] Dosovitskiy Alexey. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv preprint arXiv: 2010.11929, 2020.
Baek et al. [2018] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Augmented skeleton space transfer for depth-based hand pose estimation. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
Baek et al. [2019] Seungryul Baek, Kwang In Kim, and Tae-Kyun Kim. Pushing the envelope for rgb-based dense 3d hand pose estimation via neural rendering. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1067–1076, 2019.
Ballan et al. [2012] Luca Ballan, Aparna Taneja, Jürgen Gall, Luc Van Gool, and Marc Pollefeys. Motion capture of hands in action using discriminative salient points. In European Conference on Computer Vision (ECCV), 2012.
Boukhayma et al. [2019] Adnane Boukhayma, Rodrigo de Bem, and Philip HS Torr. 3d hand shape and pose from images in the wild. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 10843–10852, 2019.
Chang et al. [2022] Huiwen Chang, Han Zhang, Lu Jiang, Ce Liu, and William T Freeman. Maskgit: Masked generative image transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11315–11325, 2022.
Chang et al. [2023] Huiwen Chang, Han Zhang, Jarred Barber, AJ Maschinot, Jose Lezama, Lu Jiang, Ming-Hsuan Yang, Kevin Murphy, William T Freeman, Michael Rubinstein, et al. Muse: Text-to-image generation via masked generative transformers. arXiv preprint arXiv:2301.00704, 2023.
Chao et al. [2021] Yu-Wei Chao, Wei Yang, Yu Xiang, Pavlo Molchanov, Ankur Handa, Jonathan Tremblay, Yashraj S Narang, Karl Van Wyk, Umar Iqbal, Stan Birchfield, et al. Dexycb: A benchmark for capturing hand grasping of objects. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9044–9053, 2021.
Chen et al. [2023] Xingyu Chen, Baoyuan Wang, and Heung-Yeung Shum. Hand avatar: Free-pose hand animation and rendering from monocular video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2023.
Chen et al. [2021] Yujin Chen, Zhigang Tu, Di Kang, Linchao Bao, Ying Zhang, Xuefei Zhe, Ruizhi Chen, and Junsong Yuan. Model-based 3d hand reconstruction via self-supervised learning. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 10451–10460, 2021.
Cheng et al. [2023] Tianyi Cheng, Dandan Shan, Ayda Hassen, Richard Higgins, and David Fouhey. Towards a richer 2d understanding of hands at scale. Advances in Neural Information Processing Systems, 36:30453–30465, 2023.
Cho et al. [2022] Junhyeong Cho, Kim Youwang, and Tae-Hyun Oh. Cross-attention of disentangled modalities for 3d human mesh recovery with transformers. In European Conference on Computer Vision (ECCV), 2022.
Cho [2022] Youwang Kim Oh Tae-Hyun Cho, Junhyeong. Cross-attention of disentangled modalities for 3d human mesh recovery with transformers. In European Conference on Computer Vision, pages 342–359. Springer, 2022.
Damen et al. [2018] Dima Damen, Hazel Doughty, Giovanni Maria Farinella, Sanja Fidler, Antonino Furnari, Evangelos Kazakos, Davide Moltisanti, Jonathan Munro, Toby Perrett, Will Price, et al. Scaling egocentric vision: The epic-kitchens dataset. In Proceedings of the European conference on computer vision (ECCV), pages 720–736, 2018.
Devlin et al. [2019] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arxiv. arXiv preprint arXiv:1810.04805, 2019.
Ding et al. [2022] Ming Ding, Wendi Zheng, Wenyi Hong, and Jie Tang. Cogview2: Faster and better text-to-image generation via hierarchical transformers. Advances in Neural Information Processing Systems, 35:16890–16902, 2022.
Duran et al. [2024] Enes Duran, Muhammed Kocabas, Vasileios Choutas, Zicong Fan, and Michael J Black. Hmp: Hand motion priors for pose and shape estimation from video. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, pages 6353–6363, 2024.
Esser et al. [2021] Patrick Esser, Robin Rombach, and Bjorn Ommer. Taming transformers for high-resolution image synthesis. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 12873–12883, 2021.
Fang et al. [2022] Hao-Shu Fang, Jiefeng Li, Hongyang Tang, Chao Xu, Haoyi Zhu, Yuliang Xiu, Yong-Lu Li, and Cewu Lu. Alphapose: Whole-body regional multi-person pose estimation and tracking in real-time. IEEE Transactions on Pattern Analysis and Machine Intelligence, 45(6):7157–7173, 2022.
Gao et al. [2022] Chengying Gao, Yujia Yang, and Wensheng Li. 3d interacting hand pose and shape estimation from a single rgb image. Neurocomputing, 2022.
Garcia-Hernando et al. [2018] Guillermo Garcia-Hernando, Shanxin Yuan, Seungryul Baek, and Tae-Kyun Kim. First-person hand action benchmark with rgb-d videos and 3d hand pose annotations. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
Gomez-Donoso et al. [2017] Francisco Gomez-Donoso, Sergio Orts-Escolano, and Miguel Cazorla. Large-scale multiview 3d hand pose dataset. arXiv preprint arXiv:1707.03742, 2017.
Grauman et al. [2022] Kristen Grauman, Andrew Westbury, Eugene Byrne, Zachary Chavis, Antonino Furnari, Rohit Girdhar, Jackson Hamburger, Hao Jiang, Miao Liu, Xingyu Liu, et al. Ego4d: Around the world in 3,000 hours of egocentric video. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 18995–19012, 2022.
Hampali et al. [2020] Shreyas Hampali, Mahdi Rad, Markus Oberweger, and Vincent Lepetit. Honnotate: A method for 3d annotation of hand and object poses. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 3196–3206, 2020.
Hampali et al. [2022] Shreyas Hampali, Sayan Deb Sarkar, Mahdi Rad, and Vincent Lepetit. Keypoint transformer: Solving joint identification in challenging hands and object interactions for accurate 3d pose estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 11090–11100, 2022.
He et al. [2016] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 770–778, 2016.
Hoyet et al. [2012] Ludovic Hoyet, Kenneth Ryall, Rachel McDonnell, and Carol O’Sullivan. Sleight of hand: perception of finger motion from reduced marker sets. In SIGGRAPH, 2012.
Hu et al. [2018] Jie Hu, Li Shen, and Gang Sun. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 7132–7141, 2018.
Huo et al. [2023] Rongtian Huo, Qing Gao, Jing Qi, and Zhaojie Ju. 3d human pose estimation in video for human-computer/robot interaction. In Intelligent Robotics and Applications, pages 176–187, Singapore, 2023. Springer Nature Singapore.
Jiang et al. [2023] Zheheng Jiang, Hossein Rahmani, Sue Black, and Bryan M Williams. A probabilistic attention model with occlusion-aware texture regression for 3d hand reconstruction from a single rgb image. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 758–767, 2023.
Jin et al. [2020] Sheng Jin, Lumin Xu, Jin Xu, Can Wang, Wentao Liu, Chen Qian, Wanli Ouyang, and Ping Luo. Whole-body human pose estimation in the wild. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part IX 16, pages 196–214. Springer, 2020.
Kim et al. [2023] Jeonghwan Kim, Mi-Gyeong Gwon, Hyunwoo Park, Hyukmin Kwon, Gi-Mun Um, and Wonjun Kim. Sampling is matter: Point-guided 3d human mesh reconstruction. In Proceedings of the IEEE/CVF Conference on computer vision and pattern recognition, pages 12880–12889, 2023.
Kulon et al. [2019] Dominik Kulon, Haoyang Wang, Riza Alp Güler, Michael Bronstein, and Stefanos Zafeiriou. Single image 3d hand reconstruction with mesh convolutions. arXiv preprint arXiv:1905.01326, 2019.
Kulon et al. [2020] Dominik Kulon, Riza Alp Guler, Iasonas Kokkinos, Michael M Bronstein, and Stefanos Zafeiriou. Weakly-supervised mesh-convolutional hand reconstruction in the wild. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 4990–5000, 2020.
Li et al. [2024a] Bo Li, Yuanhan Zhang, Dong Guo, Renrui Zhang, Feng Li, Hao Zhang, Kaichen Zhang, Peiyuan Zhang, Yanwei Li, Ziwei Liu, et al. Llava-onevision: Easy visual task transfer. arXiv preprint arXiv:2408.03326, 2024a.
Li et al. [2024b] Mengcheng Li, Hongwen Zhang, Yuxiang Zhang, Ruizhi Shao, Tao Yu, and Yebin Liu. Hhmr: Holistic hand mesh recovery by enhancing the multimodal controllability of graph diffusion models. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 645–654, 2024b.
Lin et al. [2021a] Kevin Lin, Lijuan Wang, and Zicheng Liu. End-to-end human pose and mesh reconstruction with transformers. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 1954–1963, 2021a.
Lin et al. [2021b] Kevin Lin, Lijuan Wang, and Zicheng Liu. Mesh graphormer. In Proceedings of the IEEE/CVF international conference on computer vision, pages 12939–12948, 2021b.
Lu et al. [2024] Haofan Lu, Shuiping Gou, and Ruimin Li. Spmhand: Segmentation-guided progressive multi-path 3d hand pose and shape estimation. IEEE Transactions on Multimedia, 2024.
Markussen et al. [2014] Anders Markussen, Mikkel Rønne Jakobsen, and Kasper Hornbæk. Vulture: a mid-air word-gesture keyboard. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, page 1073–1082, New York, NY, USA, 2014. Association for Computing Machinery.
Moon et al. [2018] Gyeongsik Moon, Ju Yong Chang, and Kyoung Mu Lee. V2v-posenet: Voxel-to-voxel prediction network for accurate 3d hand and human pose estimation from a single depth map. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018.
Moon et al. [2020] Gyeongsik Moon, Shoou-I Yu, He Wen, Takaaki Shiratori, and Kyoung Mu Lee. Interhand2. 6m: A dataset and baseline for 3d interacting hand pose estimation from a single rgb image. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part XX 16, pages 548–564. Springer, 2020.
Narasimhaswamy et al. [2024] Supreeth Narasimhaswamy, Uttaran Bhattacharya, Xiang Chen, Ishita Dasgupta, Saayan Mitra, and Minh Hoai. Handiffuser: Text-to-image generation with realistic hand appearances. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 2468–2479, 2024.
Park et al. [2022] JoonKyu Park, Yeonguk Oh, Gyeongsik Moon, Hongsuk Choi, and Kyoung Mu Lee. Handoccnet: Occlusion-robust 3d hand mesh estimation network. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 1496–1505, 2022.
Pavlakos et al. [2024] Georgios Pavlakos, Dandan Shan, Ilija Radosavovic, Angjoo Kanazawa, David Fouhey, and Jitendra Malik. Reconstructing hands in 3d with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 9826–9836, 2024.
Qian et al. [2014] Chen Qian, Xiao Sun, Yichen Wei, Xiaoou Tang, and Jian Sun. Realtime and robust hand tracking from depth. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014.
Radford et al. [2021] Alec Radford, Jong Wook Kim, Chris Hallacy, Aditya Ramesh, Gabriel Goh, Sandhini Agarwal, Girish Sastry, Amanda Askell, Pamela Mishkin, Jack Clark, et al. Learning transferable visual models from natural language supervision. In International conference on machine learning, pages 8748–8763. PMLR, 2021.
Romero et al. [2017] Javier Romero, Dimitrios Tzionas, and Michael J. Black. Embodied hands: Modeling and capturing hands and bodies together. ACM Transactions on Graphics, (Proc. SIGGRAPH Asia), 36(6), 2017.
Rong et al. [2021] Yu Rong, Takaaki Shiratori, and Hanbyul Joo. Frankmocap: A monocular 3d whole-body pose estimation system via regression and integration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 1749–1759, 2021.
Simon et al. [2017] Tomas Simon, Hanbyul Joo, Iain Matthews, and Yaser Sheikh. Hand keypoint detection in single images using multiview bootstrapping. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 1145–1153, 2017.
Sridhar et al. [2013] Srinath Sridhar, Antti Oulasvirta, and Christian Theobalt. Interactive markerless articulated hand motion tracking using rgb and depth data. In IEEE International Conference on Computer Vision (ICCV), 2013.
Sridhar et al. [2015a] Srinath Sridhar, Anna Maria Feit, Christian Theobalt, and Antti Oulasvirta. Investigating the dexterity of multi-finger input for mid-air text entry. In Proceedings of the 33rd Annual ACM Conference on Human Factors in Computing Systems, page 3643–3652, New York, NY, USA, 2015a. Association for Computing Machinery.
Sridhar et al. [2015b] Srinath Sridhar, Franziska Mueller, Antti Oulasvirta, and Christian Theobalt. Fast and robust hand tracking using detection-guided optimization. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2015b.
Taylor et al. [2017] Jonathan Taylor, Vladimir Tankovich, Danhang Tang, Cem Keskin, David Kim, Philip Davidson, Adarsh Kowdle, and Shahram Izadi. Articulated distance fields for ultra-fast tracking of hands interacting. TOG, 2017.
Van Den Oord et al. [2017] Aaron Van Den Oord, Oriol Vinyals, et al. Neural discrete representation learning. Advances in neural information processing systems, 30, 2017.
Vasu et al. [2023] Pavan Kumar Anasosalu Vasu, James Gabriel, Jeff Zhu, Oncel Tuzel, and Anurag Ranjan. Fastvit: A fast hybrid vision transformer using structural reparameterization. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 5785–5795, 2023.
Wang et al. [2020] Jiayi Wang, Franziska Mueller, Florian Bernard, Suzanne Sorli, Oleksandr Sotnychenko, Neng Qian, Miguel A Otaduy, Dan Casas, and Christian Theobalt. Rgb2hands: real-time tracking of 3d hand interactions from monocular rgb video. TOG, 2020.
Wang et al. [2023] Shuaibing Wang, Shunli Wang, Dingkang Yang, Mingcheng Li, Ziyun Qian, Liuzhen Su, and Lihua Zhang. Handgcat: Occlusion-robust 3d hand mesh reconstruction from monocular images. In 2023 IEEE International Conference on Multimedia and Expo (ICME), pages 2495–2500. IEEE, 2023.
Williams et al. [2020] Will Williams, Sam Ringer, Tom Ash, David MacLeod, Jamie Dougherty, and John Hughes. Hierarchical quantized autoencoders. Advances in Neural Information Processing Systems, 33:4524–4535, 2020.
Xiang et al. [2019] Donglai Xiang, Hanbyul Joo, and Yaser Sheikh. Monocular total capture: Posing face, body, and hands in the wild. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 10965–10974, 2019.
Yang et al. [2022] Lixin Yang, Kailin Li, Xinyu Zhan, Jun Lv, Wenqiang Xu, Jiefeng Li, and Cewu Lu. Artiboost: Boosting articulated 3d hand-object pose estimation via online exploration and synthesis. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pages 2750–2760, 2022.
Yoshiyasu [2023] Yusuke Yoshiyasu. Deformable mesh transformer for 3d human mesh recovery. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 17006–17015, 2023.
Yu et al. [2022] Ziwei Yu, Linlin Yang, You Xie, Ping Chen, and Angela Yao. Uv-based 3d hand-object reconstruction with grasp optimization. arXiv preprint arXiv:2211.13429, 2022.
Zhang et al. [2020] Fan Zhang, Valentin Bazarevsky, Andrey Vakunov, Andrei Tkachenka, George Sung, Chuo-Ling Chang, and Matthias Grundmann. Mediapipe hands: On-device real-time hand tracking. arXiv preprint arXiv:2006.10214, 2020.
Zhang et al. [2023] Lvmin Zhang, Anyi Rao, and Maneesh Agrawala. Adding conditional control to text-to-image diffusion models. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 3836–3847, 2023.
Zhang et al. [2019] Xiong Zhang, Qiang Li, Hong Mo, Wenbo Zhang, and Wen Zheng. End-to-end hand mesh recovery from a monocular rgb image. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 2354–2364, 2019.
Zhang et al. [2021a] Yuxiang Zhang, Zhe Li, Liang An, Mengcheng Li, Tao Yu, and Yebin Liu. Light-weight multi-person total capture using sparse multi-view cameras. In ICCV, 2021a.
Zhang et al. [2021b] Zhu Zhang, Jianxin Ma, Chang Zhou, Rui Men, Zhikang Li, Ming Ding, Jie Tang, Jingren Zhou, and Hongxia Yang. Ufc-bert: Unifying multi-modal controls for conditional image synthesis. Advances in Neural Information Processing Systems, 34:27196–27208, 2021b.
Zhao et al. [2012] Wenping Zhao, Jinxiang Chai, and Ying-Qing Xu. Combining marker-based mocap and rgb-d camera for acquiring high-fidelity hand motion data. In SIGGRAPH, 2012.
Zhou et al. [2024] Zhishan Zhou, Shihao Zhou, Zhi Lv, Minqiang Zou, Yao Tang, and Jiajun Liang. A simple baseline for efficient hand mesh reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages 1367–1376, 2024.
Zhu et al. [2020] Xizhou Zhu, Weijie Su, Lewei Lu, Bin Li, Xiaogang Wang, and Jifeng Dai. Deformable detr: Deformable transformers for end-to-end object detection. ArXiv, abs/2010.04159, 2020.
Zimmermann and Brox [2017] Christian Zimmermann and Thomas Brox. Learning to estimate 3d hand pose from single rgb images. In Proceedings of the IEEE international conference on computer vision, pages 4903–4911, 2017.
Zimmermann et al. [2019] Christian Zimmermann, Duygu Ceylan, Jimei Yang, Bryan Russell, Max Argus, and Thomas Brox. Freihand: A dataset for markerless capture of hand pose and shape from single rgb images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, pages 813–822, 2019.

6 Supplementary Material

Appendix A Overview

The supplementary material is organized into the following sections:

•

Section B: Implementation Details
•

Section C: Ablation for VQ-MANO Pose Tokenizer
•

Section D: Generalization to Text-to-Mesh Generation
•

Section E: Effectiveness of Expectation-Approximated Differential Sampling
•

Section F: Confidence-Guided Masking
•

Section G: Pose Token Sampling Techniques
•

Section H: Impact of Control Signals for Hand Image Generation
•

Section J: Impact of Multi-Scale Features
•

Section K: Cross-Attention Layers in MMHMR
•

Section L: Qualitative Results

Appendix B Implementation Details

The implementation of MMHMR, developed using PyTorch, comprises two essential training phases: the VQ-MANO tokenizer and the context-guided masked transformer. These phases are meticulously designed to ensure accurate 3D hand mesh reconstruction while balancing computational efficiency and model robustness.

VQ-MANO. In the first phase, the VQ-MANO module is trained to learn discrete latent representations of hand poses. The pose parameters, $\theta\in\mathbb{R}^{16\times 3}$ , encapsulate the global orientation ( $\theta_{1}\in\mathbb{R}^{3}$ ) and local rotations ( $[\theta_{2},\ldots,\theta_{16}]\in\mathbb{R}^{16\times 3}$ ) of hand joints. The architecture of the tokenizer employs ResBlocks [27] and 1D convolutional layers for the encoder and decoder, with a single quantization layer mapping continuous embeddings into a discrete latent space. To train the hand pose tokenizer, we utilized a range of datasets capturing diverse hand poses, interactions, and settings. Specifically, we leveraged DexYCB [9], InterHand2.6M [43], MTC [61], and RHD [73]. These datasets collectively provide a rich spectrum of annotated data, enabling the model to generalize effectively across various real-world scenarios. The training process spans 400K iterations and uses the Adam optimizer with a batch size of 512 and a learning rate of $1\times 10^{-4}$ . The loss function combines reconstruction and regularization objectives, weighted as $\lambda_{\text{recon}}=1.0$ , $\lambda_{\text{E}}=0.02$ , $\lambda_{\theta}=1.0$ , $\lambda_{\text{V}}=0.5$ , and $\lambda_{\text{J}}=0.3$ . The final pose tokenizer is trained on DexYCB, InterHand2.6M, MTC, and RHD datasets, resulting in a model with 64 tokens and a codebook size of $2048\times 256$ .

Context-Guided Masked Transformer. The second phase involves training the context-guided masked transformer, with the pose tokenizer frozen to leverage its pre-trained pose priors. This phase is dedicated to synthesizing pose tokens conditioned on input images and refining the 3D mesh reconstruction. Multi-resolution feature maps at $1\times$ and $4\times$ scales are used to capture both global and local contextual details, allowing the model to handle complex hand articulations and occlusions. The overall architecture of the system, including the Graph-Guided Pose Modeling (GGPM) and Context-Infused Masked Synthesizer, is depicted in Figure 5. The GGPM consists of two blocks ( $xB$ ) of graph transformers to effectively model joint dependencies and ensure anatomical consistency. Meanwhile, the Context-Infused Masked Synthesizer employs four transformer layers ( $xN$ ) to integrate multi-scale image features and refine pose token predictions through deformable cross-attention and token dependencies. The default number of iterations in Confidence-Guided Sampling is 5, which we use for the ablation study. The overall loss function integrates multiple objectives to guide the model toward robust reconstructions:

\mathcal{L}_{\text{total}}=\mathcal{L}_{\text{mask}}+\mathcal{L}_{\text{MANO}}+\mathcal{L}_{\text{3D}}+\mathcal{L}_{\text{2D}},

where $\mathcal{L}_{\text{mask}}$ minimizes errors in masked token predictions, $\mathcal{L}_{\text{MANO}}$ ensures consistency in MANO shape ( $\beta$ ) and pose ( $\theta$ ) parameters, $\mathcal{L}_{\text{3D}}$ aligns the predicted and ground-truth 3D joint positions, and $\mathcal{L}_{\text{2D}}$ preserves accurate 2D joint projections. The loss weights are configured as $\lambda_{\text{mask}}=1.0$ , $\lambda_{\text{MANO}}=1.5\times 10^{-3}$ (with $\lambda_{\theta}=1\times 10^{-3}$ for pose and $\lambda_{\beta}=5\times 10^{-4}$ for shape), $\lambda_{\text{3D}}=5\times 10^{-2}$ , and $\lambda_{\text{2D}}=1\times 10^{-2}$ . This phase is trained using the Adam optimizer on NVIDIA RTX A6000 GPUs with a batch size of 48 and a learning rate of $1\times 10^{-5}$ .

Mesh-Guided Control for Hand Image Generation. To extend the utility of the reconstructed 3D hand meshes, we integrate them as control signals into the publicly available ControlNet framework [66]. This integration enables the generation of high-quality hand images guided by the reconstructed meshes. The ControlNet models are trained on hand-cropped images resized to $256\times 256$ , with a batch size of 64, using the Adam optimizer with a learning rate of $1\times 10^{-5}$ . Training is conducted over 200 epochs on eight NVIDIA RTX A6000 GPUs. During training, image captions are generated using LLaVA-OneVision [36], a vision-language model capable of producing descriptive captions based on image content. Specifically, we query LLaVA-OneVision with prompts such as “What’s in the image and how does the hand pose look like?” to obtain concise descriptions focusing on the hand’s pose, including finger positions and hand orientation. For instance, in response to an image of a hand, LLaVA-OneVision might generate a caption like “A right hand with fingers slightly bent, palm facing upward.” These captions are then utilized as text guidance during the training of ControlNet. By combining these captions with the corresponding 3D hand meshes extracted using MMHMR, we enable the ControlNet framework to effectively learn a mapping between text, mesh signals, and high-quality hand image outputs. The generation pipeline involves two stages: training and inference. During training, MMHMR extracts 3D hand meshes from images, which are paired with text prompts to guide the ControlNet model. This process ensures that the generated images are both semantically aligned with the textual descriptions and anatomically consistent with the 3D hand meshes. At inference, the model requires only text prompts and mesh signals as inputs. The text prompts provide high-level semantic guidance, such as the desired pose or hand orientation, while the mesh signals ensure that the generated images maintain accurate anatomical and spatial features. This design enables the generation of realistic and contextually appropriate hand images, demonstrating the robustness and flexibility of the proposed approach. By leveraging both text-based and mesh-based guidance, the system achieves high fidelity in image generation, even in scenarios involving complex hand poses or occlusions.

B.1 Data Augmentation

In the initial training phase, the VQ-MANO module leverages prior knowledge of valid hand poses, serving as a critical foundation for the robust performance of the overall MMHMR pipeline. To deepen the model’s understanding of pose parameters, hand poses are systematically rotated across diverse angles, enabling it to effectively learn under varying orientations. In the subsequent training phase, the robustness of MMHMR is further enhanced through an extensive augmentation strategy applied to both input images and hand poses. These augmentations—such as scaling, rotations, random horizontal flips, and color jittering—introduce significant variability into the training data. By simulating real-world challenges like occlusions and incomplete pose information, these transformations prepare the model for complex, unpredictable scenarios. This comprehensive approach to data augmentation is a cornerstone of the training process, significantly improving the model’s ability to generalize and produce reliable, precise 3D hand mesh reconstructions across a wide range of conditions.

B.2 Camera Model

In the MMHMR pipeline, a simplified perspective camera model is employed to project 3D joints onto 2D coordinates, striking a balance between computational efficiency and accuracy. The camera parameters, collectively represented by $\Pi$ , include a fixed focal length, an intrinsic matrix $K\in\mathbb{R}^{3\times 3}$ , and a translation vector $T\in\mathbb{R}^{3}$ . To streamline computations, the rotation matrix $R$ is replaced with the identity matrix $I_{3}$ , further simplifying the model. The projection of 3D joints $J_{\text{3D}}$ onto 2D coordinates $J_{\text{2D}}$ is described as $J_{\text{2D}}=\Pi(J_{\text{3D}})$ , where the operation encapsulates both the intrinsic parameters and the translation vector. This modeling approach reduces the parameter space, enabling computational efficiency while maintaining the accuracy required for robust 3D hand mesh reconstruction. By focusing on the most critical components, the model minimizes complexity without compromising performance.

Appendix C Ablation for VQ-MANO

Tables 8 and 9 summarize an ablation study on the Freihand [74] dataset, focusing on two key parameters: the number of pose tokens and the codebook size. Table 8 shows that increasing the number of pose tokens, while fixing the codebook size at $2048\times 256$ , improves performance significantly, reducing PA-MPJPE from 1.01 mm to 0.41 mm and PA-MPVPE from 0.97 mm to 0.41 mm as tokens increase from 16 to 128. Table 9 highlights the effect of increasing the codebook size with a fixed token count of 64, showing a reduction in PA-MPJPE from 0.66 mm to 0.43 mm and PA-MPVPE from 0.65 mm to 0.44 mm as the size grows from $1024\times 256$ to $4096\times 256$ . Notably, the codebook size has a stronger impact on performance than the number of pose tokens. The final configuration, with a codebook size of $2048\times 256$ and 64 tokens, balances efficiency and accuracy, achieving PA-MPJPE of 0.47 mm and PA-MPVPE of 0.44 mm. These results emphasize the importance of jointly optimizing these parameters for effective hand pose tokenization.

Table 8: Impact of Number of Pose Tokens (Codebook = 2048

\times

256) on VQ-MANO on Freihand dataset

	Number of Pose Tokens
Metric	16	32	64	128
PA-MPJPE	1.01	0.59	0.47	0.41
PA-MPVPE	0.97	0.57	0.44	0.41

Table 9: Impact of Number of Codebook Size (Pose Tokens = 64) on VQ-MANO on Freihand dataset

	Number of Codebook Size
Metric	1024 × 256	2048 × 128	2048 × 256	4096 × 256
PA-MPJPE	0.66	0.56	0.47	0.43
PA-MPVPE	0.65	0.58	0.44	0.44

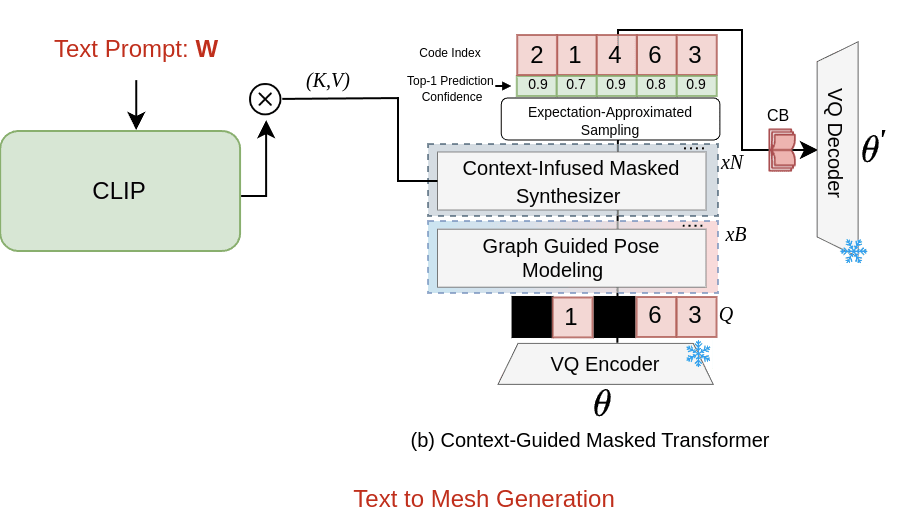
Appendix D Generalization to Text-to-Mesh Generation

The MMHMR model is designed to be highly modular and adaptable, enabling functionality beyond image-conditioned tasks. To evaluate its generalization capability, we adapted MMHMR for text-to-mesh generation by replacing image-based conditioning with text guidance as shown in Figure 6. Leveraging the generative nature of MMHMR’s Masked Synthesizer, the model can generate diverse 3D meshes based on a single text input. This adaptability was further tested by removing the 2D pose guidance from MMHMR, making the model rely solely on text for mesh generation. The model was trained on the American Sign Language (ASL) dataset, following the same configuration as the image-conditioned MMHMR model but tailored for text-conditioned mesh synthesis. During testing, a top-5% probabilistic sampling strategy was applied, allowing the generation of multiple plausible meshes from a single text prompt. This experiment showcases the versatility and robustness of MMHMR in addressing novel tasks like text-to-mesh synthesis.

American Sign Language Dataset. The American Sign Language (ASL) dataset is a widely used resource for hand-based sign language recognition in English-speaking regions such as the United States and Canada. The dataset includes 26 letters of the alphabet, expressed using one-handed gestures, making it suitable for text-to-mesh experiments. For this study, we used dataset: the ASL alphabet dataset from Kaggle [1] for text to mesh generation.

Implementation Details and Results. Since the ASL datasets lack 2D or 3D annotations, such as poses, betas, or MANO parameters, we used our model MMHMR to generate pseudo-ground-truth (p-GT) annotations for the training images. These annotations were then employed to train MMHMR with text guidance, effectively transforming it into a text-to-mesh generator. Despite being derived annotations, the p-GT annotations were accurate enough to enable the generation of high-quality 3D meshes conditioned solely on text inputs. Moreover, we utilized CLIP [48] to extract text embeddings from the provided labels, enabling seamless integration of textual information into the generative pipeline. During testing, the model’s generative capability was demonstrated by producing multiple mesh outputs for a single text condition using a top-5% sampling strategy. This approach ensured diversity in the generated meshes while maintaining plausibility and fidelity to the text prompt. The generated meshes were quantitatively evaluated using standard metrics such as Hausdorff Distance and Chamfer Distance. Additionally, PA-MPVPE (measured in millimeters), which assesses vertex-to-vertex projection error, was introduced. These metrics were averaged across all generated meshes per text condition to ensure consistency. The results, presented in Table 10, indicate that MMHMR achieves high fidelity and consistency in text-to-mesh generation, with minimal deviations across samples. The quantitative evaluation affirms the precision of the generated meshes, while qualitative examples, illustrated in Figure 7, highlight the model’s ability to produce structurally accurate and visually realistic outputs for diverse text prompts. This experiment underscores MMHMR’s potential as a versatile generative framework for text-to-mesh applications.

Table 10: Quantitative Evaluation of Text-to-Mesh Generation using MMHMR’s Masked Synthesizer. Metrics include mean and standard deviation for Hausdorff Distance, Chamfer Distance, and PA-MPVPE (in mm). Results are averaged across all generated meshes per text prompt.

Metric	Mean	Standard Deviation
Hausdorff Distance	0.0221	0.0073
Chamfer Distance	$9.73\times 10^{-5}$	$5.47\times 10^{-5}$
PA-MPVPE (mm)	12.2	3.1

Appendix E Effectiveness of Expectation-Approximated Differential Sampling

The results presented in Table 11 highlight the critical role of Expectation-Approximated Differential Sampling in enabling accurate and robust 3D hand mesh recovery. The configuration utilizing all loss components— $L_{mask}$ , $L_{MANO}$ , $L_{3D}$ , $L_{2D}$ , and $\beta$ —achieves the lowest PA-MPJPE and PA-MPVPE values of 0.70 mm on HO3Dv2 and 5.5 mm on FreiHAND, underscoring the importance of a holistic training approach. This configuration demonstrates the complementary strengths of $L_{3D}$ in enforcing anatomical coherence, $L_{2D}$ in mitigating monocular depth ambiguities, and $L_{mask}$ in iteratively refining pose token predictions. Excluding critical components such as $L_{3D}$ or $L_{2D}$ leads to substantial degradation in performance, with errors rising to 8.1 mm on HO3Dv2 and 7.0 mm on FreiHAND. These results emphasize the necessity of these constraints for accurate 2D-to-3D alignment and plausible pose synthesis. Expectation-Approximated Differential Sampling is instrumental in this process, as it facilitates seamless integration of these losses by leveraging a differentiable framework for token refinement. This approach ensures that the latent pose space is effectively optimized, enabling the model to balance fine-grained token accuracy with global pose coherence. These findings validate the pivotal role of differential sampling in guiding the learning process, resulting in precise and confident 3D reconstructions under challenging scenarios.

Table 11: Impact of different loss combinations on PA-MPJPE and PA-MPVPE errors ( in mm) for the HO3Dv2 and FreiHAND datasets.

Used Losses	HO3Dv2		FreiHAND
	PA-MPJPE ↓	PA-MPVPE ↓	PA-MPJPE ↓	PA-MPVPE ↓
$L_{mask},\beta$	7.6	7.5	6.3	6.4
$L_{mask},L_{MANO},\beta$	7.5	7.5	6.2	6.4
$L_{mask},L_{MANO},L_{3D},L_{2D},\beta$	7.0	7.0	5.7	5.5
$L_{3D},\beta$	8.1	7.9	6.8	7.0
$L_{mask},L_{MANO},L_{3D},L_{2D},\beta$	7.4	7.3	6.5	6.7

Appendix F Confidence-Guided Masking

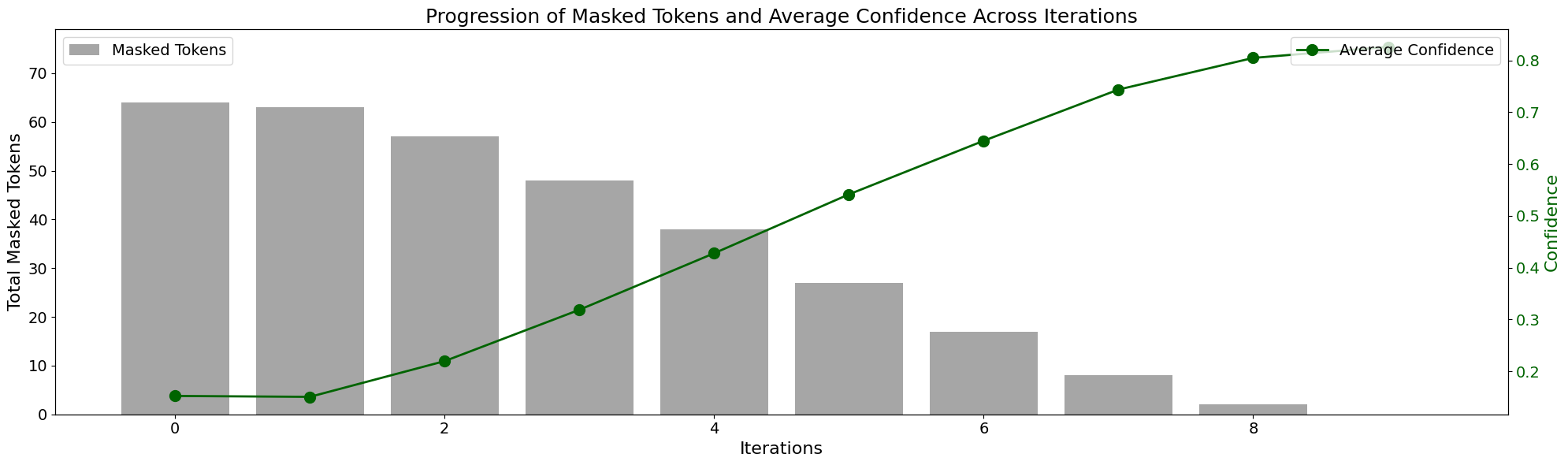
Figure 8 illustrates the iterative process of Confidence-Guided Sampling used during inference for refining pose predictions. The gray bars represent the total number of masked tokens across iterations, while the green line tracks the average confidence in the model’s predictions. At the initial iteration, the majority of pose tokens remain masked, indicating high uncertainty. As iterations progress, the number of masked tokens decreases significantly, which aligns with a steady increase in the model’s confidence. By the final iteration, only a minimal number of tokens remain masked, while the average confidence approaches its peak. This visualization highlights the systematic reduction in uncertainty and refinement of predictions over multiple iterations, enabling robust 3D pose reconstruction.

Appendix G Pose Token Sampling Techniques

The ablation study, illustrated in Table 12 and supported by Figure 9, highlights the crucial role of the Top- $k$ -th token sampling strategy in MMHMR. Top-1st token sampling, which selects the most confident token prediction for each pose token, yields the most accurate results, with the lowest PA-MPJPE (7.0 mm for HO3Dv3 and 5.7 mm for FreiHAND) and PA-MPVPE (7.0 mm for HO3Dv3 and 5.5 mm for FreiHAND). This demonstrates the model’s ability to focus on high-confidence tokens, ensuring precise 3D hand mesh reconstructions. As $k$ increases, performance degrades significantly due to the inclusion of less confident tokens. For example, with Top-20th token sampling, PA-MPJPE increases to 10.57 mm on HO3Dv3 and 10.63 mm on FreiHAND, as noise and uncertainty introduced by broader sampling reduce the accuracy of the final pose estimation. This pattern is clearly reflected in Figure 9, where reconstructions using the 1st most confident token closely resemble the ground truth, while lower-ranked tokens (e.g., 100th or 1000th token) lead to unrealistic and distorted poses. These findings underscore the necessity of prioritizing high-confidence token predictions, as seen in the Top-1st token sampling strategy, to effectively address ambiguities in 2D-to-3D mapping. Broader sampling dilutes precision by introducing irrelevant or noisy tokens. The analysis reaffirms that MMHMR’s reconstruction fidelity hinges on the fine-grained selection of tokens, emphasizing the importance of a confidence-guided approach for robust and accurate performance.

Table 12: Impact of Top-kth Sampling on MMHMR on HO3DV3 and FreiHAND dataset.

	HO3Dv3		FreiHAND
Top-K-th	PA-MPJPE	PA-MPVPE	PA-MPJPE )	PA-MPVPE
1	7.0	7.0	5.7	5.5
3	8.3	8.1	7.9	8.0
5	8.4	8.2	7.9	8.1
10	10.57	10.47	9.1	9.2
20	10.57	10.48	10.63	10.75

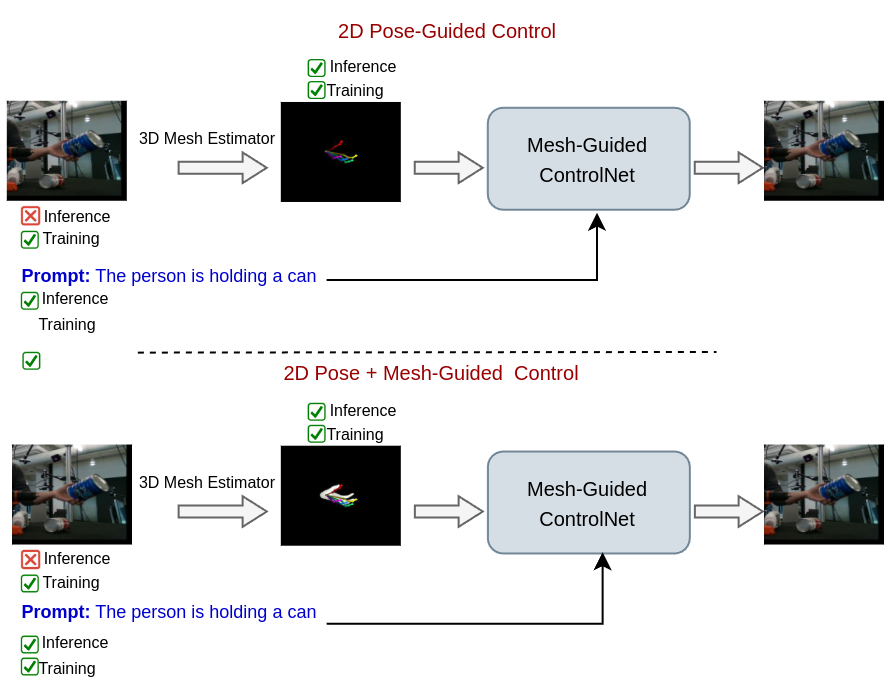
Appendix H Impact of Control Signals for Hand Image Generation

The role of control signals in guiding the generation of hand images using MMHMR’s Masked Synthesizer was evaluated through mesh-guided and pose-guided strategies. By leveraging meshes as control signals, the model demonstrated its ability to produce realistic and accurate hand images aligned with the underlying 3D structures. The results, presented in Table 13, show that mesh-guided control achieved better performance in terms of FID-H and KID-H, as well as higher hand detection confidence compared to 2D pose guidance. Notably, the combination of both mesh and 2D pose guidance further enhanced the model’s ability to generate high-quality images with fine structural details. The experiment highlighted that mesh guidance provides stronger structural constraints, leading to superior generation quality. The addition of 2D pose information complements the mesh signals by refining finer spatial details. These findings underline the versatility of MMHMR’s Masked Synthesizer in integrating multiple control modalities to achieve robust and visually coherent hand image generation, even in complex scenarios like hand-object interactions. Figures 10 and 11 demonstrate the effectiveness of mesh-guided and combined control strategies in generating realistic hand images. Mesh guidance provides strong structural constraints, while 2D pose signals refine spatial accuracy, ensuring robust and visually coherent outputs even in complex scenarios.

Table 13: Mesh-Guided Control for Hand Image Generation

HaMer Mesh Estimator	FID-H $\downarrow$	KID-H $\downarrow$	Hand Det Conf. $\uparrow$
2D Pose Guidance	45.65	0.035	0.865
Mesh Guidance	40.23	0.027	0.912
Mesh + 2D Pose Guidance	40.01	0.026	0.910

Appendix I Impact of Pose Tokenizer on MMHMR

The results presented in Table 14 demonstrate the critical influence of the Pose Tokenizer’s design on the performance of MMHMR. Increasing the codebook size from $1024\times 256$ to $2048\times 256$ yields significant improvements in both PA-MPJPE and MVE metrics across the HO3Dv3 and FreiHAND datasets. This indicates that a moderately larger codebook provides richer and more expressive pose representations, enabling better reconstruction of complex 3D hand poses. However, expanding the codebook further to $4096\times 256$ diminishes accuracy, suggesting that an overly large codebook introduces unnecessary complexity, making it harder for the model to generalize effectively.

Table 14: Impact of Codebook Size (Tokens = 96) on MMHMR.

	HO3Dv3		FreiHAND
# of code $\times$ code dimension	MPJPE ( $\downarrow$ )	MVE ( $\downarrow$ )	MPJPE ( $\downarrow$ )	MVE ( $\downarrow$ )
$1024\times 256$	7.2	7.3	6.4	6.5
$2048\times 128$	7.1	7.2	6.0	5.9
$2048\times 256$	7.0	7.0	5.7	5.7

Appendix J Impact of Multi-Scale Features

The ablation study on multi-scale feature resolutions in MMHMR (as shown in Table 15) highlights the trade-off between accuracy and computational cost. Including resolutions up to $4\times$ yields slight accuracy gains, with PA-MPJPE reducing to 7.0 mm on HO3Dv3 and 5.7 mm on FreiHAND. However, the addition of higher resolutions, such as $1\times$ and $2\times$ , results in inconsistent or degraded performance. Specifically, the inclusion of $1\times,4\times,8\times$ scales increases PA-MPJPE to 7.2 mm on HO3Dv3 and 5.8 mm on FreiHAND. Adding $2\times$ further worsens performance, reaching 7.6 mm on HO3Dv3 and 6.1 mm on FreiHAND, while significantly increasing computational overhead. Notably, the omission of lower-scale features (e.g., $1\times$ ) leads to performance degradation, highlighting the importance of combining fine-grained details with holistic structure. While multi-scale features remain critical, the study demonstrates that not all resolutions contribute equally, with $1\times$ and $4\times$ emerging as the optimal balance for accuracy and computational efficiency.

Table 15: Impact of feature resolutions on PA-MPJPE and PA-MPVPE errors for HO3Dv3 and FreiHAND datasets.

Feature Scales (Included)	HO3Dv3 ↓		FreiHAND ↓
	PA-MPJPE	PA-MPVPE	PA-MPJPE	PA-MPVPE
1 $\times$	7.1	7.1	5.9	5.8
1 $\times$ , 4 $\times$	7.0	7.0	5.7	5.5
1 $\times$ , 4 $\times$ , 8 $\times$	7.2	7.2	5.8	5.9
1 $\times$ , 8 $\times$ , 16 $\times$	7.1	7.1	6.0	5.9
1 $\times$ , 4 $\times$ , 8 $\times$ , 16 $\times$	7.6	7.5	6.1	6.3

Appendix K Cross-Attention Layers in MMHMR

The ablation study in Table 16 highlights the pivotal role of Deformable Cross-Attention Layers in the Context-Infused Masked Synthesizer of MMHMR. Increasing layers from 2 to 4 yields significant performance gains, reducing PA-MPJPE to 5.7 mm and PA-MPVPE to 5.5 mm on the FreiHAND dataset. This improvement underscores the layers’ effectiveness in fusing multi-scale contextual features and refining token dependencies for enhanced 3D hand mesh reconstruction. However, further increasing the layers beyond 4 results in diminishing returns, with slight performance degradation at 6 and 8 layers (e.g., PA-MPVPE increases to 5.8 mm and 6.1 mm, respectively). This decline suggests that additional layers introduce unnecessary complexity, potentially overfitting or disrupting the model’s ability to generalize effectively. The findings reveal that 4 layers provide the optimal balance, leveraging the benefits of cross-attention mechanisms without incurring computational overhead or accuracy trade-offs.

Table 16: Impact of Deformable Cross Attention Layers on FreiHAND dataset.

Metric	2 Layers	4 Layers	6 Layers	8 Layers
PA-MPJPE	6.6	5.7	5.7	6.0
PA-MPVPE	6.9	5.5	5.8	6.1

Appendix L Qualitative Results

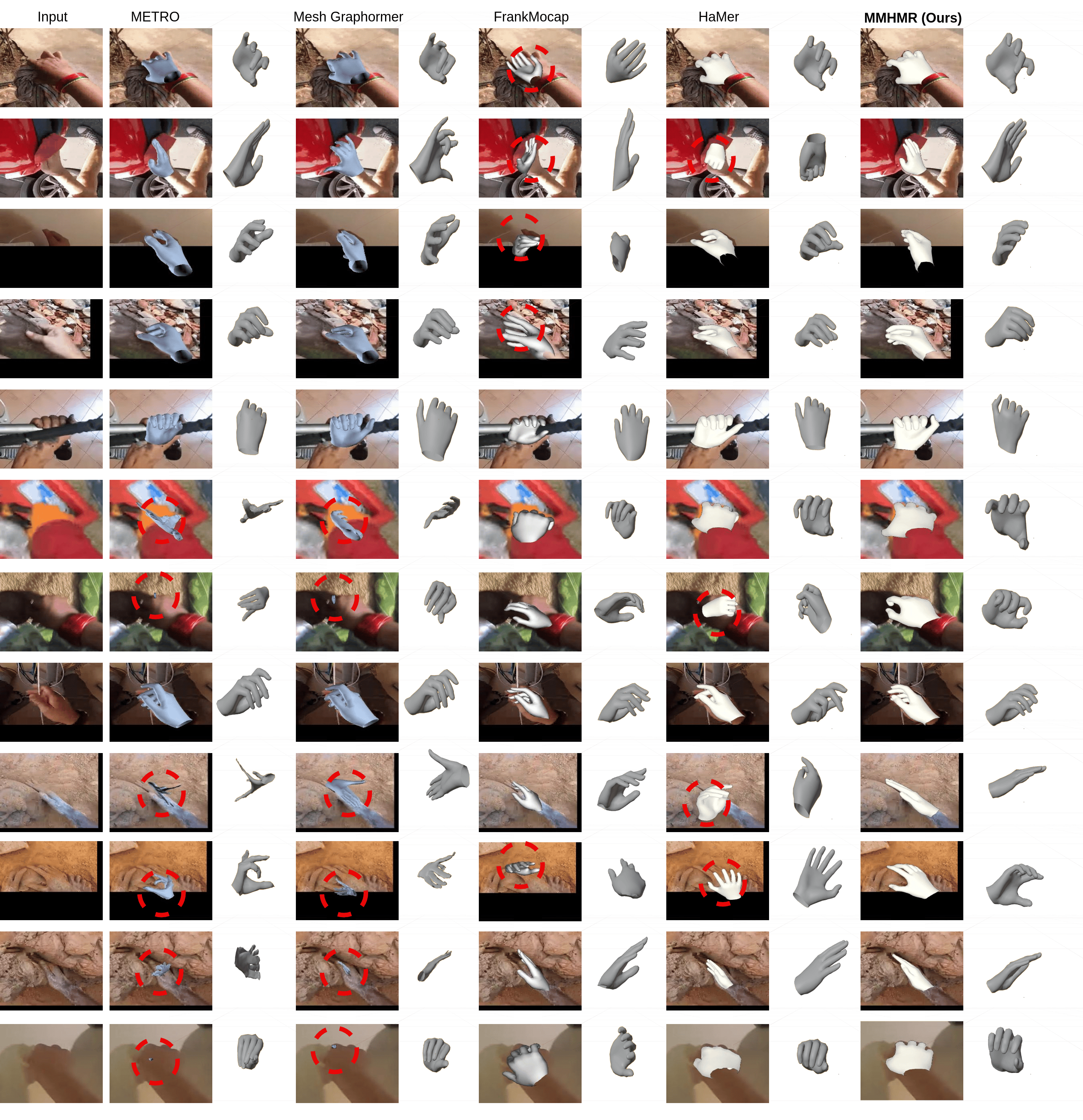
Comparison of State-of-the-Art (SOTA) Methods. Figure 12 demonstrates the superiority of MMHMR over other SOTA methods in recovering 3D hand meshes. Unlike competing approaches, MMHMR employs a generative masked modeling framework, enabling it to synthesize unobserved or occluded hand regions. This capability allows MMHMR to achieve robust and precise 3D reconstructions, even in scenarios with heavy occlusions, intricate hand-object interactions, or diverse hand poses. By refining masked tokens, MMHMR effectively addresses ambiguities in the 2D-to-3D mapping process, resulting in highly accurate reconstructions.

MMHMR’s Performance on In-the-Wild Images. Figure 13 highlights MMHMR’s robustness in real-world conditions. The model demonstrates its ability to recover accurate 3D hand meshes from single RGB images, excelling in challenging scenarios such as occlusions, hand-object interactions, and diverse hand appearances. This versatility underscores MMHMR’s applicability to real-world tasks, where robust and reliable performance is essential.

Challenging Poses from the HInt Benchmark. Figure 14 illustrates MMHMR’s effectiveness in reconstructing 3D hand meshes for challenging poses from the HInt Benchmark [46]. The model accurately handles extreme articulations and unconventional hand configurations, showcasing its ability to generalize to complex datasets and produce high-fidelity results.

Reference Key Points in the Deformable Cross-Attention. Figure 15 visualizes the interaction between reference keypoints (yellow) and sampling offsets (red) in the Deformable Cross-Attention module of MMHMR’s Masked Synthesizer. By leveraging 2D pose as guidance, the model dynamically samples and refines critical features for accurate 3D reconstruction. This mechanism proves crucial in handling severe occlusions, intricate hand-object interactions, and complex viewpoints, ensuring precise alignment between 2D observations and 3D predictions.

Impact of Pose Token Confidence on MMHMR Reconstruction. Figure 16 explores the impact of pose token confidence on reconstruction accuracy. The comparison of 3D hand meshes generated using different levels of token confidence reveals that high-confidence tokens (Top-1) produce reconstructions closely aligned with the ground truth. In contrast, lower-confidence tokens introduce distortions, highlighting the importance of prioritizing high-confidence tokens for achieving accurate and robust 3D hand mesh reconstructions.