Model-free controlled variable selection via data splitting
Abstract
Addressing the simultaneous identification of contributory variables while controlling the false discovery rate (FDR) in high-dimensional data is a crucial statistical challenge. In this paper, we propose a novel model-free variable selection procedure in sufficient dimension reduction framework via a data splitting technique. The variable selection problem is first converted to a least squares procedure with several response transformations. We construct a series of statistics with global symmetry property and leverage the symmetry to derive a data-driven threshold aimed at error rate control. Our approach demonstrates the capability for achieving finite-sample and asymptotic FDR control under mild theoretical conditions. Numerical experiments confirm that our procedure has satisfactory FDR control and higher power compared with existing methods.
Keywords: Data splitting; False discovery rate; Model-free; Sufficient dimension reduction; Symmetry
Yixin Han1, Xu Guo2 & Changliang Zou1
1School of Statistics and Data Science, LPMC KLMDASR, Nankai University
2Department of Mathematical Statistics, Beijing Normal University
1 Introduction
Sufficient dimension reduction (SDR) is a powerful technique to extract relevant information from high-dimensional data (Li, 1991; Cook and Weisberg, 1991; Xia et al., 2002; Li and Wang, 2007). We use with support to denote the univariate response, and let be the -dimensional vector of all covariates. The basic idea of SDR is to replace the predictor vector with its projection onto a subspace of the predictor space without loss of information on the conditional distribution of given . In practice, a large number of features in high-dimensional data are typically collected, but only a small portion of them are truly associated with the response variable. However, while grasping important features or patterns in the data, the reduction subspace from SDR usually includes all original variables which makes it difficult to interpret. Therefore, in this paper, we aim at developing a model-free variable selection procedure to screen out truly non-contributing variables with certain error rate control, thus making the subsequent model building feasible or simplified and helping reduce the computational cost caused by high-dimensional data.
Let denote the conditional distribution function of given . The index sets of the active and inactive variables are defined respectively as
Many prevalent variable selection procedures have been developed under the paradigm of linear models or generalized linear models, such as LASSO (Tibshirani, 1996), SCAD (Fan and Li, 2001), or adaptive LASSO (Zou, 2006). See the review of Fan and Lv (2010) and the book of Fan et al. (2020) for a fuller list of references. In contrast, model-free variable selection can be achieved by SDR since it does not require complete knowledge of the underlying model, thus researchers can avoid disposing of model misspecification.
SDR methods with variable selection aim to find the active set such that
| (1) |
where “” stands for independence, denotes the vector containing all active variables and is the complementary set of . Condition (1) implies that contains all the relevant information in terms of predicting . Li et al. (2005) proposed to combine sufficient dimension reduction and variable selection. Chen et al. (2010) proposed a coordinate-independent sparse estimation that can simultaneously achieve sparse SDR and screen out irrelevant variables efficiently. Wu and Li (2011) focused on the model-free variable selection with a diverging number of predictors. A marginal coordinate hypothesis is proposed by Cook (2004) for model-free variable selection under low-dimensional settings, and then is promoted by Shao et al. (2007) and Yu and Dong (2016). Yu et al. (2016a) constructed marginal coordinate tests for sliced inverse regression (SIR) and Yu et al. (2016b) suggested a trace-pursuit-based utility for ultrahigh-dimensional feature selection. See Li et al. (2020) and Zhu (2020) for a comprehensive review.
However, those existing approaches do not account for uncertainty quantification of the variable selection, i.e., the global error rate control in the selected subset of important covariates in high-dimensional situations. In general high-dimensional nonlinear settings, Candes et al. (2018) developed a Model-X Knockoff framework for controlling false discovery rate (FDR, Benjamini and Hochberg, 1995), which was motivated by the pioneering Knockoff filter (Barber and Candès, 2015). Their statistics constructed via “Knockoff copies” would satisfy (or roughly) joint exchangeability and thus can yield finite-sample FDR control. However, the Model-X Knockoff requires knowing the joint distribution of the covariates, which is typically difficult in high-dimensional settings. Recently, Guo et al. (2024) improved the line of marginal tests (Cook, 2004; Yu and Dong, 2016) by using decorrelated score type statistics to make inferences for a specific predictor which is of interest in advance. They further leveraged the standard Benjamini and Hochberg (1995) on -values to control FDR, but the intensive computation of the decorrelated process may limit its application to high-dimensional situations. In a different direction, Du et al. (2023) proposed a data splitting strategy, named symmetrized data aggregation (SDA), to construct a series of statistics with global symmetry property and then utilize the symmetry to derive a data-driven threshold for error rate control. Specifically, Du et al. (2023) aggregated the dependence structure into a linear model with a pseudo response and a fixed covariate, making the dependence structure become a blessing for power improvement. Similar to the Knockoff method, the SDA is also free of -values and its construction does not rely on contingent assumptions, which motivates us to employ it in sufficient dimension reduction problems.
In this paper, we propose a model-free variable selection procedure that could achieve an effective FDR control. We first recast the problem of conducting variable selection in sufficient dimension reduction into making inferences on regression coefficients in a set of linear regressions with several response transformations. A variable selection procedure is subsequently developed via error rate control for low-dimensional and high-dimensional settings, respectively. Our main contributions include: (1) This novel data-driven selection procedure can control the FDR while being combined with different existing SDR methods for model-free variable selection by choosing different response transformation functions. (2) Our method does not need to estimate any nuisance parameters such as the structural dimension in SDR. (3) Notably, the proposed procedure is computationally efficient and easy to implement since it only involves a one-time split of the data and the calculation of the product of two dimension reduction matrices obtained from two splits. (4) Furthermore, this method can achieve finite-sample and asymptotic FDR control under some mild conditions. (5) Numerical experiments indicate that our procedure exhibits satisfactory FDR control and higher power compared with existing methods.
The rest of this paper is organized as follows. In section 2, we present the problem and model formulation. In section 3, we propose a low-dimensional variable selection procedure with error rate control and then discuss its extension in high-dimensional situations. The finite-sample and asymptotic theories for controlling the FDR are developed in Section 4. Simulation studies and a real-data investigation are conducted in Section 5 to demonstrate the superior performance of the proposed method. Section 6 concludes the paper with several further topics. The main theoretical proofs are given in Appendix. More detailed proofs and additional numerical results are delineated in the Supplementary Material.
Notations. Let and denote the smallest and largest eigenvalues of square matrix . Write and . Denote and be the and norm of vector . Denote and be the expectation and covariance for random vector , respectively. Let denote that two quantities and are asymptotically equivalent, in the sense that there is a constant such that with probability tending to 1. The “” and “” are similarly defined.
2 Problem and model formulation
The variable selection in (1) can be framed as a multiple testing problem
| (2) |
This is known as the marginal coordinate hypothesis described in Cook (2004) and Yu et al. (2016a). Some related works include Li et al. (2005), Shao et al. (2007), and Yu and Dong (2016). This type of selection procedure usually uses some nonnegative marginal utility statistics ’s to measure the importance of ’s to in certain sense. However, the global error rate control within those methods is still challenging because the determination of selection thresholds generally involves the approximation to the distribution of , and the accuracy of asymptotic distributions heavily affects the error rate control.
As a remedy, we consider a reformulation for (2). Let and assume . Denote is dimension reduction subspace. For any function satisfying , it has been demonstrated by Yin and Cook (2002) and Wu and Li (2011) that
under the linearity condition Li (1991), which is usually satisfied when is elliptical distribution. The transformation is used in a way different from its traditional role of being a mechanism for improving the goodness of model fitting. It serves as an intermediate tool for performing dimension reduction. Consequently, different transformation functions correspond to different SDR methods (Dong, 2021). One can choose a series of transformation functions, , whose forms do not depend on data. The , a pre-specified integer, is usually called a working dimension and is the true structural dimension of the subspace . Given the working dimension , at the population level, define
| (3) |
Write , then , and represents the subspace spanned by the column vector of . By the following usual protocol in the literature of sufficient dimension reduction, we take one step further by assuming the coverage condition whenever . This condition often holds in practice; see Cook and Ni (2006) for further discussion.
For , let be the th element of , . If the th variable is unimportant, , where denotes the th row of . Further, implies that for and for . In other words, if belongs to the active set , response must depend on through at least one of the linear combinations. If belongs to the inactive set , none of the linear combinations involve (Yu et al., 2016a). Accordingly, the testing problem (2) is equivalent to
| (4) |
Based on the above discussion, selecting active variables in a model-free framework is equivalent to selecting important variables in multiple response linear model. Assume that there are independent and identical distributed data . Denote are the estimators of , and ’s as the marginal statistics based on the sample associated with the variants of . Its explicit form would be given in the next section. A selection procedure with a threshold is formed as
| (5) |
where is the estimate of with threshold . Obviously, plays an important role in variable selection to control the model complexity. We will construct an appropriate threshold by controlling the FDR to achieve model-free variable selection in SDR.
Denote , and assume that is dominated by , i.e., . The false discovery proportion (FDP) associated with the selection procedure (5) is
where and stands for the cardinality of an event. The FDR is defined as the expectation of the FDP, i.e., . Our main goal is to find a data-driven threshold that controls the asymptotic FDR at a target level ,
3 Variable selection via FDR control
In this section, we first provide a data-driven variable selection procedure in Subsection 3.1 to control the FDR via data splitting technique in a model-free context when , and the high-dimensional version is deferred in Subsection 3.2.
3.1 Low-dimensional procedure
We first split the full data into two independent parts and with equal size, which is respectively used to estimate the dimension reduction spaces as and , where and . One can find the unequal size data splitting investigation in Du et al. (2023). On split , , the least square estimator of
where and is the -dimensional unit vector with the th element being 1. The information from two parts is then combined to form a symmetrized ranking statistic
| (6) |
where , . For an active variable, if is large (under ), then both and have the same sign and tend to have large absolute values, thereby leading to a positive and large (Du et al., 2023). For a null feature, is symmetrically distributed around zero. It implies that demonstrates the marginal symmetry property (Barber and Candès, 2015; Du et al., 2023) for all inactive variables such that it can be used to determine active or inactive variables. This motivates us to choose a data-driven threshold as the following to control the FDR at level
| (7) |
If the above set is empty, we simply set . Then our decision rule is given by . The fraction in (7) is an estimate of the FDP since is a good approximation to by the marginal symmetry of under null. The core of our procedure is to construct marginal symmetric statistics using the data splitting technique, to obtain a data-driven threshold to realize variable selection. Therefore, we refer our method to Model-Free Selection via Data Splitting (MFSDS).
Since the estimators, and , only are two approximations of B and they are not derived by eigenvalue decomposition system (Li, 1991; Cook and Weisberg, 1991), there is no concern about that and may not be in the same subspace. Our ultimate goal is to identify the active variables rather than to recover the dimension reduction subspace. It implies that variable selection achieved through (3) requires no dimension reduction basis estimation and thus is dispensable for the knowledge of the structural dimension either. Therefore, the proposed method can be adapted to a family of inverse slice regression estimators by choosing different . In a nutshell, our method can be widely used due to its simplicity, computational efficiency, and generality. It is summarized as follows.
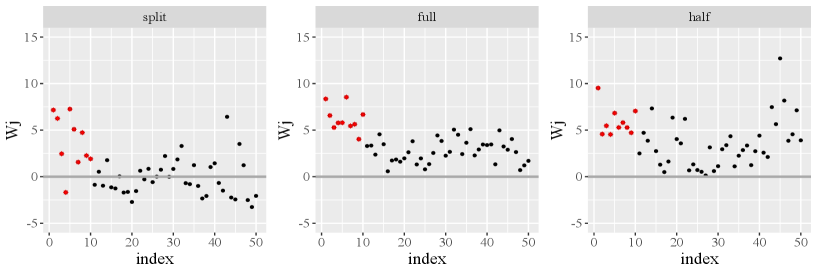
The total computational complexity of Algorithm 1 is of order so that this algorithm can be easily implemented. Practically, our method involves data splitting that may lead to some information loss concerning the full data (Du et al., 2023). Fortunately, we obtain a data-driven threshold by the marginal symmetry property of under the null, which does not need to find the null asymptotic distribution anymore. Here we use a toy example to illustrate the advantage of data splitting. Further details regarding the data generation can be found in Section 5. In Figure 1, we observe that the data splitting method (left panel) places most active variables above zero, and many inactive variables are symmetrically distributed around zero. This is a crucial property for our selection procedure while the full estimation (middle panel) and half data estimation (right panel) methods both fail to achieve this level of symmetry.
3.2 High-dimensional procedure
When the dimension is very large in practice, the above procedure does not work since the ordinary least square procedure cannot be directly implemented. Note that our data splitting procedure can be essentially extended to the version of the regularization form. Inspired by the idea of SDA filter proposed by Du et al. (2023), we then develop the following selection procedure for high-dimensional data.
To extract information from , we replace the least square solution in (3) with LASSO selector (Tibshirani, 1996) as follows
| (8) |
where is a tuning parameter. It is worth noting that although the LASSO estimator does not provide guarantees on the FDR control of the selected variables, it still serves as a useful tool here that simultaneously takes into account the sparsity and dependence structures as described in Du et al. (2023). It is not necessary to penalize slices of coefficients simultaneously to establish . This is quite different from the traditional model-free variable selection methods, such as Wu and Li (2011).
Let be the subset of variables selected by (8), where is the th element of . We then use to obtain the least square estimates in (3) for coordinates in the narrowed subset . Denote the estimates from and be and , where
Accordingly, the ranking statistics in the high-dimensional setting are constructed as
where , , with narrowed subset . The statistics has similar properties to the proposed one in (6), which is (asymptotically) symmetric with mean zero for and is a large positive value for without imposing the relationship between and . Therefore, we propose to choose a threshold
| (9) |
and select the active variables by in high-dimensional setting. The proposed in (9) shares a similar spirit to Model-X Knockoff (Candes et al., 2018) or SDA filter (Du et al., 2023) to obtain an accurate FDR control. However, in the high-dimensional variable selection problems, we usually can not collect enough information on , and the exact knockoff copies may not be available when . Fortunately, MFSDS does not require any prior information on the distribution of or the asymptotic distribution of statistics, and thus it is more suitable for high-dimensional problems.
4 Theoretical results
In this section, we entirely focus on controlling FDR. We begin by imposing a mild restriction on the response transformation function .
Assumption 1 (Response transformation).
Function satisfies and .
Assumption 1 distinguishes our approach from most model-based selection methods by transforming a general model into a multivariate response linear problem, thereby achieving model-free variable selection (Wu and Li, 2011). The transformed errors are not independent of the covariates and thus we need more effort for the theoretical analysis. Our first theorem is a finite sample theory for FDR control.
Theorem 4.1 (Finite-sample FDR control).
Suppose Assumption 1 hold. Assume that the statistics , , are well-defined. For any , the FDR of our model-free selection procedure satisfies
where and .
Theorem 4.1 holds regardless of the unknown relationship between variables and response . This result can be established using the techniques developed in Barber et al. (2020). The quantity is interpreted as a measure to investigate the effect of both the asymmetry of and the dependence between and on FDR. In asymmetric cases, it is still expected that will be small, given that both and converge to normal distributions if is not too small. Theorem 4.1 implies that tight control of ’s under asymmetric cases also results in effective FDR control.
For asymptotic FDR control of the proposed procedure, we require the following technical assumptions, which are not the weakest one but facilitate the technical proofs in the Supplementary Material. Let with , where and . Define and . Denote , and . Assume that is uniformly bounded above by some non-random sequence .
Assumption 2 (Sure screening property).
As ,
Assumption 3 (Moments).
Let . Conditioning on , there exists a positive diverging sequence and a constant such that
for . Assume that as , for some small .
Assumption 4 (Design matrix).
There exist positive constants and such that
hold with probability one.
Assumption 5 (Estimation accuracy).
Assume that uniformly holds for , where is an estimator of from , and .
Assumption 6 (Signals).
Denote . Let as .
Assumption 7 (Dependence).
Let denotes the conditional correlation between and given . Assume that for each and some , , where is some small constant, and as .
Remark 1.
Assumption 2 has been used in Meinshausen et al. (2009); Barber and Candès (2019); Du et al. (2023) to ensure that is unbiased for . Assumptions 3 and 4 are commonly used in the context of variable selection. The rate in Assumption 5 ensures that is a reasonable estimator of from . For the LASSO selector, typically satisfies the Assumption 5. Assumption 6 implies that the number of informative covariates with identifiable effect sizes is not too small as . Assumption 7 allows to be correlated with all others but requires that the correlation coefficients need to converge to zero at a log rate. This condition is similar to the weak dependence structure given in Fan et al. (2012).
Theorem 4.2 (Asymptotic FDR control).
Theorem 4.2 implies that the variable selection procedure with the data-driven threshold can control the FDR at the target level asymptotically. Further investigations are needed to better understand the condition . The conventional result of indicates that . With of LASSO selector, the condition degenerates to if is of a polynomial rate of . The above condition basically imposes restrictions on the rate of , , and . Accordingly, the screening stage on split must satisfy if we assume that and are bounded. Alternatively, if we only assume that is bounded, then a sufficient requirement for the condition in Theorem 4.2 is since . This is a reasonable rate in the problem with a diverging number of parameters, such as Fan and Peng (2004) and Wu and Li (2011).
5 Numerical studies
We evaluate the performance of our proposed procedure on several simulated datasets and a real-data example under low-dimensional and high-dimensional settings.
5.1 Implantation details
We compared our MFSDS with several benchmark methods. The first one is the marginal coordinate test in sliced inverse regression (SIR, Cook, 2004), which aims at controlling the error rate for each coordinate. To make a global error rate control, we then apply the BH procedure (Benjamini and Hochberg, 1995) to the -values. This method is implemented using functions “dr” and “drop1” in R package dr. The second method is the Model-X Knockoff (Candes et al., 2018), which also is a model-free and data-driven variable selection procedure as the proposed method. This method is implemented by the function “create.gaussian” in R package knockoff using the lasso signed maximum feature important statistics. The two methods are termed MSIR-BH and MX-Knockoff, respectively.
We set the FDR level to and conducted 500 replications for all simulation results. The performance of the proposed MFSDS is evaluated along with the above benchmarks through the comparisons of FDR, the true positive rate (TPR), and the average computing time.
5.1.1 Low-dimensional studies
We generate the covariates following three distributions: multivariate normal distribution with , ; multivariate distribution with covariance ; a mixed distribution which consists of are from , are from , and are i.i.d from a distribution. The error term is the standard normal distribution which is independent of . We fix . For a scalar , write be the -dimensional row vector of ’s. Five models have been considered:
-
•
Scenario 1a: , where .
-
•
Scenario 1b: , where , .
-
•
Scenario 1c: , where , , .
-
•
Scenario 1d: , where , , , .
-
•
Scenario 1e: , where , , , , .
We first consider three response transformation functions , for the proposed MFSDS: (1) the slice indicator function (Li, 1991) that if is in the th slice and 0 otherwise; (2) The CIRE-type response transformation (Cook and Ni, 2006) that if is in the th slice and 0 otherwise; (3) the normalized polynomial response transformation (Yin and Cook, 2002) that if is in the th slice and 0 otherwise. We name these three functions as Indicator, CIRE, and Poly, respectively.
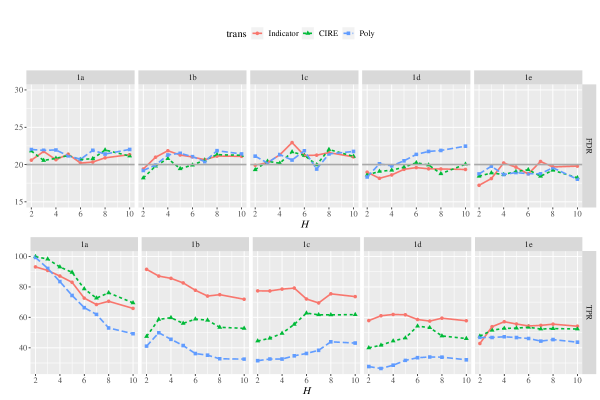
Figure 2 shows that our proposed procedure successfully controls FDR in an acceptable range of the target level, regardless of the number of working dimension and the response transformation functions. The three response transformation functions exhibit similar patterns with FDR control, and we do not address which is the “best” in this paper. Our methodology does not require the estimation of with a given . In the rest of the simulations, we focus on the slice indicator function and fix for the proposed MFSDS.
Next, we compare FDR and TPR of the proposed MFSDS under low-dimensional settings with marginal SIR and MX-Knockoff in Table 1 and Table 2. Table 1 studies how the proposed MFSDS and the benchmark methods are affected by the covariate distributions. Table 2 displays the comparisons of covariate correlation for the three methods. Across all scenarios, the FDRs of MFSDS persist at the desired level consistently and the TPRs of MFSDS are higher than MSIR-BH and MX-Knockoff in most cases. Further discussion can be found below.
-
(a)
MFSDS vs MSIR-BH. The marginal SIR (Cook, 2004) with BH procedure (Benjamini and Hochberg, 1995) controls the FDR in all settings but can be overly conservative in some cases. This is because the BH procedure controls the FDR at level in a low-dimensional setting. By contrast, MFSDS performs accurate FDR control and better TPR in both linear and nonlinear models. It seems that the power of the proposed MFSDS is slightly lower than MSIR-BH in very few cases since MFSDS involves data splitting to construct the statistic symmetry property. But additional simulations show that, as the sample size increases, our method will be more effective than others in low-dimensional settings.
-
(b)
MFSDS vs MX-Knockoff. MFSDS and MX-Knockoff are both model-free and data-driven variable selection methods. However, MX-Knockoff requires knowing the joint distribution of the covariates. The proposed MFSDS controls the FDR more accurately near the desired level, while MX-Knockoff fails to control the FDR for distribution in Column 2 of Table 1. Furthermore, Table 1 shows that MX-Knockoff works not well as our MFSDS in nonlinear cases. Table 2 indicates that the MFSDS robustly controls the FDR at the nominal level, but the MX-Knockoff exhibits more conservative FDR and lower TPR as the correlation increases across all scenarios.
| normal | t5 | mixed | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario | Method | FDR | TPR | FDR | TPR | FDR | TPR | ||
| MFSDS | 20.7 | 87.1 | 22.0 | 84.4 | 22.2 | 96.4 | |||
| 1a | MSIR-BH | 10.4 | 91.4 | 10.1 | 84.6 | 10.8 | 98.2 | ||
| MX-Knockoff | 21.0 | 99.9 | 22.4 | 100.0 | 22.8 | 100.0 | |||
| MFSDS | 21.8 | 85.6 | 19.1 | 70.4 | 21.5 | 89.7 | |||
| 1b | MSIR-BH | 10.0 | 83.1 | 13.1 | 68.3 | 10.5 | 88.9 | ||
| MX-Knockoff | 13.3 | 39.9 | 39.4 | 50.6 | 16.3 | 58.9 | |||
| MFSDS | 21.3 | 78.5 | 20.9 | 68.9 | 20.9 | 84.2 | |||
| 1c | MSIR-BH | 10.5 | 74.8 | 14.1 | 68.1 | 11.2 | 80.9 | ||
| MX-Knockoff | 13.6 | 46.0 | 38.8 | 52.4 | 19.1 | 82.2 | |||
| MFSDS | 18.6 | 61.9 | 20.0 | 51.9 | 20.0 | 61.9 | |||
| 1d | MSIR-BH | 10.6 | 57.4 | 14.1 | 48.5 | 11.6 | 56.0 | ||
| MX-Knockoff | 14.7 | 40.2 | 38.9 | 52.5 | 18.6 | 51.9 | |||
| MFSDS | 20.2 | 57.1 | 18.7 | 49.5 | 18.0 | 58.2 | |||
| 1e | MSIR-BH | 11.7 | 51.1 | 12.9 | 46.2 | 10.9 | 52.8 | ||
| MX-Knockoff | 14.5 | 40.0 | 38.8 | 52.6 | 16.0 | 33.4 | |||
| Scenario | Method | FDR | TPR | FDR | TPR | FDR | TPR | ||
|---|---|---|---|---|---|---|---|---|---|
| MFSDS | 22.6 | 99.1 | 20.7 | 87.1 | 14.6 | 27.7 | |||
| 1a | MSIR-BH | 11.0 | 99.9 | 10.4 | 91.4 | 14.0 | 10.0 | ||
| MX-Knockoff | 22.8 | 100.0 | 21.0 | 99.9 | 20.6 | 95.6 | |||
| MFSDS | 22.9 | 99.5 | 21.8 | 85.6 | 21.6 | 30.2 | |||
| 1b | MSIR-BH | 11.2 | 99.8 | 10.0 | 83.1 | 12.0 | 16.5 | ||
| MX-Knockoff | 15.9 | 54.9 | 13.3 | 39.9 | 10.1 | 20.7 | |||
| MFSDS | 21.6 | 89.9 | 21.3 | 78.5 | 20.2 | 34.9 | |||
| 1c | MSIR-BH | 11.2 | 85.9 | 10.5 | 74.8 | 11.7 | 18.4 | ||
| MX-Knockoff | 17.5 | 69.3 | 13.6 | 46.0 | 11.1 | 22.6 | |||
| MFSDS | 18.2 | 64.8 | 18.6 | 61.9 | 20.0 | 40.9 | |||
| 1d | MSIR-BH | 10.2 | 61.6 | 10.6 | 57.4 | 12.5 | 31.2 | ||
| MX-Knockoff | 16.7 | 48.0 | 14.7 | 40.2 | 11.5 | 22.5 | |||
| MFSDS | 19.1 | 64.7 | 20.2 | 57.1 | 18.1 | 45.6 | |||
| 1e | MSIR-BH | 11.2 | 61.2 | 11.7 | 51.1 | 9.6 | 40.2 | ||
| MX-Knockoff | 17.0 | 38.3 | 14.5 | 40.0 | 10.6 | 25.1 | |||
5.1.2 High-dimensional studies
In high-dimensional settings, we consider the following benchmarks. The competitor MSIR-BH in low-dimension does not work in high-dimensional settings since the -value cannot directly be obtained. Thus, the sample-splitting method (Wasserman and Roeder, 2009), which first conducts data screening using LASSO and then applies BH to the -values calculated by marginal SIR (Cook, 2004). Since the commonly used Akaike information criterion such as in Du et al. (2023) causes inaccurate model deviance after slicing responses, the cross-validation criterion is conducted to choose an overfitted model in the screening stage. The second method is named as MFSDS-DB (Javanmard and Montanari, 2014), which extends the least square solution in (3) to regularized version with penalty in (8) and makes a bias correction with R package selectiveInference. The MX-Knockoff is conducted by the function create.second-order in R package knockoff to approximate an accurate precision matrix in high-dimensional setting (Candes et al., 2018). The fourth one is the marginal independence SIR proposed in Yu et al. (2016a). We choose two model sizes , , as two simple competitors and denote them as IM-SIR1 and IM-SIR2, respectively. We consider the following models when with signal strength .
-
•
Scenario 2a: , where .
-
•
Scenario 2b: , where , .
-
•
Scenario 2c: , where ; ; .
| normal | mixed | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Method | FDR | TPR | time | FDR | TPR | time | |||
| MFSDS | 18.3 | 98.7 | 90.2 | 12.9 | 17.5 | 98.3 | 86.6 | 14.1 | ||
| MFSDS-DB | 17.1 | 57.9 | 7.0 | 75.1 | 17.0 | 77.3 | 19.8 | 65.5 | ||
| MSIR-BH | 4.5 | 32.8 | 0.0 | 11.4 | 4.2 | 32.9 | 0.0 | 12.6 | ||
| 2a | IM-SIR1 | 0.0 | 40.0 | 0.0 | 26.3 | 0.0 | 40.0 | 0.0 | 34.8 | |
| IM-SIR2 | 75.0 | 100.0 | 100.0 | 26.3 | 75.0 | 100.0 | 100.0 | 34.5 | ||
| MX-Knockoff | 6.5 | 4.3 | 0.0 | 31.8 | 26.4 | 9.2 | 0.0 | 31.6 | ||
| MFSDS | 17.0 | 94.7 | 62.0 | 12.8 | 17.5 | 94.6 | 58.8 | 14.7 | ||
| MFSDS-DB | 15.6 | 71.4 | 4.2 | 74.8 | 16.9 | 80.5 | 14.4 | 75.3 | ||
| MSIR-BH | 5.3 | 34.9 | 0.0 | 11.5 | 4.6 | 34.6 | 0.0 | 13.3 | ||
| 2b | IM-SIR1 | 0.0 | 40.0 | 0.0 | 26.3 | 0.0 | 40.0 | 0.0 | 27.3 | |
| IM-SIR2 | 75.0 | 100.0 | 100.0 | 26.3 | 75.0 | 100.0 | 100.0 | 27.1 | ||
| MX-Knockoff | 10.3 | 11.6 | 0.0 | 31.9 | 29.0 | 19.8 | 0.0 | 31.4 | ||
| MFSDS | 17.9 | 92.7 | 50.6 | 12.4 | 19.2 | 92.8 | 49.8 | 22.8 | ||
| MFSDS-DB | 17.0 | 62.1 | 8.0 | 102.3 | 17.4 | 73.2 | 6.0 | 126.8 | ||
| MSIR-BH | 6.5 | 33.4 | 0.0 | 12.2 | 6.3 | 31.1 | 0.0 | 21.8 | ||
| 2c | IM-SIR1 | 0.0 | 40.0 | 0.0 | 22.7 | 0.0 | 40.0 | 0.0 | 36.2 | |
| IM-SIR2 | 75.0 | 100.0 | 100.0 | 22.9 | 75.0 | 100.0 | 100.0 | 35.2 | ||
| MX-Knockoff | 12.1 | 12.2 | 0.0 | 28.4 | 28.8 | 19.1 | 0.0 | 42.0 | ||
Table 3 presents the comparison results for different covariate distributions to investigate the error rate control and detection power under high-dimensional settings. The FDRs of the proposed MFSDS are approximately controlled at the target level with a higher power, which is consistent with our theory. A similar analysis also can be found in the Supplementary Material Table S1 with a larger sample size. Table 3 and Table S1 further demonstrate that the MFSDS is able to detect all active variables when is large. As we can expect, although MFSDS involves data splitting which may lose some data information, its power can still be higher since the feature screening step significantly increases the signal-to-noise ratio. Besides, our method exhibits lower computing time since we avoid constructing the asymptotic distribution for each dimension in marginal coordinate test (Cook, 2004) and generating the knockoff copies in Model-X knockoff (Candes et al., 2018). We provide further explanations below.
-
(a)
MFSDS vs MFSDS-DB. The FDR of the MFSDS-DB method controls pretty well as the proposed MFSDS but it performs a lower power than MFSDS since MFSDS-DB uses bias correction instead of the screening stage which may not boost the signal-to-noise ratio. We know that the MFSDS-DB method is an extension of our low-dimensional procedure with a debiased lasso estimate but it needs to estimate the precision matrix which results in significantly higher computational costs.
-
(b)
MFSDS vs MSIR-BH. MSIR-BH method is a post-selection inference with marginal statistics, which achieves a conservative FDR control compared with MFSDS. It adopts data splitting (Meinshausen et al., 2009) but they only construct the marginal test statistics on which suffers from a serious power loss. As pointed out by reviewers, Guo et al. (2024) provided a nice refinement of MSIR-BH without data splitting, but the decorrelating process is complicated similar to the debiasing in MFSDS-DB; additional simulation in Table S2 shows that it leads intensive computation.
-
(c)
MFSDS vs IM-SIR. The hard thresholding IM-SIR methods can detect more active variables only when model size is greater than . Table 3 implies that the hard-thresholding method can not control the FDR, and thus their large powers are unreliable with user-specified model sizes.
-
(d)
MFSDS vs MX-Knockoff. MX-Knockoff offers a variable selection solution without making any modeling assumptions in high-dimensional situations. One important assumption in the theoretical development of MX-Knockoff is that the joint distribution of covariates should be either exactly known or should be estimated robustly. Moreover, MX-Knockoff usually considers Gaussian distribution or uses a second-order approximate construction, which may lead to some invalid FDR control and power loss. By contrast, MFSDS controls the FDR more accurately under mixed distribution. In addition, the symmetry property of MFSDS stems from sample splitting while MX-Knockoff requires variable augmentation, which results in a large amount of calculation.
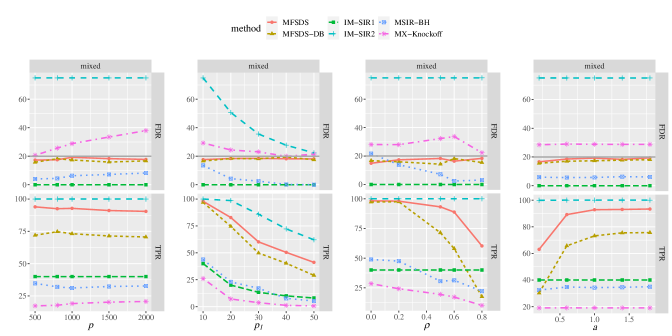
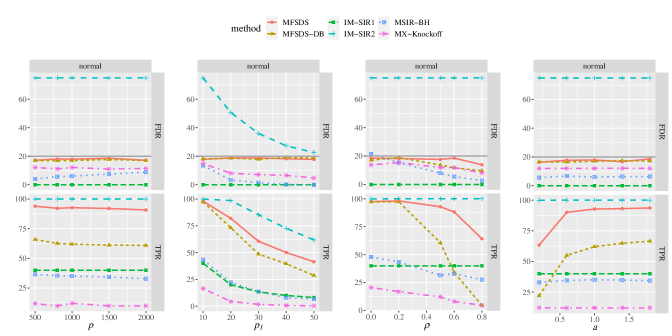
To further investigate the efficiency of our MFSDS procedure in high-dimensional settings against different covariate dimension , the signal number , covariate correlation , and signal strength , we report the corresponding FDR and TPR in Figure 3. The FDR of MFSDS remains robust in an acceptable range of the target level no matter the dimension, signal number, correlation, and signal strength varied. Our MFSDS consistently achieves the most powerful TPR than other competitors except for IM-SIR2 since IM-SIR2 can not make a fair error rate control. The practical performance between MFSDS and MX-Knockoff is quite different. It is clear that although controlling the FDR below the target level with larger in Figure 3, MX-Knockoff suffers from a larger power loss as the signal number and correlation increases. Additional numerical results with normal covariate distribution can be found in the Supplementary Material Figure S1. Figure S1 shows that the FDR of MX-Knockoff controls quite well as MFSDS under normal distribution with various combinations , , , and , but still a significant power gap compared to our proposed MFSDS.
5.2 Real data implementation
In this section, we apply our proposed MFSDS procedure to the children cancer data for classifying small round blue cell tumors (SRBCT), which has been analyzed by Khan et al. (2001) and Yu et al. (2016a). The SRBCT dataset aims to classify four classes of different childhood tumors sharing similar visual features during routine histology. Data were collected from 83 tumor samples and the expression measurements on 2308 genes for each sample are provided. In this dataset, we focus on investigating the performance of the FDR control between our MFSDS procedure and other existing methods.
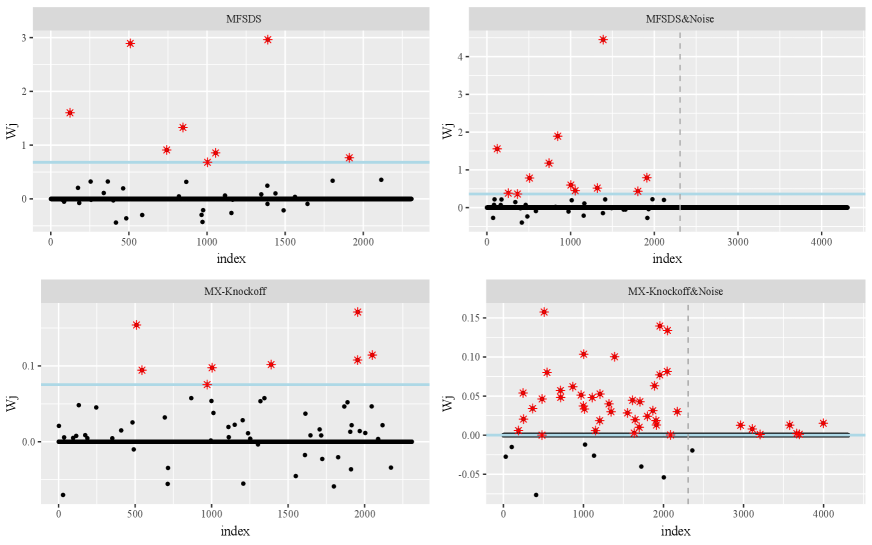
We first present the scatterplots of the ranking statistics ’s for MFSDS and MX-Knockoff in Figure 4. As we expect, genes with larger ’s are possible to be selected as influential genes (red dots), while the unselected genes (black dots) are roughly and symmetrically distributed around zero line, even though many ’s are exactly zero.
| SRBCT | SRBCT&Noise | ||||
|---|---|---|---|---|---|
| Method | ND | time | ND | time | |
| MFSDS | 8 | 1.52 | 12(0) | 1.92 | |
| MSIR-BH | 5 | 0.50 | 5(0) | 0.72 | |
| IM-SIR(c=0.05) | 1 | 130.20 | 1(0) | 1514.23 | |
| IM-SIR(c=1) | 18 | 128.31 | 18(0) | 1516.59 | |
| MX-Knockoff | 8 | 49.82 | 46(7) | 240.20 | |
Next, we introduce some simulated variables as inactive genes to further investigate the performance of our proposed method. Specifically, 1000 noise variables are from , and another 1000 noise variables are from , which are all independently and randomly generated. We refer to this dataset as SRBCT&Noise, and our main objective is to identify the important genes from the whole 4328 variables. Since and are actually inactive by construction, they can be viewed as truly false discoveries. The scatterplot of ’s and the number of discovery genes are presented in Figure 4 and Table 4. Yu et al. Yu et al. (2016a) analyzed that an average of 9 genes out of the 2308 total genes were selected, which is very close to the number of variables selected by our method. We observed that MFSDS and MX-Knockoff identified the same number of important genes without noise variables, but MX-Knockoff mistakenly selected a small number of truly noise variables, i.e., the added noise variables. Besides, the proposed MFSDS demonstrates a relatively smaller computing time than IM-SIR and MX-Knockoff.
6 Discussion
Identifying the truly contributory variables is a critical task in statistical inference. In this paper, we proposed a novel model-free variable selection procedure with a data-driven threshold in sufficient dimension reduction framework for a family of sliced methods via data splitting. The proposed MFSDS is computationally efficient in high-dimensional settings. Theoretical and numerical results show that the proposed MFSDS can asymptotically control the FDR at the target level.
Our work raises several intriguing open questions that deserve further investigation. First, it is interesting to adopt multiple data splitting in MFSDS to improve the stability and robustness but it may require intensive computations. Equal size data splitting is used in our simulation and theory for simplicity. Second, we have checked that a larger sample size for will improve TPR to some extent. In addition, we sacrifice a little detection power to obtain symmetry property via data splitting, while how to construct symmetry property without data splitting or deriving complex asymptotic distribution may be another promising direction. Third, benefiting from the use of the response transformation, the proposed method can work with many classical SDR methods (such as sliced inverse regression (Li, 1991), covariance inverse regression estimator (Cook and Ni, 2006)) and many types of response (such as continuous, discrete, or categorical data). Finally, our method may also be able to dispose of the order determination problem in many situations which merits further investigation, such as Luo and Li (2016) if the importance of slices has been determined in advance with a diverging number of . It is also worth further exploring the optimal selection of working dimension in practice.
Appendix
This Appendix gives some key lemmas and succinct proof of theorems. We only consider the proofs under a high-dimensional setting and the low-dimensional version can be easily verified. Additional lemmas used in Appendix with their proofs and some additional simulation results can be found in the Supplementary Material.
For any vector , we have
Here with . However, is not independent with nor due to the use of response transformation, which is quite different from the usual setting. To establish the FDR control result of our proposed procedure, we construct a modified statistic
where , for , and otherwise. Let , and for .
Before we present the proofs of the main theorems, we first state two key lemmas. The first lemma characterizes the closeness between and , which plays an important role in the proof.
The next lemma establishes the uniform convergence of .
Proof of Theorem 4.1
We prove the finite-sample FDR control with . The result for can be obtained similarly. The proof technique of this result has been extensively used in Barber et al. (2020) and Du et al. (2023). Fix and for any threshold , define
Define an event that . Furthermore, consider a thresholding rule that maps statistics to a threshold . Define Then for the proposed MFSDS with threshold , we can write
Next we derive an upper bound for . Note that
where the last step holds since, after conditioning on , the only unknown quantity is the sign of . Recall the definition of , we have . Thus
| (A.3) | ||||
The last expression summation in (A.3) can be simplified. If for all null , , then the summation is zero. Otherwise,
where the first equality holds by the fact: for any , if and , then ; see Barber et al. (2020) for details.
Accordingly, we have . As a result
Consequently, we can naturally get the conclusions in Theorem 4.1.
Proof of Theorem 4.2
By the definition of FDP, our test is equivalent to select the th variable if , where
We need to establish an asymptotic bound for this so that Lemmas A.1A.4 can be applied. Let . By Lemmas A.2 and A.4, it follows that
with . On the other hand, for any , where is defined in Assumption 6 and , we can show that . In fact, it is straightforward to see that
Denote . Under Assumption 6, it follows that . We then get
It follows that
the above result follows from Assumption 5 and the Lemma S.4 stated in Supplementary Material.
Thus, we get . Furthermore, we can conclude that
Then, we get an upper bound for , that is . This implies that the proposed method can detect at least signals.
Further, for any , we have
from which the second part of this theorem is proved.
References
- Barber and Candès (2015) Barber, R. F. and Candès, E. J. (2015), “Controlling the false discovery rate via knockoffs,” The Annals of Statistics, 43, 2055–2085.
- Barber and Candès (2019) — (2019), “A knockoff filter for high-dimensional selective inference,” The Annals of Statistics, 47, 2504–2537.
- Barber et al. (2020) Barber, R. F., Candes, E. J., and Samworth, R. J. (2020), “Robust inference with knockoffs,” The Annals of Statistics, 48, 1409–1431.
- Benjamini and Hochberg (1995) Benjamini, Y. and Hochberg, Y. (1995), “Controlling the false discovery rate: a practical and powerful approach to multiple testing,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 57, 289–300.
- Cai and Liu (2016) Cai, T. T. and Liu, W. (2016), “Large-scale multiple testing of correlations,” Journal of the American Statistical Association, 111, 229–240.
- Candes et al. (2018) Candes, E., Fan, Y., Janson, L., and Lv, J. (2018), “Panning for gold: ‘model-X’ knockoffs for high dimensional controlled variable selection,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 80, 551–577.
- Chen et al. (2010) Chen, X., Zou, C., and Cook, R. D. (2010), “Coordinate-independent sparse sufficient dimension reduction and variable selection,” The Annals of Statistics, 38, 3696–3723.
- Cook (2004) Cook, R. D. (2004), “Testing predictor contributions in sufficient dimension reduction,” The Annals of Statistics, 32, 1062–1092.
- Cook and Ni (2006) Cook, R. D. and Ni, L. (2006), “Using intraslice covariances for improved estimation of the central subspace in regression,” Biometrika, 93, 65–74.
- Cook and Weisberg (1991) Cook, R. D. and Weisberg, S. (1991), “Sliced inverse regression for dimension reduction: Comment,” Journal of the American Statistical Association, 86, 328–332.
- Dong (2021) Dong, Y. (2021), “A brief review of linear sufficient dimension reduction through optimization,” Journal of Statistical Planning and Inference, 211, 154–161.
- Du et al. (2023) Du, L., Guo, X., Sun, W., and Zou, C. (2023), “False discovery rate control under general dependence by symmetrized data aggregation,” Journal of the American Statistical Association, 118, 607–621.
- Fan et al. (2012) Fan, J., Han, X., and Gu, W. (2012), “Estimating false discovery proportion under arbitrary covariance dependence,” Journal of the American Statistical Association, 107, 1019–1035.
- Fan and Li (2001) Fan, J. and Li, R. (2001), “Variable selection via nonconcave penalized likelihood and its oracle properties,” Journal of the American Statistical Association, 96, 1348–1360.
- Fan et al. (2020) Fan, J., Li, R., Zhang, C.-H., and Zou, H. (2020), Statistical foundations of data science, CRC press.
- Fan and Lv (2010) Fan, J. and Lv, J. (2010), “A selective overview of variable selection in high dimensional feature space,” Statistica Sinica, 20, 101–148.
- Fan and Peng (2004) Fan, J. and Peng, H. (2004), “Nonconcave penalized likelihood with a diverging number of parameters,” The Annals of Statistics, 32, 928–961.
- Guo et al. (2024) Guo, X., Li, R., Zhang, Z., and Zou, C. (2024), “Model-Free Statistical Inference on High-Dimensional Data,” Journal of the American Statistical Association, 1–27.
- Javanmard and Montanari (2014) Javanmard, A. and Montanari, A. (2014), “Confidence intervals and hypothesis testing for high-dimensional regression,” The Journal of Machine Learning Research, 15, 2869–2909.
- Khan et al. (2001) Khan, J., Wei, J. S., Ringner, M., Saal, L. H., Ladanyi, M., Westermann, F., Berthold, F., Schwab, M., Antonescu, C. R., Peterson, C., et al. (2001), “Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks,” Nature Medicine, 7, 673–679.
- Li and Wang (2007) Li, B. and Wang, S. (2007), “On directional regression for dimension reduction,” Journal of the American Statistical Association, 102, 997–1008.
- Li (1991) Li, K.-C. (1991), “Sliced inverse regression for dimension reduction,” Journal of the American Statistical Association, 86, 316–327.
- Li et al. (2005) Li, L., Dennis Cook, R., and Nachtsheim, C. J. (2005), “Model-free variable selection,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 67, 285–299.
- Li et al. (2020) Li, L., Wen, X. M., and Yu, Z. (2020), “A selective overview of sparse sufficient dimension reduction,” Statistical Theory and Related Fields, 4, 121–133.
- Luo and Li (2016) Luo, W. and Li, B. (2016), “Combining eigenvalues and variation of eigenvectors for order determination,” Biometrika, 103, 875–887.
- Meinshausen et al. (2009) Meinshausen, N., Meier, L., and Bühlmann, P. (2009), “P-values for high-dimensional regression,” Journal of the American Statistical Association, 104, 1671–1681.
- Shao et al. (2007) Shao, Y., Cook, R. D., and Weisberg, S. (2007), “Marginal tests with sliced average variance estimation,” Biometrika, 94, 285–296.
- Svetulevičienė (1982) Svetulevičienė, V. (1982), “Multidimensional local limit theorems for probabilities of moderate deviations,” Lithuanian Mathematical Journal, 22, 416–420.
- Tibshirani (1996) Tibshirani, R. (1996), “Regression shrinkage and selection via the lasso,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 58, 267–288.
- Wasserman and Roeder (2009) Wasserman, L. and Roeder, K. (2009), “High dimensional variable selection,” The Annals of Statistics, 37, 2178–2201.
- Wu and Li (2011) Wu, Y. and Li, L. (2011), “Asymptotic properties of sufficient dimension reduction with a diverging number of predictors,” Statistica Sinica, 2011, 707–703.
- Xia et al. (2002) Xia, Y., Tong, H., Li, W., and Zhu, L.-X. (2002), “An adaptive estimation of dimension reduction space,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64, 363–410.
- Yin and Cook (2002) Yin, X. and Cook, R. D. (2002), “Dimension reduction for the conditional kth moment in regression,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 64, 159–175.
- Yu and Dong (2016) Yu, Z. and Dong, Y. (2016), “Model-free coordinate test and variable selection via directional regression,” Statistica Sinica, 26, 1159–1174.
- Yu et al. (2016a) Yu, Z., Dong, Y., and Shao, J. (2016a), “On marginal sliced inverse regression for ultrahigh dimensional model-free feature selection,” The Annals of Statistics, 44, 2594–2623.
- Yu et al. (2016b) Yu, Z., Dong, Y., and Zhu, L.-X. (2016b), “Trace pursuit: A general framework for model-free variable selection,” Journal of the American Statistical Association, 111, 813–821.
- Zhu (2020) Zhu, L. (2020), “Review of sparse sufficient dimension reduction: comment,” Statistical Theory and Related Fields, 4, 134–134.
- Zou (2006) Zou, H. (2006), “The adaptive lasso and its oracle properties,” Journal of the American Statistical Association, 101, 1418–1429.
Supplementary Material for “Model-free variable selection in
sufficient dimension reduction via FDR control”
This Supplementary Material contains the proofs of some technical lemmas and additional simulation results.
S1. Additional lemmas
The first lemma is the standard Bernstein’s inequality.
Lemma S.1 (Bernstein’s inequality).
Let be independent centered random variables a.s. bounded by in absolute value. Let . Then for all ,
The second one is a moderate deviation result for the mean of random vector; See Theorem 1 in Svetulevičienė (1982).
Lemma S.2 (Moderate deviation for the independent sum).
Suppose that are independent identically distributed random vectors with mean zero and identity covariance matrix. Let for some with . Then in the domain , one has uniformly
as . Here is the density function of .
S2. Useful lemmas
For simplicity of notation, the constant and may be slightly abused hereafter. The following lemma establishes uniform bounds for , .
-
Proof.
Note that
Recall that . Let , where for some small . In what follows, we first work on the case of the occurrence of . Denote and . The Bernstein’s inequality in Lemma S.1 yields that
holds uniformly in . here we use the condition which is implied by Assumption 3 and . Next, we turn to consider the case on . By Assumption 3 and Markov’s inequality
The lemma is proved.
The next lemma establishes uniform bounds for , .
- Proof.
S3. Proofs of lemmas in Appendix
Proof of Lemma A.1.
Define where . Hereafter for simplicity, we denote and . Thus . We observe that
Note that is a decreasing function by definition. Firstly, for the term , by Lemma S.3, we have
which implies . Recall that . By Lemma S.2 and Assumption 3, we obtain that
where . Here and . Similarly we get
Note that , from which we get and accordingly we can claim the assertion.
Proof of Lemma A.2.
We prove the first formula and the second one can be deduced similarly. By the proof of Lemma A.1, it suffices to show that
Accordingly
Thus, we need to show the following assertion
Note that the is a decreasing and continuous function. Let , and , where with and . Note that uniformly in . It is therefore enough to derive the convergence rate of the following formula
Define and then we have
Further define . Here denotes the conditional correlation between and given . Recall that It follows that
While for each and , conditional on , by Lemma 1 in Cai and Liu (2016) we have
uniformly holds, where for . From the above results and Chebyshev’s inequality, for we have
Moreover, observe that
Note that can be arbitrarily close to 1 such that . Because can be made arbitrarily large as long as , we have providing that . We need to point out that the results hold uniformly in and thus are actually unconditional results.
Proof of Lemma A.3.
Recall that
where . Firstly note that
Further observe that
While by Assumption 4, there exists a constant such that
Thus, , , and is a small order than and . By triangle inequality and Lemma S.4, .
Proof of Lemma A.4.
Recall that . By Lemma S.2, it suffices to show that
where , and are the density function and cumulative distribution function of standard normal distribution, respectively. The second to last inequality is due to
Similarly we have
S4. Additional simulations
| normal | mixed | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scenario | Method | FDR | TPR | time | FDR | TPR | time | |||
| MFSDS | 18.5 | 100.0 | 100.0 | 18.6 | 17.9 | 100.0 | 99.6 | 24.2 | ||
| MFSDS-DB | 18.1 | 93.7 | 63.4 | 213.5 | 18.1 | 96.7 | 79.0 | 209.9 | ||
| MSIR-BH | 2.7 | 37.0 | 0.0 | 14.1 | 4.4 | 38.7 | 0.0 | 20.2 | ||
| 2a | IM-SIR1 | 0.0 | 50.0 | 0.0 | 28.5 | 0.0 | 50.0 | 0.0 | 34.8 | |
| IM-SIR2 | 83.1 | 100.0 | 100.0 | 28.5 | 83.1 | 100.0 | 100.0 | 34.6 | ||
| MX-Knockoff | 71.8 | 6.0 | 0.0 | 51.6 | 27.4 | 11.9 | 0.0 | 56.7 | ||
| MFSDS | 17.7 | 99.5 | 94.6 | 18.4 | 17.9 | 99.5 | 95.2 | 27.7 | ||
| MFSDS-DB | 17.3 | 91.6 | 41.6 | 215.7 | 17.9 | 93.6 | 56.2 | 234.8 | ||
| MSIR-BH | 4.4 | 39.5 | 0.0 | 14.0 | 4.6 | 39.1 | 0.0 | 20.8 | ||
| 2b | IM-SIR1 | 0.0 | 50.0 | 0.0 | 28.6 | 0.0 | 50.0 | 0.0 | 35.5 | |
| IM-SIR2 | 83.1 | 100.0 | 100.0 | 28.6 | 83.1 | 100.0 | 100.0 | 35.9 | ||
| MX-Knockoff | 10.0 | 13.9 | 0.0 | 51.6 | 31.3 | 23.6 | 0.0 | 57.7 | ||
| MFSDS | 17.6 | 99.1 | 92.8 | 21.0 | 16.8 | 98.9 | 90.6 | 38.1 | ||
| MFSDS-DB | 18.0 | 85.6 | 25.2 | 203.4 | 16.6 | 89.8 | 38.6 | 248.7 | ||
| MSIR-BH | 5.2 | 38.4 | 0.0 | 16.1 | 4.7 | 37.8 | 0.0 | 30.0 | ||
| 2c | IM-SIR1 | 0.0 | 50.0 | 0.0 | 24.4 | 0.0 | 50.0 | 0.0 | 40.8 | |
| IM-SIR2 | 83.1 | 100.0 | 100.0 | 24.2 | 83.1 | 100.0 | 100.0 | 41.3 | ||
| MX-Knockoff | 10.3 | 11.1 | 0.0 | 54.9 | 31.5 | 23.6 | 0.0 | 60.5 | ||
| normal | mixed | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method | FDR | TPR | time | FDR | TPR | time | |||
| MFSDS | 16.4 | 63.4 | 12.9 | 16.6 | 63.0 | 20.3 | |||
| MFSDS-DB | 16.6 | 22.1 | 100.6 | 15.6 | 30.3 | 84.7 | |||
| MSIR-BH | 5.6 | 33.0 | 13.1 | 5.9 | 32.4 | 17.2 | |||
| Guo et al. (2024) | 7.1 | 47.6 | 1559.4 | 5.0 | 48.0 | 2494.9 | |||
| MFSDS | 17.9 | 92.7 | 12.4 | 19.2 | 92.8 | 22.8 | |||
| MFSDS-DB | 17.0 | 62.1 | 102.3 | 17.4 | 73.2 | 126.8 | |||
| MSIR-BH | 6.5 | 33.4 | 12.2 | 6.3 | 31.1 | 21.8 | |||
| Guo et al. (2024) | 6.5 | 94.3 | 1668.6 | 7.5 | 94.3 | 2712.1 | |||