Modeling Non-Cooperative Dialogue: Theoretical and Empirical Insights
Abstract
Investigating cooperativity of interlocutors is central in studying pragmatics of dialogue. Models of conversation that only assume cooperative agents fail to explain the dynamics of strategic conversations. Thus, we investigate the ability of agents to identify non-cooperative interlocutors while completing a concurrent visual-dialogue task. Within this novel setting, we study the optimality of communication strategies for achieving this multi-task objective. We use the tools of learning theory to develop a theoretical model for identifying non-cooperative interlocutors and apply this theory to analyze different communication strategies. We also introduce a corpus of non-cooperative conversations about images in the GuessWhat?! dataset proposed by De Vries et al. (2017). We use reinforcement learning to implement multiple communication strategies in this context and find empirical results validate our theory. 111Per-print version to appear in Transactions of the Association for Computational Linguistics published by MIT Press.
1 Introduction
A robust dialogue agent cannot always assume a cooperative conversational counterpart when deployed in the wild. Even in goal-oriented settings, where the intent of an interlocutor may seem to be granted, bad actors and disinterested parties are free to interact with our dialogue systems. These non-cooperative interlocutors add harmful noise to data, which can elicit unexpected behaviors from our dialogue systems. Thus, the need to study non-cooperation increases daily as we build and deploy conversational systems which interact with people from different demographics, political views, and intents, continuously learning from the collected data. Examples include Amazon Alexa, task-oriented systems that help patients recovering from injuries or can teach a person a new language, and systems that help predict deceptive behaviors in courtrooms. To effectively communicate in presence of unwanted behaviors like bullying Cercas Curry and Rieser (2018), systems need to understand users’ strategic behaviors Asher and Lascarides (2013) and be able to identify non-cooperative actions. Designing agents that learn to identify non-cooperative interlocutors is challenging since it requires processing the context of the dialogue in addition to modeling the choices that interlocutors make under uncertainty – choices which typically affect their ability to complete tasks unrelated to identifying non-cooperation as well. In light of this, we ask:
What communication strategies are effective for identifying non-cooperative interlocutors, while also achieving the goals of a distinct dialogue task?
To answer this question, we appeal to a simple non-cooperative version of the visual dialogue game Guess What?! De Vries et al. (2017). See Figure 1 for an example. The game consists of a multi-round dialogue between two players: a question-player and an answer-player. Both have access to the same image whereas only the answer-player has access to an image-secret; i.e., a particular goal-object for the question-player to recognize. The question-player’s goal is to ask the answer-player questions which will reveal the secret. A cooperative answer-player then provides good answers to assist in this goal. In the original game, the answer-player is always cooperative. Our modified game instead allows the answer-player to be non-cooperative with some non-zero probability. Unlike a cooperative answer-player, a non-cooperative answer-player will not necessarily act in assistance to the question-player, and instead, may attempt to reveal an incorrect secret or otherwise hinder information exchange. In experiments, the specific strategies we study are learned from human non-cooperative conversation. The question-player, importantly, does not know if answer-player is non-cooperative. At the end of the dialogue, the question-player’s final objective is not only to identify the goal-object, but also to determine if the conversation takes place with a cooperative or non-cooperative answer-player.

We propose a formal theoretical model for analyzing communication strategies in the described scenario. We frame the question-player’s objective in terms of two distinct classification tasks and use tools from the theory of learning algorithms to analyze relationships between these tasks. Our main theoretical result identifies circumstances where the question-player’s performance in identifying non-cooperation correlates with performance in identifying the goal-object. Building on this, we provide a mathematical definition of the efficacy of a non-cooperative player which is based on the conceptual idea that cooperation is necessary to make progress in dialogue. Our analysis concludes that when the answer-player is effective in this sense, the question-player can gather useful information for both the object identification task and the non-cooperation identification task by selecting a communication strategy based only on the former objective.
To test the assumptions of our theoretical model as well as the value of the aforementioned communication strategy in practice, we implement this strategy using reinforcement learning (RL). Our experiments validate our theory. As compared to heuristically justified baselines, the communication strategy motivated by our theory yields consistently better results. To conduct this experiment, we have collected a novel corpus of non-cooperative Guess What?! game instances which is publicly available.222https://github.com/anthonysicilia/modeling-non-cooperation-TACL2022 Throughout experimentation, we provide a qualitative and quantitative analysis of the non-cooperative strategies present in our corpus. These results, in particular, demonstrate that non-cooperative autonomous agents that utilize dialogue history can better deceive question-players. This contrasts the observation of Strub et al. (2017) that cooperative answer-players do not use this information.
In total, our work is positioned at the intersection of two foci: detection of non-cooperative dialogue and modeling of non-cooperative dialogue. Unlike many detection works, we consider detection in context of interaction. Additionally, while many modeling works consider the intent of conversational agents and construct strategies for non-cooperative dialogue based on this, our strategies are motivated purely from a learning theoretic argument. As we are aware, a theoretical description similar to ours has not been given before.
2 Related Works
The view that conversation is not necessarily cooperative is not novel, but the argument can be made that it has lacked sufficient investigation in the dialogue literature Lee (2000). Game theoretic investigations of non-cooperation are plentiful, perhaps beginning with work of Nash (1951). Concepts from this space, such as the stochastic games introduced by Shapley (1953), have been used to model dialogue Barlier et al. (2015) when non-cooperation between parties is allowed. Pinker et al. (2008) also consider a game-theoretic model of speech. In fact, even the dialogue game we consider in this text can be modelled through game-theoretic constructs; e.g., a Bayesian Game (Kajii and Morris, 1997). Whereas game theory focuses primarily on analysis of strategies, studying non-cooperation in dialogue requires both the learning of strategies and the learning of utterance meaning. Aptly, our use of the theory of learning algorithms (rather than game theory) is suited to handle both of these. While we are first to use learning theory, efforts to characterize non-cooperation in dialogue, learn non-cooperative strategies in autonomous agents, and detect non-cooperation in dialogue are not absent from the literature Plüss (2010); Georgila and Traum (2011a); Shim and Arkin (2013); Vourliotakis et al. (2014). We discuss these topics in detail in the following.
Modeling Non-Cooperative Dialogue.
One of the earliest works on non-cooperation – specific to dialogue – is that of Jameson et al. (1994) which considers strategic conversation for advantage in commerce. Similarly, Traum et al. (2008) focuses on negotiation and Georgila and Traum (2011b) focus on learning negotiation strategies (i.e., argumentation) through reinforcement learning (RL). More recently, Efstathiou and Lemon (2014) consider using RL to teach agents to compete in a resource-trading game and Keizer et al. (2017) use deep RL to model negotiation in a similiar game. In most of these, the intent of interlocutors is assumed and utilized in model design. In the last, strategies are learned from data similarly to our work, but objectives for learning are not motivated by learning-theoretic analysis as in ours.
Detecting Non-Cooperative Dialogue.
The work of Zhou et al. (2004) presents an early example of automated deception detection which focuses on indicators arising from the used language. Plüss (2014) also focuses on how (more general) non-cooperative dialogue can be identified at a linguistic level. Besides linguistic cues, several works employ additional features in identification of deception. These include physiological responses Abouelenien et al. (2014), human micro-expressions Wu et al. (2018), and acoustics Levitan (2019). There are also many novel scenarios for detection of deception including talk-show games Soldner et al. (2019), interrogation games Chou and Lee (2020), and news Conroy et al. (2015); Shu et al. (2017).
Other Visual Dialogue Games.
As Galati and Brennan (2021) observe, conversation involving multiple media for information transfer (instead of a single medium) typically leads to increased understanding between interlocutors. Thus, visual-dialogue is a particularly interesting setting for investigating both cooperation and non-cooperation. Appropriately, cooperative visual-dialogue games Das et al. (2017); Schlangen (2019); Haber et al. (2019) are a growing area of study. We extend, in particular, the cooperative game Guess What?! proposed by De Vries et al. (2017) to explicitly allow for non-cooperation. Whereas visual-dialogue research often focuses on mechanisms to improve task success, our work is more broadly interested in an analysis of human communication strategies within a non-cooperative, multi-task setting.
Related Learning Theoretic Work.
Classification of non-cooperative examples is similar to detection of adversarial examples; see Serban et al. (2018) for a survey. Still, most learning-theoretic work only discusses models which are robust to adversaries; e.g., see Feige et al. (2015); Cullina et al. (2018); Attias et al. (2019); Bubeck et al. (2019); Diochnos et al. (2019); and Montasser et al. (2020) to name a few. In contrast, we focus on detection. Additionally, our theoretical results are more broad and do not explicitly model adversarial intent. Identifying non-cooperation in dialogue is also related to detecting distribution shift in high-dimensional, distribution-independent settings Gretton et al. (2012); Lipton et al. (2018); Rabanser et al. (2019); Atwell et al. (2022) as well as learning to generalize in presence of such distribution shift Ben-David et al. (2010); Ganin and Lempitsky (2015); Zhao et al. (2018, 2019); Schoenauer-Sebag et al. (2019); Johansson et al. (2019); Germain et al. (2020); Sicilia et al. (2022). This connection is a strong motivation for our theoretical work, but we emphasize our results are not a trivial application of existing theory.
3 Dataset
In this section, we first describe our modified version of the GuessWhat?! game. Then, we describe the data acquisition process as well as the non-cooperative dataset used in this study. The dataset will be made publicaly available upon publication.
3.1 Proposed Dialogue Game
As noted, our proposed dialogue game is a modification of the cooperative two-player visual-dialogue game GuessWhat?! (De Vries et al., 2017). Distinctly, our version incorporates non-cooperation.
Initialization.
An image is randomly selected and an object within this image is randomly chosen to be the goal-object. With some probability, the game instance is designated as a cooperative game. Otherwise, the game is non-cooperative.
Players.
Unlike the original GuessWhat?! game, there are three (not two) player roles: the question-player, the cooperative answer-player, and the non-cooperative answer-player. For cooperative game instances (decided at initialization), the cooperative answer-player is put in play. Otherwise, the non-cooperative answer-player is put in play. The question-player always plays and does not know whether the answer-player is cooperative or non-cooperative. To start, all active players are granted access to the image. The question-player asks yes/no questions about the image and objects within the image. At the end of dialogue, the question-player will use the gathered information to guess both the unknown goal-object and the (cooperation) type of the active answer-player.333This is done simultaneously, so knowledge of the correctness of one guess cannot inform the other guess. Unlike the question-player, the active answer-player has knowledge of the game’s goal-object and responds to the question-player’s queries with yes, no, or n/a (not applicable).
Objectives.
The question-player’s goals are always to identify both the goal-object and the presence of non-cooperation if it exists (i.e., if the non-cooperative answer-player is in play). The cooperative answer-player’s goal is to reveal the goal-object to the question-player by answering the yes/no questions appropriately. The non-cooperative answer-player’s goal is instead to lead the question-player away from this goal object; i.e., to ensure the question-player does not correctly guess this object. There is no specific way in which this misleading must be done (e.g., there is not always an alternate object). Instead, during data collection, participants are simply instructed to deceive the question-player.
Gameplay.
The question-player and active answer-player converse until the question-player is ready to make a guess or a pre-specified maxium number of dialogue rounds have transpired.444For data collection, no question limit is set. Experiments in Section 5 follow Strub et al. (2017) and set the max to 5. The question-player is then presented with a list of possible objects and must guess which of these was the secret goal-object. In addition, the question-player must guess whether the answer-player was cooperative or non-cooperative.
3.2 Data Collection
Collection.
We developed a web application to collect dialogue from human participants taking the role of a non-cooperative answer-player. Participants were native English speakers recruited via an online crowd-sourcing platform and paid $15 per hour according to our institution’s human subject review board. Participants were asked to deceive an autonomous question-player pre-trained to identify the goal-object only. For pre-training, we used the original Guess What?! game corpus and supervised learning setup (De Vries et al., 2017; Strub et al., 2017). Participants received an image and a crop that indicated the goal-object. Both of these are randomly sampled from the original Guess What?! game corpus. They were tasked with leading the question-player away from this goal object by answering questions with yes, no, or n/a. Dialogue persisted until the question-player made a guess.
Dataset.
We collected 3746 non-cooperative dialogues. Dataset statistics are shown in Table 1, while visualization of the object and dialogue-length distributions are shown in Figure 2. Compared to the original Guess What?! corpus, both dialogue-length and object distributions are similar. For objects, this is expected as these are uniformly sampled from the original corpus. We see 16 of our 20 most likely objects are shared with the 20 most likely of the original GuessWhat?! object distribution, and further, the first 4 objects have identical ordering (see Figure 3). Differences here are simply attributed to randomness and the increasing uniformity as likelihood of an object decreases. For dialogue length, one might expect non-cooperative dialogue to be longer. Instead, the distributions are both right-skew with an average near 5 (i.e., 4.99 in our dataset and 5.11 in the original GuessWhat?! corpus). The primary difference is that the original corpus has more outliers, which is most probably a result of the increased sample size. We likely observe consistency between our non-cooperative corpus and the original corpus because the question-player – who controls dialogue length – is autonomous and trained on a cooperative corpus. Hence, this and other aspects of our non-cooperative corpus may be influenced by pre-conditioning the question-player for cooperation. This issue is mitigated in our experiments (Section 5) where the question-player is also trained on simulated non-cooperative dialogue. Also note, while the size of our collected dataset is smaller than the original cooperative corpus, we only use our data to train an autonomous, non-cooperative answer-player. When a larger sample is required (e.g., when training the question-player via RL), we use simulated non-cooperative data generated by the pre-trained, non-cooperative answer-player, which is a standard technique in the literature (Strub et al., 2017).
Besides the statistics shown in Table 1 and Figure 2, we also point out the question-player succeeded at identifying the goal-object in only 19% of the collected games. Comparatively, on an autonomously generated and fully cooperative test set, comparably trained question-players achieve 52.3% success (Strub et al., 2017). This indicates the deceptive strategies employed by the humans were effective at fooling the question-player to select the wrong goal-object. More detailed analysis of the strategies used by the participants is given in Section 5; these strategies are self-described by the participants and also automatically detected for a simple case. Finally, we also computed the answer distribution on the collected corpus: answers were 46% yes, 52% no, and 2% n/a.
| images | objects | words (+3) | questions | |
|---|---|---|---|---|
| Ours | 2.7K | 2.8K | 2.3K (1K) | 8.1K |
| GW | 67K | 134K | 19K (6.6K) | 277K |


4 A Theoretical Model
This section formally models the objectives of the question-player as two distinct learning tasks. We use results from the theory of learning algorithms to give a relationship between these tasks in Thm 4.1. We then use Thm 4.1 to analyze communication strategies in Section 4.3.
4.1 Setup
As described in Section 3, the question-player has two primary objectives: identification of the goal-object and identification of non-cooperation. To do so, the question-player is granted access to the image and may also converse with an answer-player. In the end, the question-player guesses based on this evidence (i.e., the image features and dialogue history). Mathematically, we encapsulate the question player’s guess as a learned hypothesis (i.e., function) from the game features to the set of object labels or the set of cooperation labels.
Key Terms.
We write to describe the finite set of object labels and for the set of cooperation labels; denotes cooperation and denotes non-cooperation. In relation to the example in Figure 1, might contain labels for the orange, apple, cups, and dining-table. In the same example, the cooperation label would be to indicate a non-cooperative answer-player. We use to denote the feature space which contains all possible game configurations. For example, each might capture the dialogue history, the image, and particular features of the image pre-extracted for the question-player (i.e., which objects are contained in the image at which locations). With this notation, the question-player’s learned hypotheses may be described as an object identification hypothesis and a cooperation identification hypothesis . The question-player learns these functions by example. In particular, we assume the question-player is given access to a random sequence of examples independently and identically distributed according to an unknown distribution over . To abbreviate, we write and assume all samples are of size for simplicity. The distribution is dependent on the question-player’s communication policy which we assume is uniquely determined by the real-vector . Later, this allows us to select communication strategies using common reinforcement learning algorithms.
We emphasize the dependence of on distinguishes our setup from typical scenarios in learning theory. Besides learning the hypotheses and , the question-player can also select the communication policy . This policy implicitly dictates the distribution over which the question-player learns, and thus, can either improve or hurt the player’s chance at success. As in reality, neither we nor the learner have knowledge of the mechanism through which changes to the communication policy modify the distribution . Our only assumption is that changing does not modify the probability of cooperation. That is, there is a constant such that for all
| (1) |
This agrees with the description in Section 3 where the game instance is designated cooperative or non-cooperative prior to dialogue. With a random sample , an unbiased estimate for is
| (2) |
where is the indicator function.
Error.
To measure the quality of the question-player’s guesses, we report the observed error-rate on the sample . In particular, the empirical object-identification error for any hypothesis is defined
| (3) |
Similarly, the cooperation identification error for any hypothesis is defined
| (4) |
In some cases, we instead restrict the sample over which we compute the empirical object-identification error. Specifically, we restrict to cooperative game instances and write
| (5) |
where is the sample with each triple where removed. The case is defined similarly. Based on these, we further define the cooperation gap
| (6) |
This gap describes observed change in (weighted) object-identification error induced by change in cooperation. We often expect to be positive.555Delta is negative when the object-identification error is higher on cooperative examples than non-cooperative examples (for simplicity, this assumes ). In practice, we rarely expect cooperation to lead to worse performance.
Finally, recall and is unknown, so in practice, we can only report the observed error discussed above. Still, we are typically more interested in the true or expected error for future samples from . This quantity tells us how the question-player’s hypotheses generalize beyond the random samples we observe. Precisely, the expected cooperation-identification error of a hypothesis is defined
| (7) |
where . The true (or expected) object-identification error is similarly defined.
4.1.1 Applicability to Distinct Contexts
While we have specified our discussion above to promote understanding, one of the benefits of our theoretical framework is that it is fairly general. In fact, the reader may be concerned that our discussion above lacks precise definitions of seemingly important terms; i.e., the feature space and the communication policy . These components are intentionally left abstract because our theoretical results make no assumptions on the mechanism through which influences – i.e., except Eq. (1). Further, our results make no assumptions on how the game configurations are represented in the feature space . This space could correspond to any set of dialogues with/without some associated data (e.g., images). Lastly, the only assumptions on the label spaces are that is finite and is binary. In this sense, our theoretical discussion is applicable to very general scenarios beyond the simple visual-dialogue game considered. We emphasize some examples later in Section 6.
4.2 Bounding Cooperation Identification Error
To motivate our main result, we informally observe that identifying non-cooperation is essentially a problem of identifying distribution-shift. Specifically, we are interested in differences between the two dialogue distributions induced by cooperative and non-cooperative answer-players, respectively. Luckily, there is a rich literature on the topic of distribution-shift. We take insight, in particular, from work of Ben-David et al. (2007, 2010) which measures shift using the symmetric difference hypothesis class. For a set of hypotheses , this class contains hypotheses characteristic to disagreements in :
| (8) |
where acts like an indicator function, returning for true arguments and otherwise. Using this class, we identify a relationship between the true error when identifying non-cooperation and the observed object-identification errors and against the cooperative and non-cooperative answer-player, respectively. While a more traditional learning-theoretic bound would relate to the empirical observation for the same task, our novel bound reveals a connection to the seemingly distinct task of object-identification. Later, this relationship is useful for analyzing how the question-player’s communication policy controls the data-distribution so that both objectives are improved. Proofs of all result are provided in Section 4.4.
Theorem 4.1.
Define as above and take to be sufficiently complex so that . Let be the VC-Dimension of . Then for any , with probability at least , for all ,
| (9) |
where , , and .
Remarks.
Notice, one sensible choice of and is to pick which minimizes the observed object-identification error and which maximizes ; this produces the tightest bound on the expected cooperation-identification error. We leave these hypotheses unspecified because later we must make limiting assumptions on the properties of and (e.g., Prop. 4.1). Greater generality here makes our results more broadly applicable. Besides this, we also observe that goes to 0 as grows. Ultimately, we ignore in interpretation, but point out that bounds based on the VC-Dimension (as above) are notoriously loose for most . As we are primarily interested in these bounds for purpose of interpretation and algorithm design, this is a non-issue. On the other hand, if practically computable bounds are desired, other (more data-dependent) techniques may be fruitful; e.g., see Dziugaite and Roy (2017).
Interpretation.
As noted, the question-player has some control over the distribution through the communication policy . So, Thm. 4.1 can be interpreted to motivate indirect mechanisms for controlling the cooperation-identification error . Specifically, with respect to , we can infer that improving performance on the object identification task should implicitly improve performance on the separate task of identifying non-cooperation. The term also offers insight. It suggests certain non-cooperative answer-players – whose actions induce a large reduction in performance as compared to the cooperative answer-player – are easy to identify. Stated more plainly, non-cooperative agents reveal themselves by their non-cooperation; this is true, in particular, when their behavior causes large performance drops. In Section 4.3, we formalize these concepts further.
4.3 Analyzing Communication Strategies
In this section, we analyze methods for the question-player to select the communication policy . In recent dialogue literature, reinforcement learning (RL) has proven successful in teaching agents effective communication strategies. For example, Strub et al. (2017) show this to be the case in the fully cooperative version of Guess What?!. Selecting an appropriate reward structure is fundamental to any RL training regime. To this end, we use Thm 4.1 to study different reward structures. We consider, in particular, an episodic RL scenario where the discount factor (often called ) is set to 1 and the only non-zero reward comes at the end of the episode. So, the question-player holds a full dialogue with the answer-player, guesses the goal-object and answer-player’s cooperation based on this dialogue, and then receives a reward dependent on whether the guesses are correct. Under these assumptions, the question-player selects the communication policy to maximize:
| (10) |
where is the reward structure to be decided. In particular, selection of can often be achieved through policy gradient methods. Williams (1992) and Sutton et al. (1999) are attributed with showing we can estimate in an un-biased manner through Monte-Carlo estimation. In our implementation in Section 5, our particular policy gradient technique is identical to previous work on communication strategies for the Guess What?! dataset Strub et al. (2017). Thus, we focus discussion on the reward structure and understanding its role through a theoretical lens.
To select , we first consider some obvious choices without appealing to complex analysis. Specifically, for fixed, define . Then,
| (11) |
Thus, maximizing is equivalent to minimizing the cooperation-identification error. This reward focuses only on identifying non-cooperation. On the other hand, if for some fixed , then
| (12) |
So, in this case, maximizing minimizes the expected object-identification error.
It is easy to see the trade-off between the two choices discussed above. Each focuses distinctly on a single objective of the question-player and it is not clear how these two objectives can relate to each other. To properly answer this, we appeal to analysis. We first give some definitions.
Definition 4.1.
We say a hypothesis is -improved by relative to if for and .
Simply, Def. 4.1 formally describes when a communication policy improves the question-player’s ability to identify the goal-object. Next, we define efficacy of an answer-player as a property of the errors induced by this player’s dialogue.
Definition 4.2.
We say a non-cooperative answer-player is effective with fixed parameter if for all there is such that for all , , and , we have
| (13) |
where , .
Def. 4.2 requires that the error of all question-players converge in probability to the same -sized region when playing against an effective answer-player. If a non-cooperative answer-player is effective, then regardless of the communication strategy employed by the question-player, we should not expect to observe large changes in object-identification performance against the non-cooperative opponent. Conceptually, this captures the following idea: Without cooperation, we cannot expect interlocutors to make significant headway. This assumption is inherently related to an answer-player’s failure to abide by Gricean maxims of conversation: uninformative and deceitful responses violate the maxim of relation and quality, respectively. Instead of explicitly modelling these violations, Def. 4.2 focuses on the effect of violations – namely, failure to progress. While violation of other Gricean maxims (i.e., quantity and manner) are less applicable to the simple game we consider, the definition of non-cooperation we give (as an observable effect) still applies.
As alluded, when the non-cooperative answer-player is effective, this non-cooperation is enough to reveal the answer-player to the question-player. The question-player may focus on communicating to identify the goal-object and this will reduce all terms in the upper-bound of Thm. 4.1; subsequently, we expect this communication strategy to be effective not only for identifying the goal-object, but also for identifying non-cooperation.
Proposition 4.1.
Let and . Suppose the non-cooperative answer-player is effective and further suppose both and are -improved by relative to with . Then, for any , there is such that for all , with probability at least we have
| (14) |
where , , , , and .
Remarks.
Notice, the result assumes the hypotheses and policies are fixed a priori to drawing . Hence, the bound is only valid for test sets independent from training. Regardless, it is still useful for interpretation and this style of bound produces tighter guarantees than conventional learning-theoretic bounds; i.e., from both analytic and empirical perspectives, respectively (Shalev-Shwartz and Ben-David, 2014; Sicilia et al., 2021). Like Thm. 4.1, we also use two hypotheses , but the result is easily specified to the one hypothesis case by taking (albeit, this may loosen the bound). In any case, the assumption is not unreasonable. A policy – optimized with respect to just one hypothesis – may also offer relative improvement for other hypotheses distinct from . For greater certainty, the term in the probability can be made arbitrarily small provided a large enough sample. Sensibly, the term indicates the probability is also proportional to how much better the communication mechanism is where “better” is given precise meaning by comparing population statistics for the objective via . At minimum, we require , but should be small for suitably effective answer-players anyway. Finally, we again, safely ignore terms, which go to 0 as grows.
Interpretation.
The takeaway from Prop. 4.1 is an unexpectedly sensible strategy for game success: the question-player focuses communication efforts only on identifying the goal-object. When the non-cooperative agent is effective, this communication strategy essentially reduces an upperbound on the true cooperation-identification error. All the while, this strategy very obviously assists the object-recognition task as well. We again note the implication that non-cooperative agents can reveal themselves by their non-cooperation. The question-player need not expend additional effort to uncover them by dialogue actions.
Comparison to Thm. 4.1.
While Thm. 4.1 alludes the interpretation given above – since the object-identification error is shown to control cooperation identification error in part –, Prop. 4.1 distinguishes itself because it considers all terms in the upperbound (not just ). This subtlety is important. In particular, a priori, one cannot be certain that improving the object-identification error from to also improves the cooperation gap . Instead, it could be the case that decreases and the overall bound on is worsened. Aptly, Prop. 4.1 isolates the circumstances (i.e., related to Def. 4.2), which ensure this adverse effect does not occur. It shows us, under reasonable assumptions, the communication strategy discussed in our interpretation controls the whole bound in Thm. 4.1 and not just some part. As noted, drawing inference from only a portion of the bound can have unexpected consequences. In fact, this is the topic of much recent work in analysis of learning algorithms (Johansson et al., 2019; Wu et al., 2019; Zhao et al., 2019; Sicilia et al., 2022).
Comparison to Cooperative Setting.
It is also worthwhile to note that setting the reward as is also an appropriate strategy in the distinct fully cooperative Guess What?! game. The authors of the original GuessWhat?! corpus propose this reward exactly in their follow-up work Strub et al. (2017) which uses RL to learn communication strategies in the fully cooperative setting. Thus, the theoretical results of this section are exceedingly practical. They suggest, for effective non-cooperative agents, we may sensibly employ the same techniques in both the fully cooperative setting and the partially non-cooperative setting. This is beneficial, because the nature of our problem anticipates we will not know the setting in which we operate.
Motivating a Mixed Objective.
As a final note, we remark on how this result may be applied to properly motivate a reward which, a priori, can only be heuristically justified. Specifically, a very reasonable suggestion would be to combine the rewards in Eq. (11) and Eq. (12) via convex sum. Prior to our theoretical analyses, it is unclear that the two strategies would be complementary. Instead, the objectives could be competing, and so, this mixed strategy could lead to sub-par performance on both tasks. In light of this, our theoretical results help to understand this heuristic more formally. They suggest the two strategies are, in fact, complementary and outline the assumptions necessary for this to be the case. In contrast, empirical analyses can be much more specific to the data used, among other factors. This, in general, is a key differentiation between the analysis we have provided here and the oft-used appeal to heuristics.
4.4 Proofs
Here, we provide proof of all theoretical results. We first remind the reader of some key definitions for easy reference:
| (15) |
Please, see Section 4.1 for additional definitions and context.
Theorem 4.1.
Claim 0.
Define as above and take to be sufficiently complex so that . Let be the VC-Dimension of . Then for any , with probability at least , for all ,
| (16) |
where , , and .
Proof.
For any and , we have
| (17) |
This is a standard VC-bound; e.g., Thm. 6.11 in Shalev-Shwartz and Ben-David (2014). Thus, it suffices to show that for any sample of size and any choice of hypotheses , we have
| (18) |
Notice first, by choice of , for any we have
| (19) |
By definition of and its relation to , for any choice of , there is some such that for all . Recall, acts like an indicator function, returning for true arguments and otherwise. Thus,
| (20) |
The equality follows by applying the definition of , appropriately grouping terms, and then using the fact: . Now, the triangle inequality for classification error Crammer et al. (2007); Ben-David et al. (2007) tells us for any and any we have
| (21) |
Applying these bounds to the result of Eqn. (20) and re-arranging terms completes the proof. ∎
Proposition 4.1.
Claim 0.
Let and . Suppose the non-cooperative answer-player is effective and further suppose both and are -improved by relative to with . Then, for any , there is such that for all , with probability at least we have
| (22) |
where , , , , and .
We first give a Lemma.
Lemma 4.1.
Let and . For any , suppose is -improved by relative to with . Then,
| (23) |
where , .
Proof.
Given samples and with and define
| (24) |
Then, and application of Hoeffding’s inequality yields
| (25) |
To finish, apply . ∎
Now, we proceed with the proof of Prop. 4.1.
Proof.
We begin by bounding the probability of a few events of interest. First,
| (26) |
as well as
| (27) |
by two applications of Lemma 4.1. Second, by Hoeffding’s Inequality, for any we know with
| (28) |
and
| (29) |
Third, by assumption on the non-cooperative agent, we know we may pick large enough samples and so
| (30) |
Applying Boole’s inequality bounds the probability that any one of these events holds by . Considering the complement event yields a lower bound on the probability that every one of these events fails to hold. Specifically, the lower bound is . Thus, it is sufficient to show
| (31) |
under assumption of the complement event. To this end, assume the complement. Then, we have directly that
| (32) |
So, in the remainder, we concern ourselves with showing . First note that for it is always true that
| (33) |
A similar equation holds for . Then, by assumption, so expanding,
| (34) |
We also assume and , so applying to both sides of Eq. (34) yields
| (35) |
Finally, the fact may be applied to both sides of Eq. (35) to attain
| (36) |
∎
5 Experimentation
In this section, we empirically study the communication strategies just discussed in a theoretical context. We also give insights on the non-cooperative strategies found in the collected data.
5.1 Implementation
Our implementation makes use of the existing framework of De Vries et al. (2017). The primary difference in the game we consider is the included possibility that the answer-player is non-cooperative. As such, many of our model components are based on those proposed by the dataset authors (De Vries et al., 2017; Strub et al., 2017).
Question-Player.
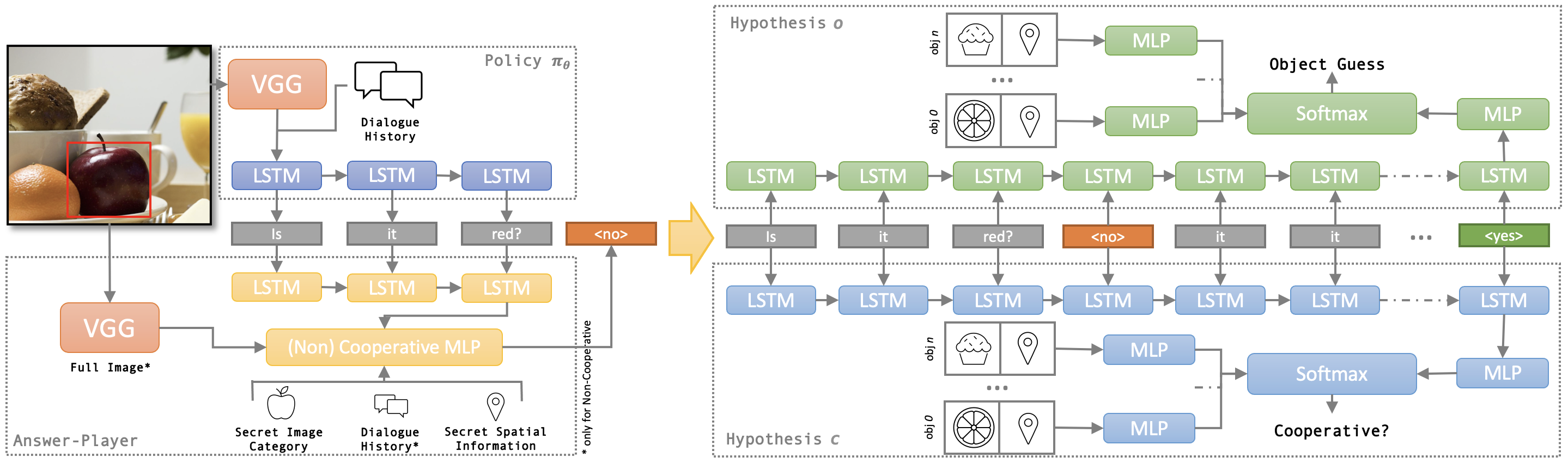
The question-player consists of: a hypothesis which predicts the goal-object given the object categories, object locations, and the dialogue-history; a hypothesis which predicts cooperation given the same information; and the communication policy which generates dialogue given the image666The image is processed by a VGG network and these features initialize the LSTM state in Figure 4. and the current dialogue-history. Each is modelled by a neural-network. Architectures of and the policy are identical to the guesser model and questioner model described by Strub et al. (2017). We give an overview of the architectures in Figure 4 as well.
Answer-Player.
The cooperative answer-player is modeled by a neural-network with binary output dependent only on the goal-object and the most immediate question. Strub et al. (2017) demonstrate – in the cooperative case – that additional features do not improve performance. On the other hand, non-cooperative behaviors may require more complex modeling. We explore different features for the network modeling the non-cooperative answer-player. During experimentation, we condition on various combinations of the full (and immediate) dialogue-history, the image, and the goal-object. The architectures in both cases are based on the oracle model described by Strub et al. (2017) with the addition of an LSTM that allows conditioning on the full dialogue-history. See Figure 4 for an overview.
Training.
As noted, is assumed fixed before considering the task of . In practice, we achieve this through supervised learning (SL) by training on human games in the Guess What?! (GW) corpus. Similarly, the cooperative answer-player is trained via SL on the GW corpus. The non-cooperative answer-player uses our novel corpus of non-cooperative games (see Section 3). Following Strub et al. (2017), we pre-train the communication policy using SL on the GW corpus. In some cases, is then taught a specific communication strategy by fine-tuning with RL on simulated dialogue. Dialogue is simulated by randomly sampling , drawing an image-object pair uniformly at random from the GW corpus, and allowing the current policy and the already trained answer-player indicated by to converse 5 rounds. The hypothesis is trained simultaneously on simulated dialogue during the RL phase of via SL. We do so because is assumed to minimize sample error in Thm 4.1. While simultaneous gradient methods only approximate this goal, it is more in line with assumptions than fixing a priori. In general, hyper-parameters are fixed for all experiments and are detailed in the code, which is publicly available. When possible, we follow the parameter choices of Strub et al. (2017). As an exception, we shorten the number of epochs in the RL phase to 10. Recall, the new network is trained in this phase as well. For , the learning rate is 1e-4. The new non-cooperative answer-players are trained similarly to the cooperative answer-players – i.e., as in Strub et al. (2017) – but we remove early-stopping to avoid the need for a validation set. Our non-cooperative corpus is thus used in its entirety for training since all trained agents are evaluated on novel generated dialogue (see Section 5.2). When training with the GW corpus, we use the original train/val split.
Comparison.
Despite some slight deviations from the original Guess What?! training setup, we point out that our fully cooperative results are fairly similar. In Figure 5, we show error-rate on simulated, cooperative, test dialogues for our question-player trained solely on object-identification; the precise error-rate is 48.8%. For the most similar training and testing setup used by Strub et al. (2017), the question-player achieves an error-rate of 46.7%.
5.2 Results

We report error for cooperation-identification and object-identification. We use a sample which has simulated dialogue (see Training) between our trained question- and answer-players using about 23K image-object pairs sampled from the GW test set. The objects/images are fixed for all experiments, but dialogue will of course change depending on the question-player. Each data-point in the figures corresponds to a single run using a specified percentage of cooperative examples; i.e., the answer-player’s type is selected by sampling and setting as the desired .
Human Non-Cooperative Strategies.
Between qualitative analysis of this data and conversations with the workers, we determined three primary human strategies for deception: spamming, absolute contradiction, and alternate goal objects. When spamming, participants would answer every question with the same answer; e.g., always answering no. Absolute contradiction was when participants determined the correct answer to the question-player’s query and then provided the negation of this. Finally, alternate goal objects describes the strategy of selecting an incorrect object in the image and providing answers as if this object was the correct goal. Of these, spamming is fairly easy to automatically detect; i.e., by searching for games where all answers are identical. We find 19% of the collected non-cooperative dialogues contain entirely spam answers. This, of course, does not account for mixed strategies within a game, but it does indicate the dataset is not dominated by the least complex strategy. Lastly, we remind the reader, some non-cooperative strategies directly describe violations of Gricean maxims. In particular, absolute contradiction and alternate goal objects violate the maxim of quality, while spamming violates the maxim of relevance. Due to the answer-player’s simple vocabulary and the greater control given to the question-player (i.e., in directing conversation topic and length), the maxims of manner and quantity are difficult for the answer-player to violate. So, it is expected observed strategies do not violate these maxims.
Modeling Human Non-Cooperation.
We further studied strategies in the autonomous non-cooperative answer-players. Notice, besides spamming, the human strategies may require knowledge of the full dialogue history as well as other objects in the image. We tested whether the autonomous answer-player utilized this information by training multiple answer-players with different information access: the first produced answers conditioned only on the goal-object and the most immediate question (1), the next two were also conditioned on the full dialogue-history (2) or the full image (3), and the last was conditioned on all of these features (4). We paired these non-cooperative answer-players with a question-player whose communication strategy focused on the object-identification task; i.e., using Eqn. (12). Answer-players 2, 3, and 4 induced an object-identification error outside a 95% confidence interval777An upper bound on true error induced by the 1st answer-player is 0.749 with confidence 95% (Hoeffding Bound 10K samples). The sample error of the 2nd, 3rd, and 4th answer-player are, respectively, 0.756, 0.757, and 0.752. of answer-player 1. In contrast, Strub et al. (2017) found that cooperative answer-players only needed access to the goal-object and the most immediate question to perform well. This result indicates the complexities inherent to deception and suggests that distinct strategies were learned when non-cooperative answer-players had access to more information. In the remainder, we focus on non-cooperative answer-player 2 with access to the full dialogue history. Our interpretation for answer-players 1, 3, and 4 is largely similar.
Empirical Validity of Def. 4.2.
Our next observation concerns the formal definition of effective given in Section 4 Def. 4.2. While the limiting property required by the definition is not easy to measure empirically, we observe in Figure 5 that the object-identification error on non-cooperative examples is relatively stable across question-player communication strategies. This fact – that the non-cooperative answer-player exhibits behavior consistent with an effective answer-player – points to the validity of our theory. Recall, an effective answer-player is assumed in Prop. 4.1.
Empirical Validity of Proposition 4.1.
Finally, the primary conclusion of our theoretical analysis was that communication strategies which focus only on the object-identification task should be effective for both object-identification and cooperation-identification. Figure 5 confirms this. Selecting a communication strategy based on improving object-identification improves object-identification as expected. Further, on the potentially opposing objective of identifying non-cooperation, this strategy is also effective. It far improves over a random baseline and also improves over the baseline which uses no RL-based strategy. On the other hand, the communication strategy which focuses only on the identification of non-cooperation fails at the opposing task of object-identification. This strategy performs almost as badly as a random baseline when the percent of non-cooperative examples is large and is also consistently worse than the baseline which uses no RL. The mixture of both strategies seems to achieve good middle ground. Recall, while this strategy may be heuristically intuited, our theoretical results formally justified this strategy as well.
6 Conclusion
Combining tools from learning theory, reinforcement learning, and supervised learning, we model partially non-cooperative communicative strategies in dialogue. Understanding such strategies is essential when building robust agents capable of conversing with parties of varying intent. Our theoretical and empirical findings suggest non-cooperative agents may sufficiently reveal themselves through their non-cooperative communicative behavior.
Although the dialogue game studied is simple, the results have ramifications for more complex dialogue systems. Our theoretical results, in particular, are not limited in this sense and may apply to designing communication strategies in distinct contexts. As noted in Section 4.1.1, the limited assumptions we make facilitate this. For example, classifying intents and asking the right clarification questions is crucial to decision making in dialogue (Purver et al., 2003; DeVault and Stone, 2007; Khalid et al., 2020). Our theory is directly applicable to this setting and could be applied to inform learning objectives for any dialogue agent that asks clarification questions to make a classification. A real-world example of this is the online-banking setting studied by Dhole (2020), in which the dialogue agent asks clarification questions to decide the type of account a user would like to open. If we suppose some users may be non-cooperative in this context, our theoretical setup is satisfied: there is some feature space (the dialogues), the label space of user-intents is finite, users are labeled with a binary indicator of cooperation, and the dialogue agent can control the distribution over which it learns by asking clarification questions. Our theoretical results should apply to many similar dialogue systems that can ask clarification questions or other types of questions. The only stipulations are that the theoretical setup is satisfied (e.g., in the manner just shown) and that our proposed assumptions on the nature of non-cooperative dialogue still hold (i.e., see Section 4.3, Def. 4.2).
To promote continued research, the collected corpus as well as our code are publicly available.888https://github.com/anthonysicilia/modeling-non-cooperation-tacl2022
7 Ethical Considerations
We have described a research prototype. The proposed dataset does not include sensitive or personal data. Our human subject board approved our protocol. Human subjects participated voluntarily and were compensated fairly for their time. The publicly available dataset is fully anonymized.
The proposed architecture relies on pretrained models such as word or image embeddings so any harm or bias associated with these models may be present in our model. We believe general methods that propose to mitigate harms can resolve these issues.
Acknowledgement
We would like to thank Matthew Stone, Raquel Fernandez, Katherine Atwell, and the anonymous reviewers for their helpful comments and suggestions. We also thank the action editors: Cindy Robinson, Ani Nenkova, and Claire Gardent.
References
- Abouelenien et al. (2014) Mohamed Abouelenien, Veronica Pérez-Rosas, Rada Mihalcea, and Mihai Burzo. 2014. Deception detection using a multimodal approach. In Proceedings of the 16th International Conference on Multimodal Interaction, pages 58–65.
- Asher and Lascarides (2013) Nicholas Asher and Alex Lascarides. 2013. Strategic conversation. Semantics and Pragmatics, 6:2–1.
- Attias et al. (2019) Idan Attias, Aryeh Kontorovich, and Yishay Mansour. 2019. Improved generalization bounds for robust learning. In Algorithmic Learning Theory, pages 162–183. PMLR.
- Atwell et al. (2022) Katherine Atwell, Anthony Sicilia, Seong Jae Hwang, and Malihe Alikhani. 2022. The change that matters in discourse parsing: Estimating the impact of domain shift on parser error. In Findings of the Association for Computational Linguistics: ACL 2022, pages 824–845, Dublin, Ireland. Association for Computational Linguistics.
- Barlier et al. (2015) Merwan Barlier, Julien Perolat, Romain Laroche, and Olivier Pietquin. 2015. Human-machine dialogue as a stochastic game. In 16th Annual SIGdial Meeting on Discourse and Dialogue (SIGDIAL 2015).
- Ben-David et al. (2010) Shai Ben-David, John Blitzer, Koby Crammer, Alex Kulesza, Fernando Pereira, and Jennifer Wortman Vaughan. 2010. A theory of learning from different domains. Machine Learning, 79(1-2):151–175.
- Ben-David et al. (2007) Shai Ben-David, John Blitzer, Koby Crammer, and Fernando Pereira. 2007. Analysis of representations for domain adaptation. In Advances in Neural Information Processing Systems, pages 137–144.
- Bubeck et al. (2019) Sébastien Bubeck, Yin Tat Lee, Eric Price, and Ilya Razenshteyn. 2019. Adversarial examples from computational constraints. In International Conference on Machine Learning, pages 831–840. PMLR.
- Cercas Curry and Rieser (2018) Amanda Cercas Curry and Verena Rieser. 2018. #MeToo Alexa: How conversational systems respond to sexual harassment. In Proceedings of the Second ACL Workshop on Ethics in Natural Language Processing, pages 7–14, New Orleans, Louisiana, USA. Association for Computational Linguistics.
- Chou and Lee (2020) Huang-Cheng Chou and Chi-Chun Lee. 2020. “Your behavior makes me think it is a lie”: Recognizing perceived deception using multimodal data in dialog games. In 2020 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC), pages 393–402. IEEE.
- Conroy et al. (2015) Nadia K. Conroy, Victoria L. Rubin, and Yimin Chen. 2015. Automatic deception detection: Methods for finding fake news. Proceedings of the Association for Information Science and Technology, 52(1):1–4.
- Crammer et al. (2007) Koby Crammer, Michael Kearns, and Jennifer Wortman. 2007. Learning from multiple sources. In Advances in Neural Information Processing Systems, pages 321–328.
- Cullina et al. (2018) Daniel Cullina, Arjun Nitin Bhagoji, and Prateek Mittal. 2018. PAC-learning in the presence of adversaries. Advances in Neural Information Processing Systems, 31.
- Das et al. (2017) Abhishek Das, Satwik Kottur, Khushi Gupta, Avi Singh, Deshraj Yadav, José M.F. Moura, Devi Parikh, and Dhruv Batra. 2017. Visual dialog. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 326–335.
- De Vries et al. (2017) Harm De Vries, Florian Strub, Sarath Chandar, Olivier Pietquin, Hugo Larochelle, and Aaron Courville. 2017. Guesswhat?! visual object discovery through multi-modal dialogue. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 5503–5512.
- DeVault and Stone (2007) David DeVault and Matthew Stone. 2007. Managing ambiguities across utterances in dialogue. In Proceedings of the 11th Workshop on the Semantics and Pragmatics of Dialogue (Decalog 2007), pages 49–56.
- Dhole (2020) Kaustubh D. Dhole. 2020. Resolving intent ambiguities by retrieving discriminative clarifying questions. arXiv preprint arXiv:2008.07559.
- Diochnos et al. (2019) Dimitrios I. Diochnos, Saeed Mahloujifar, and Mohammad Mahmoody. 2019. Lower bounds for adversarially robust PAC learning. arXiv:1906.05815v1.
- Dziugaite and Roy (2017) Gintare Karolina Dziugaite and Daniel M. Roy. 2017. Computing nonvacuous generalization bounds for deep (stochastic) neural networks with many more parameters than training data. arXiv preprint arXiv:1703.11008.
- Efstathiou and Lemon (2014) Ioannis Efstathiou and Oliver Lemon. 2014. Learning non-cooperative dialogue behaviours. In Proceedings of the 15th Annual Meeting of the Special Interest Group on Discourse and Dialogue (SIGDIAL), pages 60–68.
- Feige et al. (2015) Uriel Feige, Yishay Mansour, and Robert Schapire. 2015. Learning and inference in the presence of corrupted inputs. In Conference on Learning Theory, pages 637–657. PMLR.
- Galati and Brennan (2021) Alexia Galati and Susan E. Brennan. 2021. What is retained about common ground? Distinct effects of linguistic and visual co-presence. Cognition, 215:104809.
- Ganin and Lempitsky (2015) Yaroslav Ganin and Victor Lempitsky. 2015. Unsupervised domain adaptation by backpropagation. In International Conference on Machine Learning, pages 1180–1189.
- Georgila and Traum (2011a) Kallirroi Georgila and David Traum. 2011a. Learning culture-specific dialogue models from non culture-specific data. In International Conference on Universal Access in Human-Computer Interaction, pages 440–449. Springer.
- Georgila and Traum (2011b) Kallirroi Georgila and David Traum. 2011b. Reinforcement learning of argumentation dialogue policies in negotiation. In Twelfth Annual Conference of the International Speech Communication Association.
- Germain et al. (2020) Pascal Germain, Amaury Habrard, François Laviolette, and Emilie Morvant. 2020. PAC-bayes and domain adaptation. Neurocomputing, 379:379–397.
- Gretton et al. (2012) Arthur Gretton, Karsten M. Borgwardt, Malte J. Rasch, Bernhard Schölkopf, and Alexander Smola. 2012. A kernel two-sample test. The Journal of Machine Learning Research, 13(1):723–773.
- Haber et al. (2019) Janosch Haber, Tim Baumgärtner, Ece Takmaz, Lieke Gelderloos, Elia Bruni, and Raquel Fernández. 2019. The PhotoBook dataset: Building common ground through visually-grounded dialogue. In Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, pages 1895–1910, Florence, Italy. Association for Computational Linguistics.
- Jameson et al. (1994) Anthony Jameson, Bernhard Kipper, Alassane Ndiaye, Ralph Schäfer, Joep Simons, Thomas Weis, and Detlev Zimmermann. 1994. Cooperating to be noncooperative: The dialog system pracma. In Annual Conference on Artificial Intelligence, pages 106–117. Springer.
- Johansson et al. (2019) Fredrik D. Johansson, David Sontag, and Rajesh Ranganath. 2019. Support and invertibility in domain-invariant representations. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 527–536. PMLR.
- Kajii and Morris (1997) Atsushi Kajii and Stephen Morris. 1997. The robustness of equilibria to incomplete information. Econometrica: Journal of the Econometric Society, pages 1283–1309.
- Keizer et al. (2017) Simon Keizer, Markus Guhe, Heriberto Cuayáhuitl, Ioannis Efstathiou, Klaus-Peter Engelbrecht, Mihai Dobre, Alex Lascarides, and Oliver Lemon. 2017. Evaluating persuasion strategies and deep reinforcement learning methods for negotiation dialogue agents. In Proceedings of the 15th Conference of the European Chapter of the Association for Computational Linguistics: Volume 2, Short Papers, pages 480–484, Valencia, Spain. Association for Computational Linguistics.
- Khalid et al. (2020) Baber Khalid, Malihe Alikhani, and Matthew Stone. 2020. Combining cognitive modeling and reinforcement learning for clarification in dialogue. In Proceedings of the 28th International Conference on Computational Linguistics, pages 4417–4428.
- Lee (2000) Mark G. Lee. 2000. The ethics of deception: Why AI must study selfish behaviour. Cognitive Science Research Papers-University of Birmingham CSRP.
- Levitan (2019) Sarah Ita Levitan. 2019. Deception in spoken dialogue: Classification and individual differences. Ph.D. thesis, Columbia University.
- Lipton et al. (2018) Zachary Lipton, Yu-Xiang Wang, and Alexander Smola. 2018. Detecting and correcting for label shift with black box predictors. In International Conference on Machine Learning, pages 3122–3130. PMLR.
- Montasser et al. (2020) Omar Montasser, Steve Hanneke, and Nati Srebro. 2020. Reducing adversarially robust learning to non-robust PAC learning. Advances in Neural Information Processing Systems, 33:14626–14637.
- Nash (1951) John Nash. 1951. Non-cooperative games. Annals of Mathematics, pages 286–295.
- Pinker et al. (2008) Steven Pinker, Martin A. Nowak, and James J. Lee. 2008. The logic of indirect speech. Proceedings of the National Academy of sciences, 105(3):833–838.
- Plüss (2010) Brian Plüss. 2010. Non-cooperation in dialogue. In Proceedings of the ACL 2010 Student Research Workshop, pages 1–6.
- Plüss (2014) Brian Plüss. 2014. A Computational Model of Non-Cooperation in Natural Language Dialogue. Ph.D. thesis, The Open University.
- Purver et al. (2003) Matthew Purver, Jonathan Ginzburg, and Patrick Healey. 2003. On the means for clarification in dialogue. In Current and New Directions in Discourse and Dialogue, pages 235–255. Springer.
- Rabanser et al. (2019) Stephan Rabanser, Stephan Günnemann, and Zachary Lipton. 2019. Failing loudly: An empirical study of methods for detecting dataset shift. Advances in Neural Information Processing Systems, 32.
- Schlangen (2019) David Schlangen. 2019. Grounded agreement games: Emphasizing conversational grounding in visual dialogue settings. arXiv:1908.11279v1.
- Schoenauer-Sebag et al. (2019) Alice Schoenauer-Sebag, Louise Heinrich, Marc Schoenauer, Michele Sebag, Lani F. Wu, and Steve J. Altschuler. 2019. Multi-domain adversarial learning. In International Conference on Learning Representation.
- Serban et al. (2018) Alexandru Constantin Serban, Erik Poll, and Joost Visser. 2018. Adversarial examples - A complete characterisation of the phenomenon. arXiv:1810.01185v2.
- Shalev-Shwartz and Ben-David (2014) Shai Shalev-Shwartz and Shai Ben-David. 2014. Understanding Machine Learning: From Theory to Algorithms. Cambridge university press.
- Shapley (1953) Lloyd S. Shapley. 1953. Stochastic games. Proceedings of the national academy of sciences, 39(10):1095–1100.
- Shim and Arkin (2013) Jaeeun Shim and Ronald C. Arkin. 2013. A taxonomy of robot deception and its benefits in hri. In 2013 IEEE International Conference on Systems, Man, and Cybernetics, pages 2328–2335. IEEE.
- Shu et al. (2017) Kai Shu, Amy Sliva, Suhang Wang, Jiliang Tang, and Huan Liu. 2017. Fake news detection on social media: A data mining perspective. ACM SIGKDD Explorations Newsletter, 19(1):22–36.
- Sicilia et al. (2022) Anthony Sicilia, Katherine Atwell, Malihe Alikhani, and Seong Jae Hwang. 2022. PAC-bayesian domain adaptation bounds for multiclass learners. In The 38th Conference on Uncertainty in Artificial Intelligence.
- Sicilia et al. (2021) Anthony Sicilia, Xingchen Zhao, Anastasia Sosnovskikh, and Seong Jae Hwang. 2021. PAC bayesian performance guarantees for deep (stochastic) networks in medical imaging. In Medical Image Computing and Computer Assisted Intervention – MICCAI 2021, pages 560–570, Cham. Springer International Publishing.
- Soldner et al. (2019) Felix Soldner, Verónica Pérez-Rosas, and Rada Mihalcea. 2019. Box of lies: Multimodal deception detection in dialogues. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), pages 1768–1777.
- Strub et al. (2017) Florian Strub, Harm De Vries, Jeremie Mary, Bilal Piot, Aaron Courvile, and Olivier Pietquin. 2017. End-to-end optimization of goal-driven and visually grounded dialogue systems. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, pages 2765–2771.
- Sutton et al. (1999) Richard S. Sutton, David A. McAllester, Satinder P. Singh, Yishay Mansour, et al. 1999. Policy gradient methods for reinforcement learning with function approximation. In Advances in Neural Information Processing Systems, volume 99, pages 1057–1063. Citeseer.
- Traum et al. (2008) David Traum, William Swartout, Jonathan Gratch, and Stacy Marsella. 2008. A virtual human dialogue model for non-team interaction. In Recent Trends in Discourse and Dialogue, pages 45–67. Springer.
- Vourliotakis et al. (2014) Aimilios Vourliotakis, Ioannis Efstathiou, and Verena Rieser. 2014. Detecting deception in non-cooperative dialogue: A smarter adversary cannot be fooled that easily. In 18th Workshop on the Semantics and Pragmatics of Dialogue, pages 252–254.
- Williams (1992) Ronald J. Williams. 1992. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine Learning, 8(3-4):229–256.
- Wu et al. (2019) Yifan Wu, Ezra Winston, Divyansh Kaushik, and Zachary Lipton. 2019. Domain adaptation with asymmetrically-relaxed distribution alignment. In International Conference on Machine Learning, pages 6872–6881. PMLR.
- Wu et al. (2018) Zhe Wu, Bharat Singh, Larry S. Davis, and V.S. Subrahmanian. 2018. Deception detection in videos. In Thirty-Second AAAI Conference on Artificial Intelligence.
- Zhao et al. (2019) Han Zhao, Remi Tachet Des Combes, Kun Zhang, and Geoffrey Gordon. 2019. On learning invariant representations for domain adaptation. In International Conference on Machine Learning, pages 7523–7532. PMLR.
- Zhao et al. (2018) Han Zhao, Shanghang Zhang, Guanhang Wu, José M.F. Moura, Joao P. Costeira, and Geoffrey J. Gordon. 2018. Adversarial multiple source domain adaptation. In Advances in Neural Information Processing Systems, pages 8559–8570.
- Zhou et al. (2004) Lina Zhou, Judee K. Burgoon, Jay F. Nunamaker, and Doug Twitchell. 2004. Automating linguistics-based cues for detecting deception in text-based asynchronous computer-mediated communications. Group Decision and Negotiation, 13(1):81–106.