Modélisation micromagnétique du comportement magnéto-mécanique
Résumé
Micromagnétisme, statique, couplage, magnéto-mécanique.
keywords:
1 Introduction
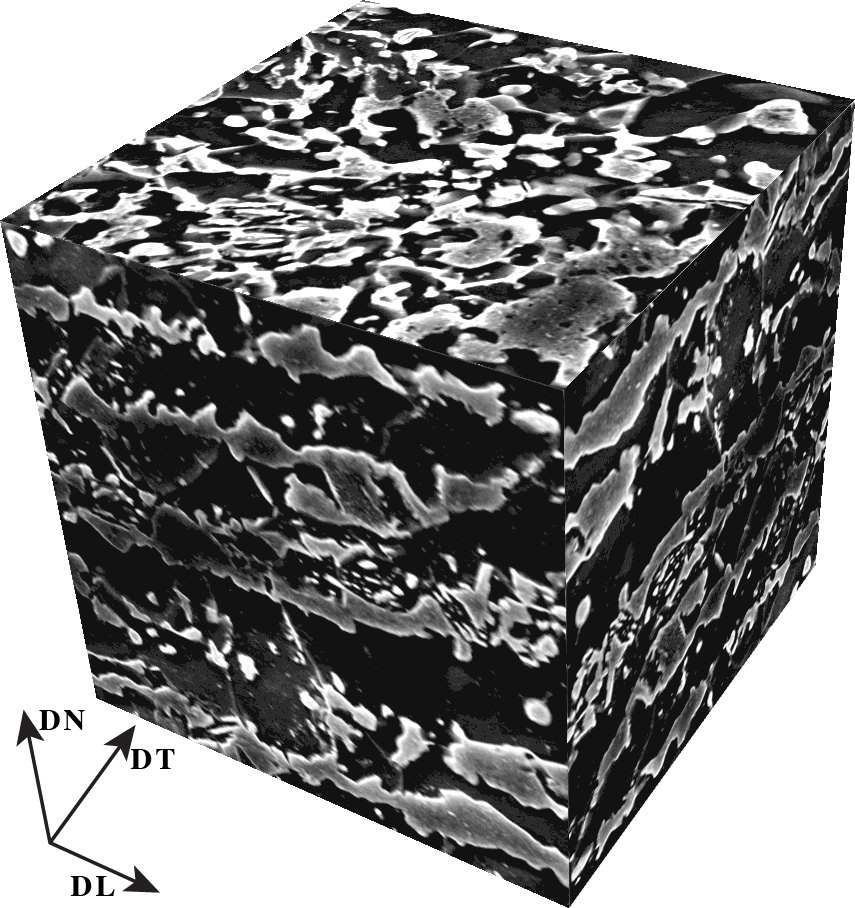
Les dernières années ont vues un intérêt grandissant des industries automobiles pour l’utilisation d’aciers à haute performance tels que les aciers dual-phases (DP). La production de ces aciers implique plusieurs procédés qui conduisent à une microstructure biphasée principalement composée d’îlots de martensite dure dispersés dans une matrice ferritique ductile en proportion variable selon l’histoire thermo-mécanique du matériau (fig 1).


Les systèmes d’évaluation non destructifs présentent un intérêt particulier pour vérifier l’homogénéité des aciers Dual Phase. Les techniques magnétiques ont montré leur efficacité à évaluer la microstructure de ces aciers en sortie de recuit/galvanisation. En particulier, le système 3MA [5] est connu pour son aptitude à évaluer de façon non destructive les propriétés mécaniques des aciers Dual Phase. Dès 2003, des essais en ligne ont permis de montrer que l’on pouvait estimer la résistance maximale avec une erreur inférieure à 4% et la limite élastique à 8-10% près. Toutefois, dans le cas des Dual Phase, la seule estimation des propriétés mécaniques n’est pas suffisante pour garantir la qualité du produit. La microstructure conditionne d’autres caractéristiques du matériau difficilement mesurables à l’aide de simples essais de traction. Ces caractéristiques (par exemple l’état de contrainte résiduel) prennent une place de plus en plus importante dans le cahier des charges des clients. Pour que la mesure magnétique donne des informations plus précises sur la microstructure du matériau, il faut pouvoir décrire suffisamment finement le lien entre la microstructure, l’état de contrainte et les propriétés magnétiques en ligne.
2 Comportement magnétique
L’application d’un champ magnétique aimante les milieux magnétiques mais peut également les déformer. Ce phénomène est appelé magnétostriction. Il s’agit d’une déformation ”spontanée”, intrinsèque au matériau. Elle ne dépend que de l’état magnétique du matériau. Aimantation et magnétostriction son liées par une relation non linéaire où est le tenseur d’ordre 4 des constantes de magnétostriction.
| (1) |
Le mécanisme d’aimantation observable macroscopiquement fut expliqué par Weiss, qui en 1907 émit l’hypothèse que le comportement magnétique des matériaux magnétiques a pour origine l’existence d’une microstructure intragranulaire organisée en domaines portant des directions d’aimantation différentes (2) et séparés par des parois (parois de Bloch). Cette interprétation fut confirmée expérimentalement lorsque Bitter (1931) observa directement les domaines de Weiss.
| (2) |
Sous l’influence d’un champ magnétique externe, la microstructure magnétique évolue par déplacement des parois et rotation des moments magnétiques. Le déplacement peut être entravé par la présence de défauts structuraux (phases, inclusions, dislocations, joints de grains …). Lorsqu’une paroi rencontre un défaut, elle se trouve ancrée. Le désancrage nécessite alors un champ appliqué légèrement supérieur au champ nécessaire au déplacement en absence de défaut. Les parois progressent alors par sauts brusques et irréversibles. Ces sauts irréversibles sont à l’origine de l’hystérésis du comportement magnétique et de sa discontinuité.
À l’échelle microscopique, la subdivision en domaines résulte de équilibre énergétique entre différentes contributions élémentaires. Trois contributions en particulier sont à l’origine de cette subdivision, l’énergie d’échange, l’énergie d’anisotropie et l’interaction dipolaire [2]. L’interaction d’échange traduit la tendance des moments magnétiques voisins à s’aligner dans la même direction. Ce phénomène se traduit à l’échelle macroscopique par un un gradient d’aimantation correspondant à une force de rappel élastique. L’interaction d’échange est une interaction purement locale qui décroit rapidement avec la distance, et ne dépend que des propriétés microscopiques du matériau. On y associe usuellement un potentiel de la forme:
| (3) |
L’anisotropie représente l’interaction des moments magnétiques avec le potentiel créé par la symétrie du cristal. Le résultat d’une telle interaction est la préférence des moments magnétiques à s’orienter dans certaines directions énergétiquement favorables (direction de symétrie du cristal). Cette interaction prend la forme d’une fonction paire s’annulant suivant les différents axes d’anisotropie () du cristal considéré.
| (4) |
Ainsi dans le cas d’une symétrie cubique, la fonction prend la forme
| (5) |
L’interaction dipolaire joue un rôle fondamental dans la formation des domaines. Celle-ci est liée à l’interaction mutuelle des moments magnétiques et à la géométrie du milieu. L’aimantation créée dans un milieu par l’action d’un champ magnétique extérieur génère en retour un champ. Ce champ appelé champ démagnétisant satisfait les équations de Maxwell et donc dérive d’un potentiel scalaire vérifiant l’ensemble des équations (6) et (7).
| (6) |
| (7) |
Le potentiel est solution du problème de Poisson (7) et traduit le caractère non local du champ démagnétisant. Ce champ conditionne un grand nombre de microstructures magnétiques observées expérimentalement. Du fait de son caractère non local, le calcul de cette grandeur est en général très coûteux en temps de calcul. On lui associe usuellement un potentiel de la forme:
| (8) |
Enfin la dernière interaction, traduit l’influence du champ appliqué sur les moments magnétiques. Il s’agit de l’énergie de Zeemann.
| (9) |
3 Modélisation Micromagnétique d’une particule ferromagnétique
Le micromagnétisme est une approche théorique permettant de décrire le processus d’aimantation à une échelle suffisamment large pour remplacer les moments magnétiques atomiques par des fonctions continues, et suffisamment fine pour rendre compte des zones de transition entre domaines magnétiques [1][3]. Cette approche continue de la théorie du ferromagnétisme fait le lien entre la description quantique de la structure des spins et la théorie de l’électromagnétisme de Maxwell où les propriétés magnétiques du matériau sont décrites par des constantes volumiques homogènes (susceptibilité et perméabilité ).
3.1 Micromagnétisme
Il s’agit d’une approximation basée sur la minimisation d’une fonctionnelle énergétique . Cette minimisation par rapport à l’aimantation donne lieu à un état d’équilibre métastable associé à une configuration particulière de la structure magnétique. La contribution apportée par Brown [1] fut de définir une expression de l’énergie libre comme somme des contributions internes et externes énoncées précédemment.
| (10) |
A l’équilibre, on doit alors satisfaire la relation de stationnarité énergétique:
| (11) |
Pour tout champ appliqué , à donné, on cherche une solution sous la contrainte
| (12) |
Pour une petite variation de l’aimantation locale , la variation de l’énergie libre totale est donnée par:
| (13) |
Soit:
| (14) |
Où est le vecteur unitaire normal à la surface qui délimite le volume . La condition de stationnarité de l’énergie totale peut donc se mettre sous la forme suivante:
| (15) |
| (16) |
Le champ effectif défini par (16) est le champ localement ressenti par chaque moment magnétique. De l’égalité (15) on tire un système appelé système de Brown [1] qui défini deux conditions à respecter à l’équilibre. Une configuration magnétique qui réalise le minimum énergétique doit vérifier le système d’équation de Brown :
| (17) |
3.2 Choix de résolution
Notre approche du problème d’optimisation (11) combine une méthode itérative (gradient conjugué) et une méthode éléments finis permettant la description du milieu. Le gradient conjugué (algorithme 1 détaillé ci-dessous) permet en général de traiter des problèmes d’optimisation. On peut montrer que cette méthode appliquée à une fonctionnelle quadratique elliptique converge en itérations. Cependant, dans le cas du micromagnétisme, la contrainte (12) imposée à l’aimantation locale associée à la non convexité de l’énergie magnétocristalline n’assurent pas l’unicité de la solution.
Le problème mathématique d’existence et d’unicité de la solution reste encore à ce jour un problème ouvert [9]. Mais, en supposant l’existence d’une solution, la problématique est alors de construire un schéma numérique conservant au mieux les propriétés du système à savoir: Les propriétés du champ démagnétisant (7), la décroissance de l’énergie, et la conservation de la norme locale de l’aimantion. Cette dernière remarque nous conduit à effectuer un changement de variable dans la définition de l’énergie, et dans la construction de la suite .
3.3 Couplage magnéto-mécanique
La variation d’aimantation d’un milieu magnétique (magnétostrictif) induit une variation de volume appelée magnétostriction spontanée. Celle-ci correspond en général à une incompatibilité (i.e. déformation ne dérivant pas d’un champ de déplacement ). La déformation élastique du milieu aimanté doit alors corriger l’incompatibilité de la magnétostriction, ce qui se traduit par un état de contrainte non nul, même en l’absence de toute sollicitation mécanique externe. On s’intéresse ici à l’évolution d’un système mécanique qui, sous l’action d’une sollicitation interne et ou externe, évolue d’un état d’équilibre à un autre. Lorsque la magnétostriction spontanée du milieu est connue, la déformation magnéto-élastique correspondante est obtenue par additivité , les déformations considérées rentrant dans le cadre de l’hypothèse des petites perturbations. La déformation magnéto-élastique totate , dérivant d’un champ de déplacement (18), et la contrainte obéissant à l’équation d’équilibre, les champs mécaniques vérifient les équations suivantes:
| (18) |
| (19) |
où désigne le tenseur d’élasticité d’ordre 4 du milieu. Les conditions aux limites du problème sont données par:
| (20) |
La linéarité des déformations permet de reformuler l’équilibre mécanique de manière à introduire explicitement une sollicitation interne d’origine magnétique (magnétostrictive).
| (21) |
Où représente la contrainte totale et la densité de forces d’origine magnétostrictive, conséquence directe de l’état d’aimantation du matériau. À l’image du micromagnétisme le problème mécanique peut également se réduire à un problème d’optimisation où le champ de déplacement minimise un potentiel donné par l’application d’une formulation variationnelle au problème (21):
| (22) |
Avec:
| (23) |
Dans le cas d’une modélisation type FEM basée sur approche en déplacement, le problème de minimisation (22) peut se simplifier sous la forme du système linéaire (24) où , et représentent respectivement la matrice de rigidité du système, le vecteur déplacement généralisé et le vecteur force généralisé traduisant les efforts d’origine magnétostrictive.
| (24) |
L’expression approchée à l’aide d’éléments finis isoparamétriques sur le domaine discrétisé est donnée pour des fonctions de forme linéaires:
| (25) |
Dans le cadre d’une approche couplée, les contributions liées à l’équilibre d’un milieu magnétique, mais aussi les contributions liées à l’équilibre d’un milieu déformable et les différentes interactions entre ces deux phénomènes participent à l’équilibre énergétique. L’ énergie libre décrivant au mieux un milieu magnétique déformable prend alors la forme suivante:
| (26) |
La condition de stabilité de l’énergie est alors obtenue si et seulement si les champs d’aimantation et de déplacement minimisent simultanément l’énergie libre totale. Cette condition s’écrit :
| (27) |
Sous les contraintes (12) , (20). Une condition de minimisation est l’annulation de toutes les dérivées partielles, ce qui permet la résolution du problème magnétique et du problème mécanique séparément. On a alors à résoudre le système.
| (28) |
La première minimisation fournit toujours la condition de couple donnée par l’équation (17). La seconde minimisation fournit toujours le système linéaire donné par l’équation (24). La subtilité cependant réside dans la définition du champ effectif, qui se voit complétée par un terme supplémentaire appelé champ d’anisotropie élastique induit, et lié à la dérivation de l’énergie magnéto-élastique par rapport à l’aimantion tel que:
| (29) |
Avec
| (30) |
Dans le cas d’un matériau à symétrie cubique et en négligeant la magnétostriction de volume (hypothèse usuelle pour les matériaux magnétiques métalliques), le tenseur de magnétostriction prend la forme simple:
| (31) |
L’énergie magnéto-élastique se développe sous la forme:
| (32) |
et on exprime le champ d’anisotropie élastique :
| (33) |
La contribution supplémentaire au champ effectif nécessite à chaque itération de connaître localement l’état de contrainte mécanique par la résolution des équations d’équilibre (19) et (20). Cette résolution se résume à l’inversion du système linéaire (24). Nous remplaçons alors l’agorithme 2 par l’algorithme 3 où la résolution du problème mécanique à chaque itération permet de redéfinir l’état de contrainte. Il s’agit de l’approche dite "constrained", qui diffère de l’approche "relaxed" où l’on néglige l’effet de la contrainte intrinsèque, en remplaçant la déformation totale par la magnétostriction . Cette approximation très répandue dans le cadre du couplage magnéto-mécanique soulève le problème de la compatibilité des déformations et de la configuration des spins obtenue [8].
4 Applications
Le code de calcul micromagnétique statique 2D "sivimm2d" [7] nous a servi de base à l’implémentation de la formulation magnéto-mécanique (algorithme 3). Nous étudions l’évolution d’un monocristal ferromagnétique à symétrie cubique dont les constantes magnétique et mécanique sont résumées dans le tableau (1). Du fait de la restriction 2D, l’hypothèse de contrainte plane a été retenue, ce qui nécessite la redéfinition du tenseur d’élasticité initialement 3D par un tenseur plan tenant compte de cette restriction.
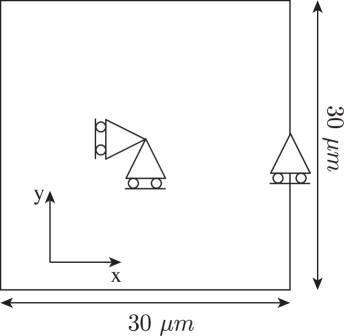
| 2 axes d’anisotropie et | |||
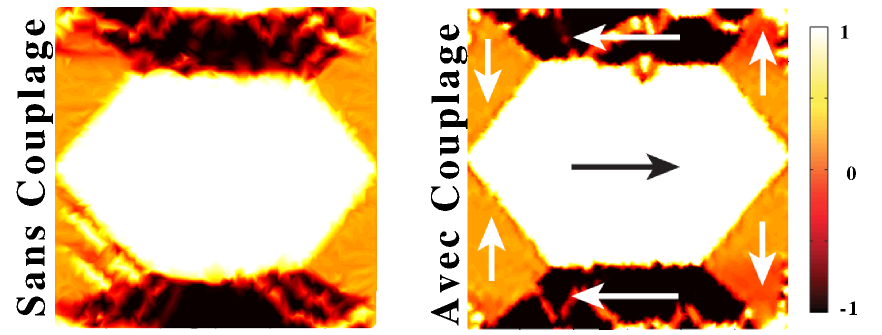
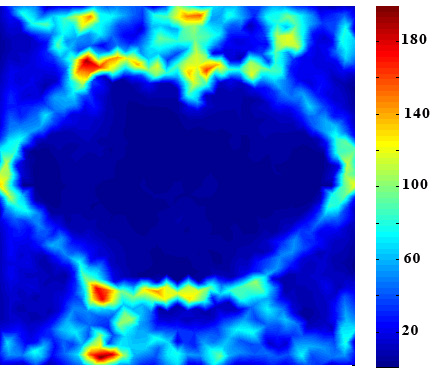
Les premières simulations sur le monocristal ont permis de mettre en évidence l’apport du couplage magnéto-mécanique (fig. 3(a)): En effet, en absence d’effet magnéto-élastique, la microstructure magnétique est dominée par les effets démagnétisant d’anisotropie qui tendent à aligner les moments magnétiques suivant les axes faciles et à favoriser l’apparition de domaines de refermeture du flux près des frontières de manière à minimiser l’énergie magnétostatique. La contrainte et son énergie associée agissent comme une source supplémentaire d’anisotropie , et en absence de sollicitation mécanique extérieure, celle ci agit sur la taille caractéristique des parois magnétiques définies respectivement par:
| (34) |
L’apport énergétique dû à l’état de contrainte intrinsèque (fig. 3(b)) a donc pour effet de stabiliser la microstructure magnétique tel qu’on peut le constater (fig. 3(a))
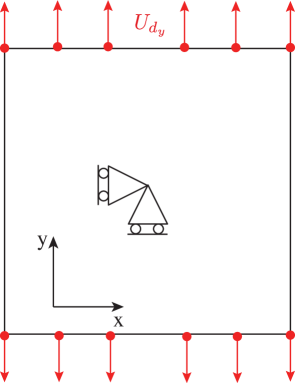
Le couplage magnéto mécanique introduit précédemment laisse la possibilité d’explorer l’influence de l’état de chargement mécanique externe sur la configuration des moments magnétiques. Ainsi sur le même domaine d’étude, on choisit, à champ fixé, d’appliquer une sollicitation mécanique perpendiculaire au champ appliqué (fig. 2(b)) et d’observer l’évolution de la microstructure magnétique sous l’action de ce chargement. définit la contrainte moyenne appliquée correspondant au déplacement imposé.

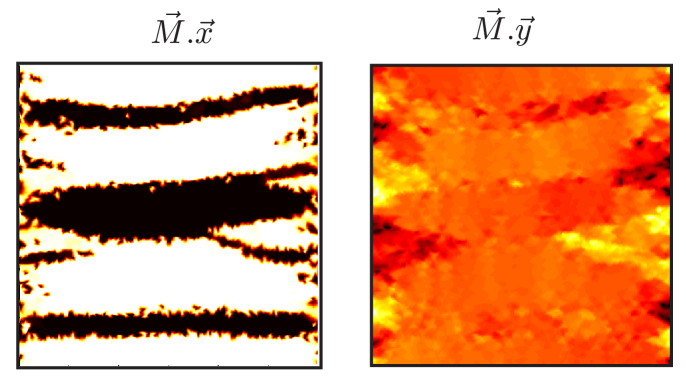
Les figures 4(a) et 4(b) rendent compte de l’évolution de la structure des domaines et des parois magnétiques. On peut y observer qu’en traction (fig. 4(a)) les domaines qui initialement étaient alignés avec le champ () disparaissent au profit des domaines orthogonaux au champ () énergétiquement favorables. En compression (fig. 4(b)) on constate l’effet inverse.
5 Conclusion
La mise en œuvre du couplage magnéto-élastique dans le cadre d’un calcul micromagnétique a montré son efficacité. Sur un monocristal nous avons montré que l’anisotropie induite par l’état de contrainte intrinsèque stabilise la microstructure magnétique, en particulier la taille des parois magnétiques. La nouvelle liberté d’explorer différents états de chargement dans le plan de contrainte (traction/compression uniaxial), nous a permis de mettre en évidence l’évolution du comportement magnétique, et la sensibilité de la microstructure magnétique à l’état de contrainte. Dans l’optique de la description du comportement magnéto-mécanique des aciers DP, la suite de ce travail consistera à introduire des microstructures de plus en plus complexes (fig. 1), l’objectif étant à terme d’obtenir des lois d’évolution du comportement magnétique en fonction de l’hétérogénéité (fraction d’îlots martensitiques, morphologie des îlots ).
Références
- [1] W. F. Brown. Micromagnetics, John Wiley & Sons, New York, 1963.
- [2] A. Hubert, R. Schäfer. Magnetic Domains. The analysis of magnetic microstructures, Springer, 2008.
- [3] Aharoni A. Introduction to the Theory of Ferromagnetism. Oxford University Press, New York, 1996.
- [4] F. Alouges. Mathematical models in micromagnetism: an introduction, ESAIM Proc, vol. 22, p 114-117, 2008.
- [5] Y. Gabi. Modélisation FEM du système de contrôle non destructif 3MA en ligne de production des aciers dual phase. ph.D Université de Grenoble. 2012.
- [6] E. Dan, Dahlberg, R. Proksch. Magnetic microscopies: the new additions, JMMM 200, p 720-728 , 1999.
- [7] M. Bernadou, S. Depeyre and S. He. Numerical Simulations of ferromagnetic microsctructures: Motion of the walls and effect on non magnetic impurities, Journal of intelligent material systems and structures,vol. 16, pp. 1015-1023, 2005.
- [8] Y. C. Shu, M. P. Lin, K. C. Wu. Micromagnetic modeling of magnetostrictive materials under intrinsic stress, Mechanics of Materials (36), p 975-997, 2004.
- [9] S. He. Modélisation et simulation numérique de matériaux magnétostrictifs, phd UPMC, p 31-36, 1999.