Modularity Enhances the Rate of Evolution in a Rugged Fitness Landscape
Abstract
Biological systems are modular, and this modularity affects the evolution of biological systems over time and in different environments. We here develop a theory for the dynamics of evolution in a rugged, modular fitness landscape. We show analytically how horizontal gene transfer couples to the modularity in the system and leads to more rapid rates of evolution at short times. The model, in general, analytically demonstrates a selective pressure for the prevalence of modularity in biology. We use this model to show how the evolution of the influenza virus is affected by the modularity of the proteins that are recognized by the human immune system. Approximately 25% of the observed rate of fitness increase of the virus could be ascribed to a modular viral landscape.
1 Introduction
Biological systems are modular, and the organization of their genetic material reflects this modularity [1, 2, 3, 4]. Complementary to this modularity is a set of evolutionary dynamics that evolves the genetic material of biological systems. In particular, horizontal gene transfer (HGT) is an important mechanism of evolution, in which genes, pieces of genes, or multiple genes are transferred from one individual to another [5, 6, 7]. Additionally, multi-body contributions to the fitness function in biology are increasingly thought to be an important factor in evolution [8], leading to a rugged fitness landscape and glassy evolutionary dynamics. The combination of modularity and horizontal gene transfer provide an effective mechanism for evolution upon a rugged fitness landscape [9]. The organization of biology into modules simultaneously restricts the possibilities for function, because the modular organization is a subset of all possible organizations, and may lead to more rapid evolution, because the evolution occurs in a vastly restricted modular subspace of all possibilities [9, 10]. Our results explicitly demonstrate this trade off, with serving as the crossover time from the latter to the former regime.
Thus, the fitness function in biology is increasingly realized to be rugged, yet modular. Nonetheless, nearly all analytical theoretical treatments assume a smooth fitness landscape with a dependence only on Hamming distance from a most-fit sequence [11], a linear or multiplicative fitness landscape for dynamical analysis of horizontal gene transfer [12, 13], or an uncorrelated random energy model [14, 15]. Horizontal gene transfer processes on more general, but still smooth, landscapes have been analyzed [16, 17, 18, 19, 20]. Here we provide, to our knowledge, the first analytical treatment of a finite-population Markov model of evolution showing how horizontal gene transfer couples to modularity in the fitness landscape. We prove analytically that modularity can enhance the rate of evolution for rugged fitness landscapes in the presence of horizontal gene transfer. This foundational result in the physics of biological evolution offers a clue to why biology is so modular. We demonstrate this theory with an application to evolution of the influenza virus.
We introduce and solve a model of individuals evolving on a modular, rugged fitness landscape. The model is constructed to represent several fundamental aspects of biological evolution: a finite population, mutation and horizontal gene transfer, and a rugged fitness landscape. For this model, we will show that the evolved fitness is greater for a modular landscape than for a non-modular landscape. This result holds for where is a crossover time, larger than typical biological timescales. The dependence of the evolved fitness on modularity is multiplicative with the horizontal gene transfer rate, and the advantage of modularity disappears when horizontal gene transfer is not allowed. Our results describe the response of the system to environmental change. In particular, we show that modularity allows the system to recover more rapidly from change, and fitness values attained during the evolved response to change increase with modularity for large or rapid environmental change.
2 Theory of the Rate of Evolution in a Rugged Fitness Landscape
We use a Markov model to describe the evolutionary process. There are individuals. Each individual replicates at a rate . The average fitness in the population is defined as . Each individual has a sequence that is composed of loci, . For simplicity, we take . Each of the loci can mutate to the opposite state with rate . Each sequence is composed of modules of length . A horizontal gene transfer process randomly replaces the th module in the sequence of individual , e.g. the sequence loci , with the corresponding sequences from a randomly chosen individual at rate . The a priori rate of sequence change in a population is, therefore, + . Since the fitness landscape in biology is rugged, we use a spin glass to represent the fitness:
| (1) |
is a quenched, Gaussian random matrix, with variance . As discussed in Appendix A, the offset value is chosen by Wigner’s semicircle law so that the minimum eigenvalue of is non-negative. The entries in the matrix are zero or one, with probability per entry, so that the average number of connections per row is . We introduce modularity by an excess of interactions in along the block diagonals of the connection matrix. There are of these block diagonals. Thus, the probability of a connection is when and when . The number of connections is . Modularity is defined by and obeys .
The Markov process describing these evolutionary dynamics includes terms for replication (), mutation (), and horizontal gene transfer ():
Here is the number of individuals with sequence , with the vector index used to label the sequences. This process conserves . The notation means the sequences created by a single mutation from sequence . The notation means the sequence created by horizontally gene transferring module from sequence into sequence .
We consider how a population of initially random sequences adapts to a given environment, averaged over the distribution of potential environments. For example, in the context of influenza evolution, these sequences arise, essentially randomly, by transmission from swine. As discussed in Appendix B, a short-time expansion for the average fitness can be derived by recursive application of this master equation:
| (3) | |||||
Result (3) is exact for all finite . Note that the effect of modularity enters at the quadratic level and requires a non-zero rate of horizontal gene transfer, . We see that for short times.
From the master equation, we also calculate the sequence divergence, defined as . As discussed in Appendix C, recursive application of Eq. (LABEL:2) gives
| (4) | |||||
The sequence divergence does not depend on modularity at second order in time. Note the terms at order not proportional are due to discontinuous changes in sequence resulting from the fixed population size constraint.
Introduction of a new sequence into an empty niche corresponds to an initial condition of identical, rather than random, sequences. The population dynamics again follows Eq. (LABEL:2). To see an effect of modularity, an expansion to 4th order in time is required. As discussed in Appendix B, we find
| (5) |
with
Interestingly, the fitness function initially increases quadratically. The modularity dependence enters at fourth order, and for short times.
3 Comparison of Theory to Simulation Results
The response function of the modular and non-modular system can be computed numerically as well. We start the system off with random initial sequences, so that the average initial is zero, and compute the evolution of the average fitness, . In Fig. 1 we show the results from a Lebowitz-Gillespie simulation. We see that for for . That is, the modular system evolves more quickly to improve the average fitness, for times less than a crossover time, . For , the constraint that modularity imposes on the connections leads to the non-modular system dominating, .
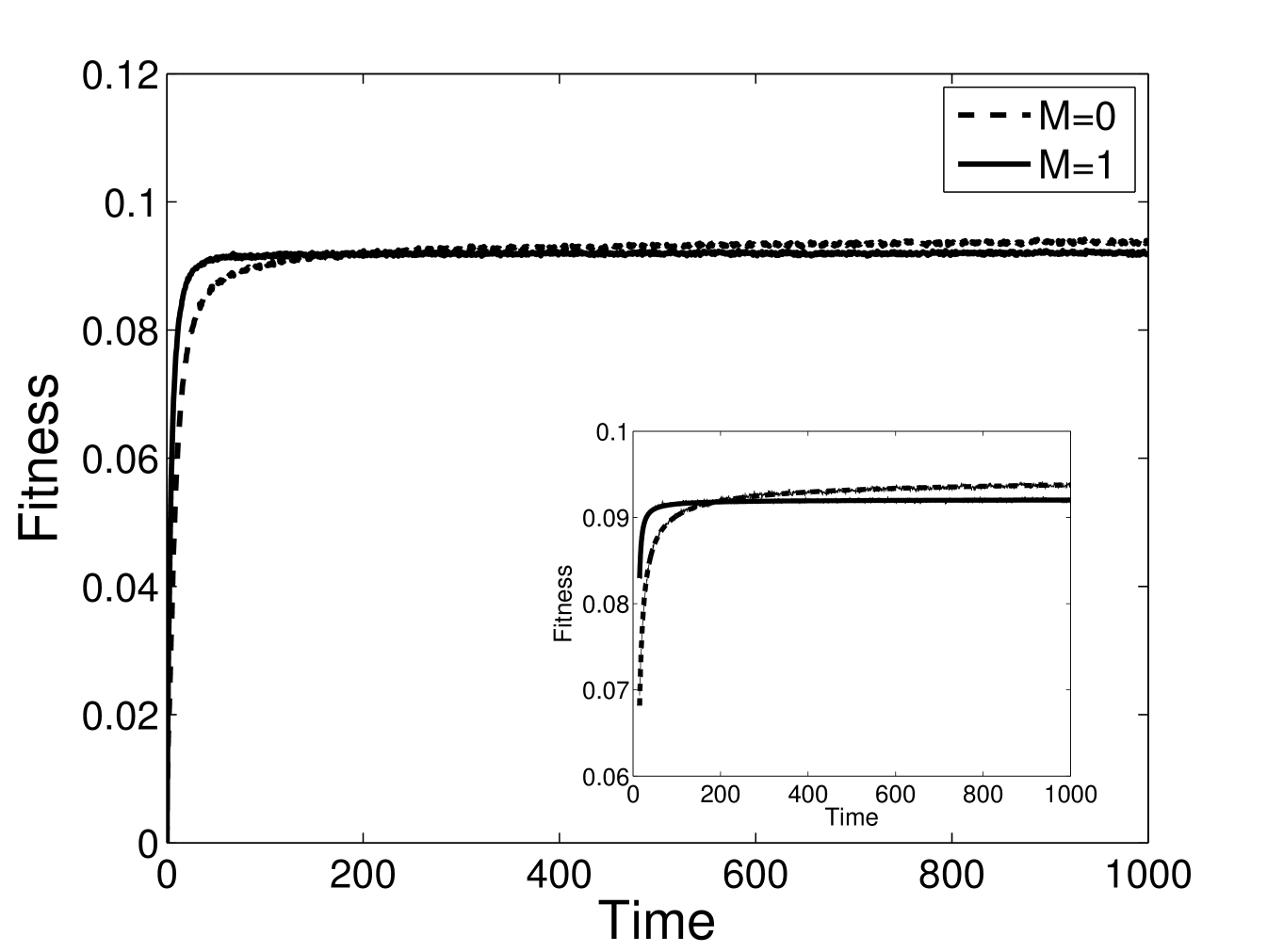
Eq. (3) shows these results analytically, and we have checked Eq. (3) by numerical simulation as well. For the parameter values of Fig. 1 and , theory predicts , , and simulation results give , . For , theory predicts , , and simulation results give ,
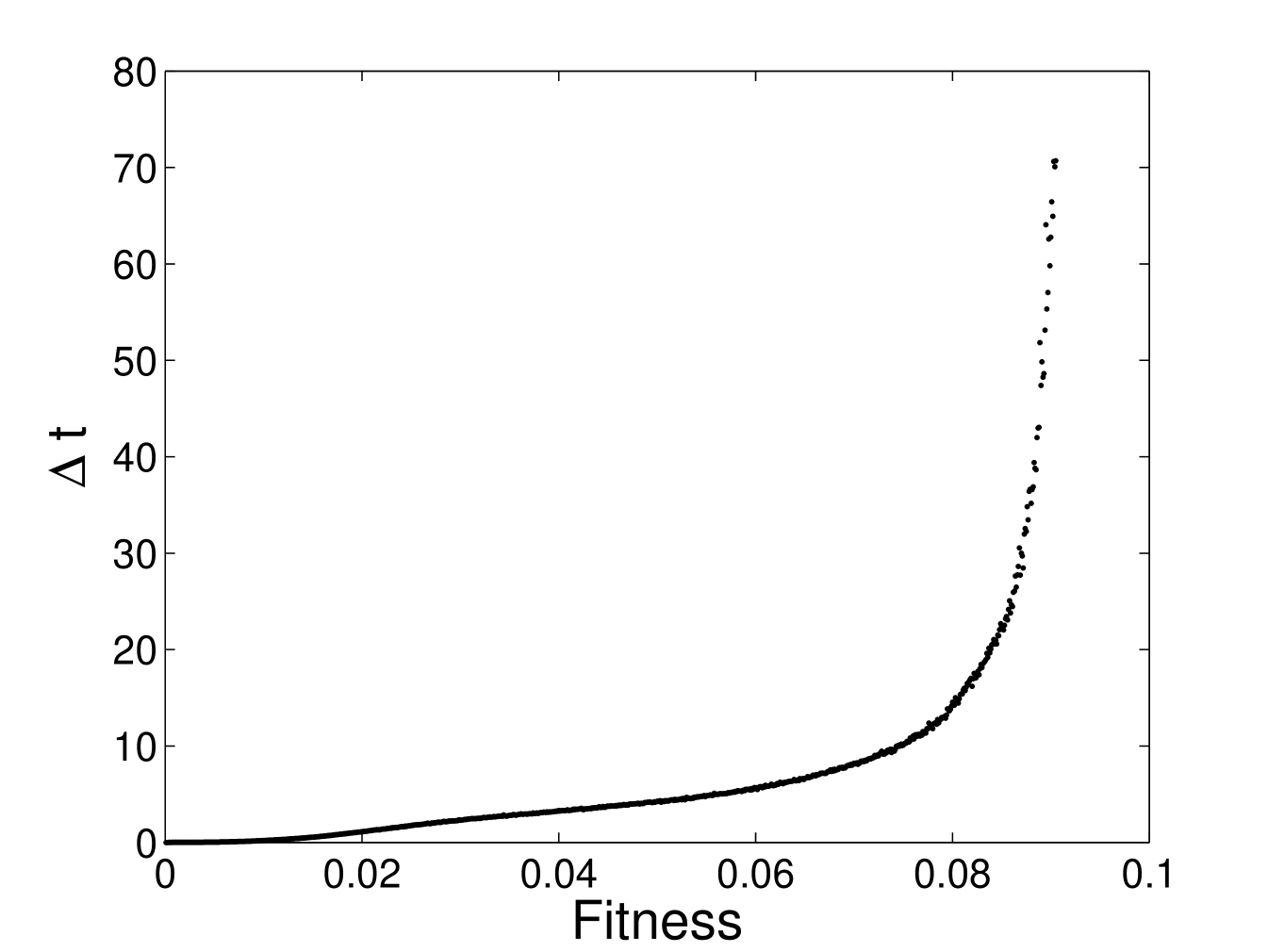
Since the landscape is rugged, we expect the time it takes the system to reach a given fitness value, , starting from random sequences to grow in a stretched exponential way at large times. Moreover, since the combination of horizontal gene transfer and modularity improves the response function at short times, we expect that the difference in times required to reach of a non-modular and modular system also increases in a stretched exponential way, by analogy with statistical mechanics, in which we expect the spin glass energy response function to converge as
| (7) |
with [21]. Figure 1 shows the fit of the data to this functional form, with , , for and , , for . Figure 2 shows the stretched exponential speedup in the rate of evolution that modularity provides.
The prediction for evolution of a population of identical sequences in a new niche is shown in Eq. (LABEL:101). Analytically, the effect of modularity shows up at 4th order rather than 2nd order when all sequences are initially identical. Qualitatively, however, at all but the very shortest times, the results for random and identical sequences are similar, as shown in Figs. 1 and 3.
4 Average Fitness in a Changing Environment
We show how to use these results to calculate the average fitness in a changing environment. We consider that every time steps, the environment randomly changes. During such an environmental change, each in the fitness, Eq. (1), is randomly redrawn from the Gaussian distribution with probability . That is, on average, a fraction of the fitness is randomized. Due to this randomization, the fitness immediately after the environmental change will be times the value immediately before the change, on average. This condition allows us to calculate the average time-dependent fitness during evolution in one environment as a function of and , given only the average fitness starting from random initial conditions, [22]. We denote the average fitness reached during evolution in one environment as . This is related to the average fitness with random initial conditions by , where is chosen to satisfy due to the above condition. Thus, for high rates or large magnitudes of environmental change, Eq. (3) can be directly used along with these two conditions to predict the steady-state average population fitness.
a)  b)
b) 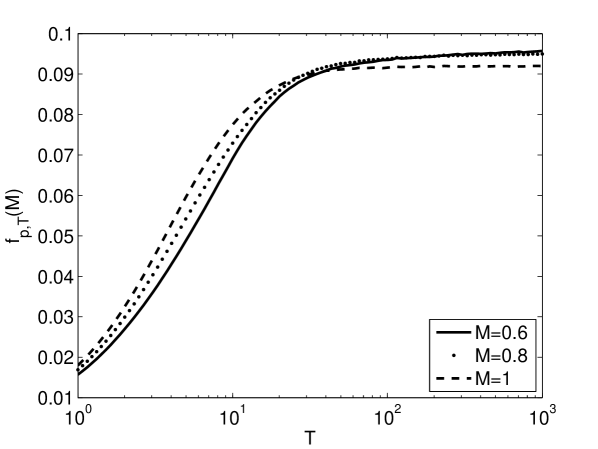
c) 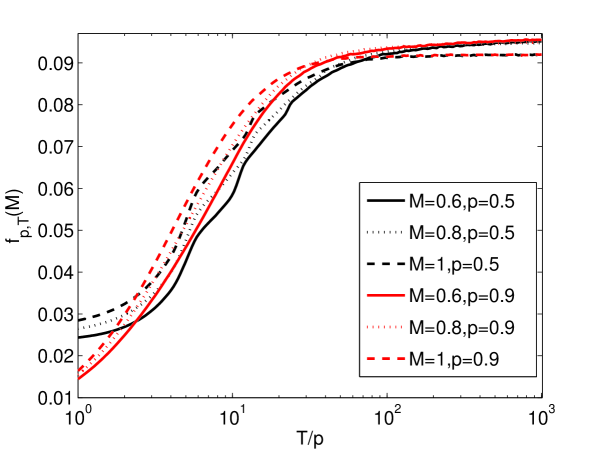
Figure 4 shows how the average fitness depends on the rate and magnitude of environmental change. The average fitness values for a given modularity are computed numerically. The figure displays a crossing of the modularity-dependent fitness curves. The curve associated with the largest modularity is greatest at short times. There is a crossing to the curve associated with the second largest modularity at intermediate times. And there is a crossing to the curve associated with the smallest modularity at somewhat longer times. In other words, the value of modularity that leads to the highest average fitness depends on time, , decreasing with increasing time.
Figure 4 demonstrates that larger values of modularity, greater , lead to higher average fitness values for faster rates of environmental change, smaller . The advantage of greater modularity persists to larger for greater magnitudes of environmental change, larger . In other words, modularity leads to greater average fitness values either for greater frequencies of environmental change, , or greater magnitudes of environmental change, .
It has been argued that an approximate measure of the environmental pressure is given by the product of the magnitude and frequency of environmental change [22]. If this is the case, then the curves in Fig. 4ab as a function of for different values of should collapse to a single curve as a function of . As shown in Fig. 4c, this is approximately true for the three cases , , and .
5 Application of Theory to Influenza Evolution Data
We here apply our theory to the evolution of the influenza virus. Influenza is an RNA virus of the Orthomyxoviridae family. The 11 proteins of the virus are encoded by 8 gene segments. Reassortment of these gene segments is common [23, 24, 25]. In addition, there is a constant source of genetic diveristy, as most human influenza viruses arise from birds, mix in pigs, with a select few transmitted to humans [23, 24, 25, 26]. We model a simplification of this complex coevolutionary dynamics with the theory presented here. We consider modules, with mutations in the genetic material encoding them leading to an effective mutation rate at the coarse-grained length scale. We do not consider individual amino acids, but rather a coarse-grained reprsentation the viral protein material. The virus is under strong selective pressure to adapt to the human host, having most often arisn in birds and trasmitted through swine. The virus is also under strong pressure from the human immune system. The virus evolves in response to this pressure, thereby increasing its fitness. The increase in fitness was estimated by tracking the increase in frequency of each viral strain, as observed in the public sequence databases: , where is the fitness of clade at time , is the frequency of clade among all clades observed at time , and is the frequency at predicted by a model that includes a description of the mutational processes [27]. Here “clade” is a term for the quasispecies of closely-related influenza sequences at time . We use these approximate fitness values, estimated from observed HA sequence patterns and an approximate point mutation model of evolution, for comparison to the present model.
Influenza evolves within a cluster of closely-related sequences for 3–5 years and then jumps to a new cluster [28, 29, 30]. Indeed, the fitness flux data over 17 years [27] shows a pattern of discontinuous changes every 3–5 years. Often these jumps are related to influx of genetic material from swine [23, 24, 25, 26]. By clustering the strains, the clusters and the transitions between them can be identified: the flu strain evolved from Wuhan/359/95 to Sydney/5/97 at 1996-1997, Panama/2007/1999 to Fujian/411/2002 at 2001-2002, California/7/2004 to Wisconsin/67/2005 at 2006-2007, Brisbane/10/2007 to BritishColumbia/RV1222/09 at 2009-2010 [30]. These cluster transitions correspond to the discontinuous jumps in the fitness flux evolution and discontinuous changes in the sequences. Our theory represents the evolution within one of these clusters, considering reassortment only among human viruses. Thus, we predict the evolution of the fitness during each of these periods. There are 4 periods within the time frame 1993–2009. Figure 5 shows the measured fitness data [27], averaged over these four time periods.
We scaled Eq. (1) by to fit the observed data. The predictions from Eq. (3) are shown in Fig. 5. We find and fit the observed data well. We assume the overall rate of evolution is equally contributed to by mutation and horizontal gene transfer. The average observed substitution rate in the 100aa epitope region of the HA protein is 5 amino acids per year [30, 27]. We interpret this result in our coarse-grained model to imply and .
The value of required to fit the non-modular model to the data is 25% greater than the value required to fit the modular model to the data. That is, approximately 25% of the observed rate of fitness increase of the virus could be ascribed to a modular viral fitness landscape. Thus, to achieve the observed rate of evolution, the virus may either have evolved modularity , or the virus may have evolved a 25% increase in its replication rate by other evolutionary mechanisms. Given the modular structure of the epitopes on the haemagglutinin protein of the virus, the modular nature of the viral segments, and the modular nature of naive, B cell, and T cell immune responses we suggest that influenza has likely evolved a modular fitness landscape.
6 Generalization to Investigate the Effect of Landscape Ruggedness
We here generalize Eq. (1) to -spin interactions, letters in the alphabet from which the sequences are constructed, and what is known as the GNK random matrix form of interactions [31]. These generalizations allow us to investigate the effect of landscape ruggedness on the rate of evolution.
6.1 Generalization to the -spin SK Model
We first generalize the SK model to interactions among spins, which we term the SK model. The SK landscape is more rugged for increasing . Thus, we might expect modularity to play a more important role for the models with larger . The generalized fitness is written as
| (8) |
The and tensors are symmetric, that is, and , where is any permutation of . The probability of a connection is inside the block, , and outside the blocks. The connections are defined as
| (9) |
Since , it follows that , and .
Increasing the value of makes the landscape more rugged, and so it is more difficult for system to reach a given value of the fitness in a finite time. Thus, modularity is expected to play a more significant role in giving the system an evolutionary advantage. Specifically we expect that the effect of modularity will show up at shorter times for larger . As shown in Appendix B, we find
| (10) | |||||
The modular terms increase faster with than the non-modular terms, so the dependence on modularity of evolution is more significant with bigger . Figure 6 shows the average fitness curves for the -spin interaction. Due to the normalization of the values, all fitness curves have the same slope at , i.e. the same values of . However, increasing leads to slower rates of fitness increase at finite time, especially for the case. At finite time, for large values of , the evolutionary advantage of larger is more pronounced. That is, modularity help the sequences to evolve more efficiently.
We also calculated the average fitness for the initial condition of all sequences identical. As discussed above, many-spin effects make the landscape more rugged for larger . We seek to understand this effect quantitatively for the case of same initial sequences as well. As shown in Appendix B, the Taylor expansion results are
6.2 Generalization to the Planar Potts Model
We here generalize the alphabet from two-states, , to states, with a planar Potts model [32] of the fitness. The model is often justified as a projection of the nucleic acid alphabet onto purines and pyrimidines. Thus, is a relevant generalization. Additional corresponds to the amino acid alphabet. The alphabet size can affect the evolutionary phase diagram [33], so is a relevant order parameter. In the planar Potts model, each vector spin takes on equidistant angles, and the angle between two is defined by . The fitness is
| (12) |
The directions of a spin are evenly spaced in the plane, so when the spin points to directions, the angle between two spins is , where can be , , …, .
The evolutionary dynamics in the planar Potts model is distinct from that in the SK model. As shown in Appendix B,
| (13) | |||||
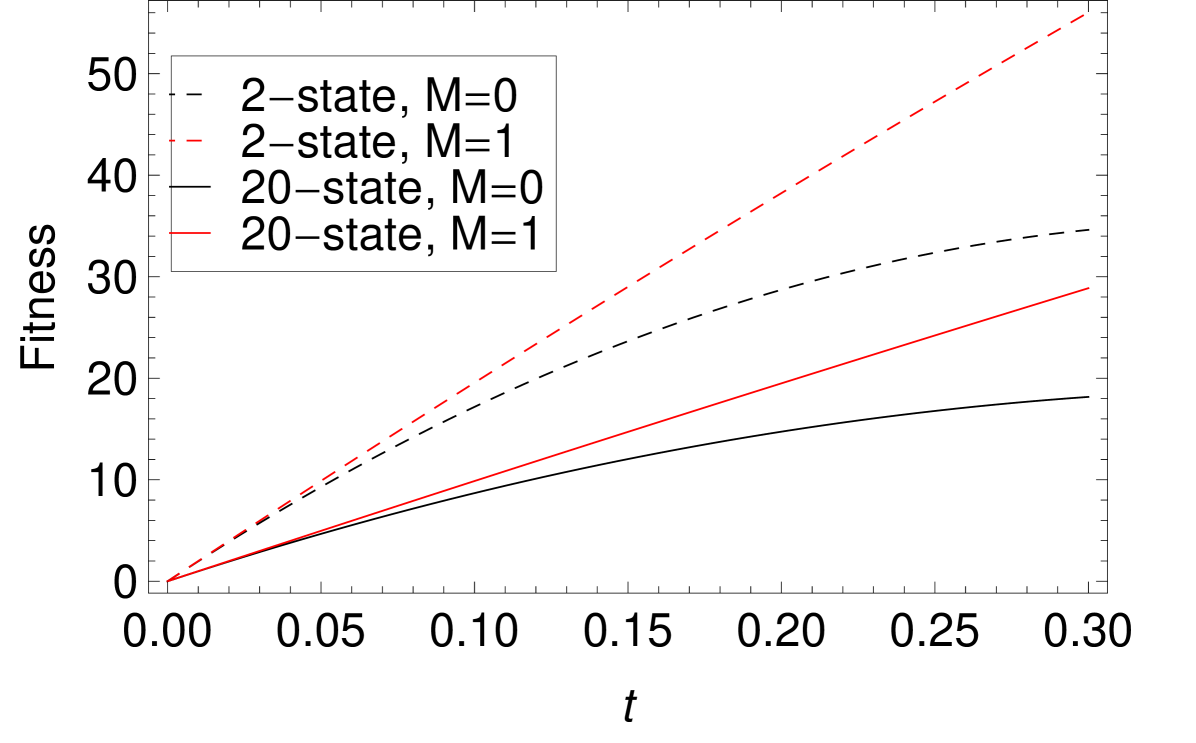
Figure 7 displays results for two values of . Increasing does increase the landscape ruggedness in the planar Potts model. There is an evolutionary speedup provided by modularity. The dependence, however, is not as dramatic as in the SK model.
6.3 Generalization to the GNK Model
A model related to the SK form is the GNK model, a simple form of which is
| (14) |
where the matrix is a symmetric matrix with random Gaussian entries, and the matrix is the same as that in Eq. (1). Other than the condition of symmetry, the entries in the matrices are independently drawn from a Gaussian distribution of zero mean and unit variance in each matrix and for different . Thus, other than the condition , the values are independent for different , , , or . This form is generalized to a -spin, -state form as
| (15) |
where can take one of the values.
For the GNK model, as shown in Appendix B, -spin -state result is
| (16) | |||||
As with previous models, modularity increases the rate of evolution.
7 Conclusion
The modular spin glass model captures several important aspects of biological evolution: finite population, rugged fitness landscape, modular correlations in the interactions, and horizontal gene transfer. We showed in both numerical simulation and analytical calculations that a modular landscape allows the system to evolve higher fitness values for times . Using this theory to analyze fitness data extracted from influenza virus evolution, we find that approximately 25% of the observed rate of fitness increase of the virus could be ascribed to a modular viral landscape. This result is consistent with the success of the modular theory of viral immune recognition, termed the theory, over the non-modular theory, termed [29]. The former correlates with human influenza vaccine effectiveness with , whereas the latter correlates with . The model, in general, analytically demonstrates a selective pressure for the prevalence of modularity in biology. The present model may be useful for understanding the influence of modularity on other evolving biological systems, for example the HIV virus or immune system cells.
Acknowledgments
This research was supported by the US National Institutes of Health under grant 1 R01 GM 100468–01. JMP was also supported by the National Research Foundation of Korea Grant (NRF-2013R1A1A2006983).
8 Appendix A: The Requirement that Fitness be Non-Negative
8.1 The SK Model
The normalization of the coupling in Eq. (1), the , affects the maximum and minimum possible values of the term. We require that the average energy per site of the sequence be finite when , i.e. that is on the order of . For the -spin, -state interaction, the Wigner semicircle law [34] shows that a rank- random symmetric matrix with has a minimum eigenvalue . Thus, if we consider the in Eq. (1) to be normalized as , the shift in Eq. (1) guarantees that . So after considering the connection matrix , we choose and .
For the SK case, we first assume that is not symmetric, i.e. with permutations of the same labels are drawn independently. We will consider the symmetrization afterward. We define
| (17) |
And for any
| (18) |
So,
| (19) | |||||
In the last step we symmetrize the matrix so that we can apply the Wigner semicircle law. From the semicircle law, if we want the minimum of the -spin interaction to be , we need for every . We, thus, find
| (20) |
So for asymmetric . We symmetrize the
| (21) |
to find
| (22) |
The Wigner approach to calculate the minimal possible value of is overly conservative, because in this approach all possible real vectors, are considered, whereas in our application . We here use extreme value theory to take this constraint into account. We use the -spin interaction to exemplify the method. As the matrix is symmetric, its elements are not independent, so the terms in are not independent. We rewrite , noting the diagonal terms are zero, as
| (23) |
The terms in are independent. After taking into account the connection matrix, there are non-zero independent elements. As is either or , multiplying them does not change the distribution of each element, so the is the sum of Gaussian variables. We choose the variance of each element as , so , and is twice of this, so
| (24) |
There are different sequences, so there are different , which differ by a few terms instead of all terms, so they are not independent. We seek the smallest . Slepian’s lemma [35] shows that for Gaussian variables and with average , if , and for all and , then for any ,
| (25) |
Thus, since and have zero mean, the minimum of the less correlated variables is smaller than that of the more correlated ones. Thus, we still use extreme value theory to determine the minimum for the same number of independent variables with the same distribution, and we use this number as an estimate of a lower bound. When we add this estimated value to , Slepian’s lemma guarantees the non-negativity of the fitness. We will show shortly that this estimated value is quite near the true value. The extreme value theory calculation proceeds as follows:
| (26) |
where is the sample space size when the spin has 2 directions. From the symmetry of Gaussian distribution and , we find
| (27) | |||||
where is the error function. Since is large, we find
| (28) |
So
| (29) |
Numerical results show that the exact value is [36], quite close to the value in Eq. (29). In this way, for the SK interaction, a normalization of
| (30) |
gives a minimum . This bound becomes exact as [37]. As becomes bigger, the landscape becomes more rugged, and the sequences becomes more uncorrelated. The correlation of general falls between that of and , so according to Slepian’s lemma, the exact minimum of any will fall between that of and that of . As and , we will neglect this factor, and set the shift to when , which guarantees .
Here we also calculate , which is used to obtain the Taylor expansion results in section 9. For a two-spin interaction we find
| (31) | |||||
We similarly calculate -spin results. We find that is always for all under this normalization scheme.
8.2 The Planar Potts Model
For the planar Potts model, we consider that is even, so the configuration space of is a subset of that of , and the minimum of is no bigger than that of Potts model, which is [36]. We consider two limiting cases to obtain the lower bound of the minimum. First, when , the planar Potts model becomes the XY model, which is defined in this case as , where is the angle between vector and , and these vectors can point to any direction in a two dimensional space. So the configuration space of the planar Potts model is a subset of that of the XY model, and the minimum of planar Potts model is no smaller than that of the XY model. Numerical results show that the ground state energy for the XY model is roughly [38].
Second, the vectors in the XY model are restricted in a two dimensional space. If we generalize it to an dimensional space, with , and , we obtain the vector model. When , the model becomes the spherical model, the exact minimum of can be calculated analytically as when [39]. Similarly, we see that the configuration space of the XY model is a subset of the spherical model, and the minimum of the XY model is no smaller than the spherical model. So considering the above two limiting cases, the minimum of the planar Potts model is no smaller than when . Thus, we set the shift as to guarantee that .
We still need to consider the effect of the connection matrix. We use extreme value theory. We consider that the matrix elements of are randomly chosen, so that becomes sum of Gaussian-like variables instead of variables, so the minimum is times that of the minimum without the connection matrix. To normalize the minimum back to , we finally choose .
We calculate for the planar Potts model. When , the average value of is , while when , the value is . Thus,
| (32) | |||||
8.3 The GNK Model
We use extreme value theory to discuss the minimum and normalization of the GNK model. When ,
| (33) |
so the distribution of the for the GNK model is the same as that of the SK model. The correlation induced by the dependence of on the is, however, different in these two models. Here we follow the method of [40]. We have two sets of variables with the same set size, one is the spin interaction GNK , denoted as , and normalized so that , and the other is a set of Gaussian variables , and , . There are variables in each set, and we know that is times the maximum of the same number of uncorrelated Gaussian variables with the same variance and average [41], so from Eq. (29) . We define a new variable, , where , and we define . So is the probability that the maximum of is smaller than , while is the probability that the maximum of is smaller than . We seek to make , so that , so we seek for . It is shown that on page 71 of [40]:
| (34) |
where is the joint distribution of . For example, the term corresponding to , is , and , as the probability that all other variables is smaller than the maximum we are looking for is approximately . for all , and is the same for pairs with the same, so we group the pairs according to their Hamming distance, and rewrite Eq. (34) as
| (35) |
where is any sequence satisfying . As the system is totally random, it does not matter what sequence is, and we can set it as the first sequence and rewrite it as
| (36) |
where is any sequence satisfying . As only the integral depends on , we can write it as
| (37) |
when , we find
| (38) |
We first calculate . The correlation is
| (39) | |||||
We initially neglect the , as among the different kinds of , there are remaining unchanged, if , otherwise it is . Now considering the connection matrix, if , the connections are randomly chosen, so we expect that the result does not change. If , all connections fall into small modules, and again the changed spins are randomly distributed in each module, so out of the spins in each module, spins have changed. Thus, in each module, out of the spins, remain unchanged, so . For general , for a given , consider that spins fall out of the module, and will fall in the module. Among the possibilities outside of the module, remain unchanged, so the ratio of unchanged over all is is . For the possible choices inside the module, is unchanged, so the ratio is . So the probability that a is unchanged is . So for all , . Also, , so
| (40) |
The integral part simplifies as
We write the joint distribution of the Gaussian variables as
| (41) |
where is the covariance matrix, and is the determinant of . For our particular case, where there are only two variables with unit variance and zero average, the covariance matrix is given by
| (42) |
where . So and
| (43) |
It follows that
| (44) |
When both variables equal , it is . So putting everything into Eq. (41), the probability that both variables are is . We calculate .
Note that , so Eq. (40) is a self-consistent equation
| (45) |
The solution for , , and is , so . With , , and , , the value of near that for infinite . We also applied this method to the SK model. For , , the correlation is . So
| (46) |
When , , and we find , and , quite near the numerical result . This self-consistent method, thus, is fairly accurate.
For a given , larger lead to smaller using Slepian’s lemma Eq. (25). To prove this, first assume and are GNK model variables with . For any sequence , we group all other sequences according to the Hamming distance between them, so the group with Hamming distance contains variables. Assume has a Hamming distance from , so , . As , , so . As the is chosen randomly, the correlation between any pair of is smaller than that of the corresponding pair of , and according to Slepian’s lemma, the minimum of is smaller. Thus, it is proved that larger lead to smaller minima.
We calculate the results for of different . Shown in Table 1 is the result of , and . We see that decreases monotonically for increasing in this range.
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.219 | 0.17 | 0.15 | 0.129 | 0.116 | 0.107 | 0.100 | 0.094 | 0.089 | 0.085 | 0.082 | 0.079 | 0.076 | 0.074 | 0.072 | 0.070 | 0.068 | 0.067 |
We also calculated for large and , Table 2.
| 40 | 80 | 160 | 320 | 640 | 1280 | 2560 | 5120 | 10240 | |
|---|---|---|---|---|---|---|---|---|---|
| 0.049 | 0.038 | 0.031 | 0.026 | 0.022 | 0.019 | 0.016 | 0.014 | 0.013 |
It is apparent that all results for fall below , so the minimum of GNK model will fall between and for any and . As , we neglect this factor, i.e. conservatively assure that the fitness is positive, not merely non-negative. When , the minimum will be .
In summary, for all models discussed in this appendix, a shift of assures that the fitness is positive.
9 Appendix B: Calculation of Taylor Series Expansion for Average Fitness
We here describe how the coefficients in the Taylor series expansion of are calculated.
9.1 Organizing the Terms in the Taylor Series Expansion
We define , the average fitness of an individual of configuration . The first order result of Eq. (LABEL:2) is a linear combination of , which can be divided into three parts: part, from natural selection; part, from mutation; part, from horizontal gene transfer. In a compact form
| (47) |
and
| (48) |
In this way we obtain the form of higher order results, for example, the second order result can be expressed as
| (49) |
which is divided into terms:
| (50) | |||||
Note that , , are not commutative with each other (but of course commutative with itself), for example , since these two correspond to different evolutionary processes of the population. As , we can divide into nine terms, and name them , , , , , , , , . Also note that the naming is in a sense inverted, for example term, which comes from , actually represents the process that a mutation happens before natural selection.
In this way, the third order term consists of terms, and the -th order term consists terms in general. Each term can be named according to the order of operators involved. Below we will discuss how to compute each part of an -th order term. First we discuss eliminating terms that do not contribute, then we calculate terms for different models. We will start with the simplest -spin, -state model, and then discuss SK model, planar Potts model, and GNK model.
9.2 Identification of the Terms that Vanish
The number of terms increases exponentially with order, so we would like to eliminate some terms that vanish from some considerations. We discuss this according to the initial conditions, that is, random initial sequences and identical initial sequences.
For both initial conditions, a term that does not contain natural selection processes vanishes. The reason is that the Taylor expansion results correspond to change of fitness, so it has a factor of proportional to some linear combinations of , which is in turn some linear combinations of or . For terms that only contain mutations and horizontal gene transfers, the result is proportional to linear combinations of or , which vanish when we take an average. Only when there is natural selection can or be multiplied into second order or higher even order forms, which are non-zero when averaged. So only terms containing natural selections can contribute.
For the random initial sequences, the modular term appears in second order. From the principle above, the first order terms and , and the second order terms , , and are all . In addition, for the term, first an individual mutates then a natural selection happens. As the initial system is totally random, the mutation in the first step does not change the system, so this term is . Then, up to second order, there are five non-zero terms: , , , and .
For the same initial sequences, the modular terms appear in the fourth order, meaning that we need to calculate terms. Fortunately, the initial conditions are so special that we can greatly reduce our burden. As discussed above, terms not containing are automatically zero, so terms can be non-zero. In addition, if a natural selection or horizontal gene transfer process happens first without a mutation, then nothing is changed as every sequence is initially the same, making this term zero. So any term not ending with is zero, leaving behind non-zero terms: first order term, second order term , third order terms satisfying three-letter-array ending with and containing a in the first two letters and fourth order terms satisfying four-letter-array ending with and containing a in the first three letters. Additionally, for a term starting with (the last process is horizontal gene transfer), if there were fewer than 2 mutational processes before horizontal gene transfer, then the term is zero. The reason is that if only one mutation happened, all mutated individuals are the same, so a horizontal gene transfer changes the population only when it involves a mutated individual and an unmutated individual. And for a change to occur, the horizontal gene transfer must transfer the part of the sequence that is mutated. The probability of the unmutated one becoming a mutated one through horizontal gene transfer is the same as the mutated one becoming an unmutated one, and the change of fitness of these two processes cancel, so the contribution is zero. In this way, is zero, and , and is zero. An additional two terms, and are found to be zero after calculation, so there is one non-zero second order term, four non-zero third order terms, and fourteen non-zero fourth order terms, totaling nineteen non-zero terms.
9.3 The SK Model with Random Initial Sequences
To illustrate the calculation for the random initial sequences, we use term as an example.
| (51) |
So
| (52) | |||||
The last equation holds because average over first order terms of is always zero. As the initial sequences are totally random, when we pick out a particular individual , we expect that from the view of , the other individuals are totally random, so their is uncorrelated with that of . As , .
So,
| (53) | |||||
and,
| (54) |
Similarly, we can obtain,
| (55) |
and
| (56) |
9.4 The SK model with Identical Initial Sequences
To illustrate how to calculate the terms for identical initial sequences we use term as an example. We assume the initial sequences are , and the initial state is . takes the state to
| (57) |
A subsequent takes the state to
| (58) | |||||
So after two operations, , and , and we find
| (59) | |||||
in which
| (60) | |||||
if we average over , we find
| (61) | |||||
So
| (62) |
and
| (63) |
Similarly, we find
| (64) |
and
| (65) | |||||
9.5 The SK Interaction
For the -spin interaction, the relationship between different is quite similar to the case, and the principles eliminating zero terms are the same. Moreover, the physical processes corresponding to each Taylor expansion term remain the same, so we just need to change the form of the . For example, to obtain term of same initial conditions, Eq. (59) still holds, but we need to use the new to calculate . For the new form,
| (66) | |||||
So . In this way, we can obtain for -spin interaction random initial sequences,
| (67) |
and
| (68) |
Also, we find for initial conditions of identical sequences,
| (69) |
and
| (70) | |||||
9.6 The Planar Potts Model with Random Initial Sequences
The non-zero terms are still , , , and . As is changed, all terms will also change. In addition, the term has a mutational process, which depends on the number of directions a spin can have. We assume that after a mutation, a spin randomly chooses a different direction as before. Using methods similar to Eq. (52), we find . Considering the different directions, we find
| (71) | |||||
where is the same as if neither nor is mutated, otherwise has the same probability to be any allowed value other than . So we only need to consider the case when either or is mutated, and obtain an extra factor of from this,
| (72) | |||||
and
| (73) | |||||
Then,
| (74) | |||||
So
| (75) |
The other terms are
| (76) |
| (77) |
and
| (78) |
9.7 GNK Model Calculation
The processes corresponding to different terms are still the same, but for the GNK model, as the is quite different, the Taylor expansion results will change. For example, for two randomly chosen sequences and , their correlation will be non-zero. Instead, it will be
| (79) | |||||
where the factor comes from the fact that only when the states of all corresponding spins match can the correlations of be nonzero.
Similarly we calculate all terms and obtain
| (80) |
and
| (81) | |||||
10 Appendix C: Calculation of the Taylor Series Expansion for the Sequence Divergence
We here describe how the Taylor expansion series of sequence divergence Eq. (4) are calculated.
As the divergence is , it is determined by the changes to the sequences of the population, which can be tracked using Eq. (LABEL:2). The order of the terms corresponds to the number of processed involved, for example, second order terms involve two processes. Using conventions developed in section 9.1, we divide the terms according to what evolutionary processes it involves, for example, the term which is the result of a mutational process followed by a horizontal gene transfer is called , similar to the naming norm used in section 9.1. So
| (82) |
We use term as an example. From Eq. (51), after a natural selection process, one sequence is replaced by sequence . If it is replaced by itself, nothing is changed. Otherwise, as the initial sequences is totally random, the number of sites changed is on average , and the probability of this is . As in the whole population, only this sequence is changed, the divergence can be calculated as
| (83) | |||||
References
- [1] C. H. Waddington. Canalization of development and the inheritance of acquired characters. Nature, 150:563–565, 1942.
- [2] H. A. Simon. The architecture of complexity. Proc. Amer. Phil. Soc., 106:467–482, 1962.
- [3] L. H. Hartwell, J. J. Hopfield, S. Leibler, and A. W. Murray. From molecular to modular cell biology. Nature, 402:C47–C52, 1999.
- [4] R. Rojas. Neural Networks: A Systematic Introduction. Springer, New York, 1996. Ch 16.
- [5] E. Grohmann. Horizontal gene transfer between bacteria under natural conditions. In I Ahmad, F. Ahmad, and J. Pichtel, editors, Microbes and Microbial Technology, pages 163–187. Springer New York, 2011.
- [6] M. B. Gogarten, J. P. Gogarten, and L. Olendzenski, editors. Horizontal Gene Transfer: Genomes in Flux. Methods in Molecular Biology, Vol. 532. Humana Press, New York, 2009.
- [7] N. Chia and N. Goldenfeld. Statistical mechanics of horizontal gene transfer in evolutionary ecology. J. Stat. Phys., 142:1287–1301, 2011.
- [8] M. S. Breen et al. Epistasis as the primary factor in molecular evolution. Nature, 490:535–538, 2012.
- [9] J. Sun and M. W. Deem. Spontaneous emergence of modularity in a model of evolving individuals. Phys. Rev. Lett., 99:228107, 2007.
- [10] N. Kashtan, M. Parter, E. Dekel, A. E. Mayo, and U. Alon. Extinctions in heterogeneous environments and the evolution of modularity. Evolution, 63:1964–1975, 2009.
- [11] J.-M. Park and M. W. Deem. Schwinger boson formulation and solution of the Crow-Kimura and Eigen models of quasispecies theory. J. Stat. Phys., 125:975–1015, 2006.
- [12] E. Cohen, D. A. Kessler, and H. Levine. Recombination dramatically speeds up evolution of finite populations. Phys. Rev. Lett., 94:098102, 2005.
- [13] S. Goyal, D. J. Balick, E. R. Jerison, R. A. Neher, B. I. Shraiman, and M. M. Desai. Dynamic mutation–selection balance as an evolutionary attractor. Genetics, 191:1309–1319, 2012.
- [14] B. Derrida and L. Peliti. Evolution in a flat fitness landscape. Bull. Math. Biol., 53:355–382, 1991.
- [15] G. Bianconi, D. Fichera, S. Franz, and L. Peliti. Modeling microevolution in a changing environment: the evolving quasispecies and the diluted champion process. J. Stat. Mech., 2011:P08022, 2011.
- [16] J.-M. Park and M. W. Deem. Phase diagrams of quasispecies theory with recombination and horizontal gene transfer. Phys. Rev. Lett., 98:058101, 2007.
- [17] E. T. Munoz, J.-M. Park, and M. W. Deem. Quasispecies theory for horizontal gene transfer and recombination. Phys. Rev. E, 78:061921, 2008.
- [18] Z. Avetisyan and D. B. Saakian. Recombination in one- and two-dimensional fitness landscapes. Phys. Rev. E, 81:051916, 2010.
- [19] D. B. Saakian. Evolutionary advantage via common action of recombination and neutrality. Phys. Rev. E, 88:052717, 2013.
- [20] D. B. Saakian, Z. Kirakosyan, and C. K. Hu. Biological evolution in a multidimensional fitness landscape. Phys. Rev. E, 86:031920, 2012.
- [21] V. S. Dotsenko. Fractal dynamics of spin glasses. J. Phys. C: Solid State Phys., 18:6023–6031, 1985.
- [22] J.-M. Park, L. R. Niestemski, and M. W. Deem. Quasispecies theory for evolution of modularity. page DOI: 10.1103/PhysRevE.00.002700, 2014. arXiv:1211.5646.
- [23] G. J. D. Smith, D. Vijaykrishna, J. Bahl, S. J. Lycett, M. Worobey, O. G. Pybus, S. K. Ma, C. L. Cheung, J. Raghwani, S. Bhatt, J. S. Malik Peiris, Y. Guan, and A. Rambaut. Origins and evolutionary genomics of the 2009 swine-origin h1n1 influenza a epidemic. Nature, 459:1122–1125, 2009.
- [24] A. Rambaut, O. G. Pybus, M. I. Nelson, C. Viboud, J. K. Taubenberger, and E. C. Holmes. The genomic and epidemiological dynamics of human influenza a virus. Nature, 453:615–619, 2008.
- [25] N. Marshall, L. Priyamvada, Z. Ende, J. Steel, and A. C. Lowen. Influenza virus reassortment occurs with high frequency in the absence of segment mismatch. PLoS Pathog., 9:e1003421, 2013.
- [26] V. Trifonov, H. Khiabanian, and Raul Rabadan. Geographic dependence, surveillance, and origins of the 2009 influenza a (h1n1) virus. N. Engl. J. Med., 361:115–119, 2009.
- [27] M. Łuksza and M. Lässig. A predictive fitness model for influenza. Nature, 507:57–61, 2014.
- [28] D. J. Smith, A. S. Lapedes, J. C. de Jong, T. M. Bestebroer, G. F. Rimmelzwaan, A. D. M. E. Osterhaus, and R. A. M. Fouchier. Mapping the antigenic and genetic evolution of influenza virus. Science, 305:371–376, 2004.
- [29] V. Gupta, D. J. Earl, and M. W. Deem. Quantifying influenza vaccine efficacy and antigenic distance. Vaccine, 24:3881–3888, 2006.
- [30] J. He and M. W. Deem. Low-dimensional clustering detects incipient dominant influenza strain clusters. PEDS, 23:935–946, 2010.
- [31] M. W. Deem and H.-Y. Lee. Sequence space localization in the immune system response to vaccination and disease. Phys. Rev. Lett., 91:068101, 2003.
- [32] F. Y. Wu. The potts model. Rev. Mod. Phys., 54:235–268, 1982.
- [33] E. T. Munoz, J.-M. Park, and M. W. Deem. Solution of the crow-kimura and eigen models for alphabets of arbitrary size by schwinger spin coherent states. J. Stat. Phys, 135:429–465, 2009.
- [34] P. E. Wigner. On the distribution of the roots of certain symmetric matrices. Annals of Mathematics, pages 325–327, 1958.
- [35] W. V. Li and Q.-M. Shao. Gaussian processes: inequalities, small ball probabilities and applications. Stochastic processes: theory and methods, 19:533–597, 2001.
- [36] S.-Y. Kim, S.-J. Lee, and J. Lee. Ground-state energy and energy landscape of the sherrington-kirkpatrick spin glass. Phys. Rev. B, 76:184412, 2007.
- [37] V. M. de Oliveira and J. F. Fontanari. Landscape statistics of the -spin ising model. Journal of Physics A: Mathematical and General, 30:8445–8457, 1997.
- [38] G. S. Grest and C. M. Soukoulis. Ground-state properties of the infinite-range vector spin-glasses. Physical Review B, 28:2886–2889, 1983.
- [39] J. M. Kosterlitz, D. J. Thouless, and R. C. Jones. Spherical model of a spin-glass. Phys. Rev. Lett., 36:1217–1220, 1976.
- [40] G. Pisier. The volume of convex bodies and Banach space geometry, volume 94. Cambridge University Press, New York, 1999.
- [41] D. B. Owen and G. P. Steck. Moments of order statistics from the equicorrelated multivariate normal distribution. The Annals of Mathematical Statistics, 33:1286–1291, 1962.