MonarchAttention: Zero-Shot Conversion to Fast, Hardware-Aware Structured Attention

We use the phrase “structured matrices” to mean those that admit sub-quadratic storage and matrix-vector multiplication, such as low-rank or sparse matrices. There are many useful classes of structured matrices, such as those with low displacement rank (Kailath et al., 1979), which includes Toeplitz, Hankel, Vandermonde, Cauchy matrices (Pan, 2001); orthogonal polynomial transforms (Chihara, 2014), which includes discrete Fourier/cosine and Hadamard transforms; butterfly factorizations (Dao et al., 2019), which implement fast matrix-vector multiplication via a recursive divide-and-conquer algorithm similar to that of fast Fourier transforms (FFTs); and Monarch matrices, an expressive family of structured matrices (generalizing butterfly matrices and thereby many fast transforms) that overcome unfavorable memory access patterns typical to FFT-like algorithms by implementing matrix products via batched dense matrix multiplications (also called matmuls) on fast tensor cores found in modern GPUs.

Nearly all approaches to sub-quadratic attention approximate the attention matrix by a structured matrix, specifically low-rank and/or sparse.

• $\bullet$

  Low-Rank. Motivated by Johnson-Lindenstrauss embeddings, Wang et al. (2020) propose sketching the key and value matrices along the sequence dimension via learnable projections. Katharopoulos et al. (2020) introduce linear attention, where the exponential kernel is approximated via inner products of queries and keys lifted via some feature map. Several follow-up works proposed various feature maps, such as the exponential linear unit (ELU) (Katharopoulos et al., 2020), random positive features (Choromanski et al., 2021), rectified linear unit (ReLU) with cosine reweighting (Qin et al., 2022), and learnable single-layer multi-layer perceptrons (MLPs) (Zhang et al., 2024). Xiong et al. (2021) use the Nyström method for computing low-rank approximations by sampling rows and columns.

• $\bullet$

  Sparse. Child et al. (2019) introduce sparsity by applying fixed, structured sparse masks on the attention matrix. In particular, Chen et al. (2022) propose a particular block butterfly matrix for the sparse mask, which is more hardware-friendly at the cost of reduced expressiveness. Those that do not enforce a structure on the sparsity pattern include Kitaev et al. (2020); Daras et al. (2020) where they utilize locality-sensitive hashing (LSH) on shared query/key vectors to only compute attention within clusters of similar tokens.

• $\bullet$

  Low-Rank + Sparse. Inspired by robust PCA, Chen et al. (2021) decompose the attention matrix into a sum of two matrices: an unstructured sparse component using LSH and a low-rank component that is constructed via linear attention. Han et al. (2024) propose to subsample columns of the non-normalized attention matrix based on row norms of the value matrix, while estimating the softmax normalization factors from a few large elements via LSH.

We note that there are significant drawbacks to the approaches described above. Pure low-rank methods are often fast and hardware-friendly, but are not typically suitable as drop-in replacements for attention in pre-trained transformers due to the prevalence of “strongly diagonal”, high-rank attention matrices where attention weights are concentrated locally in a sequence. Making up for this with a fixed sparsity pattern does not allow for data-dependent support of the attention matrix, necessary for zero-shot conversion. Finally, sparsity/LSH-based approaches that do not have a fixed sparsity pattern, improve on accuracy over low-rank approximations but suffer from significant overhead due to GPU incompatibility. MonarchAttention, on the other hand, achieves the best of both worlds: it is fast and hardware-friendly due to utilization of tensor cores for batched matmuls, while computing highly accurate approximations to the extent that it can directly replace softmax attention with no additional training.
 
We conclude this section by discussing closely related works. Dao et al. (2022b) propose FlashAttention, an IO-aware streaming algorithm for computing exact softmax attention. We show in Section 3 that each step of MonarchAttention can be written as a FlashAttention-like computation, allowing for similar IO savings to FlashAttention – in fact, we demonstrate that MonarchAttention achieves a strictly better worst-case IO complexity compared to FlashAttention. We also note that Dao et al. (2022b) propose to further accelerate FlashAttention using block butterfly attention masks, so MonarchAttention can be viewed as a generalization of block-sparse FlashAttention to more general Monarch matrices. Finally, MonarchAttention is closely related to Monarch Mixer (Fu et al., 2023), a mixer-type architecture (Tolstikhin et al., 2021) that utilizes Monarch instead of dense matrices for token and channel mixing. MonarchAttention also uses Monarch matrices for mixing tokens – however, it is based on the attention operation which is data-dependent, unlike Monarch Mixer.

In Section 2, we discuss preliminaries on (softmax) attention, and Monarch matrices. In Section 3, we describe the MonarchAttention algorithm and implementation. In Section 4, we evaluate MonarchAttention in a variety of settings for zero-shot conversion to sub-quadratic attention and benchmark its implementation. In Section 5, we discuss limitations and future directions.

We use $[N]$ to denote the index set $\{1,2,\dots,N\}$. We use $\Delta^{N}$ to denote the $(N-1)$ dimensional unit simplex, given by $\Delta^{N}=\{\bm{a}\in\mathbb{R}^{N}:\bm{a}\succeq 0,\langle\bm{1}_{N},\bm{a}\rangle=1\}$. We denote the $m\times m$ identity matrix by $\bm{I}_{m}$. We use the notation $\bm{A}_{ijk}$ to denote an element of a 3-way tensor, and $\bm{A}_{i,:,k}$ to denote a slice. We use $\delta_{kl}$ to denote the Kronecker delta that is $1$ if $k=l$ and otherwise 0.

The softmax function $\mathbb{R}^{N}\rightarrow\Delta^{N}$ maps $N$ real numbers to the $(N-1)$-dimensional unit simplex, and is defined as

An alternative definition (Blondel et al., 2019) is given by the following variational form:

where $H(\bm{a})=-\sum_{i}\bm{a}_{i}\log\bm{a}_{i}$ is Shannon entropy. See Appendix A for equivalence of (1) and (2).

Given query, key, value matrices $\bm{Q},\bm{K},\bm{V}\in\mathbb{R}^{N\times d}$, where $N$ is the sequence length and $d$ is the head dimension, a single head of standard softmax attention¹¹1Typically, the $\bm{Q}\bm{K}^{\top}$ matrix is scaled by a factor of $d^{-1/2}$, but this can be absorbed into $\bm{Q}$. computes

where the softmax function is applied across rows. The computational complexity of attention is $\Theta(N^{2}d)$ for each forward pass, because the matrices $\bm{Q},\bm{K},\bm{V}$ are data-dependent.

Given $N=m\times b$ for integers $m,b$, we define a block rank-one matrix $\bm{B}\in\mathbb{R}^{N\times N}$ as

for some $\bm{L}_{jk}\in\mathbb{R}^{m},\bm{R}_{kj}\in\mathbb{R}^{b}$ for $j\in[b]$ and $k\in[m]$. It follows that

where $\bm{L}_{j}\in\mathbb{R}^{m\times m}$ for $j\in[b]$ and $\bm{R}_{k}\in\mathbb{R}^{b\times b}$ for $k\in[m]$, and $\bm{P}\in\mathbb{R}^{N\times N}$ is a “transpose”²²2$\bm{P}\bm{x}$ corresponds to row-major reshaping $\bm{x}\in\mathbb{R}^{N}$ to $\mathbb{R}^{m\times b}$, transposing to $\mathbb{R}^{b\times m}$, then row-major flattening back to $\mathbb{R}^{N}$. See Appendix B for an example. permutation matrix whose $(i+1)$th row is given by $\bm{e}_{\sigma(i)+1}$ where

Given the above, a Monarch matrix $\bm{M}\in\mathbb{R}^{N\times N}$ is given by $\bm{M}=\bm{P}^{\top}\bm{B}$ – in other words, it is a row-permuted block rank-one matrix. When $m=b=\sqrt{N}$, storing such a matrix requires only $\Theta(N\sqrt{N})$ space, while matrix multiplication (matmul) with a matrix $\bm{V}\in\mathbb{R}^{N\times d}$ can be computed efficiently in $\Theta(N\sqrt{N}d)$ operations (as opposed to $\Theta(N^{2}d)$ for dense matrices) with batched matmuls and transposes:

for $i,j\in[b],k,l\in[m]$. A useful characterization of $\bm{M}$ is in block form:

where $\bm{M}_{lk}\in\mathbb{R}^{b\times b},\;[\bm{M}_{lk}]_{ji}=\bm{L}_{jkl}\bm{R}_{kji},\;\forall i,j\in[b],k,l\in[m]$.

First, from (2) we can write

where $\Delta^{N\times N}$ denotes a matrix whose rows lie on $\Delta^{N}$, and $H(\bm{A})=-\sum_{i,j}\bm{A}_{ij}\log\bm{A}_{ij}$. For a dense matrix $\bm{A}$, computing $f(\bm{A};\bm{Q},\bm{K})$ requires $\Theta(N^{2}d)$ operations, which is the same as computing $\sigma(\bm{Q}\bm{K}^{\top})$ directly. However, we are interested in the case where $\bm{A}$ is a Monarch matrix $\bm{M}=\bm{P}^{\top}\bm{B}$:

where $\widetilde{\bm{Q}}=\bm{P}\bm{Q}$, and $\widetilde{\bm{Q}}_{j}\in\mathbb{R}^{m\times d},\bm{K}_{k}\in\mathbb{R}^{b\times d}$ are the $j$th and $k$th block of rows of $\widetilde{\bm{Q}},\bm{K}$ respectively. Then, for each $j\in[b],k\in[m]$ we evaluate $f$ on the rank-one matrix $\bm{B}_{jk}=\bm{L}_{jk}\bm{R}_{kj}^{\top}$:

Thus, for each $j\in[b],k\in[m]$ we only need $\Theta((m+b)d)$ operations to compute $f(\bm{B}_{jk};\widetilde{\bm{Q}}_{j},\bm{K}_{k})$ due to $\widetilde{\bm{Q}}_{j}^{\top}\bm{L}_{jk}$ and $\bm{K}_{k}^{\top}\bm{R}_{kj}$. We emphasize that the rank-one structure implies separability of the entropy term, meaning we can compute the entropy on $\bm{L}_{jk}$ and $\bm{R}_{kj}$ individually and avoid the need to materialize $\bm{B}_{jk}$, which would incur $\Theta(mb)$ cost as opposed to $\Theta(m+b)$. Since there are $m\cdot b$ many $\bm{B}_{jk}$ matrices, we have in total $\Theta((m^{2}b+b^{2}m)d)$ operations to compute $f(\bm{M};\bm{Q},\bm{K})$, which for $m=b=\sqrt{N}$ is $\Theta(N\sqrt{N}d)$, improving on the dense computation by a factor of $\sqrt{N}$.

We will now explain the alternating maximization approach for optimizing $f$. When $\bm{L}$ is fixed, the objective is concave in $\bm{R}$, and vice-versa – therefore, we can derive closed form expressions via KKT conditions for $\bm{L}$ and $\bm{R}$ that maximize $f$ with one of $\bm{L}$ or $\bm{R}$ fixed, which will constitute a single update step. Evaluating (and therefore differentiating) $f$ w.r.t. $\bm{L}$ and $\bm{R}$ can be done in $\Theta(N\sqrt{N}d)$ time, which will be the same complexity as one of these steps. For $T$ steps, this will require $\Theta(TN\sqrt{N}d)$ computation; provided that $T=o(\sqrt{N})$, this will still be sub-quadratic. However, the constraint $\bm{M}\in\Delta^{N\times N}$ presents a challenge in its current form, since this requires materializing $\bm{M}$ to check that each entry is non-negative. Instead, we use the fact that

i.e., slices of $\bm{L},\bm{R}$ individually lying on the unit simplex is sufficient to enforce the constraint on $\bm{M}$. This is easily seen from (5) – obviously if $\bm{L}_{jkl},\bm{R}_{kji}\geq 0$, then $[\bm{M}_{lk}]_{ji}\geq 0$. Moreover, this also enforces the sum-to-one constraint, as rows of $\bm{M}$ sum as

We now present the updates for $\bm{L},\bm{R}$. Initializing $\bm{L}_{jkl}^{(0)}=\delta_{kl}$ as block identity, we have

for $t\in[T]$, where $\operatorname{softmax}_{k},\operatorname{softmax}_{i}$ are applied along $k$ and $i$ index dimensions respectively, and

where $\overline{\bm{Q}}_{jl},\overline{\bm{K}}_{ki}\in\mathbb{R}^{d}$ are the $(b\cdot(l-1)+j)$th and $(b\cdot(k-1)+i)$th row of $\bm{Q}$ and $\bm{K}$ respectively. The full derivation is provided in Section C.1. After $T$ steps, we obtain the final Monarch approximation $\bm{M}^{(T)}\approx\sigma(\bm{Q}\bm{K}^{\top})$ with factors $\bm{L}^{(T)}$ and $\bm{R}^{(T)}$, from which we output $\bm{M}^{(T)}\bm{V}$ using (4). A naïve implementation of the full algorithm is provided in Section C.2. We discuss in Section C.3 how padding can be incorporated into MonarchAttention for when $N$ is not divisible by $b$.

To minimize data movement and memory usage on GPU, we do not materialize $\bm{L}$ or $\bm{R}$ in high-bandwidth memory (HBM). In addition to $\bm{Q},\bm{K},\bm{V},\bm{O}$, we only need to maintain states³³3The $\bm{\alpha}$ and $\bm{c}$ variables can share the same memory location as those corresponding to $\bm{R}$ can be derived from $\bm{L}$ (and vice-versa). $\bm{\alpha}_{R}^{(t)},\bm{\alpha}_{L}^{(t)},\bm{c}_{R}^{(t)},\bm{c}_{L}^{(t)}$ from (9) and (10), resulting in $\Theta(Nd)$ additional memory. All other intermediate values are only materialized in on-chip SRAM, fusing all operations between the $\bm{\alpha}$ (and similarly $\bm{c}$) variables. For instance, from the above update equations, the computation of $\bm{\alpha}_{L}^{(t)}$ from $\bm{\alpha}_{R}^{(t)}$ is given by

which can be seen as a batched attention computation, meaning we can implement a FlashAttention-like kernel to reduce IO between HBM and on-chip SRAM. However, several aspects of this computation make it particularly IO-efficient. Besides the fact that $\overline{\bm{K}}$ acts as both the $\bm{K}$ and $\bm{V}$ matrices in (3), the effective sequence length is $\sqrt{N}$. This eliminates the need for tiling along the sequence length, except for very long sequences having $\Theta(\sqrt{N}d)>S$, where $S$ is the size of on-chip SRAM. This means that we have an optimal IO complexity of $\Theta(Nd)$ for a single call, as opposed to the worst-case $O(N^{2}d^{2}/S)$ complexity of FlashAttention. The computation of $\bm{\alpha}_{R}^{(t)}$ from $\bm{\alpha}_{L}^{(t)}$, as well as the Monarch matmul, can be written in a similar fashion. Based on this, MonarchAttention not only achieves significant speed-up over FlashAttention for longer sequences, but also for shorter ones. Python-like code for MonarchAttention is given in Figure 4.

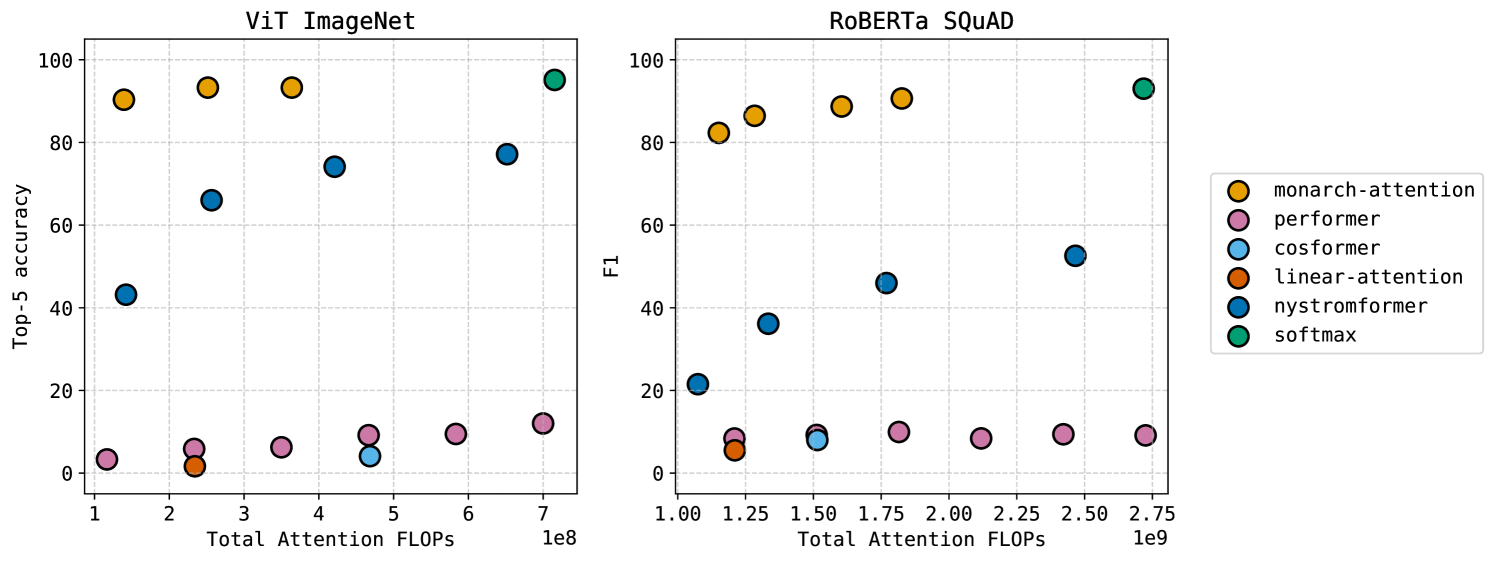
We convert all 12 attention layers, each having 12 heads with sequence length $N=197$ and head dimension $d=64$, of the 87M parameter ViT-B (Dosovitskiy et al., 2021) that has been pre-trained on ImageNet-21K (Deng et al., 2009) and fine-tuned on ImageNet-1K (Russakovsky et al., 2015) for image classification. To evaluate the performance at different FLOP counts, we vary the number of steps $T$ for MonarchAttention, and vary the rank for Performer and Nyströmformer; see Section D.2 for more details on the set-up. The results are shown in the left panel of Figure 2. MonarchAttention achieves significant improvement over other baselines – compared to the original softmax attention, MonarchAttention loses only 5% accuracy to reduce attention FLOPs by 80%, or matches the performance to reduce attention FLOPs by 50%.

We convert the initial 4 and final 4 layers of the 12 attention layers, each having 12 heads with sequence length $N=384$ and head dimension $d=64$, of the 125M parameter RoBERTa-B (Liu et al., 2019) that has been pre-trained on a large English corpus and fine-tuned on SQuAD1.1 (Rajpurkar et al., 2016) for question answering. As before, to evaluate the performance at different FLOP counts, we vary the block size $b$ for MonarchAttention, and vary the rank for Performer and Nyströmformer; see Section D.3 for more details on the set-up. The results are shown in the right panel of Figure 2. Once again, MonarchAttention achieves significant improvement over other baselines – compared to the original softmax attention, MonarchAttention loses only 10 points in F1 score to reduce attention FLOPs by 60%, or matches the performance to reduce attention FLOPs by 35%.

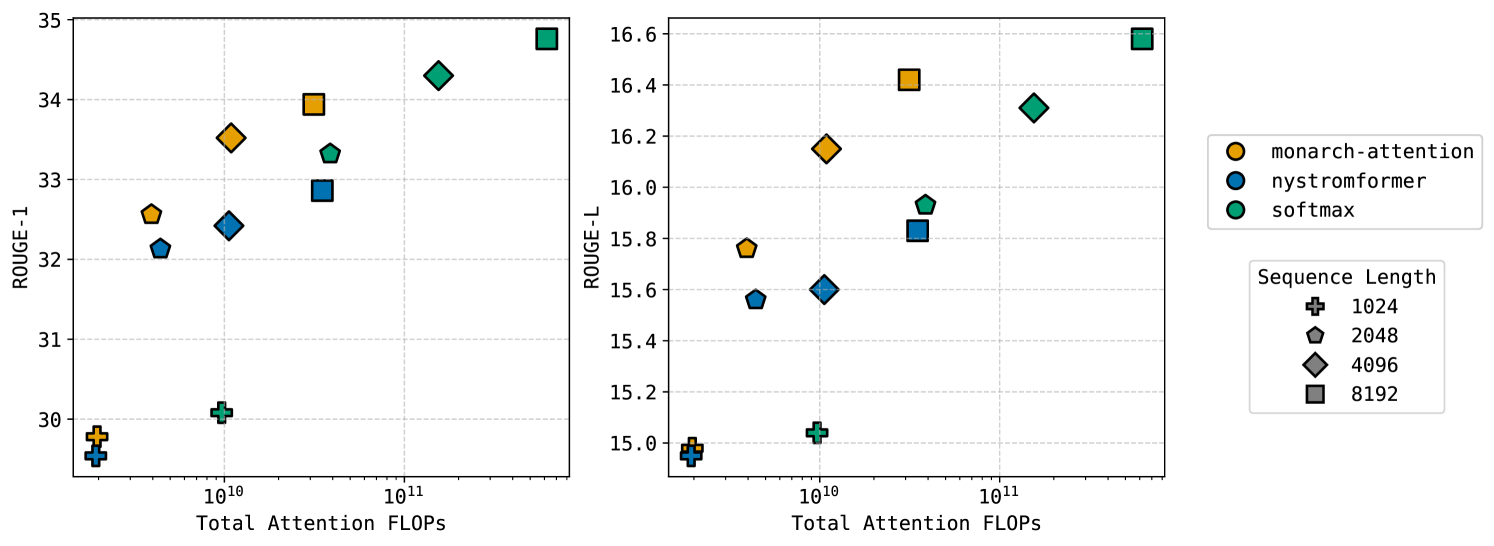
We convert all 6 attention layers, each having 12 heads with head dimension $d=64$, in the encoder of the 139M parameter BART-B (Lewis et al., 2020) that has been pre-trained on a large English corpus and fine-tuned on BookSum-chapters (Kryściński et al., 2022) for summarization. We only convert the encoder model and leave the decoder intact. To evaluate the benefits of sub-quadratic attention for processing longer sequences, we truncate the text to be summarized to various sequence lengths $N$ for each method; see Section D.4 for more details on the set-up. The results are shown in Figure 3. We see that MonarchAttention achieves a strictly better ROUGE score (Lin, 2004) vs. FLOPs tradeoff than even softmax attention, due to accurate and efficient processing of longer sequences. In particular, the $N=8192$ MonarchAttention model improves on the $N=2048$ softmax attention model by $0.75$ on ROUGE-1 and $0.5$ on ROUGE-L with slightly fewer FLOPs, while the $N=8192$ Nyströmformer model with similar FLOPs does strictly worse than softmax.

We convert a subset of the 28 attention layers, each having 16 heads with sequence length $N=256$ and head dimension $d=72$, of the 675M parameter DiT-XL (Peebles and Xie, 2023) that has been trained on ImageNet (Deng et al., 2009). We consider replacing either all layers, the first $14$ layers, or the last $14$ layers; see Section D.5 for more details on the set-up. Examples of generated images with each method for replacing the first 14 layers are shown in Figure 5, where MonarchAttention produces clear images resembling those of softmax attention, while the Nyströmformer ones are extremely noisy. We also quantitatively evaluate the (s)FID scores (Heusel et al., 2017) of MonarchAttention compared with Nyströmformer, using images generated with the original softmax attention model as reference – the results are reported in Table 1. MonarchAttention noticeably outperforms Nyströmformer with similar FLOP count. In particular, using MonarchAttention in the first half of the DiT layers results in extremely small FID and sFID from the softmax attention model’s images, while reducing FLOPs by nearly $30\%$.

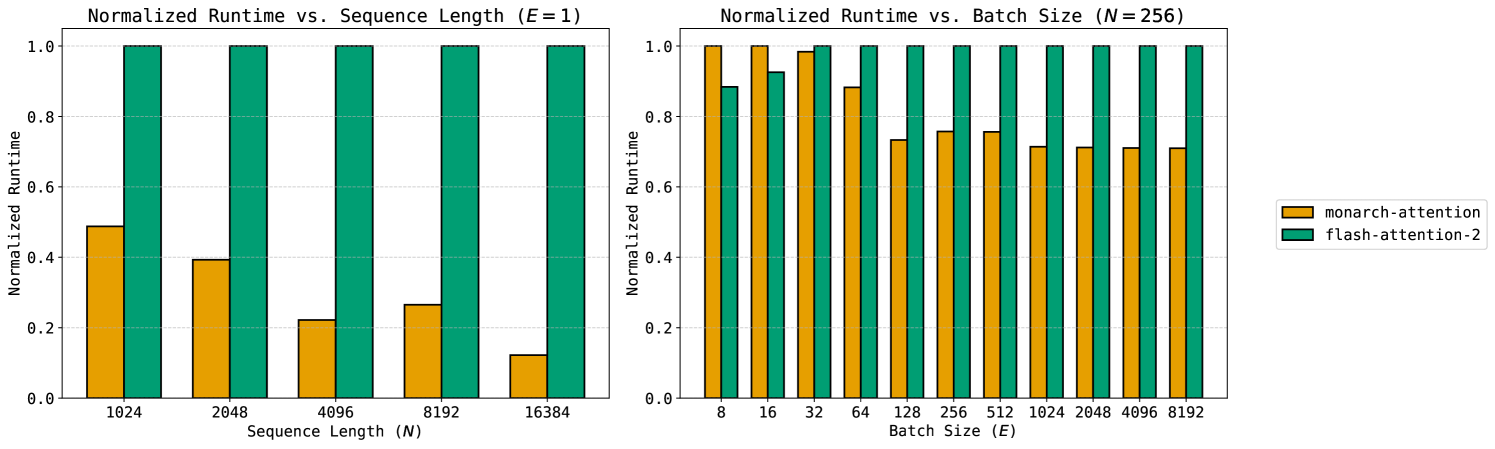
Finally, we validate that the computational/IO complexity reduction achieved by MonarchAttention translates into actual speed-ups on the NVIDIA A40, a modern GPU. We implement the pseudo-code described in Section 3 as four separate Triton kernels and compare it against the fastest available implementations of FlashAttention-2 – either the Triton implementation or PyTorch’s scaled_dot_product_attention, which calls the CUDA backend for FlashAttention-2. Using a fixed batch size $E$, number of heads $H$, and head dimension $d$, we sweep the input sequence length $N$ and compare the run-times of FlashAttention-2 and MonarchAttention (with $b=\sqrt{N}$ and $T=1$) in Figure 6 (left). As sequence length increases, MonarchAttention consistently outperforms FlashAttention-2, notably achieving up to $8.2\times$ speed-up with $N=16384$. To highlight gains for shorter sequences, we implement MonarchAttention as a single fully-fused Triton kernel, with a single thread block computing a single head. For fixed sequence length $N=256$, number of heads $H$, and head dimension $d$, we sweep the batch size $E$ and compare the run-time of the fully-fused MonarchAttention kernel against FlashAttention-2 in Figure 6 (right). With smaller batch sizes, we have low utilization of hardware, since we compute a single head with a single thread block. However, as we increase the batch size, MonarchAttention achieves up to $1.4\times$ speed-up over FlashAttention-2.