Money Pumps and Bounded Rationality
The standard criterion of rationality in economics is the maximization of a utility function that is stable across multiple observations of an agent’s choice behavior. In this paper, we discuss two notions of the money pump that characterize two corresponding notions of utility-maximization. We explain the senses in which the amount of money that can be pumped from a consumer is a useful measure of the consumer’s departure from utility-maximization.
JEL Codes: D11, D12.
Keywords: money pump, revealed preference, GARP, cyclical monotonicity, quasilinear utility, additive utility, constrained optimization
1 Introduction
It has often been argued that an agent’s vulnerability to money pumps is a sign of bounded or limited rationality. This paper is devoted to the study of money pumps and how they can be used to measure an agent’s adherence to rational principles.
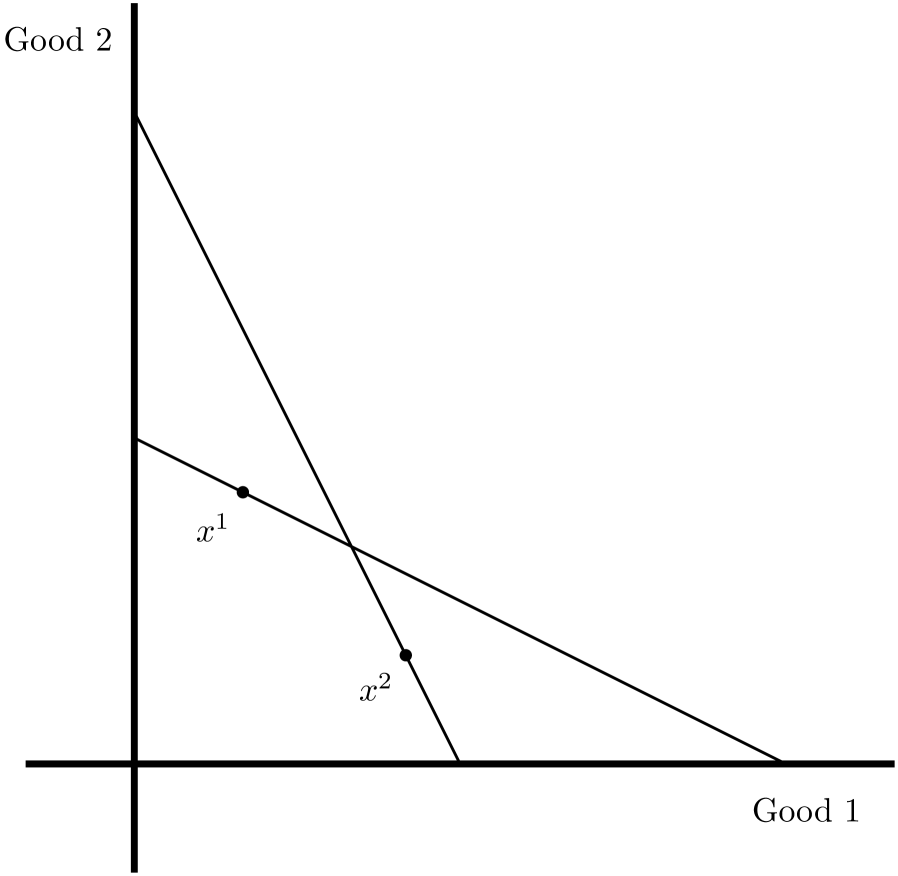
We begin our discussion with a simple example. Suppose that there are two goods and a consumer purchases the bundle when prices are and the bundle when the prices are . This situation is depicted on the left side of Figure 1 below. Note that in period 1, the bundle is cheaper than , while in period 2, is cheaper than . An arbitrageur can use this purchasing behavior to turn the consumer into a money pump. In particular, the arbitrageur may sell the consumer and purchase in period 1, which nets the arbitrageur . Then in period 2 the arbitrageur can sell the consumer and purchase , netting the arbitrageur a further . At the end of the day the consumer has been pumped for 2 dollars, while there is no net change to the arbitrageur’s stock of goods 1 and 2.
More generally, suppose that there are goods and we observe a consumer who purchases the consumption bundle when prices are , at some observation . The dataset admits a money pump if there are observations with such that an arbitrageur who purchases in period while simultaneously selling to the consumer will make a strictly positive amount of money; formally,
| (1) |
There is another way of understanding the money pump which turns out to be crucial to the formal results in the paper. Notice that if then
where we have used the requirement that . Instead of buying at , and at and so forth, the consumer could have purchased at , at , and so forth; by altering the timing of purchases in this way (interpreting the index as time), the consumer could have obtained the same set of bundles and saved money. In this sense, the consumer’s purchasing behavior is irrational and the presence of a money pump is equivalent to the presence of expenditure decisions which, taken as a whole across all observations, are cost inefficient.
But how is the presence or absence of a money pump related to the other standard by which economists judge rationality, namely, utility-maximization? Indeed, the absence of a money pump is also known as cyclical monotonicity and it is known that a dataset is cyclically monotone (i.e., free of money pumps) if and only if there is a quasilinear rationalization of , i.e., there is a well-behaved (in the sense of being continuous, strictly increasing, and concave) utility function such that maximizes , at all (see Brown and Calsamiglia (2007)). Alternatively, cyclical monotonicity is also equivalent to the additive rationalization of , by which we mean that there is a well-behaved utility function such that
for all with (see Browning (1989)). In other words, the consumer’s choices can be understood as maximizing an overall utility function that is additive across bundles at each observation, i.e.,
subject to the overall expenditure not exceeding .111Notice that in quasilinear rationalization, as opposed to additive rationalization, the consumer is not subject to a budget; she can, in principle, spend as much as she likes, but expenditure is restrained because it incurs dis-utility. It is particularly clear that a dataset that has an additive rationalization must be free of money pumps: the consumer cannot be maximizing a function like if a reshuffling of purchases leads to savings, since this frees up money that could be used to buy more goods in one or more periods and thus increase .
These characterizations of cyclical monotonicity (recall that cyclical monotonicity is equivalent to the absence of a money pump) lead naturally to the following question. For a given dataset collected from a consumer, we could work out the optimal trading strategy of the arbitrageur (the strategy which nets the most money) and consequently we could work out the amount of money which would be extracted from the consumer by an arbitrageur following this optimal strategy. We use TMP (for total money pump) to denote this amount of money. It seems sensible to regard TMP as a measure of the consumer’s departure from rationality, but in what sense does the TMP actually capture irrational behavior? In particular, can TMP be understood as a measure of the degree to which behavior departs from either quasilinear or additive utility maximization?
A natural approach to measuring deviations from quasilinear rationalization was proposed by Allen and Rehbeck (2021).222Our comments here refer to their generalized approach as discussed in their Appendix B. Notice that a well-behaved utility function is a quasilinear rationalization of if and only if
When admits a money pump, no such exists and thus, for every well-behaved utility function ,
with the inequality being strict for at least one observation . It follows that a natural measure of the consumer’s departure from quasilinear rationalization is
where the infimum is taken over all well-behaved utility functions. is a measure of inefficiency in the form of lost utility (summed across all periods).
In the case of additive rationalization, we can measure the severity of departures from this property using the cost efficiency approach advocated by Afriat (1973). Firstly, we observe that a dataset cannot be additively rationalized if and only if the consumer is cost inefficient in the following sense: for any well-behaved utility function , the required expenditure to hit the utility target is strictly lower than the amount actually spent; formally,
We can then measure the level of cost inefficiency by
where the infimum is taken over all well-behaved utility functions.
The first main result of the paper says that these three ways of measuring rationality coincide; i.e., .
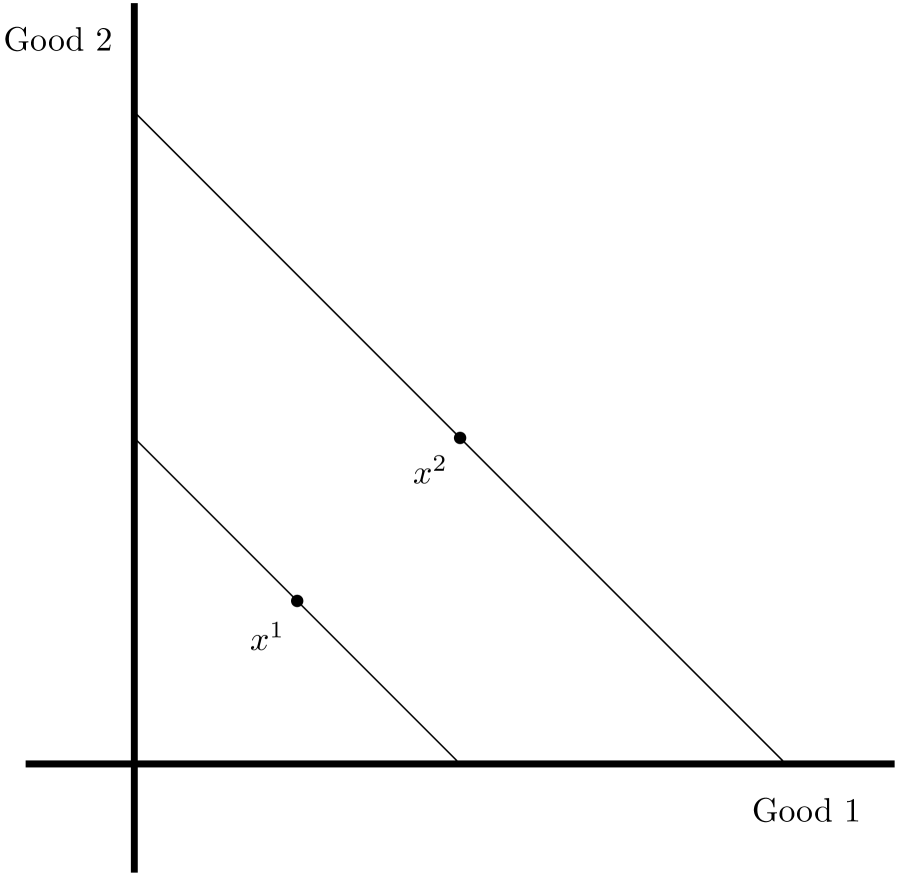
The second part of the paper begins with the observation that the existence of a money pump is not always a compelling sign of limited rationality. Suppose a consumer purchases the bundle when prices are and purchases when prices are . This situation is depicted in Figure 1(b). This behavior clearly leads to a money pump. Specifically, the arbitrageur can, in period 1, buy bundle and sell netting . Then, in period 2, the arbitrageur can buy bundle and sell to make . So the arbitrageur has extracted 2 dollars from the consumer. However, such behavior by a consumer may not be that irrational: for example, goods 1 and 2 could be festive goods which are consumed in greater quantities in the festive season (period 2), notwithstanding the higher prices. Put another way, the data has no additive rationalization because the consumer may not be maximizing an additive utility function that is symmetric across the two periods when observations are taken.
Notice also that there is a difference between the two examples depicted in Figure 1. The example depicted in Figure 1(b) clearly admits a rationalization, in the sense that there is a well-behaved utility function such that for all bundles which are cheaper than at price , i.e., for all such that . On the other hand, this is plainly not the case with the example depicted in Figure 1(a). We know from Afriat’s Theorem (see Afriat (1967), Diewert (1973), and Varian (1982)) that a dataset admits a rationalization if and only if obeys a property called the generalized axiom of revealed preference (GARP). The latter property says that the dataset does not admit a money pump (as we have defined it), with the added requirement that the arbitrageur makes money at every round of the exchange. We call a money pump with this added property a constrained money pumps. While a money pump exists in the second example depicted in Figure 1(b), it is not a constrained money pump, because the arbitrageur makes money in one round and loses in another; indeed, GARP holds because a constrained money pump is not possible and (by Afriat’s Theorem) a rationalization exists. On the other hand, in the example depicted in Figure 1(a), the money pump is a constrained money pump and thus that example violates GARP and has no rationalization.
These observations suggest that we could use the amount of money extracted from constrained money pumps as a measure of rationality; this is (in essence) the approach proposed by Echenique, Lee, and Shum (2011) and Smeulders, Cherchye, Spieksma, and De Rock (2013) in their studies of rationality and constrained money pumps.333There is a significant literature on the measurement of deviations from rationality. Afriat (1973) proposed to measure deviations in terms of the proportion of one’s budget wasted in each period and then aggregating across periods by taking the maximum waste; he refers to his proposed measure as the critical cost efficiency index. Varian (1990) generalizes Afriat’s approach by proposing other ways of aggregating waste across periods. Houtman and Maks (1985) suggest measuring violations in terms of the number of observations which need to be dropped before the remaining dataset becomes rationalizable. Apesteguia and Ballester (2015) propose measuring violations by taking the Lebesgue measure of the affordable strict upper contour set (the set preferred to the bundle actually chosen) in each period and adding up these measures across observations. (We are referring to the approach discussed in Appendix D.3; their main paper deals with a discrete choice environment.) Dean and Martin (2016) propose assigning a cost for breaking each revealed preference relation and then calculating the cheapest way of breaking every revealed preference cycle (i.e. every violation of GARP). Halevy, Persitz, and Zrill (2018) show how measures of departures from rationality can be used to perform parametric estimation of utility functions. The second main result of our paper provides a foundation for this approach.444While our index as well as those of Echenique et al. (2011) and Smeulders et al. (2013) are based on the notion of a money pump there is actually an important distinction between our different measures. See Section 3.3 for details.
Given a dataset , let be the the amount of money which would be extracted from the consumer by an arbitrageur who was following his optimal trading strategy under the provision that he cannot lose money in any round of trading. It follows immediately from the definition that and if the consumer purchasing behavior satisfies GARP. We show that coincides with appropriately modified versions of the additive cost and quasilinear utility inefficiency indices. To explain further, let denote the smallest amount of money the consumer could pay (summed across periods) to hit the utility target , provided that in each period the consumer cannot spend more than . Clearly, the additional constraint guarantees that . Analogous to the case of , we could use (where the infimum is taken over all well-behaved utility functions) as a measure of constrained additive cost inefficiency. Lastly, we can define in a way similar to our definition of , with the difference being that the suprema are taken over all bundles such that instead of over all . Like , the index is a measure how much more utility (net of expenditure) that a consumer with utility function can obtain by deviating from , but with an additional constraint on expenditure in each period. Obviously, . Our second main result states that . Additionally, we show that these measures can be calculated by solving a simple linear program.
Outline of the paper. The remainder of the paper is organized as follows. Section 2 introduces the total money pump index TMP and presents our main theorem (Theorem 2) for TMP. Section 3 introduces the constrained total money pump index and presents our main theorem for (Theorem 4). This section also has a comparison between our measure and the money pump indices introduced in Echenique et al. (2011) and Smeulders et al. (2013). Section 4 concludes. The appendix gives a more careful explanation of the relationship between our measure of additive cost inefficiency and the critical cost efficiency index introduced in Afriat (1973), as well as all proofs omitted from the body of the paper.
2 The Money Pump
We assume that we observe the consumer’s purchases of goods. A consumption bundle is denoted where is the quantity of good consumed. A price vector is denoted where is the price of good . A dataset is a finite collection of consumption bundle / price pairs denoted where intuitively means that the consumer purchased when prices were . A well-behaved utility function is a mapping which is continuous, increasing, and concave.555A function is increasing if implies and implies .
A dataset is rationalized by a utility function if
for all and all satisfying .666What we mean by this is that
for all and all satisfying , and the former inequality is strict if the latter inequality is strict. The dataset is additively rationalized by a utility function if
An additive rationalization requires that the consumer’s choices yield a higher additive (across-period) utility than any other affordable sequence of bundles . Note that if additively rationalizes the data then, for each , the choice must yield more utility than any other bundle which costs less (i.e. any bundle satisfying ). Thus, if additively rationalizes the data then rationalizes the data as well. Recall, however, the second example in the Introduction which shows that the converse does not hold. The dataset is quasilinear rationalized by a utility function if, for all ,
A quasilinear utility maximizer seeks to maximize utility net of expenditure. Note that in the case of quasilinear rationalization, the consumer is not constrained by a budget set, but expenditure leads to dis-utilty and has the effect of restraining purchases.
2.1 Money Pump and Cyclical Monotonicity
A dataset contains a money pump if there are observations (drawn from ) such that and as defined by (1) is strictly positive. A dataset that is free of money pumps is said to satisfy cyclical monotonicity. Another way of saying the same thing is that a money pump exists if there is a permutation of , denoted , where, in period , the arbitrageur sells and buys ; and the arbitrageur pumps a strictly positive amount of money,
from the consumer. We define the total money pump (TMP) as the amount of money which would be extracted from the consumer by an arbitrageur following an optimal trading strategy. That is,
| (2) |
where the supremum is taken over all permutations .
It is not hard to show that if is quasilinear rationalized by then is also additively rationalized by ; on the other hand, there is no guarantee that if is additively rationalized by , then the same provides a quasilinear rationalization of . The following result shows, among other things, that in fact these two types of rationalizations are empirically equivalent, and holds whenever .
Theorem 1.
Let be a dataset. The following are equivalent.
-
1.
.
-
2.
The dataset satisfies cyclical monotonicity.
-
3.
The dataset can be additively rationalized by a utility function .
-
4.
The dataset can be additively rationalized by a well-behaved utility function .
-
5.
The dataset can be quasilinear rationalized by a utility function .
-
6.
The dataset can be quasilinear rationalized by a well-behaved utility function .
The claims in Theorem 1 are not new in the sense that they can easily be pieced together using existing results. In particular, the equivalence between statements 1 and 2 is obvious. The equivalence between statements 2, 3, and 4 is found in Browning (1989) and the equivalence between statements 2, 5, and 6 is found in Brown and Calsamiglia (2007). To keep this article reasonably self-contained, we provide a proof of Theorem 1 in the Appendix.
The equivalence between statements 3 and 4 and the equivalence between items 5 and 6 shows that there are no additional restrictions placed on the data by assuming that is well-behaved in either the additive rationalization or the quasilinear rationalization.
The equivalence between 1, 4, and 6 shows that there is a tight relationship between the existence of a money pump and additive and quasilinear rationalizations. This suggests that the value of the total money pump may be useful as a measure of the degree to which the consumer fails to act as an additive or quasilinear utility maximizer. We address this issue in the next subsection.
2.2 TMP as a measure of rationality
By defnition, a dataset can be additively rationalized if the observations, when taken as a whole, maximize an overall utility function that is additive across bundles at each observations, i.e., , subject to the overall expenditure not exceeding the consumer’s total expenditure, which is . When cannot be additively rationalized, how should we measure the extent of the violation? The cost-efficiency approach proposed by Afriat (1973) measures the amount of money which could have been saved by the consumer were they to have acted perfectly in line with the utility maximization hypothesis under investigation (the additive utility model in our case).777Appendix A discusses in greater detail the relationship between and Afriat’s critical cost efficiency index. For a utility function let denote the smallest amount of money for which a consumer with additive (across periods) utility function could obtain utility . That is,
The additive cost inefficiency displayed by the consumer is the difference between the amount that the consumer actually spent and the smallest amount of money they could have spent to achieve the same utility. More formally, the additive cost inefficiency is the number
| (3) |
where the infimum is taken over all utility functions.
Next, let us suppose that we would like to measure the extent to which the consumer has failed to act as a quasilinear utility maximizer. One approach, which might be termed the utility efficiency approach, is to measure the additional utility which the consumer could have derived had they acted perfectly in line with the model of utility maximization under investigation. Of course, this approach only makes sense when utility is cardinal (in particular, the utility function must be identified up to translation by the consumer’s behavior). If the utility function is only identified up to monotonic transformation then it makes no sense to talk about differences in utility. As the quasilinear utility function is indeed cardinal in the requisite sense, it is reasonable to define the quasilinear utility inefficiency displayed by the consumer as
| (4) |
The term in the supremum represents the largest amount of quasilinear utility which could have been attained by the consumer in period whereas the rightmost term represents the amount of quasilinear utility actually achieved. The object was introduced in Allen and Rehbeck (2021) as a measure of deviation from quasilinear utility maximization.888What we call corresponds to the “minimum deviations” considered in Appendix B of Allen and Rehbeck (2021) when using (in their language) the aggregator .
Importantly, Allen and Rehbeck (2021) show that is easy to calculate. In particular, is equal to , the solution value for the linear programming problem of finding and to solve
{IEEEeqnarray}rCl
min& ∑_t=1^T ε_t
s.t. u_s ⩽u_t + p^t ⋅( x^s - x^t ) + ε_t, for all s,t
To recap, we have introduced three distinct ways of quantifying deviations from cyclical monotonicity. It turns out that they are all the same.
Theorem 2.
For any dataset ,
| (5) |
Moreover, there exists a well-behaved utility function that attains the infimum in the definitions of and .
As noted above, the result is shown in Allen and Rehbeck (2021). We include it here and provide a proof for the sake of completeness.
To give some insight into the proof of Theorem 2 let us focus on how we show that (the idea behind showing that is similar). The “easy direction” is showing that . Indeed, for any and permutation we have
{IEEEeqnarray*}rCl
∑_t=1^T sup_x∈R_+^L [ U(x) - p^t ⋅x] - [ U(x^t) - p^t ⋅x^t ] & ⩾ ∑_t=1^T [ U( x^σ(t) ) - p^t ⋅x^σ(t) ] - [ U(x^t) - p^t ⋅x^t ]
= ∑_t=1^T p^t ⋅( x^t - x^σ(t) )
and so the amount of quasilinear utility wasted for any is always greater than the amount of money which can be pumped for any . Thus, .
Showing that is more delicate. The key insight we utilize is that for any permutation which achieves the supremum in the definition of TMP it happens that the permuted dataset satisfies cyclical monotonicity. In other words, the purchasing behavior of the arbitrageur, which is given by , must satisfy cyclical monotonicity. Once this fact is established Theorem 1 can be applied to show that there exists a well-behaved utility function which rationalizes the permuted data. It can then be shown that the amount of money pumped via is weakly greater than the amount of quasilinear utility wasted according to which establishes that .
Recall that from items 3-6 of Theorem 1 we learned that when dealing with additive or quasilinear rationalizations there are no additional restrictions imposed on the data by requiring that the rationalizing utility function is well-behaved. This insight is preserved in Theorem 2 in the sense that the infima in the definitions of and can always be achieved by well-behaved utility functions and thus we could have defined and using infima over the collection of well-behaved utility functions without changing the content of these objects.
3 The Constrained Money Pump
3.1 GARP and the constrained money pump
A dataset satisfies the generalized axiom of revealed preferences (GARP) if, for all with satisfying
| (6) |
it is not the case that any of the inequalities in (6) hold strictly. We know from Afriat (1967) that GARP is a necessary and sufficient condition for a dataset to be rationalized by a well-behaved utility function.
A permutation of , denoted , is constrained for if for all . A constrained permutation represents a trading strategy (sell and buy in each period ) which nets the arbitrageur a weakly positive sum in each period. The constrained total money pump index, denoted , is defined as in (2), but with the supremum taken over all constrained permutations. In other words, is the amount of money which would be extracted from the consumer by an arbitrageur who was following his optimal trading strategy under the provision that he cannot lose money in any round of trading.
From Theorem 1 we know that a consumer who satisfies GARP can be turned into a money pump provided they fail to satisfy the stronger property of cyclical monotonicity. It is however plain from the definitions that the consumer who satisfies GARP cannot be turned into a constrained money pump. We next present two models of behavior which turn out to be characterized by GARP.
The dataset is constrained additively rationalized by if
where the leftmost inequality is required to be strict if any of the inequalities on the right hand side hold strictly. The constrained additive rationalization requires the consumer to maximize additive utility subject to period specific budget sets. In particular, the consumer is not allowed to reduce spending in one period in order to increasing spending in a different period. Due to this credit constraint it is easy to see that a dataset is rationalized by some utility function if and only if the dataset is constrained additively rationalized.
The dataset is constrained quasilinear rationalized by if
In a constrained quasilinear rationalization, the observed choice need only be superior (net of expenditure) to bundles which are cheaper than itself. Unlike an (unconstrained) quasilinear rationalization, it is not required that the net utility of is higher than that of all alternative bundles.
The following result relates the concepts just introduced.
Theorem 3.
Let be a dataset. The following are equivalent.
-
1.
.
-
2.
The dataset satisfies GARP.
-
3.
The dataset can be rationalized by a utility function .
-
4.
The dataset can be rationalized by a well-behaved utility function .
-
5.
The dataset can be constrained additively rationalized by a well-behaved .
-
6.
The dataset can be constrained quasilinear rationalized by an increasing and continuous .
It is easy to check that items 1 and 2 are equivalent. It is also easy to see that a utility function rationalizes if and only if constrained additively rationalizes and thus items 4 and 5 are equivalent. The equivalence between items 2, 3, and 4 is well-known and is part of Afriat’s Theorem. Thus, the only novel part of Theorem 3 is the equivalences involving item 6. Note that we do not guarantee that the constrained quasilinear utility function is well-behaved (however, it is increasing and continuous).
Theorem 3 suggests that can be used to measure the extent to which any of the equivalent conditions in the theorem are violated. This is the theme of the next subsection.
3.2 as a measure of rationality
Here we introduce constrained versions of the additive cost inefficiency and quasilinear utility inefficiency measures introduced in Section 2. Because Theorem 3 establishes that constrained additive and constrained quasilinear utility maximization are equivalent to GARP these measures can be thought of as reporting the extent to which GARP is violated.
To proceed, let be a dataset. For a utility function let denote the smallest amount of money which a consumer with additive (across periods) utility function would need in order to obtain the utility level , while not spending more than in each period , i.e.,
The constrained additive cost inefficiency displayed by the consumer is the amount of money the consumer could save while still obtaining the same additive utility provided that in each period spending is kept within the original budget set. More precisely, the constrained additive cost inefficiency is
| (7) |
where the infimum is taken over all utility functions. The interpretation of is the same as with and, in particular, it could be thought of a measure of deviation from the model of constrained additive utility maximization via the cost efficiency approach.
For a price vector and a number let denote the linear budget set . The constrained quasilinear utility inefficiency displayed by the consumer is the amount of extra quasilinear utility the consumer could have acquired by deviating from , provided that in each period the consumer’s expenditure does not exceed . Formally, the constrained quasilinear utility inefficiency is
| (8) |
where the infimum is taken over all utility functions. The interpretation of is the same as with . We know that can be calculated by solving a linear programming problem and it is natural to conjecture that can also be calculated in this fashion. Indeed, this happens to be the case. coincides with , the value of the linear programming problem of finding and to solve
{IEEEeqnarray}rCl
min& ∑_t=1^T ε_t
s.t. u_s ⩽u_t + p^t ⋅( x^s - x^t ) + ε_t, ∀s,t such that p^t ⋅x^t ⩾p^t ⋅x^s
Note that the linear programs of (2.2) and (8) are almost identical. The difference is that the constraints in (8) only apply for pairs of observations where whereas the constraints in (2.2) apply regardless of whether this condition holds or not.
The following result shows that all the measures of deviation from GARP just introduced are equivalent.
Theorem 4.
For any dataset ,
| (9) |
Moreover, there exists a continuous and increasing utility function that attains the infimum in the definitions of and .
The proof of Theorem 4 shares much in common with the proof of Theorem 2 (with a couple of added nuances). To explain further we focus on the proof that (the proof that is similar). The “easy direction” is showing that and the proof approach is essentially the same as the one we used to show in Theorem 2.
To show that we proceed as follows. Let be a constrained permutation which achieves the supremum in the definition of . The first step of our proof is to show that the permuted dataset cannot be pumped by any permutation which is constrained for (note that we consider which are constrained for and not permutations constrained for ). Once we establish that cannot be pumped in this fashion we employ Lemma 1 in the Appendix which guarantees that there exists a continuous and increasing utility function that satisfies for all . We then show that the amount of money which can be pumped with is weakly greater than the amount of quasilinear utility wasted according to ; in other words, the extra utility the consumer could have gained by deviating from , subject to any deviation costing weakly less than . This establishes .
3.3 Comparison to other money pump approaches
Here we compare our with related measures introduced in Echenique, Lee, and Shum (2011) (henceforth ELS) and Smeulders, Cherchye, Spieksma, and De Rock (2013) (henceforth SCSD). The starting point for ELS is the observation that any violation of GARP (i.e. any sequence with so that (6) holds with at least one strict inequality) can be exploited by an arbitrageur to pump money from the consumer. This observation led ELS to quantify the degree of the violation of GARP in accordance with the amount of money which could be extracted by the arbitrageur. As a single dataset can contain multiple violations of GARP it was proposed by ELS to take the average (either the mean or the median) of the amount of money which can be pumped (where the average is taken over each violation of GARP) in order to measure the degree of irrationality exhibited by the consumer. SCSD proved that calculating ELS’ average money pump (using either the mean or median) is NP-hard suggesting that this measure can be difficult to calculate in practice. SCSD proposed taking the maximum amount of money which can be pumped from the consumer through any single violation of GARP (i.e. any sequence with so that (6) holds with at least one strict inequality). They show that this maximum money pump, in contrast to the average money pump, can be calculated in polynomial time. Recall that from Theorem 4 we know that our measure can be calculated by solving a linear programming problem and thus our measure too can be calculated in polynomial time.
The main difference between our measure, , and the measures introduced by ELS and SCSD is that our index is the amount of money which can be extracted using the optimal trading strategy of the arbitrageur. On the other hand, the indices of ELS and SCSD aggregate (using either an average or a maximum) the amount of money which can be extracted over each violation of GARP whether or not the optimal strategy of the arbitrageur would actually exploit this violation (and, as we shall see in the examples below, he may not). We also note that there are no theoretical results connecting either the measure of ELS or the measure of SCSD to quasilinear or additive rationalizations (or any other rationalization concept) in the sense of our Theorem 4.
To further elucidate the differences between our and the measures of ELS and SCSD we present two examples.
Example 1.
Suppose there are two goods and three observations. Let , , and and let , , . Note that the budget set in observations 2 and 3 are the same and so the budget sets in this example are the same as those displayed in Figure 1(a). It is easy to check that the violations of GARP are observation sequences , , , and .999To confirm, for instance, that is indeed a violation of GARP just note that and and thus (6) holds with one strict inequality for . The amounts of money which can be pumped from each violation are: , , , and , respectively.101010To calculate the amount of money which can be pumped, for instance, from sequence just take . ELS’ mean and median money pumps are thus both equal to . On the other hand, the optimal strategy for the arbitrageur is to ignore observation 3 and pump via observations 1 and 2 and thus (the amount of money which can be extracted from observations 1 and 2).
Because ELS measure the average of the money pumps it is possible that a more rational dataset (in the sense that it has fewer GARP violations) can actually have a higher average money pump. For instance, if the choice in observation 3 of this example were perturbed slightly to for some small then the only GARP violations are the observation sequences and and thus ELS’ average money pump would be . Thus surprisingly, we see that a perturbation to the data which made the data more rational (it removed several violations of GARP) resulted in ELS’ index actually increasing in value. Note that this perturbation has no effect on .
Example 2.
Suppose there are four goods and four observations. In each observation the consumer purchases 1 unit of good and units of all other goods. Thus, , , , and . Let , , , and . Note that in observation 1 the consumer purchased but could have attained either or for less money. Similarly, in period 2 the consumer could have purchased for less money, in period 3 the consumer could have purchased for less money, and in period 4 the consumer could have purchased either or for less money. Using these remarks it is easy to show that the violations of GARP are observation sequences: , , and . The amounts of money which can be pumped are: , , and , respectively. The maximum money pump of SCSD is thus . Note however that the arbitrageur would not wish to pump via observations (these being the observations corresponding to the money pump amount of ) as the arbitrageur could do better by pumping via observations and (this corresponds to using the permutation which satisfies ) as following this strategy nets the arbitrageur a total of . Thus, while the maximum money pump is we see that .
The two preceding examples help make clear the distinction between our measure, which corresponds to the arbitrageur’s optimal strategy, with the measures of ELS and SCSD. In Example 1 we see that ELS’ average money pump incorporates several small violations of GARP which the arbitrageur’s optimal strategy ignores. Similarly, in Example 2 we that SCSD’s maximum money pump exploits the most severe single violation of GARP however the arbitrageur’s optimal strategy ignores this severe violation because he can make even more money by pumping two smaller violations.
4 Conclusion
In this article we propose two notions of the money pump. The total money pump (TMP) index is the total amount of money which can be extracted from the consumer via an arbitrage strategy. We show in Theorem 2 that this money pump is equivalent to a measure of additive cost inefficiency and is also equivalent to the measure of quasilinear utility inefficiency proposed by Allen and Rehbeck (2021). The constrained total money pump (TMPc) index, is the total amount of money which can be extracted from the consumer via an arbitrage strategy, with the added condition that the arbitrageur must make money in each round in which he enacts his strategy. Theorem 4 shows that the constrained total money pump is equivalent to a measure of constrained additive cost inefficiency and constrained quasilinear utility inefficiency.
References
- Afriat (1967) S. N. Afriat. The construction of utility functions from expenditure data. International Economic Review, 8(1):67–77, 1967.
- Afriat (1973) S. N. Afriat. On a system of inequalities in demand analysis: An extension of the classical method. International Economic Review, 14(2):460–472, 1973.
- Allen and Rehbeck (2021) Roy Allen and John Rehbeck. Satisficing, aggregation, and quasilinear utility. October 2021.
- Apesteguia and Ballester (2015) Jose Apesteguia and Miguel A. Ballester. A measure of rationality and welfare. Journal of Political Economy, 123(6):1278–1310, 2015. ISSN 00223808, 1537534X. URL https://www.jstor.org/stable/10.1086/683838.
- Brown and Calsamiglia (2007) Donald J. Brown and Caterina Calsamiglia. The nonparametric approach to applied welfare analysis. Economic Theory, 31(1):183–188, 2007. ISSN 09382259, 14320479. URL http://www.jstor.org/stable/27822509.
- Browning (1989) Martin Browning. A nonparametric test of the life-cycle rational expections hypothesis. International Economic Review, 30(4):979–992, 1989. ISSN 00206598, 14682354. URL http://www.jstor.org/stable/2526762.
- Dean and Martin (2016) Mark Dean and Daniel Martin. Measuring Rationality with the Minimum Cost of Revealed Preference Violations. The Review of Economics and Statistics, 98(3):524–534, 07 2016. ISSN 0034-6535.
- Diewert (1973) W. E. Diewert. Afriat and revealed preference theory. Review of Economic Studies, 40(3):419–425, 1973.
- Echenique et al. (2011) F. Echenique, S. Lee, and M. Shum. The money pump as a measure of revealed preference violations. Journal of Political Economy, 119(6):1201–1223, 2011.
- Halevy et al. (2018) Y. Halevy, D. Persitz, and L. Zrill. Parametric recoverability of preferences. Journal of Political Economy, 126(4):1558–1593, 2018.
- Houtman and Maks (1985) M. Houtman and J. A. H. Maks. Determining all maximal data subsets consistent with revealed preference. Kwantitatieve Methoden, 6(19):89–104, 1985.
- Smeulders et al. (2013) Bart Smeulders, Laurens Cherchye, Frits C. R. Spieksma, and Bram De Rock. The money pump as a measure of revealed preference violations: A comment. Journal of Political Economy, 121(6):1248–1258, 2013. ISSN 00223808, 1537534X. URL http://www.jstor.org/stable/10.1086/674077.
- Varian (1982) H. R. Varian. The nonparametric approach to demand analysis. Econometrica, 50(4):945–973, 1982.
- Varian (1990) H. R. Varian. Goodness-of-fit in optimizing models. Journal of Econometrics, 46(1-2):125–140, 1990.
Appendix A Additive Cost Efficiency and Afriat’s CCEI
Here we show that the additive cost inefficiency , as defined by (3), is in fact a version of Afriat’s CCEI (after applying a suitable normalization to ). To proceed, we normalize by dividing by total expenditure
Now, let be some dataset and let be an arbitrary utility function. Let denote the smallest amount of money which the consumer could have spent in period to acquire a bundle giving as much utility as . That is, . Let be some collection of utility functions. The CCEI for is the number111111When is the class of well-behaved utility functions then can be expressed in terms of the extent to which the budget constraints need to be relaxed in order for the data to satisfy GARP. That is, the CCEI is equal to the infimum number so that for all with we have implies that none of these inequalities hold strictly. See Halevy et al. (2018) for the proof that our definition of the CCEI and the version involving relaxed budget sets are in fact equivalent when is the collection of well-behaved utility functions.
| (10) |
In other words, the CCEI considers the percent of the budget set which is wasted in each period and aggregates the measure over periods by taking a supremum.
How does the CCEI relate to ? To answer this question let us cease to consider as separate purchasing occasions but rather let us consider as one giant purchasing occasion in which the consumer buys the bundle when prices are . Let denote the collection of utility functions which take the additive form for some . It follows that
where is the additive utility function with sub-utility function . Note that ‘1’ in the subscript of denotes the single (giant) observation where is purchased at prices . As it is clear that . Thus can be thought of as a version of Afriat’s CCEI.
Appendix B Proofs
Proof of Theorem 1..
Let be some permutation of and note that if is quasilinear rationalized by then which, after rearranging, yields and thus item 5 implies item 1.
Next, suppose satisfies cyclical monotonicity. Let be defined by
| (11) |
where the infimum is taken over all finite sequences . As satisfies cyclical monotonicity it is easy to see that the infimum in (11) is always attained by some sequence with at most elements. As such, is the pointwise infimum of finitely many well-behaved functions and is thus well-behaved. Let and let be the sequence which attains the infimum in (11) for . For any we have
where the final inequality follows from the definition of . Rearranging the previous inequality gives and so is quasilinear rationalized by . Let satisfy . Then, as is quasilinear rationalized by we see and so is additively rationalized by . We have just shown that item 2 implies items 4 and 6. It is easy to see that items 1 and 2 are equivalent and that item 4 implies item 3 and item 6 implies item 5 and so the proof is complete. ∎
Proof of Theorem 2..
To show that let be any utility function and define and . It is easy to see that these numbers and constitute a feasible solution to (2.2) and further that lies below the quantity
and so indeed .
To see that let and constitute a feasible solution to (2.2) and let be any permutation of . Using the constraint inequalities in (2.2) we see
and so indeed .
To see that let be any permutation of and note that for any utility function we have and so
from which we see that indeed .
Next, let be a permutation which achieves the supremum in the definition of the TMP (i.e. achieves the supremum in (2)). Let . We claim that satisfies cyclical monotonicity. For a contradiction suppose that this is not the case and thus there exists some permutation which “money pumps” the dataset in the sense that . We have
After rearranging we see that which contradicts the assumption that achieves the supremum in the definition of the TMP. Having achieved a contradiction we conclude that indeed satisfies cyclical monotonicity.
Lemma 1.
Let be a dataset and let be a vector satisfying for all . Suppose that for all permutations satisfying for all we have . Then, there exists a continuous and increasing utility function which satisfies for all and all satisfying .
Proof.
Let be some very large number. For each let be defined by
Note that each is increasing and continuous. Let be defined by
| (12) |
where the infimum is taken over all finite sequences . From our assumptions on we can, by taking sufficiently large, ensure that (i) for each the infimum in (12) is attained by some finite sequence which has at most elements and (ii) for all and all sequences which attain the infimum in (12) with we have and for all and .
By property (i) we see that is the pointwise infimum of finitely many increasing and continuous functions and is thus increasing and continuous. Let and let be the sequence which attains the infimum in (12) for . For any satisfying we may use property (ii) to see that
where the final inequality follows from the definition of . Rearranging the previous inequality and using the assumption that gives and thus the proof is complete. ∎
Proof of Theorem 3..
As noted, the equivalence between items 2-4 is well-known and is part of Afriat’s Theorem and so we omit the proof. Also as noted, the equivalence between items 1 and 2 and the equivalence between items 4 and 5 are obvious and so we also do not prove these results either. Clearly item 6 implies item 3 and so to complete the proof it suffices to show that item 1 implies item 6. So, suppose . Take where . It is easy to see that and satisfy the hypothesis in Lemma 1 and so the lemma provides an increasing and continuous utility function which satisfies for all satisfying . In other words, is constrained quasilinear rationalized by and so the proof is complete. ∎
Proof of Theorem 4..
To show that let be any utility function and define and where the supremum is taken over all such that . It is easy to see that these numbers and constitute a feasible solution to (8) and further that lies below the quantity
and so indeed .
To see that let and constitute a feasible solution to (8) and let be any constrained permutation of . Using the constraint inequalities in (8) we see
and so indeed .
To see that let be any constrained permutation of and note that for any utility function we have and so
from which we see that indeed .
Next, let be a constrained permutation which achieves the supremum in definition of the . Let and let where for all . We claim that and satisfy the hypotheses of Lemma 1 in the sense that for any permutation satisfying we have . For a contradiction suppose that this is not the case and thus there exists a permutation satisfying (i) for all and (ii) . Using (i) and the fact that is a constrained permutation for we see that for all we have and thus is a constrained permutation for . Using (ii) we see
After rearranging we see that which contradicts the assumption that achieves the supremum in the definition of (recall that we have shown that is a constrained permutation for ). Having achieved a contradiction we conclude that indeed and satisfy the hypotheses in Lemma 1 and so the lemma guarantees that there exists a continuous and increasing utility function which satisfies for all . Therefore, and so we see that . Noting that delivers . Thus, (9) holds and the infimum in the definitions of and are attained by the continuous and increasing utility function . ∎