Monogamy of entanglement for tripartite systems

Quantum entanglement Q1 among the subsystems of a multipartite system play significant roles in many information processing tasks. A fundamental property of quantum entanglement is the monogamy. The monogamy relations give rise to the distributions of quantum entanglement in the multipartite setting. Monogamy is also an essential feature allowing for security in quantum key distribution. For a tripartite system $A$, $B$ and $C$ associated with finite dimensional Hilbert spaces $H_{A}$, $H_{B}$ and $H_{C}$, respectively, the monogamy of an quantum entanglement measure $E$ implies that the correlation $E(\rho_{A|BC})$ between $A$ and $BC$ satisfies m1

$$E(\rho_{A|BC})\geq E(\rho_{AB})+E(\rho_{AC})$$

(1)

for any $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}$, where $\rho_{AB}=Tr_{C}(\rho_{ABC})$ and $\rho_{AC}=Tr_{B}(\rho_{ABC})$ are the corresponding reduced bipartite states. An important issue is to determine whether a given entanglement measure $E$ is monogamous or not. Considerable efforts have been devoted to this problem E1 ; E2 ; E3 ; E4 ; PRL.117.060501 ; G1 ; G2 ; G3 ; JIn for quantum correlations such as entanglement of formation (EOF) E3 , concurrence C1 ; C2 ; C3 , negativity N1 ; N2 ; N3 and concurrence of assistance zhu2 .

If $E$ does not satisfy the relation (1), it is still possible to find a positive power $\alpha\in(0,+\infty)$ such that $E^{\alpha}$ satisfies the relation (1) for $\alpha>0$ G1 ,

$$E^{\alpha}(\rho_{A|BC})\geq E^{\alpha}(\rho_{AB})+E^{\alpha}(\rho_{AC}).$$

(2)

The $\alpha$th $(\alpha\geq 2)$ power of concurrence and the $\alpha$th $(\alpha\geq\sqrt{2})$ power entanglement of formation for $n$-qubit states satisfy the relation (2) zhu1 .

In Ref. PRL.117.060501 the authors show that $E$ is monogamous if there exists a nontrivial continuous function $f$ such that the following generalized monogamy relation

$$E(\rho_{A|BC})\geq f(E(\rho_{AB}),E(\rho_{AC})),$$

(3)

is satisfied for states $\rho_{ABC}$. In Ref. JIn the authors presented a new parameterized monogamy relation of entanglement with equality,

$$E(\rho_{A|BC})=\mu E(\rho_{AB})+E(\rho_{AC}),$$

(4)

where $\mu>0$ and $E(\rho_{AB})\leq E(\rho_{AC})$. Monogamy relations satisfied by the $\alpha$th power of entanglement measures are presented based on Eq. (4) Ref. JIn .

In this paper, we investigate the monogamy properties of arbitrary quantum entanglement measures for tripartite quantum systems. We derive explicitly both the sufficient and necessary conditions for $E$ to be monogamous in terms of the $\alpha$th power of $E$, with respect to either all the quantum states. And, the monogamy conditions have been also obtained with respect to certain subsets of quantum states for quantum correlations.

In the following we say a quantum entanglement measure $E$ is $\alpha$-monogamous if there exists a real number $\alpha>0$ such that $E$ satisfies (2), and $E$ is non-monogamous if there is at least one state $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}$ such that (2) is not satisfied for any given $\alpha$.

With respect to each quantum state $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}$, we define a state dependent parameter $x_{\rho_{ABC}}$ such that the following equation is satisfied,

$$x_{\rho_{ABC}}\left(E^{y}(\rho_{A|BC})-\max\{E^{y}(\rho_{AB}),E^{y}(\rho_{AC})\}\right)=\min\{E^{y}(\rho_{AB}),E^{y}(\rho_{AC})\},$$

(5)

where $y$ is a positive number. If Eq.(5) has non-zero solution $x_{\rho_{ABC}}$ for each $\rho_{ABC}$ with $y=1$, then Eq. (5) becomes Eq.(4), i.e., $x_{\rho_{ABC}}=\frac{1}{\mu}$. Hereafter, we take $x_{\rho_{ABC}}=0$ for any $y$ when $E(\rho_{A|BC})=\max\{E(\rho_{AB}),E(\rho_{AC})$ and $\min\{E(\rho_{AB}),E(\rho_{AC})\}=0$. For simplicity, we denote the set of parameters $x_{\rho_{ABC}}$ by

$$X_{y}=\left\{x_{\rho_{ABC}}|x_{\rho_{ABC}}\left(E^{y}(\rho_{A|BC})-\max\{E^{y}(\rho_{AB}),E^{y}(\rho_{AC})\}\right)=\min\{E^{y}(\rho_{AB}),E^{y}(\rho_{AC})\},\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}\right\}.$$

[Proof]  Since as a measure of quantum entanglement, $E$ does not increase under local operations and classical communication, we have $E(\rho_{A|BC})\geq\max\{E(\rho_{AB}),E(\rho_{AC})\}$. Without loss of generality, we assume $E(\rho_{AB})\geq E(\rho_{AC})$ (The case for $E_{AC}\geq E_{AB}$ is similarly treated).

$(\Rightarrow)$   If $E$ is $\alpha$-monogamous, then $E$ satisfies (2) for any $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}$.

(Case 1) For a given state $\rho_{ABC}$, if $E(\rho_{A|BC})>E(\rho_{AB})$, we take $y=\alpha$, then $x_{\rho_{ABC}}=\frac{E^{\alpha}(\rho_{AC})}{E^{\alpha}(\rho_{A|BC})-E^{\alpha}(\rho_{AB})}.$ From (2) we have $x_{\rho_{ABC}}\leq 1.$

(Case 2) If $E(\rho_{A|BC})=E(\rho_{AB})$, since $E^{\alpha}_{A|BC}\geq E^{\alpha}_{AB}+E^{\alpha}_{AC}$, we have $E_{AC}=0$. The solution of Eq. (5) is $x_{\rho_{ABC}}=0$ for any $y$, especially for $y=\alpha$.

From Case 1 and Case 2 we have $x_{\rho_{ABC}}\in[0,1]$ for each $x_{\rho_{ABC}}\in X_{\alpha}$. Therefore, $X_{\alpha}$ is a bounded set.

$(\Leftarrow)$   If $X_{y_{0}}$ is a bounded set, then there exists a number $M>0$ such that $0\leq x_{\rho_{ABC}}\leq M$ for any $x_{\rho_{ABC}}\in X_{y_{0}}$.

(Case 1) If $x_{\rho_{ABC}}>0$, we have $E(\rho_{A|BC})>E(\rho_{AB})\geq E(\rho_{AC})>0$. Let $g(\beta)=E^{\beta}(\rho_{A|BC})-E^{\beta}(\rho_{AB})-E^{\beta}(\rho_{AC})$. We get

	$\displaystyle g(\beta)$		$\displaystyle=E^{\beta}(\rho_{A|BC})-E^{\beta}(\rho_{AB})-E^{\beta}(\rho_{AC})$
			$\displaystyle=\left(E^{y_{0}}(\rho_{AB})+\frac{1}{x_{\rho_{ABC}}}E^{y_{0}}(\rho_{AC})\right)^{\frac{\beta}{y_{0}}}-E^{\beta}(\rho_{AB})-E^{\beta}(\rho_{AC})$
			$\displaystyle=E^{\beta}(\rho_{AB})\left(1+\frac{1}{x_{\rho_{ABC}}}\frac{E^{y_{0}}(\rho_{AC})}{E^{y_{0}}(\rho_{AB})}\right)^{\frac{\beta}{y_{0}}}-E^{\beta}(\rho_{AB})-E^{\beta}(\rho_{AC})$
			$\displaystyle\geq E^{\beta}(\rho_{AB})\left(1+\frac{\beta}{x_{\rho_{ABC}}y_{0}}\frac{E^{y_{0}}(\rho_{AC})}{E^{y_{0}}(\rho_{AB})}\right)-E^{\beta}(\rho_{AB})-E^{\beta}(\rho_{AC})$
			$\displaystyle=E^{y_{0}}(\rho_{AC})\left(\frac{\beta}{x_{\rho_{ABC}}y_{0}}E^{\beta-y_{0}}(\rho_{AB})-E^{\beta-y_{0}}(\rho_{AC})\right),$

where the second equality is due to (5) and the first inequality is due to that $(1+t)^{n}\geq 1+nt$ for $n\geq 1$ and $t\geq 0$. Setting $\beta=\max\{My_{0},y_{0}\}$, we obtain $g(\beta)\geq 0$ for the given state $\rho_{ABC}$ since $0<x_{\rho_{ABC}}\leq M$ and $E(\rho_{AB})\geq E(\rho_{AC})$.

(Case 2) If $x_{\rho_{ABC}}=0$ for the quantum state $\rho_{ABC}$, one has $E(\rho_{AC})=0$. Then $E^{\alpha}(\rho_{A|BC})\geq E^{\alpha}(\rho_{AB})+E^{\alpha}(\rho_{AC})$ for any $\alpha>0$.

In conclusion, if there exists a real number $y_{0}$ such that $X_{y_{0}}$ is a bounded set, we take $\alpha=\max_{x_{\rho_{ABC}}>0}\{\beta\}=\max\{My_{0},y_{0}\}$. Then $g(\alpha)\geq 0$, i.e., $E^{\alpha}(\rho_{A|BC})\geq E^{\alpha}(\rho_{AB})+E^{\alpha}(\rho_{AC})$ for each $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}.$         

In fact, from the proof of the Theorem 1, we have $g(\beta)\geq 0$ for all $\beta\geq\alpha.$ Namely, if $E$ is $l$-monogamous, $E$ must be $L$-monogamous with $L\geq l$. From Theorem 1 we can conclude that the monogamy of $E$ is determined by $X_{y}$.

As applications let us consider the concurrence and three-qubit systems. For any arbitrary bipartite pure state $|\psi\rangle_{AB}$, the concurrence is given by $C(|\psi\rangle_{AB})=\sqrt{1-Tr(\rho^{2}_{A})}$, where $\rho_{A}=Tr_{B}(|\psi\rangle_{AB}\langle\psi|)$. We first consider the solution of Eq. (5) for three-qubit with $E=C$ and $y=2$. Any three-qubit state $|\psi\rangle_{ABC}$ can be written in the generalized Schmidt decomposition gx ,

$$\begin{array}[]{rcl}|\psi\rangle_{ABC}&=&\lambda_{0}|000\rangle+\lambda_{1}e^{i\varphi}|100\rangle+\lambda_{2}|101\rangle+\lambda_{3}|110\rangle+\lambda_{4}|111\rangle,\end{array}$$

(6)

where $\lambda_{i}\geq 0$, $i=0,...,4$, and $\sum_{i=0}^{4}\lambda_{i}^{2}=1$. We have $C_{A|BC}=2\lambda_{0}\sqrt{\lambda^{2}_{2}+\lambda^{2}_{3}+\lambda^{2}_{4}},$ $C_{AB}=2\lambda_{0}\lambda_{2}$ and $C_{AC}=2\lambda_{0}\lambda_{3}.$

Denote $\lambda=\min\{\lambda_{2},\lambda_{3}\}$. Eq. (5) becomes $x_{|\psi\rangle_{ABC}}\lambda^{2}_{0}(\lambda^{2}+\lambda^{2}_{4})=\lambda^{2}_{0}\lambda^{2}$. We obtain the following solutions,

$$x_{|\psi\rangle_{ABC}}=\left\{\begin{aligned} &~{}~{}~{}0,~{}~{}~{}~{}~{}~{}~{}~{}~{}\lambda_{0}=0;\\ &~{}~{}~{}0,~{}~{}~{}~{}~{}~{}~{}~{}~{}\lambda_{0}\not=0~{}~{}and~{}~{}\lambda=0;\\ &\frac{\lambda^{2}}{\lambda^{2}+\lambda^{2}_{4}},~{}~{}~{}\lambda_{0}\not=0~{}~{}and~{}~{}\lambda\not=0.\end{aligned}\right.$$

(7)

We have $X_{2}=\{x_{|\psi\rangle_{ABC}}|x_{|\psi\rangle_{ABC}}\lambda^{2}_{0}(\lambda^{2}+\lambda^{2}_{4})=\lambda^{2}_{0}\lambda^{2}\}$ and $\max\{x_{|\psi\rangle_{ABC}}\}=1$. According the proof of Theorem 1, we take $M=1$. Then $\alpha=\max\{2M,2\}=2$, i.e., $C^{2}(|\psi\rangle_{A|BC})\geq C^{2}(\rho_{AB})+C^{2}(\rho_{AC})$ for any pure states $|\psi\rangle_{ABC}$.

Since the concurrence of any mixed state $\rho_{AB}=\sum_{i}p_{i}|\psi\rangle_{i}\langle\psi|$ is given by the convex roof extension, $C(\rho_{AB})=\min_{\{p_{i},|\psi\rangle_{i}\}}\sum_{i}p_{i}C(|\psi\rangle_{i})$, for three-qubit mixed states $\rho_{A|BC}$, we have also $C^{2}(\rho_{A|BC})\geq C^{2}(\rho_{AB})+C^{2}(\rho_{AC})$.

In Theorem 1, we established a necessary and sufficient condition for the monogamy of a quantum entanglement measure $E$. In the following, we consider the generalized measures of quantum correlation beside entanglement measure $E$, such as entanglement of assistancega , quantum discord85040102 and quantum deficit85012103 and so on. Hereafter, we also say $Q$ is $\alpha$-monogamous if there exists a real number $\alpha>0$ such that $Q$ satisfies (2) and $Q$ is non-monogamous if there is at least one state $\rho_{ABC}\in H_{A}\otimes H_{B}\otimes H_{C}$ such that (2) is not satisfied for any given $\alpha$.

Different from the concurrence, the concurrence of assistance $C_{a}$ fails to be $\alpha$-monogamous in general. For a tripartite state $|\psi\rangle_{ABC}$, the concurrence of assistance is defined by ca

$$C_{a}(|\psi\rangle_{ABC})\equiv C_{a}(\rho_{AB})=\max_{\{p_{i},|\psi_{i}\rangle\}}\sum_{i}p_{i}C(|\psi_{i}\rangle),$$

(8)

where the maximum takes over all possible ensemble realizations of $\rho_{AB}=Tr_{C}(|\psi\rangle_{ABC}\langle\psi|)=\sum_{i}p_{i}|\psi_{i}\rangle_{AB}\langle\psi_{i}|$. Consider the $2\otimes 2\otimes 2$ pure state $|\psi\rangle_{ABC}$ given in (6). One has $C_{a}(\rho_{AB})=2\lambda_{0}\sqrt{\lambda^{2}_{3}+\lambda^{2}_{4}}$ , $C_{a}(\rho_{AC})=2\lambda_{0}\sqrt{\lambda^{2}_{2}+\lambda^{2}_{4}}$ and $C_{a}(|\psi\rangle_{A|BC}\rangle)=2\lambda_{0}\sqrt{\lambda^{2}_{2}+\lambda^{2}_{3}+\lambda^{2}_{4}}$. In particular, when $\lambda_{0}\not=0,$ $\lambda_{2}=0$ and $\lambda_{4}\not=0$, i.e., $C_{a}(|\psi\rangle_{A|BC}\rangle)=C_{a}(\rho_{AB})>0$ and $C_{a}(\rho_{AC})>0$, the Eq. (5) has no bounded solution for any $y$. The set $\Gamma=\left\{\beta\,(0<\beta<+\infty)|C^{\beta}_{a}(\rho_{A|BC})\geq C_{a}^{\beta}(\rho_{AB})+C_{a}^{\beta}(\rho_{AC})~{}for~{}all~{}\rho\in 2\otimes 2\otimes 2\right\}$ is just an empty set.

[Proof] If $\rho_{ABC}$ satisfies $Q(\rho_{A|BC})=\max\{Q(\rho_{AB}),Q(\rho_{AC})\}$ and $\min\{Q(\rho_{AB}),Q(\rho_{AC})\}>0$, then $Q^{\alpha}(\rho_{A|BC})<Q^{\alpha}(\rho_{AB})+Q^{\alpha}(\rho_{AC})$ for any $\alpha>0$.

Therefore, there is no positive number $\alpha$ such that (2) is satisfied.         

The above results show that the concurrence of assistance $C_{a}$ is non-monogamous in general for the $2\otimes 2\otimes n$ ($n\in\{2,3\}$) quantum systems. Nevertheless, for particular states, $C_{a}$ may be $\alpha$-monogamous. In zhu2 it is shown that $C_{a}$ satisfies the monogamy relation, $C_{a}^{\beta}(|\psi\rangle_{ABC})\geq C_{a}^{\beta}(\rho_{AB})+C_{a}^{\beta}(\rho_{AC})$, for the three-qubit W-class states $|\psi\rangle_{ABC}$ with $\beta\geq 2$. Therefore, with respect to a given measure of quantum correlation $Q$, there may be exist $\alpha$, which $Q$ satisfied $Q^{\alpha}(\rho_{A|BC})\geq Q^{\alpha}(\rho_{AB})+Q^{\alpha}(\rho_{AC})$ for specifically states $\rho_{ABC}$. We denote

$$X_{y,\Omega}=\left\{x_{\rho_{ABC}}|x_{\rho_{ABC}}\left(Q^{y}(\rho_{A|BC})-\max\{Q^{y}(\rho_{AB}),Q^{y}(\rho_{AC})\}\right)=\min\{Q^{y}(\rho_{AB}),Q^{y}(\rho_{AC})\},where~{}\rho_{ABC}\in\Omega\right\}.$$

Together with the Theorem 1 and Theorem 2, we have the following result.

The concurrence of assistance $C_{a}$ is an entanglement monotone for $2\otimes 2\otimes n(n\geq 2)$ pure states72042329 , i,e $C_{a}(|\psi\rangle_{A|BC})\geq\max\{C_{a}(\rho_{AB}),C_{a}(\rho_{AC})\}$ for quantum state $|\psi\rangle_{ABC}\in 2\otimes 2\otimes n(n\geq 2)$. Then we can study the monogamy of $C_{a}$ for $2\otimes 2\otimes n(n\geq 2)$ pure states by the corollary 1.

Theorem 1 and Corollary 1 provide the monogamy of $Q$ based on value of $x_{\rho_{ABC}}\in X_{y}$ for given $y$. In the following, we provide the $y$ independent monogamy with respect to a given quantum state $\rho_{ABC}$. For convenience, we denote $\Lambda=\{\rho_{ABC}|Q(\rho_{A|BC})>Q(\rho_{AB})\geq Q(\rho_{AC})>0~{}or~{}Q(\rho_{A|BC})>Q(\rho_{AC})\geq Q(\rho_{AB})>0\}$.

[Proof] Without loss of generality, we assume $Q(\rho_{A|BC})>Q(\rho_{AB})\geq Q(\rho_{AC})>0$. Set $t_{1}=\frac{Q(\rho_{AB})}{Q(\rho_{A|BC})}$, $t_{2}=\frac{Q(\rho_{AC})}{Q(\rho_{A|BC})}$ and $k=\frac{Q(\rho_{AB})}{Q(\rho_{AC})}$. It is obvious that $t_{1}\geq t_{2}$, $k\geq 1$ and $1=t^{y}_{1}+\frac{1}{x}t^{y}_{2}$, where $x$ is the solution of Eq. (5) with a given $y>0$ for $\rho_{ABC}$. Let $\alpha$ satisfy $(1+\frac{1}{k^{y}x})^{\frac{\alpha}{y}}=2$, i.e., $\alpha=\log_{\frac{Q(\rho_{A|BC})}{Q(\rho_{AB})}}2$. Next, we prove that $g(\alpha)=Q^{\alpha}(\rho_{A|BC})(1-t_{1}^{\alpha}-t_{2}^{\alpha})\geq 0$ by proving $(1-t_{1}^{\alpha}-t_{2}^{\alpha})\geq 0$,

	$\displaystyle 1-t_{1}^{\alpha}-t_{2}^{\alpha}$		$\displaystyle=(t^{y}_{1}+\frac{1}{x}t^{y}_{2})^{\frac{\alpha}{y}}-t_{1}^{\alpha}-t_{2}^{\alpha}$
			$\displaystyle=(k^{y}+\frac{1}{x})^{\frac{\alpha}{y}}t_{2}^{\alpha}-k^{\alpha}t_{2}^{\alpha}-t_{2}^{\alpha}$
			$\displaystyle=k^{\alpha}\left((1+\frac{1}{k^{y}x})^{\frac{\alpha}{y}}-1-k^{-\alpha}\right)t_{2}^{\alpha}$
			$\displaystyle=(k^{\alpha}-1)t_{2}^{\alpha}\geq 0,$

where the first equation is due to $1=t^{y}_{1}+\frac{1}{x}t^{y}_{2}$ and the inequality is due to $k\geq 1$ and $\alpha>0$. The case for $Q(\rho_{A|BC})>Q(\rho_{AC})\geq Q(\rho_{AB})>0$ is similarly proved. Therefore, $Q$ is $\log_{b}2$-monogamous for the states $\rho_{ABC}$.         

The entanglement cost $E_{C}$ of a bipartite state $\rho_{AB}$ is equal to the regularized entanglement of formation $E_{f}$ EOF , namely m1 ,

$$E_{C}(\rho_{AB})=\lim_{n\to\infty}\frac{1}{n}E_{f}(\rho^{\otimes n}_{AB}),$$

(11)

where the entanglement of formation $E_{f}$ is defined by $E_{f}(\rho_{AB})=\min_{\{p_{i},|\psi_{i}\rangle\}}\sum_{i}p_{i}S(Tr_{B}[|\psi_{i}\rangle\langle\psi_{i}|]),$ with $S(\rho)$ is the von Neumann entropy of density operator $\rho$ and the minimum is taken over all ensembles $\{p_{i},|\psi_{i}\rangle\}$ satisfying $\sum_{i}p_{i}|\psi_{i}\rangle\langle\psi_{i}|=\rho_{AB}$. It is worthwhile noting that the inequality (1) does not hold for the entanglement cost $E_{C}$ m1 .

To illustrate the Theorem 3 we consider the purification of the totally antisymmetric two-qutrit state,

$$|\psi\rangle_{ABC}=\frac{1}{\sqrt{6}}(|123\rangle-|132\rangle+|231\rangle-|213\rangle+|321\rangle-|321\rangle).$$

(12)

One has $E_{C}(|\psi\rangle_{A|BC})=\log_{2}3$ and $E_{C}(\rho_{AB})=E_{C}(\rho_{AB})=1$ m1 . According to Theorem 3, we have $b=\min\left\{\frac{E_{C}(|\psi\rangle_{A|BC})}{E_{C}(\rho_{AC})},\frac{E_{C}(|\psi\rangle_{A|BC})}{E_{C}(\rho_{AB})}\right\}=\log_{2}3$. Then $\alpha=\log_{(\log_{2}3)}2\approx 1.51.$ Therefore, $E_{C}$ is $\alpha$-monogamous for $|\psi\rangle_{ABC}$ for $\alpha\geq 1.51$. Denote $f(\alpha)=E^{\alpha}_{C}(|\psi\rangle_{A|BC})-E^{\alpha}_{C}(\rho_{AB})-E^{\alpha}_{C}(\rho_{AC})$. We have $f(\alpha)\geq 0$ for $\alpha\geq 1.51$, see the Fig. 1.

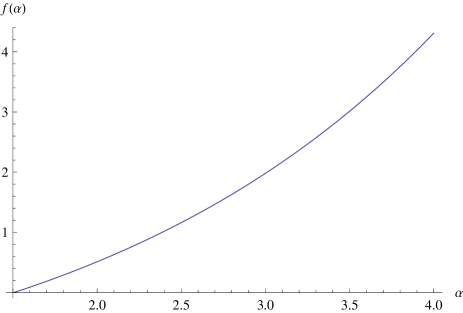
On the other hand, for the state $|\psi\rangle_{ABC}$ in (12), using the Theorem 1 and Corollary 1, we have $X_{y,|\psi\rangle_{ABC}}=\{\frac{1}{(\log_{2}3)^{y}-1}\}$ for given $y>0$. Then $E_{C}$ is $\beta$-monogamous for $|\psi\rangle_{ABC}$ with $\beta=\max\{\frac{1}{(\log_{2}3)^{y}-1}y,y\}$. Obviously, the optimal value of $\beta$ is obtained at the intersection of $z_{1}(y)=\frac{1}{(\log_{2}3)^{y}-1}y$ and $z_{2}(y)=y$ with $y>0$, i.e., $\min_{y>0}\{\beta\}=\log_{(\log_{2}3)}2$, see Fig. 2.

In the proof of the Theorem 3, if we take $1<c\leq\min\left\{\frac{Q(\rho_{A|BC})}{Q(\rho_{AC})},\frac{Q(\rho_{A|BC})}{Q(\rho_{AB})}\right\}$, then we have that $Q$ is $\log_{c}2$-monogamous for the given quantum state. For example, let $c=\frac{3}{2}\in(1,\log_{(\log_{2}3)}2]$ for the state (12). Then $E_{C}$ is $\alpha$-monogamous for $|\psi\rangle_{ABC}$ with $\alpha=\log_{\frac{3}{2}}2\approx 1.71$. More generally, for some states $\rho_{ABC}\in\Lambda$, from the proof of Theorem 3 if $T=\left\{\frac{Q(\rho_{A|BC})}{Q(\rho_{AC})},\frac{Q(\rho_{A|BC})}{Q(\rho_{AB})}\big{|}\rho_{ABC}\right\}$ has lower bound $c$ which is strictly greater than $1$, $Q$ is $\log_{c}2$-monogamous for those states $\rho_{ABC}$.

We have addressed in general the question of whether entanglement measures $E$ are monogamous in the sense of (2) introduced in Ref. G1 for tripartite quantum systems. We have presented the equations (5) and shown that the monogamy of a entanglement measure $E$ only depends on the boundedness of the solutions for the equations. Both sufficient and necessary conditions for $E$ being monogamous have been explicitly derived. Meanwhile, the monogamy conditions for a measure of quantum correlation $Q$ have been also obtained with respect to certain subsets of quantum states. According to the duality, our approach may be also applied to study the polygamy of entanglement measures $E$.