Mosaics for immersed surface-links
Abstract
The concept of a knot mosaic was introduced by Lomonaco and Kauffman as a means to construct a quantum knot system. The mosaic number of a given knot is defined as the minimum integer that allows the representation of on an mosaic board. Building upon this, the first author and Nelson extended the knot mosaic system to encompass surface-links through the utilization of marked graph diagrams and established both lower and upper bounds for the mosaic number of the surface-links presented in Yoshikawa’s table. In this paper, we establish a mosaic system for immersed surface-links by using singular marked graph diagrams. We also provide the definition and discussion on the mosaic number for immersed surface-links.
Keywords: mosaic knot, surface-link, immersed surface-link, marked graph diagram, singular vertex
2020 MSC: 57K12, 57K45, 81P99
1 Introduction
A knot mosaic is a mathematical object that represents a knot diagram composed of tiles, where each tile represents a segment of the knot. Knot mosaic diagrams provide a powerful tool for understanding and analyzing the structure of quantum knots. They allow for a visual representation of the knot and its components, enabling researchers to study the intricate connections and relationships within the knot. By utilizing knot mosaic diagrams, various properties and characteristics specific to quantum knots can be defined and investigated. Thus, knot mosaic diagrams serve as an important framework for the definition and study of quantum knots.
In 2008, Lomonaco and Kauffman [15] introduced a knot mosaic as a construction for quantum knot systems and conjectured that tame knot theory is equivalent to knot mosaic theory. In 2014, Kuriya and Shehab [14] proved this conjecture by using grid diagrams, also known as rectangular diagrams. The mosaic number of a knot is defined as the smallest number for which can be represented as an -mosaic. As a result, mathematicians have extensively studied the calculation of the mosaic number for knots, focusing on different types of knots and exploring both upper and lower bounds, among other research directions. See [14, 16, 17, 18, 19] for more information.
A surface-link is the image of a closed surface smoothly (piecewise linearly and locally flatly) embedded in (or ). If the underlying surface is connected, it is referred to as a surface-knot. Two surface-links and are said to be equivalent if there exists an orientation-preserving homeomorphism such that . In order to facilitate the study of surface-links, several descriptive tools have been developed due to the inherent complexity of directly dealing with them in 4-space. These tools include broken surface diagrams, marked graph diagrams, banded link diagrams, motion pictures, and others. Using these alternative representations allows for effective investigation and analysis of surface-links in 4-space. For more details, refer to [1, 6, 7, 11, 21]. A marked graph is a -valent graph in with a marker, which is a line segment at a -valent vertex. A marked graph diagram is a generic projection on with classical crossings and marked vertices as a link diagram. It is well known that surface-links can be represented by marked graph diagrams (cf. [1, 6, 7, 12, 20, 21]).
In 2022, the first author and Nelson [2] constructed a mosaic system for surface-links using marked graph diagrams as a tool. They established lower and upper bounds of the mosaic number for the surface-links in Yoshikawa’s table and enhanced the kei counting invariant for unoriented surface-links as well as classical knots and links using mosaic diagrams, as an application.
An immersed surface-link is a closed surface smoothly immersed in (or ) with the property of self-transversality. An immersed surface is a fundamental role in the field of low-dimensional topology, particularly in the study of -manifolds. Despite their significance, it is challenging to provide explicit descriptions of immersed surface-links and their equivalence, except for a few specific examples. Therefore, there is a pressing need for developing effective methods to represent immersed surface-links. On the other hand, extensive investigations have been conducted on representations for embedded surface-links, and recently, there has been considerable interest in extending these representations for immersed surface-links.
In 2018, Kamada and Kawamura [8] extended the concept of a normal form from surface-links to immersed surface-links and demonstrated that any immersed surface-link can be represented in a normal form. Kamada, Kawauchi, Kim, and Lee [9] introduced a diagrammatic method for representing immersed surface-links in via marked graph diagrams, using the concept of -admissibility, and then Kim [13] enumerated immersed surface-links up to ch-index . In 2019, the second author and Kawauchi [10] gave infinitely many immersed surface-links with certain types of double point singularities. In 2020, Hughes, Kim, and Miller [3] introduced a banded unlink diagrams in Kirby diagrams for surfaces embedded in any -manifold and in 2021, they extended their results to studying surfaces immersed in any -manifolds via a singular banded unlink diagram [4] and this is another diagrammatic system compared to the results in [9]. In 2022, Jabłonowski [5] constructed marked graph diagrams with singular vertices, called singular marked graph diagrams, for representing surfaces immersed in from their results.
In this paper, we extend mosaics for embedded surface-links to immersed surface-links by using singular marked graph diagrams. The paper is organized as follows. In Section 2, we review the relationship between immersed surface-links and singular marked graph diagrams. Section 3 introduced a mosaic system for embedded surface-links. Mosaics for immersed surface-links and their equivalence can be defined in Section 4. In Section 5, we calculate the mosaic number of the immersed surface-links, illustrated in [13], and suggest their lower and upper bounds.
2 Immersed surface-links and singular marked graph diagrams
We introduce the definitions and notions of singular marked graph diagrams for representing immersed surface-links in -space. See [4, 5] in details.
An immersed surface-link is the image of a closed surface smoothly immersed in (or ) such that the multiple points are transverse double points. An immersed surface-knot is an immersed surface-link whose underlying surface is connected. Clearly, if it has no transverse double points, then it is a surface-link. Two immersed surface-links and are said to be equivalent in if there exists an orientation-preserving homeomorphism such that .
We use an effective tool for describing immersed surface-links, known as a singular marked
graph diagram.
A singular marked graph is a spatial graph embedded in
possibly with -valent vertices decorated by a line segment, such as \scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x1.png) B,
or an encircled decoration, such as
\scalerel*
B,
or an encircled decoration, such as
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x2.png) B.
We call such a line segment a marker and a vertex with a marker a
marked vertex. A vertex with an encircled decoration is called a singular vertex.
In the same way as a link diagram, one can define a singular marked graph
diagram which is a diagram in with classical crossings, marked vertices, and singular vertices.
B.
We call such a line segment a marker and a vertex with a marker a
marked vertex. A vertex with an encircled decoration is called a singular vertex.
In the same way as a link diagram, one can define a singular marked graph
diagram which is a diagram in with classical crossings, marked vertices, and singular vertices.
Let be a singular marked graph diagram.
In the case of a marked vertex
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x3.png) B ,
the local diagram obtained by splicing in a direction consistent with its marker (referred to as the direction), appears as
\scalerel*
B ,
the local diagram obtained by splicing in a direction consistent with its marker (referred to as the direction), appears as
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x4.png) B .
Conversely, by applying this process in the opposite direction (referred to as the direction), the resulting local diagram appears as
\scalerel*
B .
Conversely, by applying this process in the opposite direction (referred to as the direction), the resulting local diagram appears as
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x5.png) B .
In the case of a singular vertex
\scalerel*
B .
In the case of a singular vertex
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x6.png) B ,
the local diagram obtained by choosing the arc in the circle symbol as the over arc (referred to as the direction), appears as
\scalerel*
B ,
the local diagram obtained by choosing the arc in the circle symbol as the over arc (referred to as the direction), appears as
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x7.png) B .
Conversely, the resulting local diagram by connecting the two arcs disconnected by the circle symbol (referred to as the direction), appears as
\scalerel*
B .
Conversely, the resulting local diagram by connecting the two arcs disconnected by the circle symbol (referred to as the direction), appears as
\scalerel*![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6c58e6a0-2225-4917-9c13-647e0b2e476d/x8.png) B .
Consequently, two distinct classical link diagrams, denoted by and , can be obtained from by applying all marked and singular vertices in the and directions, respectively.
Indeed, their local diagrams and neighborhoods are described in Figure 1.
We refer to and as the positive and negative resolutions of , respectively.
B .
Consequently, two distinct classical link diagrams, denoted by and , can be obtained from by applying all marked and singular vertices in the and directions, respectively.
Indeed, their local diagrams and neighborhoods are described in Figure 1.
We refer to and as the positive and negative resolutions of , respectively.
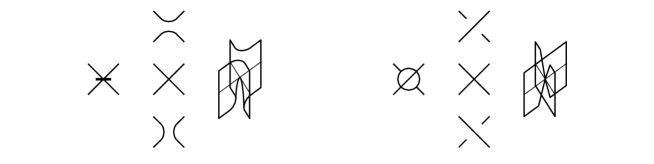
A singular marked graph diagram is said to be admissible if both resolutions and are diagrams of trivial links. A singular marked graph is said to be admissible if it has an admissible singular marked graph diagram. For example, the singular marked graph diagram as depicted in Figure 2 is admissible.

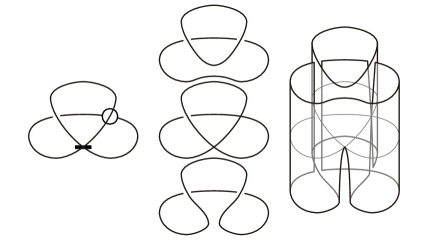
For a given admissible singular marked graph diagram , one can construct a uniquely immersed surface-link obtained from , up to equivalence. Conversely, every immersed surface-link can be expressed by an admissible singular marked graph diagram , that is, is equivalent to . See [4, 5] for more details. For example, let denote the singular marked graph diagram with one classical crossing, one marked vertex, and one singular vertex as described in Figure 3. Then one can obtain its cobordism constructed by connecting the positive and negative resolutions of .
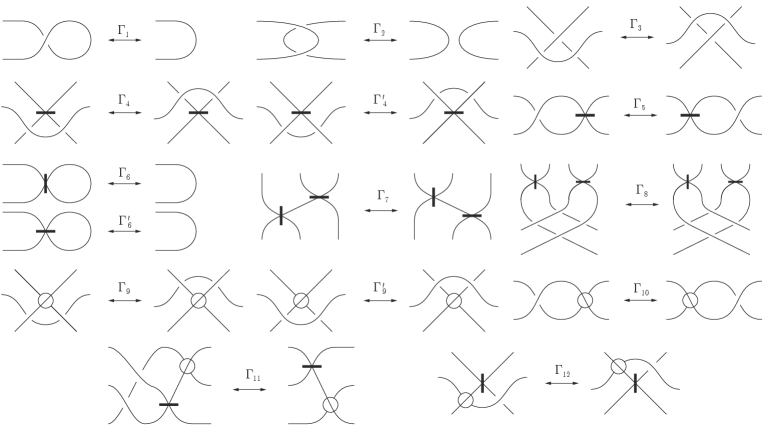
In [5], the equivalence moves for immersed surface-links are the generalized Yoshikawa moves of singular marked graph diagrams and its minimal generating set is depicted in Figure 4. In this paper, we call the generalized Yoshikawa moves the singular Yoshikawa moves.
Proposition 1 ([4, 5]).
Two singular marked graph diagrams and present equivalent immersed surface-links if and only if can be obtained from by a finite sequence of ambient isotopies in and singular Yoshikawa moves.
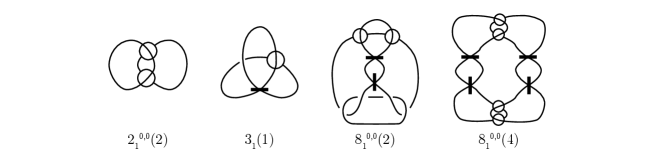
In [13], the concept of H-admissibility is used in a marked graph diagram for immersed surface-links to categorize cases up to ch-index 9 and the examples in the table of immersed surface-links that has at least one singular vertex can be illustrated in Figure 5.
A marked graph diagram is H-admissible if both positive and negative resolutions are H-trivial link diagrams where an H-trivial diagram is a diagram of a split union of trivial knots and Hopf links. During the process of constructing an immersed surface-link from an H-admissible marked graph diagram, a singular point arises when capping the Hopf link. See [9, 13] in details.
In order to convert H-admissible marked graph diagrams into admissible singular marked graph diagrams, we consider the singularities of an H-admissible marked graph diagram. Its singularities can be divided into three cases based on their location and their broken surface diagrams are shown in the first figure of each of Figures 6, 7, and 8.
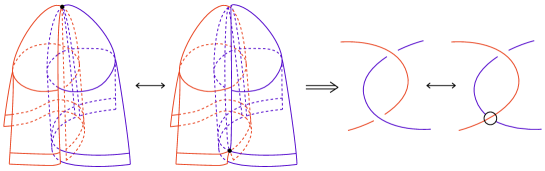
Figure 6 is the case of a singularity appearing from the positive resolution, called the upper singularity. The upper singularity can be moved down to the level where the marked graph diagram appears, to converting this H-admissible marked graph diagram to a singular marked graph diagram and its local move used to transform between them is also shown in Figure 6.
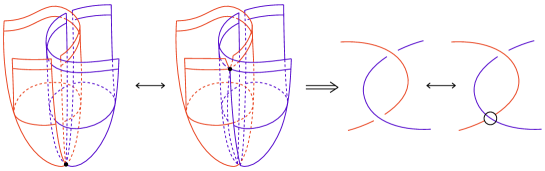
Conversely, the case of a singularity appearing from the negative resolution, called the lower singularity, is illustrated in Figure 7, similar to Figure 6.
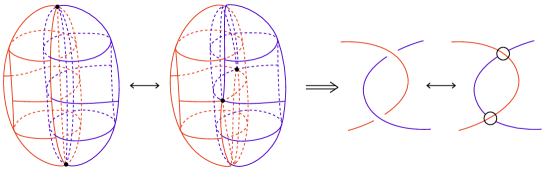
In the last case, both upper and lower singularities are present, as depicted in Figure 8, and the transformation consists of two processes. Therefore, one can deform the marked graph diagrams of Figure 5 into the singular marked graph diagrams as depicted in Figure 9.
3 Mosaics for surface-links via marked graph diagram
We review the mosaic system for surface-links using marked graph diagrams and focus on the case of unoriented surface-links. The consideration of orientation can be deferred to the last stage.
Let be the set of mosaic tiles, which are rectangles with arcs and possibly with one crossing or marked vertex as depicted in Figure 10.
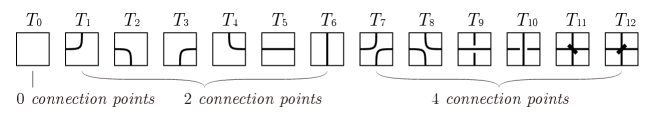
Indeed, there are exactly tiles, up to rotation. The endpoints of an arc on a mosaic tile is located the center of an edge, called connection points, and then each tile has , , or connection points.
An -mosaic is an matrix whose entries are mosaic tiles in . If it is square, i.e. , then it is called an -mosaic. The sets consisting of -mosaics and -mosaics are denoted by and , respectively.
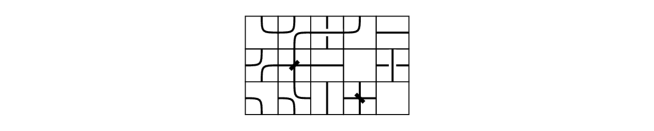
Two tiles in a mosaic are said to be contiguous if they are adjacent in either the same row or column. A tile in a mosaic is said to be suitably connected if all its connection points coincide with the connection points of contiguous tiles. Note that for a -mosaic illustrated in Figure 11, the tile at entry is suitably connected, whereas the tile at entry is not suitably connected.
Definition 1.
A marked graph -mosaic is an -mosaic in which all tiles are suitably connected. The set of all knot -mosaic is the subset of , denoted by . If , then it is called a marked graph -mosaic and its set is denoted by .
Example 1.
The spun trefoil has a marked graph -mosaic and -mosaic diagrams in Figure 12.

For representing surface-links using marked graph diagrams, one can consider the equivalence moves for surface-links, planar moves and Yoshikawa moves, [21]. The non-determistic tiles are necessary to define the moves and see [15] in detail.
The equivalence of marked graph mosaics consists of 15 types for planar isotopy, as shown in Figure 13, and Yoshikawa moves illustrated in Figure 14.
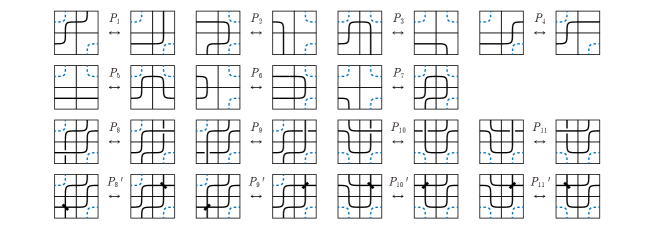

All marked graph mosaic moves are permutations on the set of -mosaics. Indeed, they are also in the group of all permutations of the set of marked graph -mosaics.
Definition 2.
The ambient isotopy group is the subgroup of the group of all permutations of the set generated by all planar isotopy moves and all Yoshikawa moves.
Two marked graph -mosaics and are said to be of the same marked graph -type, denoted by if there exists an element of such that it transforms into . Two marked graph -mosaics and are said to be of the same marked graph type if there exists a non-negative integer such that
where is the mosaic injection by adding a row and a column consisting of only empty tiles. Therefore, we can obtain the following result.
Proposition 2 ([2]).
Let and be two marked graph mosaics of two marked graphs and , respectively. Then and are of the same marked graph mosaic type if and only if and are equivalent.
Example 2.
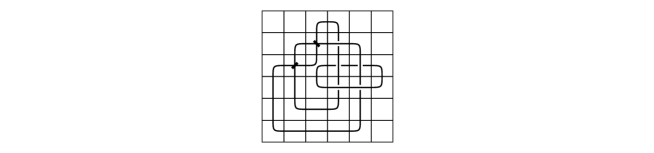
The mosaic number of is six whose mosaic diagram is described in Figure 15.
4 Mosaics for immersed surface-links via singular marked graph diagrams
We introduce the mosaic system for representing immersed surface-links in using singular marked graph diagrams and construct additional mosaic moves to the mosaic moves as shown in Figures 13 and 14, for the equivalence of immersed surface-links.
Let and denote the mosaic tiles with one singular vertex as described in Figure 16.

Note that and are identical by rotation and possess four connection points. The set is defined as the collection of all tiles , i.e. The introduction of these two additional mosaic tiles to naturally extends the various concepts defined in into .
From now on, the entries of an -mosaic are tiles in and the sets consist of -mosaics and -mosaics are denoted by and , respectively.
Definition 3.
A singular marked graph -mosaic is an -mosaic in which all tiles are suitably connected. If , then it is called a singular marked graph -mosaic. Their sets are denoted by and , respectively.
Example 3.
The immersed surface-link is represented by the singular marked graph -mosaic as illustrated in Figure 17.
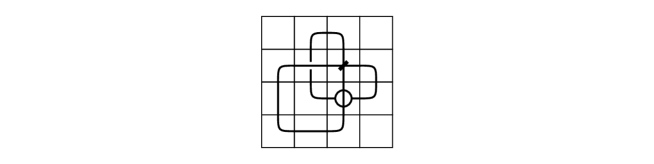
For the equivalence of immersed surafce-links, there are planar isotopy and singular Yoshikawa moves as depicted in Figrue 4. In order to construct mosaic moves for the equivalence of singular marked graph mosaics corresponding to the equivalence of immersed surafce-links, in the case of planar isotopy, we need four mosaic moves and as illustrated in Figure 18.
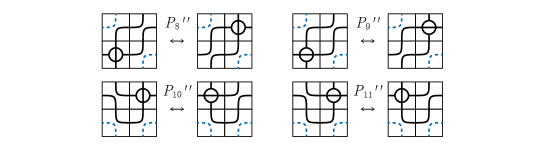
The mosaic moves for singular Yoshikawa moves are the same with marked graph mosaic moves in Figure 14. The mosaic moves for moves are as described in Figure 19.
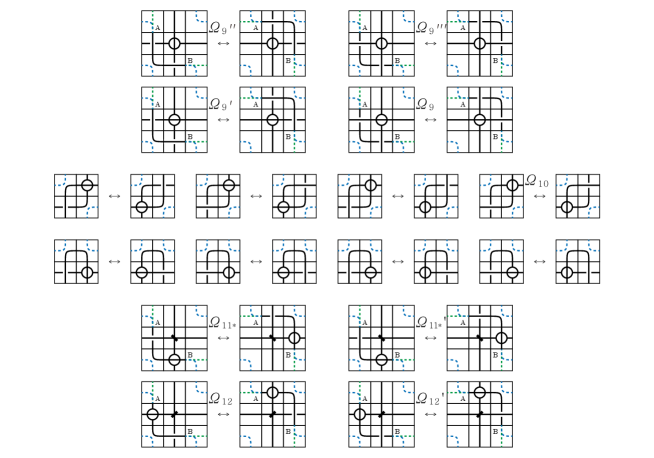
All mosaic moves are permutations on the set of -mosaics. Indeed, they are also in the group of all permutations of the set of singular marked graph -mosaics.
Definition 4.
The ambient isotopy group is the subgroup of the group of all permutations of the set generated by all planar isotopy moves and all singular Yoshiakawa moves.
Two singular marked graph -mosaics and are said to be of the same singular marked graph -type, denoted by if there exists an element of such that it transforms into . Two singular marked graph -mosaics and are said to be of the same singular marked graph type if there exists a non-negative integer such that
where is the mosaic injection by adding a row and a column consisting of only empty tiles.
By the construction of mosaic moves for singular marekd graph mosaics, we have
Theorem 3.
Let and be two singular marked graph mosaics of two immersed surface-links and , respectively. Then and are of the same singular marked graph type if and only if and are equivalent.
Therefore, by Theorem 3, two singular marked graph mosaics and are said to be of the same immersed surface-link type
if they are of the same singular marked graph type.
To illustrate the oriented case, one can explore all the potential types for assigning orientations to each unoriented mosaic tile. The oriented tiles with one singular vertex are shown in Figure 20 and the orientation of other tiles was introduced in [2, 15]. Consequently, the establishment of an oriented mosaic theory guarantees the congruence of orientations with the original theory, thereby ensuring seamless alignment between the two approaches.

5 Mosaic numbers
The mosaic number for an immersed surface-link can be defined in the same manner using singular marked graph diagrams. In this section, we only consider the case of immersed surface-links with at least one singular vertex.
Definition 5.
The mosaic number of an immersed surface-link , denoted by , is the smallest integer for which can be represented by an -mosaic.
By the construction, we have
Theorem 4.
The mosaic number is an invariant for immersed surface-links.
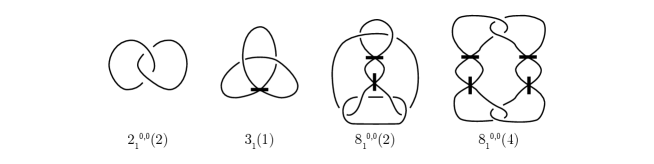
For example, the immersed surface-link whose diagram is described in Figure 2 has a -mosaic diagram and it can be changed to a -mosaic diagram as shown in Figure 21, by using mosaic moves.
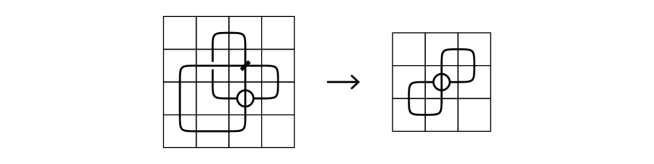
Notice that when the mosaic number is , there is exactly one case, and it is precisely . It is also obvious that the mosaic number of is as described in Figure 22.
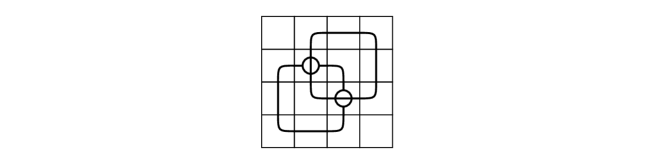
The chs-index of an immersed surface-link can be defined as the minimal number of over all singular marked graph diagrams of where is the total number of crossings, marked vertices, and singular vertices in .
Lemma 5.
Let be an immersed surface-link with the chs-index greater than or equal to . If has exactly one singular vertex, then .
The inner tiles are tiles of a -mosaic diagram whose all connection points except boundary points meet the connection points of contiguous tiles. For example, see the -mosaic diagram in the left side of Figure 23.
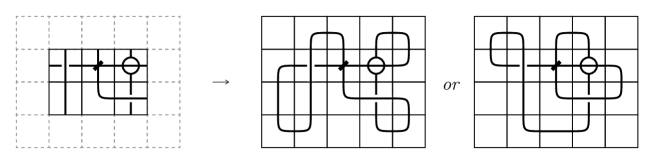
If we add boundary tiles to given inner tiles in order to connect the boundary connection points so that the whole tiles are suitably connected, then we get two mosaic diagrams. This is known as the twofold rule in [19] and it is useful to calculate the mosaic numbers. Note that from the suitably connected condition, crossings, marked vertices, and singular vertices can be located in the position of inner tiles.
Proof.
When , it is clear that . Consider the cases that or . Suppose that . Let be a -mosaic diagram of . Since the number of inner tiles in is nine and since it has only one singular vertex, there exists at least one row such that it has no singular vertices, up to rotations, as depicted in Figure 24.
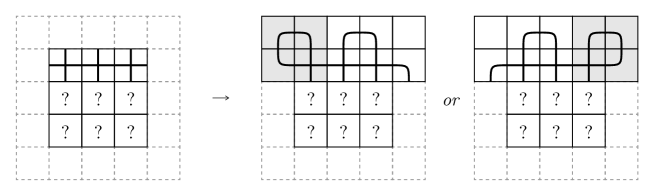
By the twofold rule, the resulting diagrams have at least one kink with one classical crossing or marked vertex.
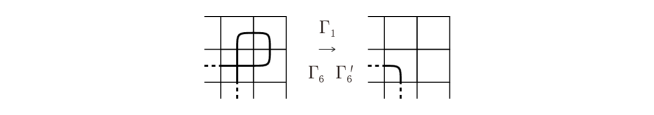
By applying Yoshikawa moves or , the kink can be removed in Figure 25. This contradicts that or . Hence .
Acknowledgement
All authors equally contribute this paper. The work of Seonmi Choi was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2021R1I1A1A01049100) and the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2022R1A5A1033624). The work of Jieon Kim was supported by Young Researchers Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science and Technology (NRF- 2018R1C1B6007021).
References
- [1] S. Carter, S. Kamada and M. Saito, Surfaces in 4-sapce, Springer, (2000).
- [2] S. Choi and S. Nelson, Marked graph mosaics, preprint, https://doi.org/10.48550/arXiv.2301.00287.
- [3] M. Hughes, S. Kim and M. Miller, Isotopies of surfaces in 4–manifolds via banded unlink diagrams, Geom. Topol., 24 (2020), 1519–1569.
- [4] M. Hughes, S. Kim and M. Miller, Banded diagrams of immersed surfaces in 4-manifolds, preprint, https://doi.org/10.48550/arXiv.2108.12794.
- [5] M. Jabłonowski, Minimal generating sets of moves for surfaces immersed in the four-space, preprint, https://doi.org/10.48550/arXiv.2208.08244.
- [6] S. Kamada, Braid and Knot Theory in Dimension Four, American Mathematical Society, (2002).
- [7] S. Kamada, Surface-knots in 4-space; An introduction, Springer, (2017).
- [8] S. Kamada and K. Kawamura, Ribbon-clasp surface-links and normal forms of immersed surface-links, Topology Appl., 230, (2017), 181–193.
- [9] S. Kamada, A. Kawauchi, J. Kim and S.Y. Lee, Presentation of immersed surface-links by marked graph diagram, J. Knot Theory Ramifications, 27 (10), (2018), 1850052(10pp).
- [10] A. Kawauchi and J. Kim, Immersed 2-knots with essential singularity, Topology Appl., 264, (2019), 462–472.
- [11] A. Kawauchi, T. Shibuya and S. Suzuki, Descriptions on surfaces in four-space I, Normal forms, Math. Sem. Notes Kobe Univ., 10, (1982), 75–125.
- [12] C. Kearton and V. Kurlin, All 2-dimensional links in 4-space live inside a universal 3-dimensional polyhedron, Algebr. Geom. Topol., 8 (3), (2008), 1223–1247.
- [13] J. Kim, An enumeration of immersed surface-links in 4-space, Topology Appl., 279, (2020), 107241(12pp).
- [14] T. Kuriya and O. Shehab, The Lomonaco-Kauffman conjecture, J. Knot Theory Ramifications, 23 (1), (2014), 1450003(20pp).
- [15] S. J. Lomonaco and L. H. Kauffman, Quantum knots and mosaics, Quantum Inf. Process., 7, (2008), 85–115.
- [16] K. Hong, H. Lee, H. J. Lee and S. Oh, Small knot mosaics and partition matrices, J. Phys. A: Math. Theor., 47 (43), (2014), 435201(13pp).
- [17] H. J. Lee, K. Hong, H. Lee and S. Oh, Mosaic number of knots, J. Knot Theory Ramifications, 23 (13), (2014), 1450069(8pp).
- [18] H. J. Lee, L. D. Ludwig, J. S. Paat and A. Peiffer, Knot mosaic tabulation, Involve, 11 (1), (2018), 13–26.
- [19] S. Oh, K. Hong, H. Lee and H. J. Lee, Quantum knots and the number of knot mosaics, Quantum Inf. Process., 14 (3), (2015), 801–811.
- [20] F. J. Swenton, On a calculus for 2-knots and surfaces in 4-space, J. Knot Theory Ramifications, 10 (8), (2001), 1133–1141.
- [21] K. Yoshikawa, An enumeration of surfaces in four-space, Osaka J. Math., 31 (3), (1994), 497–522.
Nonlinear Dynamics and Mathematical Application Center
Kyungpook National University
Daegu, 41566, Republic of Korea
Department of Mathematics
Pusan National University
Busan, 46241, Republic of Korea