Motion-selective coherent population trapping by Raman sideband cooling along two paths in a configuration
Abstract
We report our experiment on sideband cooling with two Raman transitions in a configuration that allows selective coherent population trapping (CPT) of the motional ground state. The cooling method is applied to 87Rb atoms in a circularly-polarized one-dimensional optical lattice. Owing to the vector polarizability, the vibration frequency of a trapped atom depends on its Zeeman quantum number, and CPT resonance for a pair of bound states in the configuration depends on their vibrational quantum numbers. We call this scheme motion-selective coherent population trapping (MSCPT) and it is a trapped-atom analogue to the velocity-selective CPT developed for free He atoms. We observe a pronounced dip in temperature near a detuning for the Raman beams to satisfy the CPT resonance condition for the motional ground state. Although the lowest temperature we obtain is ten times the recoil limit owing to the large Lamb-Dicke parameter of 2.3 in our apparatus, the experiment demonstrates that MSCPT enhances the effectiveness of Raman sideband cooling and enlarges the range of its application. Discussions on design parameters optimized for MSCPT on 87Rb atoms and opportunities provided by diatomic polar molecules, whose Stark shift shows strong dependence on the rotational quantum number, are included.
I INTRODUCTION
Raman sideband cooling (RSC) is by far the most effective method to laser cool trapped atoms. The method can put atoms into the motional ground state with high probability when the Lamb-Dicke condition is satisfied. Here, is the Lamb-Dicke parameter, is the vibrational frequency of a trapped atom, and is the recoil energy accompanying an emission of a photon. RSC was originally developed for an ion in a Paul trap Wineland1989 where Coulomb interaction makes the Lamb-Dicke condition well satisfied. However, it is difficult to satisfy the condition in an optical dipole trap, and only a lattice configuration with a submicron confinement has . Early experiments applied RSC to cesium atoms in an optical lattice as a precooling stage aiming at quantum degeneracy Weiss2000 ; Chu2000 . Recently, rubidium atoms were cooled by RSC to the quantum degeneracy in a dynamically controlled optical lattice without resorting to evaporative cooling Vuletic2017 . A single atom in an optical tweezer was also cooled to the motional ground state by employing either a very tight focusing Regal2012 or an RSC sequence tailored to address high-order sidebands Ni2018 .
The order of the red sideband used in RSC should be larger than a few times for the energy deficit by the red-detuned transition to exceed the recoil heating during an optical pumping (OP) cycle. When , tuning the Raman transition to the first-order red sideband achieves the net cooling, and the state is the only dark state, where atoms accumulate. Here, is the vibrational quantum number. However, as increases, should also be increased, and the state is no longer the only dark state. Atoms distribute over larger raising temperature above the recoil limit . is the Boltzmann constant. In this paper, we introduce a cooling method that incorporates -selective coherent population trapping (CPT) to RSC so that the motional ground state remains the only dark state even outside the Lamb-Dicke regime. We call this method motion-selective coherent population trapping (MSCPT), and it is a trapped-atom analogue to the velocity-selective coherent population trapping developed for subrecoil cooling of free He atoms VSCPT 1988 . We apply the method to 87Rb atoms in a 1D optical lattice. Although we cannot reach the subrecoil temperature because we use an existing apparatus, which is not optimal for MSCPT in a few regards, we achieve temperature of for the transverse motion, where , and demonstrate that the method enhances the effectiveness of RSC and enlarges the range of its application.
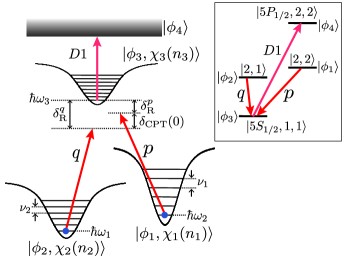
II Theory
Figure 1 shows the inverted configuration for our MSCPT experiment. In the inset, specific levels and transitions in 87Rb are assigned: , , , and . is the total angular momentum and is its component. A usual RSC consists of a red-detuned Raman transition , which we call transition, and the transition for an OP back to . To incorporate -selective CPT, we add Raman transition to form a configuration, and use a circularly polarized trap beam so that owing to the vector polarizability. Here, and are the vibration frequencies of the motional states, and , for the potential wells of and , respectively. When and pairs of Raman beams are tuned to the resonance between the and states, the motional ground states form a CPT dark state. A pair of and states, in general, are detuned from the CPT resonance by , where , and a pair with the larger is brighter. Atoms accumulate in the low- states, which are comparatively darker. in a circularly polarized trap is
| (1) |
where and are the scalar and vector polarizabilities, respectively, and is the vibration frequency in a linearly polarized trap optical Ster-Gerlach . Heavy alkali-metal atoms with large are favored for MSCPT. For 87Rb atom, if the trap wavelength is 860 nm and , Hz, while the full width at half maximum (FWHM) of the CPT resonance in our radio frequency (rf) experiment was 150 Hz M1 CPT . In our recent publication MSCPT theory , we write the master equations that describe the MSCPT scheme in Fig. 1, and solve them numerically to show that MSCPT performs better than RSC, and even at it can cool atoms below under a favorable, but experimentally feasible, condition.
Another advantage of the inverted configuration is that it is a closed system. The state decays only to one of the , , and states with the probability and , respectively. While the RSC scheme of requires repumping from and, on average, three OP cycles to pump an atom from to , MSCPT in the inverted does not require repumping, and two OP cycles are sufficient. Each OP cycle, consisting of an absorption and a spontaneous emission, causes a recoil heating of . The transition is used to avoid an off-resonant transition and subsequent decay to a state outside the . In our previous work M1 CPT , using optically trapped 7Li atoms and rf fields for and transitions, we demonstrated that the inverted exhibited CPT phenomena of a closed system in a wide range of experimental parameters.
There are a few challenges to experimentally realize the idea of MSCPT. The decoherence rate between the and states should be minimized. Noise in a magnetic field and phase of the Raman beams are the main sources, and experimental techniques normally reserved for precision spectroscopy are required. A high-density atomic sample is not suitable for MSCPT because the Raman and the OP beams, which stay on throughout the cooling process, will cause photo-associative loss of atoms. In addition, collisions between the atoms contribute to collisional dephasing . Although the experiment we report here is carried out using a medium-density sample, MSCPT is best suited for a single atom in an optical lattice or an optical tweezer. Cooling by MSCPT also proceeds slower than that by RSC because even a superposition of states is partially dark, reducing the Raman transition rate. There can also be a parasitic CPT dark state with a large .
III Apparatus
We use a double magneto-optical trap (MOT) system with an octagonal glass chamber for the second MOT. A pair of spherical mirrors, engraved on diagonal windows of the octagon, form a Fabry-Perot cavity for a 1D optical lattice PMSW RSC . At the design wavelength of 980 nm, FWHM of the cavity resonance is 13 MHz and the minimum spot size is 50 m. Optical mounts, coils, and a 6.8-GHz rf antenna surround the octagon, and a double-layer magnetic shield is installed. Fluorescence from atoms is imaged to an electron-multiplying charge-coupled device camera with a numerical aperture of 0.28 and a threefold magnification.
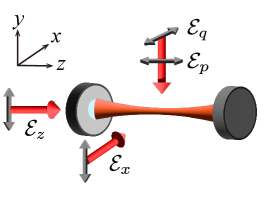
Each of the and Raman transitions in Fig. 1 requires two laser beams, and their arrangement is shown in Fig. 2. The beam propagating along and polarized along pairs with each of orthogonally polarized and applied along to drive and transitions, respectively. In this way, linear momentum transferred to an atom by a transition is the same as that by a transition, neglecting the Zeeman shift of less than 1 MHz between and . Otherwise, and make and transitions, respectively, to groups of with different , and destructive interference of the transition amplitudes for CPT is incomplete MSCPT theory . The Raman beams are linearly polarized so that they do not cause a differential ac Stark shift between the and states. The beam is blue detuned from the transition by 30 GHz, and the and beams are derived from it by using a fiber electro-optic modulator operating at 6.8 GHz and two acousto-optic modulators PMSW RSC . Oscillators driving the modulators are phase locked to an atomic clock. Furthermore, we add a phase-lock loop for beating between and , obtained immediately before the two beams enter the chamber, because phase stability between them is critical in reducing . For 3D cooling, we add an beam which plays the same role as in the plane. The beam is added to complete the inverted configuration. We take much care to control its polarization to avoid an unintended transition out of and subsequent decay outside . We use its intensity to control the effective decay rate of , and hence, the width of the Raman transitions.
IV Experiment and results
Atoms are loaded into the 1D lattice and its depth is lowered to K. At this depth, inhomogeneous broadening from the vector polarizability cancels that from anharmonicity for the red (blue) sideband of motion when the lattice beam is left (right) circularly polarized PMSW RSC . It narrows the sideband to facilitate RSC along the axis. At K and m, along the transverse direction, = 700 Hz and , being far from the Lamb-Dicke regime. At = 980 nm, and in atomic units for 87Rb, and Hz from Eq. (1). Longitudinally, kHz, , and kHz. Atoms in the lattice show a Gaussian distribution with 100 atoms per site at the center and the standard deviation of 300 sites. Their temperature is 20 K.
As a preliminary experiment, we apply RSC in the transverse plane while changing the Raman detunings, defined as and in Fig. 1. Here, () is the difference between frequencies of the () and beams in Fig. 2, and is the energy of the state for . In this experiment, we keep while detuning from the CPT resonance for the pair of states, , is close to zero. In general, CPT detuning for the th pair is
| (2) |
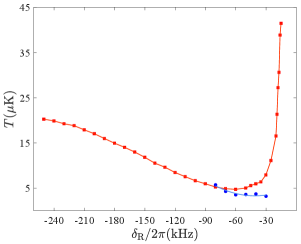
and hence, are referenced to the differences, and , which are measured by 6.8-GHz rf spectroscopy. However, in a circularly polarized lattice, the rf lineshape is asymmetric and broad rf spectroscopy , and extracting the difference by fitting a theoretical curve to a lineshape is susceptible to errors. We estimate the uncertainty to be 1 kHz. For the experiment, atoms are optically pumped to , and , , and the OP beams are applied. The quantization field is 1 G, the Rabi frequencies are kHz and kHz for and transitions, respectively, and kHz. After the beams are applied for 3 s, only 20% of the atoms are left mainly owing to the photo-associative loss. The transverse temperature is measured by the time-of-flight method. Red squares in Fig. 3 denote versus the common detuning . increases sharply near kHz, which is the minimum red detuning to overcome the recoil heating of . The lowest of 4.7 K is obtained at kHz, limited by the cross-dimensional heating by the motion. We add the beam, tuned to the red sideband of the motion, and obtain the lowest of 3.0 K at kHz, as represented by blue circles in Fig. 3. Removing the heat load from the motion allows us to use smaller , which, in turn, narrows the distribution of the atoms over . The cooling time required to reach the steady state is also reduced to 2 s. Although addition of the beam adds another configuration, it does not interfere with MSCPT in the plane because, once an atom falls into the state, transitions driven by are far-off resonant.
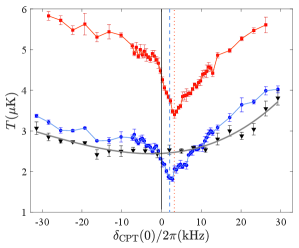
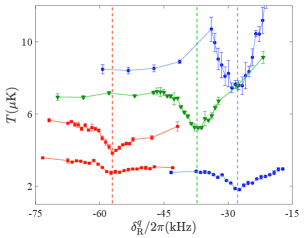
As we scan by changing , a pronounced dip in appears, demonstrating the extra cooling effect of MSCPT. Figure 4 shows the results from an experiment in 2D at kHz (red square) and that in 3D at kHz (blue circle). For a direct comparison with RSC in 3D, we alternately turn on the and beams at 1 kHz for 4 s while and stay on. The results (black triangle) show gradual change in without a dip. In the 2D MSCPT experiment, the lowest of 3.4 K occurs at kHz, and in 3D, K at kHz. Ideally, the lowest should be at , and we interpret this shift as a result of the width of the Raman transition being much smaller than . The half-width at half maximum, contributed by the power and radiative broadening, for the and transition is 3.3 kHz and 5.5 kHz, respectively. The low- states are already dark owing to the much larger Raman detuning, and the CPT does not have an impact on the atoms in those states. From Eq. (2), at positive , is CPT resonant for the states, and we conjecture that the observed position of the dip is where the CPT-induced darkness can best complement that induced by to produce the lowest . at the dip in 2D with kHz is one and a half times that in 3D with kHz, and it is consistent with the conjecture. The 1D simulations also show that MSCPT loses advantage over RSC when the Raman width is much smaller than MSCPT theory . In our experiment, the available laser power and the loss of atoms from photo-association limit and , and hence, the range of the Raman width. In addition to being the result of an extra cooling effect, the dips are, to the best of our knowledge, the first observation of CPT phenomena driven by a pair of stimulated Raman transitions. To confirm this, we repeat scans at a few . The results are shown in Fig. 5: three upper traces from the right to the left are at and -60 kHz in 2D, and two lower traces are at and -60 kHz in 3D. The dips appear when , independent of and themselves.
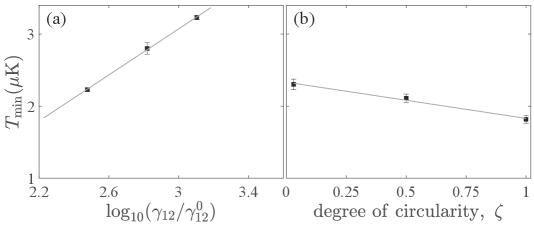
In MSCPT, it is critical to minimize the decoherence rate between and . We consider two sources for : noise in a magnetic field and phase fluctuation between the and beams. For a given , is proportional to , and we use the hyperfine transition between and as a substitute for the transition to measure . The ladder structure of the Zeeman sublevels in the state makes spectroscopy on the isolated and states difficult. In order to be free from inhomogeneous broadening, we use spin-echo spectroscopy on atoms in a linearly polarized lattice at the well depth of only 11 K. With a two-layer magnetic shield and a low-noise current supply, from at G is Hz. from , estimated from an rf spectrum of the beating between and , is Hz and it is reduced to Hz when the beating signal is phase locked to an atomic clock. Figure 6(a) shows the lowest in 3D MSCPT versus , where Hz. is increased by injecting white noise to the rf which modulates the beam. We observe gradual disappearance of the dip and an increase in . Finally, we change the degree of circularity of the lattice beam, , where is the Jones vector. For a given , in Eq. (1) is reduced to . Figure 6(b) shows the increase in the lowest in 3D MSCPT as the lattice polarization becomes linear. When the polarization is linear, a peak as well as a dip in appears as we scan , indicating unintended trapping of population at high- states.
V Summary and Discussion
In summary, we apply Raman sideband cooling in a configuration to atoms in a circularly-polarized 1D optical lattice. State-dependent variation in vibration frequency allows us to tune the Raman beams for coherent population trapping of the motional ground states. Although we observe CPT dark state of the low- states only and not the state and the lowest temperature obtained is 10 times the recoil limit, our results clearly demonstrate -selective CPT phenomena and a cooling efficiency better than that of RSC. To realize the full benefit of the MSCPT scheme, we are building an apparatus optimized for the scheme. The apparatus used in the experiment reported here has and nm, resulting in too closely spaced vibrational levels and too small , respectively. The design parameters of the present and the new apparatus are compared in Table I. Fivefold reduction of at the same well depth reduces to 1, increasing from 700 Hz to 3.5 kHz. This reduces the density of states in the plane by a factor of 25, decreasing the number of diffusive steps required to reach the ground state. At nm, increases by a factor of 2.5. With the new design parameters, increases from 5 Hz to 65 Hz, and we expect significant enhancement in the selectivity. The photon scattering rate also increases by 2.5, but it is still less than Hz. Finally, we note that a diatomic polar molecule in an optical trap polar molecule provides an excellent opportunity to apply MSCPT because its Stark shift depends strongly on the rotational quantum number. Considering a MgF molecule in a 532-nm optical trap as an example, the fractional difference between vibration frequencies of a pair of states in the same ro-vibrational level can be as large as 12%. This may be compared with of less than 2% for 87Rb in the new design.
| present apparatus | new apparatus | |
| (K) | 125 | 125 |
| (m) | 50 | 10 |
| 2.3 | 1.0 | |
| (kHz) | 0.7 | 3.5 |
| (nm) | 980 | 860 |
| (atomic unit) | -873 | -1893 |
| (atomic unit) | -25 | -139 |
| (Hz) | 5 | 65 |
| (Hz) | 0.03 | 0.07 |
ACKNOWLEDGMENTS
This work was supported by the National Research Foundation of Korea (Grant No. 2017R1A2B3002543).
References
- (1) F. Diedrich, J. C. Bergquist, W. M. Itano, and D. J. Wineland, Laser Cooling to the Zero-Point Energy of Motion, Phys. Rev. Lett. 62, 403 (1989).
- (2) D.-J. Han, S. Wolf, S. Oliver, C. McCormick, M. T. DePue, and D. S. Weiss, 3D Raman Sideband Cooling of Cesium Atoms at High Density, Phys. Rev. Lett. 85, 724 (2000).
- (3) A. J. Kerman, V. Vuletić, C. Chin, and S. Chu, Beyond Optical Molasses: 3D Raman Sideband Cooling of Atomic Cesium to High Phase-Space Density, Phys. Rev. Lett. 84, 439 (2000).
- (4) J. Hu, A. Urvoy, Z. Vendeiro, V. Crépel, W. Chen, V. Vuletić, Creation of a Bose-condensed gas of 87Rb by laser cooling, Science 358, 1078 (2017).
- (5) A. M. Kaufman, B. J. Lester, and C. A. Regal, Cooling a Single Atom in an Optical Tweezer to Its Quantum Ground State, Phys. Rev. X 2, 041014 (2012).
- (6) Y. Yu, N. R. Hutzler, J. T. Zhang, L. R. Liu, J. D. Hood, T. Rosenband, and K.-K. Ni, Motional-ground-state cooling outside the Lamb-Dicke regime, Phys. Rev. A 97, 063423 (2018).
- (7) A. Aspect, E. Arimondo, R. Kaiser, N. Vansteenkiste, and C. Cohen-Tannoudji, Laser Cooling below the One-Photon Recoil Energy by Velocity-Selective Coherent Population Trapping, Phys. Rev. Lett. 61, 826 (1988).
- (8) C. Y. Park, J. Y. Kim, J. M. Song, and D. Cho, Optical Stern-Gerlach effect from the Zeeman-like ac Stark shift, Phys. Rev. A 65, 033410 (2002).
- (9) H. Kim, H. S. Han, T. H. Yoon, and D. Cho, Coherent Population Trapping in a Configuration Coupled by Magnetic Dipole Interactions, Phys. Rev. A 89, 032507 (2014).
- (10) H. G. Lee, S. Park, M. H. Seo, and D. Cho, Motion-selective coherent population trapping for subrecoil cooling of optically trapped atoms outside the Lamb-Dicke regime, arXiv:2205.00685 [physics.atom-ph].
- (11) Y. Sagi, I. Almog, and N. Davidson, Universal Scaling of Collisional Spectral Narrowing in an Ensemble of Cold Atoms, Phys. Rev. Lett. 105, 093001 (2010).
- (12) M. H. Seo, S. Park, and D. Cho, Relaxation of atomic temperature anisotropy in a one-dimensional optical lattice enhanced by dynamic control of the aspect ratio, Phys. Rev. A 101, 043611 (2020).
- (13) S. Park, M. H. Seo, and D. Cho, Ground-state hyperfine spectroscopy of 87Rb atoms in a 1D optical lattice, J. Phys. B: At. Mol. Opt. Phys. 52, 235002 (2019).
- (14) L. Anderegg, B. L. Augenbraun, Y. Bao, S. Burchesky, L. W. Cheuk, W. Ketterle, and J. M. Doyle, Laser Cooling of Optically Trapped Molecules, Nat. Phys. 14 890 (2018).