Moving in a 360 World:
Synthesizing Panoramic Parallaxes from a Single Panorama
Abstract
We present Omnidirectional Neural Radiance Fields (OmniNeRF), the first method to the application of parallax-enabled novel panoramic view synthesis. Recent works for novel view synthesis focus on perspective images with limited field-of-view and require sufficient pictures captured in a specific condition. Conversely, OmniNeRF can generate panorama images for unknown viewpoints given a single equirectangular image as training data. To this end, we propose to augment the single RGB-D panorama by projecting back and forth between a 3D world and different 2D panoramic coordinates at different virtual camera positions. By doing so, we are able to optimize an Omnidirectional Neural Radiance Field with visible pixels collecting from omnidirectional viewing angles at a fixed center for the estimation of new viewing angles from varying camera positions. As a result, the proposed OmniNeRF achieves convincing renderings of novel panoramic views that exhibit the parallax effect. We showcase the effectiveness of each of our proposals on both synthetic and real-world datasets.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/b9a152d0-c23f-4473-8564-9744a35cc75f/x1.png)
1 Introduction
Synthesizing novel views with parallax provides immersive 3D experiences [26]. Traditional computer vision solutions employ reconstruction techniques (e.g., structure from motion [5] and image-based rendering [24, 25]) using a set of densely captured images. However, these approaches suffer from the cost of matching and reconstruction computation for both time and capacity. The recent development in this field focuses on deep learning methods for its strong capability of modeling 3D geometry and rendering new frames.
While many techniques are proposed to synthesize novel views by taking the perspective image(s) as the input, prior work rarely considers the panorama image as a single source for modeling and rendering. Although perspective images can be acquired conveniently, in order to construct a full scene, it requires a set of dense samples. Furthermore, additional camera variables are essential for estimating relative poses and matching. Recently, 360 cameras have become more easily accessible, with a growing number of panoramas shared on media and 360 datasets released. In a snapshot, it provides an omnidirectional field-of-view, facilitating structure inference and 3D modeling [35]. This work is in the intersection of novel view synthesis and panoramic imaging, and we propose the first method to animate a single static panoramic photo with motion parallax.
We aim to take the full advantage of a single panorama, which collects a set of viewing directions intersecting at a center and thus suffers no matching problems. The panorama can further be projected to 3D coordinates with auxiliary depth information. In this work, we transform the view synthesis problem into a subsampling task respect to the full scene, without using additional images and camera parameters. With the implicit representation of Neural Radiance Field (NeRF) [16], the full scene is formed by a continuous function , which maps 5D coordinates to actual color and density. In NeRF, the whole 3D scene is encoded in weights of a deep fully-connected neural network (a multi-layer perceptron model), which takes the ray origin and ray direction as input. For 2D perspective images, emitted viewing directions are computed from camera parameters. Real-world data might be captured by different cameras with distinct parameters, and to calculate these parameters entails an additional effort. Accordingly, we propose to derive the NeRF-based representation from the viewpoint of 360 panorama. The ray origin is simply the coordinate center. Ray directions are the unit vectors from 3D pixel coordinates to the center, which can be obtained by mapping 2D image coordinates to its 3D position along horizontal and vertical axis respectively, based on the auxiliary depth information. These unit vectors are fixed for every panorama, which alleviates the complexity of calculating viewing directions for different input images.
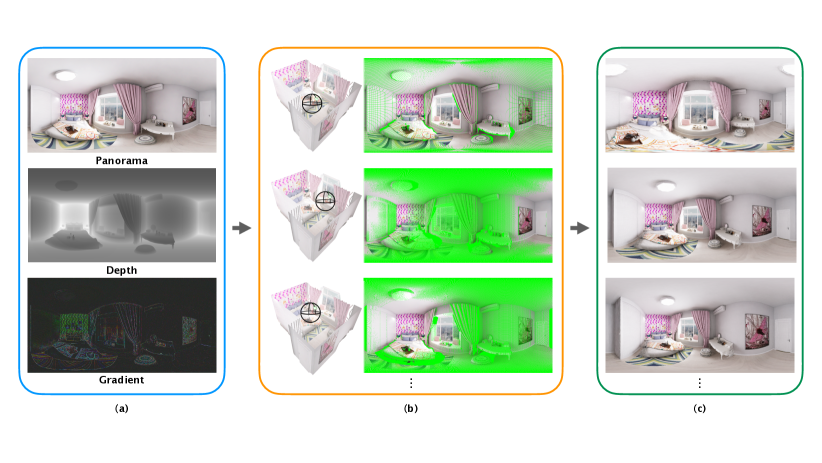
For a reconstruction task, training with merely a single input sample is apparently not sufficient to create convincing results. Methods trained on perspective images usually require to or more samples, depending on the size of the scene and the camera moving distance. We propose a method to augment omnidirectional training data from size one to any desired amount. With an auxiliary depth map being provided, we can retrieve a portion of the actual coordinates of the scene, through multiplying the directional unit vectors by the depth values. To generate a training image at an arbitrary camera position, we translate the center to a target position and project the 3D coordinates back to 2D image space, so that we can produce a ‘likely-to-be’ panorama from a novel viewpoint. However, this panorama is incomplete and the information would be missing due to limited resolution and occlusion. Therefore, cracks and seams appear between pixels when the camera moves. We leverage the pixel-based representation in NeRF and present Omnidirectional Neural Radiance Field (OmniNeRF) to solve the problem. With the new OmniNeRF representation we are free to ignore the missing parts caused by camera translation, and only take account of the valid parts for constructing our training data. Fig. 2 shows an overview of OmniNeRF.
With the operations under OmniNeRF, camera parameters are not needed, and thus we subside the cost and reduce the error for calculating correspondences between different input images in common perspective settings. The partially available 3D coordinates from a single RGB-D panorama enable free camera movements and allow back-and-forth projections between 3D and 2D spaces for augmenting the training data. We show that the proposed OmniNeRF can render visually plausible results on the new application of novel panoramic view synthesis with parallax effects.
2 Related work
Novel view synthesis
Novel view synthesis has a long history in computer vision for reconstructing or modeling a scene from the acquisition of multi-view 2D pictures of the surroundings. Traditionally, the reference of 3D reconstruction could be a precise 3D model or an approximated representation. Previous methods mainly address 3D reconstruction by applying multi-view stereo and warping strategies for aggregating information among images. Structure from motion [5] is able to produce sparse point clouds and retrieve camera parameters. Previous methods on novel view synthesis often rely on solving structure from motion, including directly using the point cloud and extracted features [20], or leveraging generated camera parameters [10]. Mesh-based approaches are more common in 3D model reconstruction [2, 4, 6, 7, 30, 31], and they may be used to create 360 view around center object. However, acquiring sufficient information to model an entire scene with detailed 3D meshes cannot be easily done in real world, and thus is less practical for applications. Another way to achieve novel view synthesis without the need of 3D model is to represent the world in different scales of multi-plane images (MPI). MPI provides foreground and background information to solve visibility problems better for synthesizing novel views [10, 15, 37] or adapting it into inpainting-like tasks [23]. These methods have proposed various representations for deriving more realistic results by incorporating deep learning techniques. While many previous approaches take the perspective image(s) as the input to synthesize novel views, very little prior work has considered synthesizing novel panoramas from a single panorama, except recent methods like [11], which uses concentric mosaics and GAN for stereo panorama conversion, but cannot be easily extended to the application of synthesizing freely-moving novel panoramas as our method.
Neural 3D representation
Recent research on mapping 3D spatial location to an implicit representation has shown promising results on encoding the entire scene into weights of a multi-layer perceptron model. In particular, the technique of neural radiance field (NeRF) [16], presented by Mildenhall et al., has shown its power of rendering complex objects with both high quality and high resolution. NeRF describes the world as a continuous function that maps a 5D coordinates to pixel color and density, where the 5D coordinates include the 3D position of a viewpoint and the horizontal and vertical viewing angles from that view point. Furthermore, NeRF jointly adopts i) positional encoding [29] to embed the input into higher frequency domain and ii) alpha composition [15, 19, 21, 27] to simulate the formation of color for a ray, and, as a result, can achieve impressive results. Niemeyer et al. [17] propose Differentiable Volumetric Rendering (DVR), which is also aimed at learning implicit representation of continuous 3D shapes. DVR does not require ground-truth 3D geometry and can learn the implicit shape and texture representations simply from multi-view 2D images.
The aforementioned neural rendering methods are based on 2D perspective images. These methods need to acquire a sufficient number of images from the scene for learning the implicit representations. Some NeRF variants allow more dynamic or less constrained settings of data acquisition. [18, 22, 33]. Some approaches use online in-the-wild photos to augment the dataset for learning to render identical view but at different time or under different lighting [10, 12, 14]. In our work, the input and output data are 360 panorama images. From a single RGB-D panorama, our method can augment the training data and learn an MLP as implicit scene representation for synthesizing novel 360 panoramas at different locations in the scene.

3 OmniNeRF
We propose OmniNeRF to achieve the goal of synthesizing novel panoramas of a scene at arbitrary viewpoints. The only information available is from an omnidirectional RGB-D image, which would be too limited to train a typical convolutional network directly. The proposed OmniNeRF addresses this issue by augmenting the single RGB-D panorama through back-and-forth projections between 3D world and different 2D panoramic coordinates of different camera poses. The data augmentation mechanism allows us to optimize an Omnidirectional Neural Radiance Field with visible pixels collecting from omnidirectional viewing angles at varying camera locations, and is thus able to train a multi-layer perceptron (MLP) for predicting each pixel in the panorama being viewed from an arbitrary location.
3.1 Generating training samples
Generating novel panoramic views with only one omnidirectional image of the scene is a challenging task. Previous perspective-based methods show promising results on scene reconstruction and new viewpoints rendering by using multi-view data with known camera parameters. Our idea is to adapt a similar process to our scenario by simulating multi-view images from the single RGB-D panorama image. We first produce a set of 3D points from the given RGB-D panorama and then reproject these 3D points into multiple panoramas that correspond to different virtual camera locations. The generated omnidircetional images are likely to be imperfect as there might be gaps and cracks between pixels due to occlusion or limited resolution. OmniNeRF solves this problem by taking advantage of the pixel-based prediction property of its MLP model, which takes a single pixel rather than an entire image as the input. By considering valid pixels only, we are able to augment our training set given that we have a sparse point cloud of the scene derived from the auxiliary depth map of the input RGB-D panorama.
We project the current panorama into 3D coordinates by the following procedure. First, all pixels can be projected to a uniform sphere by their 2D coordinates. For a pixel on the panorama, its vertical and horizontal viewing angles can be defined by , , where and are the height and width of the panorama. The coordinate center would be the current camera position, namely the ray origin. Likewise, a ray direction simply means a unit vector from the center to the sphere. A novel panoramic view can therefore be determined by moving the camera to a new position and examining what would be sampled on the new sphere by the emitted rays based on the above equations. Not all pixels are supposed to be visible from the new viewpoint. Moreover, the sparse source input might wrongly allow a ray to pass through some occluding object, which causes a visibility problem needed to be solved. (We will come back to address this issue in the next section.) Assuming that we have removed the false visible pixels, we then project the points from the new sphere back to the original pose to obtain the final training image. This transformation is crucial because the scene coordinates are defined by the original source image; the coordinate frame should be kept consistent across all camera poses. As a result, the key of our data augmentation mechanism is to verify which parts of the ground truth will be visible to a given ray origin.
To fully sample the scene, our strategy is to transform views along each axis. We uniformly sample the camera poses along x-axis and y-axis, within a range of multiplied a scaling factor . The range is divided into equal intervals to collect the training views. A smaller means that samples would be closer to the center. A larger guarantees better performance while moving farther away from the original center, but the number of applicable pixels would also decrease. We set to balance between quality and displacement. All experiments are trained on incomplete panoramas derived from a single input panorama and its auxiliary depth map.
3.2 Visibility
To produce self-simulated multi-viewpoint panoramic images, we transform an image from the original camera pose to any desired pose. One critical issue is the ambiguity of ray visibility from new viewpoints due to the sparsity of the projected 3D points from only a single image. More specifically, a ray from a translated camera view could “see through” the sparse points of an obstacle and reach a 3D point visible to the original view (see the left-most image in Fig. 3 for an illustration). To mask out the “see-through” rays, we first apply a median filter on the depth map of the translated view. Note that only valid pixels on the depth map should be considered. We then simply filter out pixels whose depth values are larger than the local median depth multiplied by a tolerance ratio (which is set to in this work). With this simple modification, we can remove most of the incorrect “see-through” samples. A visualization demonstrating the effectiveness of our filtering strategy is shown in Fig. 3.
3.3 Concatenating multiple panoramas
Although our method only needs one input panorama, it can also combine multiple omnidirectional images once their relative camera positions are known. Since Matterport3D dataset [3] is the only dataset with multi-view panoramas, we could only apply this experiment on Matterport3D dataset.
3.4 Regressing with gradient
Our initial attempt with the basic setting occasionally suffers from the artifacts of blurry edges, which might come from forcing the model to predict the uncertain regions of the scene. The given training data are not dense enough to cover all areas in the scene; therefore, to render images at new positions would force the model to predict some regions that the model has never seen before. We introduce an additional loss term to improve our model’s performance regarding color gradient prediction. The key of OmniNeRF is to predict unseen pixels between neighboring samples. The model should be able to learn to interpolate from one pixel to another according to ray origin and direction information. Inspired by recent depth estimation methods, e.g. [9], we include a gradient loss term to enforce the structure-preserving property for color prediction. We use a Laplacian filter to obtain the gradient of the ground truth. The gradient loss can help produce smoother color prediction as well as reduce artifacts. However, we are not able to directly compute the output gradient because the input pixels are shuffled (due to 3D reprojection) and thus the neighbor ordering is not maintained. Instead, we add one more head which is parallel to color output in the MLP model to predict gradient. Gradient contains information about neighboring pixels and thus can improve the quality of generated images near boundaries.
3.5 Optimization
The purpose of an implicit neural representation model is to learn a mapping between 3D coordinates and RGB color space. At each discrete sample on the ray , where and denote the ray origin and ray direction, the final RGB values are optimized from aggregation of color and opacity . A positional encoding technique [29] is applied to rays for capturing high frequency information. The function of color composition follows the rule in volume rendering [13]:
| (1) | |||
and is the interval between two adjacent samples. The overall volume sampling principles are done in a hierarchical way: a ‘coarse’ and a ‘refined’ stage. The coarse and refined networks are identical except the process of sampling pixels on a ray. At the coarse stage, intervals are uniformly sampled alone the ray, while at the refined stage, intervals are decided in accordance with densities from the coarse stage. These two predictions would be optimized by the ground-truth color respectively. The overall loss is the sum of two terms: the color loss and the gradient loss. The color loss is simply the loss between the observed color in Eq. (1) and the ground truth. Both the coarse and refined models participate in the optimization process for the composite color. Gradient is aggregated by the same principle as the color term; its loss is also the total squared error between the estimated results and the ground truth.
4 Experiments
4.1 Datasets
We test our method on both synthetic and real-world datasets. In this work, all the panorama images are under equirectangular projection at the resolution of .
Structured3D [36] Structured3D dataset has 3,500 synthetic departments with 18,332 photorealistic panoramas rendering. As the original virtual environment is not publicly accessible, we use the rendered panoramas directly.
Matterport3D [3] Matterport3D dataset is a large-scale indoor real-world 360 dataset, captured by Matterport’s Pro 3D Camera in 90 furnished houses. The dataset provides 10,800 RGB-D panorama images in total, where we find the RGB-D signals near the polar region are missing.
Google Street View [1] Google Street View images are captured by 360 cameras on top of the Street View vehicles or uploaded by users to provide the Google Maps street view services. The accompanied depth is rendered from a facade approximation, so it does not carry detailed information.
For each dataset, we discard scenes that are not feasible for our application, i.e., more than of the pixels do not have depth values. Since our task is to generate novel panoramic views from a single panorama, consequently, the only supervision to the model comes from those pixels with depths, and it is not applicable to learn from a scene with too many missing depths. For Matterport3D, we exclude the polar regions (corresponding to ceiling and floor in most cases) as the RGB-D information is unavailable.
4.2 Implementation details
Training protocol
The Adam optimizer [8] is used for the overall training process. The learning rate is initialized to , which is then exponentially reduced to . The model is trained by 200,000 epochs for each experiment with a batch-size of 1,400 on a GTX 1080 Ti GPU. We follow NeRF [16] to set and in the coarse and refined networks.
 |
 |
 |
 |
 |
 |
 |
 |
 |
| (a) NeRF | (b) OmniNeRF (color only) | (c) OmniNeRF (color + gradient) |
Evaluation protocol
The standard evaluation for perspective novel view synthesis is dividing the images of a scene into training and test sets. Unfortunately, most panoramas we use have no ground-truth nearby panoramic views. Structured3D rendered panoramas with limited view overlapping. Some panoramas in Matterport3D do overlap one another. However, the missing pole region in different views highly affect the quality of rendering outputs, so it is not applicable to evaluate quantitative results on adjacent views. For Google Street View, the relative camera distances are too far. For all datasets, we report the statistics by training the model only on translated camera centers and evaluate the generated results at the original camera position with ground truth RGB on account of the lack of ground-truth nearby views. The quantitative results are reported in Table 1 using PSNR, SSIM [32], and LPIPS [34] to assess the quality of synthesized images.
4.3 Comparison with baselines
Single image training
To showcase the proposed learning method’s effectiveness, we compare it with NeRF, which is trained on one translated nearby view to serve as the baseline. Based on the quantitative evaluation shown in Table 1, it is clear that using the original NeRF setting to learn from a single image leads to inferior results. The proposed OmniNeRF, which learns from a wide range of virtual viewpoints, can significantly outperform the baseline on all datasets and all metrics.
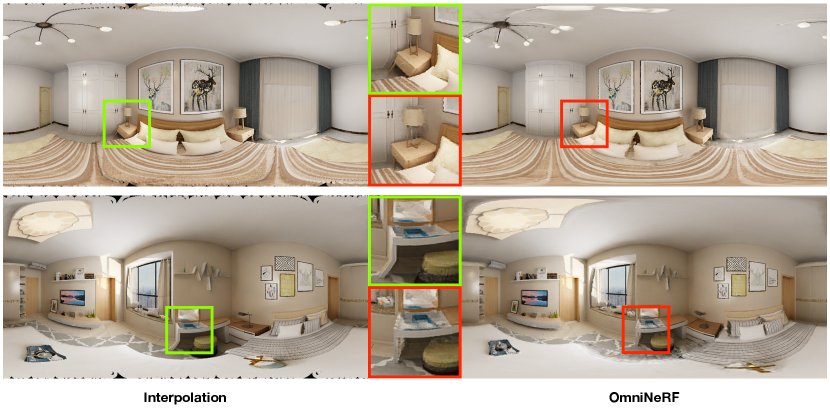
Interpolation from layout
The layout model captures the gist of a scene’s structure, so it is suitable to synthesize new views with camera translation using the layout model. We first obtain the 3D layout output, which is 2D coordinates for 8 indoor room corners, of each scene by running the HorizonNet [28] pre-trained on the Structured3D dataset; then, given the new camera position, we generate the panorama by interpolation from the 3D layout. As there are no ground-truth nearby views, we can only compare with the layout interpolation method qualitatively in Fig. 4.
| Learning method | Aux. gradient loss | PSNR | SSIM | LPIPS |
| Structured3D [36] dataset | ||||
| NeRF | ✓ | 22.459 | 0.842 | 0.136 |
| OmniNeRF | 33.147 | 0.969 | 0.077 | |
| ✓ | 33.249 | 0.968 | 0.073 | |
| Matterport3D [3] dataset | ||||
| NeRF | ✓ | 17.269 | 0.737 | 0.350 |
| OmniNeRF | 31.565 | 0.945 | 0.132 | |
| ✓ | 33.943 | 0.965 | 0.108 | |
| Google Street View [1] dataset | ||||
| NeRF | ✓ | 18.518 | 0.762 | 0.273 |
| OmniNeRF | 33.043 | 0.970 | 0.100 | |
| ✓ | 33.766 | 0.979 | 0.078 | |
4.4 Ablation study
We compare the detailed settings of the objective function for the proposed OmniNeRF in Table 1. Our augmented method significantly improve the performance to a plausible level. Learning with additional gradient supervision further uplifts the resemblance between the generated image and the ground truth. Gradient information carries supervision for local structure-preserving, and it also generates more fine details in the scene. See Fig. 5 for the visualization.
 |
 |
 |
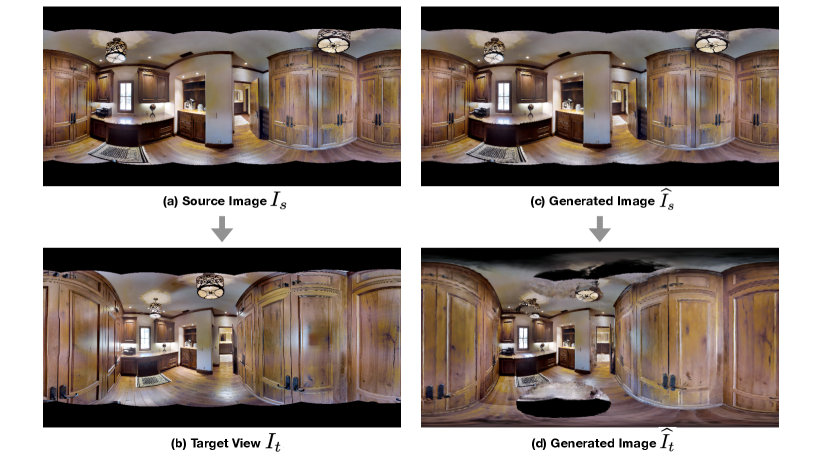
4.5 Comparison with ground truth nearby view
4.6 Qualitative results
We encourage the reader to see the supplementary video demonstration for a fly-through experience provided by our method from just a single panorama.
4.7 Limitation
To examine the limitation of the proposed OmniNeRF for scene coverage from only a single panorama, we render images at a broader range of camera viewpoints and check the quality of the outcomes. Specifically, we manually draw a path to render images at some sample positions in a scene. Some representative results on the three datasets with diverse scenes are visualized in Fig. 6. For irregular or complicated scenes, the single source image does not contain enough information to infer the occlusion and the opposite side of objects, and thus the results are degraded. Our model shows better results for simpler scenes with less occlusion, and the range it can render is therefore broader.
5 Conclusion
This paper presents OmniNeRF, which learns an implicit representation for 360 image rendering from only one single RGB-D panorama. OmniNeRF can synthesize novel panoramic views with the camera moving in the scene. We demonstrate that our augmentation strategy is efficient for providing enough self-simulated multi-viewpoint training samples by leveraging reprojections, transformations, and filtering. Also, it benefits from the property of the MLP model as a pixel-based method, to make use of incomplete appearance. Another advantage of developing rendering techniques for 360 images is that no camera parameters are needed in this pipeline, which alleviates the computation cost and the error from matching between different images. The additional gradient loss also improves the performance to generate realistic images.We show that with OmniNeRF, information embedded in a single RGB-D panorama is capable of constructing novel parallax-enabled panoramas.
References
- [1] Dragomir Anguelov, Carole Dulong, Daniel Filip, Christian Früh, Stéphane Lafon, Richard Lyon, Abhijit S. Ogale, Luc Vincent, and Josh Weaver. Google street view: Capturing the world at street level. Computer, 43(6):32–38, 2010.
- [2] Abhishek Badki, Orazio Gallo, Jan Kautz, and Pradeep Sen. Meshlet priors for 3d mesh reconstruction. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, June 13-19, 2020, pages 2846–2855. IEEE, 2020.
- [3] Angel X. Chang, Angela Dai, Thomas A. Funkhouser, Maciej Halber, Matthias Nießner, Manolis Savva, Shuran Song, Andy Zeng, and Yinda Zhang. Matterport3d: Learning from RGB-D data in indoor environments. In 2017 International Conference on 3D Vision, 3DV 2017, Qingdao, China, October 10-12, 2017, pages 667–676. IEEE Computer Society, 2017.
- [4] Thibault Groueix, Matthew Fisher, Vladimir G. Kim, Bryan C. Russell, and Mathieu Aubry. Atlasnet: A papier-mâché approach to learning 3d surface generation. CoRR, abs/1802.05384, 2018.
- [5] Richard Hartley and Andrew Zisserman. Multiple View Geometry in Computer Vision. Cambridge University Press, 2004.
- [6] Angjoo Kanazawa, Shubham Tulsiani, Alexei A. Efros, and Jitendra Malik. Learning category-specific mesh reconstruction from image collections. In Vittorio Ferrari, Martial Hebert, Cristian Sminchisescu, and Yair Weiss, editors, Computer Vision - ECCV 2018 - 15th European Conference, Munich, Germany, September 8-14, 2018, Proceedings, Part XV, volume 11219 of Lecture Notes in Computer Science, pages 386–402. Springer, 2018.
- [7] Hiroharu Kato, Yoshitaka Ushiku, and Tatsuya Harada. Neural 3d mesh renderer. In 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, June 18-22, 2018, pages 3907–3916. IEEE Computer Society, 2018.
- [8] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In Yoshua Bengio and Yann LeCun, editors, 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings, 2015.
- [9] Zhengqi Li, Tali Dekel, Forrester Cole, Richard Tucker, Noah Snavely, Ce Liu, and William T. Freeman. Learning the depths of moving people by watching frozen people. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 4521–4530. Computer Vision Foundation / IEEE, 2019.
- [10] Zhengqi Li, Wenqi Xian, Abe Davis, and Noah Snavely. Crowdsampling the plenoptic function. In Proc. European Conference on Computer Vision (ECCV), 2020.
- [11] Jie Lu, Yang Yang, Ruiyang Liu, Sing Bing Kang, and Jingyi Yu. 2d-to-stereo panorama conversion using GAN and concentric mosaics. IEEE Access, 7:23187–23196, 2019.
- [12] Ricardo Martin-Brualla, Noha Radwan, Mehdi S. M. Sajjadi, Jonathan T. Barron, Alexey Dosovitskiy, and Daniel Duckworth. Nerf in the wild: Neural radiance fields for unconstrained photo collections. CoRR, abs/2008.02268, 2020.
- [13] Nelson L. Max. Optical models for direct volume rendering. IEEE Trans. Vis. Comput. Graph., 1(2):99–108, 1995.
- [14] Moustafa Meshry, Dan B. Goldman, Sameh Khamis, Hugues Hoppe, Rohit Pandey, Noah Snavely, and Ricardo Martin-Brualla. Neural rerendering in the wild. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 6878–6887. Computer Vision Foundation / IEEE, 2019.
- [15] Ben Mildenhall, Pratul P. Srinivasan, Rodrigo Ortiz Cayon, Nima Khademi Kalantari, Ravi Ramamoorthi, Ren Ng, and Abhishek Kar. Local light field fusion: practical view synthesis with prescriptive sampling guidelines. ACM Trans. Graph., 38(4):29:1–29:14, 2019.
- [16] Ben Mildenhall, Pratul P. Srinivasan, Matthew Tancik, Jonathan T. Barron, Ravi Ramamoorthi, and Ren Ng. Nerf: Representing scenes as neural radiance fields for view synthesis. In ECCV, 2020.
- [17] Michael Niemeyer, Lars M. Mescheder, Michael Oechsle, and Andreas Geiger. Differentiable volumetric rendering: Learning implicit 3d representations without 3d supervision. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, June 13-19, 2020, pages 3501–3512. IEEE, 2020.
- [18] Keunhong Park, Utkarsh Sinha, Jonathan T. Barron, Sofien Bouaziz, Dan B Goldman, Steven M. Seitz, and Ricardo Martin-Brualla. Deformable neural radiance fields, 2020.
- [19] Eric Penner and Li Zhang. Soft 3d reconstruction for view synthesis. ACM Trans. Graph., 36(6):235:1–235:11, 2017.
- [20] Francesco Pittaluga, Sanjeev J. Koppal, Sing Bing Kang, and Sudipta N. Sinha. Revealing scenes by inverting structure from motion reconstructions. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 145–154. Computer Vision Foundation / IEEE, 2019.
- [21] Thomas K. Porter and Tom Duff. Compositing digital images. In Hank Christiansen, editor, Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1984, Minneapolis, Minnesota, USA, July 23-27, 1984, pages 253–259. ACM, 1984.
- [22] Albert Pumarola, Enric Corona, Gerard Pons-Moll, and Francesc Moreno-Noguer. D-nerf: Neural radiance fields for dynamic scenes, 2020.
- [23] Meng-Li Shih, Shih-Yang Su, Johannes Kopf, and Jia-Bin Huang. 3d photography using context-aware layered depth inpainting. In 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition, CVPR 2020, Seattle, WA, USA, June 13-19, 2020, pages 8025–8035. IEEE, 2020.
- [24] Heung-Yeung Shum, Shing-Chow Chan, and Sing Bing Kang. Image-based rendering. Springer, 2007.
- [25] Heung-Yeung Shum and Li-wei He. Rendering with concentric mosaics. In Warren N. Waggenspack, editor, Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH 1999, Los Angeles, CA, USA, August 8-13, 1999, pages 299–306. ACM, 1999.
- [26] Heung-Yeung Shum, King To Ng, and Shing-Chow Chan. A virtual reality system using the concentric mosaic: construction, rendering, and data compression. IEEE Trans. Multim., 7(1):85–95, 2005.
- [27] Pratul P. Srinivasan, Richard Tucker, Jonathan T. Barron, Ravi Ramamoorthi, Ren Ng, and Noah Snavely. Pushing the boundaries of view extrapolation with multiplane images. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 175–184. Computer Vision Foundation / IEEE, 2019.
- [28] Cheng Sun, Chi-Wei Hsiao, Min Sun, and Hwann-Tzong Chen. Horizonnet: Learning room layout with 1d representation and pano stretch data augmentation. In IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2019, Long Beach, CA, USA, June 16-20, 2019, pages 1047–1056. Computer Vision Foundation / IEEE, 2019.
- [29] Matthew Tancik, Pratul P. Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan T. Barron, and Ren Ng. Fourier features let networks learn high frequency functions in low dimensional domains. CoRR, abs/2006.10739, 2020.
- [30] Maxim Tatarchenko, Alexey Dosovitskiy, and Thomas Brox. Multi-view 3d models from single images with a convolutional network. In Bastian Leibe, Jiri Matas, Nicu Sebe, and Max Welling, editors, Computer Vision - ECCV 2016 - 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part VII, volume 9911 of Lecture Notes in Computer Science, pages 322–337. Springer, 2016.
- [31] Nanyang Wang, Yinda Zhang, Zhuwen Li, Yanwei Fu, Wei Liu, and Yu-Gang Jiang. Pixel2mesh: Generating 3d mesh models from single RGB images. In Vittorio Ferrari, Martial Hebert, Cristian Sminchisescu, and Yair Weiss, editors, Computer Vision - ECCV 2018 - 15th European Conference, Munich, Germany, September 8-14, 2018, Proceedings, Part XI, volume 11215 of Lecture Notes in Computer Science, pages 55–71. Springer, 2018.
- [32] Zhou Wang, Alan C. Bovik, Hamid R. Sheikh, and Eero P. Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process., 13(4):600–612, 2004.
- [33] Kai Zhang, Gernot Riegler, Noah Snavely, and Vladlen Koltun. Nerf++: Analyzing and improving neural radiance fields, 2020.
- [34] Richard Zhang, Phillip Isola, Alexei A. Efros, Eli Shechtman, and Oliver Wang. The unreasonable effectiveness of deep features as a perceptual metric. In 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, June 18-22, 2018, pages 586–595. IEEE Computer Society, 2018.
- [35] Yinda Zhang, Shuran Song, Ping Tan, and Jianxiong Xiao. Panocontext: A whole-room 3d context model for panoramic scene understanding. In David J. Fleet, Tomás Pajdla, Bernt Schiele, and Tinne Tuytelaars, editors, Computer Vision - ECCV 2014 - 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part VI, volume 8694 of Lecture Notes in Computer Science, pages 668–686. Springer, 2014.
- [36] Jia Zheng, Junfei Zhang, Jing Li, Rui Tang, Shenghua Gao, and Zihan Zhou. Structured3d: A large photo-realistic dataset for structured 3d modeling. In Proceedings of The European Conference on Computer Vision (ECCV), 2020.
- [37] Tinghui Zhou, Richard Tucker, John Flynn, Graham Fyffe, and Noah Snavely. Stereo magnification: learning view synthesis using multiplane images. ACM Trans. Graph., 37(4):65:1–65:12, 2018.