MUC: Mixture of Uncalibrated Cameras for
Robust 3D Human Body Reconstruction
Abstract
Multiple cameras can provide comprehensive multi-view video coverage of a person. Fusing this multi-view data is crucial for tasks like behavioral analysis, although it traditionally requires camera calibration—a process that is often complex. Moreover, previous studies have overlooked the challenges posed by self-occlusion under multiple views and the continuity of human body shape estimation. In this study, we introduce a method to reconstruct the 3D human body from multiple uncalibrated camera views. Initially, we utilize a pre-trained human body encoder to process each camera view individually, enabling the reconstruction of human body models and parameters for each view along with predicted camera positions. Rather than merely averaging the models across views, we develop a neural network trained to assign weights to individual views for all human body joints, based on the estimated distribution of joint distances from each camera. Additionally, we focus on the mesh surface of the human body for dynamic fusion, allowing for the seamless integration of facial expressions and body shape into a unified human body model. Our method has shown excellent performance in reconstructing the human body on two public datasets, advancing beyond previous work from the SMPL model to the SMPL-X model. This extension incorporates more complex hand poses and facial expressions, enhancing the detail and accuracy of the reconstructions. Crucially, it supports the flexible ad-hoc deployment of any number of cameras, offering significant potential for various applications. Our code is available at https://github.com/AbsterZhu/MUC.
Introduction
Recently, there has been a growing interest in creating 3D whole-body models from 2D images, especially for virtual reality and 3D animation. This process, known as expressive whole-body mesh recovery, combines the estimation of 3D human body pose, hand gesture, and facial expression. The progress is remarkable in single camera (monocular) setting such as SMPLer-X (Cai et al. 2023), which has become a foundation model in this field. Yet using a single camera still faces challenges such as occlusions, which can severely degrade the reconstruction quality.
Utilizing multiple camera views, multi-view videos provide essential visual cues from various angles and are widely used in applications like behavioral studies, where they facilitate the detailed observation of children’s behaviors in natural settings (Ballan et al. 2010; Schmidt et al. 2008). While the first step in many traditional approaches involves spatial camera calibration (He et al. 2020), this process is often cumbersome, requiring specialized tools and complex optimizations. Such time-consuming requirements hinder the efficient and convenient deployment of multi-camera setups across numerous sites. In response, this paper proposes a novel method for fusing data from multiple uncalibrated cameras to reconstruct 3D human bodies more effectively.
Many multi-view methods build on single-view approaches, typically by averaging predictions from individual views to estimate 3D human body pose and shape, which can lead to incoherence and reduced accuracy (Kanazawa et al. 2018; Kolotouros et al. 2019; Jafarian and Park 2021). Others map features from multiple views onto a common space for fusion (Yu et al. 2022), requiring complex coordinate transformations that increase method complexity. In contrast, the pixel-aligned feedback fusion method (Jia et al. 2023) iteratively refines estimations through aligned mesh vertex features, boosting accuracy without complex spatial mappings but necessitating multiple iterations. Additionally, the scarcity of multi-view data compared to single-view data complicates the direct training of multi-view models for optimal performance.
In this study, we introduce the Mixture of Uncalibrated Cameras (MUC), a novel pipeline for 3D human body reconstruction from multiple uncalibrated camera views, combining single-view encoding and multi-view fusion. Recognizing that early single-view methods effectively capture the relationship between observation angle and human pose, we apply a proven single-view model to each camera to independently reconstruct body parts. Notably, parts captured closer and without occlusion are more accurately reconstructed due to fewer self-occlusions. Therefore, we assess the quality of these single-view reconstructions, dynamically weighting key body parts across views to optimally fuse multi-view data.
It is critical for our method to assess the quality of the single-view reconstuctions. To this end, we propose two strategies. (1) Joint Reweighting. For all body joints predicted from each view, we use a joint reweighting network to acquire the weights of the human body joints based on the predicted camera positions. We also implement a distance-based distribution loss function, aiming to reduce the weights of body parts that have high uncertainty in reconstruction. (2) Surface Reweighting. To integrate facial expression with body smoothly, we design a surface reweighting network. This network utilizes UV map, corresponding to vertex normals of the mesh of human body, to estimate dynamic weighting toward seamless combination of facial expressions and body shape.
Contributions: The contributions of this work can be summarized in three items.
-
(1)
We present a groundbreaking multi-view method for reconstructing human pose, shape and facial expression. Our method does not require calibration or geometric mapping among views. It is scalable to an arbitrary number of cameras (including single view) out of the box.
-
(2)
We develop a novel distribution prediction strategy based on distance to assess the joint importance from various viewpoints, coupled with surface reweighting for continuous fusion of facial expression and body shape.
-
(3)
Our method establishes a new benchmark in calibration-free 3D human body reconstruction, surpassing existing state-of-the-art approaches and expanding upon previous work by transitioning from the SMPL human model to the more detailed SMPL-X model.
Related Work
Rising demand for 3D human body reconstruction has catalyzed a division in research into single-view and multi-view methods. Single-view approaches, bolstered by richly annotated datasets, have reached high levels of accuracy but often falter when dealing with occlusions. Conversely, multi-view methods excel at managing occlusions but are hindered by the scarcity of multi-view datasets (i.e., datasets with multiple observation angles), leading to ongoing research aimed at improving feature fusion techniques in these frameworks.
Single-View Human Body Reconstruction. In the context of 3D human body reconstruction from a single viewpoint, models like SMPL (Loper et al. 2023) and SMPL-X (Pavlakos et al. 2019) provide effective low-dimensional parameterizations for human poses and shapes. Despite numerous applications using these models (Feng et al. 2021; Choutas et al. 2020; Rong, Shiratori, and Joo 2021; Zhou et al. 2021), resolution constraints and limited field-of-view often hinder accurate facial and finger estimation. To address this, some methods, such as ExPose (Choutas et al. 2020), incorporate body-driven attention mechanisms and refinements from specialized datasets for enhanced detail, while OSX (Lin et al. 2023) presents a unified end-to-end model for comprehensive pose and shape estimation, achieving remarkable outcomes. Extensive datasets, both real and synthesized (Lin et al. 2014; Patel et al. 2021; Huang et al. 2022; Ionescu et al. 2013), and targeted non-full-body datasets (Lin et al. 2023) are crucial in overcoming occlusion challenges in single-view reconstruction. SMPLer-X (Cai et al. 2023) leverages 4.5 million images from 32 datasets to become the state-of-the-art foundation model in this domain.
Multi-View Human Body Reconstruction
The primary approach to multi-view reconstruction employs calibration parameters (intrinsic and extrinsic), as demonstrated by SMPLify-X (Pavlakos et al. 2019), which reduces 2D keypoint and silhouette reprojection errors in a unified system (Li, Oskarsson, and Heyden 2021). Although effective, this method’s heavy reliance on precise camera calibration can be impractical in dynamic environments.
When camera parameters are not available, alternative methods are used. A simple approach is averaging results from single-view models to achieve multi-view fusion. More complex learning-based methods include warping feature maps to align views without calibration (Qiu et al. 2019) and fusing images by mapping features onto a semantic model of the human body, utilizing self-attention to integrate features (Yu et al. 2022). These methods manage to bypass traditional calibration but can struggle with complex mappings and self-occlusion. The pixel-aligned feedback fusion technique iteratively refines body parameters by aligning features on mesh vertices. While this enhances accuracy, the multiple iterations required reduce computational efficiency, potentially limiting its suitability for real-time applications (Jia et al. 2023). Overall, these methods depend on the SMPL model, which falls short in detailing hand movements and facial expressions, underscoring the need for advanced models like SMPL-X to better tackle these issues.
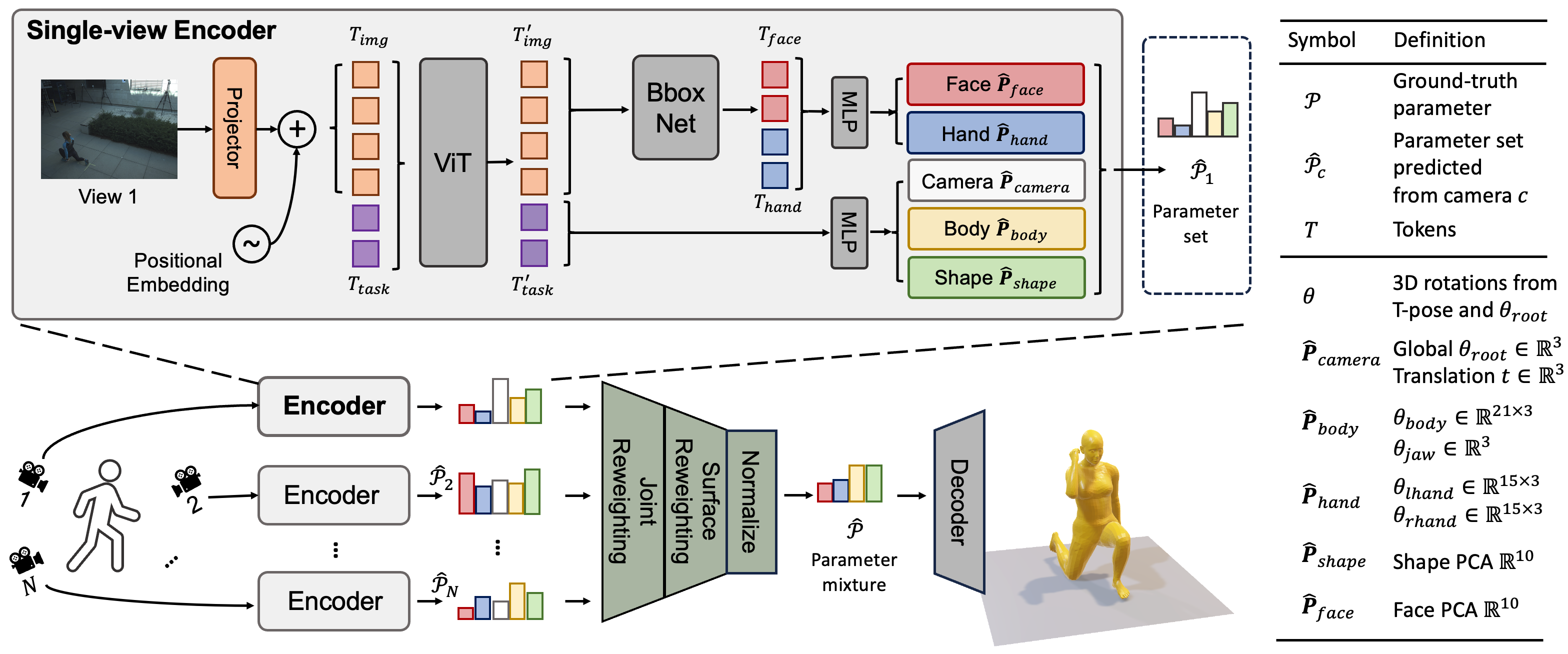
Method
Our work introduces an innovative approach to reconstruct 3D human body using multi-view images from multiple uncalibrated cameras as shown in Figure 1. We adopt a pre-trained single-view Vision Transformer (ViT) based foundation model SMPLer-X (Cai et al. 2023) as encoder for each view. The core of our approach comprises two key reweighting networks: a Joint Reweighting Network (JRN) and a Surface Reweighting Network (SRN). They cleverly figures out which parts of the images are reliable and use this information to reconstruct better joints and surface.
The sequence of reweighting first the joints and then the surface is intentional, as the surface mesh is contingent upon the underlying joint-based skeleton structure. Upon the completion of the reweighting processes, we normalize and amalgamate all reweighted parameters into a unified parameter set. The parameter set is then fed into a decoder, which reconstructs the 3D human body.
Single-view Encoder
To exploit the benefits of extensive datasets in single-view 3D human body reconstruction, we adopt a pre-trained encoder from SMPLer-X, a generalist foundation model specialized for monocular tasks. The encoder is portrayed in the top of Figure 1.
We introduce how the single-view encoder works briefly, which is important to subsequent multi-view fusion. First, a human body image is split into a sequence of fixed-size non-overlapping patches, which are linearly projected to image tokens . They are then concatenated with learnable task tokens , which are transformed by ViT to and . A BboxNet module predicts bounding boxes to localize face and hands in the feature map. Subsequently, MLPs are employed to regress a set of parameters . Notably, are joints parameter in rotation , are surface parameter in PCA top-10 components to control the curvature of different parts of the mesh. This encoder is tailored to minimize the difference between the estimated parameters and the ground-truth , focusing particularly on areas rich in details such as the hands and face. Further, a SMPL-X layer, as described in (Pavlakos et al. 2019), can be the decoder to derive the 3D mesh of human body from .
Multi-view Joint Reweighting
In the last section, we brief the single-view encoder. In this section, we introduce how the proposed Joint Reweighting Network (JRN) can mix the joint parameters from multiple uncalibrated cameras.
Network architecture The JRN employs two MLPs to mix joint landmark and hand landmark based on camera position for the -th camera.
-
•
The first MLPbody gets task token and camera parameter , and outputs the score . And is mixed as
(1) -
•
The second MLPhand gets hand token and camera parameter . The hand token is localized and cropped from image token by BboxNet as shown in Figure 1: . And is mixed as
(2)
Optimization Objective Previous studies using single-camera setups have indicated that reconstruction inaccuracies primarily stem from incorrect limb assessments, with errors increasing as the distance from the human body to the camera grows due to self-occlusion. To address this, we have integrated the joint distance distribution loss as a spatial prior to refining JRN’s learning process.
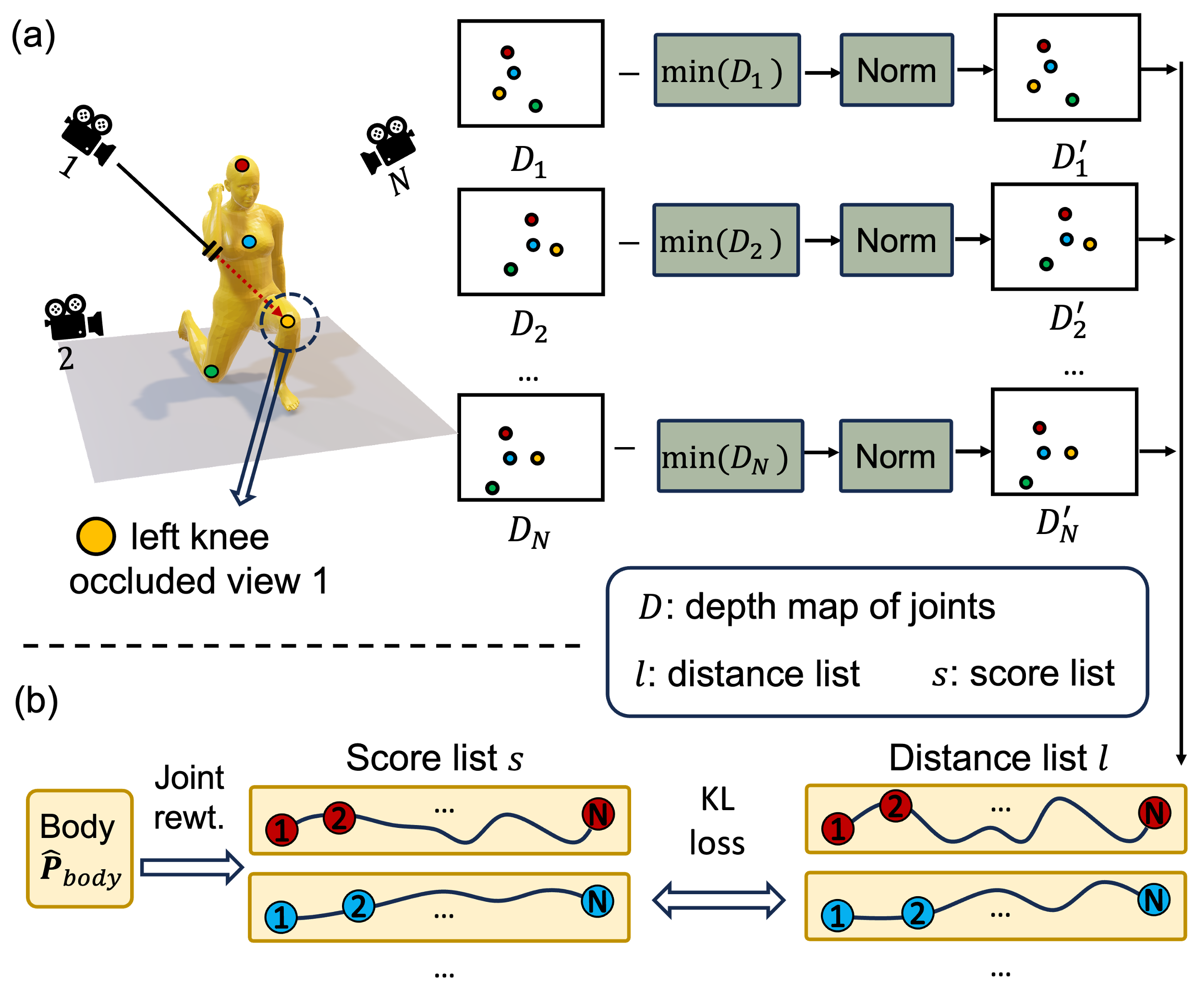
The optimization process is illustrated in Figure 2. Joint distance distribution loss is applied to 21 body joints, but for clarity we draw only 4 joint landmarks in Figure 2. Initially, 3D joints from view point are projected onto a 2D distance map in camera ’s image coordinate system. We subtract the minimal distance value from each distance map and normalize these values to a range from 0 to 1. Through this process, we obtain an approximate representation of the self-occlusion probability distribution.
The distance lists are captured as . We collect reweighting scores for these joints from different cameras () into , aiming for the Joint Reconstruction Network (JRN) to assign higher scores to joints with a lower probability of self-occlusion across views. We then use the Kullback-Leibler divergence to quantify the difference between and . Below is the definition of the joint distance distribution loss function:
| (3) |
Multi-view Surface Reweighting
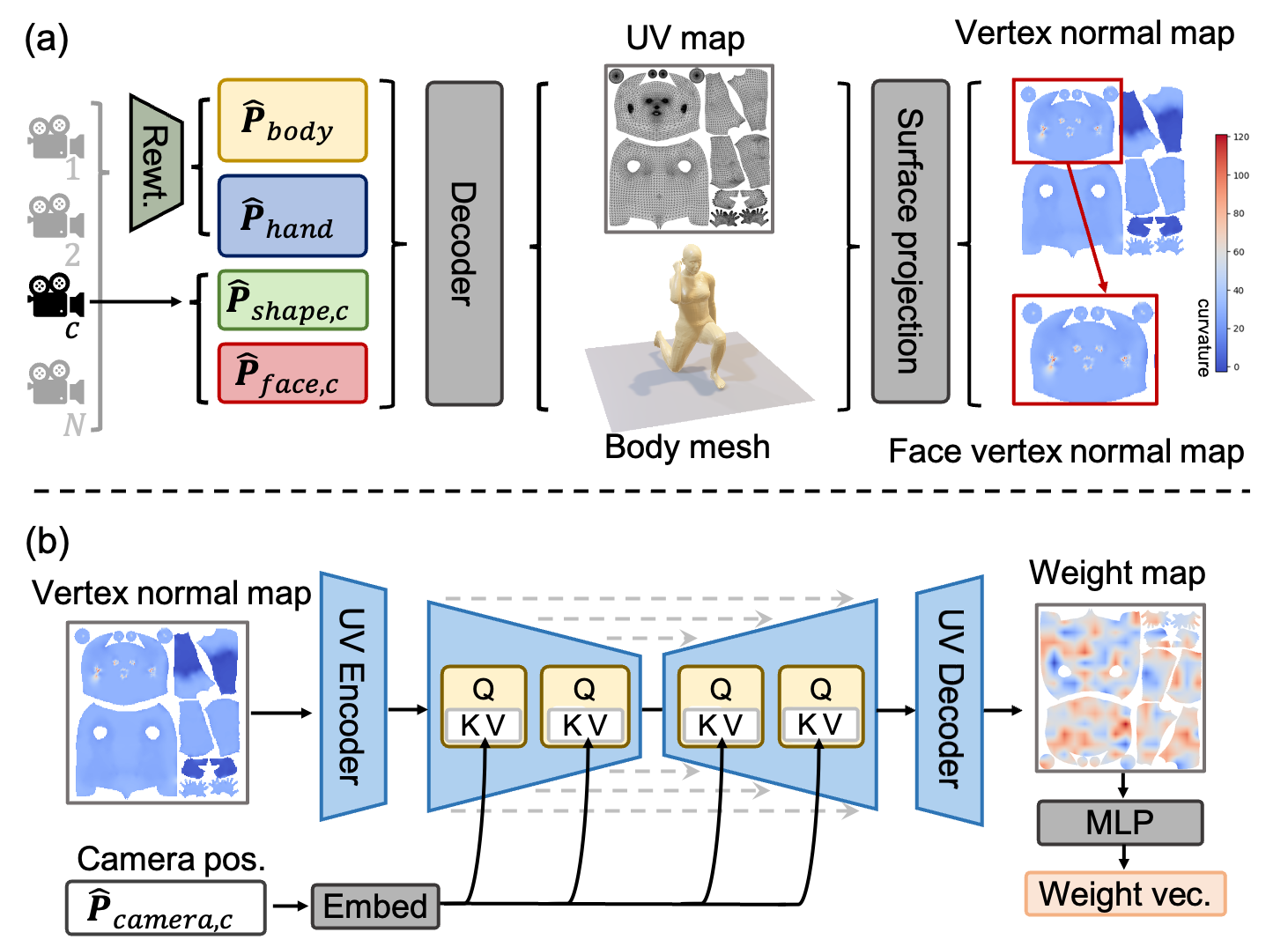
In the last section, we have introduced joint reweighting network, which can mix joint landmarks from multiple cameras. This section introduces the Surface Reweighting Network (SRN), which amalgamates the body surface attached to joint from multiple cameras. However, the direct fusion of 10,475 vertices of a 3D body presents a significant challenge for current hardware capabilities and poses difficulties in optimizing the reweighting network. To address this, we propose a novel surface reweighting method that concentrates on the continuous representation of these parameters. This approach facilitates a more refined understanding of the 3D human form. The overview of SRN is illustrated in Figure 3.
As shown in Figure 3 (a), initially, the mixed and parameters, obtained from the JRN, are inputted into a SMPL-X layer alongside the and parameters encoded from view . This will generate a reconstructed human body mesh, from which vertex normals are projected onto a downsampled UV map. This projection yields the vertex normal map . Similarly, the face vertex normal map can be cropped from .
We employed a conditional U-Net, which is a simplified version akin to the latent diffusion model described by Rombach et al. (Rombach et al. 2022). This U-Net is specifically informed by the predicted camera position . The architecture of the model is shown in Figure 3 (b). Specifically, it contains two Downsample Blocks and two Upsample Blocks with skip connections. For each block, we use as K and V, and features from vertex normal map as Q to compute the cross-attention. This network predicts the weight maps and . These weight maps are essential for reweighting the body and facial surface features for each camera view, focusing on capturing the continuous variations in body shape and facial expressions. The final and can be obtained by weighted normalization and can be supervised by the real vertex normal map generated by ground truth.
Following this, the predicted weight maps and are converted into weight vectors and through MLPs which bring more reasonable and reweighting. The final and can be obtained by weighted normalization as well.
Implementation
We train our model end-to-end by minimizing a several loss functions: , , , . Each component of the loss function serves a specific purpose in the learning process. The loss is computed as the L1 distance between the ground truth and predicted SMPL-X parameters, providing explicit supervision for whole body joints, body shape, facial expressions, and camera position. The loss is a regression loss for the projected 2D landmarks of the whole body, ensuring the accuracy of landmark localization in two-dimensional space. The loss, as defined in Eq. 3, is used for training JRN to learn the importance of different body joints across various camera views. Finally, the loss is calculated as the L1 distance between the ground truth and the predicted fused surface feature maps, offering direct supervision for SRN.
All model are trained using single A100 with pytorch. Adam optimizer with an initial learning rate of for 20 epochs. The initialization weight of encoder from SMPLer-X (Cai et al. 2023).
| Scenes | Train | Validate | Test |
|---|---|---|---|
| BBQ | 8 | N/A | N/A |
| Gym | 7 | N/A | 3-4 |
| LectureHall | 7 | 7 | 3-4 |
| ParkingLot 1 | 8 | 8 | N/A |
| ParkingLot 2 | 6 | 6 | 3-4 |
| Pavallion | 7 | 7 | N/A |
| Method | Camera(s) | Model type | Multi-view reconstruction | Single-view reconstruction | ||
|---|---|---|---|---|---|---|
| PA-MPJPE | PA-MPVPE | PA-MPJPE | PA-MPVPE | |||
| SMPLify (2016) | Single | SMPL | N/A | N/A | 82.3 | N/A |
| HMR (2018) | Single | SMPL | 57.8 | 67.7 | 56.8 | 65.5 |
| GraphCMR (2019) | Single | SMPL | 50.9 | 59.1 | 50.1 | 56.9 |
| SPIN (2019) | Single | SMPL | 44.5 | 51.5 | 41.1 | 49.3 |
| DecoMR (2020) | Single | SMPL | 42.0 | 50.5 | 39.3 | 47.6 |
| Pose2Mesh (2020) | Single | SMPL | N/A | N/A | 47.0 | N/A |
| I2lMeshnet (2020) | Single | SMPL | N/A | N/A | 41.1 | N/A |
| PyMAF (2021) | Single | SMPL | N/A | N/A | 40.5 | N/A |
| SMPLer-X-base (2023) | Single | SMPL-X | 38.3 | 41.3 | 45.1 | 47.8 |
| SMPLer-X-large (2023) | Single | SMPL-X | 33.4 | 37.1 | 38.9 | 42.8 |
| Liang (2019) | Multi | SMPL | 48.5 | 57.5 | 59.1 | 69.2 |
| ProHMR (2021) | Multi | SMPL | 34.5 | N/A | 41.2 | N/A |
| Yu (2022) | Multi | SMPL | 33.0 | 34.4 | 41.6 | 46.4 |
| PaFF (2023) | Multi | SMPL | 28.2 | N/A | N/A | N/A |
| MUC-base | Multi | SMPL-X | 31.9 | 33.4 | 44.3 | 45.8 |
| MUC-base (with translation) | Multi | SMPL | 27.1 | N/A | 39.5 | N/A |
Experiments
In our experiments, we demonstrate the effectiveness and robustness of our proposed MUC method for calibration-free multi-view fusion.
-
•
Initially, we benchmark our method against state-of-the-art 3D human body reconstruction techniques, providing a detailed comparison on accuracy and robustness.
-
•
Subsequently, we delve into the core of our contributions, evaluating the performance with an increasing number of cameras. This involves a systematic analysis to illustrate the scalability and impact of multi-view geometry on reconstruction accuracy.
-
•
Lastly, we conduct an ablation study to reveal the significance of our proposed JRN and SRN based on joint distribution loss, isolating their effects and demonstrating their contributions to the overall performance.
Datasets and Metrics
Two datasets are used to train and evaluate our method.
-
•
Human3.6M (Ionescu et al. 2013) is a large-scale multi-view dataset with ground-truth 3D human pose annotation. We follow the standard training/testing split: using subjects S1, S5, S6, S7 and S8 for training, and subjects S9 and S11 for testing. The SMPL/SMPL-X pseudo-GTs are obtained from NeuralAnnot (Moon, Choi, and Lee 2022). This dataset is widely used in multiple human body reconstruction tasks and helps us to compare with other state-of-the-art methods.
-
•
RICH (Huang et al. 2022) is an in-the-wild and indoor multi-view dataset annotated with ground-truth 2D keypoints and 3D body mesh. We adopt the intrinsic training/testing split in the dataset. The SMPL-X pseudo-GTs are obtained from SMPLify-X. This dataset contains human body joints, shape, hand joints and facial expression annotations, which can be used to prove the effectiveness of our multi-view fusion method. The distribution of camera numbers is shown in Table 1. For each sample in the training and validation sets, we randomly split it into two samples, each with a camera count equal to 4.
Both of these datasets are based on video capture, where the positions of individuals relative to the cameras are constantly changing, hence it can be considered suitable for assessing the generalization ability of our method to camera positions.
For 3D whole-body mesh reconstruction, we utilize the mean per-vertex position error (MPVPE) and mean per-joint position error (MPJPE) as our primary metrics. In addition, we apply procrustes analysis (PA) to the recovered mesh, and report PA-MPVPE and PA-MPJPE after rigid alignment. PA-MPJPE primarily evaluates the pose estimation accuracy of the human body model, whereas PA-MPVPE evaluates the accuracy of the reconstructed 3D model. PA-MPJPE and PA-MPVPE are reported in millimeter (mm).

Comparative Analysis with SOTA Methods
In this subsection, we present a comprehensive comparison of our proposed calibration-free multi-view fusion model with current SOTA methods in the domain of 3D human body reconstruction. We employ both multi-view and single-view reconstruction methods on the Human3.6M dataset to gauge the performance of our method against an array of established techniques. The results are presented in Table 2.
Our comparison includes 3D human body reconstruction methods from 2016 to 2023. Most of them are in the category of single view, while a few are in the multi-view category. Meanwhile, many methods adopt the SMPL model, which can only represent human body pose and body shape. A more sophisticated SMPL-X, as adopted by our method, can reconstruct human body pose, hand pose, body shape and facial expression jointly. Specifically, we can treat SMPLer-X (Cai et al. 2023) as SOTA method for single-view fusion method and PaFF (Jia et al. 2023) as SOTA method for multi-view fusion method. To eliminate differences between using different templates, we not only evaluated using the SMPL-X template but also utilized the conversion tool provided by SMPL-X (Pavlakos et al. 2019) to transform our prediction results into the SMPL template for evaluation.
From Table 2, we can observe the following.
-
•
Our Method’s Edge: Our approach outperforms other methods in multi-view reconstruction, achieving a PA-MPJPE of 27.1mm, which surpasses the previous best multi-view method by 1.1mm. It also performs better than models with larger parameter counts, such as SMPLer-X-large. Additionally, it maintains a leading position in both PA-MPJPE and PA-MPVPE metrics in single-view scenarios.
-
•
Model Bias: Under different model types (SMPL and SMPL-X), our approach demonstrates significant performance improvements in multi-view reconstruction compared to single view. Moreover, it achieves a notable enhancement in joints accuracy compared to previous methods. Since our model utilizes the SMPL-X model for both training and prediction, and the vertex count of the SMPL-X model is roughly twice that of the SMPL model, forcibly converting results to the SMPL model introduces some errors in the overall vertex alignment. Therefore, we only present results in terms of PA-MPJPE.
From Table 3, we can observe that our method outperforms SMPLer-X on the RICH dataset, which features more complex scenes and diverse camera settings. Our method’s visualization results are depicted in Figure 4. Compared to single-view models, our approach better compensates for the information loss caused by different viewpoints, resulting in superior reconstruction outcomes.
| Method | Multi-view | |
|---|---|---|
| PA-MPJPE | PA-MPVPE | |
| SMPLer-X-base (2023) | 42.1 | 37.1 |
| MUC-base | 37.5 | 33.5 |
Performance across Multi-view Configurations
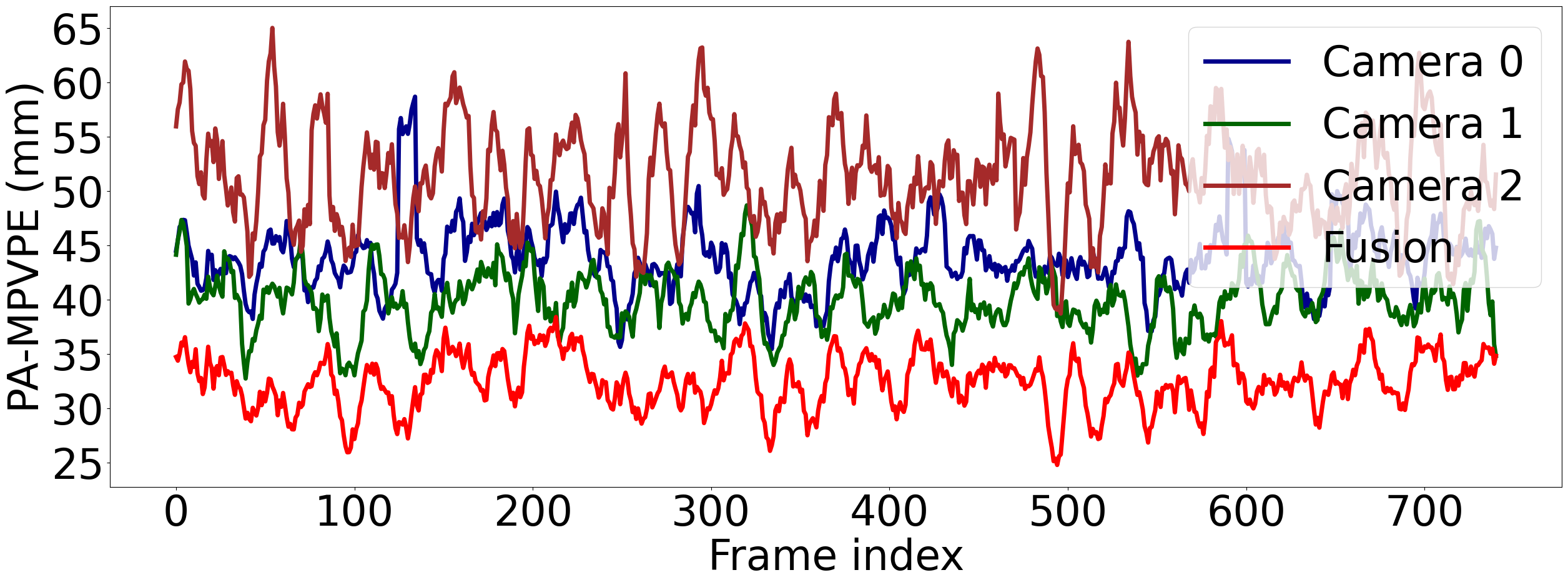
To evaluate the effectiveness of our calibration-free multi-view fusion method, we first present a frame-based analysis for a video of three cameras. As illustrated in Figure 5, our multi-view method effectively compensates for the target’s movement in the wild, maintaining a stable PA-MPVPE fluctuation.
Our method is scalable to an arbitrary number of cameras out of the box, so we conduct quantitative validation to assess the impact of adding more cameras for each case. The goal is to determine how the number of cameras influences the reconstruction precision of different human body parts.
The results, shown in Tables 4, underscore our method’s effectiveness in utilizing additional camera angles. For body reconstruction, there is a marked decrease in PA-MPJPE when increasing the camera count from one to four. Similar enhancements are observed in the hand and face reconstructions. Notably, the transition from one to two cameras yields the most significant improvement, highlighting the value of multi-view geometry. While the incremental gains diminish with each additional camera, the consistent improvements across all metrics reinforce our approach’s effectiveness in leveraging multiple uncalibrated views for 3D human body reconstruction in various settings. The same conclusions are also demonstrated on the Human3.6M dataset, with results presented in Table 5.
| # Cam | Body | Hand | Face | ||
|---|---|---|---|---|---|
| PA-MPJPE | PA-MPVPE | PA-MPJPE | PA-MPVPE | PA-MPVPE | |
| 1 | 52.8 | 47.7 | 8.4 | 8.2 | 4.1 |
| 2 | 43.7 | 38.9 | 7.4 | 7.2 | 3.5 |
| 3 | 40.4 | 35.8 | 7.0 | 6.8 | 3.3 |
| 4 | 38.6 | 34.5 | 6.8 | 6.7 | 3.2 |
| # Cam | Body | Hand | Face | ||
|---|---|---|---|---|---|
| PA-MPJPE | PA-MPVPE | PA-MPJPE | PA-MPVPE | PA-MPVPE | |
| 1 | 47.0 | 49.2 | 1.1 | 1.3 | 5.0 |
| 2 | 37.1 | 38.8 | 0.9 | 1.0 | 4.2 |
| 3 | 34.5 | 36.4 | 0.9 | 0.9 | 4.1 |
| 4 | 31.9 | 33.4 | 0.8 | 0.9 | 3.9 |
Impact of Joint and Surface Reweighting
Our qualitative evaluation focuses on the influence of the JRN and SRN on the 3D reconstruction of human body poses and shape. Figure 6 visually demonstrates the effect of reweighting across different camera views.
In Figure 6, the size of the red circles superimposed on the model’s joints indicates the importance level that JRN assigns to each joint. Larger circles indicate a higher score, suggesting that these joints exert a more significant influence during the multi-view joint reweighting process. It is evident that with the aid of the joint distance distribution loss, the JRN assigns lower weights to joints with a higher probability of self-occlusion. This strategy effectively harnesses the more accurate parts of predictions from each single viewpoint for fusion. Similarly, predictions using the SRN feature more precise estimates of body shape.

| Human3.6M | RICH | ||||
|---|---|---|---|---|---|
| JRN | SRN | PA-MPJPE | PA-MPVPE | PA-MPJPE | PA-MPVPE |
| 33.8 | 34.8 | 42.1 | 37.1 | ||
| ✓ | 32.5 | 34.3 | 39.4 | 34.2 | |
| ✓ | ✓ | 31.9 | 33.4 | 37.5 | 33.5 |
| Hand | Face | |||
|---|---|---|---|---|
| JRN | SRN | PA-MPJPE | PA-MPVPE | PA-MPVPE |
| 7.2 | 7.0 | 5.0 | ||
| ✓ | 7.0 | 6.8 | 3.5 | |
| ✓ | ✓ | 6.9 | 6.7 | 3.3 |
We further perform two quantitative ablation studies experiments to objectively measure the effectiveness of the JRN and SRN: one focusing on whole body reconstruction and the other on detailed hand and face reconstruction.
Whole Body Reconstruction We utilized the Human3.6M and RICH datasets to evaluate the performance improvements. The results are compiled in Table 6. The inclusion of JRN alone, and in combination with SRN, shows a consistent decrease in PA-MPJPE and PA-MPVPE across both datasets, highlighting the benefits of the reweighting mechanisms.
Hand and Face Reconstruction The results on RICH are presented in Table 7. The quantitative analysis clearly demonstrates that the combined use of JRN and SRN yields the best performance, as indicated by the bold values for PA-MPJPE and PA-MPVPE, underscoring their importance in enhancing the precision of 3D human pose reconstruction.
Conclusion and Discussion
In this paper, we present a new method for creating 3D meshes from images taken by uncalibrated cameras, removing the need for complex setup. Our approach scales easily to any number of cameras and uses distance distribution to estimate self-occlusion, enhanced by our SRN for smooth surface fusion. The technique determines the reliability of image segments to improve 3D reconstruction and assesses the positioning confidence of body parts from different views. Currently limited to static images, future updates could extend to video for more precise pose estimation. This method is not only more practical for everyday use but also surpasses current leading techniques in accuracy.
References
- Ballan et al. (2010) Ballan, L.; Brostow, G. J.; Puwein, J.; and Pollefeys, M. 2010. Unstructured video-based rendering: Interactive exploration of casually captured videos. In ACM SIGGRAPH 2010 papers, 1–11.
- Bogo et al. (2016) Bogo, F.; Kanazawa, A.; Lassner, C.; Gehler, P.; Romero, J.; and Black, M. J. 2016. Keep it SMPL: Automatic estimation of 3D human pose and shape from a single image. In Computer Vision–ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part V 14, 561–578. Springer.
- Cai et al. (2023) Cai, Z.; Yin, W.; Zeng, A.; Wei, C.; Sun, Q.; Wang, Y.; Pang, H. E.; Mei, H.; Zhang, M.; Zhang, L.; et al. 2023. Smpler-x: Scaling up expressive human pose and shape estimation. arXiv preprint arXiv:2309.17448.
- Choi, Moon, and Lee (2020) Choi, H.; Moon, G.; and Lee, K. M. 2020. Pose2mesh: Graph convolutional network for 3d human pose and mesh recovery from a 2d human pose. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part VII 16, 769–787. Springer.
- Choutas et al. (2020) Choutas, V.; Pavlakos, G.; Bolkart, T.; Tzionas, D.; and Black, M. J. 2020. Monocular expressive body regression through body-driven attention. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part X 16, 20–40. Springer.
- Elhayek et al. (2015) Elhayek, A.; De Aguiar, E.; Jain, A.; Tompson, J.; Pishchulin, L.; Andriluka, M.; Bregler, C.; Schiele, B.; and Theobalt, C. 2015. Efficient convnet-based marker-less motion capture in general scenes with a low number of cameras. In Proceedings of the IEEE conference on computer vision and pattern recognition, 3810–3818.
- Feng et al. (2021) Feng, Y.; Choutas, V.; Bolkart, T.; Tzionas, D.; and Black, M. J. 2021. Collaborative regression of expressive bodies using moderation. In 2021 International Conference on 3D Vision (3DV), 792–804. IEEE.
- He et al. (2020) He, Y.; Yan, R.; Fragkiadaki, K.; and Yu, S.-I. 2020. Epipolar transformers. In Proceedings of the ieee/cvf conference on computer vision and pattern recognition, 7779–7788.
- Huang et al. (2022) Huang, C.-H. P.; Yi, H.; Höschle, M.; Safroshkin, M.; Alexiadis, T.; Polikovsky, S.; Scharstein, D.; and Black, M. J. 2022. Capturing and inferring dense full-body human-scene contact. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 13274–13285.
- Ionescu et al. (2013) Ionescu, C.; Papava, D.; Olaru, V.; and Sminchisescu, C. 2013. Human3. 6m: Large scale datasets and predictive methods for 3d human sensing in natural environments. IEEE transactions on pattern analysis and machine intelligence, 36(7): 1325–1339.
- Jafarian and Park (2021) Jafarian, Y.; and Park, H. S. 2021. Learning high fidelity depths of dressed humans by watching social media dance videos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 12753–12762.
- Jia et al. (2023) Jia, K.; Zhang, H.; An, L.; and Liu, Y. 2023. Delving deep into pixel alignment feature for accurate multi-view human mesh recovery. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 37, 989–997.
- Kanazawa et al. (2018) Kanazawa, A.; Black, M. J.; Jacobs, D. W.; and Malik, J. 2018. End-to-end recovery of human shape and pose. In Proceedings of the IEEE conference on computer vision and pattern recognition, 7122–7131.
- Kolotouros et al. (2019) Kolotouros, N.; Pavlakos, G.; Black, M. J.; and Daniilidis, K. 2019. Learning to reconstruct 3D human pose and shape via model-fitting in the loop. In Proceedings of the IEEE/CVF international conference on computer vision, 2252–2261.
- Kolotouros, Pavlakos, and Daniilidis (2019) Kolotouros, N.; Pavlakos, G.; and Daniilidis, K. 2019. Convolutional mesh regression for single-image human shape reconstruction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 4501–4510.
- Kolotouros et al. (2021) Kolotouros, N.; Pavlakos, G.; Jayaraman, D.; and Daniilidis, K. 2021. Probabilistic modeling for human mesh recovery. In Proceedings of the IEEE/CVF international conference on computer vision, 11605–11614.
- Li, Oskarsson, and Heyden (2021) Li, Z.; Oskarsson, M.; and Heyden, A. 2021. 3D human pose and shape estimation through collaborative learning and multi-view model-fitting. In Proceedings of the IEEE/CVF winter conference on applications of computer vision, 1888–1897.
- Liang and Lin (2019) Liang, J.; and Lin, M. C. 2019. Shape-aware human pose and shape reconstruction using multi-view images. In Proceedings of the IEEE/CVF international conference on computer vision, 4352–4362.
- Lin et al. (2023) Lin, J.; Zeng, A.; Wang, H.; Zhang, L.; and Li, Y. 2023. One-Stage 3D Whole-Body Mesh Recovery with Component Aware Transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 21159–21168.
- Lin et al. (2014) Lin, T.-Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; and Zitnick, C. L. 2014. Microsoft coco: Common objects in context. In Computer Vision–ECCV 2014: 13th European Conference, Zurich, Switzerland, September 6-12, 2014, Proceedings, Part V 13, 740–755. Springer.
- Loper et al. (2023) Loper, M.; Mahmood, N.; Romero, J.; Pons-Moll, G.; and Black, M. J. 2023. SMPL: A skinned multi-person linear model. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2, 851–866.
- Moon, Choi, and Lee (2022) Moon, G.; Choi, H.; and Lee, K. M. 2022. NeuralAnnot: Neural annotator for 3D human mesh training sets. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2299–2307.
- Moon and Lee (2020) Moon, G.; and Lee, K. M. 2020. I2l-meshnet: Image-to-lixel prediction network for accurate 3d human pose and mesh estimation from a single rgb image. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part VII 16, 752–768. Springer.
- Patel et al. (2021) Patel, P.; Huang, C.-H. P.; Tesch, J.; Hoffmann, D. T.; Tripathi, S.; and Black, M. J. 2021. AGORA: Avatars in geography optimized for regression analysis. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 13468–13478.
- Pavlakos et al. (2019) Pavlakos, G.; Choutas, V.; Ghorbani, N.; Bolkart, T.; Osman, A. A.; Tzionas, D.; and Black, M. J. 2019. Expressive body capture: 3d hands, face, and body from a single image. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 10975–10985.
- Qiu et al. (2019) Qiu, H.; Wang, C.; Wang, J.; Wang, N.; and Zeng, W. 2019. Cross view fusion for 3d human pose estimation. In Proceedings of the IEEE/CVF international conference on computer vision, 4342–4351.
- Rombach et al. (2022) Rombach, R.; Blattmann, A.; Lorenz, D.; Esser, P.; and Ommer, B. 2022. High-resolution image synthesis with latent diffusion models. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 10684–10695.
- Rong, Shiratori, and Joo (2021) Rong, Y.; Shiratori, T.; and Joo, H. 2021. Frankmocap: A monocular 3d whole-body pose estimation system via regression and integration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 1749–1759.
- Schmidt et al. (2008) Schmidt, M. E.; Pempek, T. A.; Kirkorian, H. L.; Lund, A. F.; and Anderson, D. R. 2008. The effects of background television on the toy play behavior of very young children. Child development, 79(4): 1137–1151.
- Yu et al. (2022) Yu, Z.; Zhang, L.; Xu, Y.; Tang, C.; Tran, L.; Keskin, C.; and Park, H. S. 2022. Multiview Human Body Reconstruction from Uncalibrated Cameras. Advances in Neural Information Processing Systems, 35: 7879–7891.
- Zeng et al. (2020) Zeng, W.; Ouyang, W.; Luo, P.; Liu, W.; and Wang, X. 2020. 3d human mesh regression with dense correspondence. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 7054–7063.
- Zhang et al. (2021) Zhang, H.; Tian, Y.; Zhou, X.; Ouyang, W.; Liu, Y.; Wang, L.; and Sun, Z. 2021. Pymaf: 3d human pose and shape regression with pyramidal mesh alignment feedback loop. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 11446–11456.
- Zhou et al. (2021) Zhou, Y.; Habermann, M.; Habibie, I.; Tewari, A.; Theobalt, C.; and Xu, F. 2021. Monocular real-time full body capture with inter-part correlations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 4811–4822.