Multi-level Protein Representation Learning for
Blind Mutational Effect Prediction

Yang Tan ^∗
East China University of Science and Technology
Shanghai, China, 200237
tyang@mail.ecust.edu.cn
&Bingxin Zhou
Shanghai Jiao Tong University
Shanghai, China, 200240
bingxin.zhou@sjtu.edu.cn
Yuanhong Jiang
Shanghai Jiao Tong University
Shanghai, China, 200240
william_jiang@sjtu.edu.cn
&Yu Guang Wang
Shanghai Jiao Tong University
Shanghai, China, 200240
yuguang.wang@sjtu.edu.cn
&Liang Hong
Shanghai Jiao Tong University
Shanghai, China, 200240
hongl3liang@sjtu.edu.cn
equal contribution.

Abstract

Directed evolution plays an indispensable role in protein engineering that revises existing protein sequences to attain new or enhanced functions. Accurately predicting the effects of protein variants necessitates an in-depth understanding of protein structure and function. Although large self-supervised language models have demonstrated remarkable performance in zero-shot inference using only protein sequences, these models inherently do not interpret the spatial characteristics of protein structures, which are crucial for comprehending protein folding stability and internal molecular interactions. This paper introduces a novel pre-training framework that cascades sequential and geometric analyzers for protein primary and tertiary structures. It guides mutational directions toward desired traits by simulating natural selection on wild-type proteins and evaluates the effects of variants based on their fitness to perform the function. We assess the proposed approach using a public database and two new databases for a variety of variant effect prediction tasks, which encompass a diverse set of proteins and assays from different taxa. The prediction results achieve state-of-the-art performance over other zero-shot learning methods for both single-site mutations and deep mutations.

1 Introduction

The analysis of protein sequence–function relationships provides valuable insights for enzyme engineering to develop new or enhanced functions. Predicting the effects of point mutations in proteins allow researchers to dissect how changes in the amino acid (AA) sequence can impact the protein’s structure, stability, function, and interactions with other molecules [44]. While direct projection to protein functionality may encompass numerous uncharacterized molecular interactions, the advent of high-throughput experimental techniques has enabled the measurement of sequence-function mappings, thereby expanding the range of observable biochemical functions [6, 27, 33, 40]. Currently, hundreds of well-studied proteins have documented tens of thousands of mutational effects on their functions, such as ParD-ParE complexes for binding preferences [1], and ubiquitin for thermodynamic stability [41], and green fluorescent proteins for fluorescence [42], to name but a few. Systematic exploration of sequence variants offers copious evidence for characterizing the evolutionary space of mutants. However, this approach heavily depends on the domain-specific knowledge of individual proteins and their functionalities, thereby generalizing these specifically-designed mapping rules to a vast array of protein families poses a significant challenge.

Deep learning methods have been applied to expedite protein research, particularly in bridging protein sequences to functions. Analogous to how language models analyze the semantics and syntax of human language, these methods interpret protein sequences as raw text and utilize self-attention mechanisms [3, 29, 39] and/or autoregressive inference methods [23, 31] to reveal hidden long-range sequential dependencies. In addition, multiple sequence alignments (MSAs) have been wildly applied in predicting protein sequence [5, 12, 26, 35] or structure [2, 16] to augment the contextual information gleaned from sets of relevant sequences. While language models reveal sophisticated projections from protein sequence to functionality, inferring hundreds to thousands of uncharacterized molecular interactions demands considerable input samples and computationally intensive propagation modules. Alternatively, the structure of a protein, governed by its AA sequence, not only guides molecular interactions but also determines its functionality. Studies have derived the latent representation of AAs’ local environment based on protein topology or geometry [15, 49, 55]. They assume that an accurate description of a protein’s microenvironment is essential for determining its properties or functionality. Given that core mutations often induce functional defects through subtle disruptions to structure or dynamics [41], incorporating protein topology or geometry into the learning process can offer valuable insights into stabilizing protein functioning.

Both sequence and structure-oriented deep learning approaches have contributed to significant scientific discoveries [22, 23, 47]. However, they exhibit limitations when implemented individually. Structure encoders fail to capture long-range sequential connections for an AA beyond its contact region, and they overlook any correlations that do not conform to the ‘structure-function determination’ heuristic. On the other hand, sequential encoders struggle to capture the spatial molecular interactions of long-range elements and require an excessive number of protein instances to implicitly unravel the deep connection between protein topology and functionality. Although sequence-based learning might or might not find a better solution than human beings, language models demand significantly more resources for data processing and model training. In natural language processing, large models claim to consume more than $10^{12}$ documents to achieve quantitative changes in inference [36, 46].

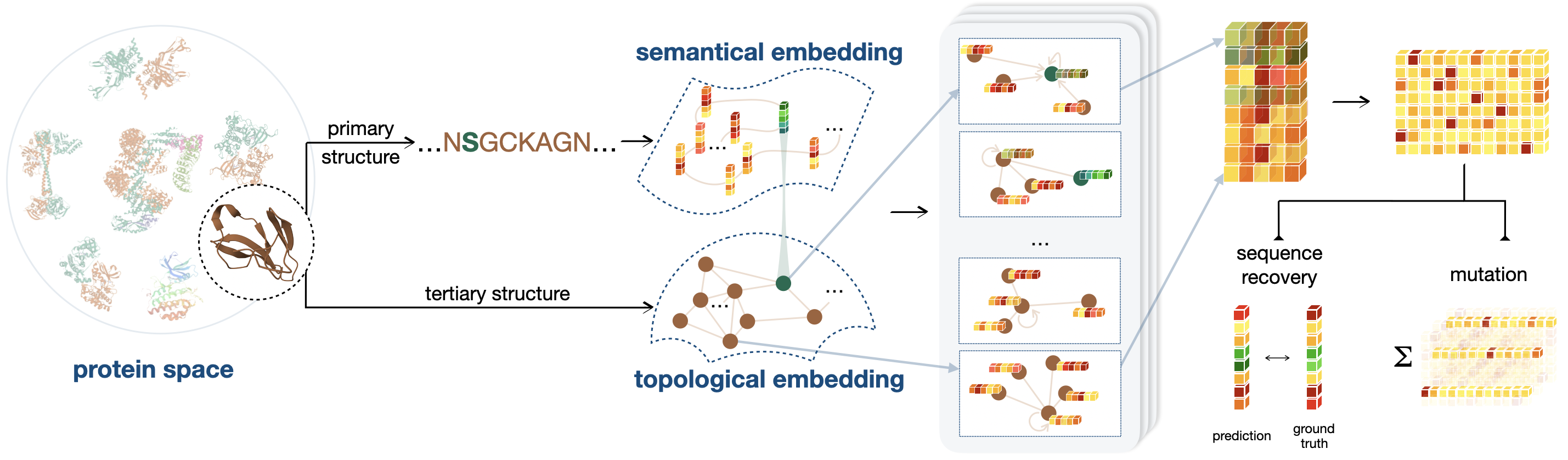
Refer to caption — Figure 1: An illustration of P¹³LG that extracts the semantics and topology of a protein by learning its primary and tertiary structures. The hidden representation can be decoded for variants effect prediction that recognizes the impact of mutating a few sites of a protein on its functionality.

We believe incorporating the intermediate state of protein structures can facilitate the discovery of an efficient and effective trajectory for mapping protein sequences to functionalities. To this end, we introduce P¹³LG , a framework designed to assimilate the semantics and topology of Proteins from their primary (1) and tertiary (3) structure with Language and Graph models. The developed model extends the generalization and robustness of self-supervised protein language models while maintaining low computational costs, thereby facilitating self-supervised training and task-specific customization. A funnel-shaped learning pipeline, as depicted in Figure 1, is designed due to the limited availability of crystallized protein structures compared to observed protein sequences. Initially, the linguistic embedding establishes the semantic and grammatical rules in AA chains by inspecting over $60$ million protein sequences [21]. Then, the topological embedding encodes the microenvironment of AAs, supplementing sequential relationships with spatial connections. Since a geometry can be placed or observed by different angles and positions in space, we represent proteins’ topology by graphs and enhance the model’s robustness and efficiency with a rotation and translation equivariant graph representation learning scheme. Consequently, the trained model is capable of interpreting the characterization of proteins in dimensions closely related to their functionality.

The developed model for directed evolution fulfills practical requirements in enzyme engineering from three perspectives. (i) The model gains interpretability by simulating natural selection. During training, random perturbations are assigned to AA types to encourage the model to recover advantageous protein sequences found in nature. (ii) The trained model provides robust and meaningful approximations to the joint distribution of the complete AA chain, enhancing the epistatic effect [17, 42] in deep mutations by considering the nonlinear combinatorial effects of AA sites. (iii) The model deploys self-supervised learning during training to eliminate the need for further supervision on downstream tasks. This zero-shot scenario is desirable due to the scarcity of experimental results as well as the ‘cold-start’ situation common in many wet lab experiments.

The pre-trained P¹³LG demonstrates its feasibility across a broad range of variant effect prediction benchmarks. These benchmarks include a general deep mutational effect prediction benchmark, ProteinGym [31], which comprises over $80$ proteins of varying assays and taxa. In addition, we have prepared two niche single-site mutation benchmarks. They measure thermodynamic stability using $\Delta$ Tm and $\Delta\Delta$ G values and $2,967$ mutants across $90$ protein-condition combinations. These two databases supplement the existing publicly available benchmarks with assay-specific deep mutational scanning (DMS) records, which facilitate the establishment of well-defined evaluation criteria for future methods that are specifically designed and assessed based on protein stability.

2 Zero-shot Multi-level Protein Representation Learning

Labeled data are usually scarce in biomolecule research, which demands designing a general model for predicting variant effects on unknown proteins and protein functions. Given a three-dimensional protein backbone structure, this study utilizes a self-supervised learning model that recovers AA types from noisy local environment observations. It simulates nature’s iterative selection of well-functioning mutated proteins from harmful random mutations.

2.1 Multi-level Protein Representation

Protein Primary Structure (Noised)

For a given observation with an AA type $\tilde{{\bm{v}}}$ , it is assumed that this observation is randomly perturbed. The model then learns a revised state ${\bm{v}}$ that is less likely to be eliminated by natural selection due to unfavorable properties such as instability or inability to fold. Formally, we define the perturbed observation by a Bernoulli distribution as follows:

\bm{\pi}(\tilde{{\bm{v}}}\mid{\bm{v}})=p\bm{\Theta}(\pi_{1},\pi_{2},\dots,\pi_{20})+(1-p)\delta(\tilde{{\bm{v}}}-{\bm{v}}),

(1)

where an AA in a protein chain has a chance of $p$ to mutate to one of $20$ AAs following the replacement distribution $\bm{\Theta}(\cdot)$ and $(1-p)$ of remaining unchanged. We consider $p$ as a tunable parameter and define $\bm{\Theta}(\cdot)$ based on the frequency of AA types observed in wild-type proteins in the training dataset.

Protein Tertiary Structure

The geometry of a protein is described by ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}},{\bm{W}}_{V},{\bm{W}}_{E},{\bm{X}}_{V})$ , a residue graph by the $k$ -nearest neighbor ( $k$ NN). Each node $v_{i}\in{\mathcal{V}}$ represents an AA in the protein connected to up to $k$ other nodes in the graph that are the closest in Euclidean distance within a contact region of $30$ Å. Node attributes ${\bm{W}}_{V}$ are hidden semantic embeddings of AA types, and edge attributes ${\bm{W}}_{E}\in\mathbb{R}^{93}$ feature relationships of connected nodes based on inter-atomic distances, local N-C positions, and sequential position encoding. Additionally, ${\bm{X}}_{V}$ records 3D coordinates of AAs in the Euclidean space, which plays a crucial role in the subsequent topological embedding stage to preserve roto-translation equivariance.

2.2 Semantic Encoding of Protein Sequence

Although it is generally believed by the community that a protein’s sequence determines its biological function via the folded structure, following strictly to this singular pathway risks overlooking other unobserved yet potentially influential inter-atomic communications impacting protein fitness. In line with this reasoning, our proposed model, P¹³LG , begins by extracting pairwise relationships for residues through an analysis of proteins’ primary structure from $\tilde{{\bm{V}}}$ and embed them to hidden representations ${\bm{W}}_{V}$ for residues. At each update, the information and representations of the noisy AA sequence are encoded from the noisy input via an Evolutionary Scale Modeling ESM-2 [21]¹¹1Official implementation released at https://github.com/facebookresearch/esm.. This approach employs a BERT-style masked language modeling (MLM) objective that predicts the identity of randomly selected AAs in a protein sequence by observing their context within the remainder of the sequence. Note that during training, the sequence embedding operates in every epoch as AA types are subject to independent random perturbations. For alternative encoding strategies, please refer to the discussion in Appendix B.

2.3 Topological Encoding of Protein Structure

Proteins are structured in 3D space, which requires the geometric encoder to possess roto-translation equivariance to node positions as well as permutation invariant to node attributes. This design is vital to avoid the implementation of costly data augmentation strategies. We practice Equivariant Graph Neural Networks (EGNN) [43] to acquire the hidden representation to node properties ${\bm{W}}_{V}^{l+1}=\left\{{\bm{w}}_{v_{1}}^{l+1},\dots,{\bm{w}}_{v_{n}}^{l+1}\right\}$ and node coordinates ${\bm{X}}_{\text{pos}}^{l+1}=\left\{{\bm{x}}_{v_{1}}^{l+1},\dots,{\bm{x}}_{v_{n}}^{l+1}\right\}$ at the $l+1$ th layer by

$\displaystyle{\bm{m}}_{ij}$	$\displaystyle=\phi_{e}\left({\bm{w}}_{v_{i}}^{l},{\bm{w}}_{v_{j}}^{l},\left\\|{\bm{x}}_{v_{i}}^{l}-{\bm{x}}_{v_{j}}^{l}\right\\|^{2},{\bm{w}}_{e_{ij}}\right),$	(2)
$\displaystyle{\bm{x}}_{v_{i}}^{l+1}$	$\displaystyle=\mathbf{x}_{v_{i}}^{l}+\frac{1}{n}\sum_{j\neq i}\left(\mathbf{x}_{v_{i}}^{l}-\mathbf{x}_{v_{j}}^{l}\right)\phi_{x}\left(\mathbf{m}_{{ij}}\right),\quad$
$\displaystyle{\bm{w}}_{v_{i}}^{l+1}$	$\displaystyle=\phi_{v}\big{(}{\bm{w}}_{i}^{l},\sum_{j\neq i}{\bm{m}}_{ij}\big{)}.$

In these equations, ${\bm{w}}_{e_{ij}}$ represents the input edge attribute on ${\mathcal{V}}_{ij}$ , which is not updated by the network. The propagation rules $\phi_{e},\phi_{x}$ and $\phi_{v}$ are defined by differentiable functions, e.g., multi-layer perceptrons (MLPs). The final hidden representation on nodes ${\bm{W}}_{V}^{L}$ embeds the microenvironment and local topology of AAs, and it will be carried on by readout layers for label predictions.

3 Blind Variant Effect Prediction

Our method is specifically designed for protein engineering that is trained with a self-supervised learning scheme. The model’s capability extends to blind variant effect prediction on an unknown protein, and it can generate the joint distribution for all AA sites as one of the 20 possible types, conditioned on their spatial and sequential neighbors. This process accounts for the epistatic effect and concurrently returns all AA sites in a sequence. Below we detail the workflow for training the zero-shot model and scoring the mutational effect of a specific mutant.

3.1 Model Pipeline

Training

The fundamental model architecture cascades a frozen sequence encoding module and a trainable tertiary structure encoder. Initially, a protein language model encodes pairwise hidden relationships of AAs by analyzing the input protein sequence and produces a vector representation ${\bm{w}}_{v_{i}}\in{\bm{W}}_{V}$ for an arbitrary AA, where ${\bm{W}}_{V}=\text{LM}_{\text{frozen}}(\tilde{{\bm{V}}})$ with $\tilde{{\bm{V}}}$ be the perturbed initial AA-type encoding. The language model $\text{LM}_{\text{frozen}}(\cdot)$ , ESM-2 [21] for instance, has been pre-trained on a massive protein sequence database (e.g., UniRef50 [48]) to understand the semantic and grammatical rules of wild-type proteins. It conceals high-dimensional AA-level long-short-range interactions that may or may not have been investigated and explained by scientists. Next, we represent proteins by $k$ NN graphs with model-encoded node attributes, handcrafted edge attributes, and 3D positions of the corresponding AAs. This representation is embedded using a stack of $L$ EGNN [43] layers to yield ${\bm{W}}_{V}^{L}=\text{EGNN}({\mathcal{G}})$ . This process extracts the geometric and topological embedding for protein graphs with AAs represented by ${\bm{w}}_{v_{i}}$ . During the pre-training phase for protein sequence recovery, the output layer $\phi(\cdot)$ provides the probability of AA types on each residue, i.e., ${\bm{Y}}=\phi({\bm{W}}_{V}^{L})\in\mathbb{R}^{n\times 20}$ for a protein comprising $n$ AAs. The model’s learnable parameters are refined by minimizing the cross-entropy of the recovered AAs with respect to the ground-truth AAs in wild-type proteins.

Inference

For a given mutant, its fitness score is derived from the joint distribution of the altered AA types on associated nodes that provides a preliminary assessment based on natural observations. We consider the AA type in the wild-type protein as a reference state and compare it with the predicted probability of AAs at the mutated site. Formally, for a mutant with mutated sites ${\mathcal{T}}$ ( $|{\mathcal{T}}|\geq 1$ ), we define its fitness score by the corresponding log-odds-ratio, i.e., $\sum_{t\in{\mathcal{T}}}\log p({\bm{y}}_{t})-\log p({\bm{v}}_{t})$ , where ${\bm{y}}_{t}$ and ${\bm{v}}_{t}$ denote the mutated and the wild-type AA at site $t$ , respectively.

3.2 Evaluation Metrics

It is critical to evaluate the developed model’s effectiveness using quantitative, computable measurements before proceeding to wet lab validations. Within the scope of mutational effect prediction, each raw protein in the database maintains dozens to tens of thousands of mutants with varying depths of mutation sites. Considering that protein functions are sensitive to the external environment and experimental methods, the absolute values measured by individual labs are typically not directly comparable. Consequently, we evaluate the performance of pre-trained models on a diverse set of proteins and protein functions using two quantitative measurements for ordinal and categorical data.

Spearman’s $\rho$ Correlation

Spearman’s correlation is commonly applied in mutational effect prediction tasks to measure the strength and direction of the monotonic relationship between two ranked sequences i.e., experimentally evaluated mutants and model-inferred mutants. This non-parametric rank measure is robust to outliers and asymmetry in mutational scores, does not assume any specific distribution of mutational scores, and captures non-linear correlations between the two sequences. The scale of $\rho$ ranges from $-1$ to $1$ which indicates whether the predicted sequence is negatively or positively related to the ground truth. Ideally, a result close to $1$ is preferred.

True Positive Rate

The true positive rate (TPR), also known as recall, is a key performance measure for the proportion of actual positives that are correctly identified. In the context of directed evolution tasks, this refers to the proportion of top beneficial mutations that are accurately predicted as most beneficial. A high TPR for the predicted results indicates that the trained model is likely to provide reliable mutational recommendations for wet labs. The following section will test TPR for baseline models on each of the proteins at $5\%$ , $25\%$ , and $50\%$ . For instance, TPR at $5\%$ defines the top $5\%$ mutants (in terms of the highest ground-truth score) as ‘positive samples’ and measures the proportion of these samples that are also ranked in the top $5\%$ by the model.

4 Numerical Experiments

We validate the efficacy of P¹³LG on zero-shot mutational effect prediction tasks on $186$ diverse proteins. The performance is compared with other SOTA models of varying scales (i.e., number of parameters). The implementations (https://anonymous.4open.science/r/plg-1B02) are programmed with PyTorch-Geometric (ver 2.2.0) and PyTorch (ver 1.12.1) and executed on an NVIDIA^® Tesla A100 GPU with $6,912$ CUDA cores and $80$ GB HBM2 installed on an HPC cluster.

4.1 Experimental Protocol

Training Setup

We train P¹³LG on a non-redundant subset of CATH v4.3.0 [32] domains, which contains $30,948$ experimental protein structures with less than $40$ % sequence identity. We further remove $\sim 6\%$ of proteins that exceed $2,000$ AAs in length. Each protein domain is transformed into a $k$ NN graph as following Section 2, with node features extracted by a frozen ESM2-t33 [21] prefix model. Protein topology is inferred by a $6$ -layer EGNN [43] with the hidden dimension tuned from $\{512,768,1280\}$ . Adam [18] is used for backpropagation with the learning rate set to $0.0001$ . To avoid training instability or CUDA out-of-memory errors, we limit the maximum input to $8,192$ AA tokens per batch, constituting approximately $32$ residue graphs.

Baseline Methods

We undertake an extensive comparison with baseline methods of self-supervised SOTA models on the fitness of mutation effects prediction. These methods utilize protein sequences and/or structures for learning. Sequence models employ position embedding strategies such as autoregression (Tranception [31], RITA [10], and ProGen2 [29]), masked language modeling (ESM-1b [39], ESM-1v [26], and ESM2 [21]), and a combination of the both (ProtTrans [5]). As our model acquires structural encoding, we also compare with ESM-IF1 [12] which incorporates mask language modeling objectives with GVP [14]. ProteinGym exhibits diverse protein types and assays, we thus include additional baselines that utilize MSA for model training (DeepSequence [38], WaveNet [45], MSA-Transformer [35], SiteIndep, and EVmutation [11]).

Benchmark Datasets

We conduct a comprehensive comparison of diverse mutation effect predictors in different regimes. Following [31, 38], we prioritize experimentally-measured properties that possess a monotonic relationship with protein fitness, such as protein stability and relative activity. For protein stability, we generate $90$ experimentally-measured sets of protein-condition combination assays from ProThermDB ²²2Retrieved from https://web.iitm.ac.in/bioinfo2/prothermdb/index.html., containing $2,967$ single-site mutants in environments with different pH levels, where $60$ of them are measured by $\Delta$ Tm (the change of melting temperature) and the rest $30$ assays are by $\Delta\Delta$ G (the change in the change in Gibbs free energy). The two datasets are named according to their scoring metrics: DTm and DDG, respectively. See Appendix A for additional descriptions. We also examine the fitness prediction of the proteins in ProteinGym, which constitutes $86$ ³³3We exclude A0A140D2T1_ZIKV_Sourisseau_growth_2019, the longest protein of over $3,000$ AAs in ProteinGym because it fails to be folded by AlphaFold2. DMS assays of different taxa (e.g., prokaryotes, humans, other eukaryotes, viruses).

Table 1: Variant Effect Prediction on DTm and DDG.

Model	version	TPR $\uparrow$ (DTm)			TPR $\uparrow$ (DDG)
Model	version	5%	25%	50%	5%	25%	50%
ProGen2	oas	0.033	0.286	0.537	0.000	0.339	0.515
	medium	0.117	0.367	0.582	0.072	0.443	0.615
	base	0.212	0.362	0.585	0.231	0.408	0.621
	large	0.132	0.323	0.557	0.117	0.320	0.597
	BFD90	0.178	0.333	0.589	0.206	0.451	0.644
	xlarge	0.118	0.353	0.578	0.144	0.383	0.603
Tranception	medium	0.188	0.359	0.564	0.083	0.367	0.527
Tranception	large	0.149	0.371	0.586	0.072	0.395	0.540
PortTrans	bert	0.131	0.364	0.586	0.122	0.424	0.635
	bert_bfd	0.168	0.336	0.579	0.136	0.423	0.589
	t5_xl_uniref50	0.184	0.412	0.593	0.147	0.425	0.640
	t5_xl_bfd	0.136	0.350	0.587	0.106	0.419	0.610
ESM-1v	-	0.216	0.386	0.602	0.231	0.451	0.622
ESM-1b	-	0.151	0.402	0.606	0.211	0.424	0.642
ESM-if1	-	0.188	0.418	0.656	0.258	0.469	0.641
ESM-2	t30	0.139	0.397	0.598	0.172	0.453	0.646
	t33	0.239	0.407	0.601	0.181	0.438	0.637
	t36	0.152	0.408	0.634	0.169	0.405	0.641
	t48	0.232	0.430	0.607	0.189	0.400	0.606
P¹³LG	k20_h1280	0.304	0.419	0.642	0.267	0.454	0.676
$\dagger$ The top three are highlighted by First, Second, Third.

4.2 Variant Effect Prediction

Our model has demonstrated exceptional predictive performance compared to other SOTA models in forecasting the stability of protein mutation sequences in both DTm and DDG. P¹³LG learns residue graphs with $k=20$ and deploys $1,280$ hidden neurons in each EGNN layer. Table 1 evaluates $100$ protein assays using TPR at $5\%$ , $25\%$ , and $50\%$ , wherein P¹³LG consistently outperforms competitors of varying model sizes. To further examine how our model efficiently achieves top performance relative to other large models, Figure 2 visualizes Spearman’s correlation from predictions of pre-trained models at different model scales. Our model occupies the most desirable upper-left corner spot, where it reaches top-rank correlation with minimal computational cost, or equivalently, the smallest number of parameters to learn.

In addition to single-site predictions, we also test P¹³LG ’s performance on deep mutations using $86$ protein assays in ProteinGym and compare its ranking with $27$ baselines. For the Spearman’s correlation scores reported in Table 2, we reproduce ESM series (including MSA-Transformer) and ProtTrans, and retrieve scores for the remaining methods from ProteinGym’s repository ⁴⁴4https://github.com/OATML-Markslab/ProteinGym. Our method consistently predicts the most aligned ranks, regardless of mutational depth or the predicted taxon. Notably, we include 6 additional MSA-based models, which require fewer parameters but significantly longer inference times due to the need to query and process supplementary information in MSA for the target protein. Consequently, MSA-based methods achieve the second-best overall performance on ProteinGym, following closely behind P¹³LG .

Table 2: Variant Effect Prediction on ProteinGym.

	Model	Version	# Params	$\rho$ (by depth) $\uparrow$			$\rho$ (by taxon) $\uparrow$
	Model	Version	(million)	Single	Double	All	Prokaryote	Human	Eukaryote	Virus
MSA	SiteIndep	-	-	0.378	0.322	0.378	0.343	0.375	0.401	0.406
	EVmutation	-	-	0.423	0.401	0.423	0.499	0.396	0.429	0.381
	Wavenet	-	-	0.399	0.344	0.400	0.492	0.373	0.442	0.321
	DeepSequence	-	-	0.411	0.357	0.415	0.497	0.396	0.461	0.332
	MSA-Transfomer	msa1	100	0.310	0.232	0.308	0.292	0.302	0.392	0.278
	MSA-Transfomer	msa1b	100	0.291	0.275	0.290	0.268	0.282	0.365	0.279
non-MSA	RITA	small	85	0.324	0.211	0.329	0.311	0.314	0.330	0.372
		medium	300	0.372	0.237	0.377	0.356	0.370	0.399	0.398
		large	680	0.372	0.227	0.383	0.353	0.380	0.404	0.405
		xlarge	1,200	0.385	0.234	0.389	0.405	0.364	0.393	0.407
	ProGen2	small	151	0.346	0.249	0.352	0.364	0.376	0.396	0.273
		medium	764	0.394	0.274	0.395	0.434	0.393	0.411	0.346
		base	764	0.389	0.323	0.394	0.426	0.396	0.427	0.335
		large	2,700	0.396	0.333	0.396	0.431	0.396	0.436	0.336
		xlarge	6,400	0.404	0.358	0.404	0.480	0.349	0.452	0.383
	PortTrans	bert	420	0.339	0.279	0.336	0.403	0.300	0.345	0.317
		bert_bfd	420	0.311	0.336	0.308	0.471	0.328	0.338	0.087
		t5_xl_uniref50	3,000	0.384	0.284	0.378	0.485	0.375	0.369	0.277
		t5_xl_bfd	3,000	0.355	0.356	0.351	0.490	0.399	0.349	0.131
	Tranception	large	700	0.399	0.398	0.406	0.447	0.369	0.426	0.407
	ESM-1v	-	650	0.376	0.290	0.372	0.496	0.409	0.398	0.233
	ESM-1b	-	650	0.371	0.325	0.366	0.507	0.416	0.360	0.150
	ESM-if1	-	142	0.359	0.279	0.368	0.445	0.358	0.339	0.322
	ESM-2	t30	150	0.345	0.296	0.344	0.437	0.419	0.401	0.045
		t33	650	0.392	0.317	0.389	0.515	0.433	0.454	0.155
		t36	3,000	0.384	0.261	0.383	0.495	0.419	0.429	0.195
		t48	15,000	0.394	0.313	0.391	0.457	0.402	0.442	0.251
	P¹³LG	k20_h512	148	0.424	0.395	0.426	0.516	0.425	0.480	0.297
$\dagger$ The top three are highlighted by First, Second, Third.

4.3 Ablation Study

This section evaluates the prediction performance of ProteinGym based on Spearman’s correlation on different modular designs of P¹³LG . The results are visualized in Figure 3 with additional details supplemented in Appendix F. In this section, we mix the inference results for each primary criterion with diverse secondary arguments. For instance, in the top orange box of Figure 3(a), we report all ablation results that utilize $6$ EGNN layers for graph convolution, regardless of the different scales of ESM-2 or the definitions of node attributes. For all modules investigated in this section, we separately discuss their influence on predicting mutational effects when modifying a single site or an arbitrary number of sites. These two cases are marked respectively as ‘single’ and ‘all’ on the y-axis.

Inclusion of Roto-Translation Equivariance

We assess the effect of incorporating rotation and translation equivariance during protein geometric and topological encoding. Three types of graph convolutions are compared, including GCN [19], GAT [51], and EGNN [43]. The first two are classic non-equivariant graph convolutional methods, while the last one, which we apply in the main algorithm, preserves roto-translation equivariance. We fix the number of EGNN layers to $6$ and examine the performance of the other two methods with either $4$ or $6$ layers. We find that integrating equivariance when embedding protein geometry significantly improves prediction performance.

Sequence Encoding

We next investigate the benefits of defining data-driven node attributes for protein representation learning. We compare the performance of models trained on two sets of graph inputs: the first set defines its AA node attributes through trained ESM2 [21], while the second set uses one-hot encoded AA types for each node. A clear advantage of using hidden representations by prefix models over hardcoded attributes is evident from the results presented in Figure 3(b).

Depth of EGNN

Although graph neural networks can extract topological information from geometric inputs, it is vital to select an appropriate number of layers for the module to deliver the most expressive node representation without encountering the oversmoothing problem. We investigate a wide range of choices for the EGNN layers among $\{6,12,18\}$ . As reported in Figure 3(c), embedding graph topology with deeper networks does not lead to performance improvements. A moderate choice of $6$ EGNN layers is sufficient for our learning task.

Scale of ESM

We also evaluate our models on different choices of language embedding dimensions to study the trade-off between the computational cost and input richness. Various scales of prefix models, including $\{8,150,650,3000\}$ millions of parameters, have been applied to produce different sequential embeddings with $\{320,640,1280,2560\}$ dimensions, respectively. Figure 3(d) reveals a clear preference for ESM-2-t33, which employs $650$ million parameters to achieve optimal model performance with the best stability. Notably, a higher dimension and richer semantic expression do not always yield better performance. In fact, performance degradation is observed when using the t36 version of the prefix model with 3 billion parameters.

5 Related Work

Protein Primary Structure Embedding

Self-supervised protein language models play the predominant role in the training of large quantities of protein sequences for protein representation learning. These methodologies draw parallels between protein sequences and natural language, encoding amino acid tokens using the Transformer model [50] to extract pairwise relationships among tokens. These methods typically pre-train on extensive protein sequence databases to autoregressively recover protein sequences [23, 31]. Alternatively, masked language modeling objectives develop attention patterns that correspond to the residue-residue contact map of the protein [21, 26, 34, 39, 52]. Other methods start from a multiple sequence alignment, summarizing the evolutionary patterns in target proteins [7, 35, 38]. Both aligned and non-aligned methods result in a strong capacity for discovering the hidden protein space, but this often comes at the expense of excessive training input or the use of substantial learning resources. This trade-off underlines the need for efficient and cost-effective approaches in self-supervised protein modeling.

Protein Tertiary Structure Embedding

Protein structures directly dictate protein functions and are essential to de novo protein design, which is a critical challenge in bioengineering. The remarkable success of accurate protein folding by AlphaFold2 [16] and the subsequent enrichment of the structure-aware protein repository have motivated a series of research initiatives focused on learning protein geometry. Recent efforts have been made to encode geometric information of proteins [9, 14, 54] for topology-sensitive tasks such as molecule binding [13, 20, 28], protein interface analysis [24, 37], and protein properties prediction [53].

Variant Effect Prediction

Variant effect predictions quantify the fitness of a mutant protein in comparison to its wild-type counterpart. For well-studied proteins, it is feasible to fit a supervised model on the hidden representation of amino acid local environments to infer fitness scores [8, 22, 25, 55]. However, in many cases, labeled data is either scarce or inaccessible. To overcome this, zero-shot methods have been developed to infer the fitness of a mutation from the evolutionary landscape of the original protein using sequence alignments [11, 38, 45]. Alternatively, hybrid models [31, 35] utilize retrieval or attention mechanisms to extract patterns from Multiple Sequence Alignments (MSAs) in conjunction with protein language or structure models.

6 Conclusion and Discussion

The development of dependable computational methodologies for protein engineering is a crucial facet of in silico protein design. Accurately assessing the fitness of protein mutants not only supports cost-effective experimental validations but also guides the modification of proteins to enhance existing or introduce new functions. Most recent deep learning solutions employ a common strategy that involves establishing a hidden protein representation and masking potential mutation sites for amino acid generation. Previous research has primarily focused on extracting protein representations from either their sequential or structural modalities, with many treating the prediction of mutational effects merely as a secondary task following inverse folding or de novo protein design. These approaches often overlook the importance of comprehending various levels of protein structures that are critical for determining protein function. Furthermore, they seldom implement model designs tailored specifically for mutation tasks. In this work, we introduce P¹³LG , a denoising framework that effectively cascades protein primary and tertiary structure embedding for the specific task of predicting mutational effects. This framework first employs a prefix protein language model to decode sequence representation and identify residue-wise intercommunications. This is subsequently enhanced by a roto-translation equivariant graph neural network, which encodes geometric representations for amino acid microenvironments. We have extensively validated the efficacy of P¹³LG across various protein function assays and taxa, including two thermal stability databases that were prepared by ourselves. Our approach consistently demonstrates substantial promise for protein engineering applications, particularly in facilitating the design of mutation sequences with improved thermal stability.

Broader Impact

The intersection of deep learning and structural biology, as showcased in this study, has the potential to transform our approach to protein engineering challenges, paving the way for sustainable and efficient solutions. Algorithms, such as P¹³LG , are primarily designed to enhance enzymes to support initiatives in drug discovery, biofuel production, and other relevant industries. However, given the pervasive presence of proteins across numerous scenarios and organisms, it is feasible that these methods could be employed to modify dangerous species, such as harmful viruses. Therefore, it is crucial to regulate the use of these deep learning methods, akin to the oversight required for any other powerful tools. Interestingly, our model demonstrates suboptimal performance when applied to such categories of proteins (refer to Table 2), suggesting an inherent limitation in its potential misuse.

Limitation

The consumption of training resources for AI-driven protein engineering techniques has surged considerably nowadays. For instance, ESM-IF1, which is another geometric model that utilizes structural information of proteins, necessitates months of processing time and hundreds of machines to integrate sequence and topological data. Owing to these computational cost constraints, our approach does not train on such an extensive corpus from scratch. Instead, we harness publicly-available language models to extract hidden representations for amino acids. Nevertheless, training and inference in such an integrated model require geometric information from proteins in addition to sequential data. The current data repositories are rich with protein structures experimentally solved by biologists and supplemented by high-quality protein geometries from contemporary techniques such as AlphaFold2, and they are adequate for training our model. However, it’s plausible that a revised protein could have an excessively long sequence that lacks a crystallized structure and cannot be folded by computational tools. An example of such a limitation is evident in our experiment, where a protein with an extended length was removed from the ProteinGym database.

References

[1] Christopher D Aakre, Julien Herrou, Tuyen N Phung, Barrett S Perchuk, Sean Crosson, and Michael T Laub. Evolving new protein-protein interaction specificity through promiscuous intermediates. Cell, 163(3):594–606, 2015.
[2] Minkyung Baek, Frank DiMaio, Ivan Anishchenko, Justas Dauparas, Sergey Ovchinnikov, Gyu Rie Lee, Jue Wang, Qian Cong, Lisa N Kinch, R Dustin Schaeffer, et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science, 373(6557):871–876, 2021.
[3] Nadav Brandes, Dan Ofer, Yam Peleg, Nadav Rappoport, and Michal Linial. ProteinBERT: A universal deep-learning model of protein sequence and function. Bioinformatics, 38(8):2102–2110, 2022.
[4] Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv:1810.04805, 2018.
[5] Ahmed Elnaggar, Michael Heinzinger, Christian Dallago, Ghalia Rehawi, Wang Yu, Llion Jones, Tom Gibbs, Tamas Feher, Christoph Angerer, Martin Steinegger, Debsindhu Bhowmik, and Burkhard Rost. ProtTrans: Towards cracking the language of lifes code through self-supervised deep learning and high performance computing. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.
[6] Douglas M Fowler and Stanley Fields. Deep mutational scanning: a new style of protein science. Nature Methods, 11(8):801–807, 2014.
[7] Jonathan Frazer, Pascal Notin, Mafalda Dias, Aidan Gomez, Joseph K Min, Kelly Brock, Yarin Gal, and Debora S Marks. Disease variant prediction with deep generative models of evolutionary data. Nature, 599(7883):91–95, 2021.
[8] Jonathan Frazer, Pascal Notin, Mafalda Dias, Aidan Gomez, Joseph K Min, Kelly Brock, Yarin Gal, and Debora S Marks. Disease variant prediction with deep generative models of evolutionary data. Nature, 599(7883):91–95, 2021.
[9] Vladimir Gligorijević, P Douglas Renfrew, Tomasz Kosciolek, Julia Koehler Leman, Daniel Berenberg, Tommi Vatanen, Chris Chandler, Bryn C Taylor, Ian M Fisk, Hera Vlamakis, et al. Structure-based protein function prediction using graph convolutional networks. Nature Communications, 12(1):3168, 2021.
[10] Daniel Hesslow, Niccoló Zanichelli, Pascal Notin, Iacopo Poli, and Debora Marks. Rita: a study on scaling up generative protein sequence models. arXiv:2205.05789, 2022.
[11] Thomas A Hopf, John B Ingraham, Frank J Poelwijk, Charlotta PI Schärfe, Michael Springer, Chris Sander, and Debora S Marks. Mutation effects predicted from sequence co-variation. Nature Biotechnology, 35(2):128–135, 2017.
[12] Chloe Hsu, Robert Verkuil, Jason Liu, Zeming Lin, Brian Hie, Tom Sercu, Adam Lerer, and Alexander Rives. Learning inverse folding from millions of predicted structures. In International Conference on Machine Learning, pages 8946–8970. PMLR, 2022.
[13] Wengong Jin, Jeremy Wohlwend, Regina Barzilay, and Tommi S Jaakkola. Iterative refinement graph neural network for antibody sequence-structure co-design. In International Conference on Learning Representations, 2021.
[14] Bowen Jing, Stephan Eismann, Patricia Suriana, Raphael JL Townshend, and Ron Dror. Learning from protein structure with geometric vector perceptrons. arXiv:2009.01411, 2020.
[15] Derek Jones, Hyojin Kim, Xiaohua Zhang, Adam Zemla, Garrett Stevenson, WF Drew Bennett, Daniel Kirshner, Sergio E Wong, Felice C Lightstone, and Jonathan E Allen. Improved protein–ligand binding affinity prediction with structure-based deep fusion inference. Journal of Chemical Information and Modeling, 61(4):1583–1592, 2021.
[16] John Jumper, Richard Evans, Alexander Pritzel, Tim Green, Michael Figurnov, Olaf Ronneberger, Kathryn Tunyasuvunakool, Russ Bates, Augustin Žídek, Anna Potapenko, et al. Highly accurate protein structure prediction with AlphaFold. Nature, 596(7873):583–589, 2021.
[17] Olga Khersonsky, Rosalie Lipsh, Ziv Avizemer, Yacov Ashani, Moshe Goldsmith, Haim Leader, Orly Dym, Shelly Rogotner, Devin L Trudeau, Jaime Prilusky, et al. Automated design of efficient and functionally diverse enzyme repertoires. Molecular Cell, 72(1):178–186, 2018.
[18] Diederik P Kingma and Jimmy Ba. ADAM: A method for stochastic optimization. In Proceedings of International Conference on Learning Representation (International Conference on Learning Representations), 2015.
[19] Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In International Conference on Learning Representations, 2017.
[20] Xiangzhe Kong, Wenbing Huang, and Yang Liu. Conditional antibody design as 3D equivariant graph translation. In The Eleventh International Conference on Learning Representations, 2023.
[21] Zeming Lin, Halil Akin, Roshan Rao, Brian Hie, Zhongkai Zhu, Wenting Lu, Nikita Smetanin, Robert Verkuil, Ori Kabeli, Yaniv Shmueli, et al. Evolutionary-scale prediction of atomic-level protein structure with a language model. Science, 379(6637):1123–1130, 2023.
[22] Hongyuan Lu, Daniel J Diaz, Natalie J Czarnecki, Congzhi Zhu, Wantae Kim, Raghav Shroff, Daniel J Acosta, Bradley R Alexander, Hannah O Cole, Yan Zhang, et al. Machine learning-aided engineering of hydrolases for PET depolymerization. Nature, 604(7907):662–667, 2022.
[23] Ali Madani, Ben Krause, Eric R Greene, Subu Subramanian, Benjamin P Mohr, James M Holton, Jose Luis Olmos Jr, Caiming Xiong, Zachary Z Sun, Richard Socher, et al. Large language models generate functional protein sequences across diverse families. Nature Biotechnology, pages 1–8, 2023.
[24] Sazan Mahbub and Md Shamsuzzoha Bayzid. EGRET: edge aggregated graph attention networks and transfer learning improve protein–protein interaction site prediction. Briefings in Bioinformatics, 23(2):bbab578, 2022.
[25] Céline Marquet, Michael Heinzinger, Tobias Olenyi, Christian Dallago, Kyra Erckert, Michael Bernhofer, Dmitrii Nechaev, and Burkhard Rost. Embeddings from protein language models predict conservation and variant effects. Human Genetics, 141(10):1629–1647, 2022.
[26] Joshua Meier, Roshan Rao, Robert Verkuil, Jason Liu, Tom Sercu, and Alex Rives. Language models enable zero-shot prediction of the effects of mutations on protein function. In Advances in Neural Information Processing Systems, volume 34, pages 29287–29303, 2021.
[27] Daniel Melamed, David L Young, Caitlin E Gamble, Christina R Miller, and Stanley Fields. Deep mutational scanning of an RRM domain of the Saccharomyces cerevisiae poly (A)-binding protein. RNA, 19(11):1537–1551, 2013.
[28] Yoochan Myung, Douglas EV Pires, and David B Ascher. CSM-AB: graph-based antibody–antigen binding affinity prediction and docking scoring function. Bioinformatics, 38(4):1141–1143, 2022.
[29] Erik Nijkamp, Jeffrey Ruffolo, Eli N Weinstein, Nikhil Naik, and Ali Madani. ProGen2: exploring the boundaries of protein language models. arXiv:2206.13517, 2022.
[30] Rahul Nikam, A Kulandaisamy, K Harini, Divya Sharma, and M Michael Gromiha. ProThermDB: thermodynamic database for proteins and mutants revisited after 15 years. Nucleic Acids Research, 49(D1):D420–D424, 2021.
[31] Pascal Notin, Mafalda Dias, Jonathan Frazer, Javier Marchena Hurtado, Aidan N Gomez, Debora Marks, and Yarin Gal. Tranception: protein fitness prediction with autoregressive transformers and inference-time retrieval. In International Conference on Machine Learning, pages 16990–17017. PMLR, 2022.
[32] CA Orengo, AD Michie, S Jones, DT Jones, MB Swindells, and JM Thornton. CATH – a hierarchic classification of protein domain structures. Structure, 5(8):1093–1109, 1997.
[33] Anna I Podgornaia and Michael T Laub. Pervasive degeneracy and epistasis in a protein-protein interface. Science, 347(6222):673–677, 2015.
[34] Roshan Rao, Joshua Meier, Tom Sercu, Sergey Ovchinnikov, and Alexander Rives. Transformer protein language models are unsupervised structure learners. In International Conference on Learning Representations, 2021.
[35] Roshan M Rao, Jason Liu, Robert Verkuil, Joshua Meier, John Canny, Pieter Abbeel, Tom Sercu, and Alexander Rives. MSA transformer. In International Conference on Machine Learning, pages 8844–8856. PMLR, 2021.
[36] Jeff Rasley, Samyam Rajbhandari, Olatunji Ruwase, and Yuxiong He. Deepspeed: System optimizations enable training deep learning models with over 100 billion parameters. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, pages 3505–3506, 2020.
[37] Manon Réau, Nicolas Renaud, Li C Xue, and Alexandre MJJ Bonvin. DeepRank-GNN: a graph neural network framework to learn patterns in protein–protein interfaces. Bioinformatics, 39(1):btac759, 2023.
[38] Adam J Riesselman, John B Ingraham, and Debora S Marks. Deep generative models of genetic variation capture the effects of mutations. Nature Methods, 15(10):816–822, 2018.
[39] Alexander Rives, Joshua Meier, Tom Sercu, Siddharth Goyal, Zeming Lin, Jason Liu, Demi Guo, Myle Ott, C Lawrence Zitnick, Jerry Ma, et al. Biological structure and function emerge from scaling unsupervised learning to 250 million protein sequences. Proceedings of the National Academy of Sciences, 118(15):e2016239118, 2021.
[40] Philip A Romero, Tuan M Tran, and Adam R Abate. Dissecting enzyme function with microfluidic-based deep mutational scanning. Proceedings of the National Academy of Sciences, 112(23):7159–7164, 2015.
[41] Benjamin P Roscoe, Kelly M Thayer, Konstantin B Zeldovich, David Fushman, and Daniel NA Bolon. Analyses of the effects of all ubiquitin point mutants on yeast growth rate. Journal of Molecular Biology, 425(8):1363–1377, 2013.
[42] Karen S Sarkisyan, Dmitry A Bolotin, Margarita V Meer, Dinara R Usmanova, Alexander S Mishin, George V Sharonov, Dmitry N Ivankov, Nina G Bozhanova, Mikhail S Baranov, Onuralp Soylemez, et al. Local fitness landscape of the green fluorescent protein. Nature, 533(7603):397–401, 2016.
[43] Vıctor Garcia Satorras, Emiel Hoogeboom, and Max Welling. E(n) equivariant graph neural networks. In International Conference on Machine Learning, pages 9323–9332, 2021.
[44] Jung-Eun Shin, Adam J Riesselman, Aaron W Kollasch, Conor McMahon, Elana Simon, Chris Sander, Aashish Manglik, Andrew C Kruse, and Debora S Marks. Protein design and variant prediction using autoregressive generative models. Nature Communications, 12(1):2403, 2021.
[45] Jung-Eun Shin, Adam J Riesselman, Aaron W Kollasch, Conor McMahon, Elana Simon, Chris Sander, Aashish Manglik, Andrew C Kruse, and Debora S Marks. Protein design and variant prediction using autoregressive generative models. Nature Communications, 12(1):2403, 2021.
[46] Mohammad Shoeybi, Mostofa Patwary, Raul Puri, Patrick LeGresley, Jared Casper, and Bryan Catanzaro. Megatron-lm: Training multi-billion parameter language models using model parallelism. arXiv:1909.08053, 2019.
[47] Raghav Shroff, Austin W Cole, Daniel J Diaz, Barrett R Morrow, Isaac Donnell, Ankur Annapareddy, Jimmy Gollihar, Andrew D Ellington, and Ross Thyer. Discovery of novel gain-of-function mutations guided by structure-based deep learning. ACS Synthetic Biology, 9(11):2927–2935, 2020.
[48] Baris E Suzek, Yuqi Wang, Hongzhan Huang, Peter B McGarvey, Cathy H Wu, and UniProt Consortium. UniRef clusters: a comprehensive and scalable alternative for improving sequence similarity searches. Bioinformatics, 31(6):926–932, 2015.
[49] Wen Torng and Russ B Altman. High precision protein functional site detection using 3D convolutional neural networks. Bioinformatics, 35(9):1503–1512, 2019.
[50] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Advances in Neural Information Processing Systems, 2017.
[51] Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. Graph attention networks. In International Conference on Learning Representations, 2018.
[52] Jesse Vig, Ali Madani, Lav R Varshney, Caiming Xiong, Nazneen Rajani, et al. BERTology meets biology: Interpreting attention in protein language models. In International Conference on Learning Representations, 2021.
[53] Ningyu Zhang, Zhen Bi, Xiaozhuan Liang, Siyuan Cheng, Haosen Hong, Shumin Deng, Jiazhang Lian, Qiang Zhang, and Huajun Chen. Ontoprotein: Protein pretraining with gene ontology embedding. arXiv:2201.11147, 2022.
[54] Zuobai Zhang, Minghao Xu, Arian Jamasb, Vijil Chenthamarakshan, Aurelie Lozano, Payel Das, and Jian Tang. Protein representation learning by geometric structure pretraining. arXiv:2203.06125, 2022.
[55] Bingxin Zhou, Outongyi Lv, Kai Yi, Xinye Xiong, Pan Tan, Liang Hong, and Yu Guang Wang. Accurate and definite mutational effect prediction with lightweight equivariant graph neural networks. arXiv:2304.08299, 2023.

Appendix A Dataset Description

A.1 New Benchmarks: DTm and DDG

We have established two novel benchmarks, namely DTm and DDG, to assess model accuracy in predicting the stability of proteins that have single-site mutations. The proteins included in both benchmarks have been sourced from ProThermDB [30]. Given the profound influence experimental conditions exert on protein stability, we have made it a point to denote the pH (potential of hydrogen) environment and have assigned each protein-environment pairing a name that follows the format “PDB ID-pH level" (refer to Figure 4). For instance, “O00095-8.0" in DDG signifies that the mutational records were conducted and evaluated under a pH of $8.0$ for protein O00095.

A sample of the acquired “protein-environment" source records is presented in Figure 5. We further process the attributes “mutant", “score", and “UniProt_ID". Initially, we curated all sets in ProThermDB containing at least $10$ records to achieve statistically significant correlation and TPR evaluations. Next, we manually scrutinized the mutation points relative to their raw sequences and removed records with continuous mutations. In other words, we exclude mutations upon mutations, concentrating instead on the single-site mutations compared to wild-type proteins. Furthermore, we employ UniProt ID to pair protein sequences with folded structures predicted by AlphaFold2 [16] from https://alphafold.ebi.ac.uk. We abstain from querying the protein structure by their PDB ID to prevent dealing with partial or misaligned protein sequences due to incompleteness in wet experimental procedures. In total, DTm consists of $60$ such protein-environment pairs, and DDG encompasses $30$ .

A.2 From Tranception: ProteinGym

We also validate our model’s ability to predict deep mutational effects using ProteinGym [31]. It is currently the most extensive protein substitution benchmark, comprising roughly $1.5M$ missense variants across $87$ DMS assays. These DMS assays cover a broad spectrum of functional properties (e.g., , thermostability, ligand binding, aggregation, viral replication, drug resistance) and span diverse protein families (e.g., , kinases, ion channel proteins, g-protein coupled receptors, polymerases, transcription factors, tumor suppressors) across different taxa (e.g., , humans, other eukaryotes, prokaryotes, viruses). In this study, we evaluated $86$ variants from the full set. We excluded one protein, namely A0A140D2T1_ZIKV_Sourisseau_growth_2019, due to its failure to be folded by AlphaFold2.

Appendix B Noise Addition Strategies

In the primary algorithm, noise sampling is utilized at each epoch on the node attributes to emulate random mutations in nature. This introduction of noise directly affects the node attribute input to the graphs. Alongside the “mutate-then-recode" method we implemented in the main algorithm, we examined four additional strategies to perturb the input data during training. The construction of these strategies is detailed below, and the corresponding model performance is reported in Table 3, which returns Spearman’s correlation on ProteinGym.

Table 3: Performance comparison on different noise addition strategies.

strategy	Mean	Sliding Window	Gaussian Noise	Mask	Mutate&Recode
$\rho$	0.245	0.215	0.229	0.396	0.426

Mean

Suppose the encoded sequential representation of a node is predominantly determined by its amino acid (AA) type. In essence, the protein sequence encoder will return similar embeddings for nodes of the same AA type, albeit at different positions within a protein. With this premise, the first method replaces the node embedding for perturbed nodes with the average representations from the same AA types. For example, a random node ${\bm{v}}_{i}$ in a protein is of type L. If it is altered in the current epoch, $\tilde{{\bm{v}}}_{i}$ is designated as the average sequential embedding of all other nodes of type L.

Sliding Window

The presumption in the previous method neither aligns with the algorithmic design nor biological heuristics. Self-attention discerns the interaction of the central token with its neighbors across the entire document (protein), and AAs, inclusive of their types and properties, are thought to be closely aligned with its local environment. Thus, averaging embeddings of AAs from varying positions is likely to forfeit positional information of the modified AA. Consequently, the second method designs a sliding window along the protein sequence for perturbing node noise. By setting the window size to $k$ , a corrupted node will update its representation by averaging the node representation of the nearest $k$ neighbor AAs along the AA chain.

Gaussian Noise

The subsequent method regards node embeddings of AA as hidden vectors and imposes white noise on the vector values. We define the mean and variance of the noise as 0 and 0.5, respectively, making the revised node representation $\tilde{{\bm{v}}}={\bm{v}}+{\mathcal{N}}(0,0.5)$ .

Mask

Finally, we employ the masking technique prevalent in masked language modeling and substitute the perturbed AA token with a special <mask> token. The prefix language model will interpret it as a novel token and employ self-attention mechanisms to assign a new representation to it. We utilize the same hyperparameter settings as that of BERT [4] and choose $15\%$ of tokens per iteration as potential influenced subjects. Specifically, $80\%$ of these subjects are replaced with <mask>, $10\%$ of them are replaced randomly (to other AA types), and the rest $10\%$ stay unchanged.

Appendix C Baseline Method Implementation Details

In our series of experiments, we compared a wide array of baseline methods across three benchmarks. All baseline methods were evaluated on two new datasets, namely DTm and DDG. We conducted these evaluations by independently reproducing the methods based on the algorithms or pre-trained models available in their respective official repositories. The names of the models along with pertinent details are provided in Table 4.

Table 4: Details of Baseline Models.

Model	Description	URL
DeepSequence [38]	a VAE-based model trained for every target protein with their MSAs	https://github.com/debbiemarkslab/DeepSequence
Tranception [31]	an autoregressive model for variant effect prediction task with retrieve machine	https://github.com/OATML-Markslab/Tranception
ESM-1b [39]	masked language model-based pre-train method with various pre-training dataset and positional embedding strategies	https://github.com/facebookresearch/esm
MSA-Transformer [35]
ESM-1v [26]
ESM2 [21]
ESM-if1 [12]	an inverse folding method with both mask language modeling and Geometric Vector Perceptron (GVP)
RITA [10]	a generative protein language model with billion-level parameters	https://github.com/lightonai/RITA
ProGen2 [29]	a generative protein language model with billion-level parameters	https://github.com/salesforce/progen
ProtTrans [5]	Transformer-based models trained on large protein sequence corpus	https://github.com/agemagician/ProtTrans

To ensure fair comparisons in the baseline models, we took two specific measures. First, the retrieval module in Tranception was removed when assessing its performance on the ProteinGym dataset. This step was taken as this model had been specifically tailored for this particular dataset. Second, the comprehensive version of ESM-1v averages model predictions from five different variants of diverse setups and parameters. However, as the rest of the baseline methods did not implement ensemble strategies, we tested ESM-1v using only its first variant.

For the rest methods we compared on the ProteinGym benchmark, the results are retrieved from https://marks.hms.harvard.edu/proteingym/scores_all_models_proteingym_substitutions.zip except for MSA Transformer, which is reproduced by ourselves.

Appendix D Varient Effect Prediction on Individual Proteins

Figures 7 through 9 illustrate the correlation performance for individual proteins within the DTm, DDG, and ProteinGym benchmarks. Results are color-coded according to their model types, with varying degrees of transparency indicating different versions of the same baseline method. Across the majority of proteins and protein-environment combinations, our developed P¹³LG consistently outperforms competitor models. For ProteinGym, we have intentionally excluded alignment-based methods (including SiteIndep, EVmutation, Wavenet, and DeepSequence) from our comparisons, focusing instead on assessing the performance of general-purpose pre-trained models.

In addition to Spearman’s $\rho$ correlation, TPR scores for protein assays across all three benchmarks are presented in Figures 10 through 12. It should be noted that several protein assays within DTm and DDG have been subjected to a limited number of tests in the source database, ProtThermDB, which leads to the frequent occurrence of extreme TPR values ( $0$ or $1$ ) at the top $5\%$ threshold. Consequently, interpretation of TPR scores is considered more meaningful at $25\%$ or $50\%$ positive rates, or at $5\%$ within the ProteinGym benchmark. Despite these challenges, our P¹³LG model delivers exceptional overall performance, clearly surpassing the baseline methods on all considered test sets.

Appendix E Learning Curve

We compared the learning curve of P¹³LG for 9 combinations of the number of $k$ nearest neighbors used in constructing protein graphs from $\{10,20,30\}$ , and hidden dimension from $\{512,768,1280\}$ , with respect to both training and validation. In all cases, we have used early stopping to ensure the convergence of training loss and sufficient learning. However, the validation loss varies depending on the scenario. Notably, for each value of $k$ , there exists a corresponding hidden dimension scenario that converges consistently with training.

There is typically a gap between validation and training loss, indicating that there is a room of improving generalizability of the model. One possible approach to address this issue is to increase the size of both the encoder and training datasets.

Table 5: Detailed Correlation Scores in Ablation Study by ProteinGym.

Noise Encoding	Noise Rate	Convolution	ESM-2 scale (million)	EGNN Depth	$\rho$ $\uparrow$
Noise Encoding	Noise Rate	Convolution	ESM-2 scale (million)	EGNN Depth	Single	All
mask	0.15	GCN	650	6	0.124	0.210
mask	0.15	GAT	650	6	0.077	0.177
noise	0.4	GCN	NA	4	0.102	0.126
noise	0.4	GAT	NA	4	0.070	0.144
noise	0.15	GCN	650	6	0.103	0.187
noise	0.15	GAT	650	6	0.101	0.131
noise	0.4	EGNN	NA	6	0.311	0.341
mask	0.15	EGNN	8	6	0.308	0.357
noise	0.15	EGNN	8	6	0.319	0.366
mask	0.15	EGNN	150	6	0.372	0.408
mask	0.15	EGNN	150	12	0.370	0.409
noise	0.15	EGNN	150	6	0.307	0.365
noise	0.15	EGNN	150	12	0.317	0.364
mask	0.15	EGNN	650	6	0.373	0.386
mask	0.15	EGNN	650	12	0.403	0.405
mask	0.3	EGNN	650	12	0.381	0.394
mask	0.4	EGNN	650	12	0.395	0.403
noise	0.15	EGNN	650	6	0.417	0.415
noise	0.15	EGNN	650	12	0.342	0.352
noise	0.3	EGNN	650	12	0.404	0.402
noise	0.4	EGNN	650	12	0.401	0.401
noise	0.25	EGNN	650	6	0.404	0.417
noise	0.1	EGNN	650	6	0.409	0.409
noise	0.01	EGNN	650	6	0.356	0.414
noise	0.05	EGNN	650	6	0.412	0.356
mask	0.15	EGNN	3000	18	0.057	0.146
noise	0.15	EGNN	3000	18	0.165	0.227

Appendix F Ablation Study

In Section 4.3, we conducted a comprehensive analysis of the configurations of several key components in our main algorithm. The results, which are represented by box plots in Figure 3, amalgamate a wide array of hyper-parameter combinations. For thoroughness, we enumerate the testing scores of models associated with all these combinations in Table 5. Note that for one-hot encoded input node features, no ESM-2 version was involved, we thus use NA to indicate this scenario. For noise encoding types, we include both our denoising method (named as noise in the table) and masked tokens (named as mask, which refers to the last of the four noise addition strategies introduced earlier).

Multi-level Protein Representation Learning for Blind Mutational Effect Prediction