Multi-neutron transfer in ⁸He induced reactions near the Coulomb barrier

Before discussing the origin of the ⁴He production we consider that of ⁶He in detail. The measured ⁶He yield gloria1 could result from the following four processes:

1. 1.

   ²⁰⁸Pb(⁸He,⁷He+n$\rightarrow$⁶He+n+n)²⁰⁸Pb (1n breakup)

2. 2.

   ²⁰⁸Pb(⁸He,⁶He+2n)²⁰⁸Pb (2n breakup)

3. 3.

   ²⁰⁸Pb(⁸He,⁷He$\rightarrow$⁶He+n)²⁰⁹Pb (1n transfer)

4. 4.

   ²⁰⁸Pb(⁸He,⁶He)²¹⁰Pb (2n transfer)

In Ref. gloria1 we adduced arguments in favor of breakup processes providing an essentially negligible contribution to the inclusive ⁶He yield in the angular range considered; there may be some small “background” from these reactions that falls off approximately exponentially with scattering angle. This leaves us with 1n and 2n transfer reactions. It is possible to assess the relative 1n and 2n contributions via DWBA calculations since these can show the kinematic differences between the two reactions. The one neutron transfer has an optimum Q value of around $-0.4$ MeV, leading to population of low-lying bound states of ²⁰⁹Pb with well known spectroscopic factors, thus enabling quantitative DWBA calculations. Since the entrance channel elastic scattering was also measured, in principle the only unknown is the exit channel ⁷He + ²⁰⁹Pb distorting potential. For the 2n cluster transfer, the optimum Q-value is $-0.8$ MeV gloria1 . This reaction should therefore in principle preferentially populate excited states of ²¹⁰Pb at energies around $E_{\mathrm{x}}$ = 8 MeV, very close to the two-neutron binding energy (S_2n=9.1 MeV), in good agreement with the measured ⁶He energy spectrum gloria1 . At this high excitation energy the structure of ²¹⁰Pb is not known so that only qualitative DWBA calculations can be performed. However, the range of allowed excitation energies of the ²¹⁰Pb residual can be fixed from the observed two-dimensional ⁶He total energy versus scattering angle spectrum purely by kinematics.

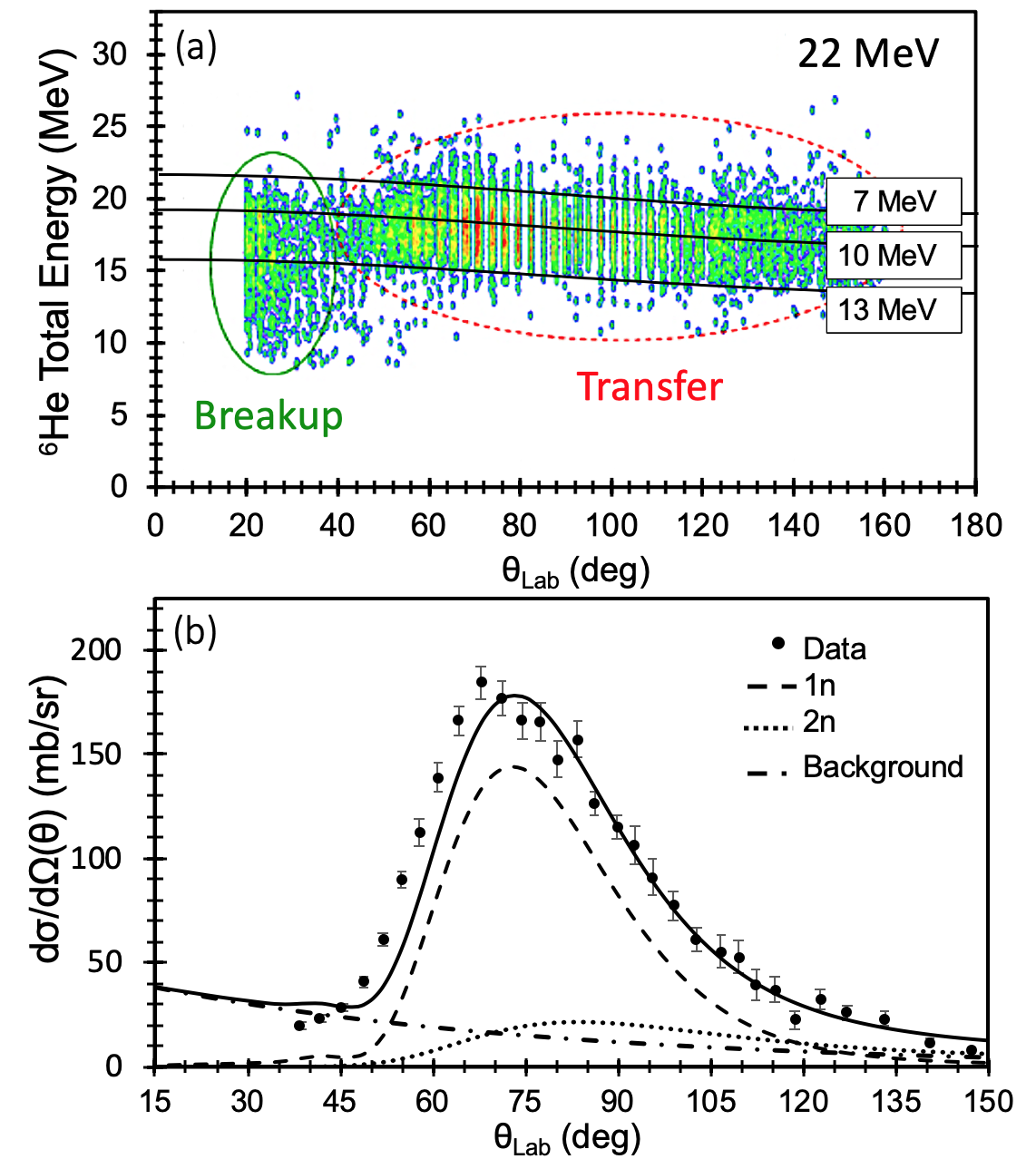
Figure 1 (a) clearly shows that if we assume direct 2n stripping as the ⁶He production mechanism then only states in ²¹⁰Pb with excitation energies in the range $7\leq E_{\mathrm{x}}\leq 13$ MeV can be populated, with $E_{\mathrm{x}}\approx 10$ MeV, slightly larger than that corresponding to the calculated $\mathrm{Q_{opt}}$ value, being most likely.

We therefore performed DWBA calculations of the ²⁰⁸Pb(⁸He,⁶He)²¹⁰Pb reaction subject to these constraints in order to ascertain the angular position of the peak of the predicted ⁶He angular distribution for comparison with the measured inclusive ⁶He angular distribution at 22 MeV gloria1 . All DWBA calculations were performed with the code fresco thompson . The entrance channel potential used the same parameters as in Ref. gloria1 and the exit channel ⁶He + ²¹⁰Pb potential used the 22 MeV parameters of Ref. San08 . The bound state potentials for the 2n cluster bound to the ⁶He and ²⁰⁸Pb cores were of standard Woods-Saxon form, with $r_{0}=1.38\times\mathrm{A}_{\mathrm{core}}^{1/3}$ fm and $a=0.7$ fm for the $\left<{}^{8}\mathrm{He}\mid{{}^{6}\mathrm{He}}+2n\right>$ overlap keeley1 and $r_{0}=1.25\times\mathrm{A}_{\mathrm{core}}^{1/3}$ fm and $a=0.7$ fm for the $\left<{}^{210}\mathrm{Pb}\mid{{}^{208}\mathrm{Pb}}+2n\right>$. The 2n cluster was assumed to have spin-parity $0^{+}$. Since these calculations were purely qualitative the spectroscopic factors for both overlaps were set to 1.0.

Calculations were performed for transfers leading to states in ²¹⁰Pb at excitation energies of $E_{\mathrm{x}}=7$, 10 and 13 MeV, covering the kinematically allowed range, and several values of the transferred angular momentum $L$ for each $E_{\mathrm{x}}$. The dotted curve in Fig. 1 (b) denotes the result of the DWBA 2n-stripping calculation for $E_{\mathrm{x}}=10$ MeV and $L=4\hbar$, approximately the best matched $L$ value. The shape of the calculated angular distribution does not reproduce the measured one and it peaks at $\theta_{\mathrm{lab}}\approx 84^{\circ}$, about $10^{\circ}$ larger than the measured ⁶He angular distribution. While the detailed shape of the calculated angular distribution depends slightly on $L$ and the choice of exit channel optical potential, the position of the peak is essentially fixed by kinematics, i.e. the value of $E_{\mathrm{x}}$, variations due to different input choices being of the order of $3^{\circ}$ at most. The exit channel ⁶He + ²¹⁰Pb optical potentials are rather well determined since the relevant incident energy range is covered by the ⁶He + ²⁰⁸Pb potentials of Ref. San08 , which should not differ significantly from those for a ²¹⁰Pb target. If $\alpha$-particle optical potentials are used instead in the exit channel—a rather extreme assumption—the stripping peak is shifted by about $3^{\circ}$ to larger angles, i.e. making the description of the data worse. This relative insensitivity to the choice of exit channel optical potential is to be expected since the energies of the ⁶He recoils when populating the levels of ²¹⁰Pb concerned are at or below the relevant Coulomb barrier. Reducing $E_{\mathrm{x}}$ by a few MeV moves the peak cross section to more forward angles but it is clear from Fig. 1 (a) that the 2n-stripping cross section for such values of $E_{\mathrm{x}}$ must be negligible, since little or no ⁶He are observed with the required energy. The shape is also not improved. We therefore arrive at the inescapable conclusion that direct 2n stripping can only make a minor contribution to the ⁶He production on kinematical grounds alone, since no variation of the input parameters will enable the shape of the measured angular distribution to be reproduced by DWBA calculations if $E_{\mathrm{x}}$ remains within the kinematically allowed limits.

Since we argue elsewhere gloria1 that breakup will only make a small contribution to the ⁶He yield in the angular region considered here, essentially constituting an approximately exponentially falling background, this leaves one neutron stripping as the main ⁶He production process. The one neutron stripping process can, at least in principle, be calculated quantitatively using a direct reaction theory since all of the inputs are reasonably well known from other sources with the exception of the ⁷He + ²⁰⁹Pb exit channel optical potential. In Ref. gloria1 we performed such calculations using a few “physically reasonable” choices for the exit channel potential, fixing the other inputs—the entrance channel distorting potential and $\left<{}^{8}\mathrm{He}\mid{{}^{7}\mathrm{He}}+n\right>$ and $\left<{}^{209}\mathrm{Pb}\mid{{}^{208}\mathrm{Pb}}+n\right>$ overlaps—at values taken from the literature. The resulting cross sections accounted for about one third of the total ⁶He cross section at 22 MeV, clearly a significant underestimate in the light of the kinematical considerations detailed in the preceding paragraph. We therefore performed new calculations in order to determine whether it was in fact possible to account for most of the ⁶He cross section by the one neutron stripping process while remaining within the bounds of what is physically acceptable with regard to the inputs.

The potentials binding the transferred neutron to the ⁷He and ²⁰⁸Pb cores were of standard Woods-Saxon form with radius and diffuseness parameters $r_{0}=1.25\times\mathrm{A}_{\mathrm{core}}^{1/3}$ fm and $a=0.65$ fm and the spectroscopic factors for the $\left<{}^{8}\mathrm{He}\mid{{}^{7}\mathrm{He}}+n\right>$ and $\left<{}^{209}\mathrm{Pb}\mid{{}^{208}\mathrm{Pb}}+n\right>$ overlaps were set to 4 and 1 respectively, the theoretical maximum values under the conventions used by the fresco code. The entrance channel distorting potential was as in Ref. gloria1 . The exit channel distorting potential remains an unknown since ⁷He is unbound. In order to apply some physical constraints to the choice of this potential we calculated the real part using the double-folding procedure and a theoretical ⁷He density Neff04 . This was then held fixed and the three parameters of the standard Woods-Saxon form imaginary potential varied to give the largest possible cross section. In the event, this was achieved with a so-called “interior” potential, the parameters being: $W=50$ MeV, $R_{W}=1.0\times 209^{1/3}$ fm, $a_{W}=0.3$ fm. The result is plotted on Fig. 1 (b) as the dashed curve.

We note here that, in contrast to the 2n-stripping calculations, the resulting angular distribution is sensitive to the choice of exit channel optical potential, cf. Fig. 4 (b) of Ref. gloria1 . This is due to the kinematics of the reaction, since in the 1n-stripping case the energies of the ⁷He ejectiles (before decaying into ${}^{6}\mathrm{He}+n$) are relatively well above the relevant Coulomb barrier, unlike for the 2n-stripping. While the choice of the imaginary part of the exit channel potential merely affects the height of the peak relative to the backward angle cross section the peak position is sensitive to the choice of the real part, with shifts of up to $10^{\circ}$ for a given imaginary potential. The calculation using the double-folded real potential based on the ⁷He matter density of Ref. Neff04 gives the result closest to the measured ⁶He angular distribution. Using a ⁸He real potential, either double-folded or the real part of the Woods-Saxon entrance potential, combined with the “interior” imaginary potential gives a similar result, the peak cross section being shifted by approximately $2^{\circ}$ to larger angles. Use of ⁶He, ⁶Li or ⁷Li real potentials as in Ref. gloria1 (but retaining the same “interior” imaginary potential referred to above) shifts the peak of the calculated angular distribution to even larger angles, by up to about $10^{\circ}$.

The measured inclusive ⁶He angular distribution was fitted by summing the calculated one-neutron and two-neutron stripping cross sections together with a background function (denoted by the dot-dashed curve on Fig. 1 (b)), the magnitudes of the two-neutron stripping and background being varied to give the best agreement with the data. The resulting sum is plotted on Fig. 1 (b) as the solid curve, approximately 67% of the total (812 mb, cf. the experimental value of $871\pm 31$ mb gloria1 ) coming from one-neutron stripping, 16% from two-neutron stripping and 17% from the background (including any contribution from breakup of ⁸He). An upper limit on the two-neutron stripping contribution is reasonably well defined by the measured backward angle ⁶He cross section. The maximum value of the calculated 2n-stripping cross section consistent with this is about one third of the total, with essentially no contribution from the background. The lower limit on the two-neutron stripping contribution is about 12% of the total, this being the minimum consistent with a good description of the measured ⁶He angular distribution, with a corresponding increase in the background contribution. Assessing the uncertainty on the 1n-stripping contribution is more difficult, but any variation greater than about $\pm 10$% would lead to a significant degradation of the description of the ⁶He angular distribution.

We therefore conclude that the measured inclusive ⁶He angular distribution for the interaction of a 22 MeV ⁸He beam with a ²⁰⁸Pb target is indeed consistent with one-neutron stripping as the dominant ⁶He production mechanism, with two-neutron stripping playing a minor role, contributing at most about one third of the total. This has important implications for the ⁴He production mechanism which we address in the following section.

We now turn to a detailed consideration of the ⁴He production. In addition to neutron transfer processes the measured inclusive ⁴He angular distribution will contain any contribution from breakup of the ⁸He projectile, as in the ⁶He case, but may also include $\alpha$ particles arising from fusion-evaporation events. In our analysis of the inclusive ⁴He production cross section these latter two processes are subsumed into the background since they are expected to be small compared to the transfer yield.

The following neutron transfer processes could contribute to the inclusive ⁴He yield (we do not consider transfers with more than two steps):

1. 1.

   ²⁰⁸Pb(⁸He,⁴He)²¹²Pb

2. 2.

   ²⁰⁸Pb(⁸He,⁵He$\rightarrow$⁴He+n)²¹¹Pb

3. 3.

   ²⁰⁸Pb(⁸He,⁶He^∗$\rightarrow$⁴He+2n)²¹⁰Pb

4. 4.

   ²⁰⁸Pb(⁸He,⁶He)²¹⁰Pb(⁶He,⁴He)²¹²Pb

5. 5.

   ²⁰⁸Pb(⁸He,⁷He^∗$\rightarrow$(⁶He^∗$\rightarrow$⁴He+2n)+n)²⁰⁹Pb

6. 6.

   ²⁰⁸Pb(⁸He,⁷He)²⁰⁹Pb(⁷He,⁶He^∗$\rightarrow$⁴He+2n)²¹⁰Pb

7. 7.

   ²⁰⁸Pb(⁸He,⁷He)²⁰⁹Pb(⁷He,⁴He)²¹²Pb

We may immediately rule out any significant contribution from 4), the sequential transfer of two 2n clusters, since we have shown in the previous section that the initial step must have a small cross section on purely kinematic grounds. Processes 6) and 7) at first sight appear possible significant contributors due to the strong population of the intermediate step, as demonstrated in the previous section. However, they may be ruled out on structural grounds: In process 6) the intermediate step populates low-lying single particle levels in ²⁰⁹Pb below 4 MeV in excitation energy which are unlikely to have significant overlap with levels in ²¹⁰Pb in the required excitation energy range, around 8 MeV or so. For process 7) to contribute significantly the second step would require a significant overlap between the ground state of ⁷He and the $\alpha$ + 3n configuration, which seems unlikely given the accepted status of ⁷He as a ⁶He + n resonance (see, e.g., Ref. Aks13 ). Process 5) is unlikely since there appears to be little overlap between the ground state of ⁸He and excited states of ⁷He, see e.g. the ⁸He(p,d) work of Ref. keeley1 , and in any case the known levels are broad, with widths of a few MeV Fos18 . Process 3) also seems unlikely since the overlap between the ground state of ⁸He and at least the 1.8 MeV $2^{+}$ excited state of ⁶He is small keeley1 , although this need not necessarily be the case for the other known low-lying levels of ⁶He at 2.6 and 5.3 MeV Mou12 . However, test calculations of 2n stripping populating these levels in ⁶He found that not only was the cross section significantly smaller than for populating the ground state (even with the same spectroscopic factor) but the angular distributions peaked at larger angles as the excitation energy of the ⁶He resonance increased, moving the peak of the corresponding ⁴He distribution further away from the peak of the observed inclusive ⁴He angular distribution. Finally, process 2) does not seem a likely candidate since it would require a sizeable overlap between the ground state of ⁸He and the ⁵He + 3n configuration in order to make a significant contribution and we are not aware of any structure calculations that explicitly mention significant 3n clustering in the ground state of ⁸He.

We are thus left with process 1), direct 4n stripping, as our candidate main mechanism for production of ⁴He. Transfer of four neutrons can in principle populate states in ²¹²Pb from the ground state (Q = $+14.99$ MeV) up to the four-neutron separation energy at $E_{\mathrm{x}}=18.08$ MeV (Q = $-3.11$ MeV), or even beyond if resonant-like states are considered. However, as discussed in Ref. gloria1 , the optimum Q value for this process is Q = $-1.7$ MeV so that final states around 16.7 MeV in excitation energy are expected to be preferentially populated. A consideration of the observed two-dimensional ⁴He total energy versus scattering angle spectrum together with the kinematics of the ²⁰⁸Pb(⁸He,⁴He)²¹²Pb reaction, assumed to be direct 4n transfer, enables us to fix the range of allowed excitation energies of the residual ²¹²Pb nucleus. Under this assumption only states in ²¹²Pb with $14\;\;\mathrm{MeV}\leq E_{\mathrm{x}}\leq 22\;\;\mathrm{MeV}$ can be populated, see Fig. 2 (a).

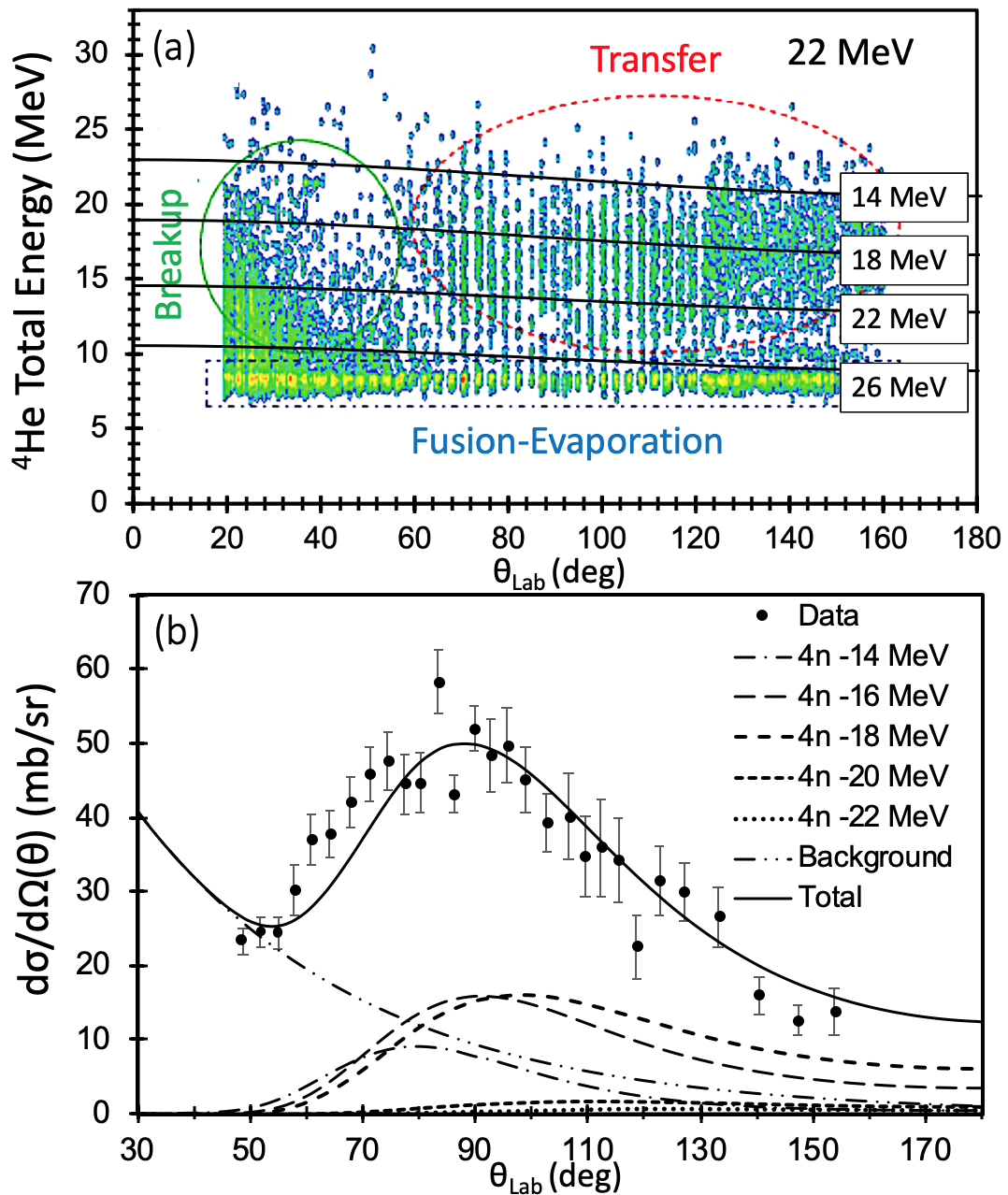
To test whether such a process, subject to these kinematic constraints, can reproduce the shape of the measured inclusive ⁴He angular distribution DWBA calculations were performed for direct 4n transfer to states in ²¹²Pb at excitation energies of 14, 16, 18, 20 and 22 MeV, covering the observed energy range of ⁴He recoils, with angular momentum $L=6\hbar$ relative to the ²⁰⁸Pb core, approximately the best matched $L$ value. The shape of the angular distribution is only weakly dependent on the value of $L$. The potentials binding the 4n cluster to the ⁴He and ²⁰⁸Pb cores were of Woods-Saxon form with parameters $r_{0}=1.0\times(4+\mathrm{A}_{\mathrm{core}}^{1/3})$ fm and $a=0.65$ fm. The spin-parity of the 4n cluster was assumed to be $0^{+}$, the simplest possibility consistent with the presence of such a cluster in the ground state of ⁸He. The optical potential in the entrance channel was the same as in the previous section. The ⁴He+²⁰⁸Pb optical potential parameters of Ref. hudson were used in the exit channel. Since the calculations were purely qualitative all spectroscopic factors were set equal to 1.0. The form factors for the states at $E_{\mathrm{x}}=20$ and 22 MeV were calculated assuming nominal binding energies of 0.01 MeV for the 4n cluster with respect to the ²⁰⁸Pb core since these values of $E_{\mathrm{x}}$ are above the 4n emission threshold of ²¹²Pb.

The inclusive ⁴He angular distribution for 22 MeV ⁸He incident on a ²⁰⁸Pb target of Ref. gloria1 was fitted by adjusting the normalizations of the DWBA curves and the parameters of an exponential background function (including any contributions from breakup of the ⁸He projectile and fusion-evaporation) to give the best description of the data. The data were obtained by integrating, for each laboratory scattering angle, the energy distribution above the 8.78 MeV alpha peak arising from the decay of the ²¹²Po ground state. To assist in fixing the parameters of the background function the angular range of the data was slightly extended to more forward angles than in Ref. gloria1 . Care was also taken to avoid unrealistically large contributions from the calculations with $E_{\mathrm{x}}$ values at the limits of the kinematically allowed range. The results of this analysis are displayed in Fig. 2 (b). As in the case of the 2n cluster transfer, the calculated shapes of the angular distributions were not very sensitive to the transferred angular momentum but did depend on the excitation energy of the recoil ²¹²Pb nucleus, see Fig. 2 (b).

Our results suggest that the ⁴He yield can be well described by a combination of direct 4n transfer and an exponential background function, the transfer accounting for 73% of the total (355 mb, cf. the experimental value of $393^{+10}_{-33}$ mb gloria1 ).