Multi-Objective Complementary Control
Abstract
This paper proposes a novel multi-objective control framework for linear time-invariant systems in which performance and robustness can be achieved in a complementary way instead of a trade-off. In particular, a state-space solution is first established for a new stabilizing control structure consisting of two independently designed controllers coordinated with a Youla-type operator . It is then shown by performance analysis that these two independently designed controllers operate in a naturally complementary way for a tracking control system, due to the coordination function of driven by the residual signal of a Luenberger observer. Moreover, it is pointed out that could be further optimized with an additional gain factor to achieve improved performance, through a data-driven methodology for a measured cost function.
Index Terms:
Multi-objective control, complementary control, Youla-Kučera parameterization, robustnessI Introduction
There are usually multiple objectives or specifications required to be achieved by various control systems in practice [1, 2, 3, 4, 5, 6, 7, 8, 9], such as optimality of tracking performance, robustness to some unknown/uncertain disturbances or parameter variations, passivity, etc. Various formulated multi-objective (MO) control problems have received considerable attention in the control community, for example, the MO control [10, 11, 12, 13, 14, 15, 4], where optimization of performance in the norm and robustness in the norm are considered simultaneously and are heavily studied in 1990’s. Other kinds of MO optimal control problems have also been extensively explored, for example, in [1, 3, 15, 7, 6], where the concept of Pareto optimality is used with respect to multiple optimization criteria.
It can be observed that the common feature of these traditional MO control problems is the fact that a single-controller structure is applied which poses challenges for the design methodologies, especially, when the involved objectives are inherently conflicting. A typical example is the well-known conflicting pair of robustness and optimal performance in a traditional robust control design. When conflicting objectives could not be achieved at their best by the single controller, the trade-off is normally the only choice, which results in a compromised single controller, as can be seen in many mixed control results [10, 11, 12, 14, 15, 4]. There are some research reported for controller designs in the two-degree-of-freedom (2DoF) form [16, 17, 18]. The reference [16] is concerned with 2DoF optimal design for a quadratic cost. In particular, the class of all stabilizing 2DoF controllers which give finite cost is characterized. In [17], the class of all stabilizing 2DoF controllers which achieve a specified closed-loop transfer matrix is characterized in terms of a free stable parameter. Inspired by the generalized internal model control (GIMC) developed in [19], a bi-objective high-performance control design for antenna servo systems is studied in [18]. Performance limitation problems are also studied for 2DoF controllers in [20, 21], with tracking and/or regulation as a sole objective. However, there is, essentially, a lack of a fundamental and general framework that can assemble two controllers together in a complementary way for MO control design purposes. That said, it is desired to develop a new framework for MO control problems that can overcome the curse of trade-offs and achieve non-compromised MO performances, which is the main goal of this paper.
This work is closely related to the GIMC structure [19], a multi-block implementation of the famous Youla-Kučera parameterization of all stabilizing 1DoF and 2DoF controllers [22]. In this implementation, the Youla-type parameter becomes an explicit design factor driven by the residual signal, instead of functioning as an optional parameter to deliver a specific stabilizing controller. Although this GIMC structure provides hope for the desired two-controller complementary structure to address MO control problems, no further details are given for the systematic design of in [19]. Motivated by the GIMC, in this paper a new two-controller design framework called ‘Multi-Objective Complementary Control’ (MOCC) is proposed and explored in detail with rigorous performance analysis, aiming to achieve MO performances while alleviating trade-offs. In particular, state-space formulas are provided for the MOCC framework. A tracking control setting is utilized as a platform to demonstrate the said advantages of MOCC, that is, overcoming the trade-off in the conventional MO control to achieve nominal tracking performance and robustness in a complementary way. Furthermore, a data-driven optimization approach is also sketched for the design of Youla-type operator to turn a robust controller into an optimal one, when performing the tracking task repetitively over a finite time interval in the presence of an unknown but repetition-invariant disturbance.
This paper is organized as follows: in Section II, the motivation of this paper is explained in detail using a tracking control case as well as some preliminaries of GIMC and Youla-Kučera parameterization; Section III presents a new two-controller structure which enables the MOCC design in the later section; in Section IV, a tracking control problem is addressed in the new framework with a rigorous performance analysis, illustrating the design features and the advantages of MOCC; the data-driven performance optimization is sketched in Section V; simulation results can be found in Section VI and conclusions in Section VII.
Notations: Throughout this paper, the symbol of transfer matrices or systems will be in bold to distinguish them from constant matrices. A system and its transfer function are denoted by the same symbol and whenever convenient, the dependence on the frequency variable or for a transfer function may be omitted. The set consists of all -dimensional real vectors. The unsubscripted norm denotes the standard Euclidean norm on vectors. For a matrix or vector , denotes its transpose. For a rational transfer matrix , denotes or complex conjugation of . () denotes the space of all rational (and stable) functions with the norm for any , where represents the largest singular value. A rational proper transfer matrix in terms of state-space data is simply denoted by .
II Motivation
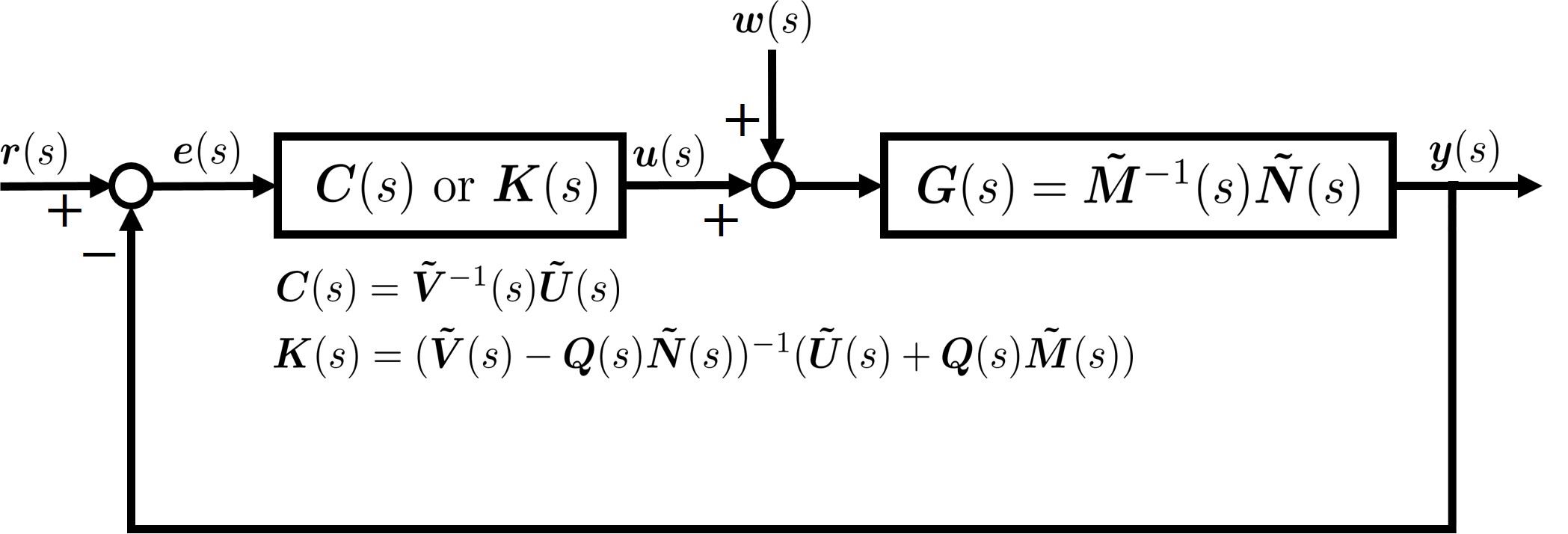
Transfer functions shall be utilized to motivate our idea, though this paper mainly works on state space. Consider a tracking control system shown in Fig. 1. Let be a linear time-invariant (LTI) plant with a left coprime factorization and , be a stabilizing controller with a left coprime factorization and , be a reference signal to be tracked, and be an uncertain or unknown disturbance signal. It is well-known that all stabilizing controllers can be characterized in the format of Youla-Kučera parameterization
for the same plant , with and [19], [22, Chapter 5], [23]. The tracking error with either or is given by
It can be seen that the single controller (or ) has to be designed to deal with both the tracking performance for the reference signal and the robustness against the disturbance simultaneously. In practice, trade-off usually should be carried out to compromise the design difficulty of the single (or ) between the tracking performance and the disturbance attenuation. On the other hand, considering the challenge posed for the selection of under a given performance expectation of , one can conclude that finding a is not necessarily easier than designing when both performance and robustness need to be addressed.
An interesting controller architecture called GIMC was proposed in [19] which provides a promising approach to overcome the trade-off in the traditional design. The GIMC is shown in Fig. 2, featuring the parameter as a separate design factor in the structure, instead of being buried in . By direct algebra, the tracking error in Fig. 2 can be derived as
It is clear from the above expression that different from the control structure in Fig. 1, there are potentially two separate design degrees of freedom for tracking control in GIMC: for tracking performance and for disturbance attenuation. In addition, if there is no uncertainty, i.e., , then and thus the nominal tracking error signal is recovered. These attractive features motivate us to revisit MO control problems through the design of and , instead of the traditional design of a single controller or . Noting that, for a given , if can be determined then is derived and vice verse. Hence, design of and can be reduced to the design of and even if is not explicitly seen in Fig 2. It is noted that how to coordinate and using such that specified performances are achieved and rigorous performance analysis for GIMC have not systematically and profoundly been investigated so far. In [24], a solution to is derived in state space for a robust LQG control problem through the design with a modified control structure from GIMC, although it is still not clear how to systematically use to coordinate and in the Youla-Kučera parameterization.
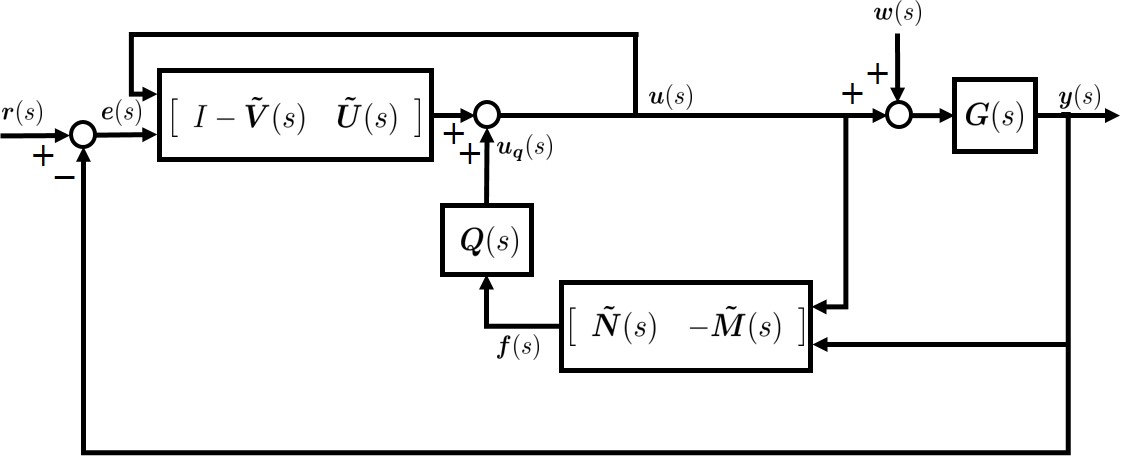
In the following sections of this paper, a two-controller structure is proposed in state space, motivated from the analysis above. In particular, how can be constructed from two independently designed controllers and to coordinate and is explored systematically. To showcase the superior performance of this new control design framework, a tracking control problem is presented to demonstrate how and can be coordinated through to address MO tracking performance and robustness in a complementary way, together with a rigorous performance analysis.
Remark 1
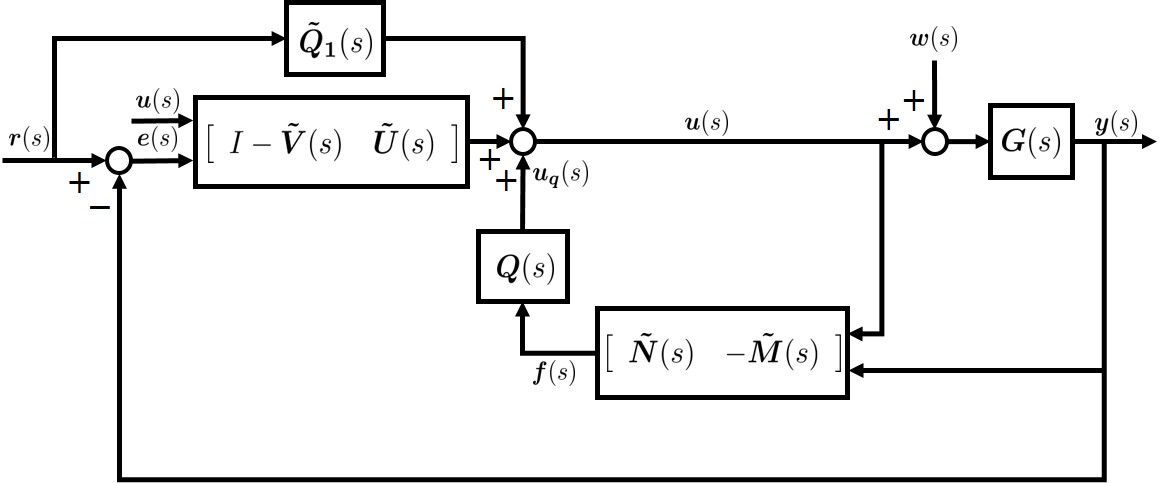
Note that the GIMC structure in Fig. 2 can be extended to an equivalent 2DoF controller structure with an additional feed-forward parameter , shown in Fig 3. Indeed, the controller in Fig. 3 can be deemed as with
which in fact parameterizes all stabilizing 2DoF controllers in terms of free parameters and [22, Theorem 5.6.3]. In this case, the controller can be obtained as . Since occurs in the feed-forward channel, without loss of generality, the GIMC in Fig. 2 is adopted as the beginning structure in this paper.
III Two-Controller Structure
This section presents a new stabilizing control structure motivated by GIMC. Consider the following finite-dimensional linear time-invariant (FDLTI) system
| (3) |
where , and are the state, control input, and sensor output, respectively. All matrices are real constant and have compatible dimensions. The following assumption is required throughout the remainder of this paper.
Assumption 1
is stabilizable and is detectable.
A full-order Luenberger observer for system (3) can be given by
| (4) |
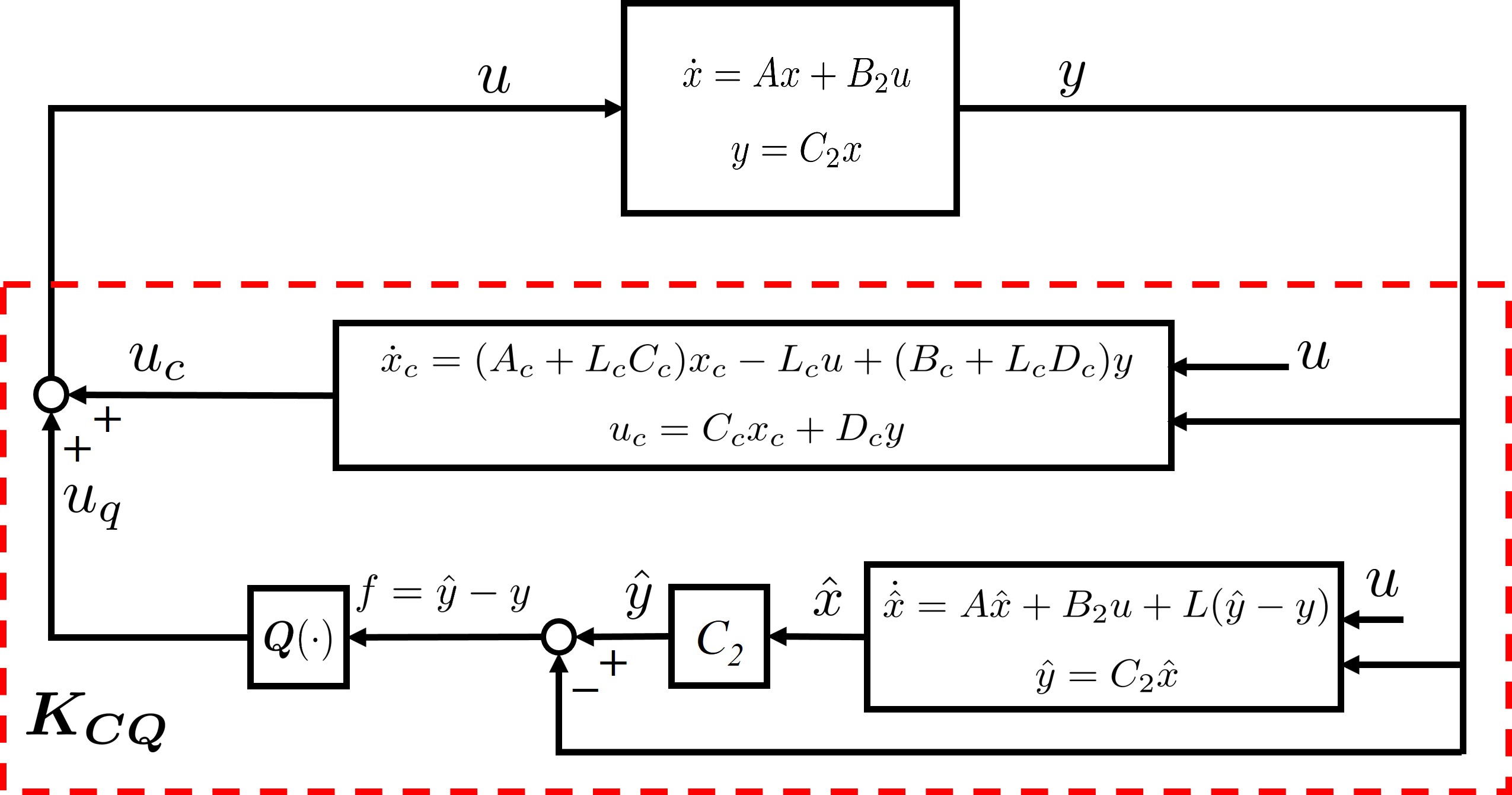
where is the residual signal and is any matrix such that is stable. Note that the Luenberger observer (4) is very related to the GIMC structure in Fig. 2. Specifically, by letting in the GIMC structure, a state-space realization of and can be obtained as
and it is not difficult to observe that is the residual signal generated by the Luenberger observer (4).
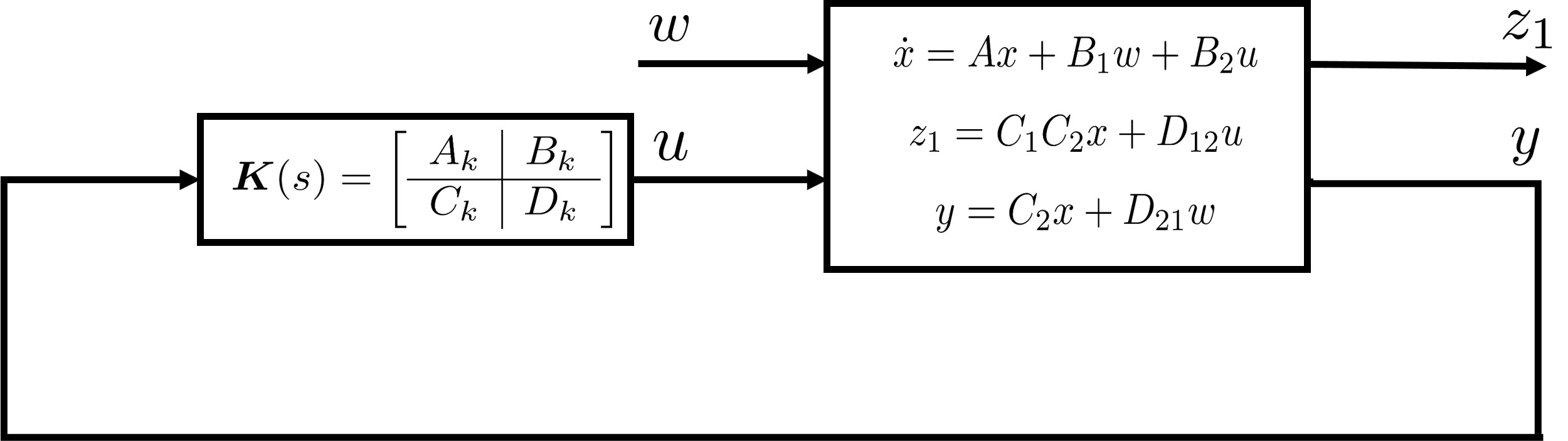
For the system in (3), consider a dynamic output-feedback stabilizing controller :
| (7) |
Clearly, is stabilizable and detectable, since stabilizes if and only if stabilizes [22, Section 5.1]. Then there exists a matrix , such that is stable. Motivated from the GIMC structure in Fig. 2, we present the following composite controller :
| (13) |
based on the observer (4) and the controller in (7), where is a stable dynamic operator driven by the residual signal to be designed in the following form:
| (16) |
with stable.
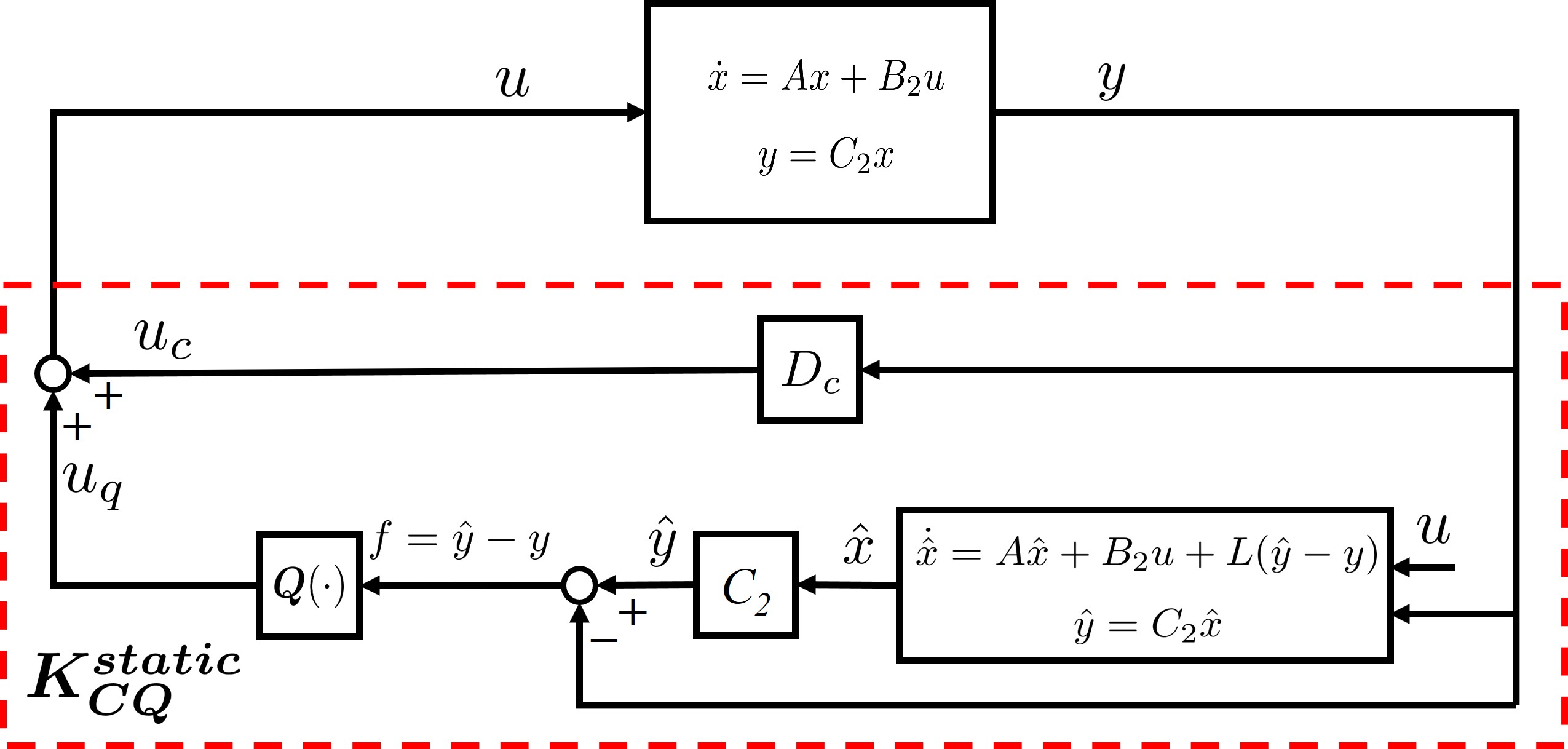
The significant feature of the composite controller is that if the output signal of is zero, then and is the same as the controller in (7). On the other hand, if , then the composite controller behaves like a different one. Therefore, can be viewed as a two-controller structure to stabilize the system in (3), as shown in Fig. 4.
Now consider another dynamic output-feedback stabilizing controller designed in the following form:
| (19) |
Then we give the solution of in state space such that when , which is presented in the following proposition.
Proposition 1
| (16) |
Proof:
First, is obviously stable, as and are both stable. Note that is the closed-loop matrix for the system with controller . For the system in (3) with the controller in (13), by letting as the closed-loop system state, we obtain the following closed-loop matrix
The above matrix is stable, as , , and are all stable. Thus stabilizes . Next we shall show that if is realized by (23), then . It follows from the composite controller (13) that
where the state is . Substituting in (23) into the above formula and using the similarity transformation
we obtain , where the detailed derivation is shown in (16) in the bottom of the next page. ∎
Remark 2
It follows from in (23) that in fact consists of three parts in terms of controller , the Luenberger observer (4), and controller . Specifically, writing , then can be described as
Considering in described by (13), it is interesting to have the following relationship:
| (32) |
which suggests that the state of corresponds to the states of , the Luenberger observer (4), and . Note that the parameters in (23) can be derived by letting and using the tool of linear fractional transformations [25, Chapter 10].
Remark 3
In the sequel, two interesting cases: shared observer and static stabilizing controllers, are considered.
III-A Two-controller structure with shared observer
Now consider the controller in (7) to be in the observer-based state-feedback structure with feedback gain and observer gain , such that both and are stable. Then, with , , , , and , the dynamic output-feedback controller (7) becomes the following observer-based state-feedback form:
| (35) |
and the controller in (13) is rewritten as
| (41) |
Note that is stable here. A new controller structure with shared observer is proposed by forcing as follows:
| (46) |
The resulting control system is shown in Fig. 5.

Proposition 2 (Shared Observer)
Proof:
III-B Two-controller structure with static controllers
Assume that there exists a static controller stabilizing system (3). Then let controller be static:
| (55) |
The controller in (13) becomes
| (60) |
The resulting control system is shown in Fig. 6. The solution to in state space is presented in the following proposition and its proof is similar to that of the previous two propositions and thus is omitted.
Proposition 3 (Static Controller)
If controller is also static, i.e., , then reduces to
| (68) |
State feedback: The static state feedback is a special static case when . In this case, the observer gain can be simply chosen as , as is stable.
IV Multi-Objective Complementary Control (MOCC)
In general, a typical MO control problem specifies different objectives on different channels of the closed-loop system [10, 13, 14, 2, 15, 4, 7]. The objectives under consideration can be roughly divided into two classes: performance involving commands and robustness against unknown disturbances. Performance is meant for transient process, tracking accuracy, passivity requirement [26], etc, while robustness is meant to keep healthy performance in an uncertain or partially unknown environment. It has been pointed out in the Introduction that the traditional design technique using a single controller to address multiple objectives of the closed-loop system usually renders trade-off solutions with compromised performance and robustness in some sense, and for 2DoF controllers there does not exist a general and systematic design method so far to address both performance and the robustness. In contrast, we shall show that MO control problems can be handled effectively by applying the two-controller structures presented in the previous section with two independently designed controllers operating in a naturally complementary way, leading to a MO complementary control (MOCC) framework.
In the sequel, a specific robust tracking control problem is presented to demonstrate the advantages of the proposed MOCC framework. The MO tracking problem under consideration has two objectives: tracking performance and robustness. In the new control structure, is designed to address the tracking performance without disturbances, and is designed to address the robustness with respect to unknown/uncertain disturbances.
Consider a perturbed FDLTI system (3), described by
| (72) |
where is the system state, is the control input, is the measured output, is the unknown disturbance input, known or measurable reference signal, and consisting of tracking error and control input is an output variable evaluating the tracking performance.
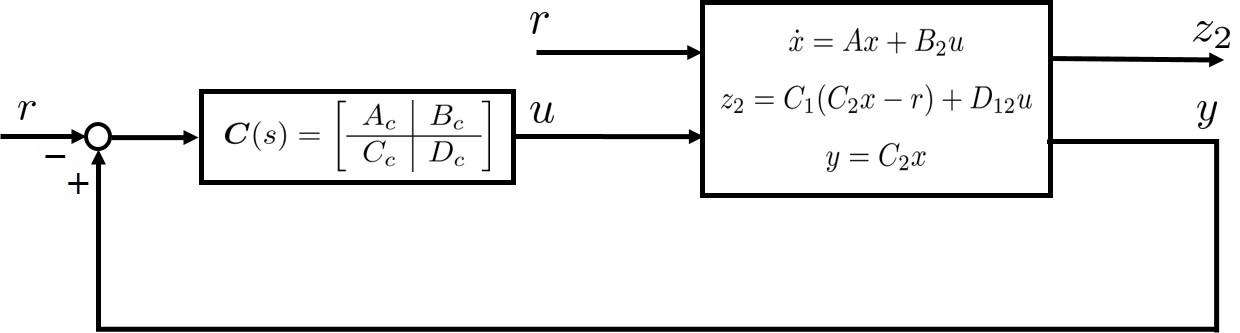
Assume that an admissible tracking controller is designed as the following form
| (75) |
for the system in (72) with , i.e.,
| (79) |
as shown in Fig. 7.
On the other hand, assume that a robust controller having the form of
| (82) |
is designed for the system in (72) with , i.e,
| (86) |
as shown in Fig. 8.
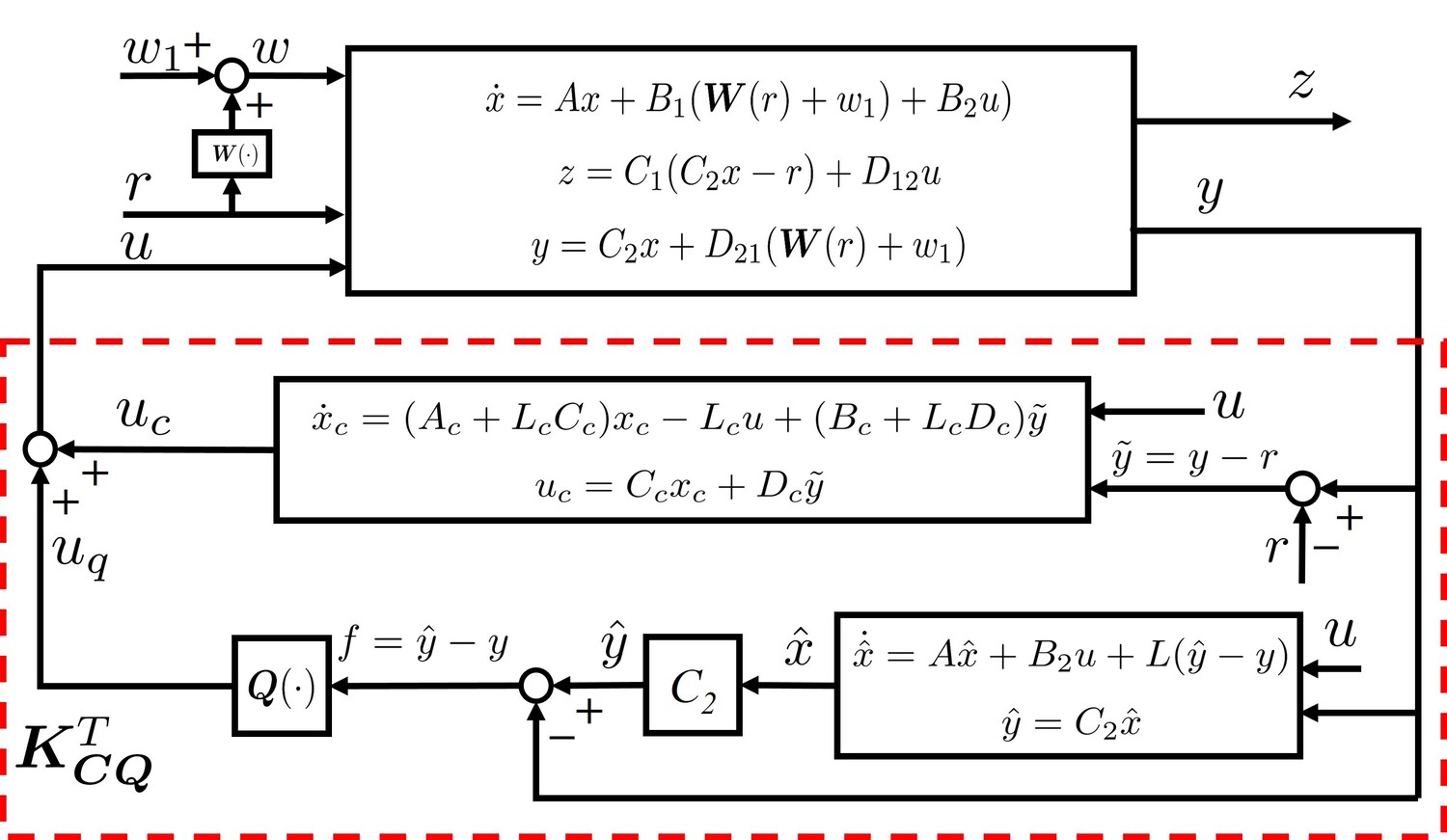
Then by applying the two-controller structure in Fig. 4, a MO tracking controller (the superscript “” stands for tracking) can be obtained shown in Fig. 9, where the state-space model of is constructed as that in Proposition 1:
with given by (23). Note that the difference between the controller in Fig. 4 and the tracking controller in Fig. 9 is that for , the reference signal is also as an input to generate the control signal . Then it follows from Proposition 1 that for the tracking control system with , the transfer matrix from to is .
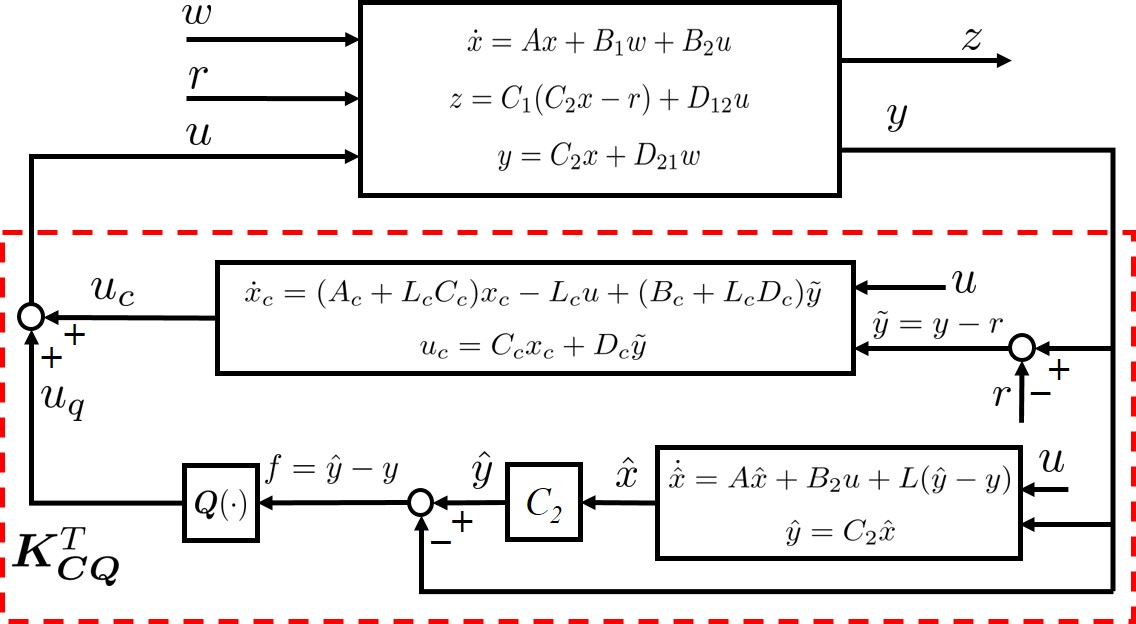
Remark 5
As the two-controller structure studied in Section III, the tracking controller can also have shared-observer and static structures. If the tracking controller in (75) is observer-based with , , , , and , then in becomes
Write above as a sum of two terms: , such that
Then similar to the controller in (46), the tracking controller with shared observer is described as
The parameters of are given by Proposition 2. If the tracking controller in (75) is static as , the tracking controller is simply given by
with given by Proposition 3.
Next, we shall conduct a performance analysis for the resulting tracking controller . It will be shown that the tracking controller consisting of for the nominal tracking performance and for the robustness leads to a decoupled design and the two controllers and operate in a complementary way.
IV-A Performance analysis
In principle, the objective of performance analysis in this paper is to determine the closed-loop performance generated by under certain specified criteria such as the norm and norm of . Here, we shall choose the power norm of bounded power signals, since it can be used for persistent signals and is related to the quadratic criterion and the norm. It is common to use the power norm of bounded power signals in the analysis of control systems, e.g. [13, 14, 4, 27, 28]. All signals considered in this paper are assumed to be deterministic. In the sequel, the notion of bounded power signals is introduced.
Given a real vector signal that is zero for , its asymptotically stationary autocorrelation matrix is defined as
The Fourier transform of called the (power) spectral density of , if exists, is
Then the bounded power signals are defined as follows.
Definition 1 ([13])
A signal is said to have bounded power if it satisfies the following conditions:
-
1.
is bounded for all ;
-
2.
The autocorrelation matrix exists for all and the spectral density matrix exists;
-
3.
.
The set of all signals having bounded power is denoted by . A seminorm can be defined on :
| (89) |
The power seminorm of a signal can also be computed from its spectral density matrix by using the inverse Fourier transform of :
| (90) |
which is derived from the Parseval theorem in the average power case [29, Section 3.5.7] with being the Laplace transform of . The cross-correlation between two real signals and is defined as
and its Fourier transform is denoted by , called cross (power) spectral density.
Now consider the tracking control system in Fig. 9, with constructed according to Proposition 1. Both the disturbance signal and the reference signal are assumed to be bounded power signals, i.e., . The closed-loop performance will be measured in terms of the power norm of the performance output , i.e., . First, the closed-loop system can be described by
| (93) |
where and
The following decoupled result is important in this paper, which characterizes the nature of the closed-loop system with the controller .
| (30) | ||||
| (38) |
Lemma 1
The closed-loop system (93) can be represented as the following form of transfer matrix in terms of state-space matrices:
| (97) |
where
Proof:
It is clearly seen that the closed-loop transfer function consists of and which depend on the controller and the controller separately, and does not depend on and . Note that and are the closed-loop transfer matrices in Figs. 8 and 7, respectively. The total performance achieved by and is characterized in the analysis below, through the power norm of . Due to the neat separate transfer matrices and , we shall analyze in the frequency domain.
Defining , then the spectral density matrix of can be written as
From the spectral analysis [13] and (90), we get
| (104) |
and
| (105) |
Generally, the disturbance signal and the reference signal could be independent or dependent on each other. Signals and are said to be orthogonal or independent if [30, 13]. For example, any two sinusoidal signals and with different frequencies are orthogonal since the cross-correlation matrix which is the orthogonal case. The dependent case could happen when is induced by plant parameter uncertainties, which in turn is related to the reference signal in some way. Performance evaluations are carried out for both orthogonal and dependent cases and summarized in the following two theorems.
Theorem 1
Proof:
Remark 6
It is clear that the nominal tracking performance is characterized in with respect to the reference signal and the impact of disturbance (hence, the robustness) is measured in . Since only depends on and is only related to , Theorem 1 shows that if and are orthogonal, there is no trade-off between the design of for the nominal tracking performance and the design of for the robustness. In other words, the two independently designed controllers and operate in a naturally complementary way, and, obviously, when , the nominal tracking performance can be fully kept by . Furthermore, it can also be seen that, to achieve better robust tracking performance, should be designed to bring low, while can be designed to be a robust controller. For example, if is designed to be an control for a given , then . In general, for a given , . In this sense, the operator obtained in Proposition 1 achieves the two objectives of nominal tracking performance and minimization of simultaneously.
Remark 7
It is also noted that the controller could itself be designed to address multiple optimal performance objectives such as the controller in Lemma 1 of [31] that is derived from the Youla parameter to optimize multiple costs simultaneously. Since no impact of uncertain disturbance is counted, this controller could be complemented by the constructed in the MOCC design of this paper to achieve non-compromised robust optimal performance with respect to uncertain disturbance.
The performance analysis for the dependent case could be more complicated due to the complexity of dependency between and . In this paper, performance analysis is done for the case that , where is assumed to be a mapping satisfying , and is the orthogonal part of with both and , i.e., and . The system in (72) then becomes
| (110) |
The MO tracking control system in Fig. 9 can be modified as Fig. 10.
For a linear time-invariant mapping , denoting the Laplace transform of as , then
and . Now we are ready to present the following performance analysis result in the dependent case.
Theorem 2
For dependent and as in , where is an LTI mapping with , and is orthogonal of both and in the sense that and , given any controllers and in (75) and (82), the following equations hold:
| (111) | ||||
| (112) |
where is a scalar level constant,
and and are derived in Lemma 1. Moreover, if is designed to be an control for a given such that , then, regardless of , we have
| (113) |
with the worst dependent weighting , and
| (114) |
Proof:
Remark 8
If no dependence is assumed between and , that is , then , thus, resulting in Theorem 1.
Remark 9
From Theorem 2, one can derive
where the fact that is applied. It can be seen that the upper bound above is a sum of two terms that depend on controllers and separately. Hence, it is clear that, for any and , the same observation as that from Theorem 1 can be drawn: to achieve better robust tracking performance, should be designed to bring the nominal tracking performance low and should be designed to address the robustness against . It should be pointed out that the dependency may not be always harmful to the tracking performance, since the case could happen. In case it poses a negative impact, Theorem 2 gives the worst possible linear dependency for an controller .
IV-B A specific MOCC design: LQ tracking (LQT)
In this section, a specific MO complementary tracking controller is presented based on the performance analysis results in Theorems 1 and 2. That is, controllers and are designed according to the LQ optimal criterion and the criterion, respectively. Besides Assumption 1, the following standard assumption is made on the system (72) in this subsection [32, 25]:
Assumption 2
(i) has full row rank for all ; (ii) has full column rank for all ; (iii) and .
Step 1: Design controller to be the LQ optimal tracking controller. The design of the LQ optimal tracking controller is based on the FDLTI system (72) with , i.e., system (79) and, is to minimize the following quadratic cost function:
| (115) |
The optimal control law, which is a 2DoF form111Though the tracking controller in (75) is in the 1DoF form, there is no restriction for the proposed MOCC framework to be applied to the case of a 2DoF controller , as discussed in Remark 1., is given by [33, Chapter 4][34]
| (119) |
and the minimal cost is
| (120) |
where is the observer gain matrix with stable, , , and . Here, is the stabilizing solution to the following algebraic Riccati equation:
Notice that the dynamics of in (119) is anticausal such that is bounded [33, Chapter 4].
Step 2: Design controller to be an controller. Now consider the FDLTI system (72) with , i.e., system (86). The controller is designed according to the following performance criterion:
| (121) |
where is a prescribed value. It follows from [25, 32] that the central controller satisfying (121) is
| (122) |
where
Here, and are the stabilizing solutions to the following algebraic Riccati equations:
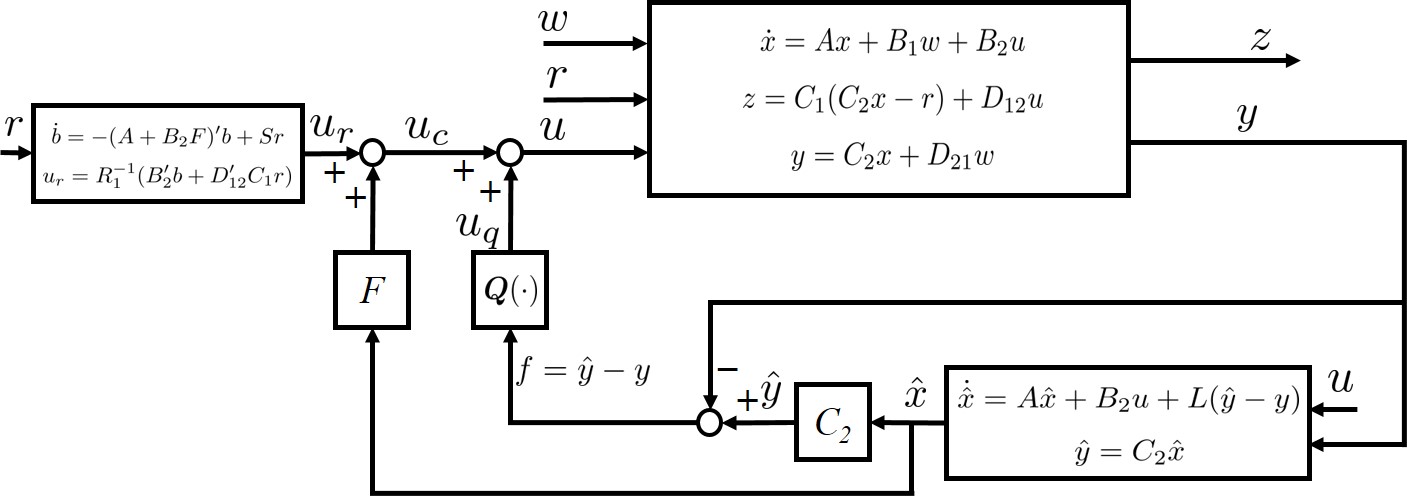
Step 3: Design of MOCC: controller.
Applying the two-controller structure with shared observer (Proposition 2) gives the following MO complementary tracking controller :
| (129) |
where , and by (51) in Proposition 2,
The diagram of controller by the MOCC framework is shown in Fig. 11. Similarly, by applying the two-controller structure in the state-feedback case in subsection III-B, the controller of the state-feedback version can be obtained.
V Data-driven Optimization of Performance
Theorems 1 and 2 show the total tracking performance achieved by and . Note that, if is designed as the controller shown in Subsection IV-B, it is still the worst-case design. Hence, in order to further improve the robust performance, an extra gain factor can be introduced into the operator :
| (133) |
with given in (23). This can be further optimized through a data-driven approach. Let us denote the MO tracking controller with as . Apparently, the two special cases and correspond to the nominal controller and the MO complementary controller , respectively.
With being the state of the closed-loop system, the closed-loop system matrix becomes
Obviously, is a stable matrix for all , so that the stability of the closed-loop is guaranteed for any . The system performance can be further improved by through a data-driven approach. In this regard, let us consider the task of tracking a desired trajectory within a specified finite time interval, with the task repeating over multiple iterations. It is assumed that the disturbance is iteration-invariant; in other words, when the tracking task is repetitive, the unknown disturbance also repeats. This scenario closely resembles the setting in [35], where PID parameters are iteratively tuned. Thus, the performance optimization problem can be dealt with in the framework of iterative learning control (ILC) [36, 37], and the following finite-horizon cost function is introduced:
| (134) |
where is the measured version of . Then an optimal minimizing the cost function (134) can be found by an extremum seeking (ES) algorithm [38, 39, 35], which requires the following assumption.
Assumption 3
For the closed-loop system with the controller and in the presence of a deterministic and repeating disturbance , the cost function defined by (134) has a minimum at , and the following holds:
| (135) |
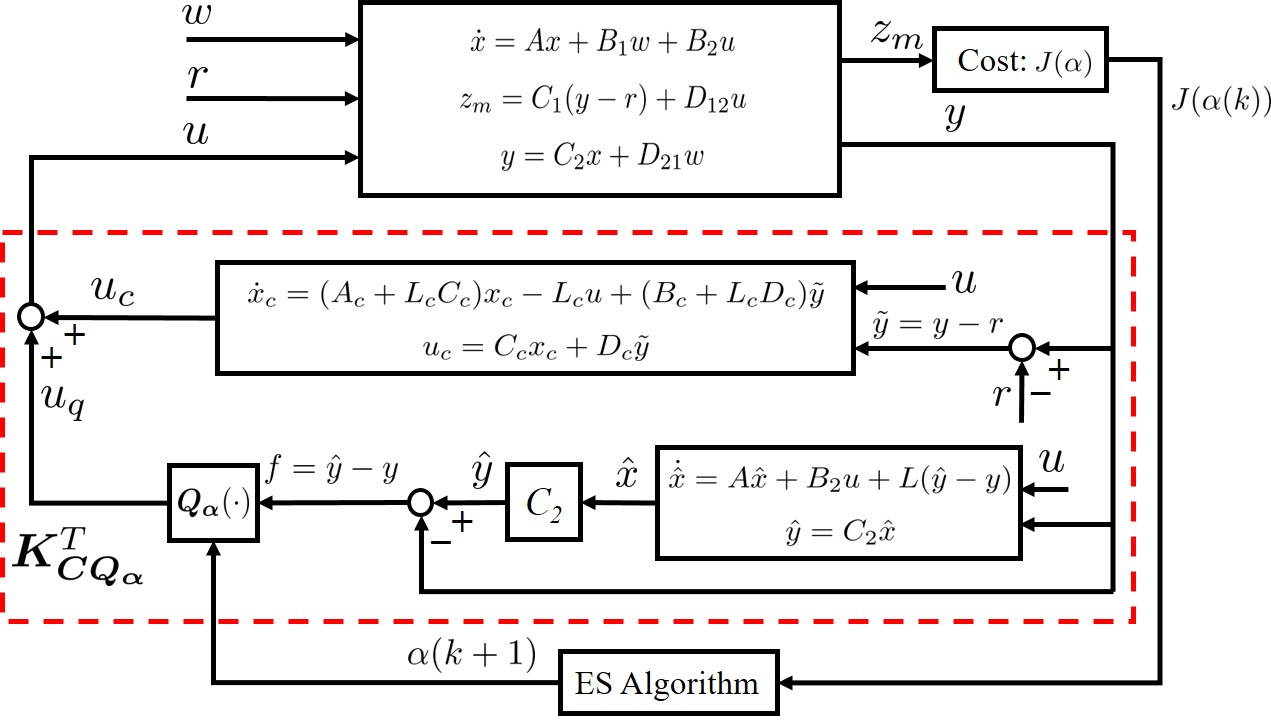
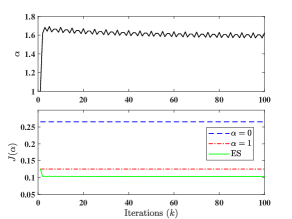
Under Assumption 3, an ES algorithm can be used to tune the parameter for a given disturbance by repeatedly running the closed-loop system with the controller over the finite time . ES is a data-driven optimization method which uses input-output data to seek an optimal input with respect to a selected cost [38]. The ES algorithm adopted here is in the iteration domain, which can be, for example, that presented in [35]. The overall ES tuning scheme for is delineated in Fig. 12. By tuning the parameters of the ES algorithm appropriately, the parameter will converge to a small neighborhood of iteratively as shown in our work [40].
VI Example
To demonstrate the advantages of the developed MO control framework, a comparative example of tracking control is worked out. Consider the following double integrator system
with the performance variable
The reference signal is . Thus, the tracking task is to design a controller such that the first state can track the reference signal while the control effort is taken into account. To make comparisons, four different tracking control methods are considered: the proposed MOCC in (129), LQT control in (119), tracking control [34], and disturbance observer-based control (DOBC) [41]. For the MO complementary controller (129),
and the robustness level is chosen as , which is the minimum value (tolerance of ). The LQT controller uses the same and , and the tracking controller uses the same . Here, the DOBC combines a disturbance observer and a disturbance compensation gain, whose structure is similar to the proposed two-controller structure with shared observer in Fig. 5. The disturbance observer is to jointly estimate the system state and disturbance:
where and are the estimated state and disturbance, respectively, and and are the preassumed disturbance model. The selection of , and needs to make the error matrix stable. The disturbance compensation gain can be chosen as [41, 42]
Then the tracking controller based on the DOBC method is designed to be .
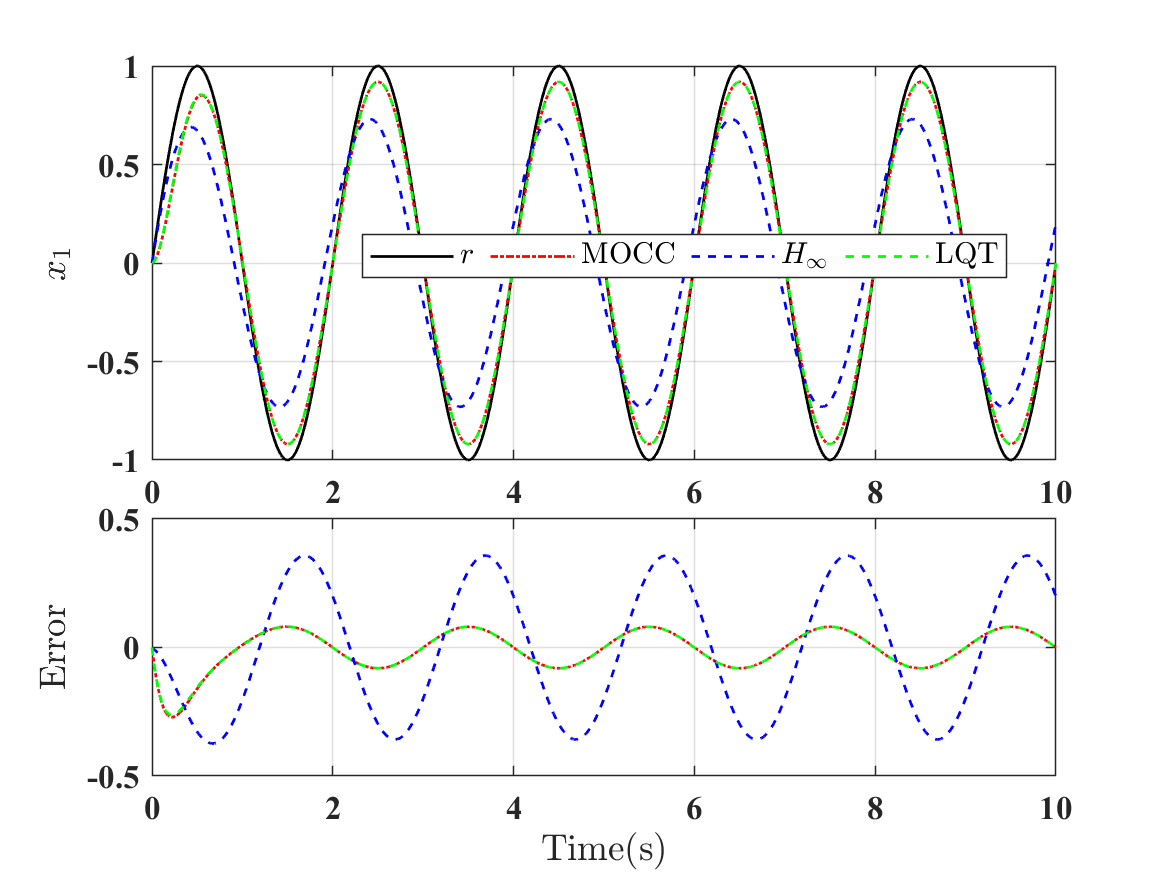
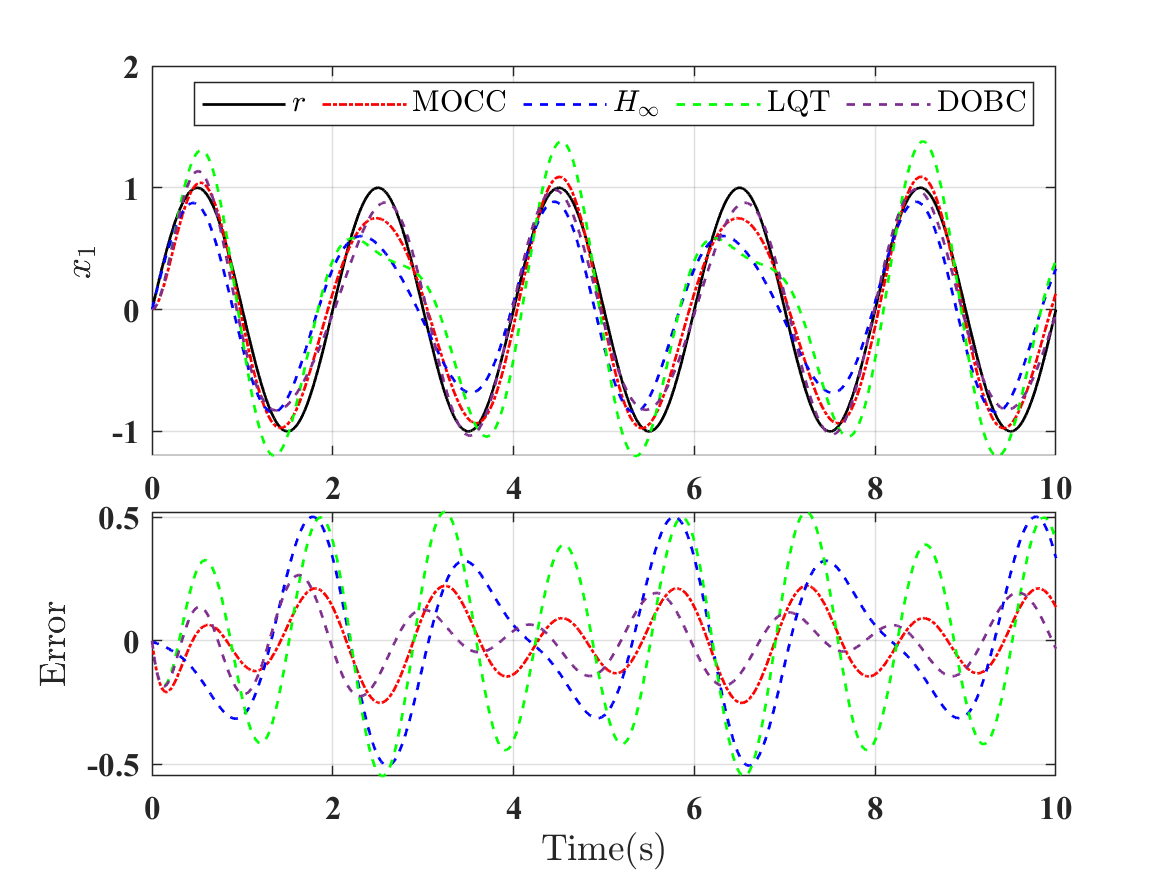
First, we consider the scenario in the absence of disturbance. In this scenario, the DOBC is not included for comparison as no disturbance is considered. The tracking response and tracking error are shown in Fig. 13 and the average quadratic costs for MOCC, LQT control, and tracking control are , and , respectively. Thus, it is verified that the MOCC has the same tracking performance as LQT control when , while, on the other hand, it is shown that the control has a significant performance loss () compared with the LQT control.
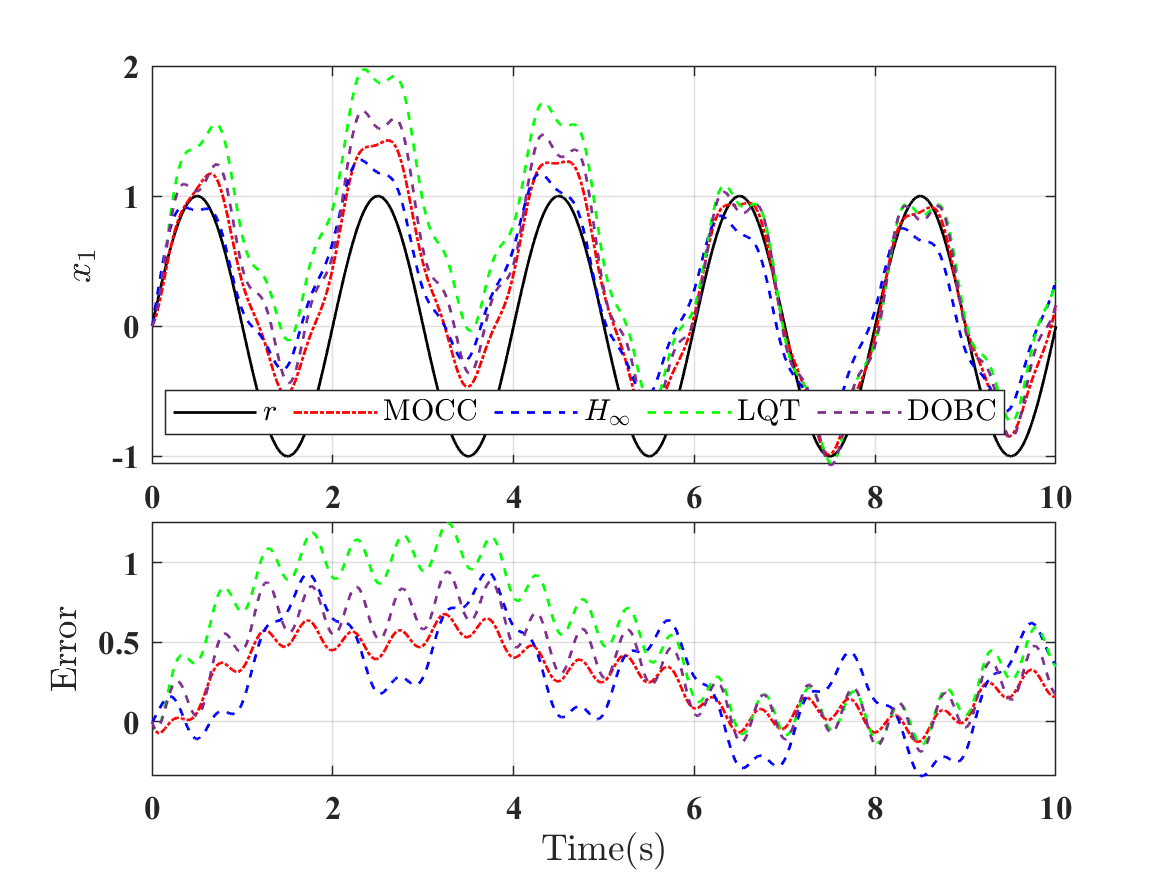
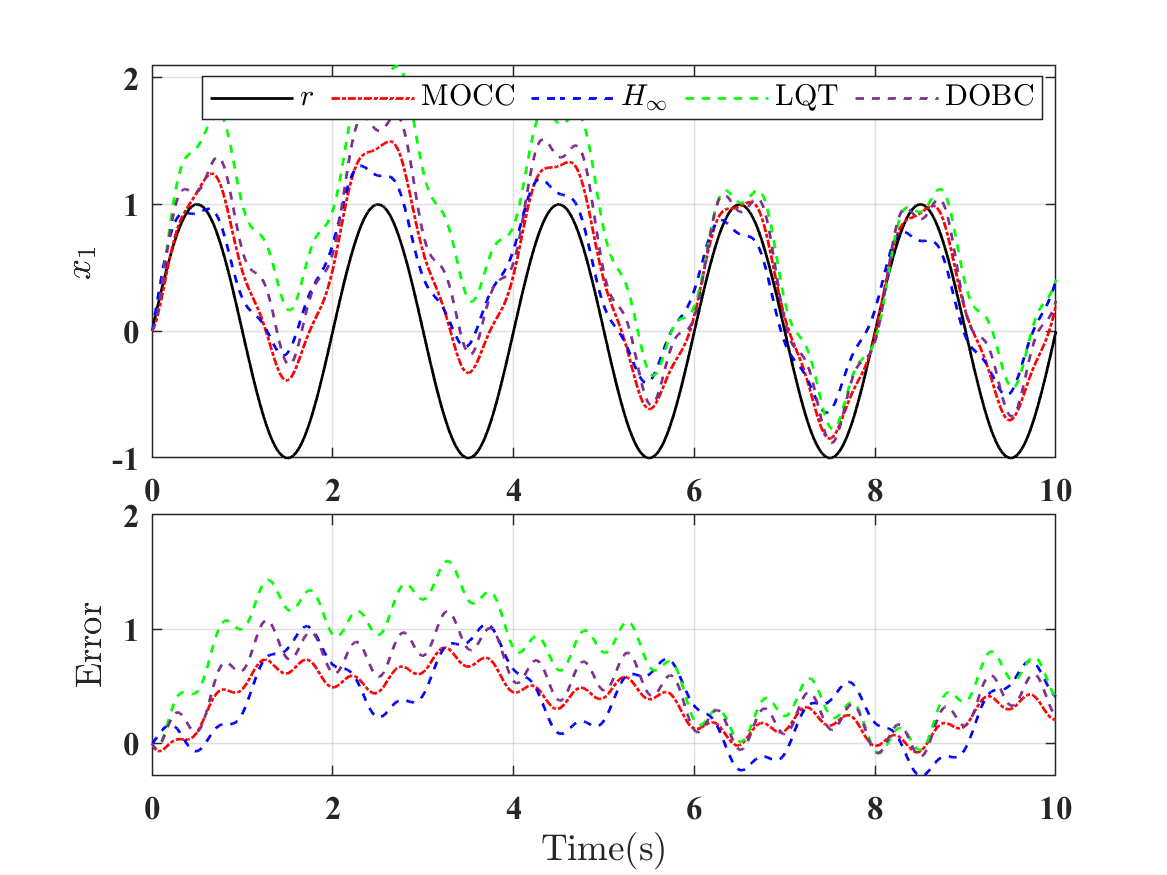
Now three different disturbances are considered:
For the DOBC method, the matrices and use the model of , i.e., . Choosing and such that the eigenvalues of the error matrix are . The tracking results for are shown in Figs. 14–16. It can be observed in Fig. 14 that the DOBC is comparable to MOCC in terms of tracking error in the presence of . This is not surprising, as the DOBC uses the exact disturbance model of . We can calculate the quadratic costs () generated by the four controllers for , , and . Also, the robust performance of the four controllers can be compared by computing the norm of the closed-loop transfer matrix from to . The quadratic cost and the norm for the four controllers are summarized in Table I. It can be seen that the proposed MOCC method generates the minimum tracking cost for the three specific disturbances and has the minimum norm for robustness. In summary, the proposed MOCC method does not require a prior knowledge of the disturbance model and guarantees a certain robustness level compared to the LQT and the DOBC, and performs better than the method due to the proposed complementary structure.
| MOCC | LQT | DOBC | ||
|---|---|---|---|---|
| norm |
Finally, we provide a simulation to illustrate the performance optimization idea with a factor discussed in Section V. We will use the ES algorithm in the iteration domain from [35] to find an optimal . The quadratic cost in (134) is used with . The disturbance signal is considered in the tuning process and the result is shown in Fig. 17. It is seen that the parameter converges to a small neighborhood of which yields a lower cost compared with the cases when (, LQT performance) and (, MOCC performance).
VII Conclusion
A multi-objective complementary control (MOCC) framework that can assemble two independently designed controllers in a complementary way instead of a trade-off is proposed. A state-space realization for the Youla-type operator is provided to manage the two controllers. In particular, an MO complementary tracking control is applied to demonstrate the advantages of MOCC. Rigorous performance analysis shows that the tracking performance and robustness can be addressed separately, especially when the disturbance signal is independent of the reference signal. Simulation results validate the advantages of MOCC, especially, when the disturbance signal is completely unknown. Furthermore, it is shown that this framework can be potentially extended to improve the total performance through a data-driven approach with an extra gain factor to .
References
- [1] P. P. Khargonekar and M. A. Rotea, “Multiple objective optimal control of linear systems: The quadratic norm case,” IEEE Transactions on Automatic Control, vol. 36, no. 1, pp. 14–24, 1991.
- [2] C. Scherer, P. Gahinet, and M. Chilali, “Multiobjective output-feedback control via LMI optimization,” IEEE Transactions on Automatic Control, vol. 42, no. 7, pp. 896–911, 1997.
- [3] N. Elia and M. A. Dahleh, “Controller design with multiple objectives,” IEEE Transactions on Automatic Control, vol. 42, no. 5, pp. 596–613, 1997.
- [4] X. Chen and K. Zhou, “Multiobjective / control design,” SIAM Journal on Control and Optimization, vol. 40, no. 2, pp. 628–660, 2001.
- [5] C. Lin and B.-S. Chen, “Achieving pareto optimal power tracking control for interference limited wireless systems via multi-objective optimization,” IEEE Transactions on Wireless Communications, vol. 12, no. 12, pp. 6154–6165, 2013.
- [6] L. Menini, C. Possieri, and A. Tornambè, “Algebraic methods for multiobjective optimal design of control feedbacks for linear systems,” IEEE Transactions on Automatic Control, vol. 63, no. 12, pp. 4188–4203, 2018.
- [7] D. V. Balandin and M. M. Kogan, “Multi-objective generalized control,” Automatica, vol. 99, pp. 317–322, 2019.
- [8] P. Bhowmick and S. Patra, “Solution to negative-imaginary control problem for uncertain LTI systems with multi-objective performance,” Automatica, vol. 112, p. Art. no. 108735, 2020.
- [9] H.-G. Han, C. Chen, H.-Y. Sun, and J.-F. Qiao, “Multiobjective integrated optimal control for nonlinear systems,” IEEE Transactions on Cybernetics, early access, 2022, doi: 10.1109/TCYB.2022.3204030.
- [10] D. Bernstein and W. Haddad, “LQG control with an performance bound: A Riccati equation approach,” IEEE Transactions on Automatic Control, vol. 34, no. 3, pp. 293–305, 1989.
- [11] P. P. Khargonekar and M. A. Rotea, “Mixed control: A convex optimization approach,” IEEE Transactions on Automatic Control, vol. 36, no. 7, pp. 824–837, 1991.
- [12] D. J. Limebeer, B. D. Anderson, and B. Hendel, “A Nash game approach to mixed control,” IEEE Transactions on Automatic Control, vol. 39, no. 1, pp. 69–82, 1994.
- [13] K. Zhou, K. Glover, B. Bodenheimer, and J. Doyle, “Mixed and performance objectives I: Robust performance analysis,” IEEE Transactions on Automatic Control, vol. 39, no. 8, pp. 1564–1574, 1994.
- [14] J. Doyle, K. Zhou, K. Glover, and B. Bodenheimer, “Mixed and performance objectives II: Optimal control,” IEEE Transactions on Automatic Control, vol. 39, no. 8, pp. 1575–1587, 1994.
- [15] H. A. Hindi, B. Hassibi, and S. P. Boyd, “Multiobjective -optimal control via finite dimensional -parametrization and linear matrix inequalities,” in Proceedings of the 1998 American Control Conference (ACC), 1998, pp. 3244–3249.
- [16] D. Youla and J. Bongiorno, “A feedback theory of two-degree-of-freedom optimal Wiener-Hopf design,” IEEE Transactions on Automatic Control, vol. 30, no. 7, pp. 652–665, 1985.
- [17] J. Moore, L. Xia, and K. Glover, “On improving control-loop robustness of model-matching controllers,” Systems & Control Letters, vol. 7, no. 2, pp. 83–87, 1986.
- [18] C. Wen, J. Lu, and W. Su, “Bi-objective control design for vehicle-mounted mobile antenna servo systems,” IET Control Theory & Applications, vol. 16, no. 2, pp. 256–272, 2022.
- [19] K. Zhou and Z. Ren, “A new controller architecture for high performance, robust, and fault-tolerant control,” IEEE Transactions on Automatic Control, vol. 46, no. 10, pp. 1613–1618, 2001.
- [20] J. Chen, S. Hara, and G. Chen, “Best tracking and regulation performance under control energy constraint,” IEEE Transactions on Automatic Control, vol. 48, no. 8, pp. 1320–1336, 2003.
- [21] J. Chen, L. Qiu, and O. Toker, “Limitations on maximal tracking accuracy,” IEEE Transactions on Automatic Control, vol. 45, no. 2, pp. 326–331, 2000.
- [22] M. Vidyasagar, Control Systems Synthesis: A Factorization Approach, Part I. Switzerland: Springer, 2022.
- [23] B. D. Anderson, “From Youla–Kucera to identification, adaptive and nonlinear control,” Automatica, vol. 34, no. 12, pp. 1485–1506, 1998.
- [24] X. Chen, K. Zhou, and Y. Tan, “Revisit of LQG control–A new paradigm with recovered robustness,” in Porceedings of the IEEE 58th Conference on Decision and Control (CDC), 2019, pp. 5819–5825.
- [25] K. Zhou, J. Doyle, and K. Glover, Robust and optimal control. Englewood Cliffs, NJ, USA: Prentice-Hall, 1996.
- [26] A. Q. Keemink, H. van der Kooij, and A. H. Stienen, “Admittance control for physical human–robot interaction,” Int. J. Robot. Res., vol. 37, no. 11, pp. 1421–1444, 2018.
- [27] P. Mäkilä, J. Partington, and T. Norlander, “Bounded power signal spaces for robust control and modeling,” SIAM Journal on Control and Optimization, vol. 37, no. 1, pp. 92–117, 1998.
- [28] Y. Wan, W. Dong, H. Wu, and H. Ye, “Integrated fault detection system design for linear discrete time-varying systems with bounded power disturbances,” International Journal of Robust and Nonlinear Control, vol. 23, no. 16, pp. 1781–1802, 2013.
- [29] A. V. Oppenheim, A. S. Willsky, S. H. Nawab, and J.-J. Ding, Signals and systems, 2nd ed. Upper Saddle River, NJ, USA: Prentice-Hall, 1997.
- [30] W. A. Gardner and E. A. Robinson, Statistical spectral analysis: A nonprobabilistic theory. Englewood Cliffs, NJ, USA: Prentice-Hall, 1988.
- [31] F. J. Vargas, E. I. Silva, and J. Chen, “Stabilization of two-input two-output systems over SNR-constrained channels,” Automatica, vol. 49, no. 10, pp. 3133–3140, 2013.
- [32] K. Glover and J. C. Doyle, “State-space formulae for all stabilizing controllers that satisfy an -norm bound and relations to relations to risk sensitivity,” Systems & Control Letters, vol. 11, no. 3, pp. 167–172, 1988.
- [33] B. D. Anderson and J. B. Moore, Optimal control: Linear quadratic methods. Englewood Cliffs, NJ, USA: Prentice-Hall, 1989.
- [34] U. Shaked and C. E. de Souza, “Continuous-time tracking problems in an setting: A game theory approach,” IEEE Transactions on Automatic Control, vol. 40, no. 5, pp. 841–852, 1995.
- [35] N. J. Killingsworth and M. Krstic, “PID tuning using extremum seeking: Online, model-free performance optimization,” IEEE Control Systems Magazine, vol. 26, no. 1, pp. 70–79, 2006.
- [36] D. A. Bristow, M. Tharayil, and A. G. Alleyne, “A survey of iterative learning control,” IEEE Control Systems Magazine, vol. 26, no. 3, pp. 96–114, 2006.
- [37] S. Z. Khong, D. Nešić, and M. Krstić, “Iterative learning control based on extremum seeking,” Automatica, vol. 66, pp. 238–245, 2016.
- [38] K. B. Ariyur and M. Krstic, Real-time optimization by extremum-seeking control. NJ: John Wiley & Sons, 2003.
- [39] Y. Tan, D. Nešić, and I. Mareels, “On non-local stability properties of extremum seeking control,” Automatica, vol. 42, no. 6, pp. 889–903, 2006.
- [40] J. Xu, Y. Tan, and X. Chen, “Robust tracking control for nonlinear systems: Performance optimization via extremum seeking,” in Proceedings of the 2023 American Control Conference (ACC), 2023, pp. 1523–1528.
- [41] W.-H. Chen, J. Yang, L. Guo, and S. Li, “Disturbance-observer-based control and related methods—An overview,” IEEE Transactions on Industrial Electronics, vol. 63, no. 2, pp. 1083–1095, 2016.
- [42] J. Yang, A. Zolotas, W.-H. Chen, K. Michail, and S. Li, “Robust control of nonlinear MAGLEV suspension system with mismatched uncertainties via DOBC approach,” ISA Transactions, vol. 50, no. 3, pp. 389–396, 2011.