Multiple Domain Experts Collaborative Learning:
Multi-Source Domain Generalization For Peron Re-Identification

Shijie Yu,^1,2 Feng Zhu,³ Dapeng Chen,³ Rui Zhao,^3,5 Haobin Chen,^1,2
Jinguo Zhu,³ Shixiang Tang,³ Yu Qiao,^1,4 This work was done when Shijie Yu was an intern at SenseTime (sj.yu@siat.ac.cn).Corresponding author (yu.qiao@siat.ac.cn).

Abstract

Recent years have witnessed significant progress in person re-identification (ReID). However, current ReID approaches still suffer from considerable performance degradation when unseen testing domains exhibit different characteristics from the source training ones, known as the domain generalization problem. Given multiple source training domains, previous Domain Generalizable ReID (DG-ReID) methods usually learn all domains together using a shared network, which can’t learn sufficient knowledge from each domain. In this paper, we propose a novel Multiple Domain Experts Collaborative Learning (MECL) framework for better exploiting all training domains, which benefits from the proposed Domain-Domain Collaborative Learning (DDCL) and Universal-Domain Collaborative Learning (UDCL). DDCL utilizes domain-specific experts for fully exploiting each domain, and prevents experts from over-fitting the corresponding domain using a meta-learning strategy. In UDCL, a universal expert supervises the learning of domain experts and continuously gathers knowledge from all domain experts. Note, only the universal expert will be used for inference. Extensive experiments on DG-ReID benchmarks demonstrate the effectiveness of DDCL and UDCL, and show that the whole MECL framework significantly outperforms state-of-the-arts. Experimental results on DG-classification benchmarks also reveal the great potential of applying MECL to other DG tasks. Code will be released.

Introduction

Person re-identification (ReID) which aims to associate the corresponding person across non-overlapped cameras given query person images or videos, has attracted more and more attention due to its promising application in public security and smart city. Recently, person ReID methods (Chen et al. 2019; Hou et al. 2019; Liu, Chang, and Shen 2020) based on deep learning have achieved significant performance improvement. However, an assumption in their settings is that the training set and testing set are collected from the same domain, which limits their practical applications because the domains vary with the background, illumination and so on in the real-world scenarios, leading to drastic performance degradation of ReID models. Unsupervised domain adaptation (UDA) ReID methods (Fu et al. 2019; Ge, Chen, and Li 2020; Kumar et al. 2020; Song et al. 2020) tackle the domain shift problem in a domain adaptation manner, that is to adapt a trained model to the target domain based on unlabeled target-domain training data, but can not guarantee the performance on unseen target domains.

Refer to caption — Figure 1: The overall framework of our MECL. Each domain is associated with a specific expert. Domain experts and the universal expert are jointly learned through domain-domain and universal-domain collaborative learning. The universal expert is used for inference.

Compared with UDA, domain generalization (DG) (Li et al. 2018b; Muandet, Balduzzi, and Schölkopf 2013) is more challenging but practical because it doesn’t require any prior knowledge about the target domain during training, that is, target domains are unknown to the models. DG methods aim to improve the model’s generalization capability across domains so that they can be applied to any unseen domain once trained, i.e., “train once, run everywhere”. Most previous DG methods (Matsuura and Harada 2020; Li et al. 2018a; Muandet, Balduzzi, and Schölkopf 2013) reach a consensus that the data from different domains share the same label space. However, there is usually no ID overlap between source domains and target domains in ReID tasks, making domain generalization learning for ReID (DG-ReID) more challenging. Following Zhao et al. (2020), we focus on a more practical setting of DG-ReID, referred as multi-source DG-ReID, where the datasets for training are collected from multiple domains.

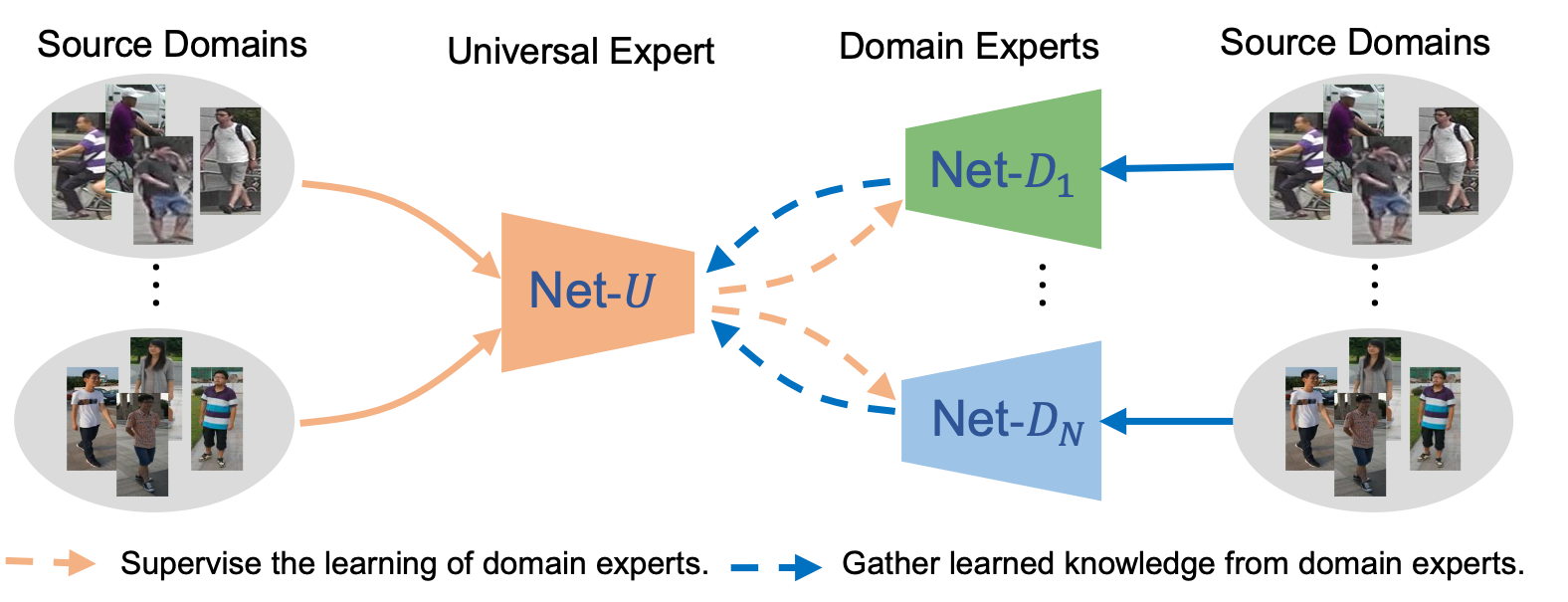
Existing works (Choi et al. 2020; Zhao et al. 2020) on the multi-source DG-ReID task usually share the same feature extractor among multiple domains. We argue that it can’t exploit each domain sufficiently because the optimization directions of different domains may have dramatic differences which will affect the learning of the single network. To alleviate this problem, we propose a novel model-agnostic learning framework (as shown in Fig. 1), named Multiple Domain Experts Collaborative Learning (MECL), which jointly trains multiple domain-specific experts and one universal expert in a collaborative learning manner. Compared to other single model based methods, MECL requires no additional computation cost in testing as only the universal expert will be used for inference.

In greater detail, two collaborative learning algorithms work together organically in MECL: (1) Domain-Domain Collaborative Learning (DDCL). Each domain expert associated with a specific domain concentrates on exploiting the corresponding domain sufficiently. Meanwhile, to avoid over-fitting one specific domain, domain experts will communicate with others to regulate its learning procedure during training using a meta-learning strategy. Vividly speaking, a good expert should not only be good at his major but also know something about other areas. (2) Universal-Domain Collaborative Learning (UDCL). The universal expert supervises the learning of domain experts and continuously gathers learned knowledge from all domain experts. Specifically, at the beginning of each training iteration, the universal expert will review the duplicated mini-batch data from all source domains and then provide supervision to the domain experts through the alignment loss and uniformity loss. At the end of the iteration, it will gather the learned knowledge from all domain experts to update its parameters by exponential moving average (EMA). DDCL and UDCL complement each other, and can significantly improve the generalization capability of learned models when applied together in our MECL framework.

In summary, the main contributions of this paper are three-fold: (1) We propose a novel model-agnostic learning framework called Multiple Domain Experts Collaborative Learning (MECL) for multi-source Domain Generalizable person ReID (DG-ReID), in which Domain-Domain Collaborative Learning (DDCL) and Universal-Domain Collaborative Learning (UDCL) organically work together to improve the model’s generalization capability across domains. (2) We establish a simple but rather strong multi-source DG-ReID baseline method named Multi-Domain Equality (MDE) which outperforms the conventional baseline by a large margin. This strong baseline method will facilitate future works in this area. (3) We perform extensive experiments on both DG-ReID and DG-classification benchmarks, not only demonstrate the effectiveness of our MECL framework on improving the model’s generalization capability for person ReID, but also reveal the great potential of applying MECL to other DG tasks.

Related Work

Person ReID. Person ReID (Chen et al. 2019; Li et al. 2014a; Sun et al. 2018; Park and Ham 2020; Luo et al. 2019; Li, Zhu, and Gong 2018) based on deep learning has made remarkable progress recently. However, these methods mainly focus on learning discriminative intra-domain person features, that is, training and evaluating on the same domain, ignoring the model’s generalization capability to unseen domains. As shown by Luo et al. (2019), the model trained on Market1501 (Zheng et al. 2015) dataset suffers from dramatic performance degradation when it is tested on DukeMTMC-reID (Ristani et al. 2016), which heavily impedes the practical applications of ReID systems. Recently, Unsupervised domain adaptation (UDA) methods (Kumar et al. 2020; Zhai et al. 2020a; Song et al. 2020) are proposed to adapt ReID models from a labeled source domain to an unlabeled target domain. This adaptation paradigm requires amounts of unlabeled target-domain training data, thus can not guarantee the performance on unseen target domains.

Domain Generalization (DG). DG is more challenging but practical than UDA, because it doesn’t require any data of target domains during training. Recent works on this topic mainly concentrate on (1) learning domain-invariant features by minimizing the inter-domain discrepancy of the same identity (Akuzawa, Iwasawa, and Matsuo 2019; Xiao et al. 2021; Li et al. 2018b), or (2) optimizing the network using meta-learning strategy to improve the generalization capability (Li et al. 2018a; Dou et al. 2019). These DG methods are usually developed on classification tasks, where source and target domains share the same label space. However, for DG-ReID tasks, there are few overlapped identities across domains, which makes DG-ReID more challenging.

Domain Generalization for Person ReID. Conventional DG methods developed on classification can not be directly applied to DG-ReID as different domain doesn’t share label space. There are three main categories of DG-ReID methods. (1) Normalization-based methods (Jin et al. 2020; Choi et al. 2020; Jia, Ruan, and Hospedales 2019). These methods mainly utilize batch normalization (BN) (Ioffe and Szegedy 2015) and instance normalization (IN) (Ulyanov, Vedaldi, and Lempitsky 2016) to filter out the identity-irrelevant information. Jin et al. (2020) proposed the style normalization and restitution (SNR) module based on IN to further disentangle the identity-relevant features and identity-irrelevant features. (2) Adversarial learning based methods (Lin, Li, and Kot 2020; Tamura and Murakami 2019). Lin, Li, and Kot (2020) employed an adversarial auto-encoder module and a discriminator to guide feature extractor to extract domain-invariant features across domains. (3) Meta-learning based methods (Choi et al. 2020; Li et al. 2018a; Song et al. 2019). Zhao et al. (2020) proposed M³L approach which employs meta-learning to train the whole feature extractor network. Choi et al. (2020) proposed the MetaBIN that not only employs normalization layers, but also uses meta-learning to learn the balance weight of BIN layers.

The above methods usually share a single network among multiple source domains. Differently, our MECL framework assigns a network (domain expert) to each source domain to exploit the source domain sufficiently, and jointly train multiple domain experts and a universal expert through domain-domain and universal-domain collaborative learning. Besides, MECL is a general DG framework that can be applied to both DG-ReID and DG-classification tasks.

Collaborative Learning. Our collaborative learning is also inspired by some similar works from the semi-supervised learning (Tarvainen and Valpola 2017; Qiao et al. 2018), the knowledge distillation (Hinton, Vinyals, and Dean 2015; Tian, Krishnan, and Isola 2019), the self-supervised learning (Grill et al. 2020; He et al. 2020; Chen and He 2020), etc. In ReID, Ge, Chen, and Li (2020) proposed the mutual mean-teaching framework and Zhai et al. (2020b) proposed the multiple experts brainstorming method for the UDA task.

Methodology

Problem Definition

At the beginning, we formally give the definition of the multi-source DG-ReID problem. Assume that we have access to $N$ source domains, i.e., $N$ person ReID datasets denoted as $\mathcal{D}^{s}=\{\mathcal{D}^{s}_{n}\}_{n=1}^{N}$ for training, and $M$ target domains denoted as $\mathcal{D}^{t}=\{\mathcal{D}^{t}_{m}\}_{m=1}^{M}$ for testing. Note that there is no overlap between source and target domains, which means $\mathcal{D}^{s}\cap\mathcal{D}^{t}=\emptyset$ . The $k$ -th source domain $\mathcal{D}^{s}_{k}\in\mathcal{D}^{s}$ with $P^{k}$ images is denoted as $\{(\mathcal{I}_{i}^{k},y_{i}^{k})\}^{P^{k}}_{i=1}$ where $\mathcal{I}_{i}^{k}$ is the $i$ -th image and $y^{k}_{i}$ is the corresponding identity label from the label space $\mathcal{Y}^{k}$ . Different with the DG-classification problem, the source domains in the multi-source DG-ReID don’t share the label space, i.e., $\bigcap_{n=1}^{N}\mathcal{Y}^{n}=\emptyset$ . The goal of the multi-source DG-ReID is to fully exploit the $N$ source domains to train a more generalizable model which is expected to have a better performance on the $M$ target domains.

Baseline Methods

We introduce the two baseline methods used in this paper in detail, including the traditional DAG baseline and our proposed stronger MDE baseline.

Domain Aggregation (DAG) Baseline. The DAG baseline is the most commonly used baseline approach in multi-source DG-ReID (Choi et al. 2020; Lin, Li, and Kot 2020; Zhao et al. 2020). In particular, it firstly merges all the source datasets into a single dataset $\mathcal{D}^{s}_{agg}$ without regard to which domain they are from, where $\mathcal{D}^{s}_{agg}=\bigcup_{n=1}^{N}\mathcal{D}^{s}_{n}$ . Then, the model will be trained on $\mathcal{D}^{s}_{agg}$ in a standard ReID training procedure (Luo et al. 2019). There are at least three reasons that cause this baseline is not sufficient: (1) The label space of $D^{s}_{agg}$ is relatively larger, which makes the training of the classifier more difficult. (2) The source datasets are usually not balanced, and the large-scale datasets will be dominated in $D^{s}_{agg}$ . (3) The domain discrepancy is totally ignored in training. We introduced another stronger baseline setting inspired by multi-task learning as follows.

Multi-Domain Equality (MDE) Baseline. The MDE baseline has addressed the aforementioned three deficiencies of the DAG baseline from the view of multi-task learning. In the settings of MDE, each source domain has its own classifier and shares the feature extractor network with others. During training, all domains are treated equally. Specifically, in each iteration, we will sample a mini-batch with $B$ images from each domain for training, denoted as $\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}$ , and the loss is formulated as follows:

\mathcal{L}_{mde}=\frac{1}{N}\sum_{n=1}^{N}(\mathcal{L}_{id}(\bm{\mathcal{I}}^{n},\bm{y}^{n})+\lambda\mathcal{L}_{tri}(\bm{\mathcal{I}}^{n},\bm{y}^{n})).

(1)

The $\mathcal{L}_{id}$ and $\mathcal{L}_{tri}$ balanced by $\lambda$ are the commonly used softmax classification loss (cross entropy loss) and triplet loss, which are in form of

\mathcal{L}_{id}=\frac{1}{B}\sum\limits_{i=1}^{B}\mathcal{L}_{ce}(\mathcal{C}(\mathcal{F}(\bm{\mathcal{I}}_{i}^{n};\bm{\theta});\bm{\phi}_{n}),\bm{y}_{i}^{n}),

(2)

	$\displaystyle\mathcal{L}_{tri}=\frac{1}{B}\sum\limits_{i=1}^{B}\max($	$\displaystyle\|\|(\mathcal{F}(\bm{\mathcal{I}}_{i}^{n};\bm{\theta})-\mathcal{F}(\bm{\mathcal{I}}_{i,+}^{n};\bm{\theta}))\|\|+m$		(3)
	$\displaystyle-$	$\displaystyle\|\|\mathcal{F}(\bm{\mathcal{I}}_{i}^{n};\bm{\theta})-\mathcal{F}(\bm{\mathcal{I}}_{i,-}^{n};\bm{\theta})\|\|,0),$		(3)

where $\mathcal{F}(\cdot;\bm{\theta})$ and $\mathcal{C}(\cdot;\bm{\phi}_{n})$ denote the shared feature extractor and the $n$ -th domain classifier, $\bm{\mathcal{I}}_{i,+}^{n}$ and $\bm{\mathcal{I}}_{i,-}^{n}$ indicate the farthest positive and nearest negative sample of $\bm{\mathcal{I}}_{i}^{n}$ , and $m$ fixed to 0.3 is the triplet distance margin. Extensive experiments have shown that the MDE baseline has a better performance on unseen domains than the DAG baseline.

Multiple Domain Experts Collaborative Learning

In this subsection, we dive into the proposed Multiple Domain Experts Collaborative Learning (MECL) framework. The network architecture and the collaborative learning algorithm will be detailedly explained.

Overall Framework. The overall framework of MECL is illustrated in Fig. 1, which mainly consists of $N$ domain experts and one universal expert. During training, the domain experts and the universal expert interact with each other through the proposed collaborative learning approach, which can be further divided into domain-domain collaborative learning (DDCL) and universal-domain collaborative learning (UDCL). The detailed end-to-end algorithm of MECL is shown in Algorithm. 1.

Network Architecture. Each domain expert is composed of three components, a feature extractor, a classifier and a projector. For simplicity, we formulate the $N$ domain experts as $\{\mathcal{F}(\cdot;\bm{\theta}_{n})\}_{n=1}^{N}$ , $\{\mathcal{C}(\cdot;\bm{\phi}_{n})\}_{n=1}^{N}$ and $\{\mathcal{P}(\cdot;\bm{\psi}_{n})\}_{n=1}^{N}$ in terms of the component categories, where $\bm{\theta}_{n},\bm{\phi}_{n},\bm{\psi}_{n}$ denote the corresponding model parameters of the $n$ -th domain expert. The universal expert only consists of a feature extractor parameterized by $\bm{\nu}$ , denoted as $\mathcal{F}(\cdot;\bm{\nu})$ . Note that, the feature extractors of the domain experts and the universal expert use the same type of backbones. In addition, the universal expert is employed to extract features in the inference stage.

Input:

N

source domains:

\{\mathcal{D}^{s}_{n}\}_{n=1}^{N}

;

N

domain experts, including the feature extractors:

\{\mathcal{F}(\cdot;\bm{\theta}_{n})\}_{n=1}^{N}

, the classifiers:

\{\mathcal{C}(\cdot;\bm{\phi}_{n})\}_{n=1}^{N}

and the projectors:

\{\mathcal{P}(\cdot;\bm{\psi}_{n})\}_{n=1}^{N}

; One universal expert:

\mathcal{F}(\cdot;\bm{\nu})

; Maximum training iteration

T^{*}

; Learning rate

\beta

; Step size

\alpha

; Ensembling momentum

\epsilon

;

Output: The universal expert

\mathcal{F}(\cdot;\bm{\nu}^{*})

Initialization:

\bm{\nu}^{(0)}=\bm{\theta}_{1}^{(0)}=\cdot\cdot\cdot=\bm{\theta}_{N}^{(0)}

;

\bm{\psi}_{1}^{(0)}=\cdot\cdot\cdot=\bm{\psi}_{N}^{(0)}

for $T\leftarrow 1$ to $T^{*}$ do

Sample

N

mini-batches from

N

source domains, denoted as

\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}

;

for $k\leftarrow 1$ to $N$ do

Meta-Train:

Select

(\bm{\mathcal{I}}^{k},\bm{y}^{k})\in\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}

as the meta-train data;

Compute the meta-train loss:

\mathcal{L}_{mtr}(\bm{\mathcal{I}}^{k},\bm{y}^{k};\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k})

;

Compute the adapted parameter:

\bm{\theta}_{k}^{{}^{\prime}}=\bm{\theta}_{k}-\alpha\nabla_{\bm{\theta}_{k}}\mathcal{L}_{mtr}(\bm{\mathcal{I}}^{k},\bm{y}^{k};\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k})

;

Meta-Test:

Randomly select the meta-test data

(\bm{\mathcal{I}}^{j},\bm{y}^{j})

from

\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}

where

j\neq k

;

Compute the meta-test loss using

\bm{\theta}_{k}^{{}^{\prime}}

\mathcal{L}_{mte}(\bm{\mathcal{I}}^{j},\bm{y}^{j};\bm{\theta}_{k}^{{}^{\prime}},\hat{\bm{\phi}}_{j},\hat{\bm{\psi}}_{j})

Optimization of the

k

-th domain expert:

Compute the uniformity loss

\mathcal{L}_{unif}

;

Compute the overall loss

\mathcal{L}_{total}

;

Update the model parameters of the

k

-th domain expert:

\bm{\theta}_{k}^{(T)}=\bm{\theta}_{k}^{(T-1)}-\beta\nabla_{\bm{\theta}_{k}}\mathcal{L}_{total}

;

\bm{\phi}_{k}^{(T)}=\bm{\phi}_{k}^{(T-1)}-\beta\nabla_{\bm{\phi}_{k}}\mathcal{L}_{total}

;

\bm{\psi}_{k}^{(T)}=\bm{\psi}_{k}^{(T-1)}-\beta\nabla_{\bm{\psi}_{k}}\mathcal{L}_{total}

Optimization of the universal expert:

Update the model parameters of the universal expert using exponential moving average:

\bm{\nu}^{(T)}=\epsilon~{}\bm{\nu}^{(T-1)}+(1-\epsilon)\frac{1}{N}\sum_{n=1}^{N}\bm{\theta}_{n}^{(T)}

At the end of the training:

\mathcal{F}(\cdot;\bm{\nu}^{*})=\mathcal{F}(\cdot;\bm{\nu}^{(T^{*})})

Algorithm 1 Multiple Domain Experts Collaborative Learning (MECL)

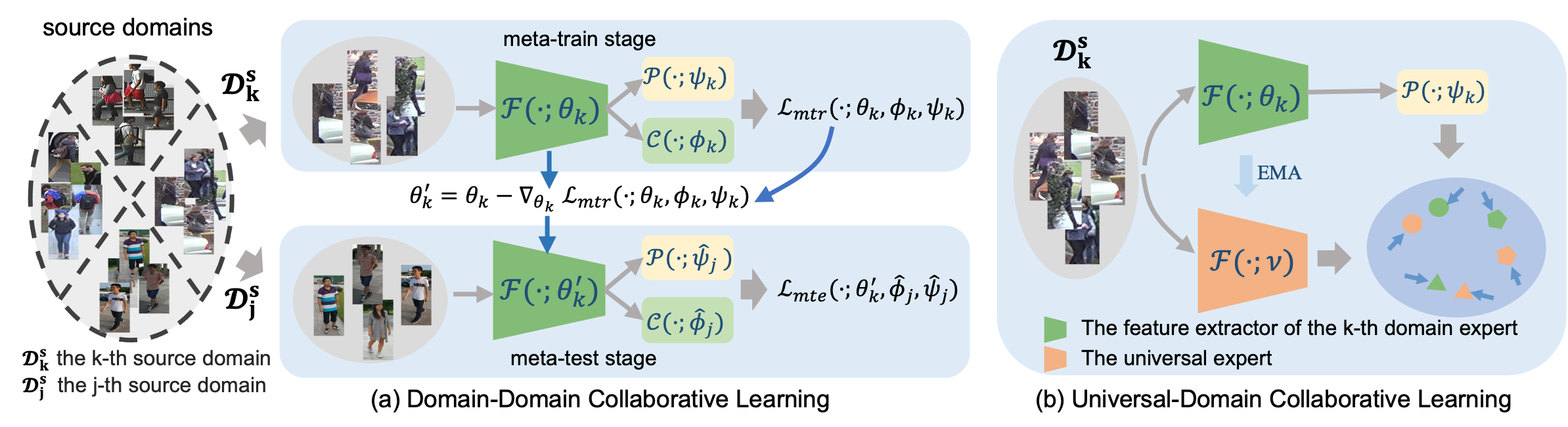
Domain-Domain Collaborative Learning. To avoid overfitting the specific domains, the domain experts should communicate with others periodically to regulate their learning process. Following Li et al. (2018a); Zhao et al. (2020); Song et al. (2019), we apply the model-agnostic meta-learning (MAML) (Finn, Abbeel, and Levine 2017) to the training of each domain expert, because it can not only further improve the generalization capability of models (Li et al. 2018a), but also strengthen the interaction among domain experts by dynamically combining the three components of the feature extractors, classifiers and projectors in the meta-test stage as shown in Fig. 2-a.

At the beginning of each training iteration, we will randomly sample a mini-batch with $B$ image-label pairs from each domain, denoted as $\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}$ , where $(\bm{\mathcal{I}}^{n},\bm{y}^{n})$ comes from $\mathcal{D}^{s}_{n}$ . Take the training of the $k$ -th domain expert for example. The mini-batch $(\bm{\mathcal{I}}^{k},\bm{y}^{k})$ is treated as meta-train samples while the meta-test samples $(\bm{\mathcal{I}}^{j},\bm{y}^{j})$ are randomly selected from the left mini-batches, that is, $(\bm{\mathcal{I}}^{j},\bm{y}^{j})\in\{(\bm{\mathcal{I}}^{n},\bm{y}^{n})\}_{n=1}^{N}$ where $j\neq k$ .

In the meta-train stage, the meta-train loss with respect to $(\bm{\mathcal{I}}^{k},\bm{y}^{k})$ is denoted as $\mathcal{L}_{mtr}(\bm{\mathcal{I}}^{k},\bm{y}^{k};\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k})$ , where $\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k}$ are the model parameters of the $k$ -th domain expert. Moreover, $\mathcal{L}_{mtr}$ is the combination of Eq. 2, 3 and 6, i.e., $\mathcal{L}_{mtr}=\mathcal{L}_{id}+\mathcal{L}_{tri}+\mathcal{L}_{align}$ . Then, we compute the adapted parameters of $\bm{\theta}_{k}$ by

\bm{\theta}_{k}^{{}^{\prime}}=\bm{\theta}_{k}-\alpha\nabla_{\bm{\theta}_{k}}\mathcal{L}_{mtr}(\bm{\mathcal{I}}^{k},\bm{y}^{k};\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k}),

(4)

where $\alpha$ is the step size which is fixed to 0.1 here. Note that, only $\bm{\theta}_{k}$ needs to be meta-learned.

In the meta-test stage, the meta-test loss with respect to $(\bm{\mathcal{I}}^{j},\bm{y}^{j})$ should be calculated under the condition of $\bm{\theta}_{k}^{{}^{\prime}}$ , denoted as $\mathcal{L}_{mte}(\bm{\mathcal{I}}^{j},\bm{y}^{j};\bm{\theta}_{k}^{{}^{\prime}},\hat{\bm{\phi}}_{j},\hat{\bm{\psi}}_{j})$ , where $\hat{\bm{\phi}}_{j},\hat{\bm{\psi}}_{j}$ belong to the $j$ -th domain expert, and $\hat{\cdot}$ denotes that the parameters will not be optimized here. Note, $\mathcal{L}_{mte}$ and $\mathcal{L}_{mtr}$ have the same form with different inputs and parameters.

Finally, we combine $\mathcal{L}_{mtr}$ and $\mathcal{L}_{mte}$ to optimize $\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k}$ , respectively, i.e.

\mathop{\arg\min}\limits_{\bm{\theta}_{k},\bm{\phi}_{k},\bm{\psi}_{k}}\frac{1}{2}(\mathcal{L}_{mtr}+\mathcal{L}_{mte}).

(5)

Universal-Domain Collaborative Learning. During the training stage of MECL, the universal expert takes responsibility for providing supervision to the domain experts and periodically gathering what they have learned to improve itself. Each domain expert and the universal expert will learn mutually as illustrated in Fig. 2-b.

At first, the universal expert will review the $N$ mini-batch data, i.e., project the images into the feature vectors by $\mathcal{F}(\cdot;\bm{\nu})$ . Then, $\mathcal{F}(\bm{\mathcal{I}}^{k};\bm{\nu})$ will be used to supervise the $k$ -th domain expert using the alignment loss in terms of

\mathcal{L}_{align}=\frac{1}{B}\sum_{i=1}^{B}||\mathcal{P}(\mathcal{F}(\bm{\mathcal{I}}^{k}_{i};\bm{\theta}_{k});\bm{\psi}_{k})-\mathcal{F}(\bm{\mathcal{I}}^{k}_{i};\bm{\nu})||,

(6)

where $||\cdot||$ denotes the Euclidean distance between two feature vectors. The projector $\mathcal{P}(\cdot;\bm{\psi}_{k})$ (Grill et al. 2020) attempts to bridge the gap between the universal expert and the $k$ -th domain expert to make the optimization easier.

The alignment loss provides the supervision from the perspective of pushing the positive samples (two types of features of the same image). Inspired by Wang and Isola (2020), we employ the uniformity loss which fully exploits the negative samples to encourage the feature distribution more uniform among domains. For the training of $k$ -th domain expert, it is defined as follows:

\mathcal{L}_{unif}=\frac{1}{B}\sum_{i=1}^{B}\log\frac{1}{N}\sum_{n=1}^{N}(\frac{1}{Q}\sum^{Q}_{q=1}e^{-2||\bm{f}^{k}_{i}-\bm{\bar{f}}^{n}_{q}||}),

(7)

where $\bm{f}_{i}^{k}=\mathcal{F}(\bm{\mathcal{I}}_{i}^{k};\bm{\theta}_{k})$ , $\bm{\bar{f}}_{q}^{n}=\mathcal{F}(\bm{\bar{\mathcal{I}}}_{q}^{n};\bm{\nu})$ , $\bm{\bar{\mathcal{I}}}_{q}^{n}$ is the negative sample of $\bm{\mathcal{I}}_{i}^{k}$ and $Q$ is the number of the negative samples in the $n$ -th domain. Actually, minimizing $\mathcal{L}_{unif}$ is equal to maximize the distance of a sample of $D^{s}_{k}$ to its negative samples which are sampled from $\{D^{s}_{n}\}_{n=1}^{N}$ . Intuitively, a sample is closer to its negative samples from the same domain than those from others, but the ideal situation is that a sample should be far away from the negative samples no matter what the domain they are from, $\mathcal{L}_{unif}$ is therefore used to make each sample keep away from the negative samples from any domain.

After one iteration of all domain experts, the universal expert will gather the learned knowledge from each domain expert to improve itself. We update the parameters of the universal expert in the manner of the exponential moving average (EMA) (Tarvainen and Valpola 2017), which is defined as follows:

\bm{\nu}^{(T)}=\epsilon~{}\bm{\nu}^{(T-1)}+(1-\epsilon)\frac{1}{N}\sum_{n=1}^{N}\bm{\theta}_{n}^{(T)},

(8)

where $\bm{\nu}^{(T-1)}$ denotes the parameters of the universal expert in the previous iteration $(T-1)$ , $\bm{\theta}_{n}^{(T)}$ is the feature extractor parameters of the $n$ -th domain expert in the current iteration $(T)$ , and $\epsilon$ is the ensembling momentum usually set to 0.999. The initialization of these parameters are $\bm{\nu}^{(0)}=\bm{\theta}^{(0)}_{1}=\cdot\cdot\cdot=\bm{\theta}_{N}^{(0)}$ .

Totally, the overall loss function are in the form of

\mathcal{L}_{total}=\frac{1}{2}(\mathcal{L}_{mtr}+\mathcal{L}_{mte})+\gamma\mathcal{L}_{unif},

(9)

where $\gamma=0.1$ is to balance the influence of $\mathcal{L}_{unif}$ .

Table 1: Ablation studies of MECL. ‘DDCL’ is the domain-domain collaborative learning of multiple domain experts (ME) with the meta-learning strategy (ML). ‘EMA’ means exponential moving average of domain experts to the universal expert. ‘

L_{a}

’ and ‘

L_{u}

’ denote the alignment and uniformity loss, respectively. ‘pro’ denotes the projector. ‘UDCL’ is the universal-domain collaborative learning, featured with EMA,

L_{a}

and

L_{u}

. ‘M’ is Market1501, ‘D’ is DukeMTMC-reID, ‘MS’ is MSMT17 and ‘C’ is CUHK03. ‘MS+D+C

\to

M’ means training on MSMT17, DukeMTMC-reID and CUHK03, and testing on Market1501.

No.	Experimental Settings	Train/Test Domain Settings								Average
		MS+D+C $\to$ M		MS+M+C $\to$ D		M+D+C $\to$ MS		MS+M+D $\to$ C		Average
		mAP	Top-1	mAP	Top-1	mAP	Top-1	mAP	Top-1	mAP	Top-1
1	DAG Base.	47.7	73.5	45.7	63.5	8.7	22.9	29.3	29.3	32.9	47.3
2	MDE Base.	53.9	77.7	52.0	67.7	12.7	31.4	28.9	29.6	36.9	51.6
3	MDE Base.+ML	55.2	79.2	52.7	68.9	12.9	31.9	31.0	31.7	38.0	52.9
4^∗	DDCL(ME+ML)	57.8	80.8	53.8	70.7	13.6	33.5	33.6	35.1	39.7	55.0
5	DDCL+EMA	58.7	81.5	54.4	71.4	15.1	36.2	35.6	36.8	41.0	56.5
6	DDCL w/o ML+EMA	37.0	62.7	41.6	58.1	8.2	21.9	17.7	17.1	26.1	40.0
7	DDCL+EMA+ $L_{a}$ w/o pro	59.1	82.0	55.4	72.0	17.2	40.0	35.2	36.0	41.7	57.5
8	DDCL+EMA+ $L_{a}$	60.1	82.2	56.7	73.0	17.4	40.5	36.2	37.4	42.6	58.3
9	DDCL+UDCL(EMA+ $L_{a}$ + $L_{u}$ )	60.9	83.2	57.2	74.1	18.0	41.2	37.3	38.1	43.4	59.2

*

Report the results of the best domain expert.

Table 2: Performance (%) on the three domain experts. The results are permuted according to the source domains order. Take ‘MS+D+C’ for example, the 1st domain expert belongs to MSMT17, and the 2nd and 3rd belongs to DukeMTMC and CUHK03.

No.	Experimental Settings	MS+D+C $\to$ M		MS+M+C $\to$ D		M+D+C $\to$ MS		MS+M+D $\to$ C
No.	Experimental Settings	mAP	Top-1	mAP	Top-1	mAP	Top-1	mAP	Top-1
1	DDCL+EMA	56.6/56.5/57.8	81.1/80.0/80.8	53.8/53.9/53.6	70.7/71.1/71.1	13.5/13.6/13.5	33.0/33.5/33.1	33.6/33.4/33.1	35.1/33.9/33.8
2	DDCL+EMA+ $L_{a}$ w/o pro	58.9/58.6/59.2	82.2/82.1/81.9	56.0/55.9/55.4	72.2/72.2/72.3	16.6/16.6/16.5	38.9/38.7/38.6	35.1/35.1/35.4	35.4/35.9/36.3
3	DDCL+UDCL(EMA+ $L_{a}$ )	59.9/59.1/60.4	82.7/82.4/83.2	57.0/56.9/56.7	73.1/72.7/73.0	16.3/16.2/16.4	38.7/38.7/38.7	36.1/35.3/36.1	37.4/35.9/36.1

Experiments

Datasets & Evaluation Metrics

Datasets. We follow the large-scale dataset setting of multi-source DG-ReID proposed in Zhao et al. (2020). This setting employs four large-scale person ReID datasets from different domains, including Market1501 (Zheng et al. 2015), DukeMTMC-reID (Ristani et al. 2016; Zheng, Zheng, and Yang 2017), CUHK03 (Li et al. 2014b) and MSMT17 (Wei et al. 2018), which are widely used in recent ReID tasks. Following Zhao et al. (2020); Gulrajani and Lopez-Paz (2020), we use the leave-one-domain-out protocol to split the four datasets (domains) into training/testing domains, specifically, three datasets are used as source training domains and the left one is used as the unseen target domain. The detailed information of the large-scale dataset setting and another small-scale dataset setting (Song et al. 2019; Lin, Li, and Kot 2020) in multi-source DG-ReID will be introduced in the Supplementary Materials.

Evaluation Metrics. We follow the commonly used evaluation metrics in ReID to quantitatively evaluate the performance by mean Average Precision (mAP) and Cumulative Matching Characteristic (CMC) curve at Top- $k$ .

Implementation Details

We utilize the ResNet50 (He et al. 2016), ResNet50-IBN (Pan et al. 2018) and OSNet (Zhou et al. 2021) as the backbones in the following experiments. The projector is a simple MLP network composed of Linear-BN-ReLU-Linear where the shapes of the two Linear layers are (2048, 512) and (512, 2048), respectively. We employ the iteration-based way to train those models where the max iteration is set to 12,000 per GPU and 8 GTX-1080TI GPUs are used. We optimize the model parameters of each domain-specific network by Adam (Kingma and Ba 2014) optimizer with the weight decay $5\times 10^{-4}$ . The learning rate is initialized to $1\times 10^{-5}$ , and warmed up to $1\times 10^{-3}$ gradually in the previous 1,000 iterations and then decay to $1\times 10^{-4}$ and $1\times 10^{-5}$ at the 4,000-th iteration and the 8,000-th iteration, respectively. At the beginning of each iteration, we randomly sample 32 images of 8 identities, i.e., 4 images per identity, from each source domain. Besides, some data augmentation methods used in conventional person ReID approaches are also employed, including random flipping, random cropping and random erasing (Zhong et al. 2020).

Ablation Study

We have conducted comprehensive ablation studies using ResNet50-IBN as the backbone to analyze each component of the MECL learning framework. Besides, This section also reflects how MECL come into being step by step. More ablation studies (e.g. visualization, hyper-parameter analysis) please refer to the Supplementary Materials.

Comparison of Baseline Methods. We firstly compare the two baseline methods, the traditional DAG baseline and our proposed MDE baseline. As shown in Tab. 1-1, 2, our proposed MDE baseline outperforms the DAG baseline by a large margin on most current ReID benchmarks. On average, DAG falls behind MDE about 4.0% and 4.3% in mAP and Top-1 accuracy, indicating that MDE provides a stronger baseline than DAG in the multi-source DG-ReID task.

Effectiveness of Meta-Learning. Following MLDG (Li et al. 2018a), we also apply meta-learning (Finn, Abbeel, and Levine 2017) strategy to train the MDE baseline to explore its effectiveness on domain generalization. As shown in Tab. 1-3, compared with the pure MDE baseline, training in the meta-learning manner obtains about 1.1% in mAP and 1.3% in Top-1 accuracy gains on average, proving that the meta-learning strategy is able to improve the model’s generalization capability.

Table 3: Compared with the state-of-the-arts on multi-source DG-ReID benchmarks. The first group are the results of SOTAs, the second and third are the results of MDE and MECL using different backbones.

Method	Backbone	MS+D+C $\to$ M		MS+M+C $\to$ D		M+D+C $\to$ MS		MS+M+D $\to$ C		Average
Method	Backbone	mAP	Top-1	mAP	Top-1	mAP	Top-1	mAP	Top-1	mAP	Top-1
QAConv	ResNet50	35.6	65.7	47.1	66.1	7.5	24.3	21.0	23.5	27.8	44.9
CBN	ResNet50	47.3	74.7	50.1	70.0	15.4	37.0	25.7	25.2	34.6	51.7
SNR	SNR	48.5	75.2	48.3	66.7	13.8	35.1	29.0	29.1	34.9	51.5
M³L	ResNet50	48.1	74.5	50.5	69.4	12.9	33.0	29.9	30.7	35.4	51.9
M³L	ResNet50-IBN	50.2	75.9	51.1	69.2	14.7	36.9	32.1	33.1	37.0	53.8
OSNet	OSNet	44.2	72.5	47.0	65.2	12.6	33.2	23.3	23.9	31.8	48.7
OSNet-IBN	OSNet-IBN	44.9	73.0	45.7	64.6	16.2	39.8	25.4	25.7	33.0	50.8
OSNet-AIN	OSNet-AIN	45.8	73.3	47.2	65.6	16.2	40.2	27.1	27.4	34.1	51.6
MDE Base.	ResNet50	49.2	75.2	44.2	60.6	9.3	23.6	23.0	22.8	31.4	45.6
	ResNet50-IBN	53.9	77.7	52.0	67.7	12.7	31.4	28.9	29.6	36.9	51.6
	SNR	53.8	77.7	52.5	69.5	16.8	39.5	30.5	30.4	38.4	54.3
	OSNet-IBN	48.6	75.0	48.0	66.7	16.5	40.3	26.8	26.2	35.0	52.0
MECL	ResNet50	56.5	80.0	53.4	70.0	13.3	32.7	31.5	32.1	38.7	53.7
	ResNet50-IBN	60.9	83.2	57.2	74.1	18.0	41.2	37.3	38.1	43.4	59.2
	SNR	60.2	82.4	57.6	75.0	21.7	47.7	38.3	38.5	44.5	60.9
	OSNet-IBN	52.3	77.6	51.3	68.8	18.1	43.0	29.3	29.9	37.8	54.8

Table 4: Compared with SOTAs^∗ on DG-classification benchmarks. Top: PACS; Bottom: OfficeHome.

Method	Art	Cartoon	Photo	Sketch	Avg
ERM	83.2 $\pm$ 1.3	76.8 $\pm$ 1.7	97.2 $\pm$ 0.3	74.8 $\pm$ 1.3	83.0
Mixup	85.2 $\pm$ 1.9	77.0 $\pm$ 1.7	96.8 $\pm$ 0.8	73.9 $\pm$ 1.6	83.2
MLDG	81.4 $\pm$ 3.6	77.9 $\pm$ 2.3	96.2 $\pm$ 0.3	76.1 $\pm$ 2.1	82.9
MTL	85.6 $\pm$ 1.5	78.9 $\pm$ 0.6	97.1 $\pm$ 0.3	73.1 $\pm$ 2.7	83.7
RSC	83.7 $\pm$ 1.7	82.9 $\pm$ 1.1	95.6 $\pm$ 0.7	68.1 $\pm$ 1.5	82.6
MECL	86.5 $\pm$ 1.2	80.5 $\pm$ 0.8	96.2 $\pm$ 0.3	77.7 $\pm$ 0.1	85.3
Method	Art	Clipart	Product	RealWorld	Avg
ERM	61.1 $\pm$ 0.9	50.7 $\pm$ 0.6	74.6 $\pm$ 0.3	76.4 $\pm$ 0.6	65.7
Mixup	61.4 $\pm$ 0.5	53.0 $\pm$ 0.3	75.8 $\pm$ 0.2	77.7 $\pm$ 0.3	67.0
MLDG	60.5 $\pm$ 1.4	51.9 $\pm$ 0.2	74.4 $\pm$ 0.6	77.6 $\pm$ 0.4	66.1
MTL	59.1 $\pm$ 0.3	52.1 $\pm$ 1.2	74.7 $\pm$ 0.4	77.0 $\pm$ 0.6	65.7
RSC	61.6 $\pm$ 1.0	51.1 $\pm$ 0.8	74.8 $\pm$ 1.1	75.7 $\pm$ 0.9	65.8
MECL	65.9 $\pm$ 1.3	58.3 $\pm$ 0.5	76.9 $\pm$ 1.0	79.8 $\pm$ 0.4	70.2

*

All results of SOTAs are based on Gulrajani and Lopez-Paz (2020).

Effectiveness of Domain-Domain Collaborative Learning. We argue that using a shared backbone can’t learn each domain sufficiently, so we propose that each domain is associated with a specific network (domain expert), and employ the meta-learning strategy to strengthen the interaction among the multiple domain experts by the meta-test stage. Tab. 1-4 has reported the performance of the best domain expert, specifically, the performance increases by 1.7% in mAP and 2.1% in Top-1 accuracy on average with the help of the collaborative learning. Besides, meta-learning plays an important roles in the domain-domain collaborative learning, removing it causes great performance degradation as shown in Tab. 1-6.

Effectiveness of EMA. To study the effectiveness of UDCL, we firstly observe the performance of the universal expert after gathering the knowledge from the domain experts in the manner of exponential moving average (EMA) (Tarvainen and Valpola 2017). As shown in the Tab. 1-5, the universal expert outperforms the best domain experts by 1.3% and 1.5% in mAP and Top-1 accuracy on average, indicating that the universal expert is more generalizable than the domain experts for the reason that it has absorbed the knowledge of all domains.

Effectiveness of Alignment Loss. We have conducted two studies to show the powerful capability of the alignment loss which provides a supervision signal from the perspective of pushing positive samples. The first is to directly minimize the Euclidean distance between the features of the same image extracted from the universal expert and domain experts respectively. The second is that the features output from the domain experts will be transformed by a projector according to Eq. 6. As shown in the Tab. 1-5,7,8, the alignment loss without projectors can bring slight improvements to most benchmarks , but it has a negative effect on CUHK03. However, with the addition of the projectors, the generalization capability of the universal expert is further improved, i.e., 1.6% in mAP and 1.8% Top-1 accuracy gains on average based on Tab. 1-5. Furthermore, we also observe the performance of the three domain experts as shown in the Tab. 2. With the alignment loss, the generalization capability of the domain experts are improved as well. Notice that, the best domain experts in some experiments even outperform the universal expert when using the alignment loss.

Effectiveness of Uniformity Loss. Different with the alignment loss, the uniformity loss supervises the training of the domain experts by fully exploiting the negative samples. As shown in Tab. 1-9, with the addition of the uniformity loss, the generalization capability of the universal expert are further improved. Specifically, the uniformity loss increases the performance by 0.8% in mAP and 0.9% in Top-1 accuracy on average.

Compare with State-of-the-Arts

To demonstrate the novelty and versatility of the proposed MECL, we compare it with some state-of-the-arts on both DG-ReID and DG-classification tasks.

Results on Multi-Source DG-ReID. We compare our proposed MECL with the state-of-the-arts (SOTAs) using multi-source DG-ReID setting, including QAConv (Liao and Shao 2020),CBN (Zhuang et al. 2020), SNR (Jin et al. 2020), M³L (Zhao et al. 2020) and OSNet (Zhou et al. 2021). Notice that, we adapt the single source based methods (e.g., CBN, SNR) to multi-source setting in the traditional DAG baseline manner. As shown in Tab. 3, MECL has achieved the best performance among these SOTAs under different types of backbones. Furthermore, because MECL is a model-agnostic training framework, some SOTAs with more generalizable networks can be trained using MECL to further improve the model’s generalization capability, like SNR, OSNet, etc. Specifically, when SNR meets MECL, the performance is increased from 34.9% to 44.5% in mAP and from 51.5% to 60.9% in Top-1 accuracy on average. Besides, the proposed MDE baseline performs better on most of the backbones, indicating its superiority as the baseline of the multi-source DG-ReID task.

Results on DG-Classification. MECL is not ReID-specific, and it also can be applied to the traditional DG-classification task with slight modification, i.e., a classifier using EMA to update is added to the universal expert. The details of modification and training will be demonstrated in Supplementary Materials. The studies are conducted around two common benchmarks in the DG-classification task, PACS (Li et al. 2017) and OfficeHome (Venkateswara et al. 2017). As the results shown in Tab. 4, MECL outperforms the current SOTAs by a large margin, including ERM (Gulrajani and Lopez-Paz 2020), Mixup (Xu et al. 2020), MLDG (Li et al. 2018a), MTL (Blanchard et al. 2017) and RSC (Huang et al. 2020). Specifically, MECL respectively surpasses the best SOTAs (MTL & Mixup) by 1.6% and 3.2% on the two benchmarks on average.

Conclusion

In this paper, we have proposed a novel model-agnostic learning framework for multi-source DG-ReID, named Multiple Domain Experts Collaboration Learning (MECL). Domain-Domain Collaborative Learning (DDCL) and Universal-Domain Collaborative Learning (UDCL) organically work together in MECL to improve the model’s generalization capability. Extensive experiments on both DG-ReID and DG-classification benchmarks show that, without additional inference computation cost, our MECL framework significantly outperforms state-of-the-arts. We also establish a simple but rather strong multi-source DG-ReID baseline method named Multi-Domain Equality (MDE) that will facilitate future works in this area.

References

Akuzawa, Iwasawa, and Matsuo (2019) Akuzawa, K.; Iwasawa, Y.; and Matsuo, Y. 2019. Domain Generalization via Invariant Representation under Domain-Class Dependency.
Blanchard et al. (2017) Blanchard, G.; Deshmukh, A. A.; Dogan, U.; Lee, G.; and Scott, C. 2017. Domain generalization by marginal transfer learning. arXiv preprint arXiv:1711.07910.
Chen et al. (2019) Chen, T.; Ding, S.; Xie, J.; Yuan, Y.; Chen, W.; Yang, Y.; Ren, Z.; and Wang, Z. 2019. Abd-net: Attentive but diverse person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 8351–8361.
Chen and He (2020) Chen, X.; and He, K. 2020. Exploring Simple Siamese Representation Learning. arXiv preprint arXiv:2011.10566.
Choi et al. (2020) Choi, S.; Kim, T.; Jeong, M.; Park, H.; and Kim, C. 2020. Meta Batch-Instance Normalization for Generalizable Person Re-Identification. arXiv preprint arXiv:2011.14670.
Dou et al. (2019) Dou, Q.; Coelho de Castro, D.; Kamnitsas, K.; and Glocker, B. 2019. Domain generalization via model-agnostic learning of semantic features. Advances in Neural Information Processing Systems, 32: 6450–6461.
Finn, Abbeel, and Levine (2017) Finn, C.; Abbeel, P.; and Levine, S. 2017. Model-agnostic meta-learning for fast adaptation of deep networks. In International Conference on Machine Learning, 1126–1135. PMLR.
Fu et al. (2019) Fu, Y.; Wei, Y.; Wang, G.; Zhou, Y.; Shi, H.; and Huang, T. S. 2019. Self-similarity grouping: A simple unsupervised cross domain adaptation approach for person re-identification. In Proceedings of the IEEE/CVF International Conference on Computer Vision, 6112–6121.
Ge, Chen, and Li (2020) Ge, Y.; Chen, D.; and Li, H. 2020. Mutual mean-teaching: Pseudo label refinery for unsupervised domain adaptation on person re-identification. arXiv preprint arXiv:2001.01526.
Grill et al. (2020) Grill, J.-B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P. H.; Buchatskaya, E.; Doersch, C.; Pires, B. A.; Guo, Z. D.; Azar, M. G.; et al. 2020. Bootstrap your own latent: A new approach to self-supervised learning. arXiv preprint arXiv:2006.07733.
Gulrajani and Lopez-Paz (2020) Gulrajani, I.; and Lopez-Paz, D. 2020. In search of lost domain generalization. arXiv preprint arXiv:2007.01434.
He et al. (2020) He, K.; Fan, H.; Wu, Y.; Xie, S.; and Girshick, R. 2020. Momentum contrast for unsupervised visual representation learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9729–9738.
He et al. (2016) He, K.; Zhang, X.; Ren, S.; and Sun, J. 2016. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, 770–778.
Hinton, Vinyals, and Dean (2015) Hinton, G.; Vinyals, O.; and Dean, J. 2015. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531.
Hou et al. (2019) Hou, R.; Ma, B.; Chang, H.; Gu, X.; Shan, S.; and Chen, X. 2019. Interaction-and-aggregation network for person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9317–9326.
Huang et al. (2020) Huang, Z.; Wang, H.; Xing, E. P.; and Huang, D. 2020. Self-challenging improves cross-domain generalization. In Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part II 16, 124–140. Springer.
Ioffe and Szegedy (2015) Ioffe, S.; and Szegedy, C. 2015. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In International conference on machine learning, 448–456. PMLR.
Jia, Ruan, and Hospedales (2019) Jia, J.; Ruan, Q.; and Hospedales, T. M. 2019. Frustratingly easy person re-identification: Generalizing person re-id in practice. arXiv preprint arXiv:1905.03422.
Jin et al. (2020) Jin, X.; Lan, C.; Zeng, W.; Chen, Z.; and Zhang, L. 2020. Style normalization and restitution for generalizable person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 3143–3152.
Kingma and Ba (2014) Kingma, D. P.; and Ba, J. 2014. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
Kumar et al. (2020) Kumar, D.; Siva, P.; Marchwica, P.; and Wong, A. 2020. Unsupervised domain adaptation in person re-id via k-reciprocal clustering and large-scale heterogeneous environment synthesis. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, 2645–2654.
Li et al. (2018a) Li, D.; Yang, Y.; Song, Y.-Z.; and Hospedales, T. 2018a. Learning to generalize: Meta-learning for domain generalization. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 32.
Li et al. (2017) Li, D.; Yang, Y.; Song, Y.-Z.; and Hospedales, T. M. 2017. Deeper, broader and artier domain generalization. In Proceedings of the IEEE international conference on computer vision, 5542–5550.
Li et al. (2018b) Li, H.; Pan, S. J.; Wang, S.; and Kot, A. C. 2018b. Domain generalization with adversarial feature learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 5400–5409.
Li et al. (2014a) Li, W.; Zhao, R.; Xiao, T.; and Wang, X. 2014a. Deepreid: Deep filter pairing neural network for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 152–159.
Li et al. (2014b) Li, W.; Zhao, R.; Xiao, T.; and Wang, X. 2014b. Deepreid: Deep filter pairing neural network for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 152–159.
Li, Zhu, and Gong (2018) Li, W.; Zhu, X.; and Gong, S. 2018. Harmonious attention network for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 2285–2294.
Liao and Shao (2020) Liao, S.; and Shao, L. 2020. Interpretable and Generalizable Person Re-Identification with Query-Adaptive Convolution and Temporal Lifting. In European Conference on Computer Vision (ECCV).
Lin, Li, and Kot (2020) Lin, S.; Li, C.-T.; and Kot, A. C. 2020. Multi-Domain Adversarial Feature Generalization for Person Re-Identification. IEEE Transactions on Image Processing.
Liu, Chang, and Shen (2020) Liu, C.; Chang, X.; and Shen, Y.-D. 2020. Unity style transfer for person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 6887–6896.
Luo et al. (2019) Luo, H.; Gu, Y.; Liao, X.; Lai, S.; and Jiang, W. 2019. Bag of tricks and a strong baseline for deep person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, 0–0.
Matsuura and Harada (2020) Matsuura, T.; and Harada, T. 2020. Domain generalization using a mixture of multiple latent domains. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, 11749–11756.
Muandet, Balduzzi, and Schölkopf (2013) Muandet, K.; Balduzzi, D.; and Schölkopf, B. 2013. Domain generalization via invariant feature representation. In International Conference on Machine Learning, 10–18. PMLR.
Pan et al. (2018) Pan, X.; Luo, P.; Shi, J.; and Tang, X. 2018. Two at once: Enhancing learning and generalization capacities via ibn-net. In Proceedings of the European Conference on Computer Vision (ECCV), 464–479.
Park and Ham (2020) Park, H.; and Ham, B. 2020. Relation network for person re-identification. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, 11839–11847.
Qiao et al. (2018) Qiao, S.; Shen, W.; Zhang, Z.; Wang, B.; and Yuille, A. 2018. Deep co-training for semi-supervised image recognition. In Proceedings of the european conference on computer vision (eccv), 135–152.
Ristani et al. (2016) Ristani, E.; Solera, F.; Zou, R.; Cucchiara, R.; and Tomasi, C. 2016. Performance measures and a data set for multi-target, multi-camera tracking. In European conference on computer vision, 17–35. Springer.
Song et al. (2019) Song, J.; Yang, Y.; Song, Y.-Z.; Xiang, T.; and Hospedales, T. M. 2019. Generalizable person re-identification by domain-invariant mapping network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 719–728.
Song et al. (2020) Song, L.; Wang, C.; Zhang, L.; Du, B.; Zhang, Q.; Huang, C.; and Wang, X. 2020. Unsupervised domain adaptive re-identification: Theory and practice. Pattern Recognition, 102: 107173.
Sun et al. (2018) Sun, Y.; Zheng, L.; Yang, Y.; Tian, Q.; and Wang, S. 2018. Beyond part models: Person retrieval with refined part pooling (and a strong convolutional baseline). In Proceedings of the European conference on computer vision (ECCV), 480–496.
Tamura and Murakami (2019) Tamura, M.; and Murakami, T. 2019. Augmented hard example mining for generalizable person re-identification. arXiv preprint arXiv:1910.05280.
Tarvainen and Valpola (2017) Tarvainen, A.; and Valpola, H. 2017. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. arXiv preprint arXiv:1703.01780.
Tian, Krishnan, and Isola (2019) Tian, Y.; Krishnan, D.; and Isola, P. 2019. Contrastive representation distillation. arXiv preprint arXiv:1910.10699.
Ulyanov, Vedaldi, and Lempitsky (2016) Ulyanov, D.; Vedaldi, A.; and Lempitsky, V. 2016. Instance normalization: The missing ingredient for fast stylization. arXiv preprint arXiv:1607.08022.
Venkateswara et al. (2017) Venkateswara, H.; Eusebio, J.; Chakraborty, S.; and Panchanathan, S. 2017. Deep hashing network for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 5018–5027.
Wang and Isola (2020) Wang, T.; and Isola, P. 2020. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. In International Conference on Machine Learning, 9929–9939. PMLR.
Wei et al. (2018) Wei, L.; Zhang, S.; Gao, W.; and Tian, Q. 2018. Person transfer gan to bridge domain gap for person re-identification. In Proceedings of the IEEE conference on computer vision and pattern recognition, 79–88.
Xiao et al. (2021) Xiao, Z.; Shen, J.; Zhen, X.; Shao, L.; and Snoek, C. G. M. 2021. Variational Invariant Learning for Bayesian Domain Generalization.
Xu et al. (2020) Xu, M.; Zhang, J.; Ni, B.; Li, T.; Wang, C.; Tian, Q.; and Zhang, W. 2020. Adversarial domain adaptation with domain mixup. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 34, 6502–6509.
Zhai et al. (2020a) Zhai, Y.; Lu, S.; Ye, Q.; Shan, X.; Chen, J.; Ji, R.; and Tian, Y. 2020a. Ad-cluster: Augmented discriminative clustering for domain adaptive person re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 9021–9030.
Zhai et al. (2020b) Zhai, Y.; Ye, Q.; Lu, S.; Jia, M.; Ji, R.; and Tian, Y. 2020b. Multiple expert brainstorming for domain adaptive person re-identification. arXiv preprint arXiv:2007.01546.
Zhao et al. (2020) Zhao, Y.; Zhong, Z.; Yang, F.; Luo, Z.; Lin, Y.; Li, S.; and Sebe, N. 2020. Learning to Generalize Unseen Domains via Memory-based Multi-Source Meta-Learning for Person Re-Identification. arXiv preprint arXiv:2012.00417.
Zheng et al. (2015) Zheng, L.; Shen, L.; Tian, L.; Wang, S.; Wang, J.; and Tian, Q. 2015. Scalable person re-identification: A benchmark. In Proceedings of the IEEE international conference on computer vision, 1116–1124.
Zheng, Zheng, and Yang (2017) Zheng, Z.; Zheng, L.; and Yang, Y. 2017. Unlabeled samples generated by gan improve the person re-identification baseline in vitro. In Proceedings of the IEEE International Conference on Computer Vision, 3754–3762.
Zhong et al. (2020) Zhong, Z.; Zheng, L.; Kang, G.; Li, S.; and Yang, Y. 2020. Random erasing data augmentation. In Proceedings of the AAAI Conference on Artificial Intelligence.
Zhou et al. (2021) Zhou, K.; Yang, Y.; Cavallaro, A.; and Xiang, T. 2021. Learning generalisable omni-scale representations for person re-identification. IEEE Transactions on Pattern Analysis and Machine Intelligence.
Zhuang et al. (2020) Zhuang, Z.; Wei, L.; Xie, L.; Zhang, T.; Zhang, H.; Wu, H.; Ai, H.; and Tian, Q. 2020. Rethinking the distribution gap of person re-identification with camera-based batch normalization. In European Conference on Computer Vision, 140–157. Springer.

Multiple Domain Experts Collaborative Learning: Multi-Source Domain Generalization For Peron Re-Identification