Multispace and Multilevel BDDC
Abstract
BDDC method is the most advanced method from the Balancing family of iterative substructuring methods for the solution of large systems of linear algebraic equations arising from discretization of elliptic boundary value problems. In the case of many substructures, solving the coarse problem exactly becomes a bottleneck. Since the coarse problem in BDDC has the same structure as the original problem, it is straightforward to apply the BDDC method recursively to solve the coarse problem only approximately. In this paper, we formulate a new family of abstract Multispace BDDC methods and give condition number bounds from the abstract additive Schwarz preconditioning theory. The Multilevel BDDC is then treated as a special case of the Multispace BDDC and abstract multilevel condition number bounds are given. The abstract bounds yield polylogarithmic condition number bounds for an arbitrary fixed number of levels and scalar elliptic problems discretized by finite elements in two and three spatial dimensions. Numerical experiments confirm the theory.
AMS Subject Classification: 65N55, 65M55, 65Y05
Key words: Iterative substructuring, additive Schwarz method, balancing domain decomposition, BDD, BDDC, Multispace BDDC, Multilevel BDDC
1 Introduction
The BDDC (Balancing Domain Decomposition by Constraints) method by Dohrmann [4] is the most advanced method from the BDD family introduced by Mandel [12]. It is a Neumann-Neumann iterative substructuring method of Schwarz type [5] that iterates on the system of primal variables reduced to the interfaces between the substructures. The BDDC method is closely related to the FETI-DP method (Finite Element Tearing and Interconnecting - Dual, Primal) by Farhat et al. [6, 7]. FETI-DP is a dual method that iterates on a system for Lagrange multipliers that enforce continuity on the interfaces, with some “coarse” variables treated as primal, and it is a further development of the FETI method by Farhat and Roux [8]. Polylogarithmic condition number estimates for BDDC were obtained in [13, 14] and a proof that the eigenvalues of BDDC and FETI-DP are actually the same except for eigenvalue equal to one was given in Mandel et al. [14]. Simpler proofs of the equality of eigenvalues were obtained by Li and Widlund [10], and also by Brenner and Sung [3], who also gave an example when BDDC has an eigenvalue equal to one but FETI-DP does not. In the case of many substructures, solving the coarse problem exactly becomes a bottleneck. However, since the coarse problem in BDDC has the same form as the original problem, the BDDC method can be applied recursively to solve the coarse problem only approximately. This leads to a multilevel form of BDDC in a straightforward manner, see Dohrmann [4]. Polylogarithmic condition number bounds for three-level BDDC (BDDC with two coarse levels) were proved in two and three spatial dimensions by Tu [20, 19].
In this paper, we present a new abstract Multispace BDDC method. The method extends a simple variational setting of BDDC from Mandel and Sousedík [15], which could be understood as an abstract version of BDDC by partial subassembly in Li and Widlund [11]. However, we do not adopt their change of variables, which does not seem to be suitable in our abstract setting. We provide a condition number estimate for the abstract Multispace BDDC method, which generalizes the estimate for a single space from [15]. The proof is based on the abstract additive Schwarz theory by Dryja and Widlund [5]. Many BDDC formulations (with an explicit treatment of substructure interiors, after reduction to substructure interfaces, with two levels, and multilevel) are then viewed as abstract Multispace BDDC with a suitable choice of spaces and operators, and abstract condition number estimates for those BDDC methods follow. This result in turn gives a polylogarithmic condition number bound for Multilevel BDDC applied to a second-order scalar elliptic model problems, with an arbitrary number of levels. A brief presentation of the main results of the paper, without proofs and with a simplified formulation of the Multispace BDDC estimate, is contained in the conference paper [16].
The paper is organized as follows. In Sec. 2 we introduce the abstract problem setting. In Sec. 3 we formulate an abstract Multispace BDDC as an additive Schwarz preconditioner. In Sec. 4 we introduce the settings of a model problem using finite element discretization. In Sec. 5 we recall the algorithm of the original (two-level) BDDC method and formulate it as a Multispace BDDC. In Sec. 6 we generalize the algorithm to obtain Multilevel BDDC and we also give an abstract condition number bound. In Sec. 7 we derive the condition number bound for the model problem. Finally, in Sec. 8, we report on numerical results.
2 Abstract Problem Setting
We wish to solve an abstract linear problem
| (1) |
where is a finite dimensional linear space, is a symmetric positive definite bilinear form defined on , is the right-hand side with denoting the dual space of , and is the duality pairing. The form is also called the energy inner product, the value of the quadratic form is called the energy of , and the norm is called the energy norm. The operator associated with is defined by
A preconditioner is a mapping and we will look for preconditioners such that is also symmetric and positive definite on . It is well known that then has only real positive eigenvalues, and convergence of the preconditioned conjugate gradients method is bounded using the condition number
which we wish to bound above.
All abstract spaces in this paper are finite dimensional linear spaces and we make no distinction between a linear operator and its matrix.
3 Abstract Multispace BDDC
To introduce abstract Multispace BDDC preconditioner, suppose that the bilinear form is defined and symmetric positive semidefinite on some larger space . The preconditioner is derived from the abstract additive Schwarz theory, however we decompose some space between and rather than as it would be done in the additive Schwarz method: In the design of the preconditioner, we choose spaces , , such that
| (2) |
Assumption 1
The form is positive definite on each separately.
Algorithm 2 (Abstract Multispace BDDC)
Given spaces and linear operators , such that is positive definite on each space , and
define the preconditioner by
| (3) |
We formulate the condition number bound first in the full strength allowed by the proof. The bound used in the rest of this paper will be a corollary.
Theorem 3
Define for all the spaces by
If there exist constants and a symmetric matrix , such that
| (4) | |||
| (5) | |||
| (6) |
then the preconditioner from Algorithm 2 satisfies
Proof. We interpret the Multispace BDDC preconditioner as an abstract additive Schwarz method. An abstract additive Schwarz method is specified by a decomposition of the space into subspaces,
| (7) |
and by symmetric positive definite bilinear forms on . The preconditioner is a linear operator
defined by solving the following variational problems on the subspaces and adding the results,
| (8) |
Dryja and Widlund [5] proved that if there exist constants and a symmetric matrix , such that
| (9) | ||||
| (10) | ||||
| (11) |
then
where is the spectral radius.
Now the idea of the proof is essentially to map the assumptions of the abstract additive Schwarz estimate from the decomposition (7) of the space to the decomposition (2). Define the spaces
We will show that the preconditioner (3) satisfies (8), where is defined by
| (12) |
with the operators defined by
| (13) |
First, from the definition of operators , spaces and because is positive definite on by Assumption (1), it follows that and in (12) exist and are unique, so is defined correctly. To prove (8), let be as in (3) and note that is the solution of
Consequently, the preconditioner (3) is an abstract additive Schwarz method and we only need to verify the inequalities (9)–(11). To prove (9), let . Then, with from the assumption (4) and with as in (12), it follows that
Next, let . From the definitions of and , it follows that there exist unique such that . Using the assumption (5) and the definition of in (12), we get
The next Corollary was given without proof in [16, Lemma 1]. This is the special case of Theorem 3 that will be actually used. In the case when , this result was proved in [15].
Corollary 4
Assume that the subspaces are energy orthogonal, the operators are projections, is positive definite on each space , and
| (14) |
Then the abstract Multispace BDDC preconditioner from Algorithm 2 satisfies
| (15) |
Proof. We only need to verify the assumptions of Theorem 3. Let and choose as the energy orthogonal projections of on . First, since the spaces are energy orthogonal, , are projections, and from (14) , we get that which proves (4) with . Next, the assumption (5) becomes the definition of in (15). Finally, (6) with follows from the orthogonality of subspaces .
4 Finite Element Problem Setting
Let be a bounded domain in , or , decomposed into nonoverlapping subdomains , , which form a conforming triangulation of the domain . Subdomains will be also called substructures. Each substructure is a union of Lagrangian or finite elements with characteristic mesh size , and the nodes of the finite elements between substructures coincide. The nodes contained in the intersection of at least two substructures are called boundary nodes. The union of all boundary nodes is called the interface . The interface is a union of three different types of open sets: faces, edges, and vertices. The substructure vertices will be also called corners. For the case of regular substructures, such as cubes or tetrahedrons, we can use standard geometric definition of faces, edges, and vertices; cf., e.g., [9] for a more general definition.
In this paper, we find it more convenient to use the notation of abstract linear spaces and linear operators between them instead of the space and matrices. The results can be easily converted to the matrix language by choosing a finite element basis. The space of the finite element functions on will be denoted as . Let be the space of finite element functions on substructure , such that all of their degrees of freedom on are zero. Let
and consider a bilinear form arising from the second-order scalar elliptic problem as
| (16) |
Now is the subspace of all functions from that are continuous across the substructure interfaces. We are interested in the solution of the problem (1) with ,
| (17) |
where the bilinear form is associated on the space with the system operator, defined by
| (18) |
and is the right-hand side. Hence, (17) is equivalent to
| (19) |
Define as the subspace of functions that are zero on the interface , i.e., the “interior” functions. Denote by the energy orthogonal projection from onto ,
Functions from , i.e., from the nullspace of are called discrete harmonic; these functions are -orthogonal to and energy minimal with respect to increments in . Next, let be the space of all discrete harmonic functions that are continuous across substructure boundaries, that is
| (20) |
In particular,
| (21) |
A common approach in substructuring is to reduce the problem to the interface. The problem (17) is equivalent to two independent problems on the energy orthogonal subspaces and , and the solution satisfies , where
| (22) | ||||
| (23) |
The solution of the interior problem (22) decomposes into independent problems, one per each substructure. The reduced problem (23) is then solved by preconditioned conjugate gradients. The reduced problem (23) is usually written equivalently as
where is the form restricted on the subspace , and is the reduced right hand side, i.e., the functional restricted to the space . The reduced right-hand side is usually written as
| (24) |
because by (21). In the implementation, the process of passing to the reduced problem becomes the elimination of the internal degrees of freedom of the substructures, also known as static condensation. The matrix of the reduced bilinear form in the basis defined by interface degrees of freedom becomes the Schur complement, and (24) becomes the reduced right-hand side. For details on the matrix formulation, see, e.g., [17, Sec. 4.6] or [18, Sec. 4.3].
The BDDC method is a two-level preconditioner characterized by the selection of certain coarse degrees of freedom, such as values at the corners and averages over edges or faces of substructures. Define as the subspace of all functions such that the values of any coarse degrees of freedom have a common value for all relevant substructures and vanish on and as the subspace of all function such that their coarse degrees of freedom vanish. Next, define as the subspace of all functions such that their coarse degrees of freedom between adjacent substructures coincide, and such that their energy is minimal. Clearly, functions in are uniquely determined by the values of their coarse degrees of freedom, and
| (25) |
We assume that
| (26) |
That is the case when is positive definite on the space , where the problem (1) is posed, and there are sufficiently many coarse degrees of freedom. We further assume that the coarse degrees of freedom are zero on all functions from , that is,
| (27) |
In other words, the coarse degrees of freedom depend on the values on substructure boundaries only. From (25) and (27), it follows that the functions in are discrete harmonic, that is,
| (28) |
Next, let be a projection from onto , defined by taking some weighted average on substructure interfaces. That is, we assume that
| (29) |
Since a projection is the identity on its range, it follows that does not change the interior degrees of freedom,
| (30) |
since . Finally, we show that the operator is a projection. From (30) it follows that does not change interior degrees of freedom, so . Then, using the fact that and are projections, we get
| (31) | ||||
Remark 6
In [14, 15], the whole analysis was done in spaces of discrete harmonic functions after eliminating , and the space was the solution space. In particular, consisted of discrete harmonic functions only, while the same space here would be . The decomposition of this space used in [14, 15] would be in our context written as
| (32) |
In the next section, the space will be either or .
5 Two-level BDDC as Multispace BDDC
We show several different ways the original, two-level, BDDC algorithm can be interpreted as multispace BDDC. We consider first BDDC applied to the reduced problem (23), that is, (1) with . This was the formulation considered in [14]. Define the space of discrete harmonic functions with coarse degrees of freedom continuous across the interface
Because we work in the space of discrete harmonic functions and the output of the averaging operator is not discrete harmonic, denote
| (33) |
In an implementation, discrete harmonic functions are represented by the values of their degrees of freedom on substructure interfaces, cf., e.g. [18]; hence, the definition (33) serves formal purposes only, so that everything can be written in terms of discrete harmonic functions without passing to the matrix formulation.
Algorithm 7 ([15], BDDC on the reduced problem)
Define the preconditioner by
| (34) |
Proposition 8 ([15])
Proof. We only need to note that the bilinear form is positive definite on by (26), and the operator defined by (33) is a projection by (31). The projection is onto because is onto by (29), and maps onto by the definition of in (20).
Using the decomposition (32), we can split the solution in the space into the independent solution of two subproblems: mutually independent problems on substructures as the solution in the space , and a solution of global coarse problem in the space . The space has a decomposition
| (36) |
the same as the decomposition (32), and Algorithm 7 can be rewritten as follows.
Algorithm 9 ([14], BDDC on the reduced problem)
Define the preconditioner by , where
| (37) | ||||
| (38) |
Proposition 10
Proof. Let . Define the vectors , in Multispace BDDC by (3) with and given by (39). Let be the quantities in Algorithm 9, defined by (37)-(38). Using the decomposition (36), any can be written uniquely as + for some and corresponding to (3) as and , and .
To verify the assumptions of Corollary 4, note that the decomposition (36) is orthogonal, is positive definite on both and as subspaces of by (26), and is a projection by (31).
Next, we present a BDDC formulation on the space with explicit treatment of interior functions in the space as in [4, 13], i.e., in the way the BDDC algorithm was originally formulated.
Algorithm 11 ([4, 13], original BDDC)
Define the preconditioner as follows. Compute the interior pre-correction
| (40) |
Set up the updated residual
| (41) |
Compute the substructure correction
| (42) |
Compute the coarse correction
| (43) |
Add the corrections
Compute the interior post-correction
| (44) |
Apply the combined corrections
| (45) |
The interior corrections (40) and (44) decompose into independent Dirichlet problems, one for each substructure. The substructure correction (42) decomposes into independent constrained Neumann problems, one for each substructure. Thus, the evaluation of the preconditioner requires three problems to be solved in each substructure, plus solution of the coarse problem (43). In addition, the substructure corrections can be solved in parallel with the coarse problem.
Remark 12
As it is well known [4], the first interior correction (40) can be omitted in the implementation by starting the iterations from an initial solution such that the residual in the interior of the substructures is zero,
i.e., such that the error is discrete harmonic. Then the output of the preconditioner is discrete harmonic and thus the errors in all the CG iterations (which are linear combinations of the original error and outputs from the preconditioner) are also discrete harmonic by induction.
The following proposition will be the starting point for the multilevel case.
Proposition 13
Proof. Let . Define the vectors , , in Multispace BDDC by (3) with the spaces given by (46) and with the operators given by (47). Let , , , , , , and be the quantities in Algorithm 11, defined by (40)-(45).
Next, consider defined in (42). We show that satisfies (3) with , i.e., . So, let be arbitrary. From (42) and (41),
| (48) |
Now from the definition of by (40) and the fact that , we get
| (49) |
and subtracting (49) from (48) gives
because by orthogonality. To verify (3), it is enough to show that then . Since is an -orthogonal projection, it holds that
| (50) |
where we have used following the assumption (30) and the equality
for any , which follows from (41) and (40). Since is positive definite on by assumption (26), it follows from (50) that .
In exactly the same way, from (43) – (45), we get that if is defined by (43), then satisfies (3) with . (The proof that can be simplified but there is nothing wrong with proceeding exactly as for .)
Finally, from (44), , so
It remains to verify the assumptions of Corollary 4.
First, the spaces and are -orthogonal by (25) and, from (27),
thus . Clearly, . Since consists of discrete harmonic functions from (28), so , it follows that the spaces , , given by (46), are -orthogonal.
It remains to prove the decomposition of unity (14). Let
| (51) |
and let
From (51), since and . Then by (29), so
because both and are discrete harmonic.
The next Theorem shows an equivalence of the three Algorithms introduced above.
Theorem 14
Proof. From the decomposition (36), we can write any uniquely as for some and , so the preconditioned operators from Algorithms 7 and 9 are spectrally equivalent and we need only to show their spectral equivalence to the preconditioned operator from Algorithm 11. First, we note that the operator defined by (18), and given in the block form as
with blocks
is block diagonal and for any , written as , because . Next, we note that the block is the Schur complement operator corresponding to the form . Finally, since the block is used only in the preprocessing step, the preconditioned operator from Algorithms 7 and 9 is simply
Let us now turn to Algorithm 11. Let the residual be written as , where and . Taking , we get , and it follows that , so . On the other hand, taking gives , , and finally , so . This shows that the off-diagonal blocks of the preconditioner are zero, and therefore it is block diagonal
Next, let us take and consider . The algorithm returns , and finally . This means that so . The operator , and the block preconditioned operator from Algorithm 11 can be written, respectively, as
where the right lower block is exactly the same as the preconditioned operator from Algorithms 7 and 9.
The BDDC condition number estimate is well known from [13]. Following Theorem 14 and Corollary 4, we only need to estimate on .
Theorem 15 ([13])
The condition number of the original BDDC algorithm satisfies , where
| (52) |
Remark 16
Before proceeding into the Multilevel BDDC section, let us write concisely the spaces and operators involved in the two-level preconditioner as
We are now ready to extend this decomposition into the multilevel case.
6 Multilevel BDDC and an Abstract Bound
In this section, we generalize the two-level BDDC preconditioner to multiple levels, using the abstract Multispace BDDC framework from Algorithm 2. The substructuring components from Section 5 will be denoted by an additional subscript as , etc., and called level . The level coarse problem (43) will be called the level problem. It has the same finite element structure as the original problem (1) on level , so we put . Level substructures are level elements and level coarse degrees of freedom are level degrees of freedom. Repeating this process recursively, level substructures become level elements, and the level substructures are agglomerates of level elements. Level substructures are denoted by and they are assumed to form a conforming triangulation with a characteristic substructure size . For convenience, we denote by the original finite elements and put . The interface on level is defined as the union of all level boundary nodes, i.e., nodes shared by at least two level substructures, and we note that . Level coarse degrees of freedom become level degrees of freedom. The shape functions on level are determined by minimization of energy with respect to level shape functions, subject to the value of exactly one level degree of freedom being one and others level degrees of freedom being zero. The minimization is done on each level element (level substructure) separately, so the values of level degrees of freedom are in general discontinuous between level substructures, and only the values of level degrees of freedom between neighboring level elements coincide.
The development of the spaces on level now parallels the finite element setting in Section 4. Denote . Let be the space of functions on the substructure , such that all of their degrees of freedom on are zero, and let
Then is the subspace of all functions from that are continuous across the interfaces . Define as the subspace of functions that are zero on, i.e., the functions “interior” to the level substructures. Denote by the energy orthogonal projection from onto ,
Functions from , i.e., from the nullspace of are called discrete harmonic on level ; these functions are -orthogonal to and energy minimal with respect to increments in . Denote by the subspace of discrete harmonic functions on level, that is
| (53) |
In particular, . Define as the subspace of all functions such that the values of any coarse degrees of freedom on level have a common value for all relevant level substructures and vanish on and as the subspace of all functions such that their level coarse degrees of freedom vanish. Define as the subspace of all functions such that their level coarse degrees of freedom between adjacent substructures coincide, and such that their energy is minimal. Clearly, functions in are uniquely determined by the values of their level coarse degrees of freedom, and
| (54) |
We assume that the level coarse degrees of freedom are zero on all functions from , that is,
| (55) |
In other words, level coarse degrees of freedom depend on the values on level substructure boundaries only. From (54) and (55), it follows that the functions in are discrete harmonic on level, that is
| (56) |
Let be a projection from onto , defined by taking some weighted average on
Since projection is the identity on its range, does not change the level interior degrees of freedom, in particular
| (57) |
Finally, we introduce an interpolation from level degrees of freedom to functions in some classical finite element space with the same degrees of freedom as . The space will be used for comparison purposes, to invoke known inequalities for finite elements. A more detailed description of the properties of and the spaces is postponed to the next section.
The hierarchy of spaces and operators is shown concisely in Figure 1. The Multilevel BDDC method is defined recursively [4, 16] by solving the coarse problem on level only approximately, by one application of the preconditioner on level . Eventually, at level, , the coarse problem, which is the level problem, is solved exactly. We need a more formal description of the method here, which is provided by the following algorithm.
Algorithm 17 (Multilevel BDDC)
Define the preconditioner as follows:
for ,
-
Compute interior pre-correction on level ,
(58) -
Get updated residual on level ,
(59) -
Find the substructure correction on level :
(60) -
Formulate the coarse problem on level ,
(61) -
If , solve the coarse problem directly and set ,
otherwise set up the right-hand side for level ,(62)
end.
for
-
Average the approximate corrections on substructure interfaces on level ,
(63) -
Compute the interior post-correction on level ,
(64) -
Apply the combined corrections,
(65)
end.
We can now show that the Multilevel BDDC can be cast as the Multispace BDDC on energy orthogonal spaces, using the hierarchy of spaces from Figure 1.
Lemma 18
Proof. Let . Define the vectors by (3) with the spaces and operators given by (66)-(67), and let , , , , , , , and be the quantities in Algorithm 17, defined by (58)-(65).
First, with , the definition of in (3) is (58) with and . We show that in general, for level , and space we get (3) with , so that and in particular . So, let , be arbitrary. From (58) using (62) and (59),
| (68) | ||||
Since from (58) using the fact that it follows that
we get from (68),
and because by orthogonality, we get
Repeating this process recursively using (68), we finally get
Next, consider defined by (60). We show that for , and , we get (3) with , so that and in particular . So, let be arbitrary. From (60) using (59),
| (69) |
From the definition of by (58) and since it follows that
so (69) gives
Next, because by orthogonality, and using (62),
Repeating this process recursively, we finally get
To verify (3), it remains to show that then . Since is an -orthogonal projection, it holds that
where we have used following the assumption (57) and the equality
and, in particular for ,
It remains to verify the assumptions of Corollary 4.
The spaces and , for all , are -orthogonal by (54) and from (55),
thus is -orthogonal to . Since consists of discrete harmonic functions on level from (56), and , it follows by induction that the spaces , given by (66), are -orthogonal.
We now show that the operators defined by (67) are projections. From our definitions, coarse degrees of freedom on substructuring level (from which we construct the level problem) depend only on the values of degrees of freedom on the interface and for . Then,
| (70) |
It remains to prove the decomposition of unity (14). Let , such that
| (71) | ||||
| (72) |
and
| (73) |
From (71), since and . Then by (57), so
because and are discrete harmonic on level . The fact that in (71) and (73) are the same on arbitrary level can be proved in exactly the same way using induction and putting in (71) as
and in (73) as
The following bound follows from writing of the Multilevel BDDC as Multispace BDDC in Lemma 18 and the estimate for Multispace BDDC in Corollary 4.
Lemma 19
Proof. Choose the spaces and operators as in (66)-(67) so that , , , . The bound now follows from Corollary 4.
Lemma 20
Proof. Note from Lemma 19 that , , and generally ,
7 Condition Number Bound for the Model Problem
Let be the energy norm of a function restricted to subdomain , i.e., and let be the norm obtained by piecewise integration over each . To apply Lemma 20 to the model problem presented in Section 5, we need to generalize the estimate from Theorem 15 to coarse levels. To this end, let be an interpolation from the level coarse degrees of freedom (i.e., level degrees of freedom) to functions in another space and assume that, for all and the interpolation satisfies for all and for all the equivalence
| (76) |
which implies by Lemma 22 also the equivalence
| (77) |
with bounded independently of .
Remark 21
Since , the two norms are the same on
For the three-level BDDC in two dimensions, the result of Tu [20, Lemma 4.2], which is based on the lower bound estimates by Brenner and Sung [2], can be written in our settings for all and for all as
| (78) |
where is a piecewise (bi)linear interpolation given by values at corners of level substructures, and independently of .
For the three-level BDDC in three dimensions, the result of Tu [19, Lemma 4.5], which is based on the lower bound estimates by Brenner and He [1], can be written in our settings for all and for all as
| (79) |
where is an interpolation from the coarse degrees of freedom given by the averages over substructure edges, and independently of .
We note that the level substructures are called subregions in [20, 19]. Since , with the equivalence (78) corresponds to (76), and (79) to (77).
The next Lemma establishes the equivalence of seminorms on a factor space from the equivalence of norms on the original space. Let be finite dimensional spaces and a norm on and define
| (80) |
We will be using (80) for the norm on the space of discrete harmonic functions with as the space of interior functions , and also with as the space . In particular, since , we have
| (81) |
Lemma 22
Let , be norms on , and
| (82) |
Then for any subspace ,
resp.,
| (83) |
Proof. From the definition (80) of the norm on a factor space, we get
for some . Let be defined similarly. Then
which is the right hand side inequality in (83). The left hand side inequality follows by switching the notation for and .
Lemma 23
For all , and ,
| (84) |
with , independently of ,…, .
Proof. The proof follows by induction. For , (84) holds because . Suppose that (84) holds for some and let . From the definition of by energy minimization,
| (85) |
From (85), the induction assumption, and Lemma 22 eq. (83), it follows that
| (86) | ||||
From the assumption (76), applied to the functions of the form on ,
| (87) |
with , bounded independently of . Then (85), (86) and (87) imply (84) with .
Next, we generalize the estimate from Theorem 15 to coarse levels.
Lemma 24
For all substructuring levels ,
| (88) |
Proof. From (84), summation over substructures on level gives
| (89) |
Next, in our context, using the definition of and (83), we get
so from (52) for some and all ,
| (90) |
Similarly, from (89) and (90) it follows that
which is (88) with
and from Lemma 23.
Theorem 25
The Multilevel BDDC for the model problem and corner coarse function in 2D and edge coarse functions in 3D satisfies the condition number estimate
Remark 27
While for standard (two-level) BDDC it is immediate that increasing the coarse space and thus decreasing the space cannot increase the condition number bound, this is an open problem for the multilevel method. In fact, the 3D numerical results in the next section suggest that this may not be the case.
Corollary 28
In the case of uniform coarsening, i.e. with and the same geometry of decomposition on all levels we get
| (91) |
8 Numerical Examples
| C | C+E | |||||
| iter | cond | iter | cond | |||
| at all levels. | ||||||
| 2 | 8 | 1.92 | 5 | 1.08 | 144 | 80 |
| 3 | 13 | 3.10 | 7 | 1.34 | 1296 | 720 |
| 4 | 17 | 5.31 | 9 | 1.60 | 11,664 | 6480 |
| 5 | 23 | 9.22 | 10 | 1.85 | 104,976 | 58,320 |
| 6 | 31 | 16.07 | 11 | 2.12 | 944,748 | 524,880 |
| 7 | 42 | 28.02 | 13 | 2.45 | 8,503,056 | 4,723,920 |
| at all levels. | ||||||
| 2 | 9 | 2.20 | 6 | 1.14 | 256 | 112 |
| 3 | 15 | 4.02 | 8 | 1.51 | 4096 | 1792 |
| 4 | 21 | 7.77 | 10 | 1.88 | 65,536 | 28,672 |
| 5 | 30 | 15.2 | 12 | 2.24 | 1,048,576 | 458,752 |
| 6 | 42 | 29.7 | 13 | 2.64 | 16,777,216 | 7,340,032 |
| at all levels. | ||||||
| 2 | 10 | 2.99 | 7 | 1.33 | 1024 | 240 |
| 3 | 19 | 7.30 | 11 | 2.03 | 65,536 | 15,360 |
| 4 | 31 | 18.6 | 13 | 2.72 | 4,194,304 | 983,040 |
| 5 | 50 | 47.38 | 15 | 3.40 | 268,435,456 | 62,914,560 |
| at all levels. | ||||||
| 2 | 11 | 3.52 | 8 | 1.46 | 2304 | 368 |
| 3 | 21 | 10.12 | 12 | 2.39 | 331,776 | 52,992 |
| 4 | 39 | 29.93 | 15 | 3.32 | 47,775,744 | 7,630,848 |
| at all levels. | ||||||
| 2 | 11 | 3.94 | 8 | 1.56 | 4096 | 496 |
| 3 | 23 | 12.62 | 13 | 2.67 | 1,048,576 | 126,976 |
| 4 | 43 | 41.43 | 16 | 3.78 | 268,435,456 | 32,505,856 |
| E | C+E | C+E+F | ||||||
| iter | cond | iter | cond | iter | cond | |||
| at all levels. | ||||||||
| 2 | 10 | 1.85 | 8 | 1.47 | 5 | 1.08 | 1728 | 1216 |
| 3 | 14 | 3.02 | 12 | 2.34 | 8 | 1.50 | 46,656 | 32,832 |
| 4 | 18 | 4.74 | 18 | 5.21 | 11 | 2.20 | 1,259,712 | 886,464 |
| 5 | 23 | 7.40 | 26 | 14.0 | 16 | 3.98 | 34,012,224 | 23,934,528 |
| at all levels. | ||||||||
| 2 | 10 | 1.94 | 9 | 1.66 | 6 | 1.16 | 4096 | 2368 |
| 3 | 15 | 3.51 | 14 | 3.24 | 10 | 1.93 | 262,144 | 151,552 |
| 4 | 20 | 6.09 | 22 | 9.95 | 14 | 3.05 | 16,777,216 | 9,699,328 |
| at all levels. | ||||||||
| 2 | 12 | 2.37 | 11 | 2.24 | 8 | 1.50 | 32,768 | 10,816 |
| 3 | 19 | 5.48 | 20 | 7.59 | 14 | 3.32 | 16,777,216 | 5,537,792 |
| at all levels. | ||||||||
| 2 | 12 | 2.56 | 12 | 2.47 | 9 | 1.69 | 64,000 | 17,344 |
| 3 | 20 | 6.39 | 22 | 10.1 | 16 | 3.85 | 64,000,000 | 17,344,000 |
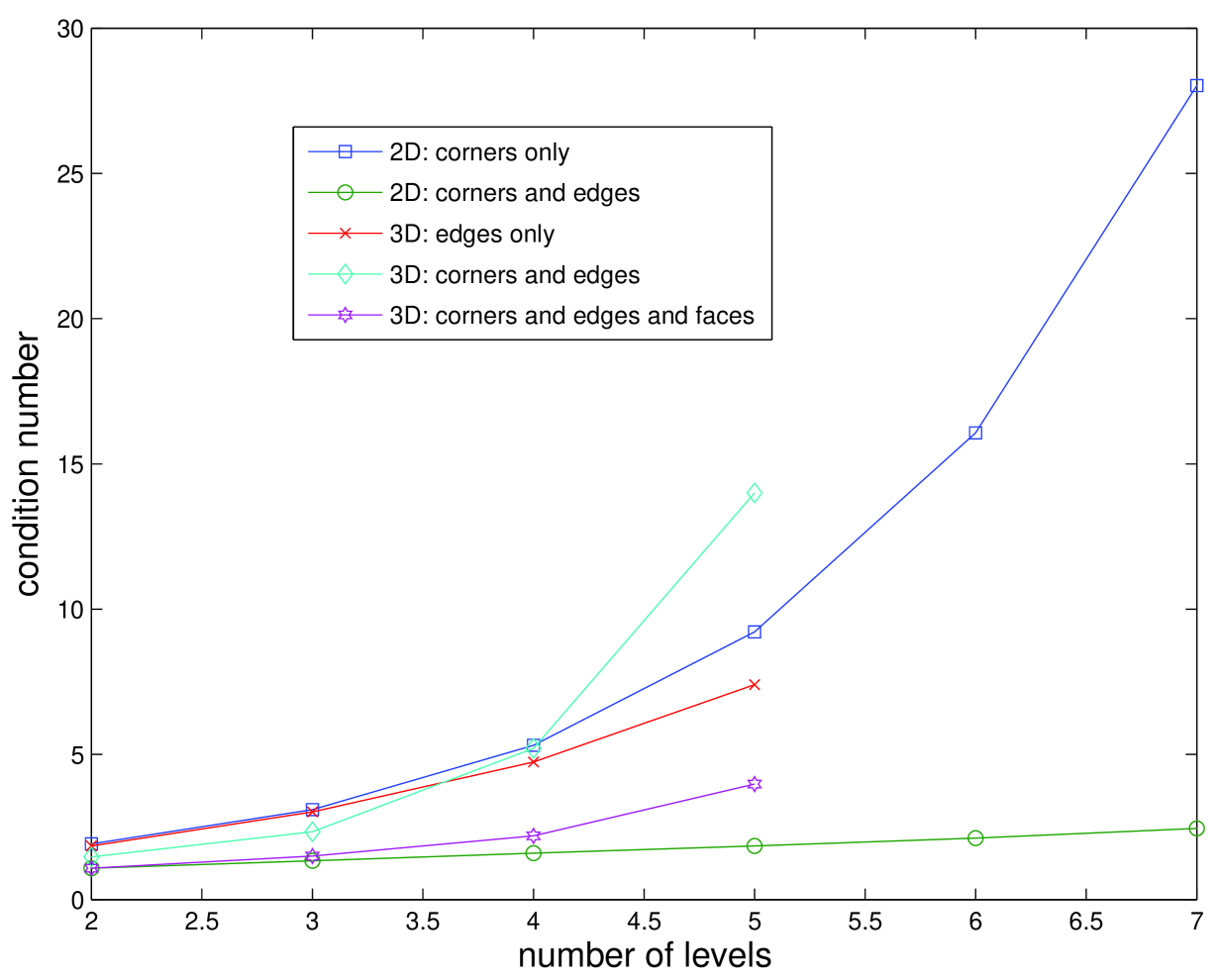
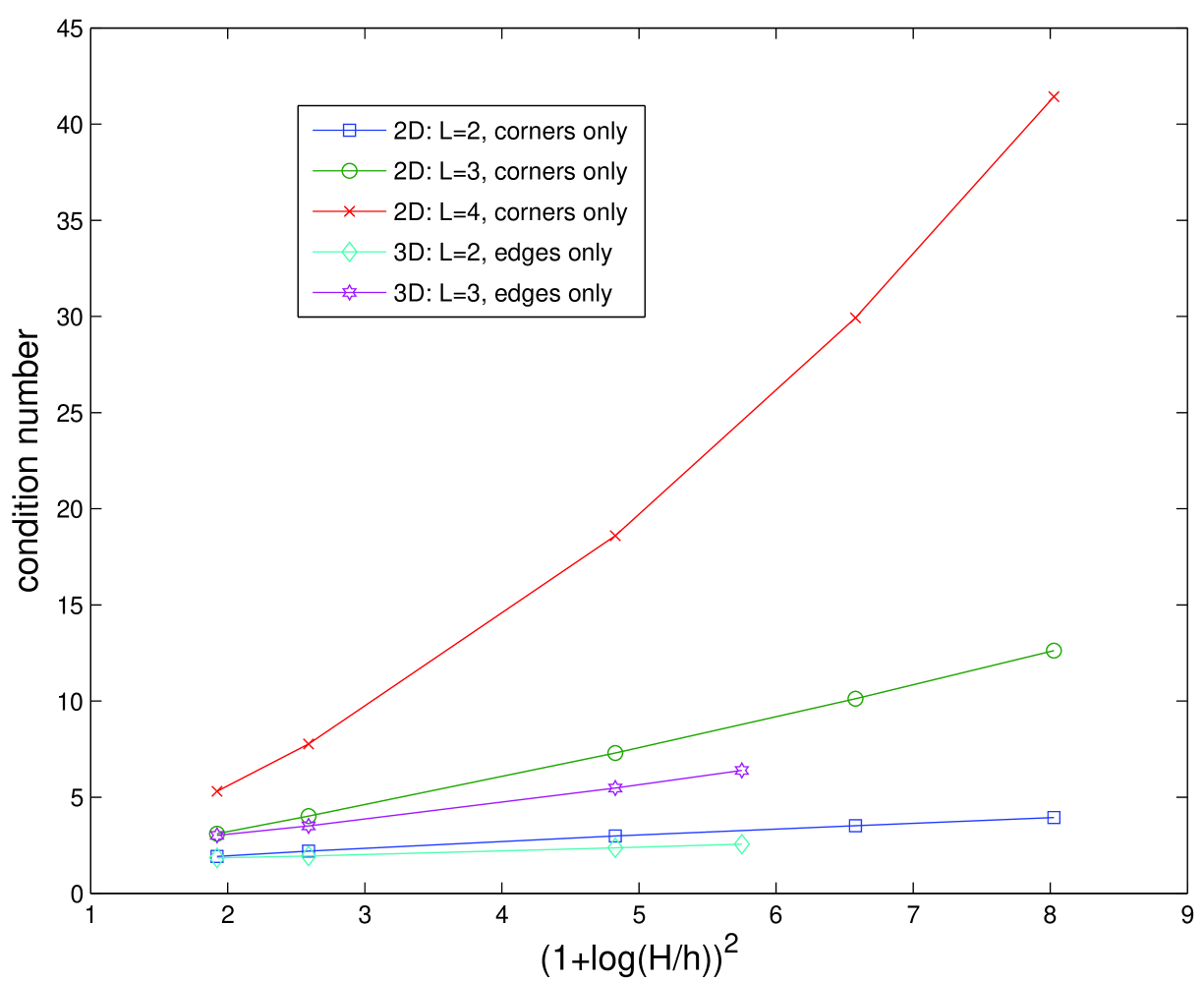
Numerical examples are presented in this section for the Poisson equation in two and three dimensions. The problem domain in 2D (3D) is the unit square (cube), and standard bilinear (trilinear) finite elements are used for the discretization. The substructures at each level are squares or cubes, and periodic essential boundary conditions are applied to the boundary of the domain. This choice of boundary conditions allows us to solve very large problems on a single processor since all substructure matrices are identical for a given level.
The preconditioned conjugate gradient algorithm is used to solve the associated linear systems to a relative residual tolerance of for random right-hand-sides with zero mean value. The zero mean condition is required since, for periodic boundary conditions, the null space of the coefficient matrix is the unit vector. The coarse problem always has () subdomains at the coarsest level for 2D (3D) problems.
The number of levels (), the number of iterations (iter), and condition number estimates (cond) obtained from the conjugate gradient iterations are reported in Tables 1 and 2. The letters C, E, and F designate the use of corners, edges, or faces in the coarse space. For example, C+E means that both corners and edges are used in the coarse space. For 2D and 3D problems, the theory is applicable to coarse spaces C and E, respectively. Also shown in the tables are the total number of unknowns () and the number of unknowns () on subdomain boundaries at the finest level.
The results in Tables 1 and 2 are displayed in Figure 2 for a fixed value of . In two dimensions we observe very different behavior depending on the particular form of the coarse space. If only corners are used in 2D, then there is very rapid growth of the condition number with increasing numbers of levels as predicted by the theory. In contrast, if both corners and edges are used in the 2D coarse space, then the condition number appears to vary linearly with for the the number of levels considered. Our explanation is that a bound similar to Theorem 25 still applies to the favorable 2D case, though possibly with (much) smaller constants, so the exponential growth of the condition number is no longer apparent. The results in Tables 1 and 2 are also displayed in Figure 3 for fixed numbers of levels. The observed growth of condition numbers for the case of uniform coarsening is consistent with the estimate in (91).
Similar trends are present in 3D, but the beneficial effects of using more enriched coarse spaces are much less pronounced. Interestingly, when comparing the use of edges only (E) with corners and edges (C+E) in the coarse space, the latter does not always lead to smaller numbers of iterations or condition numbers for more than two levels. The fully enriched coarse space (C+E+F), however, does give the best results in terms of iterations and condition numbers. It should be noted that the present 3D theory in Theorem 25 covers only the use of the edges only, and the present theory does not guarantee that the condition number (or even its bound) decrease with increasing the coarse space (Remark 27).
In summary, the numerical examples suggest that better performance, especially in 2D, can be obtained when using a fully enriched coarse space. Doing so does not incur a large computational expense since there is never the need to solve a large coarse problem exactly with the multilevel approach. Finally, we note that a large number of levels is not required to solve very large problems. For example, the number of unknowns in 3D for a 4-level method with a coarsening ratio of at all levels is .
References
- [1] S. C. Brenner and Q. He, Lower bounds for three-dimensional nonoverlapping domain decomposition algorithms, Numer. Math., 93 (2003), pp. 445–470.
- [2] S. C. Brenner and L.-Y. Sung, Lower bounds for nonoverlapping domain decomposition preconditioners in two dimensions, Math. Comp., 69 (2000), pp. 1319–1339.
- [3] , BDDC and FETI-DP without matrices or vectors, Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 1429–1435.
- [4] C. R. Dohrmann, A preconditioner for substructuring based on constrained energy minimization, SIAM J. Sci. Comput., 25 (2003), pp. 246–258.
- [5] M. Dryja and O. B. Widlund, Schwarz methods of Neumann-Neumann type for three-dimensional elliptic finite element problems, Comm. Pure Appl. Math., 48 (1995), pp. 121–155.
- [6] C. Farhat, M. Lesoinne, P. LeTallec, K. Pierson, and D. Rixen, FETI-DP: a dual-primal unified FETI method. I. A faster alternative to the two-level FETI method, Internat. J. Numer. Methods Engrg., 50 (2001), pp. 1523–1544.
- [7] C. Farhat, M. Lesoinne, and K. Pierson, A scalable dual-primal domain decomposition method, Numer. Linear Algebra Appl., 7 (2000), pp. 687–714. Preconditioning techniques for large sparse matrix problems in industrial applications (Minneapolis, MN, 1999).
- [8] C. Farhat and F.-X. Roux, A method of finite element tearing and interconnecting and its parallel solution algorithm, Internat. J. Numer. Methods Engrg., 32 (1991), pp. 1205–1227.
- [9] A. Klawonn and O. B. Widlund, Dual-primal FETI methods for linear elasticity, Comm. Pure Appl. Math., 59 (2006), pp. 1523–1572.
- [10] J. Li and O. B. Widlund, FETI-DP, BDDC, and block Cholesky methods, Internat. J. Numer. Methods Engrg., 66 (2006), pp. 250–271.
- [11] , On the use of inexact subdomain solvers for BDDC algorithms, Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 1415–1428.
- [12] J. Mandel, Balancing domain decomposition, Comm. Numer. Methods Engrg., 9 (1993), pp. 233–241.
- [13] J. Mandel and C. R. Dohrmann, Convergence of a balancing domain decomposition by constraints and energy minimization, Numer. Linear Algebra Appl., 10 (2003), pp. 639–659. Dedicated to the 70th birthday of Ivo Marek.
- [14] J. Mandel, C. R. Dohrmann, and R. Tezaur, An algebraic theory for primal and dual substructuring methods by constraints, Appl. Numer. Math., 54 (2005), pp. 167–193.
- [15] J. Mandel and B. Sousedík, Adaptive selection of face coarse degrees of freedom in the BDDC and the FETI-DP iterative substructuring methods, Comput. Methods Appl. Mech. Engrg., 196 (2007), pp. 1389–1399.
- [16] J. Mandel, B. Sousedík, and C. R. Dohrmann, On multilevel BDDC, Lecture Notes in Computational Science and Engineering, 60 (2007), pp. 287–294. Domain Decomposition Methods in Science and Engineering XVII.
- [17] B. F. Smith, P. E. Bjørstad, and W. D. Gropp, Domain decomposition, Cambridge University Press, Cambridge, 1996. Parallel multilevel methods for elliptic partial differential equations.
- [18] A. Toselli and O. Widlund, Domain decomposition methods—algorithms and theory, vol. 34 of Springer Series in Computational Mathematics, Springer-Verlag, Berlin, 2005.
- [19] X. Tu, Three-level BDDC in three dimensions, SIAM J. Sci. Comput., 29 (2007), pp. 1759–1780.
- [20] , Three-level BDDC in two dimensions, Internat. J. Numer. Methods Engrg., 69 (2007), pp. 33–59.