Mushroom-instability-driven Magnetic Reconnections in Collisionless Relativistic Jets
Abstract
We study the kinetic plasma dynamics in collisionless relativistic jets with velocity shear, by carrying out particle-in-cell simulations in the transverse plane of a jet. It is discovered that intermittent magnetic reconnections (MRs) are driven by Mushroom instability (MI), which is an important kinetic-scale plasma instability in the plasma shear-flows with relativistic bulk speed. We refer to this sequence of kinetic plasma phenomena as ”MI-driven MR”. The MI-driven MRs intermittently occur with moving the location of the reconnection points from the vicinity of the initial velocity-shear surface towards the center of the jet. As a consequence, the number density of high energy electrons, which are accelerated by MI-driven MRs, increases with time in the region inside the initial velocity-shear surface with accompanying the generation and subsequent amplification of magnetic fields by MI. The maximum Lorentz factor of electrons increases with initial bulk Lorentz factor of the jet. A possible relation of MI-driven MR to the bright synchrotron emission in jet-spine of active galactic nucleus jets is also discussed.
1 Introduction
The relativistic jets launched from the supermassive black holes (Blandford et al., 2019) show or imply the enigmatic sub-structure inside them. The elliptical galaxy M87 is one of the best laboratories to study the relativistic jet because it possesses one of the closest jets, so that its jet structure is best resolved (Hada et al., 2011; Walker et al., 2018). Recently, very long baseline interferometer (VLBI) observation in radio band revealed the triple-ridge structure in M87 jet at a distance of from the central supermassive black hole (Asada et al., 2016; Mertens et al., 2016; Hada, 2017), where the distance is projected on the sky plane. Here, is the gravitational radius of the central black hole with its mass , is the gravitational constant, and is the speed of light. The triple-ridge structure can be interpreted as the observational feature of the spine-sheath structure of the jet, which is composed of the fast flowing spine and the slow flowing sheath (Laing & Bridle, 2002). The spine-sheath structure is also proposed to explain the short-term variation of TeV -ray emission in blazars (e.g., Mrk 501 and PKS 2155-304) and may be ubiquitous in the relativistic jet (Ghisellini et al., 2005).
In order to understand the physics and the observed features of the relativistic jets, a number of magnetohydrodynamic (MHD) simulations have been performed (Koide et al., 1999; McKinney, 2006; Mizuno et al., 2007; Tchekhovskoy et al., 2011; Porth & Komissarov, 2015; Gourgouliatos & Komissarov, 2018; Nakamura et al., 2018; Davelaar et al., 2019; Matsumoto & Masada, 2019). The general relativistic radiation MHD (GRRMHD) simulations qualitatively reproduced the sheath brightened structure (Chael et al., 2019). In addition, a possible formation of the plasmoids in the sheath is proposed by general relativistic MHD simulations (Nakamura et al., 2018) and general relativistic resistive MHD simulations (Ripperda et al., 2020). However, GR(R)MHD simulations could not explain the formation of the jet spine up to today111Alternatively, it has long been known that the natural place for under expanded hypersonic jets (in rocket jets, in particular) to dissipate is at the center line. Particles are energized downstream of Mach disks (shocks) that form along the center-line due to compressive waves emanating from the boundary (Sanders, 1983; Edgington-Mitchell et al., 2014)..
Meanwhile, a limited number of particle-in-cell (PIC) simulations of jets have been carried out as a strong tool to explore the kinetic plasma processes of jets (Nishikawa et al., 2003, 2016; Alves et al., 2018; Davelaar et al., 2020). In the 2010s, an important electron-scale shear-instability called Mushroom instability (MI; Alves et al., 2012) was found in the plasma with relativistic bulk shear flow. Importantly, the MI dominates the electron-scale Kelvin-Helmholtz instability when relative bulk speed is greater than (Alves et al., 2015). Based on kinetic plasma simulations (Alves et al., 2012; Grismayer et al., 2013; Liang et al., 2013; Alves et al., 2014, 2015), the mechanism of MI is the following: At first, the interchanging thermal motion of electrons across the shear surface, which is faster than proton motions, results in the electric currents along the jet bulk-motion near the shear surface. Then, the magnetic field is generated mainly parallel to the shear surface. The generated magnetic field further induces the interchanging electron motion across the velocity-shear surface, and the perturbation grows into a number of electron channel-flows.
In this paper, we study the kinetic plasma dynamics triggered by the MI, namely Mushroom-instability-driven magnetic reconnection (MI-driven MR), by carrying out two-dimensional particle-in-cell (PIC) simulations on the transverse plane of the relativistic jets with velocity-shear surface. Here, MR is the topological rearrangement of magnetic fields with dissipation of magnetic energy and resultant heating and acceleration of plasma particles (Parker, 1979; Horiuchi & Sato, 1999; Biskamp, 2000; Zenitani & Hoshino, 2001; Drake et al., 2006; Yamada et al., 2010; Sironi & Spitkovsky, 2014). We demonstrate that the intermittent MI-driven MR results in the electron concentration to the center (i.e., spine). We propose that this new kinetic plasma dynamics will lead to the formation of the jet spine in the relativistic jets.
2 Model Setup
We perform fully kinetic PIC simulations of the relativistic jets of electron-proton plasma. The simulations are carried out by using a two-dimensional relativistic PIC simulation code PASTEL (Moritaka et al., 2016) in the Cartesian coordinate system with – plane, which can explicitly solve the Maxwell equations and the Newton-Lorentz equation in a self-consistent way (e.g., Birdsall & Langdon, 1991; Hockney & Eastwood, 1988; Esirkepov, 2001). We set the – plane in the transverse direction of the jet, i.e., the propagation direction of the jet is perpendicular to the computational domain. Although the computational domain is in two-dimension, the physical quantities have three dimension in space, i.e., -component of physical quantities of the plasma and electromagnetic fields are also time integrated.
The size of the simulation domain is , where the unit of the length is the electron skin depth , where is the plasma frequency of electrons. This simulation domain is resolved by grid cells, and the cell size is one-half of the Debye length of the electrons. The periodic boundary condition is imposed at each boundary of the computational domain.
The initial condition of the simulation is as follows. We define the cylindrical radius and that of the initial velocity-shear surface . We set the high-bulk velocity plasma with the speed whose corresponding Lorentz factor is in the region . We note that, in this work, we assume the bulk speed to be zero in the region to focus on kinetic plasma phenomena in a simplified model setup, rather than setting a structured jet with velocity shear inside a static ambient plasma, which may be realized in a more realistic situation. We examine a moderately relativistic bulk velocity model with () and a highly relativistic bulk velocity model with (i.e., ). The temperatures of the electrons and protons are constant in space, and their thermal velocities equal to and , respectively. The particles are also uniformly distributed and neither magnetic field nor electric current is assumed. We add no artificial initial perturbation to the plasma. The adequacy of our simple assumption on no initial magnetic field, which is expected to be consistent for the jet plasma far from the central black hole, will be discussed in §4.
Since the injection mechanism of the plasmas into the jet is an open question, we simply assumed the initially uniform density plasma composed of protons and electrons as described above. The protons and electrons might be injected into the jet base as a result of the MRs triggered at the interface of jet and turbulent accretion flow (Tchekhovskoy et al., 2011) or the decay of the neutrons generated via the accelerated proton in the underlying accretion flows (Toma & Takahara, 2012).
3 Results
3.1 Moderately Relativistic Bulk Speed Model )
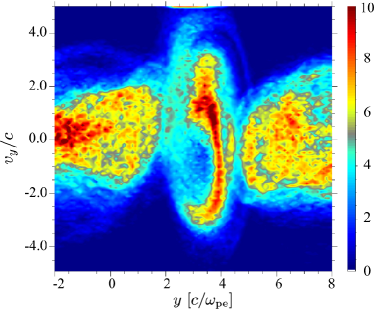
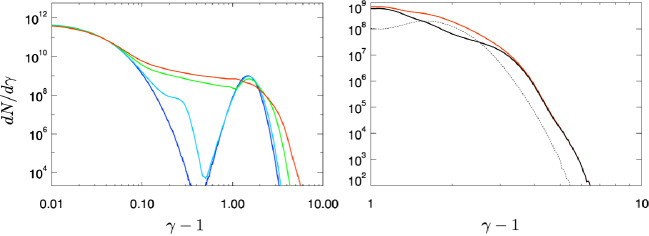
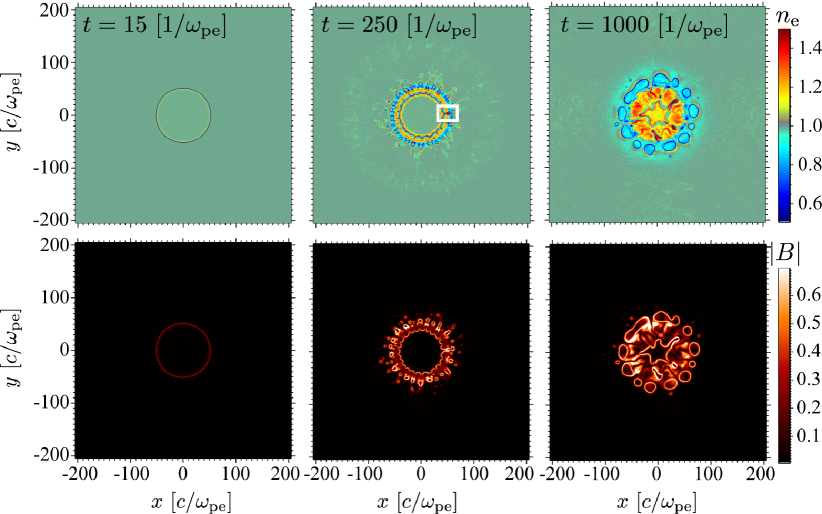
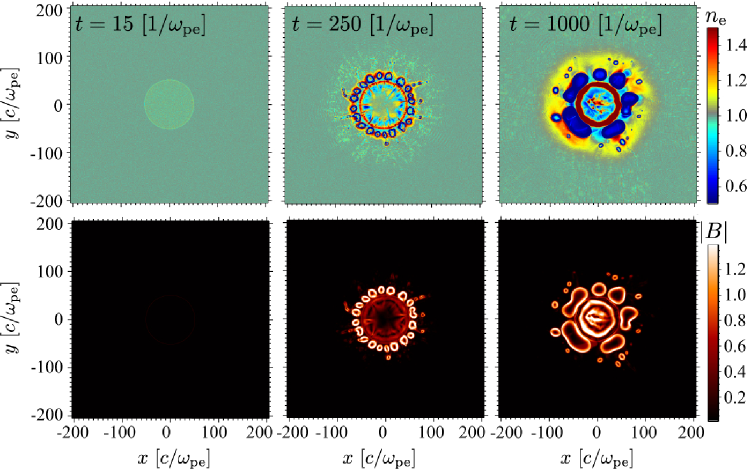
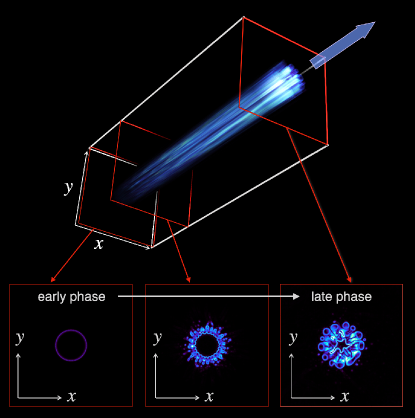
Figure 1 demonstrates the overview of the time sequence of our PIC simulation in the entire simulation box. Although the magnetic field is initially zero, the MI generates and subsequently amplifies the magnetic field (bottom panels), as shown in the next paragraph in detail. The electrons concentrate in the center of the jet region, as the relativistic jet propagates (top panels). This is due to the combination of magnetic pinching force induced by MI and the high energy electron ejections by the subsequent, intermittent MRs. We refer to this new type MR as MI-driven MR. The electrons are accelerated via the MRs. Since the high energy electrons concentrate in the jet-center region together with amplified magnetic field, the jet-center is expected to be bright in the synchrotron emission as discussed in §4.
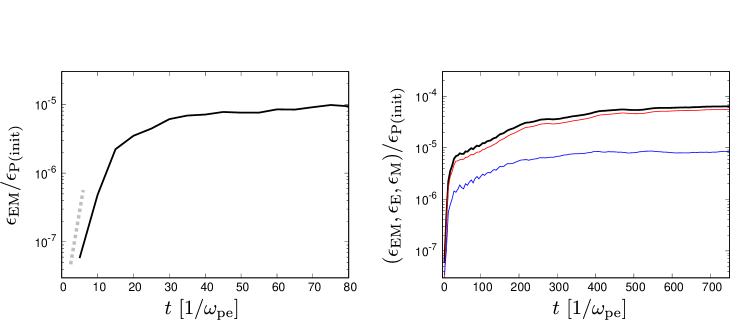
We overview the time evolution of MI in the linear-stage and subsequent MI-driven MRs in the non-linear stage. At the early stage of our simulation (up to ), the MI exponentially grows near the velocity-shear surface as follows: (1) the thermal electron motion across the velocity-shear surface leads to the generation of electric current in direction in the vicinity of the velocity-shear surface. (2) The magnetic fields surrounding the jet center (i.e., high-bulk-Lorentz-factor region) are subsequently generated near the shear surface (left-bottom panel of Figure 1). (3) Then, the electrons experience the Lorentz force, which enhances the electron motion to cross the shear surface. This is the linear stage of MI and the timescale of the instability is consistent with the growth timescale of MI assuming cold plasma obtained by the linear analysis (Alves et al., 2015, see also Appendix). The left panel of Figure 2 shows that the MI exponentially grows in this timescale and the growth rate of the electromagnetic energy is consistent with the maximum linear growth rate obtained by the linear analysis of the MI.
In the non-linear stage of the MI, the channel flow is evidently formed into the direction parallel to the shear surface, as a consequence of the earlier linear growth (Alves et al., 2015). The MR is recurrently induced in this channel-flow region (that is, MI-driven-MR). The channel flow of electrons in the radial direction, which is induced by the Lorentz force due to the magnetic field generated in the azimuthal direction, accompanies the strong electric current in the direction and the anti-parallel configuration of the magnetic field elongated in the radial direction (Figure 3 as discussed later). Then, the MR is triggered near the shear surface and the heated and/or accelerated electrons are ejected towards the regions inside and outside the shear surface as shown in the next paragraph. At the early non-linear stage (), the electromagnetic energy intermittently varies. This is due to the episodic MI-driven MR; the MRs convert the electromagnetic energy amplified by the MI to the electron energy, while the MI recovers the magnetic energy lost by the MRs and forms new electric current sheets followed by subsequent MRs. We note that the MI-driven MR continues to occur, although the time variation of the electromagnetic energy in the whole simulation domain is not remarkable after the early non-linear stage. In the later non-linear stage of MI (), the electromagnetic energy is amplified up to of the initial particle energy in the whole simulation domain. Throughout the simulation, the magnetic energy dominates the electric energy since the simulated plasma is mildly relativistic. These are shown in the right panel of Figure 2.
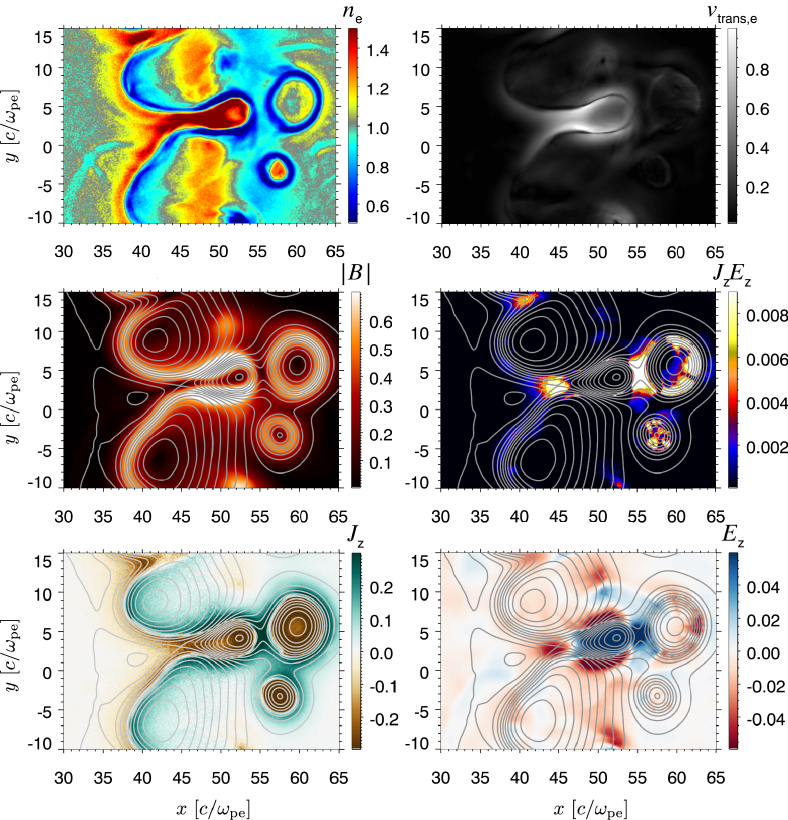
Next, we present the detail of MI-driven MR near the velocity-shear surface. Figure 3 displays magnified view of the electron density, transverse electron velocity, magnetic field strength, energy conversion rate from the electromagnetic field to electrons, electric current density, and electric field at . As a result of the nonlinear evolution of the MI, an elongated current sheet surrounded by anti-parallel magnetic fields grows in the radial direction (see in the bottom-left panel). The direction of the electric current density is anti-parallel to the bulk-jet motion, since the electric current is generated via the MI. Importantly, X-shaped singular points of magnetic field lines (”reconnection points”) appear at the center of the current sheet, in which the reconnection component (-component) of electric field is generated along the electric current density through a microscopic kinetic process (Ishizawa & Horiuchi, 2005), and thus the field energy is strongly converted to electrons. In other words, the subsequent heating and acceleration of the electrons occur via the MI-driven MR. We note that the acceleration of electrons to the highest energy in our simulation is due to the electric field of MRs.
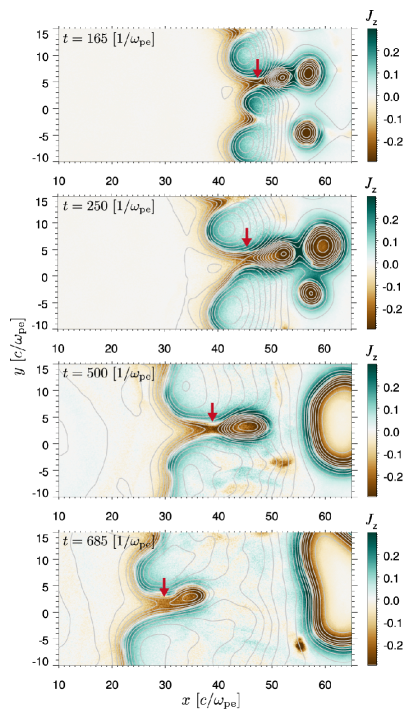
The high-energy electrons concentrate to the region inside the initial velocity-shear surface as the intermittent MI-driven MRs evolve. In Figure 4, we show time evolution of the episodic MI-driven MRs. One can find that the reconnection point moves towards the jet center as time increases, which results in the contraction of the current sheet surrounding the jet center. This is because the electrons which generate the electric current move towards the jet center due to the MRs and the Lorentz force (the magnetic pinch force) as a consequence of MI. As the current sheet contracts, the reconnection point moves towards the jet center. Then, the accelerated and/or heated electrons concentrate in the jet center, i.e., the jet spine is formed.
Here, we confirm that the MRs are physically triggered in our simulation. Figure 5 displays a phase-space (–) plot of electrons at in a region where an MR expected to be taking place at , i.e., the region near the red arrow in the second top panel in Figure 4. One can clearly find the appearance of the hole structure at around and . This hole structure in the phase-space is a consequence of the stochastic motion of electrons in the vicinity of the magnetic neutral sheet, i.e., meandering motion (Speiser, 1965). The hole structure in the phase space is a strong evidence of the MRs (Horiuchi & Ohtani, 2008).
The MI-driven-MRs accelerate electrons. Figure 6 displays the time evolution of electron energy-spectra in the whole computational domain. Initially, the electrons outside the velocity-shear surface shows the Maxwell distribution, while the shifted-Maxwellian appears inside the shear surface because the electrons have the bulk velocity of . One can find that the more electrons are accelerated with time via MI-driven MR and the power-law spectra with narrow energy range appear as explained below.
Just after the MI grows, the electrons outside the shear surface are mainly accelerated and the Maxwell distribution starts to be distorted around at . The MRs intermittently take place with their reconnection points, which move towards the center of the cylindrical jet with time as shown in Figure 4. At , the power-law spectra with narrow energy range is formed at . As shown in the right panel of Figure 6, the highly accelerated particles are distributed inside the initial shear surface, indicating that the jet spine is composed of high energy electrons. The high energy electrons are mainly accelerated to the jet direction (-direction) by virtue of the electric fields of MI-driven MRs. The maximum Lorentz factor of electrons reaches at the end of our simulations in this model.
3.2 Highly Relativistic Bulk Speed Model
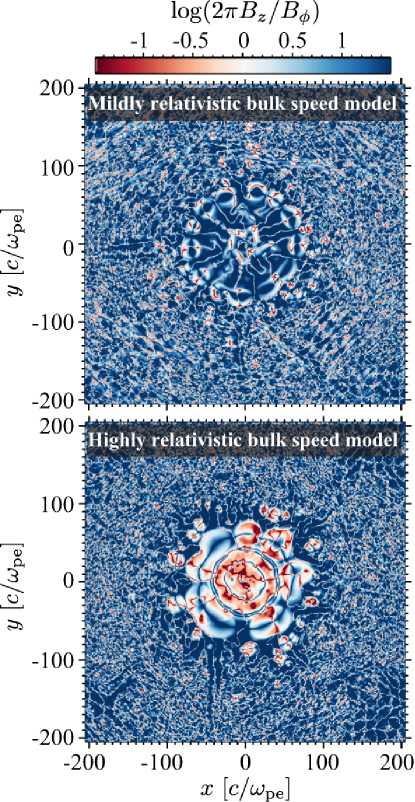
A model with highly relativistic bulk speed is examined here. Figure 7 displays the time evolution of the MI-driven MRs in the plasma with high velocity shear. As in the case of moderately relativistic bulk speed model, the MI-driven MR occurred. The highly relativistic shear flow brings much stronger magnetic field via the MI compared with the moderately relativistic former model. The electron number density in a part of the high-bulk-Lorentz-factor region () is small, while it is high in the rest of the high-bulk-Lorentz-factor region (i.e., messy region in the center and the high density ring-like region )) at . This is due to the strongly amplified magnetic field near the strong velocity-shear region, since the stronger magnetic field results in the smaller gyro-radius of electrons and a smaller number of the electrons move towards the jet center. It should be noted that the generated magnetic field will be so strong that the kink instability can occur, which will be discussed in §4.
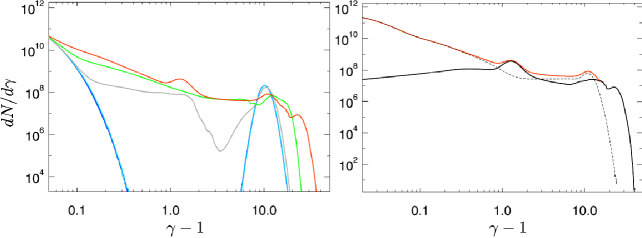
Figure 8 shows the time evolution of the electron spectrum. By virtue of the strong velocity shear, which is an energy source of the electron acceleration via MI-driven MRs, the electrons are accelerated up to (left panel), which is significantly larger than that of the mildly relativistic case, in which the electrons are accelerated up to . The accelerated electrons exists inside the initial velocity-shear surface (right panel) as is the same as the moderately relativistic bulk velocity model. Since we focus on the discovery of the MI-driven MR, the detailed acceleration mechanism of electrons will be left as a future work.
4 Summary and Discussion
We carried out two dimensional PIC simulations to study the kinetic plasma dynamics in the transverse direction of the relativistic jet with velocity-shear surface. Although we start the simulation with no initial magnetic field, the magnetic fields are generated by MI near the velocity-shear surface, and it is discovered that intermittent MRs induced by MI, which we refer to as ”MI-driven MRs”, occur in the transverse plane of the jet. As a result, the number density of high energy electrons increases with time in the jet-center region accompanying with the generation and amplification of magnetic field by MI. The maximum Lorentz factor of the accelerated electrons increases with the initial bulk Lorentz factor inside the velocity-shear surface.
We discuss the consistency of our numerical setup for the dynamics of MI-driven MRs with no initial magnetic field. The necessary condition is that the Larmor radius of the electrons in the jets in which the MI-driven MRs are expected to take place is larger than the length of our simulation domain. In this case, the effects of the initial magnetic field can be reasonably neglected. The Larmor radius of the electrons before the acceleration via the MI-driven MRs (i.e., ) is expected to be cm, as the magnetic field could be dissipated and its strength would be mG (e.g., MAGIC Collaboration et al., 2020) while that near the black hole is indicated to be G (Event Horizon Telescope Collaboration, 2021). On the other hand, the simulation box size is cm. This is because the electron skin depth in the jet can be roughly estimated to be , where the number density of electrons of the distant jet will be less than that near the black hole (see, e.g., Event Horizon Telescope Collaboration, 2019; Kawashima et al., 2021). Our simulation setup with no initial magnetic field will be reasonable, at least to study the dynamics of MI-driven MR itself, because of , while the PIC simulation with initial magnetic field will be performed in forthcoming papers to confirm the results.
In the highly relativistic bulk speed model, the stronger magnetic field surrounding the jet-center region is generated, which results in less concentration of the accelerated electrons in the jet center by suppressing the electron motion across the strong magnetic field via the Lorentz force. However, the strong magnetic field surrounding the high-bulk-Lorentz-factor region can be unstable against the kink instability. Here, we consider the Kruskal–Shafranov stability criterion which proposes that the jet is kink unstable if is satisfied, where , , and are the cylindrical radius of the jet, typical length scale of the jet in the direction, magnetic field strength in the direction, and the magnetic field strength in the azimuthal direction of the cylindrical jet, respectively. Here, is the azimuthal angle in the cylindrical coordinate system defined as . Figure 9 shows the distribution of , which means that the plasma jet with , which can be easily realized because of the narrow opening angle of the relativistic jets observed in active galactic nuclei, can be unstable in the region with (i.e., red colored region). Figure 9 represents that the jetted plasma can be kink unstable for the highly relativistic bulk speed model (bottom panel), while it will be stable for the mildly relativistic bulk speed model (top panel). In the highly relativistic bulk Lorentz factor model, strong MI growth results in the generation of intense magnetic field in the -direction, which suppresses the transverse motion of electrons (i.e., suppression of the generation of the magnetic field in -direction). As a consequence, the electric current in -direction is suppressed and the generation of the magnetic field in the -direction is reduced. It can be proposed that the highly relativistic shear plasma flow will generate strong magnetic fields with accompanying the MI-driven MRs, and as a consequence, the large scale MRs with drastic deformation of jet structure triggered by the kink-instability and accelerate the electrons more. After the large scale MRs, it is expected that the MI-driven MRs will restart to transport the electrons towards the jet center because a part of the strong magnetic field surrounding the jet center will disappear just after the large scale MRs induced by the kink instability, although 3D PIC simulations are needed to confirm the expected behavior of the plasma including kink instability.
Shown in Appendix (Figure 11), the MI will dominate the electron-scale Kelvin-Helmholtz instability in our relativistic velocity-shear flow, however, it may not be completely negligible. We should emphasize that the three-dimensional effects can lead to the significant destruction/suppression of the large-scale, coherent plasma structure shown in our two-dimensional simulations, since non-linear behavior of structure formation often depends on the spatial dimension of the system. Three-dimensional PIC simulations to simultaneously solve the MI-driven MRs, electron-scale Kelvin-Helmholtz instability, kink instability, and others are out of the scope of this paper, so that these remain as future works.
It should be mentioned that there is a gap between the length-scales of PIC simulations and realistic jets in the universe. The observed jet-spine seems to have the scale with cm, while the diameter of high-Lorentz-factor region in our simulation is cm, i.e., the length-scale of the simulation is much smaller than that of the observed jet-spine. The MI-driven MR may not directly but indirectly form the jet spine via triggering an MHD scale mechanism. Another possible scenario is that the MI-driven MRs continuously occur with moving their reconnection points towards inward until the high energy electrons reaches near the jet-center (see Figure 4). The intermittent MRs would enable the electrons to reach the realistic jet-center because of the acceleration of the electrons and the prompt change of the magnetic field topology during MRs, while the initial and amplified magnetic field may arrest the approach of the electrons towards the jet-center. Alternatively, successive shear-driven acceleration mechanism may work on the electrons after the acceleration via MI-driven MRs, and helps the electrons to penetrate the jet-center region, which is motivated by the recent work on the shear-driven acceleration of electrons after the MRs induced by Kelvin-Helmholtz instability (Sironi et al., 2021). More realistic studies with long term PIC simulations with larger simulation box including a finite initial magnetic field and a finite width of shear-layer, which will give us more insight whether the above scenario solving the scale gap problem is correct, remain as a future work.
Here, in order to demonstrate the possible brightening in the jet-center region as a consequence of the MI-driven MRs, Figure 10 displays the electron density multiplied by the strength of the magnetic field, which qualitatively agrees with the synchrotron emissivity, in the moderately relativistic bulk speed model. One may find that the jet-center region becomes brighter with time. In terms of the timescale, if the straightforward extrapolation of the length scale discussed above is correct and is also applicable to non-linear structure-formation in three-dimensional plasma, the concentration of electrons in the jet spine triggered by MI is not inconsistent with the observation of M87. The typical propagation timescale of the relativistic jet up to the distance with appearance of triple-ridge structure for M87 () is s. On the other hand, the growth timescale of MI is much shorter than the jet propagation timescale. In practice, the structure-formation timescale via the MI-driven MR should be estimated by , where is the radius of high-bulk-Lorentz-factor region and the transverse electron velocity is roughly equal to the initial thermal velocity of electrons. Since the radius of M87 jet at from the BH is (Asada & Nakamura, 2012; Nakamura & Asada, 2013; Hada, 2017) and the thermal velocity of electrons is expected to be , the formation timescale of the jet spine is estimated to be (several) s.222The important point is the ratio of the jet-spine width to the distance from the BH. If this ratio is kept, the same scenario can be applied, even if the jet-spine is found in the region closer to the BH. Hence, with respect to the timescale, our scenario of the jet-spine formation via MI-driven MR is consistent with the observed M87 jet.
If the MI-driven MRs take place in the relativistic jets, the azimuthal component of magnetic fields surrounding the jet spine will be generated via the MI. The linearly polarized radio emission will be detected by VLBI observations. The shear-driven acceleration through the MI-driven MRs may also generate the VHE gamma-ray emissions.
Appendix A The maximum linear growth rate of the Mushroom instability
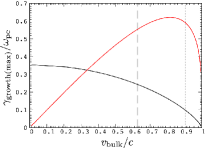
We demonstrate the maximum linear growth rate of the MI in the appendix. Fist of all, the maximum growth rate of MI estimated for our simulations is shown in Figure 11 with including that of electron-scale Kelvin-Helmholtz instability for comparison, by following Alves et al. (2015). In both of our moderately and highly relativistic bulk velocity models, the bulk Lorentz factor is high enough that the MI dominates the electron-scale Kelvin-Helmholtz instability. The linear analysis is carried out in the frame with zero-net-velocity in the whole simulation domain, i.e., the flow velocity has the same absolute value but opposite direction against the velocity-shear surface and . The maximum growth rate of the MI is , where is the the Lorentz factor of . Our moderately relativistic bulk velocity model of corresponds to , where these are related by and . It should be noted that this dispersion relation is derived by assuming that the number density of the plasma is uniform in the zero-net-velocity frame, although in our simulations it is uniform in the rest frame of the plasma outside the velocity-shear surface and the plasma has moderately high thermal velocity (. For the moderately relativistic bulk velocity model, however, the relative velocity between these frame is and the Lorentz factor is almost unity (), so that the deviation is expected to be small enough in the context of the Lorentz contraction.333For the highly relativistic bulk velocity model, the discrepancy would be not negligible since the corresponding Lorentz factor is , i.e., the density inside and outside the velocity-shear surfaces are enhanced and reduced by the factor of . The plasma is also assumed to be cold in the linear analysis while our simulation assumed to be moderately warm (initial thermal velocity is set to be ). The finite thermal motion will slightly modify the maximum growth rate of our simulations but still agree with the linear analysis results as shown in Figure 2.
References
- Alves et al. (2014) Alves, E. P., Grismayer, T., Fonseca, R. A., & Silva, L. O. 2014, New Journal of Physics, 16, 035007, doi: 10.1088/1367-2630/16/3/035007
- Alves et al. (2015) —. 2015, Phys. Rev. E, 92, 021101, doi: 10.1103/PhysRevE.92.021101
- Alves et al. (2012) Alves, E. P., Grismayer, T., Martins, S. F., et al. 2012, ApJ, 746, L14, doi: 10.1088/2041-8205/746/2/L14
- Alves et al. (2018) Alves, E. P., Zrake, J., & Fiuza, F. 2018, Phys. Rev. Lett., 121, 245101, doi: 10.1103/PhysRevLett.121.245101
- Asada & Nakamura (2012) Asada, K., & Nakamura, M. 2012, ApJ, 745, L28, doi: 10.1088/2041-8205/745/2/L28
- Asada et al. (2016) Asada, K., Nakamura, M., & Pu, H.-Y. 2016, ApJ, 833, 56, doi: 10.3847/1538-4357/833/1/56
- Birdsall & Langdon (1991) Birdsall, C. K., & Langdon, A. B. 1991, Plasma Physics via Computer Simulation
- Biskamp (2000) Biskamp, D. 2000, Magnetic Reconnection in Plasmas, Vol. 3
- Blandford et al. (2019) Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467, doi: 10.1146/annurev-astro-081817-051948
- Chael et al. (2019) Chael, A., Narayan, R., & Johnson, M. D. 2019, MNRAS, 486, 2873, doi: 10.1093/mnras/stz988
- Davelaar et al. (2020) Davelaar, J., Philippov, A. A., Bromberg, O., & Singh, C. B. 2020, ApJ, 896, L31, doi: 10.3847/2041-8213/ab95a2
- Davelaar et al. (2019) Davelaar, J., Olivares, H., Porth, O., et al. 2019, A&A, 632, A2, doi: 10.1051/0004-6361/201936150
- Drake et al. (2006) Drake, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553, doi: 10.1038/nature05116
- Edgington-Mitchell et al. (2014) Edgington-Mitchell, D., Honnery, D. R., & Soria, J. 2014, Physics of Fluids, 26, 096101, doi: 10.1063/1.4894741
- Esirkepov (2001) Esirkepov, T. Z. 2001, Computer Physics Communications, 135, 144, doi: 10.1016/S0010-4655(00)00228-9
- Event Horizon Telescope Collaboration (2019) Event Horizon Telescope Collaboration. 2019, ApJ, 875, L5, doi: 10.3847/2041-8213/ab0f43
- Event Horizon Telescope Collaboration (2021) —. 2021, ApJ, 910, L13, doi: 10.3847/2041-8213/abe4de
- Ghisellini et al. (2005) Ghisellini, G., Tavecchio, F., & Chiaberge, M. 2005, A&A, 432, 401, doi: 10.1051/0004-6361:20041404
- Gourgouliatos & Komissarov (2018) Gourgouliatos, K. N., & Komissarov, S. S. 2018, Nature Astronomy, 2, 167, doi: 10.1038/s41550-017-0338-3
- Grismayer et al. (2013) Grismayer, T., Alves, E. P., Fonseca, R. A., & Silva, L. O. 2013, Phys. Rev. Lett., 111, 015005, doi: 10.1103/PhysRevLett.111.015005
- Hada (2017) Hada, K. 2017, Galaxies, 5, 2, doi: 10.3390/galaxies5010002
- Hada et al. (2011) Hada, K., Doi, A., Kino, M., et al. 2011, Nature, 477, 185, doi: 10.1038/nature10387
- Hockney & Eastwood (1988) Hockney, R. W., & Eastwood, J. W. 1988, Computer simulation using particles
- Horiuchi & Ohtani (2008) Horiuchi, R., & Ohtani, H. 2008, Communications in Computational Physics, 4, 496
- Horiuchi & Sato (1999) Horiuchi, R., & Sato, T. 1999, Physics of Plasmas, 6, 4565, doi: 10.1063/1.873744
- Ishizawa & Horiuchi (2005) Ishizawa, A., & Horiuchi, R. 2005, Phys. Rev. Lett., 95, 045003, doi: 10.1103/PhysRevLett.95.045003
- Kawashima et al. (2021) Kawashima, T., Toma, K., Kino, M., et al. 2021, ApJ, 909, 168, doi: 10.3847/1538-4357/abd5bb
- Koide et al. (1999) Koide, S., Shibata, K., & Kudoh, T. 1999, ApJ, 522, 727, doi: 10.1086/307667
- Laing & Bridle (2002) Laing, R. A., & Bridle, A. H. 2002, MNRAS, 336, 328, doi: 10.1046/j.1365-8711.2002.05756.x
- Liang et al. (2013) Liang, E., Boettcher, M., & Smith, I. 2013, ApJ, 766, L19, doi: 10.1088/2041-8205/766/2/L19
- MAGIC Collaboration et al. (2020) MAGIC Collaboration, Acciari, V. A., Ansoldi, S., et al. 2020, MNRAS, 492, 5354, doi: 10.1093/mnras/staa014
- Matsumoto & Masada (2019) Matsumoto, J., & Masada, Y. 2019, MNRAS, 490, 4271, doi: 10.1093/mnras/stz2821
- McKinney (2006) McKinney, J. C. 2006, MNRAS, 368, 1561, doi: 10.1111/j.1365-2966.2006.10256.x
- Mertens et al. (2016) Mertens, F., Lobanov, A. P., Walker, R. C., & Hardee, P. E. 2016, A&A, 595, A54, doi: 10.1051/0004-6361/201628829
- Mizuno et al. (2007) Mizuno, Y., Hardee, P., & Nishikawa, K.-I. 2007, ApJ, 662, 835, doi: 10.1086/518106
- Moritaka et al. (2016) Moritaka, T., Kuramitsu, Y., Liu, Y.-L., & Chen, S.-H. 2016, Physics of Plasmas, 23, 032110, doi: 10.1063/1.4942028
- Nakamura & Asada (2013) Nakamura, M., & Asada, K. 2013, ApJ, 775, 118, doi: 10.1088/0004-637X/775/2/118
- Nakamura et al. (2018) Nakamura, M., Asada, K., Hada, K., et al. 2018, ApJ, 868, 146, doi: 10.3847/1538-4357/aaeb2d
- Nishikawa et al. (2003) Nishikawa, K. I., Hardee, P., Richardson, G., et al. 2003, ApJ, 595, 555, doi: 10.1086/377260
- Nishikawa et al. (2016) Nishikawa, K. I., Frederiksen, J. T., Nordlund, Å., et al. 2016, ApJ, 820, 94, doi: 10.3847/0004-637X/820/2/94
- Parker (1979) Parker, E. N. 1979, Cosmical magnetic fields. Their origin and their activity
- Porth & Komissarov (2015) Porth, O., & Komissarov, S. S. 2015, MNRAS, 452, 1089, doi: 10.1093/mnras/stv1295
- Ripperda et al. (2020) Ripperda, B., Bacchini, F., & Philippov, A. A. 2020, ApJ, 900, 100, doi: 10.3847/1538-4357/ababab
- Sanders (1983) Sanders, R. H. 1983, ApJ, 266, 73, doi: 10.1086/160760
- Sironi et al. (2021) Sironi, L., Rowan, M. E., & Narayan, R. 2021, ApJ, 907, L44, doi: 10.3847/2041-8213/abd9bc
- Sironi & Spitkovsky (2014) Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21, doi: 10.1088/2041-8205/783/1/L21
- Speiser (1965) Speiser, T. W. 1965, J. Geophys. Res., 70, 4219, doi: 10.1029/JZ070i017p04219
- Tchekhovskoy et al. (2011) Tchekhovskoy, A., Narayan, R., & McKinney, J. C. 2011, MNRAS, 418, L79, doi: 10.1111/j.1745-3933.2011.01147.x
- Toma & Takahara (2012) Toma, K., & Takahara, F. 2012, ApJ, 754, 148, doi: 10.1088/0004-637X/754/2/148
- Walker et al. (2018) Walker, R. C., Hardee, P. E., Davies, F. B., Ly, C., & Junor, W. 2018, ApJ, 855, 128, doi: 10.3847/1538-4357/aaafcc
- Yamada et al. (2010) Yamada, M., Kulsrud, R., & Ji, H. 2010, Reviews of Modern Physics, 82, 603, doi: 10.1103/RevModPhys.82.603
- Zenitani & Hoshino (2001) Zenitani, S., & Hoshino, M. 2001, ApJ, 562, L63, doi: 10.1086/337972