Nearly optimal coloring of some -free graphs
Abstract
A class of graphs is -polydet if has a polynomial binding function and there is a polynomial time algorithm to determine an -coloring of . Let and denote a path and a cycle on vertices, respectively. A bull consists of a triangle with two disjoint pendant edges, a hammer is obtained by identifying an end of with a vertex of a triangle, a fork+ is obtained from by subdividing an edge twice. Let be a bull or a hammer, and be a or a fork+. We determine all -free graphs without clique cutsets and universal cliques, and present a close relation between -free graphs and the Petersen graph. As a consequence, we show that the classes of -free graphs are -polydet with nearly optimal linear binding functions.
Key words and phrases: -free, decomposition, chromatic number, clique number
AMS 2000 Subject Classifications: 05C15, 05C75
1 Introduction
All graphs considered in this paper are finite and simple. We follow [2] for undefined notations and terminologies. Let be a graph, let , and let and be two subsets of . Let be the set of edges with one end in and the other in . We say that is complete (resp. anticomplete) to if (resp. ), and say that is complete (resp. anticomplete) to if each vertex of is complete (resp. anticomplete) to .
Let be the set of vertices adjacent to , . Let has a neighbor in , and . Let be the subgraph of induced by . If it does not cause any confusion, we usually omit the subscript . For , , we write if , and write if . For and , let .
We say that a graph contains a graph if is isomorphic to an induced subgraph of , and say that is -free if it does not contain . For a family of graphs, is -free if is -free for every .
A clique (resp. stable set) of is a set of mutually adjacent (resp. non-adjacent) vertices in . The clique number (resp. stability number) of , denoted by (resp. ), is the maximum size of a clique (resp. stable set) in .
Let be a graph with . A clique blowup of is any graph such that can be partitioned into cliques, say , such that is complete to in if in , and is anticomplete to in if in . Let be a clique blowup of . We call a -clique blowup of if for all , and call a nonempty clique blowup of if for all . Under this literature, an induced subgraph of can be viewed as a clique blowup of with of sizes 1 or 0, for all .
Let be a positive integer. A -coloring of is a function such that if . The chromatic number of is the minimum number for which has a -coloring. A graph is perfect if all its induced subgraphs satisfy . An induced cycle of length at least 4 is called a hole, and its complement is called an antihole. A -hole is a hole of length . A hole or antihole is odd or even if it has odd or even number of vertices. In 2006, Chudnovsky et al [12] proved the Strong Perfect Graph Theorem.
Theorem 1.1
[12] A graph is perfect if and only if it is (odd hole, odd antihole)-free.
Let be a hereditary family of graphs. If there is a function such that for each graph in , then we say that is -bounded, and call a binding function of [19]. Gyárfás [19], and Sumner [35] independently, conjectured that the class of -free graphs is -bounded for any forest . Interested readers are referred to [28, 31, 32] for its related problems and progresses.
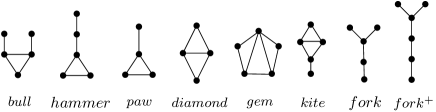
Some configurations used in this paper such as paw, diamond, gem, kite, fork, and fork+ are shown in Figure 1. Since every antihole with at least six vertices has a 4-hole , the -boundedness of subclasses of -free graphs are studies extensively. Choudum et al [6] proved if is -free. Chudnovsky et al [10] proved if is (fork, )-free. Gasper and Huang [16] proved that for -free graph , and Karthick and Maffray [22] improved the upper bound to . Huang [20] proved that if is -free, which is optimal. Generalize some results of Choudum et al [7], the current authors and Wu proved [4] that if is (, diamond)-free, and if is (, gem)-free, and they also proved that if is (, kite)-free.
Motivated by a new concept Polyanna introduced by Chudnovsky et al [8], and by the above mentioned linear binding function of subclasses of -free graphs, we studied , bull)-free graphs and , hammer)-free graphs in [5], and proved the following conclusion.
Theorem 1.2
[5] Let be a -bounded class of graphs. Let be a bull or a hammer, and let be a connected -free graph which has no clique cutsets or universal cliques. Then,
-
•
is a clique blowup of some graph of girth at least if is a bull, and has girth at least 5 if is a hammer.
-
•
-free graphs of are always linearly -bounded.
Note that the paths and stars are the two extremal classes of trees. There are a lot of results on binding functions of -free or -free related graphs. Gyárfás [19] proved that for all -free graphs, and this upper bound was improved to by Gravier et al [18]. On -free graphs, its best known binding function,due to Scott et al [33], is for . Chudnovsky et al [13] proved that a connected -free graphs with satisfies . Liu et al [24] proved that if is fork-free, which answers a problem raised in [21, 28]. Chudnovsky et al [10] proved that if is (fork, )-free. Interested readers can find more results and problems on binding functions of subclasses of fork-free graphs in [9, 21, 28, 37].
Let be a bull or a hammer. From Theorem 1.2, both -free graphs and (, fork-free graphs are linearly -bounded. We can do better on these two classes of graphs. In this paper, we prove the following Theorems 1.3 and 1.4 on the structural decompositions of (, fork-free graphs and -free graphs, which show that these graphs are closely related to the Petersen graph. Then, we deduce polynomial time algorithms to optimally color these graphs.
Let be the graphs as shown in Figure 2, where is just the Petersen graph, and the parameter and appeared in and are positive integers. When , we particularly refer to the graph as . Let and, let . A clique cutset of is a clique in such that has more components than , and a cutvertex is a clique cutset of size 1. A clique is call a universal clique of if is complete to .
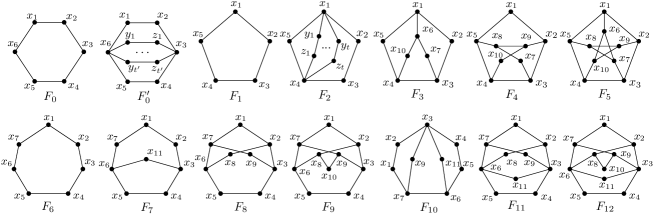
Theorem 1.3
Let be a bull or a hammer, and let be a connected -free graph without clique cutsets or universal cliques. Then, if is a hammer, and is a nonempty clique blowup of a graph in if is a bull.
Theorem 1.4
Let be a bull or a hammer, and let be a connected -free graph without clique cutsets or universal cliques. Then, if is a hammer, and is a nonempty clique blowup of a graph in if is a bull.
It is easy to check that is isomorphic to . Since is just the Petersen graph, we have that can be obtained from the Petersen graph by deleting a vertex and adding a path of length 3 to join some two vertices of degree 3. Since , , , and are all induced subgraphs of , and since are all induced subgraphs of , Theorems 1.3 and 1.4 assert that (, fork-free graphs and -free graphs are closely related to the Petersen graph, where is a bull or a hammer.
Notice that all graphs in are 3-colorable, and clique cutsets and universal cliques are reducible in coloring of graphs. As an immediate consequence of Theorems 1.3 and 1.4, one can prove the following Corollary 1.1 by a simple induction on .
Corollary 1.1
Let be a or a fork+, and let be a , hammer)-free graph. Then, .
Let be a positive integer. We use to denote the -clique blowup of a graph . We can easily verify that both and are (, bull)-free for being a or a fork+, and is (, fork+, bull)-free. Also, we have that , , and . We will show that by excluding and further, (, bull)-free graphs satisfy if is a , and if is a fork+.
Theorem 1.5
Let be a or a fork+, and let be a , bull)-free graph. Then,
-
•
, and if is further -free.
-
•
if and is further -free.
-
•
if and is further -free.
Where all the bounds , and are reachable.
A class of graphs is said to be -polydet [31] if has a polynomial binding function and there is a polynomial time algorithm to determine an -coloring for each .
Suppose that has a clique cutset , and suppose that is partitioned into two nonempty subsets and that are anticomplete to each other. Let and . By repeating this procedure to both and until all the resulted subgraphs have no clique cutsets, can be partitioned into a collection of subsets of which each induces a subgraph without clique cutsets. We can use a binary tree to represent this process, and call a clique-cutsets-decomposition.
Tarjan [34] showed that for a connected graph with vertices and edges, its clique-cutsets-decomposition (not necessarily unique) can be found in times. Tarjan also showed that if the maximum weight clique of each subgraph induced by a leaf of can be found, then one can find the maximum weight clique of in times.
Chudnovsky et al [11] showed that an optimal coloring of any -free perfect graph can be found in . If has maximal cliques, then we can take times to find them [26, 36]. Since a -free graph has maximal cliques [1, 15], we can find the maximum weight cliques for any -free graph in times. Let be a or a fork+, and let be a bull or a hammer. By Theorems 1.3 and 1.4, if is a -free graph, then in its clique-cutsets-decomposition, each leaf represents a subset of vertices which induces a well-defined graph with a universal clique (maybe empty). Applying Tarjan’s algorithm, we can, in at most times, find a nearly optimal coloring and the maximum weight cliques of a )-free graph. Therefore, we have
Corollary 1.2
Let be a or a fork+, and let be a bull or a hammer. Then, )-free graphs are -polydet with linear binding functions.
2 Proof of Theorem 1.3
This section is devoted to prove Theorem 1.3. We begin from (fork-free graphs.
Lemma 2.1
Let be a connected perfect (fork)-free graph without clique cutsets. If is not a complete graph, then is an even-hole.
Proof. By Theorem 1.1, is odd-hole-free. If is even-hole-free, then is a chordal graph, and so is complete as it has no clique cutsets. Suppose that has an even-hole, say , where . If , let and suppose, without loss of generality, that , then is anticomplete to , and so is a fork+, a contradiction. Therefore, , and so is an even-hole.
Lemma 2.2
Let be a connected imperfect -free graph without clique cutsets. If is not an odd-hole, then is isomorphic to a graph in {}.
Proof. Since is not perfect, it follows from Theorem 1.1 that has an odd-hole. Let be an odd-hole of , where , and let and . Since is not an odd hole, we have that . Without loss of generality, suppose that has a vertex adjacent to .
Suppose that . Then, is anticomplete to to avoid a or , and to avoid an induced fork+ on . But then, , which forces to be an induced fork+, a contradiction. Therefore, . During the following proof of Lemma 2.2, every subscript is understood to be modulo 5.
Since has girth at least 5, we have that each vertex of has exactly one neighbor in . Let . We define , and let . Then, , and .
If , then is a 4-hole for some and . If is not complete to , then for some and , is a fork+. If has two vertices, say and , then is a triangle if , and is a fork+ if . This shows that
| , is anticomplete to and complete to . | (1) |
In this section, we always assume that if . We show next that
| (2) |
Suppose . We may assume, by symmetry, that for some . Let be the component of that contains . If , then by (1), and so is a fork+. If , then by (1), and so is a fork+. This shows that . Since is not a cutvertex of , we may assume by symmetry that and . With a similar argument as above used to deal with , we can show that . Then, is a clique cutset of . Therefore, (2) holds.
Now, we have that , where . Suppose, without loss of generality, that . Since is anticomplete to by (1), and since is not a cutvertex, we may by symmetry assume that . Then, by (1).
If , then as otherwise is a cutvertex by (1), and thus is isomorphic to . Suppose by symmetry that . By (1), and . If and , then by (1), we have , , and , and thus is isomorphic to . If , then is isomorphic to . If and , then by (1), and is isomorphic to . The same happens if and . Therefore, is isomorphic to a graph in . This completes the proof of Lemma 2.2.
Lemma 2.3
Let be a connected (fork+,)-free graph without clique cutsets. If is not a complete graph, then is in .
3 Proof of Theorem 1.4
The aim of this section is to prove Theorem 1.4, which characterizes the structures of -free graphs and -free graphs. First, we discuss -free graphs.
Lemma 3.1
Let be a connected imperfect -free graph without clique cutsets. Then is isomorphic to a graph in (see Figure 2).
Proof. Since is not perfect, it follows from Theorem 1.1 that contains a 5-hole. Let be a 5-hole of . Let , and let . Since has no triangles and no s, we have that each vertex of has exactly one neighbor in . For each , we define that , and let . Then, , and for each ,
| is a stable set, and is anticomplete to , | (3) |
where the summation of subindexes is taken modulo 5.
Next, we prove that
| (4) |
Suppose not. Since is connected, we may assume by symmetry that and such that . Let be the component of which contains . Since is -free and is an induced , we have that is complete to . So, because is triangle-free. If has a neighbor, say , in , then is an induced by (3). So, is anticomplete to , and is anticomplete to by symmetry. If has a neighbor, say , in , then is a 7-hole if , and is a triangle if , both are contradictions. Therefore, is anticomplete to , and is anticomplete to similarly. Since is -free, we have that is the unique neighbor of in , and so is a cutvertex of , a contradiction. This proves (4).
Now, we have that , and is stable by (3). Let be the set of edges between and . We show next that for each ,
| is a matching, and if for some then . | (5) |
Let . It suffices to prove, by symmetry, that has at most one neighbor in , and if has a neighbor in then has no neighbor in . If has two neighbors, say and , in , then a 4-hole appears, a contradiction. If has a neighbor in , and some vertex has a neighbor in , then a 7-hole appears. Both are contradictions. Therefore, (5) holds.
| (6) |
Without loss of generality, we take , and suppose that . Choose with and . By (5), , and thus . Since is a stable set and is not a cutvertex, we have that each vertex in must have a neighbor in . Similarly, each vertex in must have a neighbor in . Therefore, , and so is a matching of size by (5). This proves (6).
Recall that . If then is isomorphic to . So, we suppose that , and suppose, without loss of generality, that . By (5), . Since is not a cutvertex, we may assume by symmetry that . Then, by (5) and (6), and is a matching.
Let and such that . We first consider the case that .
Claim 3.1
If then is isomorphic to a graph in .
Proof. Suppose that is not anticomplete to . Since , we have that is anticomplete to by (5), and and by (6), with both and being matchings. Therefore, . Let . Then, such that .
First, we suppose that . By (5) and (6), . Let . Now, we have that such that by (3). If , then is isomorphic to . Otherwise, let . By (3), , and so must have a neighbor in since cannot be a cutvertex. Without loss of generality, we suppose . Then, for avoiding an induced , and thus by (6), which forces that is isomorphic to .
Similarly, we may deduce that is isomorphic to or if . Next, we suppose that .
If , let , then by (3), and so must have a neighbor, say , in as otherwise is a cutvertex. But now, is an induced as and by (3). A similar contradiction happens if . Therefore, , and . Now we have that is isomorphic to . This proves Claim 3.1.
By Claim 3.1 and by symmetry, we may suppose that . If , let , then by (3), and by the fact that cannot be a cutvertex, must have a neighbor, say , in which forces an induced , a contradiction. So, . Similarly, , and thus as otherwise is a cutvertex. Now, we have that , , and is a matching of size . Therefore, is isomorphic to . This completes the proof of Lemma 3.1.
Lemma 3.2
Let be a connected -free graph without clique cutsets. If contains a -hole, then is isomorphic to a graph in {}.
Proof. Let be a 7-hole of . Let and . For each , we define . During the proof of Lemma 3.2, every subscript is understood to be modulo 7. Let .
Let . Without loss of generality, suppose that . Since has girth at least 5, we have that is anticomplete to , and thus must have a neighbor in to avoid an induced . Obviously, has exactly one neighbor in , and hence if and if . Therefore, , and .
Since has girth at least 5, we have that for each . In this section, we always assume that
| if . | (7) |
Let .
If for some , then has a 4-hole if , and has a triangle if . If and , then has a 4-hole if , and has an induced otherwise. Both are contradictions. Therefore,
| , and either or . | (8) |
Next, we show that
| if and , then and . | (9) |
Without loss of generality, we set . Then, and by (7), and by (8). Let . Then, to avoid an induced . This implies that . Similarly, we can show , and thus . Since is triangle-free, must be a stable set, and any two distinct vertices and in would produce a 4-hole . Therefore, . This proves (9).
Recall that . We may assume that as otherwise is isomorphic to . Without loss of generality, suppose . If , then as otherwise is a cutvertex, and so is isomorphic to . So, we further suppose that .
Since , by (8), we have that , and contains at most two nonempty sets. By symmetry, we may assume that . Then, equals one of the set in . We deal with the three cases separately.
Claim 3.2
If , then is isomorphic to or .
Proof. Suppose that . Then, , and by (8). If , then is isomorphic to . So, we suppose that . Since is connected, we may suppose that by (9). If , we may choose an , then has an induced . Therefore, , and is isomorphic to .
Claim 3.3
If , then is isomorphic to .
Proof. Suppose that . Then, , and by (8). We show that . Suppose not, we may assume by symmetry that . Let , and let be the component of which contains . To avoid an induced which contains , we have that must be complete to , and hence since is triangle-free. But then, to avoid a 4-hole , which forces to be a cutvertex , contradicting the choice of . Therefore, , and must be isomorphic to .
Claim 3.4
If , then is isomorphic to or .
Proof. Suppose that . Then, , and is a stable set by (8). If then is isomorphic to . So, we suppose that .
We show first that . Suppose to its contrary, let , and let be the component of which contains . Then, must be complete to to avoid an induced which contains , and hence since is triangle-free. But now, to avoid a 4-hole , and to avoid a 4-hole , which imply that is a cutvertex of , contradicting the choice of . Therefore, , and so .
By (9), we suppose that . If , we may choose , then has an induced , a contradiction. Therefore, , and is isomorphic to .
Lemma 3.3
Let be a connected perfect ()-free graph without clique cutsets. If is not a complete graph, then is isomorphic to either or .
Proof. Since is perfect, we have that is ()-free by Theorem 1.1. If is -free, then is a chordal graph, which must be complete of order 1 or 2 as it is triangle-free and has no clique cutsets. So, we suppose that has a 6-hole, say . Let and . During the proof of Lemma 3.3, every subscript is understood to be modulo 6. Since has girth at least 6, we have that each vertex of has exactly one neighbor in . For each , we define , and let . Then, .
If , let and suppose by symmetry that for some , then is an induced . Therefore, , and hence .
If then is isomorphic to . Suppose so that , and suppose, without loss of generality, that .
Let . If and , let and , then is an induced if , and is an induced if . Therefore, either or .
Since by our assumption, we have . If , then , which implies that is a clique cutsets. So, , and by symmetry. Now, we have that . Since both and cannot be cutvertices, and since and are both stable, we have that each vertex in must have a neighbor in , and each vertex in must have a neighbor in . If some vertex of has two neighbors, say and , in , then would be a 4-hole. A similar contradiction happens if some vertices of has two neighbors in . Therefore, is a matching of size , and . Now, is isomorphic to . This completes the proof of Lemma 3.3.
Lemma 3.4
Let be a connected -free graph without clique cutsets. If is not a complete graph, then is in .
Proof of Theorem 1.4: Let be a bull or a hammer, and let be a connected -free graph without clique cutsets or universal cliques. By Theorem 1.2, is a clique blowup of some -free graph if is a bull, and is -free if is a hammer. If is a hammer, then is in by Lemma 3.4.
Suppose that is a bull, and suppose that is a nonempty clique blowup of a graph . Since is connected and has no clique cutsets or universal cliques, we have that is connected, not complete, and has no clique cutsets. Therefore, is in by Lemma 3.4.
This completes the proof of Theorem 1.4.
4 Chromatic bound for clique blowups
In this section, we will prove Theorem 1.5. Before that, we first color some special clique blowups. Throughout this section, we will use the following notations. Suppose that is a clique blowup of with . Let be partitioned into cliques , , , , such that is the clique of corresponding to the vertex of . We simply write instead of for . We say that two sets and meet if . Let be a graph and be a stable set, we say is good if it meets every clique of size .
Lemma 4.1
[22] Let be a graph such that every proper induced subgraph of satisfies . Suppose that has a vertex of degree at most , or has a good stable set, or has a stable set such that is perfect. Then, .
In [22], Karthick and Maffray proved that if is a clique blowup of the Petersen graph. Since , , , and are all induced subgraphs of the Petersen graph , we have the following lemma directly.
Lemma 4.2
if is a clique blowup of some graph in .
Lemma 4.3
[25] Clqiue blowups of perfect graphs are perfect.
Recall that we use to denote the nonempty clique blowup of such that each vertex is blewup into a clique of size .
Lemma 4.4
.
Proof. It is certain that , and .
In , we may color , , with (taken modulo 5), and color and , , with and , respectively. Hence, .
For , we can define a 5-coloring as follows: , , , , , , , , . This proves Lemma 4.4.
Lemma 4.5
Let be a graph, with . Let be a clique blowup of with . Then, , and unless .
Proof. It is certain that since . If , then we are done. Suppose . Then, . If , then and , and so , a contradiction. Therefore, . Since , we have that , which implies that .
Lemma 4.6
Let be a triangle-free graph with , and let be a clique blowup of such that for every proper induced subgraph of . Suppose that for every edge with . Then, .
Proof. We may suppose that is a connected imperfect graph. So, . If , then is an induced subgraph of and for every edge . If , then for some edge since is triangle-free. Both contradict while . Therefore, .
Let be a maximal clique of . Then, for some edge since is triangle-free. Choose a subset of such that for each . If , then because . Suppose that . If , then , and thus . If , then . Therefore, .
Since , we have that . This proves Lemma 4.6.
Before proving Theorem 1.5, we present a number of lemmas of which all are proved by induction on the number of vertices. In the following proofs, we always suppose that
| (10) |
We begin from the clique blowups of odd holes.
Lemma 4.7
Let , let , and let be a clique blowup of . Then, for every positive integer , and .
Proof. Let be a positive integer. Then, , and . We can construct a -coloring of by coloring with , where the colors are taken modulo . Therefore, .
Next, we prove by induction on . If there exists for some , then is a clique blowup of a path, and the lemma holds by Lemma 4.3. So, suppose that for all . If is not a maximum clique of , let , then is a good stable set of , and so by induction. So, we may suppose by symmetry that is a maximum clique of for all . Now, is a -clique blowup of , and thus . This proves Lemma 4.7.
Lemma 4.8
Let be a clique blowup of (see Figure 2). Then, .
Proof. The lemma holds trivially if is an induced subgraph of . By (10), we have if . If for some , then is perfect, and the lemma follows from Lemma 4.1. So, suppose that if .
To avoid a good stable set , must be a maximum clique of . Similarly, is a maximum clique of also. Let and . Then, and . We can deduce similarly that, for each , if , and if . So, if or for some maximum clique , then we may by symmetry suppose that and .
Suppose . Then, , and thus because , which contradicts that . A similar contradiction happens if . Therefore, for each , if then . By Lemmas 4.4 and 4.6, we have that .
By Lemma 4.2, we have that if is a clique blowup of some graph in . By Lemma 4.7, we have that if is a clique blowup of . Our next lemma deals with the cases for and .
Lemma 4.9
Let be a clique blowup of . Then .
Proof. We take to show the proving procedure. It holds trivially if is an induced subgraph of . We may suppose by Lemma 4.1. By (10), , and are all nonempty. By Lemma 4.1, we may suppose that for each , as otherwise is perfect. Then, for . Since , we have that by Lemma 4.5.
Now, we can easily deduce that, for each edge , if . Lemma 4.9 follows immediately from Lemmas 4.4 and 4.6.
Lemma 4.10
Let be a clique blowup of . Then .
Proof. It holds clearly if is an induced subgraph of . We suppose that by Lemmas 4.1. If or , then is a clique blowup of and we are done by Lemma 4.9. Suppose so that and . By Lemma 4.5, for each .
If , then because is connected and has no clique cutsets. Now, is a clique blowup of , and we are done by Lemma 4.2. So, we further suppose, by symmetry, that and . By Lemma 4.5, we have for each . Now, we can deduce that for all . Therefore, for each edge with . Lemma 4.10 follows from Lemmas 4.4 and 4.6.
Lemma 4.11
Let be a clique blowup of . Then .
Proof. It holds trivially if is an induced subgraph of . We suppose by Lemma 4.1.
If , then as otherwise is a clique cutset of or is a complete graph. Now, is a clique blowup of , and the lemma holds by Lemma 4.2. So, suppose by symmetry that and . With the same argument, we may suppose that and . Since , by Lemma 4.5, we have that for each . Then, for all , and so for each with . Lemma 4.11 follows from Lemmas 4.4 and 4.6.
Lemma 4.12
Let be a clique blowup of . Then .
Proof. It holds clearly if is an induced subgraph of . We suppose that by Lemma 4.1.
If , then is a clique blowup of . If or , then is a clique blowup of . If , then since is connected, imperfect and has no clique cutsets, and is a clique blowup of . Therefore, by Lemmas 4.2, 4.9 and 4.11, we suppose by symmetry that for each .
By Lemma 4.5, for each . Now for all , and so for each edge with . Lemma 4.12 follows from Lemmas 4.4 and 4.6.
Lemma 4.13
Let be a clique blowup of . Then .
Proof. It holds if is an induced subgraph of . We still suppose that by Lemma 4.1.
If or then is a clique blowup of . If then is a clique blowup of . If , then since is connected, imperfect and has no clique cutsets, and so is a clique blowup of . So, we suppose, by Lemmas 4.2, 4.10 and 4.12, that for each .
By Lemma 4.5, for each . Now, for all , and for each edge with . Lemma 4.13 follows from Lemmas 4.4 and 4.6.
Up to now, we have proved the first conclusion of Theorem 1.5, i.e., for all -free graphs. In the following Lemmas 4.144.18, we show that we can do better by excluding some further configurations.
Lemma 4.14
Let be a -free clique blowup of or . Then .
Proof. It holds clearly if is an induced subgraph of or . Let be a clique blowup of or , and suppose that .
Let be a stable set of . If is a good stable set, then by induction. If is perfect, then . We say a graph is good if has a stable set such that either is a good stable set or is perfect. Next, we show that is good, and thus satisfies by induction. Suppose that
| is imperfect for any stable set . | (11) |
Claim 4.1
If is a clique blowup of , then is good.
Proof. It is certain that for each , since cannot be perfect. Since is -free, we have that , and for each . Without loss of generality, we suppose that . For , let such that . Then, is a good stable set of . This proves Claim 4.1.
Next, we suppose that is a clique blowup of . Note that and are both induced subgraphs of . We first discuss the cases that is a clique blowup of or .
Claim 4.2
Let be a clique blowup of or . Then, is good.
Proof. First suppose that is a clique blowup of . Following from (10), we have that for all as otherwise is a clique blowup of and we are done. By Lemma 4.5, for each . Since is -free, we have that . Then, either or , and so is good because both and are perfect, which contradicts (11).
Suppose now that is a clique blowup of . Then, for all as otherwise is a clique blowup of and we are done. By Lemma 4.5, for each . Since is -free, we have that for . Now, is a stable set and is perfect, which contradicts (11). This proves Claim 4.2.
We now suppose that is a nonempty clique blowup of by Claim 4.2. By (11), we have that
| is not a stable set | (12) |
for any three distinct vertices . Particularly, is not a stable set, and so for all .
Since is -free, we suppose, without loss of generality, that . Since none of , , and can be a , and since is not a stable set by (12), we may suppose by symmetry that . Now, we have that for by (12), and so since is not a .
If , then to avoid being stable, and to avoid a on . But then, is a good stable set of as .
Suppose that .Then, for avoiding a stable set on , and for avoiding a on . But then, is a good stable set of as . This completes the proof of Lemma 4.14.
Lemma 4.15
Let be a clique blowup of such that has no good stable sets, and meets no maximum clique of . Then, is isomorphic to . And, if for each and every proper induced subgraph satisfies , then .
Proof. Since meets no maximum clique of , we have that, for each , for avoiding a good stable set , where the subscript are taken modulo 7. Therefore, is isomorphic to .
Let , and suppose that for each . If or 2, then, by Lemma 4.13. So, suppose that .
If , then we can construct a 7-coloring of as follows: , , , , , , , , , , and . So, .
Let be a subset of obtained by taking vertices from for each vertex . Clearly, as shown above. Then, . This proves Lemma 4.15.
Lemma 4.16
Let be a connected -free clique blowup of such that and has no good stable sets. If is not a clique blowup of , then has a stable set such that is perfect, or is isomorphic to for some and for each .
Proof. Suppose that is not a clique blowup of . Clearly, is not a clique blowup of . We divide the proof into several claims.
Claim 4.3
If is a clique blowup of , then the lemma holds.
Proof. For , since is perfect, we may suppose as otherwise is perfect and so we are done. If , then by Lemma 4.5, and so is a . This shows that . Similarly, . Since has no clique cutsets by (10), we may suppose that and as otherwise is a clique blowup of . Again by Lemma 4.5, we have for , and so for . Recall that . Now, meets no maximum clique of , and by Lemma 4.15, is a . This proves Claim 4.3.
Claim 4.4
If is a clique blowup of , then the lemma holds.
Proof. If for some then is a clique blowup of since is a connected imperfect graph without clique cutsets by (10). If for some , then is a clique blowup of . So, we suppose that for all , and so for each by Lemma 4.5. Then, since is -free, and so is a stable set with perfect. This proves Claim 4.4.
Claim 4.5
If is a clique blowup of , then the lemma holds.
Proof. By Claim 4.3, we may suppose that and as otherwise is a clique blowup of . We may also suppose for each as otherwise is a clique blowup of . Then, for each by Lemma 4.5, and since is -free, and so meets no maximum clique of . Now, is by Lemma 4.15. This proves Claim 4.5.
Claim 4.6
If is a clique blowup of , then the lemma holds.
Proof. By (10), we may suppose for each as otherwise is a clique blowup of , or , or , and we are done by Claims 4.3 and 4.5. Then, for each by Lemma 4.5, and since is -free. If , then is a stable set with perfect. If , then since is -free. Hence, meets no maximum clique of , and now is by Lemma 4.15. This proves Claim 4.6.
Now, we may suppose that is a nonempty clique blowup of , as otherwise the statement holds by Claims 4.34.6. Then, by Lemma 4.5, for each , and so since is -free. Now, is a stable set and is perfect. This completes the proof of Lemma 4.16.
Lemma 4.17
Let be a -free clique blowup of . Then, .
Proof. It holds trivially if is an induced subgraph of . We may suppose by induction that , has no good stable sets, and has no stable set such that is perfect.
By Lemma 4.16, either is a clique blowup of , or is isomorphic to for some and for . Recall that is an induced subgraph of . Then, Lemma 4.17 follows from Lemmas 4.14 and 4.15.
Lemma 4.18
Let be a -free clique blowup of . Then .
Proof. The statement holds easily if is an induced subgraph of . Suppose by induction that , has no good stable sets, and has no stable set such that is perfect.
By Lemma 4.16, either is a clique blowup of , or is isomorphic to and for each . If is a clique blowup of , we are done by Lemma 4.14. So, suppose that satisfies the latter. Since is -free, we have that , and so by Lemma 4.17. This completes the proof of Lemma 4.18.
Now, we are ready to prove Theorem 1.5.
Proof of Theorem 1.5: Let be a or a fork+, and let be a (, bull)-free graph. We may suppose that is connected, imperfect and has no clique cutsets or universal cliques. By Theorems 1.4, 1.3, and Lemma 4.3, is a nonempty clique blowup of an imperfect graph, where the graph is in if is a , and is in if is a fork+.
Lemmas 4.2, 4.7, 4.8 and 4.13, assert that , and Lemmas 4.7, 4.14 and 4.17 assert that if is (, bull, )-free.
Suppose finally that is (, fork+, bull, )-free. Then, is a nonempty clique blowup of a graph . If then by Lemma 4.14. If then we are done by Lemma 4.18. If for some or , then by Lemmas 4.3 and 4.7, . This completes the proof of of Theorem 1.5.
Remark: Let denote the maximum degree of . Brooks [3] showed that if is a graph with and , then . Reed [29] conjectured that every graph satisfies . This conjecture is still widely open. Gernet et al [17] showed that Reed’s conjecture holds for graphs with , and Karthick et al [23] showed that Reed’s conjecture holds for graphs with . Combining these two conclusions with Corollary 1.1 and Theorem 1.5, we have immediately the following theorem.
Theorem 4.1
Let be a or a fork+, and let be a bull or a hammer. Then, Reed’s conjecture holds for -free graphs.
References
- [1] V. E. Alekseev, On the number of maximal independence sets in graphs from hereditary classes, Combinatorial-algebraic methods in applied mathematics (V. N. Shevchenko, ed.), Gorkiy University Press, Gorky, 1991, pp. 5-8.
- [2] J. A. Bondy and U. S. R. Murty, Graph Theory, Springer, New York, 2008.
- [3] R. L. Brooks, On colouring the nodes of a network, Proc. Cambridge Philos. Soc. 37 (1941) 194-197.
- [4] R. Chen, D. Wu and B. Xu, Structure and coloring of some )-free graphs, Disc. Appli. Math. 357 (2024) 14-23.
- [5] R. Chen and B. Xu, Structure and linear-Pollyanna of some square-free graphs, arXiv:2407.18506, 2024.
- [6] S. A. Choudum and T. Karthick, Maximal cliques in {}-free graphs, Disc. Math. 310 (2010) 3398-3403.
- [7] S. A. Choudum, T. Karthick and M. M. Belavadi, Structural domination and coloring of some -free graphs, Disc. Math. 344 (2021) 112244.
- [8] M. Chudnovsky, L. Cook, J. Davies and S. Oum, Reuniting -boundedness with polynomial -boundedness, arXiv preprint arXiv:2310.11167, 2023.
- [9] M. Chudnovsky, L. Cook and P. Seymour, Excluding the fork and antifork, Disc. Math. 343 (2020) 111786.
- [10] M. Chudnovsky, S. Huang, T. Karthick and J. Kaufmann, Squeare-free graphs with no inducec fork, The Elec. J. of Combin. 28 (2021) P2-20.
- [11] M. Chudnovsky, I. Lo, F. Maffray, N. Trotignon and K. Vušković, Coloring square-free Berge graphs, J. Combin. Theory Ser. B. 135 (2019) 96-128.
- [12] M. Chudnovsky, N. Robertson, P. Seymour and R. Thomas, The strong perfect graph theorem, Annals of Mathematics 164 (2006) 51–229.
- [13] M. Chudnovsky, P. Seymour, Claw-free graphs vi colouring , J. Combin. Theory Ser. B. 100 (6) (2010) 560-572.
- [14] L. Esperet, Graph colorings, flows and perfect matchings, Habilitation Thesis, Université Grenoble Alpes, 2017.
- [15] M. Farber, On diameters and radii of bridged graphs, Disc. Math. 73 (1989) 249-260.
- [16] S. Gaspers and S. Huang, Linearly -Bounding -free graphs, J. Graph Theory 92 (2019) 322-342.
- [17] D. Gernet and L. Rabern, A computerized system for graph theory, illustrated by partial proofs for graph-coloring problems, Graph Theory Notes of New York LV (2008) 14-24.
- [18] S. Gravier, C. T. Hoáng and F. Maffray, Coloring the hypergraph of maximal cliques of a graph with no long path, Disc. Math. 272 (2003) 285-290.
- [19] A. Gyárfás, On Ramsey covering-numbers, Infinite and Finite Sets 2 (1975) 801-816.
- [20] S. Huang, The optimal -bound for -free graphs, Disc. Math. 347 (2024) 114036.
- [21] T. Karthick, J. Kaufmann and V. Sivaraman, Coloring graph classes with no induced fork via perfect divisibility, The Electronic J. of Combinatorics (2022) 29(3) P3.19.
- [22] T. Karthick and F. Maffray, Square-free graphs with no six-vertex induced path, SIAM J. on Disc. Math. 33 (2019) 874-909.
- [23] T. Karthick and F. Maffray, coloring (gem, co-gem)-free graphs, J. Graph Theory 89 (2018) 288-303.
- [24] X. Liu, J. Schroeder, Z. Wang and X. Yu, Polynomial -binding functions for -broom-free graphs, J. Combin. Theorey Ser. B 162 (2023) 118-133.
- [25] L. Lovász, A characterization of perfect graph, J. Combin. Theorey Ser. B 13 (1972) 95-98.
- [26] K. Makino and T. Uno, New algorithms for enumerating all maximal cliques, Lecture Notes in Compute Science 3111 (2004), 260¨C272.
- [27] B. Randerath, The Vizing bound for the chromatic number based on forbidden Pairs (Ph. D. Thesis), Shaker Verlag, Aachen, (1998).
- [28] B. Randerath and I. Schiermeyer, Vertex colouring and forbidden subgraphs-A survey, Graphs and Combinatorics 20 (2004) 1-40.
- [29] B. Reed, , and , J. Graph Theory 27 (1998) 177-212.
- [30] I. Schiermeyer, Chromatic number of -free graphs: Reed’s conjecture, Disc. Math. 339 (2016) 1940-1943.
- [31] I. Schiermeyer and B. Randerath, Polynomial -binding functions and forbidden induced subgraphs: A survey, Graphs and Combinatorics 35 (2019) 1-31.
- [32] A. Scott and P. Seymour, A survey of -boundedness, J. of Graph Theory 95 (2020) 473-504.
- [33] A. Scott, P. Seymour, S. Spirkl, Polynomial Bounds for Chromatic Numbr. IV: A Near-polynomial Bounds for Excluding the Five-vertex Path, Combinatorica 43 (2023) 845-852.
- [34] R. E. Tarjan, Decomposition by clique separators, Disc. Math. 55 (1985) 221-232.
- [35] D. P. Sumner, Subtrees of a graph and chromatic number. in The Theory and Applications of Graphs, John Wiley & Sons, New York (1981) 557-576.
- [36] S. Tsukiyama, M. Ide, H. Ariyoshi, and I. Shirakawa, A new algorithm for generating all the maximal independent sets, SIAM Journal on Computing 6 (1977), 505-517.
- [37] D. Wu and B. Xu, Perfect divisibility and coloring of some fork-free graphs, Disc. Math. 347 (2024) 114121.