Necessary and sufficient condition for constructing
a single qudit insertion/deletion code
and its decoding algorithm

Taro Shibayama Kaijo Junior and Senior High School, 3-6-1 Okubo, Shinjuku, Tokyo, Japan, 169-0072. E-mail: shibayama@kaijo.ed.jp

Abstract

This paper shows that Knill-Laflamme condition, known as a necessary and sufficient condition for quantum error-correction, can be applied to quantum errors where the number of particles changes before and after the error. This fact shows that correctabilities of single deletion errors and single insertion errors are equivalent. By applying Knill-Laflamme condition, we generalize the previously known correction conditions for single insertion and deletion errors to necessary and sufficient level. By giving an example that satisfies this condition, we construct a new single qudit insertion/deletion code and explain its decoding algorithm.

1 Introduction

Quantum error-correcting codes play an important role in quantum information theory and have been actively studied since the 1990s[22, 3, 5]. The necessary and sufficient condition for quantum error-correction (KL condition) given by Knill-Laflamme in 1997[9] is extremely useful. Quantum errors in KL condition are mainly assumed to be those in which the number of particles does not change before and after the error, such as errors represented by unitary matrices. Recently, however, quantum errors where the number of particles changes, such as quantum insertion/deletion errors, have been attracting attention. Since 2020, several examples of quantum insertion/deletion error-correcting codes have been reported[13, 7, 17, 16, 19, 6, 12], and applications of quantum deletion codes have also been reported recently[1].

Classical insertion/deletion error-correcting codes were first given by Levenstein in 1966[11] and have been actively studied in recent years since then[8, 2, 15, 23, 4]. The most important property of classical codes is the equivalence between the error-correctability of insertion and deletion errors[11, 8]. Although it has been an open problem whether the equivalence holds in quantum theory, it has recently been shown that KL condition for deletions is equivalent to that for insertions of separable states[21]. In this paper, we first prove that KL condition can be used as a necessary and sufficient condition for error-correction even when the number of particles changes before and after the error.

By using KL conditions, the single deletion error-correction condition by Nakayama-Hagiwara[14] and the single insertion error-correction condition by Shibayama-Hagiwara[20] are improved to reach the necessary and sufficient level. These are also greatly generalized in that they give construction conditions not only for binary codes but also for non-binary codes. We also construct a new single qudit insertion/deletion code by giving an example that satisfies these conditions, and explain its decoding algorithm in detail.

This paper is organized as follows. Section 2 describes the variables and notations used in this paper. Section 3 explains that KL condition is also available for errors that change the number of particles. In Section 4, we define single deletion and single insertion errors and show that their correctabilities are equivalent. Section 5 gives necessary and sufficient conditions for the correction of single insertion/deletion errors. In Section 6, we give an example of the code and explain its decoding algorithm. Finally, Section 7 summarizes.

2 Preliminaries

The symbols and notations defined in this section will be used throughout this paper. Let $n$ be a positive integer and $[n]:=\{1,2,\dots,n\}$ . We denote by $\mathbb{C}^{l}$ the $l$ -dimensional vector space over a complex field $\mathbb{C}$ for an integer $l\geq 2$ . Let $|0\rangle,|1\rangle,|2\rangle,\dots,|l-1\rangle$ be the standard orthogonal basis of $\mathbb{C}^{l}$ and $\mathcal{L}:=\{0,1,2,\dots,l-1\}$ . Set $|\bm{x}\rangle:=|x_{1}\rangle\otimes|x_{2}\rangle\otimes\dots\otimes|x_{n}\rangle\in\mathbb{C}^{l\otimes n}$ for an $n$ -tuple $\bm{x}=x_{1}x_{2}\dots x_{n}\in\mathcal{L}^{n}$ . Here $\otimes$ is the tensor product operation. Let $\langle\bm{x}|:=|\bm{x}\rangle^{\dagger}$ denote the conjugate transpose of $|\bm{x}\rangle$ . A positive semi-definite Hermitian matrix of trace $1$ is called a density matrix. We denote by $S(\mathbb{C}^{l\otimes n})$ the set of all density matrices of order $l^{n}$ . An element of $S(\mathbb{C}^{l\otimes n})$ is called an $n$ -qudit quantum state. In this paper, we also use a complex vector $|\phi\rangle\in\mathbb{C}^{l\otimes n}$ for representing a pure state $|\phi\rangle\langle\phi|\in S(\mathbb{C}^{l\otimes n})$ .

For vectors $|0_{L}\rangle,|1_{L}\rangle,|2_{L}\rangle,\dots,|l-1_{L}\rangle\in\mathbb{C}^{l\otimes n}$ of length $1$ orthogonal to each other, the image of a linear map ${\rm Enc}$ that satisfies

	$\displaystyle\|\psi\rangle$	$\displaystyle:=\sum_{i\in\mathcal{L}}\alpha_{i}\|i\rangle\in\mathbb{C}^{l},$
	$\displaystyle\|\Psi\rangle$	$\displaystyle:=\sum_{i\in\mathcal{L}}\alpha_{i}\|i_{L}\rangle\in\mathbb{C}^{l\otimes n},$

and ${\rm Enc}(|\psi\rangle)=|\Psi\rangle$ is called a quantum code, and the map ${\rm Enc}$ is called the encoder for the code. Here, vectors $|0_{L}\rangle,|1_{L}\rangle,|2_{L}\rangle,\dots,|l-1_{L}\rangle\in\mathbb{C}^{l\otimes n}$ are collectively called logical codewords.

Definition 2.1 (Quantum error).

For positive integers $n,n^{\prime}$ , take a set $\mathcal{A}=\{A_{a}\}$ of $l^{n^{\prime}}$ -by- $l^{n}$ matrices such that $\sum_{a}A_{a}^{\dagger}A_{a}$ is the identity operator on $S(\mathbb{C}^{l\otimes n})$ . The map $E:S(\mathbb{C}^{l\otimes n})\rightarrow S(\mathbb{C}^{l\otimes n^{\prime}})$ defined by

\displaystyle E(\rho):=\sum_{a}A_{a}\rho A_{a}^{\dagger}

is called a quantum error. Here, $\mathcal{A}$ is called a Kraus set for the error $E$ and an element of $\mathcal{A}$ is called a Kraus operator.

If $n=n^{\prime}$ and a linear map $E$ is a quantum channel, that is, completely positive and trace-preserving, then $E$ is a quantum error[10]. Definition 2.1 extends the ordinary definition of quantum error to include the case of $n\neq n^{\prime}$ . This allows the case where the number of particles changes before and after an error, such as quantum insertion or quantum deletion, to be considered a quantum error.

If $|\psi\rangle\in S(\mathbb{C}^{l})$ can be obtained by the operations allowed by quantum mechanics on $E({\rm Enc}(|\psi\rangle))\in S(\mathbb{C}^{l\otimes n^{\prime}})$ , then the quantum code $C$ is correctable for the quantum error $E$ . In this paper, the quantum code $C$ is called $\mathcal{A}$ -correcting when $|0\dots 0\rangle\otimes|\psi\rangle\in S(\mathbb{C}^{l\otimes n^{\prime}})$ can be obtained by a finite number of measurements and unitary transformations. When $C$ is an $\mathcal{A}$ -correcting code, the original state $|\psi\rangle\in S(\mathbb{C}^{l})$ can be obtained by deleting the $1$ st through the $(n^{\prime}-1)$ th particles. The decoding in this paper uses the measurement described by the measurement operator $\mathcal{M}=\{M_{k}\}$ that satisfies the completeness relation $\sum_{k}M_{k}^{\dagger}M_{k}=I$ . If we perform a measurement $\mathcal{M}$ under a state $\rho\in S(\mathbb{C}^{l\otimes n^{\prime}})$ , the probability to get an outcome $k$ is $p(k)={\rm Tr}(M_{k}^{\dagger}M_{k}\rho)$ and the after measurement state is $M_{k}\rho M_{k}^{\dagger}/p(k)$ . Here, we denote the sum of the diagonal elements of the square matrix $M$ by ${\rm Tr}(M)$ and the identity operator by $I$ .

3 Correctable condition for quantum errors with non-square Kraus operators

This paper extends the recovery superoperator given in Ref.[9] to apply to non-square Kraus operators.

Definition 3.1 (Recovery superoperator).

The set $\mathcal{R}=\{R_{r}\}$ of square matrices of order $l^{n^{\prime}}$ such that the following two conditions are satisfied is called a recovery superoperator of $(C,\mathcal{A})$ .

•

For any $i\in\mathcal{L}$ , $R_{r}\in\mathcal{R}$ , $A_{a}\in\mathcal{A}$ , there exists $\lambda_{r,a}\in\mathbb{C}$ such that

$\displaystyle R_{r}A_{a}|i_{L}\rangle=\lambda_{r,a}|0\dots 0i\rangle.$
•

$\mathcal{R}$ satisfies the completeness relation $\sum_{r}R_{r}^{\dagger}R_{r}=I$ .

In Theorem 3.2, the case $n=n^{\prime}$ is a well-known fact, and the 3rd condition in the theorem is known as KL condition[9]. Here we extend it and claim that it also holds for the case of non-square Kraus operators.

Theorem 3.2.

For a quantum code $C$ with logical codewords $|0_{L}\rangle,|1_{L}\rangle,|2_{L}\rangle,\dots,|l-1_{L}\rangle\in\mathbb{C}^{l\otimes n}$ and a quantum error $E:S(\mathbb{C}^{l\otimes n})\rightarrow S(\mathbb{C}^{l\otimes n^{\prime}})$ with the Kraus set $\mathcal{A}$ , the following three conditions are equivalent to each other:

${\it 1.}$

The quantum code $C$ is $\mathcal{A}$ -correcting.
${\it 2.}$

There exists a recovery superoperator of $(C,\mathcal{A})$ .
${\it 3.}$

(KL condition) For any $A_{a},A_{b}\in\mathcal{A}$ , and any $i,j\in\mathcal{L}$ , there exists $\mu_{a,b}\in\mathbb{C}$ such that

$\displaystyle\langle i_{L}|A_{a}^{\dagger}A_{b}|j_{L}\rangle=\mu_{a,b}\delta_{i,j},$

where $\delta_{i,j}$ denotes the Kronecker delta function.

In the case of non-square Kraus operators, it may not be possible to correct to the post-encoding state because the number of particles has changed, but it is possible to correct to the pre-encoding state. The concept of the proof of Theorem 3.2 is based on the one by Knill-Laflamme[9], but needs some modifications in this sense.

Proof.

This proof consists of three steps.

(Step 1) First, we prove that ${\it 1}\Rightarrow{\it 2}$ .

Assume that the outcomes obtained in the decoding process are in turn $k_{1},k_{2},\dots,k_{m}$ , and the operators corresponding to them are in turn

\displaystyle U_{0},\mathcal{M}^{1},U_{1},\mathcal{M}^{2},U_{2},\dots,\mathcal{M}^{m},U_{m},

where, $U_{0},U_{1},U_{2},\dots,U_{m}$ are unitary operators and $\mathcal{M}^{1}=\{M^{1}_{k_{1}}\},\mathcal{M}^{2}=\{M^{2}_{k_{2}}\},\dots,\mathcal{M}^{m}=\{M^{m}_{k_{m}}\}$ are measurement operators. Since the product of unitary matrices is a unitary matrix and the identity matrix is a unitary matrix, we may assume that the measurement and unitary transformation are performed alternately as described above. Note that the operator used may vary depending on the outcomes obtained each time. In this case, define $R_{\bm{k}}=U_{m}M_{k_{m}}^{m}\dots U_{2}M_{k_{2}}^{2}U_{1}M_{k_{1}}^{1}U_{0}$ with $\bm{k}=k_{1}k_{2}\dots k_{m}$ , we can show that $\mathcal{R}=\{R_{\bm{k}}\}$ is a recovery superoperator. Since

	$\displaystyle R_{\bm{k}}\left(\sum_{a}A_{a}\left(\sum_{i\in\mathcal{L}}\alpha_{i}\|i_{L}\rangle\right)\left(\sum_{i\in\mathcal{L}}\overline{\alpha_{i}}\langle i_{L}\|\right)A_{a}^{\dagger}\right)R_{\bm{k}}^{\dagger}$
		$\displaystyle=\prod_{j=1}^{m}p_{j}(k_{j})\left(\sum_{i\in\mathcal{L}}\alpha_{i}\|0\dots 0i\rangle\right)\left(\sum_{i\in\mathcal{L}}\overline{\alpha_{i}}\langle 0\dots 0i\|\right)$

for any $|\psi\rangle=\sum_{i\in\mathcal{L}}\alpha_{i}|i\rangle\in\mathbb{C}^{l}$ , we have

\displaystyle R_{\bm{k}}A_{a}|i_{L}\rangle=\sqrt{\prod_{j=1}^{m}p_{j}(k_{j})}|0\dots 0i\rangle,

where $p_{j}(k_{j})$ is the probability of obtaining the outcome $k_{j}$ in the measurement $\mathcal{M}^{j}$ for $1\leq j\leq m$ . We can also check that $\sum_{\bm{k}}R_{\bm{k}}^{\dagger}R_{\bm{k}}=I$ by considering that $\sum_{M_{k}\in\mathcal{M}}M_{k}^{\dagger}M_{k}=I$ for the same measurement $\mathcal{M}$ and $U^{\dagger}U=I$ for any unitary matrix $U$ .

(Step 2) Next, we prove that ${\it 2}\Rightarrow{\it 3}$ .

For any $A_{a},A_{b}\in\mathcal{A}$ , and any $i,j\in\mathcal{L}$ , we obtain

	$\displaystyle\langle i_{L}\|A_{a}^{\dagger}A_{b}\|j_{L}\rangle$	$\displaystyle=\langle i_{L}\|A_{a}^{\dagger}\left({\sum_{r}R_{r}^{\dagger}R_{r}}\right)A_{b}\|j_{L}\rangle$
		$\displaystyle=\sum_{r}\langle i_{L}\|A_{a}^{\dagger}R_{r}^{\dagger}R_{r}A_{b}\|j_{L}\rangle$
		$\displaystyle=\sum_{r}\overline{\lambda_{r,a}}\lambda_{r,b}\langle 0\dots 0i\|0\dots 0j\rangle$
		$\displaystyle=\left(\sum_{r}\overline{\lambda_{r,a}}\lambda_{r,b}\right)\delta_{i,j}.$

Thus, KL condition is satisfied.

(Step 3) Finally, we prove that ${\it 3}\Rightarrow{\it 1}$ .

Fix $i\in\mathcal{L}$ and let $V^{i}\subset\mathbb{C}^{l^{n^{\prime}}}$ be the vector space spanned by $A_{a}|i_{L}\rangle$ for all Kraus operators $A_{a}\in\mathcal{A}$ . We define the basis $\{|u_{1}^{i}\rangle,|u_{2}^{i}\rangle,\dots,|u_{d}^{i}\rangle\}$ of $V^{i}$ by applying the Gram-Schmidt orthonormalization as follows. We define

	$\displaystyle\|\tilde{u}_{1}^{i}\rangle$	$\displaystyle:=A_{1}\|i_{L}\rangle,$
	$\displaystyle\|\tilde{u}_{k}^{i}\rangle$	$\displaystyle:=A_{k}\|i_{L}\rangle-\sum_{p=1}^{k-1}\frac{\langle\tilde{u}_{p}^{i}\|A_{k}\|i_{L}\rangle}{\langle\tilde{u}_{p}^{i}\|\tilde{u}_{p}^{i}\rangle}\|\tilde{u}_{p}^{i}\rangle$

for $k\geq 2$ to obtain vectors $|\tilde{u}_{1}^{i}\rangle,|\tilde{u}_{2}^{i}\rangle,\dots,|\tilde{u}_{d}^{i}\rangle\in V^{i}$ that are orthogonal to each other. Note that even if the Kraus set $\mathcal{A}$ is an infinite set, the above inductive operation must finish because the dimension $d$ of $V^{i}$ is finite. In addition, even if the Kraus set $\mathcal{A}$ is uncountable, the orthogonal vectors $|\tilde{u}_{1}^{i}\rangle,|\tilde{u}_{2}^{i}\rangle,\dots,|\tilde{u}_{d}^{i}\rangle\in V^{i}$ can be obtained by selecting the Kraus operators $A_{1},A_{2},\dots,A_{d}$ in any order such that $A_{1}|i_{L}\rangle,A_{2}|i_{L}\rangle,\dots,A_{d}|i_{L}\rangle$ are linearly independent. By adjusting the lengths of all the obtained orthogonal vectors $|\tilde{u}_{1}^{i}\rangle,|\tilde{u}_{2}^{i}\rangle,\dots,|\tilde{u}_{d}^{i}\rangle\in V^{i}$ to $1$ , the basis $\{|u_{1}^{i}\rangle,|u_{2}^{i}\rangle,\dots,|u_{d}^{i}\rangle\}$ of $V^{i}$ is obtained. Note here that $d$ is independent of $i$ .

From the definition of the basis $\{|u_{1}^{i}\rangle,|u_{2}^{i}\rangle,\dots,|u_{d}^{i}\rangle\}$ , we can represent

\displaystyle|u_{k}^{i}\rangle=c_{k,1}A_{1}|i_{L}\rangle+c_{k,2}A_{2}|i_{L}\rangle+\dots+c_{k,k}A_{k}|i_{L}\rangle

(1)

for $k\in[d]$ . Note that $c_{k,1},c_{k,2},\dots,c_{k,k}\in\mathbb{C}$ do not depend on $i$ . This fact can be proved by mathematical induction as follows. From $\langle\tilde{u}_{1}^{i}|\tilde{u}_{1}^{i}\rangle=\langle i_{L}|A_{1}^{\dagger}A_{1}|i_{L}\rangle=\mu_{1,1}$ for any $i\in\mathcal{L}$ ,

\displaystyle|u_{1}^{i}\rangle=\frac{|\tilde{u}_{1}^{i}\rangle}{\||\tilde{u}_{1}^{i}\rangle\|}=\frac{A_{1}|i_{L}\rangle}{\sqrt{\mu_{1,1}}}

holds and $\mu_{1,1}$ does not depend on $i$ , thus it holds when $k=1$ . When $k\leq m$ for an integer $m\in[d-1]$ , assume that

\displaystyle|\tilde{u}_{k}^{i}\rangle=c^{\prime}_{k,1}A_{1}|i_{L}\rangle+c^{\prime}_{k,2}A_{2}|i_{L}\rangle+\dots+c^{\prime}_{k,k}A_{k}|i_{L}\rangle

and $c^{\prime}_{k,1},c^{\prime}_{k,2},\dots,c^{\prime}_{k,k}\in\mathbb{C}$ are all independent of $i$ . Then,

	$\displaystyle\langle\tilde{u}_{k}^{i}\|\tilde{u}_{k}^{i}\rangle$	$\displaystyle=\sum_{p=1}^{k}\sum_{q=1}^{k}\overline{c^{\prime}_{k,p}}c^{\prime}_{k,q}\langle i_{L}\|A_{p}^{\dagger}A_{q}\|i_{L}\rangle$
		$\displaystyle=\sum_{p=1}^{k}\sum_{q=1}^{k}\overline{c^{\prime}_{k,p}}c^{\prime}_{k,q}\mu_{p,q}$

and

	$\displaystyle\langle\tilde{u}_{k}^{i}\|A_{m+1}\|i_{L}\rangle$	$\displaystyle=\sum_{p=1}^{k}\overline{c^{\prime}_{k,p}}\langle i_{L}\|A_{p}^{\dagger}A_{m+1}\|i_{L}\rangle$
		$\displaystyle=\sum_{p=1}^{k}\overline{c^{\prime}_{k,p}}\mu_{p,m+1}$

are both independent of $i$ . Therefore, every coefficient of

	$\displaystyle\|\tilde{u}_{m+1}^{i}\rangle$	$\displaystyle=A_{m+1}\|i_{L}\rangle-\sum_{p=1}^{m}\frac{\langle\tilde{u}_{p}^{i}\|A_{m+1}\|i_{L}\rangle}{\langle\tilde{u}_{p}^{i}\|\tilde{u}_{p}^{i}\rangle}\|\tilde{u}_{p}^{i}\rangle$
		$\displaystyle=A_{m+1}\|i_{L}\rangle-\sum_{p=1}^{m}\left(\frac{\langle\tilde{u}_{p}^{i}\|A_{m+1}\|i_{L}\rangle}{\langle\tilde{u}_{p}^{i}\|\tilde{u}_{p}^{i}\rangle}\sum_{q=1}^{p}c^{\prime}_{p,q}A_{q}\|i_{L}\rangle\right)$

does not depend on $i$ . Hence, all coefficients of $|u_{m+1}^{i}\rangle$ are also independent of $i$ , and it is shown that it holds for $k=m+1$ .

Define $M_{k}:=\sum_{i\in\mathcal{L}}|u_{k}^{i}\rangle\langle u_{k}^{i}|$ for $k\in[d]$ . For the space $V\subset\mathbb{C}^{l\otimes n^{\prime}}$ with the basis $\{|u_{k}^{i}\rangle\mid k\in[d],i\in\mathcal{L}\}$ , choose a basis $\{|e_{j}\rangle\}$ of its orthogonal complementary space $V^{\perp}$ and define $M_{\emptyset}:=\sum_{j}|e_{j}\rangle\langle e_{j}|$ . Then $\mathcal{M}:=\{M_{\emptyset}\}\cup\{M_{k}\mid k\in[d]\}$ is a set of measurement operators because the completeness relation

\displaystyle M_{\emptyset}^{\dagger}M_{\emptyset}+\sum_{k\in[d]}M_{k}^{\dagger}M_{k}=I

is satisfied. Here, $I$ is the identity matrix of order $l^{n^{\prime}}$ .

The measurement $\mathcal{M}$ is performed on the state after the quantum error $E$ of the encoded state $|\Psi\rangle\in S(\mathbb{C}^{l\otimes n})$ . Then, the probability to get the outcome $k\in[d]$ is

	$\displaystyle p(k)$	$\displaystyle={\rm Tr}\left(M_{k}^{\dagger}M_{k}\left(\sum_{a}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}\right)\right)$
		$\displaystyle=\sum_{\bm{x}\in\mathcal{L}^{n^{\prime}}}\sum_{a}\langle\bm{x}\|M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}\|\bm{x}\rangle$
		$\displaystyle=\sum_{a}\langle\Psi\|A_{a}^{\dagger}\left(\sum_{\bm{x}\in\mathcal{L}^{n^{\prime}}}\|\bm{x}\rangle\langle\bm{x}\|\right)M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle$
		$\displaystyle=\sum_{a}\langle\Psi\|A_{a}^{\dagger}M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle.$

Since $\langle u_{k}^{i}|A_{a}|i_{L}\rangle$ does not depend on $i$ from Equation (1), if we set this value to $\beta_{k,a}\in\mathbb{C}$ , then

\displaystyle\langle u_{k}^{i}|A_{a}|j_{L}\rangle=\begin{cases}\beta_{k,a}&i=j\\ 0&i\neq j\end{cases}

holds. Therefore, we obtain

$\displaystyle M_{k}A_{a}\|\Psi\rangle$	$\displaystyle=\sum_{i\in\mathcal{L}}\|u_{k}^{i}\rangle\langle u_{k}^{i}\|A_{a}\sum_{j\in\mathcal{L}}\alpha_{j}\|j_{L}\rangle$
	$\displaystyle=\sum_{i\in\mathcal{L}}\sum_{j\in\mathcal{L}}\alpha_{j}\|u_{k}^{i}\rangle\langle u_{k}^{i}\|A_{a}\|j_{L}\rangle$
	$\displaystyle=\sum_{i\in\mathcal{L}}\alpha_{i}\beta_{k,a}\|u_{k}^{i}\rangle$
	$\displaystyle=\beta_{k,a}\sum_{i\in\mathcal{L}}\alpha_{i}\|u_{k}^{i}\rangle.$	(2)

Hence, we have

	$\displaystyle p(k)$	$\displaystyle=\sum_{a}\overline{\beta_{k,a}}\beta_{k,a}\left(\sum_{i\in\mathcal{L}}\overline{\alpha_{i}}\langle u_{k}^{i}\|\right)\left(\sum_{i\in\mathcal{L}}\alpha_{i}\|u_{k}^{i}\rangle\right)$
		$\displaystyle=\sum_{a}\|\beta_{k,a}\|^{2}.$		(3)

The state after the measurement $\mathcal{M}$ when the outcome $k$ is obtained is $\sum_{i\in\mathcal{L}}\alpha_{i}|u_{k}^{i}\rangle\in S(\mathbb{C}^{l\otimes n^{\prime}})$ , since

	$\displaystyle M_{k}\left(\sum_{a}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}\right)M_{k}^{\dagger}$	$\displaystyle=\sum_{a}M_{k}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}M_{k}^{\dagger}$
		$\displaystyle=\sum_{a}\beta_{k,a}\overline{\beta_{k,a}}\left(\sum_{i\in\mathcal{L}}\alpha_{i}\|u_{k}^{i}\rangle\right)\left(\sum_{i\in\mathcal{L}}\overline{\alpha_{i}}\langle u_{k}^{i}\|\right)$
		$\displaystyle=p(k)\left(\sum_{i\in\mathcal{L}}\alpha_{i}\|u_{k}^{i}\rangle\right)\left(\sum_{i\in\mathcal{L}}\overline{\alpha_{i}}\langle u_{k}^{i}\|\right)$

from Equation (2). On the other hand, from the definition of $M_{\emptyset}$ , the probability of obtaining the outcome $\emptyset$ is $0$ .

For each $k\in[d]$ , take one unitary matrix $U_{k}$ such that $U_{k}|u_{k}^{i}\rangle=|0\dots 0i\rangle$ for any $i\in\mathcal{L}$ . When the outcome $k$ is obtained, applying the unitary operator $U_{k}$ to the state after the measurement $\mathcal{M}$ , we obtain

\displaystyle U_{k}\left(\sum_{i\in\mathcal{L}}\alpha_{i}|u_{k}^{i}\rangle\right)=\sum_{i\in\mathcal{L}}\alpha_{i}|0\dots 0i\rangle=|0\dots 0\rangle\otimes|\psi\rangle.

Therefore, the code $C$ is $\mathcal{A}$ -correcting. The original state $|\psi\rangle=\sum_{i\in\mathcal{L}}\alpha_{i}|i\rangle\in S(\mathbb{C}^{l})$ can be obtained by deleting the $1$ st through the $(n^{\prime}-1)$ th particles and error-correction is completed. ∎

4 Equivalence of quantum single deletion and single insertion error-correctabilities

As typical errors that change the number of particles, this section defines single deletion errors and single insertion errors using Kraus operators.

Let $m\geq 0$ be an integer and let $|\phi\rangle\in\mathbb{C}^{l}$ with $\langle\phi|\phi\rangle=1$ . For an integer $p\in[m+1]$ , we define a $l^{m}$ -by- $l^{m+1}$ matrix $D_{p,|\phi\rangle}^{m}$ and a $l^{m+1}$ -by- $l^{m}$ matrix $I_{p,|\phi\rangle}^{m}$ as

	$\displaystyle D_{p,\|\phi\rangle}^{m}$	$\displaystyle:=\underbrace{\mathbb{I}_{l}\otimes\dots\otimes\mathbb{I}_{l}}_{(p-1)\,{\rm times}}\otimes\langle\phi\|\otimes\underbrace{\mathbb{I}_{l}\otimes\dots\otimes\mathbb{I}_{l}}_{(m-p+1)\,{\rm times}},$
	$\displaystyle I_{p,\|\phi\rangle}^{m}$	$\displaystyle:=\underbrace{\mathbb{I}_{l}\otimes\dots\otimes\mathbb{I}_{l}}_{(p-1)\,{\rm times}}\otimes\|\phi\rangle\otimes\underbrace{\mathbb{I}_{l}\otimes\dots\otimes\mathbb{I}_{l}}_{(m-p+1)\,{\rm times}}.$

Here, $\mathbb{I}_{l}$ denotes the identity matrix of order $l$ .

Definition 4.1 (Single deletion error).

For a quantum state $\rho\in S(\mathbb{C}^{l\otimes n})$ , we define a quantum single deletion error as a map $E^{del}:S(\mathbb{C}^{l\otimes n})\rightarrow S(\mathbb{C}^{l\otimes(n-1)})$ expressed as

\displaystyle E^{del}(\rho):=\sum_{p\in[n]}\left(p^{-}(p)\sum_{b\in\mathcal{L}}D_{p,|b\rangle}^{n-1}\rho{D_{p,|b\rangle}^{n-1}}^{\dagger}\right),

with $\sum_{p\in[n]}p^{-}(p)=1$ for a non-negative-valued function $p^{-}$ . I.e., the Kraus set for the single deletion error $E^{del}$ is

\displaystyle\mathcal{D}_{1}:=\left\{\sqrt{p^{-}(p)}D_{p,|b\rangle}^{n-1}\,\middle|\,p\in[n],b\in\mathcal{L}\right\}.

(4)

Although quantum single deletion error is often defined as a partial trace at an unknown position, it can also be defined as in Definition 4.1 from the discussion in Ref. [21].

Definition 4.2 (Single insertion error).

Suppose that a single qudit $\sigma\in S(\mathbb{C}^{l})$ is represented as $\sigma=\sum_{b\in\mathcal{L}}p_{b}|\phi_{b}\rangle\langle\phi_{b}|$ in the form of a spectral decomposition. For a quantum state $\rho\in S(\mathbb{C}^{l\otimes n})$ , we define a quantum single insertion error of $\sigma$ as a map $E^{ins}_{\sigma}:S(\mathbb{C}^{l\otimes n})\rightarrow S(\mathbb{C}^{l\otimes(n+1)})$ expressed as

\displaystyle E^{ins}_{\sigma}(\rho):=\sum_{p\in[n+1]}\left(p^{+}(p)\sum_{b\in\mathcal{L}}p_{b}I_{p,U|b\rangle}^{n}\rho{I_{p,U|b\rangle}^{n}}^{\dagger}\right),

with $\sum_{p\in[n+1]}p^{+}(p)=1$ for a non-negative-valued function $p^{+}$ . Here, $U$ is a unitary matrix such that $U|b\rangle=|\phi_{b}\rangle$ for every $b\in\mathcal{L}$ . I.e., the Kraus set for the single insertion error $E^{ins}_{\sigma}$ is

\displaystyle\mathcal{I}_{1}:=\left\{\sqrt{p^{+}(p)p_{b}}I_{p,U|b\rangle}^{n}\,\middle|\,p\in[n+1],b\in\mathcal{L}\right\}.

(5)

Quantum single insertion error is often defined as the insertion of a quantum state into an unknown position, but it is known that if the state before the error is pure, it can be expressed in a Kraus representation as in Definition 4.2[20]. Throughout this paper, the discussion is based on the assumption that the quantum state before the error is pure. This means that the codeword is pure, which is a weak assumption.

It is pointed out that the following theorem presented by the author in 2022 does not show the equivalence of error-correctability[20].

Theorem 4.3.

[Theorem III.4,[20]] KL condition for single deletion error is equivalent to that for single insertion error.

From Theorem 3.2, reported for the first time in this paper, the equivalence of error-correctability is also shown.

Theorem 4.4.

It is equivalent for quantum code to be $\mathcal{D}_{1}$ -correcting and $\mathcal{I}_{1}$ -correcting.

5 A necessary and sufficient condition for single qudit insertion/deletion error-correction

This section discusses the code $C$ defined by the following logical codewords. Take $A_{i}\subset\mathcal{L}^{n}$ for every $i\in\mathcal{L}$ and define

\displaystyle|i_{L}\rangle:=\frac{1}{\sqrt{|A_{i}|}}\sum_{{\bm{a}}\in A_{i}}|\bm{a}\rangle.

A necessary and sufficient condition for the correction of single deletion errors in the code $C$ is as follows:

Theorem 5.1.

It is a necessary and sufficient condition for the code $C$ to be $\mathcal{D}_{1}$ -correcting that the following two conditions are satisfied simultaneously.

•

(C1^del: ratio condition): For each $p_{1},p_{2}\in[n]$ and $b_{1},b_{2}\in\mathcal{L}$ , the following values are constant regardless of $i\in\mathcal{L}$ :

$\displaystyle{|\Delta^{-}_{p_{1},b_{1}}(A_{i})\cap\Delta^{-}_{p_{2},b_{2}}(A_{i})|}\,/\,{|A_{i}|}.$
•

(C2^del: distance condition): For any $p_{1},p_{2}\in[n]$ and any $b_{1},b_{2},i,j\in\mathcal{L}$ , if $i\neq j$ , then

$\displaystyle|\Delta^{-}_{p_{1},b_{1}}(A_{i})\cap\Delta^{-}_{p_{2},b_{2}}(A_{j})|=0.$

We refer to (C1^del) and (C2^del) collectively as (C^del). Here,

\displaystyle\Delta_{p,b}^{-}(A):=\{a_{1}\dots a_{p-1}a_{p+1}\dots a_{n}\mid a_{1}\dots a_{p-1}ba_{p+1}\dots a_{n}\in A\}

for a non-empty set $A\subset\mathcal{L}^{n}$ and $p\in[n]$ , $b\in\mathcal{L}$ .

Proof.

For $p\in[n]$ and $b,i\in\mathcal{L}$ , we have

\displaystyle D_{p,|b\rangle}^{n-1}|i_{L}\rangle

\displaystyle=\frac{1}{\sqrt{|A_{i}|}}\sum_{\bm{a}\in A_{i}}D_{p,|b\rangle}^{n-1}|\bm{a}\rangle=\frac{1}{\sqrt{|A_{i}|}}\sum_{\tilde{\bm{a}}\in\Delta^{-}_{p,b}(A_{i})}|\tilde{\bm{a}}\rangle.

Hence, for $p_{1},p_{2}\in[n]$ and $b_{1},b_{2},i,j\in\mathcal{L}$ , we obtain

\displaystyle\langle i_{L}|{D_{p_{1},|b_{1}\rangle}^{n-1}}^{\dagger}D_{p_{2},|b_{2}\rangle}^{n-1}|j_{L}\rangle

\displaystyle=\frac{|\Delta^{-}_{p_{1},b_{1}}(A_{i})\cap\Delta^{-}_{p_{2},b_{2}}(A_{j})|}{\sqrt{|A_{i}||A_{j}|}}.

Therefore, from Theorem 3.2, the condition (C^del) is a necessary and sufficient condition for $\mathcal{D}_{1}$ -correcting. ∎

Theorem 5.1 extends the code by Nakayama-Hagiwara[14] with $l=2$ to the case where $l$ is any positive integer, and further generalizes it to be necessary and sufficient level of error-correction. Note that the decoder shown in Ref.[14] is consequently the same as the decoder shown in the proof of Theorem 3.2 in this paper.

A necessary and sufficient condition for the correction of single insertion errors in the code $C$ is as follows:

Theorem 5.2.

It is a necessary and sufficient condition for the code $C$ to be $\mathcal{I}_{1}$ -correcting that the following two conditions are satisfied simultaneously.

•

(C1^ins: ratio condition): For each $p_{1},p_{2}\in[n+1]$ and $b_{1},b_{2}\in\mathcal{L}$ , the following values are constant regardless of $i\in\mathcal{L}$ :

$\displaystyle|\Delta^{+}_{p_{1},b_{1}}(A_{i})\cap\Delta^{+}_{p_{2},b_{2}}(A_{i})|\,/\,|A_{i}|.$
•

(C2^ins: distance condition): For any $p_{1},p_{2}\in[n+1]$ and any $b_{1},b_{2},i,j\in\mathcal{L}$ , if $i\neq j$ , then

$\displaystyle|\Delta^{+}_{p_{1},b_{1}}(A_{i})\cap\Delta^{+}_{p_{2},b_{2}}(A_{j})|=0.$

We refer to (C1^ins) and (C2^ins) collectively as (C^ins). Here,

\displaystyle\Delta_{p,b}^{+}(A)\coloneqq

\displaystyle\{a_{1}\dots a_{p-1}ba_{p}\dots a_{n}\mid a_{1}\dots a_{p-1}a_{p}\dots a_{n}\in A\}

for a non-empty set $A\subset\mathcal{L}^{n}$ and $p\in[n+1]$ , $b\in\mathcal{L}$ .

Proof.

For $p\in[n+1]$ and $b,i\in\mathcal{L}$ , we have

\displaystyle I_{p,|b\rangle}^{n}|i_{L}\rangle

\displaystyle=\frac{1}{\sqrt{|A_{i}|}}\sum_{\bm{a}\in A_{i}}I_{p,|b\rangle}^{n}|\bm{a}\rangle=\frac{1}{\sqrt{|A_{i}|}}\sum_{\tilde{\bm{a}}\in\Delta^{+}_{p,b}(A_{i})}|\tilde{\bm{a}}\rangle.

Hence, for $p_{1},p_{2}\in[n+1]$ and $b_{1},b_{2},i,j\in\mathcal{L}$ , by noting that there exists a unitary matrix $U_{p_{1},p_{2}}$ such that $I_{p_{1},U|b_{1}\rangle}^{n}=U_{p_{1},p_{2}}I_{p_{1},|b_{1}\rangle}^{n}$ and $I_{p_{2},U|b_{2}\rangle}^{n}=U_{p_{1},p_{2}}I_{p_{2},|b_{2}\rangle}^{n}$ , we obtain

	$\displaystyle\langle i_{L}\|{I_{p_{1},U\|b_{1}\rangle}^{n}}^{\dagger}I_{p_{2},U\|b_{2}\rangle}^{n}\|j_{L}\rangle$	$\displaystyle=\langle i_{L}\|{I_{p_{1},\|b_{1}\rangle}^{n}}^{\dagger}I_{p_{2},\|b_{2}\rangle}^{n}\|j_{L}\rangle$
		$\displaystyle=\frac{\|\Delta^{+}_{p_{1},b_{1}}(A_{i})\cap\Delta^{+}_{p_{2},b_{2}}(A_{j})\|}{\sqrt{\|A_{i}\|\|A_{j}\|}}.$

Therefore, from Theorem 3.2, the condition (C^ins) is a necessary and sufficient condition for $\mathcal{I}_{1}$ -correcting. ∎

Theorem 5.2 extends $l$ to any positive integer for codes with $l=2$ in Ref.[20] and greatly generalizes the error-correction condition to necessary and sufficient level. Note that although the 4-qubit code satisfies the condition (C^ins), the decoder given in the proof of Theorem 3.2 in this paper is not the one by Hagiwara[6], but corresponds to the one given in Ref.[18].

Theorem 5.3.

Conditions (C^del) and (C^ins) are equivalent.

Theorem 5.3 follows immediately from Theorem 5.1, Theorem 5.2 and Theorem 4.4, but can also be proved classically as follows:

Classical proof of Theorem 5.3.

For integers $p_{1},p_{2}\in[n]$ , assume that $p_{1}\leq p_{2}$ without loss of generality. The sequence $\bm{x}\in\Delta_{p_{1},b_{1}}^{-}(A)\cap\Delta_{p_{2},b_{2}}^{-}(A)$ and the sequence $\tilde{\bm{x}}\in\Delta_{p_{1},b_{1}}^{+}(A)\cap\Delta_{p_{2}+1,b_{2}}^{+}(A)$ correspond one-to-one, where

	$\displaystyle\bm{x}$	$\displaystyle=x_{1}\dots x_{p_{1}-1}x_{p_{1}}\dots x_{p_{2}-1}x_{p_{2}+1}\dots x_{n-1},$
	$\displaystyle\tilde{\bm{x}}$	$\displaystyle=x_{1}\dots x_{p_{1}-1}b_{1}x_{p_{1}}\dots x_{p_{2}-1}b_{2}x_{p_{2}+1}\dots x_{n-1}.$

Therefore, we obtain

\displaystyle|\Delta_{p_{1},b_{1}}^{-}(A)\cap\Delta_{p_{2},b_{2}}^{-}(A)|=|\Delta_{p_{1},b_{1}}^{+}(A)\cap\Delta_{p_{2}+1,b_{2}}^{+}(A)|.

On the other hand, we have

\displaystyle|\Delta_{p,b_{1}}^{+}(A)\cap\Delta_{p,b_{2}}^{+}(A)|=\begin{cases}|A|&b_{1}=b_{2}\\ 0&b_{1}\neq b_{2}\end{cases}

for any $p\in[n+1]$ . From the above, it is shown that (C1^del) and (C1^ins) are equivalent.

From the equivalence of classical insertion codes and classical deletion codes, the equivalence of (C2^del) and (C2^ins) is obvious. ∎

6 Example of insertion/deletion qudit code and its decoding algorithm

By defining the sets $A_{0},A_{1}$ , and $A_{2}$ as follows, we can construct an example of a $6$ -qudit single insertion/deletion error-correcting code with $l=3$ :

	$\displaystyle A_{0}$	$\displaystyle=\{001122,112200,220011\},$
	$\displaystyle A_{1}$	$\displaystyle=\{002211,110022,221100\},$
	$\displaystyle A_{2}$	$\displaystyle=\{001100,112211,220022\}.$

We can easily check that these sets satisfy the condition (C^del) by Table 1.

Table 1:

\Delta^{-}_{p,b}(A_{i})

for

p\in[6]

and

b,i\in\{0,1,2\}

$\Delta^{-}_{p,b}(A_{0})$	$A_{0}=\{001122,112200,220011\}$
$\Delta^{-}_{p,b}(A_{0})$	$b=0$	$b=1$	$b=2$
$p=1$	$\{01122\}$	$\{12200\}$	$\{20011\}$
$p=2$	$\{01122\}$	$\{12200\}$	$\{20011\}$
$p=3$	$\{22011\}$	$\{00122\}$	$\{11200\}$
$p=4$	$\{22011\}$	$\{00122\}$	$\{11200\}$
$p=5$	$\{11220\}$	$\{22001\}$	$\{00112\}$
$p=6$	$\{11220\}$	$\{22001\}$	$\{00112\}$

$\Delta^{-}_{p,b}(A_{1})$	$A_{1}=\{002211,110022,221100\}$
$\Delta^{-}_{p,b}(A_{1})$	$b=0$	$b=1$	$b=2$
$p=1$	$\{02211\}$	$\{10022\}$	$\{21100\}$
$p=2$	$\{02211\}$	$\{10022\}$	$\{21100\}$
$p=3$	$\{11022\}$	$\{22100\}$	$\{00211\}$
$p=4$	$\{11022\}$	$\{22100\}$	$\{00211\}$
$p=5$	$\{22110\}$	$\{00221\}$	$\{11002\}$
$p=6$	$\{22110\}$	$\{00221\}$	$\{11002\}$

$\Delta^{-}_{p,b}(A_{2})$	$A_{2}=\{001100,112211,220022\}$
$\Delta^{-}_{p,b}(A_{2})$	$b=0$	$b=1$	$b=2$
$p=1$	$\{01100\}$	$\{12211\}$	$\{20022\}$
$p=2$	$\{01100\}$	$\{12211\}$	$\{20022\}$
$p=3$	$\{22022\}$	$\{00100\}$	$\{11211\}$
$p=4$	$\{22022\}$	$\{00100\}$	$\{11211\}$
$p=5$	$\{00110\}$	$\{11221\}$	$\{22002\}$
$p=6$	$\{00110\}$	$\{11221\}$	$\{22002\}$

By Theorem 5.3, these sets also satisfy the condition (C^ins). Therefore, the quantum code whose logical codewords are

	$\displaystyle\|0_{L}\rangle$	$\displaystyle:=\frac{1}{\sqrt{3}}(\|001122\rangle+\|112200\rangle+\|220011\rangle),$
	$\displaystyle\|1_{L}\rangle$	$\displaystyle:=\frac{1}{\sqrt{3}}(\|002211\rangle+\|110022\rangle+\|221100\rangle),$
	$\displaystyle\|2_{L}\rangle$	$\displaystyle:=\frac{1}{\sqrt{3}}(\|001100\rangle+\|112211\rangle+\|220022\rangle),$

is $\mathcal{D}_{1}$ -correcting and $\mathcal{I}_{1}$ -correcting. Using the decoding algorithm presented under Theorem 3.2, we can correct any single deletion error or any single insertion error as follows.

6.1 Decoding algorithm for single deletion errors

Since $n=6$ , from Equation (4) there are 18 Kraus operators for the single deletion error, which are labeled newly as $A_{a}$ , where $a\in\{1,2,\dots,18\}$ . The dimension of the vector space $V^{i}$ spanned by $A_{a}|i_{L}\rangle$ for all Kraus operators $A_{a}$ is $9$ , and its basis $\{|u_{1}^{i}\rangle,|u_{2}^{i}\rangle,\dots,|u_{9}^{i}\rangle\}$ is defined by applying the Gram-Schmidt orthonormalization. For example, for $i=0$ , we have the following results. Compare with Table 1.

	$\displaystyle\|u_{1}^{0}\rangle=\|01122\rangle,$
	$\displaystyle\|u_{2}^{0}\rangle=\|22011\rangle,$
	$\displaystyle\|u_{3}^{0}\rangle=\|11220\rangle,$
	$\displaystyle\|u_{4}^{0}\rangle=\|12200\rangle,$
	$\displaystyle\|u_{5}^{0}\rangle=\|00122\rangle,$
	$\displaystyle\|u_{6}^{0}\rangle=\|22001\rangle,$
	$\displaystyle\|u_{7}^{0}\rangle=\|20011\rangle,$
	$\displaystyle\|u_{8}^{0}\rangle=\|11200\rangle,$
	$\displaystyle\|u_{9}^{0}\rangle=\|00112\rangle.$

When the measurement $\mathcal{M}$ is performed on the quantum state $E^{del}(\alpha_{0}|0_{L}\rangle+\alpha_{1}|1_{L}\rangle+\alpha_{2}|2_{L}\rangle)\in S(\mathbb{C}^{3\otimes 5})$ , the probability of obtaining the outcome $k\in[9]$ is

\displaystyle p(k)=\begin{cases}\displaystyle\frac{1}{3}(p^{-}(1)+p^{-}(2))&k=1,4,7\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle\frac{1}{3}(p^{-}(3)+p^{-}(4))&k=2,5,8\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle\frac{1}{3}(p^{-}(5)+p^{-}(6))&k=3,6,9\end{cases}

from Equation (3). Then, the unitary operator $U_{k}$ corresponding to each outcome $k\in[9]$ is applied and the $1$ st through $4$ th particles are deleted. Thus, the original quantum state $\alpha_{0}|0\rangle+\alpha_{1}|1\rangle+\alpha_{2}|2\rangle)\in S(\mathbb{C}^{3})$ can be obtained.

6.2 Decoding algorithm for single insertion errors

From Equation (5) there are $21$ Kraus operators for the single insertion error, which are labeled newly as $A_{a}$ , where $a\in\{1,2,\dots,21\}$ . The dimension of the vector space $V^{i}$ spanned by $A_{a}|i_{L}\rangle$ for all Kraus operators $A_{a}$ is $21$ , and its basis $\{|u_{1}^{i}\rangle,|u_{2}^{i}\rangle,\dots,|u_{21}^{i}\rangle\}$ is defined by applying the Gram-Schmidt orthonormalization. We have

$\displaystyle\|u_{7j+1}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!I_{1,\|j\rangle}^{6}\|i_{L}\rangle,$
$\displaystyle\|u_{7j+2}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{9}{8}}\bigg{(}-\frac{1}{3}I_{1,\|j\rangle}^{6}\|i_{L}\rangle+I_{2,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$
$\displaystyle\|u_{7j+3}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{6}{5}}\bigg{(}-\frac{1}{4}I_{1,\|j\rangle}^{6}\|i_{L}\rangle-\frac{1}{4}I_{2,\|j\rangle}^{6}\|i_{L}\rangle+I_{3,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$
$\displaystyle\|u_{7j+4}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{15}{13}}\bigg{(}\frac{1}{10}I_{1,\|j\rangle}^{6}\|i_{L}\rangle+\frac{1}{10}I_{2,\|j\rangle}^{6}\|i_{L}\rangle-\frac{2}{5}I_{3,\|j\rangle}^{6}\|i_{L}\rangle+I_{4,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$
$\displaystyle\|u_{7j+5}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{39}{32}}\bigg{(}\frac{1}{13}I_{1,\|j\rangle}^{6}\|i_{L}\rangle+\frac{1}{13}I_{2,\|j\rangle}^{6}\|i_{L}\rangle-\frac{4}{13}I_{3,\|j\rangle}^{6}\|i_{L}\rangle-\frac{3}{13}I_{4,\|j\rangle}^{6}\|i_{L}\rangle+I_{5,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$
$\displaystyle\|u_{7j+6}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{96}{83}}\bigg{(}-\frac{1}{32}I_{1,\|j\rangle}^{6}\|i_{L}\rangle-\frac{1}{32}I_{2,\|j\rangle}^{6}\|i_{L}\rangle+\frac{1}{8}I_{3,\|j\rangle}^{6}\|i_{L}\rangle+\frac{3}{32}I_{4,\|j\rangle}^{6}\|i_{L}\rangle$
$\displaystyle\!\!\!\!-\frac{13}{32}I_{5,\|j\rangle}^{6}\|i_{L}\rangle+I_{6,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$
$\displaystyle\|u_{7j+7}^{i}\rangle$	$\displaystyle=$	$\displaystyle\!\!\!\!\sqrt{\frac{83}{68}}\bigg{(}-\frac{2}{83}I_{1,\|j\rangle}^{6}\|i_{L}\rangle-\frac{2}{83}I_{2,\|j\rangle}^{6}\|i_{L}\rangle+\frac{8}{83}I_{3,\|j\rangle}^{6}\|i_{L}\rangle+\frac{6}{83}I_{4,\|j\rangle}^{6}\|i_{L}\rangle$
$\displaystyle\!\!\!\!-\frac{26}{83}I_{5,\|j\rangle}^{6}\|i_{L}\rangle-\frac{19}{83}I_{6,\|j\rangle}^{6}\|i_{L}\rangle+I_{7,\|j\rangle}^{6}\|i_{L}\rangle\bigg{)},$

for $i,j\in\{0,1,2\}$ . Unlike the deletion case, since $A_{a}|i_{L}\rangle$ are not all orthogonal to each other, the result is complicated.

When the measurement $\mathcal{M}$ is performed on the quantum state $E^{ins}(\alpha_{0}|0_{L}\rangle+\alpha_{1}|1_{L}\rangle+\alpha_{2}|2_{L}\rangle)\in S(\mathbb{C}^{3\otimes 7})$ , the probability of obtaining the outcome $k\in[21]$ is

\displaystyle p(k)=\begin{cases}\displaystyle p_{j}\left(p^{+}(1)+\frac{1}{9}p^{+}(2)+\frac{1}{9}p^{+}(3)\right)&k=7j+1\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{8}{9}p^{+}(2)+\frac{1}{18}p^{+}(3)\right)&k=7j+2\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{5}{6}p^{+}(3)+\frac{2}{15}p^{+}(4)+\frac{2}{15}p^{+}(5)\right)&k=7j+3\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{13}{15}p^{+}(4)+\frac{3}{65}p^{+}(5)\right)&k=7j+4\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{32}{39}p^{+}(5)+\frac{13}{96}p^{+}(6)+\frac{13}{96}p^{+}(7)\right)&k=7j+5\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{83}{96}p^{+}(6)+\frac{361}{7968}p^{+}(7)\right)&k=7j+6\vskip 6.0pt plus 2.0pt minus 2.0pt\\ \displaystyle p_{j}\left(\frac{68}{83}p^{+}(7)\right)&k=7j+7\end{cases}

for $j\in\{0,1,2\}$ from Equation (3). Then, the unitary operator $U_{k}$ corresponding to each outcome $k\in[21]$ is applied and the $1$ st through $6$ th particles are deleted. Thus, the original quantum state $\alpha_{0}|0\rangle+\alpha_{1}|1\rangle+\alpha_{2}|2\rangle)\in S(\mathbb{C}^{3})$ can be obtained.

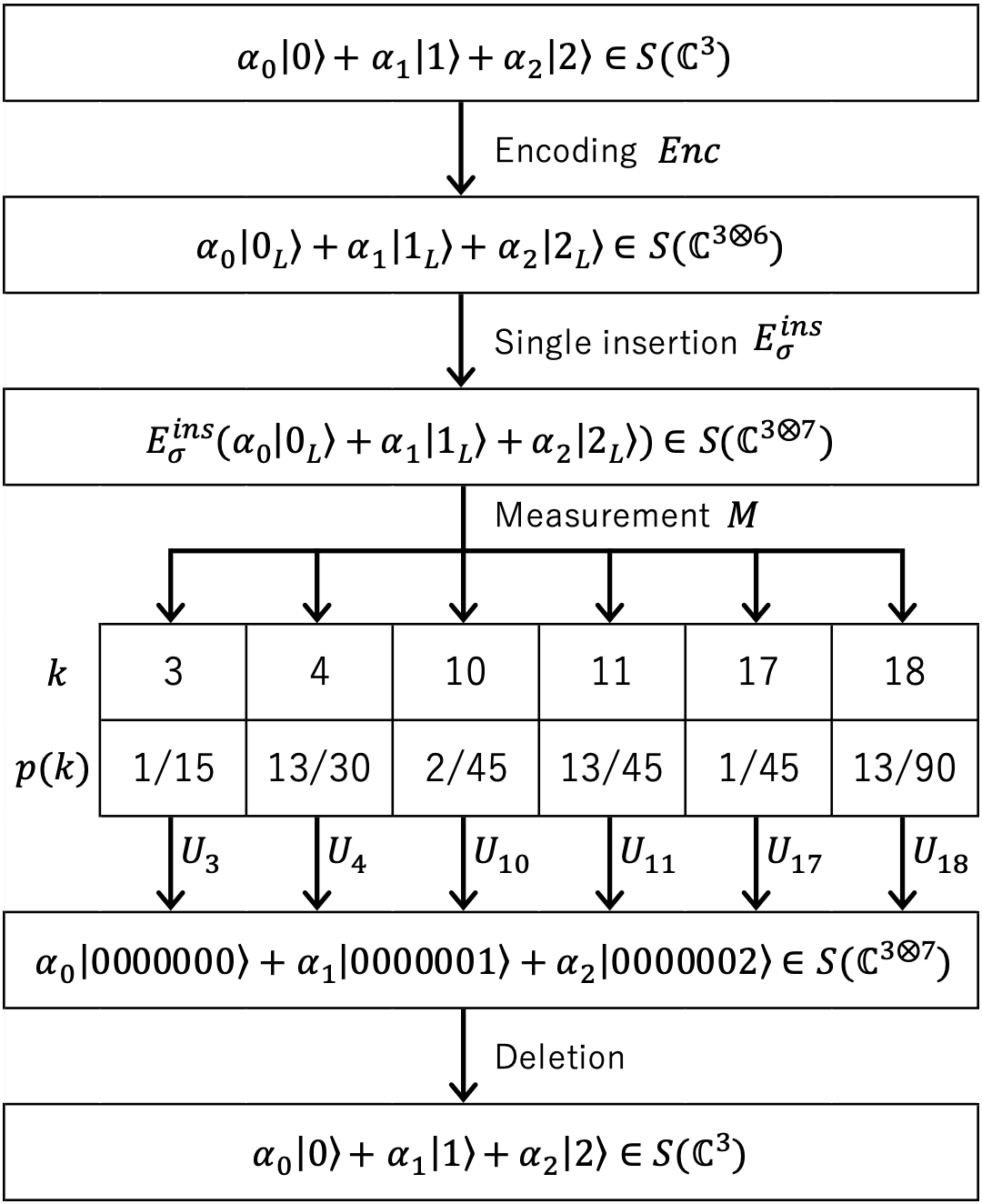
For example, if $\sigma=\frac{1}{2}|0\rangle\langle 0|+\frac{1}{3}|1\rangle\langle 1|+\frac{1}{6}|2\rangle\langle 2|\in S(\mathbb{C}^{3})$ is inserted in the $4$ th position, that is, if we consider the single insertion error where $p^{+}(4)=1$ , $p^{+}(p)=0$ for any $p\neq 4$ , and $p_{1}=1/2$ , $p_{2}=1/3$ , $p_{3}=1/6$ , the error-correction process is as shown in Figure 1.

Refer to caption — Figure 1: Error-correction process for the 6-qudit insertion code when $\sigma=\frac{1}{2}|0\rangle\langle 0|+\frac{1}{3}|1\rangle\langle 1|+\frac{1}{6}|2\rangle\langle 2|\in S(\mathbb{C}^{3})$ is inserted in the 4th position

7 Conclusion

In this paper, we proved that KL condition [9] can be used as a necessary and sufficient condition for correcting quantum errors with changing number of particles. By using KL condition, we showed that the error-correctabilities of single deletion and single insertion are equivalent. Furthermore, the error-correctability conditions for single deletion given by Nakayama-Hagiwara[14] and for single insertion given by Shibayama-Hagiwara[20] were improved to necessary and sufficient level. We also constructed a new single qudit insertion/deletion code by giving an example that satisfies the conditions, and provided a decoding algorithm for the code.

References

[1] Yuta Aoki and Mitsuru Tada. A quantum secret sharing scheme using a 4-qubit code. IEICE Tech. Rep., IT2023-38, in Japanese, 123(338):45–50, 2024.
[2] Tilo Buschmann and Leonid V. Bystrykh. Levenshtein error-correcting barcodes for multiplexed dna sequencing. BMC Bioinformatics, 14(1), 2013.
[3] A. Robert Calderbank and Peter W. Shor. Good quantum error-correcting codes exist. Physical Review A, 54(2):1098–1105, 1996.
[4] Roni Con, Amir Shpilka, and Itzhak Tamo. Explicit and efficient constructions of linear codes against adversarial insertions and deletions. IEEE Transactions on Information Theory, 68(10):6516–6526, 2022.
[5] Daniel Gottesman. Stabilizer codes and quantum error correction. arXiv preprint arXiv:9705052, 1997.
[6] Manabu Hagiwara. The four qubits deletion code is the first quantum insertion code. IEICE Communications Express, 10(5):243–247, 2021.
[7] Manabu Hagiwara and Ayumu Nakayama. A four-qubits code that is a quantum deletion error-correcting code with the optimal length. In The Proceedings of 2020 IEEE International Symposium on Information Theory (ISIT2020), pages 1870–1874, 2020.
[8] Albertus S. J. Helberg and Hendrik C. Ferreira. On multiple insertion/deletion correcting codes. IEEE Transactions on Information Theory, 48(1):305–308, 2002.
[9] Emanuel Knill and Raymond Laflamme. Theory of quantum error-correcting codes. Physical Review A, 55(2):900–911, 1997.
[10] K. Kraus, A. Böhm, J.D. Dollard, and W.H. Wootters. States, Effects, and Operations: Fundamental Notions of Quantum Theory. Lecture Notes in Physics. Springer Berlin Heidelberg, 1983.
[11] Vladimir I Levenshtein. Binary codes capable of correcting deletions, insertions, and reversals. Soviet physics doklady, 10:707–710, 1966.
[12] Ken Nakamura and Takayuki Nozaki. Decoding algorithm correcting single-insertion plus single-deletion for non-binary quantum codes. arXiv preprint arXiv:2409.10924, 2024.
[13] Ayumu Nakayama and Manabu Hagiwara. The first quantum error-correcting code for single deletion errors. IEICE Communications Express, 9(4):100–104, 2020.
[14] Ayumu Nakayama and Manabu Hagiwara. Single quantum deletion error-correcting codes. In The Proceedings of 2020 International Symposium on Information Theory and Its Applications (ISITA2020), pages 329–333, 2020.
[15] Takayuki Nozaki. Bounded single insertion/deletion correcting codes. In The Proceedings of 2019 IEEE International Symposium on Information Theory (ISIT2019), pages 2379–2383, 2019.
[16] Yingkai Ouyang. Permutation-invariant quantum coding for quantum deletion channels. In The Proceedings of 2021 IEEE International Symposium on Information Theory (ISIT2021), pages 1499–1503, 2021.
[17] Taro Shibayama. Construction of single quantum deletion codes via combinatorial conditions and adjacency matrices. Quantum Information Processing, 20(9), 2021.
[18] Taro Shibayama. A generalization of the four qubits single insertion error-correcting code. IEICE Communications Express, 13(4):126–129, 2024.
[19] Taro Shibayama and Manabu Hagiwara. Permutation-invariant quantum codes for deletion errors. In The Proceedings of 2021 IEEE International Symposium on Information Theory (ISIT2021), pages 1493–1498, 2021.
[20] Taro Shibayama and Manabu Hagiwara. Equivalence of quantum single insertion and single deletion error-correctabilities, and construction of codes and decoders. In The Proceedings of 2022 IEEE International Symposium on Information Theory (ISIT2022), pages 2957–2962, 2022.
[21] Taro Shibayama and Yingkai Ouyang. The equivalence between correctability of deletions and insertions of separable states in quantum codes. In The Proceedings of 2021 IEEE Information Theory Workshop (ITW2021), pages 1–6, 2021.
[22] Peter W. Shor. Scheme for reducing decoherence in quantum computer memory. Physical Review A, 52:R2493–R2496, 1995.
[23] Evagoras Stylianou, Lorenz Welter, Rawad Bitar, Antonia Wachter-Zeh, and Eitan Yaakobi. Equivalence of insertion/deletion correcting codes for d-dimensional arrays. In The Proceedings of 2022 IEEE International Symposium on Information Theory (ISIT2022), pages 814–819, 2022.

	$\displaystyle\|\psi\rangle$	$\displaystyle:=\sum_{i\in\mathcal{L}}\alpha_{i}\|i\rangle\in\mathbb{C}^{l},$
	$\displaystyle\|\Psi\rangle$	$\displaystyle:=\sum_{i\in\mathcal{L}}\alpha_{i}\|i_{L}\rangle\in\mathbb{C}^{l\otimes n},$

	$\displaystyle\langle i_{L}\|A_{a}^{\dagger}A_{b}\|j_{L}\rangle$	$\displaystyle=\langle i_{L}\|A_{a}^{\dagger}\left({\sum_{r}R_{r}^{\dagger}R_{r}}\right)A_{b}\|j_{L}\rangle$
		$\displaystyle=\sum_{r}\langle i_{L}\|A_{a}^{\dagger}R_{r}^{\dagger}R_{r}A_{b}\|j_{L}\rangle$
		$\displaystyle=\sum_{r}\overline{\lambda_{r,a}}\lambda_{r,b}\langle 0\dots 0i\|0\dots 0j\rangle$
		$\displaystyle=\left(\sum_{r}\overline{\lambda_{r,a}}\lambda_{r,b}\right)\delta_{i,j}.$

	$\displaystyle\|\tilde{u}_{1}^{i}\rangle$	$\displaystyle:=A_{1}\|i_{L}\rangle,$
	$\displaystyle\|\tilde{u}_{k}^{i}\rangle$	$\displaystyle:=A_{k}\|i_{L}\rangle-\sum_{p=1}^{k-1}\frac{\langle\tilde{u}_{p}^{i}\|A_{k}\|i_{L}\rangle}{\langle\tilde{u}_{p}^{i}\|\tilde{u}_{p}^{i}\rangle}\|\tilde{u}_{p}^{i}\rangle$

	$\displaystyle p(k)$	$\displaystyle={\rm Tr}\left(M_{k}^{\dagger}M_{k}\left(\sum_{a}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}\right)\right)$
		$\displaystyle=\sum_{\bm{x}\in\mathcal{L}^{n^{\prime}}}\sum_{a}\langle\bm{x}\|M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle\langle\Psi\|A_{a}^{\dagger}\|\bm{x}\rangle$
		$\displaystyle=\sum_{a}\langle\Psi\|A_{a}^{\dagger}\left(\sum_{\bm{x}\in\mathcal{L}^{n^{\prime}}}\|\bm{x}\rangle\langle\bm{x}\|\right)M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle$
		$\displaystyle=\sum_{a}\langle\Psi\|A_{a}^{\dagger}M_{k}^{\dagger}M_{k}A_{a}\|\Psi\rangle.$

$\displaystyle M_{k}A_{a}\|\Psi\rangle$	$\displaystyle=\sum_{i\in\mathcal{L}}\|u_{k}^{i}\rangle\langle u_{k}^{i}\|A_{a}\sum_{j\in\mathcal{L}}\alpha_{j}\|j_{L}\rangle$
	$\displaystyle=\sum_{i\in\mathcal{L}}\sum_{j\in\mathcal{L}}\alpha_{j}\|u_{k}^{i}\rangle\langle u_{k}^{i}\|A_{a}\|j_{L}\rangle$
	$\displaystyle=\sum_{i\in\mathcal{L}}\alpha_{i}\beta_{k,a}\|u_{k}^{i}\rangle$
	$\displaystyle=\beta_{k,a}\sum_{i\in\mathcal{L}}\alpha_{i}\|u_{k}^{i}\rangle.$	(2)

Necessary and sufficient condition for constructing a single qudit insertion/deletion code and its decoding algorithm

Abstract

1 Introduction

2 Preliminaries

Definition 2.1 (Quantum error).

3 Correctable condition for quantum errors with non-square Kraus operators

Definition 3.1 (Recovery superoperator).

Theorem 3.2.

Proof.

4 Equivalence of quantum single deletion and single insertion error-correctabilities

Definition 4.1 (Single deletion error).

Definition 4.2 (Single insertion error).

Theorem 4.3.

Theorem 4.4.

5 A necessary and sufficient condition for single qudit insertion/deletion error-correction

Theorem 5.1.

Proof.

Theorem 5.2.

Proof.

Theorem 5.3.

Classical proof of Theorem 5.3.

6 Example of insertion/deletion qudit code and its decoding algorithm

6.1 Decoding algorithm for single deletion errors

6.2 Decoding algorithm for single insertion errors

7 Conclusion

References

Necessary and sufficient condition for constructing
a single qudit insertion/deletion code
and its decoding algorithm