Nematic and chiral superconductivity induced by odd-parity fluctuations

The theoretical identification of time-reversal invariant topological insulatorsKane and Mele (2005); Fu et al. (2007) has sparked a great discovery of topological states in various forms of matter, including insulatorsHasan and Kane (2010); Qi and Zhang (2011), superconductorsQi and Zhang (2011) and semimetalsLiu et al. (2014); Xu et al. (2015). A topological superconductor is enriched by its intrinsic particle-hole symmetry, which protects zero-energy Majorana modes on boundaries and in vorticesQi and Zhang (2011). Topological superconductivity is being actively studied in both theoryFu and Kane (2008); Qi et al. (2009); Sau et al. (2010); Lutchyn et al. (2010) and experimentNadj-Perge et al. (2014); Albrecht et al. (2016).

Recent experiments have identified Bi₂Se₃ intercalated with Cu, Nb or Sr as a candidate system for topological superconductor. Many bulk properties in the superconducting state of doped Bi₂Se₃ display a uniaxial anisotropy in response to an in-plane magnetic field, which include Knight shiftMatano et al. (2016), upper critical fieldYonezawa et al. (2017); Pan et al. (2016), magnetic torqueAsaba et al. (2017) and specific heatYonezawa et al. (2017). Therefore, the superconducting state breaks the lattice discrete rotational symmetry, and can be termed as nematic. Specific heatKriener et al. (2011) and penetration depth measurementSmylie et al. (2016) have shown the absence of line nodes in the superconducting state. Given these experimental observations, the nematic state is most consistent with an $E_{u}$ pairing channel that has two components and odd-parity symmetryFu (2014). Here $E_{u}$ is one of the symmetry representations allowed by the $D_{3d}$ point group of Bi₂Se₃. The odd-parity nematic state can be a fully-gapped time-reversal-invariant topological superconductorFu (2014). So far, experimental evidence of surface Majorana states associated with topological superconductivity has been not conclusiveSasaki et al. (2011); Levy et al. (2013). On the theoretical side, different aspects of the nematic states have been explored, including bulk propertiesHashimoto et al. (2013); Nagai and Ota (2016); Venderbos et al. (2016a), surface statesYang et al. (2014), vortex statesWu and Martin (2017); Zyuzin et al. , and the interplay between $E_{u}$ superconductivity and magnetismYuan et al. (2017); Chirolli et al. (2017).

The basic question, which remains largely openFu (2016); Behnia (2017), is the underlying microscopic mechanism for the odd-parity nematic superconductivity in doped Bi₂Se₃. In the pioneering work of Fu and Berg(Fu and Berg, 2010), they demonstrated that pairing instability in the odd-parity channels can be generated by a simple type of attractive interaction in doped Bi₂Se₃. However, the odd-parity $A_{1u}$ pairing channel has a higher critical temperature than the $E_{u}$ pairing channel in their model.

Odd-parity pairing can be induced by magnetic fluctuations, as in the case of superfluid Helium-3Leggett (1975) and in strongly correlated materials like Sr₂RuO₄Rice and Sigrist (1995) and UPt₃Nomoto and Ikeda (2016). It has recently been proposed that odd-parity pairing can also be induced by odd-parity fluctuations in a system with strong spin-orbit coupling, time reversal and inversion symmetriesKozii and Fu (2015); Wang et al. (2016); Ruhman et al. (2017). As doped Bi₂Se₃ is likely a weakly correlated material, we study superconductivity induced by odd-parity fluctuations in this paper.

In Ref. Kozii and Fu, 2015, Kozii and Fu have studied the most symmetric group $O(3)$ in three dimensions, and found that odd-parity fluctuation in pseudoscalar and vector representations generate attractive interaction in both conventional even-parity $s$-wave pairing channel and odd-parity pairing channels, while fluctuation in the multipolar channel only generates attractive interaction in the $s$-wave channel. Our work builds upon Ref. Kozii and Fu, 2015. We apply a similar approach to doped Bi₂Se₃ which has a $D_{3d}$ point group symmetry. Symmetry classifications of odd-parity fluctuations for $O(3)$ and $D_{3d}$ groups are different. Our main results can be summarized as follows. Odd-parity fluctuations in the $E_{u}$ representation of the $D_{3d}$ point group can induce attractive interaction in both the $s$-wave and odd-parity $E_{u}$ pairing channels, but repulsive interaction in the other two odd-parity $A_{1u}$ and $A_{2u}$ pairing channels. The competition between $s$-wave and $E_{u}$ pairings can be further tuned by Coulomb repulsion, which has the strongest pair-breaking effect in the $s$-wave channel.

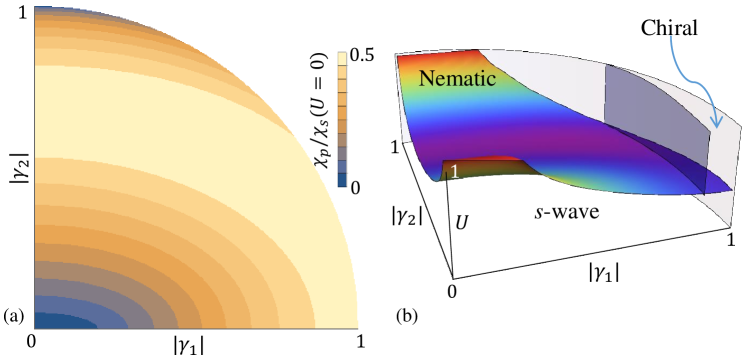
The organization of this paper is the following. In Sec. II, we study odd-parity fluctuations and superconductivity. The fluctuations are possibly induced by electron-phonon interaction. We use an approach that closely follow that in Ref. Kozii and Fu, 2015. Essential details of the approach will be presented to make the discussion self-contained. We obtain a phase diagram (Fig. 1) as a function of phenomenological parameters $\gamma_{i}$ (i=1,2,3) and $U$. $\gamma_{i}$, introduced in Eq. (5), parametrize odd-parity particle-hole fluctuations in $E_{u}$ representation. $U$ is the repulsive interaction in the $s$-wave pairing channel, which can arise from Coulomb repulsion. There is a critical $U_{c}$, above which $E_{u}$ pairing has a higher critical temperature compared to the $s$-wave pairing. $E_{u}$ superconductivity supports two distinct phasesVenderbos et al. (2016b): nematic and chiral, both of which can be realized in the parameter space of $\gamma_{i}$. In Sec. III, we study a phase in the vicinity of $U_{c}$, where even-parity $s$-wave and odd-parity $E_{u}$ pairing can coexist. The coexistence phase spontaneously breaks both time-reversal and lattice discrete rotational symmetries. The gap structures in different superconductivity phases are reviewed. In Sec. IV, we discuss our work in the context of previous studies. We present some related materials in the Appendixes. Appendix A shows that an on-site repulsion in Bi₂Se₃ generates repulsive interaction in both $s$-wave and $A_{2u}$ pairing channels, but not in the $E_{u}$ channel. In Appendixes B and C, we show that odd-parity fluctuations in $A_{1u}$ ($A_{2u}$) representation can generate $A_{1u}$ ($A_{2u}$) Cooper pairing besides the usual $s$-wave pairing.

Before ending the Introduction section, we mention that odd-parity particle-hole fluctuations can become unstable and lead to spontaneous parity-breaking phasesFu (2015), which have been recently observed in Cd₂Re₂O₇Harter et al. (2017).

Electronic bands in Bi₂Se₃ are doubly degenerate at every $\boldsymbol{k}$ point due to the presence of both time-reversal and inversion symmetries. When Bi₂Se₃ is intercalated with Cu, Nb or Sr, the chemical potential lies in the conduction bands. As attractive interaction induced by fluctuations typically occurs in a small energy window around chemical potential, we will only retain the lowest conduction bands in our theory. The Fermi surface of Bi₂Se₃ at low electron doping level is approximately sphericalWray et al. (2010); Lawson et al. (2012). Therefore, we approximate the conduction band by a parabolic dispersion:

which is intended to describe physics near the chemical potential $\mu$. $c_{\boldsymbol{k}}^{\dagger}$ represents a two-component spinor $(c_{\boldsymbol{k}\uparrow}^{\dagger},c_{\boldsymbol{k}\downarrow}^{\dagger})$, which is understood to be in the “manifestly covariant Bloch basis”(MCBB)Fu (2015). Here $\uparrow$ and $\downarrow$ represent pseudospin instead of real spin because of strong spin-orbit coupling. Nevertheless, the pseudospin in the MCBB transforms in the same way as the real spin of a free electron under symmetry operations. In particular, the transformations under time reversal ($\hat{\mathcal{T}}$) and inversion ($\hat{\mathcal{P}}$) operations are:

where $\epsilon_{\alpha\beta}$ is the fully antisymmetric tensor with $\epsilon_{\uparrow\downarrow}=1$.

To study electron-phonon interaction, we focus on phonons at the Brillouin zone center, which can be classified by the $D_{3d}$ point group of Bi₂Se₃. To be specific, we consider $E_{u}$ phonons that are odd under inversion and have two degenerate modes. The coupling between electrons and $E_{u}$ phonons can be expressed as:

where the Hermitian operators $(\phi_{x},\phi_{y})$ represent the $E_{u}$ phonons, and also take into account all coupling constants. $\Gamma_{x,y}(\boldsymbol{k})$ are $2\times 2$ matrices in the pseudospin space. As $H_{el-ph,0}$ should be invariant under all symmetries that the system has, the operators $\hat{Q}_{x,y}$ are Hermitian, time reversal symmetric and form a two-component $E_{u}$ representation. By Hermiticity, we can express $\Gamma_{x,y}(\boldsymbol{k})$ using identity matrix $s_{0}$ and Pauli matrices $\boldsymbol{s}$:

where both the scalar $\tilde{D}_{a}$ and the vector $\boldsymbol{D}_{a}$ are real. By time reversal symmetry, we require $\tilde{D}_{a}(\boldsymbol{k})=\tilde{D}_{a}(-\boldsymbol{k})$ and $\boldsymbol{D}_{a}(\boldsymbol{k})=-\boldsymbol{D}_{a}(-\boldsymbol{k})$. On the other hand, $\hat{Q}_{a}$ is odd under inversion, which leads to $\Gamma_{a}(\boldsymbol{k})=-\Gamma_{a}(-\boldsymbol{k})$. Therefore, $\tilde{D}_{a}(\boldsymbol{k})$ must vanish. In our low-energy theory, odd-parity phonons couple to electron’s spin, which is possible due to the presence of strong spin-orbit coupling.

The form factors $\Gamma_{x,y}(\boldsymbol{k})$ are further restricted by other point group symmetries. There are three basis functions separately for $\Gamma_{x}$ and $\Gamma_{y}$ to first order of $\boldsymbol{k}$ in the $E_{u}$ representation, as listed in Table 1. In general, $\Gamma_{x,y}(\boldsymbol{k})$ is a linear combination of these three basis functions:

where $\gamma_{i}$ are real parameters that are not fixed by symmetries. We will take $\gamma_{i}$ as free parameters and study phase diagrams in this parameter space.

$H_{el-ph,0}$ describes the coupling between electrons and zone-center phonon modes. We generalize the coupling to include phonon modes at finite momentum:

In the generalization, we assume that the phonon modes vary smoothly in real space.

The electron-phonon coupling generates an effective electron-electron interaction:

where $\Omega$ is the system size. By the definition in (6), we have $\hat{Q}_{a}(-\boldsymbol{q})=\hat{Q}_{a}^{\dagger}(\boldsymbol{q})$.

In $H_{int}$, we neglect the frequency dependence of $V_{\boldsymbol{q}}$ for simplicity. The point group symmetries put constraints on the momentum dependence of $V_{\boldsymbol{q}}$: (1) $V_{\boldsymbol{q}}$ is an even function of $\boldsymbol{q}$ and (2) it is invariant under a three-fold rotation of $\boldsymbol{q}$ along $\hat{z}$ direction.

We now restrict the interaction to the Bardeen-Cooper-Schrieffer (BCS) channel:

The expression for the interaction vertex $V_{\alpha\beta\gamma\delta}(\boldsymbol{k},\boldsymbol{k}^{\prime})$ is given by:

where $\boldsymbol{D}_{a}$ and $\boldsymbol{D}_{a}^{\prime}$ are respectively shorthand notations for $\boldsymbol{D}_{a}(\boldsymbol{k})$ and $\boldsymbol{D}_{a}(\boldsymbol{k}^{\prime})$. Here $\boldsymbol{D}_{a}(\boldsymbol{k})$ is the vector representation of $\Gamma_{a}(\boldsymbol{k})$, as introduced in (4).

To minimize the number of parameters in our phenomenogical study, we further approximate $V_{\boldsymbol{q}}$ by its value at zero momentum $V_{0}$. Here $V_{0}<0$, representing attractive interaction induced by phonon fluctuations. Under this simplification, it is convenient to separate $V_{\alpha\beta\gamma\delta}$ to two parts: $V_{\alpha\beta\gamma\delta}=(V^{e}+V^{o})_{\alpha\beta\gamma\delta}$. The expressions for $V^{e,o}$ are as follows:

Here $V^{e}$ and $V^{o}$ are respectively even and odd functions of $\boldsymbol{k}$ and $\boldsymbol{k}^{\prime}$, and, therefore, generate correspondingly even and odd parity pairings. In (10), the final expressions of $V^{e,o}$ are presented in a form that is suitable for BCS decomposition. In the following subsections II.1 and II.2, we study the pairing instabilities in even and odd parity channels separately and finally compare them.

At $U=U_{c}$, the $s$-wave and $E_{u}$ channel have the same critical temperature $T_{c,s}=T_{c,p}=T_{c}^{*}$. To pin down the nature of the superconductivity below $T_{c}^{*}$, we study the Ginzburg-Landau free energy that includes both $s$-wave and $E_{u}$ pairing order parameters:

where $\mathcal{F}_{s}$ is the free energy for $s$-wave pairing characterized by the order parameter $\eta_{s}$, $\mathcal{F}_{p}$ is give in (24) and $\mathcal{F}_{sp}$ describes the coupling between $s$-wave and $E_{u}$ pairings. Parameters in the free energy are again obtained using weak-coupling analysis: $r_{0}=2\kappa(1-|V_{0}|\chi_{s})/|V_{0}|$, $b_{0}=\frac{1}{2}\langle\text{Tr}[g_{0}(\boldsymbol{k})s_{0}]^{4}\rangle\beta_{0}$ and $b_{3}=\frac{1}{2}\langle\text{Tr}[g_{x}^{2}(\boldsymbol{k})g_{0}^{2}(\boldsymbol{k})]\rangle\beta_{0}$. Here $b_{0}$ and $b_{3}$ are always positive.

To minimize $\mathcal{F}$ below $T_{c}^{*}$ at $U=U_{c}$, it is most instructive to consider the case $b_{2}<0$. $\mathcal{F}$ is then minimized by a state where the $s$-wave and nematic superconductivity coexist and have a relative phase difference $\pm\pi/2$, i.e. $\eta_{s}=\pm i|\eta_{s}|$ and $(\eta_{x},\eta_{y})=|\eta_{p}|(\cos\theta,\sin\theta)$. $|\eta_{s}|$ and $|\eta_{p}|$ are given by:

The coexistence of the two superconductivity order parameters requires the expressions for $|\eta_{s}|^{2}$ and $|\eta_{p}|^{2}$ in (27) to be positive, which we find to be generally satisfied in the $\gamma_{i}$ parameter space.

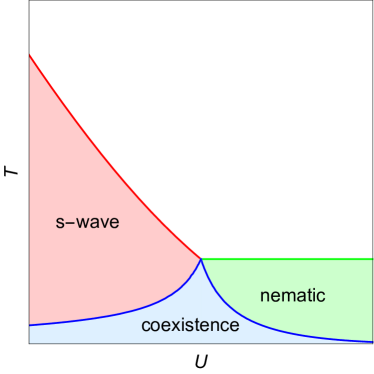
When $U$ is away from $U_{c}$, the coexistence state can still develop, but at a temperature lower than $T_{c,s}$ when $U<U_{c}$ or $T_{c,p}$ when $U>U_{c}$. The schematic phase diagram as a function of $U$ and $T$ is shown in Fig. 2. This coexistence phase not only breaks lattice discrete rotational symmetry because of the presence of nematic order parameter, but also breaks time reversal symmetry because of the relative phase difference $\pm\pi/2$ between the even and odd parity order parameters.

In the case of $b_{2}>0$, there can also be an intermediate phase between $s$-wave and chiral phases in the vicinity of $U_{c}$. This intermediate phase is characterized by non-zero order parameters $(\eta_{s},\eta_{+},\eta_{-})$, where $\eta_{\pm}=\eta_{x}\pm i\eta_{y}$. $|\eta_{+}|$ and $|\eta_{-}|$ are generally unequal so both time reversal and discrete rotational symmetries are also broken.

We now discuss gap structures in different phases. In the $s$-wave phase, the superconductivity gap is proportional to $g_{+}(\boldsymbol{k})$ on the Fermi surface, which is fully gapped for weak repulsion $U$.

To study gap structure in the nematic phase, we express $g_{a}(\boldsymbol{k})$ for $a=x$ and $y$ in terms of a vector:

For order parameter $(\eta_{x},\eta_{y})$ given by $|\eta_{p}|(\cos\theta,\sin\theta)$, the gap is proportional to $|\boldsymbol{d}|$ on the Fermi surface, where the vector $\boldsymbol{d}$ is defined as $\cos\theta\boldsymbol{d}_{x}+\sin\theta\boldsymbol{d}_{y}$. $|\boldsymbol{d}|$ is finite everywhere on the Fermi surface unless $\theta=n\pi/3$ (integer $n$ takes value from 0 to 5). The nematic phase realizes a fully gapped topological superconductor when $\theta\neq n\pi/3$, as it has odd parity pairing and the Fermi surface encloses only one time reversal invariant momentumFu and Berg (2010). A hallmark of a time-reversal invariant topological superconductor is that it supports Majorana modes bound to surfaces and time-reversal-invariant vortex defectsQi et al. (2009); Wu and Martin (2017). When $\theta=n\pi/3$, the nematic pairing preserves one of the mirror symmetries and the gap vanishes at two opposite momenta located on the corresponding mirror-invariant plane in the Brillouin zoneFu (2014). Therefore, the nematic phase with $\theta=n\pi/3$ realizes a topological Dirac superconductor with Dirac point nodes in the bulk and Majorana arcs on certain surfacesYang et al. (2014).

In the coexistence phase where $s$-wave and nematic order parameter has a phase difference $\pm\pi/2$, the Bogoliubov-de Gennes Hamiltonian is:

which is expressed in the basis $(c_{\boldsymbol{k}\uparrow}^{\dagger},c_{\boldsymbol{k}\downarrow}^{\dagger},c_{-\boldsymbol{k}\downarrow},-c_{-\boldsymbol{k}\uparrow})$. $\varepsilon_{0}(\boldsymbol{k})=\hbar^{2}\boldsymbol{k}^{2}/(2m)-\mu$, and $\tau_{x,y,z}$ are Pauli matrices in the Nambu space. Here $|\eta_{p}|$ and $|\eta_{s}|$ are respectively coupled to $\tau_{x}$ and $\tau_{y}$, reflecting the $\pi/2$ phase difference. The energy spectrum of $\mathcal{H}(\boldsymbol{k})$ is $\pm\sqrt{\varepsilon_{0}(\boldsymbol{k})^{2}+|\eta_{p}|^{2}|\boldsymbol{d}(\boldsymbol{k})|^{2}+|\eta_{s}|^{2}g_{+}(\boldsymbol{k})^{2}}$, which is fully gapped for any value of $\theta$. The surface Majorana zero modes presented in the nematic phase also become gapped in the coexistence phase because of broken time reversal symmetry. Such a state represents a superconducting analog of an axion insulatorQi et al. (2008), and can have thermal Hall effect on the surface. Similar phase with coexistence of even and odd parity pairing have been studied in Ref. Goswami and Roy, 2014 and recently in Ref. Wang and Fu, . A distinct feature of the coexistence phase that we obtain is that it spontaneously breaks discrete rotational symmetry besides time reversal symmetry. We also note an additional symmetry breaking in the coexistence phase. In (29), $\mathcal{H}(\boldsymbol{k})$ satisfies an inversion symmetry $\mathcal{H}(\boldsymbol{k})=\mathcal{H}(-\boldsymbol{k})$ when $|\eta_{p}|=0$, or an inversion-gauge symmetry $\tau_{z}\mathcal{H}(\boldsymbol{k})\tau_{z}=\mathcal{H}(-\boldsymbol{k})$ when $|\eta_{s}|=0$. In the coexistence phase, neither the inversion nor inversion-gauge symmetry remains.

The chiral phase characterized by $(\eta_{x},\eta_{y})\propto(1,\pm i)$ realizes a topological Weyl superconductor with bulk Weyl point nodes. The nodal structure has been extensively discussed in Refs. Venderbos et al., 2016b and Kozii et al., 2016. When there is some mixing between $s$-wave and chiral superconductivity near $U_{c}$, the Weyl points remain robust unless two Weyl points with opposite chiralities meet and annihilate each other.

We discuss connections between our work and previous studies. Reference Brydon et al., 2014 reached a general conclusion that pure electron-phonon interaction in a system with time-reversal and inversion symmetries can generate odd-parity superconductivity, but its instability temperature can not be larger than that of the $s$-wave superconductivity. Our results are consistent with this general statement, and we also show that local Coulomb repulsion can tip the balance in favor of odd-parity pairing. In Ref. Wan and Savrasov, 2014, Wan and Savrasov presented a first principle study of phonon mediated superconductivity in Cu doped Bi₂Se₃. Encouragingly, they found that pure electron-phonon interaction does generate odd-parity pairings in both $E_{u}$ and $A_{2u}$ channels besides the usual even-parity channel. Their calculation indicated that the phonon-mediated instability is stronger in $A_{2u}$ channel compared to $E_{u}$ channel. In Appendix A, we show that an on-site repulsive interaction in Bi₂Se₃ generates repulsion in both the $s$-wave channel and $A_{2u}$ channel, but not in $E_{u}$ channel. In general a finite-range repulsive interaction could also suppress $E_{u}$ pairingFu and Berg (2010). However, the on-site interaction presumably leads to the most dominant repulsion, which could make $E_{u}$ pairing more favorable compared to $s$-wave and $A_{2u}$ pairings. It is interesting to reexamine electron-phonon interaction in metal doped Bi₂Se₃ using ab initio calculation. In particular, parameters $\gamma_{i}$, which determine whether nematic or chiral superconductivity is realized in our theory, could be extracted from such a study. In our work, we do not attempt to determine the critical temperature of $E_{u}$ superconductivity. Such a task requires a detailed knowledge about electron-phonon interaction, which we leave for ab initio calculation. The study of Wan and SavrasovWan and Savrasov (2014) has shown that the electron-phonon interaction is capable of producing a critical temperature of $3\sim 5$ K in the $A_{2u}$ channel.

In summary, we studied odd-parity fluctuations as a possible mechanism for the nematic superconductivity observed in doped Bi₂Se₃.

F.W. thanks J.W.F. Venderbos for stimulating discussion. We acknowledge support from Department of Energy, Office of Basic Energy Science, Materials Science and Engineering Division.