Nemo/Hecke: Computer Algebra and Number Theory Packages for the Julia Programming Language
Abstract.
We introduce two new packages, Nemo and Hecke, written in the Julia programming language for computer algebra and number theory. We demonstrate that high performance generic algorithms can be implemented in Julia, without the need to resort to a low-level C implementation. For specialised algorithms, we use Julia’s efficient native C interface to wrap existing C/C++ libraries such as Flint, Arb, Antic and Singular. We give examples of how to use Hecke and Nemo and discuss some algorithms that we have implemented to provide high performance basic arithmetic.
1. Introduction
Nemo111http://nemocas.org. Nemo and Hecke are BSD licensed. is a computer algebra package for the Julia programming language. The eventual aim is to provide highly performant commutative algebra, number theory, group theory and discrete geometry routines. Hecke is a Julia package that builds on Nemo to cover algebraic number theory.
Nemo consists of two parts: wrappers of specialised C/C++ libraries (Flint (flint, ), Arb (arb, ), Antic (antic, ) and Singular (singular, )), and implementations of generic algorithms and mathematical data structures in the Julia language. So far the fully recursive, generic constructions include univariate and multivariate polynomial rings, power series rings, residue rings (modulo principal ideals), fraction fields, and matrices.
We demonstrate that Julia is effective for implementing high performance computer algebra algorithms. Our implementations also include a number of improvements over the state of the art in existing computer algebra systems.
2. Computer algebra in Julia
Julia (julia, ) is a modern programming language designed to be both performant and flexible. Notable features include an innovative type system, multiple dispatch, just-in-time (JIT) compilation supported by dynamic type inference, automatic memory management (garbage collection), metaprogramming capabilities, high performance builtin collection types (dictionaries, arrays, etc.), a powerful standard library, and a familiar imperative syntax (like Python). Julia also has an efficient native C interface, and more recently a C++ interface. In addition, Julia provides an interactive console and can be used with Jupyter notebooks.
Julia was designed with high performance numerical algorithms in mind, and provides near C or Fortran performance for low-level arithmetic. This allows low-level algorithms to be implemented in Julia itself. However, for us, the main advantage of Julia is its ability to JIT compile generic algorithms for specific types, in cases where a specific implementation does not exist in C.
One of the most important features from a mathematical point of view is Julia’s parametric type system. For example, in Julia, a 1-dimensional array of integers has type Array{Int, 1}. We make heavy use of the parametric type system in Nemo and Hecke. Generic polynomials over a ring have type GenPoly{T} where is the type of elements of the ring . Parametric types bear some resemblance to C++ template classes, except that in Julia the type can be constrained to belong to a specified class of types.
2.1. Modelling domains in Julia
Julia provides two levels of types: abstract and concrete types. Concrete types are like types in Java, C or C++, etc. Abstract types can be thought of as collections of types. They are used when writing generic functions that should work for any type in a collection.
To write such a generic function, we first create an abstract type, then we create the individual concrete types that belong to that abstract type. The generic function is then specified with a type parameter, T say, belonging to the abstract type.
In Julia, the symbol ¡: is used to specify that a given type belongs to a given abstract type. For example the built-in Julia type Int64 for 64-bit machine integers belongs to the Julia abstract type Integer.
Abstract types in Julia can form a hierarchy. For example, the Nemo.Field abstract type belongs to the Nemo.Ring abstract type. An object representing a field in Nemo has type belonging to Nemo.Field. But because we define the inclusion Nemo.Field ¡: Nemo.Ring, the type of such an object also belongs to Nemo.Ring. This means that any generic function in Nemo which is designed to work with ring objects will also work with field objects.
Julia always picks the most specific function that applies to a given type. This allows one to implement a function at the most general level of a type hierarchy at which it applies. One can also write a version of a given function for specific concrete types. For example, one may wish to call a specific C implementation for a multiplication algorithm, say, when arguments with a certain very specific given type are passed.
Another way that we make use of Julia’s abstract type system in Nemo/Hecke is to distinguish between the type of elements of fields, and the fields themselves, and similarly for all other kinds of domains in Nemo.
Figure 1 shows the abstract type hierarchy in Nemo.
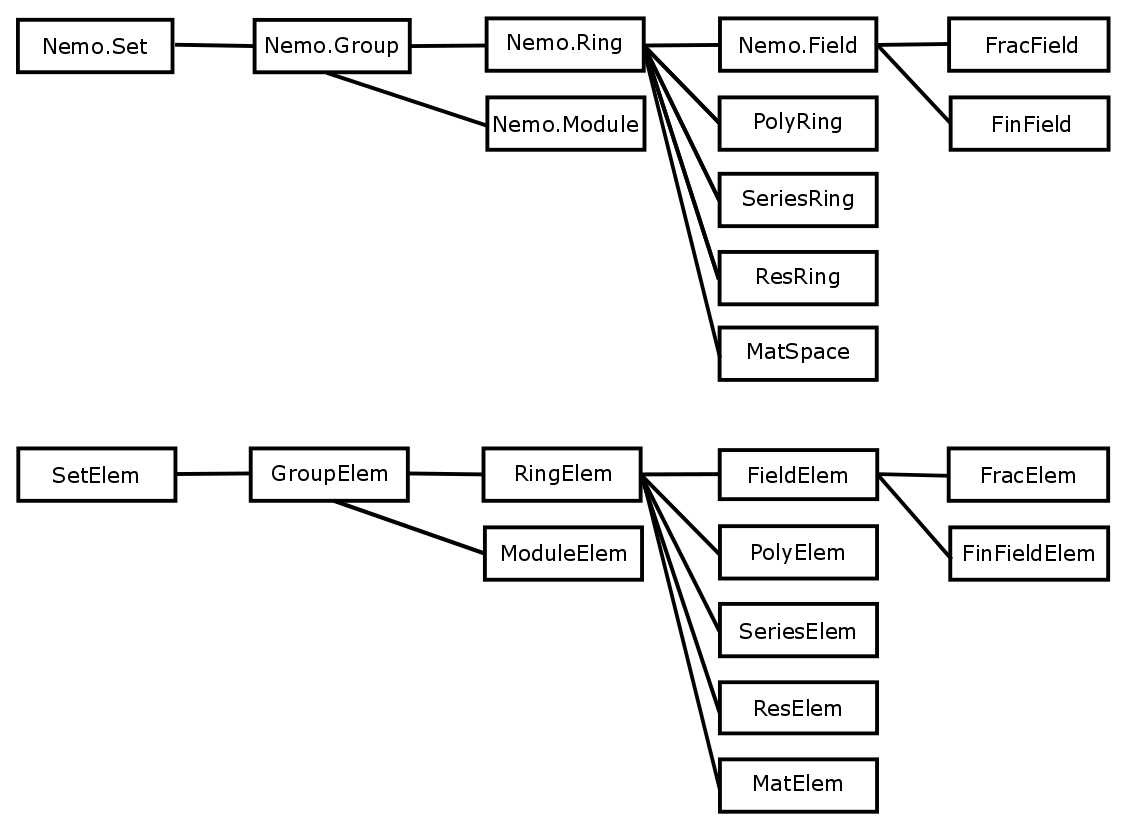
Naively, one may expect that specific mathematical domains in Nemo/Hecke can be modeled as types and their elements as objects of the given type. But there are various reasons why this is not a good model.
As an example, consider the ring . If we were to model the ring as a type, then the type would need to contain information about the modulus . This is not possible in Julia if is an object, e.g. a multiprecision integer. Further, Julia dispatches on type, and each time we call a generic function with values of a new type, the function is recompiled by the JIT compiler for that new type. This would result in very poor performance if we were writing a multimodular algorithm, say, as recompilation would be triggered for each distinct modulus . For this reason, the modulus needs to be attached to the elements of the ring, not to the type associated with those elements.
The way we deal with this is to have special (singleton) objects, known as parent objects, that act like types, but are in fact ordinary Julia objects. As ordinary objects, parents can contain arbitrary information, such as the modulus in . Each object representing an element of the ring then contains a pointer to this parent object.
This model of mathematical parent objects is taken from SageMath (sage, ) which in turn followed Magma (magma, ).
Julia allows ordinary objects to be made callable. We make use of the facility to write coercions and constructors for elements of mathematical domains in Nemo/Hecke. For example, the following code constructs .
R = ResidueRing(ZZ, 7) a = R(3)
We also make use of the parent object system to encode information such as context objects needed by C libraries. As Julia objects can have precisely the same bit representation as native C objects, parent objects can be passed directly to C functions. Additional fields in these objects can be safely appended if it is desirable to retain more information at the Julia level than the C/C++ level.
Nemo wraps C types provided by libraries such as Flint for ground domains. For example, Nemo’s ZZ wraps Flint’s fmpz integer type. Nemo also uses specialised C implementations for nested structures where available. For instance, PolynomialRing(R, "x") which constructs the univariate polynomial ring automatically switches to a wrapper of Flint’s fmpz_poly when instead of using the Julia implementation designed for generic .
2.2. In-place operations
C libraries such as Flint allow mutating objects in-place, which improves performance especially when making incremental updates to large objects. Nemo objects are ostensibly immutable, but special mutation methods are provided for use in critical spots. Instead of writing
s += a * b
in Nemo, which creates an object for a * b and then replaces s with yet another new object, we create a reusable scratch variable t with the same type as a, b and s and use
mul!(t, a, b) addeq!(s, t)
which creates no new objects and avoids making a copy of the data in s that is not being modified.
In Julia, in-place operators save not only memory allocation and copying overheads, but also garbage collection costs, which may be substantial in the worst case.
3. Nemo examples
We present a few Nemo code examples which double as benchmark problems.
3.1. Multivariate polynomials
The Fateman benchmark tests arithmetic in by computing where . In Nemo, this is expressed by the following Julia code:
R,x,y,z,t = PolynomialRing(ZZ, ["x","y","z","t"]) f = (1+x+y+z+t)^30 f*(f+1)
Table 1 shows timing results compared to SageMath 7.4, Magma V2.22-5 and Giac-1.2.2 on a 2.2 GHz AMD Opteron 6174. We used sparse multivariate polynomials in all cases (this benchmark could also be performed using nested dense univariate arithmetic, i.e. in ).
Nemo (generic) is our Julia implementation of Johnson’s sparse multiplication algorithm which handles for generic coefficient rings . Flint (no asm) is a reimplementation of the same algorithm in C for the special case , and Flint (asm) is an assembly optimised version of this code. Finally, Flint (array) and Giac implement an algorithm designed for dense polynomials, in which terms are accumulated into a big array covering all possible exponents.
Table 2 shows timing results on the Pearce benchmark, which consists of computing where , . This problem is too sparse to use the big array method, so only the Johnson algorithm is used.
| Sage- | Magma | Nemo | Flint | Flint | Flint | Giac | |
|---|---|---|---|---|---|---|---|
| Math | (generic) | (no asm) | (asm) | (array) | |||
| 5 | 0.008 | 0.01 | 0.004 | 0.002 | 0.002 | 0.0003 | 0.0002 |
| 10 | 0.53 | 0.12 | 0.11 | 0.04 | 0.02 | 0.005 | 0.006 |
| 15 | 10 | 1.9 | 1.6 | 0.53 | 0.30 | 0.08 | 0.11 |
| 20 | 76 | 16 | 14.3 | 6.3 | 2.8 | 0.53 | 0.62 |
| 25 | 426 | 98 | 82 | 39 | 17.4 | 2.5 | 2.8 |
| 30 | 1814 | 439 | 362 | 168 | 82 | 11 | 14 |
By default, Nemo uses Flint for multivariate polynomials over instead of the generic Julia code 222The new Flint type fmpz_mpoly is presently available in the git version of Flint. The mul_johnson (with and without asm enabled) and mul_array methods were timed via Nemo.. We have timed both versions here to provide a comparison between Julia and C. It is somewhat remarkable that the generic Julia code comes within a factor two of our C version in Flint (without asm), and even runs slightly faster than the C code in Magma.
| SageMath | Magma | Nemo | Flint | Flint | Giac | |
| (generic) | (no asm) | (asm) | ||||
| 4 | 0.01 | 0.01 | 0.008 | 0.003 | 0.002 | 0.004 |
| 6 | 0.20 | 0.08 | 0.07 | 0.03 | 0.03 | 0.03 |
| 8 | 2.0 | 0.68 | 0.56 | 0.16 | 0.15 | 0.28 |
| 10 | 11 | 3.0 | 2.2 | 0.77 | 0.71 | 1.45 |
| 12 | 57 | 11.3 | 8.8 | 3.7 | 3.2 | 4.8 |
| 14 | 214 | 36.8 | 32.3 | 16 | 12 | 14 |
| 16 | 785 | 94.0 | 85.5 | 44 | 32 | 39 |
3.2. Generic resultant
The following Nemo example code computes a resultant in the ring , demonstrating generic recursive rings and polynomial arithmetic. Flint is used for univariate polynomials over a finite field.
R, x = FiniteField(17, 11, "x") S, y = PolynomialRing(R, "y") T = ResidueRing(S, y^3 + 3x*y + 1) U, z = PolynomialRing(T, "z") f = (3y^2+y+x)*z^2 + ((x+2)*y^2+x+1)*z + 4x*y + 3 g = (7y^2-y+2x+7)*z^2 + (3y^2+4x+1)*z + (2x+1)*y + 1 s = f^12 t = (s + g)^12 resultant(s, t)
This example takes 179907 s in SageMath 6.8, 82 s in Magma V2.21-4 and 0.2 s in Nemo 0.4.
3.3. Generic linear algebra
We compute the determinant of a random matrix with entries in a cubic number field. This benchmark tests generic linear algebra over a field with coefficient blowup. The number field arithmetic is provided by Antic.
QQx, x = PolynomialRing(QQ, "x")
K, a = NumberField(x^3 + 3*x + 1, "a")
M = MatrixSpace(K, 80, 80)()
for i in 1:80
for j in 1:80
for k in 0:2
M[i, j] = M[i, j] + a^k * (rand(-100:100))
end
end
end
det(M)
This takes 5893 s in SageMath 6.8, 21.9 s in Pari/GP 2.7.4 (pari, ), 5.3 s in Magma V2.21-4, and 2.4 s in Nemo 0.4.
4. Generic algorithms in Nemo
Many high level algorithms in number theory and computer algebra rely on the efficient implementation of fundamental algorithms. We next discuss some of the algorithms used in Nemo for generic polynomials and matrices.
4.1. Polynomial algorithms
For generic coefficient rings, Nemo implements dense univariate polynomials, truncated power series (supporting both relative and absolute precision models), and multivariate polynomials in sparse distributed format.
The generic polynomial resultant code in Nemo uses subresultant pseudoremainder sequences. This code can even be called for polynomials over a ring with zero divisors, so long as impossible inverses are caught. The exception can be caught using a try/catch block in Julia and a fallback method called, e.g. the resultant can be computed using Sylvester matrices. This allows an algorithm with quadratic complexity to be called generically, with an algorithm of cubic complexity only called as backup.
We make use of variants of the sparse algorithms described by Monagan and Pearce for heap-based multiplication (heapmul, ), exact division and division with remainder (heapdiv, ) and powering (heappow, ). For powering of polynomials with few terms, we make use of the multinomial formula. For multivariate polynomials over , we used the generic Julia code as a template to implement a more optimised C version in Flint.
In the case of pseudodivision for sparse, multivariate polynomials, we extract one of the variables and then use a heap-based, univariate pseudoremainder algorithm inspired by an unpublished manuscript of Monagan and Pearce.
We make use of this pseudoremainder implementation to implement the subresultant GCD algorithm. To speed the latter up, we make use of a number of tricks employed by the Giac/XCAS system (giac, ), as taught to us by Bernard Parisse. The most important of these is cheap removal of the content that accumulates during the subresultant algorithm by analysing the input polynomials to see what form the leading coefficient of the GCD can take.
We also use heuristics to determine which permutation of the variables will lead to the GCD being computed in the fastest time. This heuristic favours the variable with the lowest degree as the main variable for the computation, with the other variables following in increasing order of degree thereafter. But our heuristic heavily favours variables in which the polynomial is monic.
4.2. Matrix algorithms
For computing the determinant over a generic commutative ring, we implemented a generic algorithm making use of Clow sequences (clow, ) which uses only ring operations in the dimension of the matrix. However, two other approaches seem to always outperform it. The first approach makes use of a generic fraction free LU decomposition. This algorithm may fail if an impossible inverse is encountered. However, as a fallback, we make use of a division free determinant algorithm. This computes the characteristic polynomial and then extracts the determinant from that.
For determinants of matrices over polynomial rings, we use an interpolation approach.
We implemented an algorithm for computing the characteristic polynomial due to Danilevsky (see below) and an algorithm that is based on computing the Hessenberg form. We also make use of a generic implementation of the algorithm of Berkowitz which is division free.
As is well known, fraction free algorithms often improve the performance of matrix algorithms over an integral domain. For example, fraction free Gaussian elimination for LU decomposition, inverse, determinant and reduced row echelon form are well-known.
We have also been able to use this strategy in the computation of the characteristic polynomial. We have adapted the well-known 1937 method of Danilevsky (danilevsky, ) for computing the characteristic polynomial, into a fraction-free version.
Danilevsky’s method works by applying similarity transforms to reduce the matrix to Frobenius form. Normally such computations are done over a field, however each of the outer iterations in the algorithm introduce only a single denominator. Scaling by this denominator allows us to avoid fractions. The entries become larger as the algorithm proceeds because of the scaling, but conveniently it is possible to prove that the introduced scaling factor can be removed one step later in the algorithm. This is an exact division and does not lead to denominators.
Removing such a factor has to be done in a way that respects the similarity transforms. We achieve this by making two passes over the matrix to remove the common factor.
4.2.1. Minimal polynomial
Next we describe an algorithm we have implemented for efficient computation of the minimal polynomial of an integer matrix . A standard approach to this problem is known as “spinning” (steel, ). We provide a brief summary of the main ideas, to fix notation and then describe our contribution, which is a variant making use of Chinese remaindering in a provably correct way.
We first summarise the theory for matrices over a field . The theory relies on the following result, e.g. (vinberg, ).
Theorem 4.1.
Suppose is a linear operator on a -vector space , and that for invariant subspaces . Then the minimal polynomial of is LCM, where is the minimal polynomial of restricted to .
The subspaces we have in mind are the following.
Definition 4.2.
Given a vector in a vector space the Krylov subspace associated to is the linear subspace spanned by .
Krylov subspaces are invariant subspaces and so these results lead to an algorithm for computing the minimal polynomial as follows.
Start with and let . For each let be the first standard basis vector that is linearly independent of . Set . By construction, , and the minimal polynomial of is the least common multiple of the minimal polynomials of restricted to the .
The minimal polynomials are easy to compute. For, if , , is a basis for , there is a linear relation
for some , and no smaller such relation. Letting
we have . One sees that for all polynomials and so annihilates all of . Thus is the required minimal polynomial.
To efficiently implement this algorithm, we keep track of and (incrementally) reduce a matrix whose rows consist of all the linearly independent vectors from the Krylov sequences computed so far. Any column without a pivot in this reduced matrix corresponds to a standard basis vector independent of the Krylov subspaces computed so far. As each new Krylov subspace is computed, we append the corresponding vectors to the matrix , and reduce them.
It is also possible to define the minimal polynomial of a matrix over , since the null ideal of a matrix over an integrally closed domain is principal (brown, ).
In the case , we can define the minimal polynomial of to be a (primitive) generator of this ideal. We have that is monic since the characteristic polynomial of is monic and an element of the null ideal. By Gauss’ Lemma for polynomials, this argument also shows that the minimal polynomial of is the same as that of considered as a matrix over .
We have been informed by personal communication that the algorithm used by Magma (magma, ) for minimal polynomial computation over uses spinning, however it uses a -adic approach. Unfortunately we have been unable to find a publication outlining their method.
We describe a multimodular variant of the spinning approach. The idea is to reduce the matrix modulo many small primes and apply the method described above over the field , for each prime . We then combine the minimal polynomials modulo the various primes using Chinese remaindering.
The minimal polynomial of the reduction of modulo is the reduction modulo of the minimal polynomial of for all but finitely many “bad” primes (see (giesbrecht, ) Lemma 2.3). Bad primes are detected if the degrees of the minimal polynomials modulo change at any point during the algorithm.
Whilst bounds on the number of primes required in the Chinese remaindering exist, e.g. based on Ovals of Cassini, these bounds are typically extremely pessimistic. It is also unfortunately too expensive to simply evaluate the minimal polynomial at the matrix and compare with zero.
We obtain a better termination criterion by allowing a small amount of information to ’leak’ from the modulo minimal polynomial computations. Namely, for one of the (good) primes , we record which standard basis vectors were used to generate the Krylov subspaces when computing the minimal polynomial of . Recall that , where is thought of as a linear operator on .
Thinking of as a linear operator on a -vector space , and letting , where is the lift of to , it is clear that .
Thus, if is believed to be the minimal polynomial of , e.g. because the Chinese remaindering has stabilised, then if for all , then is the minimal polynomial of over . This follows because if then annihilates all of for each . Thus it annihilates all of .
The cost of computing the is usually low compared to computing directly, since it consists of matrix-vector rather than matrix-matrix multiplications.
In the worst case this algorithm requires operations over (once we encounter a good prime), but this is far from the generic case, even when the minimal polynomial is not the characteristic polynomial.
In practice our multimodular algorithm seems to slightly outperform Magma on the examples we have tried, including matrices with minimal polynomial smaller than the characteristic polynomial. A generic version of the algorithm over fields is implemented in Julia code in Nemo, and an efficient version over using the Chinese remaindering trick is implemented in Flint and made available in Nemo.
5. C/C++ wrappers in Nemo
5.1. Flint: arithmetic and number theory
Flint provides arithmetic over , , , as well as matrices, polynomials and power series over most of these ground rings. Nemo implements elements of these rings as thin wrappers of the Flint C types.
Flint uses a number of specialised techniques for each domain. For example, Flint’s multiplication in uses a best-of-breed algorithm which selects classical multiplication, Karatsuba multiplication, Kronecker segmentation or a Schönhage-Strassen FFT, with accurate cutoffs between algorithms, depending on the degrees and coefficient sizes.
In some cases, Flint provides separate implementations for word-size and arbitrary-size coefficients. Nemo wraps both versions and transparently selects the optimised word-size version when possible.
Additional Flint algorithms wrapped by Nemo include primality testing, polynomial factorisation, LLL, and Smith and Hermite normal forms of integer matrices.
5.2. Arb: arbitrary precision ball arithmetic
Computing over and requires using some approximate model for these fields. The most common model is floating-point arithmetic. However, for many computer algebra algorithms, the error analysis necessary to guarantee correct results with floating-point arithmetic becomes impractical. Interval arithmetic solves this problem by effectively making error analysis automatic.
Nemo includes wrapper code for the C library Arb, which implements real numbers as arbitrary-precision midpoint-radius intervals (balls) and complex numbers as rectangular boxes + . Nemo stores the precision in the parent object. For example, R = ArbField(53) creates a field of Arb real numbers with 53-bit precision. Arb also supplies types for polynomials, power series and matrices over and , as well as transcendental functions. Like Flint, Arb systematically uses asymptotically fast algorithms for operations such as polynomial multiplication, with tuning for different problem sizes.
Many problems can be solved using lazy evaluation: the user can try a computation with some tentative precision and restart with precision if that fails. The precision can be set optimally when a good estimate for the minimal required is available; that is, the intervals can be used as if they were plain floating-point numbers, and the automatic error bounds simply provide a certificate.
Alternative implementations of and may be added to Nemo in the future. For example, it would sometimes be more convenient to use a lazy bit stream abstraction in which individual numbers store a symbolic DAG representation to allow automatically increasing their own precision.
5.3. Antic: algebraic number fields
Antic is a C library, depending on Flint, for doing efficient computations in algebraic number fields. Nemo uses Antic for number field element arithmetic. We briefly describe some of the techniques Antic uses for fast arithmetic, but refer the reader to the article (antic, ) for full details.
Antic represents number field elements as Flint polynomials thereby benefiting from the highly optimised polynomial arithmetic in Flint. However, a few more tricks are used.
Firstly, Antic makes a number of precomputations which are stored in a context object to speed up subsequent computations with number field elements. Number field parent objects in Nemo consist precisely of these context objects.
The first is a precomputed inverse of the leading coefficient of the defining polynomial of the number field. This helps speed up reduction modulo the defining polynomial.
The second is an array of precomputed powers modulo the defining polynomial . This allows fast reduction of polynomials whose degree exceeds that of the defining polynomial, e.g. in multiplication of number field elements and where one wants wants to compute .
The third precomputation is of Newton sums where the are the roots of the defining polynomial . These Newton sums are precomputed using recursive formulae as described in (Cohen1993, ). They are used to speed up the computation of traces of elements of the number field.
Norms of elements of number fields are computed using resultants, for which we use the fast polynomial resultant code in Flint. Inverses of elements are computed using the fast polynomial extended GCD implementation in Flint.
Antic also offers the ability to do multiplication of number field elements without reduction. This is useful for speeding up the dot products that occur in matrix multiplication, for example. Instead of reducing after every multiplication, the unreduced products are first accumulated and their sum can be reduced at the end of the dot product.
To facilitate delayed reduction, all Antic number field elements are allocated with sufficient space to store a full polynomial product, rather than the reduction of such a product.
5.4. Singular: commutative algebra
Singular (singular, ) is a C/C++ package for polynomial systems and algebraic geometry. Recently, we helped prepare a Julia package called Singular.jl, which is compatible with Nemo. It will be described in a future article.
6. Hecke: algebraic number theory in Julia
Hecke is a tool for algebraic number theory, written in Julia. Hecke includes the following functionality:
-
•
element and ideal arithmetic in orders of number fields,
-
•
class group and unit group computation,
-
•
verified computations with embeddings and
-
•
verified residue computation of Dedekind zeta functions.
Hecke is written purely in Julia, though it makes use of Flint, Arb and Antic through the interface provided by Nemo. Hecke also applies the generic constructions and algorithms provided by Nemo to its own types. This allows for example to work efficiently with polynomials or matrices over rings of integers without the necessity to define special types for these objects.
For most computational challenges we rely on well known techniques as described in (Cohen1993, ; Pohst1997, ; Belabas2004, ) (with a few modifications). However, we use new strategies for ideal arithmetic and computations with approximations.
6.1. Fast ideal arithmetic in rings of integers
A classical result is that in Dedekind domains, as for the ring of integers of a number field, any ideal can be generated using only two elements, one of which can be chosen at random in the ideal. This representation is efficient in terms of space compared to storing a -basis. However, the key problem is the lack of efficient algorithms for working with two generators. We remark that one operation is always efficient using two generators: powering of ideals.
A refinement of this idea, due to Pohst and Zassenhaus (Pohst1997, , p. 400), is a normal presentation. Here a finite set of prime numbers is fixed, typically containing at least all prime divisors of the norm of the ideal. Then, based on this set, the two generators are chosen: The first as an integer having only divisors in —but typically with too high multiplicities. The second generator then has the correct multiplicity at all prime ideals over primes in —but is allowed to have other divisors as well.
For the remainder of this section, let be a number field of degree and be its ring of integers.
Definition 6.1.
Let be a finite set of prime numbers and a nonzero ideal such that all primes dividing the norm are in . A tuple is an -normal presentation for if and only if
-
•
we have , ,
-
•
for all prime ideals over we have for the exponential valuation associated to ,
-
•
for all prime ideals over we have .
A direct application of the Chinese remainder theorem shows the existence of such normal presentations. The algorithmic importance comes from the following result.
Theorem 6.2.
Let be an ideal in -normal presentation. Then the following hold:
-
(1)
We have .
-
(2)
If is a second ideal in -normal presentation for the same set , then is also a -normal presentation.
-
(3)
Let , , with coprime , and only divisible by primes not in . Then is an -normal presentation.
-
(4)
If is a prime number and a prime ideal over in -normal presentation, then the -normal presentation of yields a valuation element, that is, for all .
It should be noted that (almost all) prime ideal are naturally computed in -normal presentation. The key problem in using the theorem for multiplication is that both ideals need to be given by an -normal presentation for the same set , which traditionally is achieved by recomputing a suitable presentation from scratch, taking random candidates for the second generator until it works. Based on the following lemma, we have developed a new algorithm that manages it at the cost of a few integer operations only.
Lemma 6.3.
Let be a finite set of prime numbers and an ideal in -normal presentation. Let be a second set of primes and set as well as . If , then is an -normal presentation, where .
Proof.
By definition, has only prime divisors in , so and are coprime. Also, is a possible first generator for the -normal presentation. Let be a prime ideal over a prime , then since due to and by definition. For coming from , we have since and as well. ∎
Using this lemma on both input ideals, we can obtain compatible -normal presentations at the cost of two computations, a few integer multiplications and two products of integers with algebraic numbers. The final ideal multiplication is then a single integer product and a product of algebraic numbers. Thus the asymptotic cost is that of a single multiplication of two algebraic numbers. In contrast, all previous algorithms require a linear algebra step.
Finally, we improve on the computation of an -normal presentation.
Lemma 6.4.
If , then where is minimal such that .
Theorem 6.5 ((Pohst1997, )).
Let be a nonzero ideal. Then the tuple is an -normal presentation of if and only if , where .
Together with the above lemma, this allows for the rapid computation of a normal presentation: Choose at random until a normal presentation is obtained. It can be shown that, unless involves many ideals of small norm, this is very efficient.
To illustrate the speed of our algorithm, we created a list of ideals of bounded norm (here: 400) and took random products of 100 ideals in the field defined by the polynomial for . The results are presented in Table 3. Times are given in seconds.
| Magma | Pari | Hecke | |
|---|---|---|---|
| 16 | 8.44 | 0.05 | 0.02 |
| 32 | 235.82 | 0.18 | 0.04 |
| 64 | 905.44 | 0.96 | 0.06 |
| 128 | 7572.19 | 5.40 | 0.08 |
6.2. The use of interval arithmetic
One is often forced to study algebraic number fields in a real or complex setting, e.g. embeddings into an algebraically closed field, or computing Dedekind zeta functions. This can be due to an intrinsic property of the problem, or it may be the fastest (known) way to solve the problem. Either way, the price is working with approximations. We give a few examples of this and show how the ball arithmetic provided by Arb is employed in Hecke for this purpose.
6.2.1. Computing conjugates
Let be an algebraic number field, where is an irreducible polynomial of degree . We represent the elements of as polynomials of degree less than . Denoting by the roots of in , the distinct embeddings are given by . For an element of the complex numbers , are called the conjugates of . Since for the conjugates are irrational, it is clear that we must rely on approximations.
In Hecke this is done using ball arithmetic. Let be an element of . Assume that we want to find with for some precision . Using Arb’s polynomial root finding functionality and some initial precision we find balls such that and . Ball arithmetic then yields balls with
Finally we check whether . If not, we increase the working precision and repeat. When finished, the midpoints of the balls are approximations with the desired property. The following Hecke code illustrates this.
QQx, x = PolynomialRing(QQ, "x")
K, a = NumberField(x^3 + 3*x + 1, "a")
alpha = a^2 + a + 1
p = 128; p’ = p
while true
CCy, y = PolynomialRing(AcbField(p’), "y")
g = CCy(x^3 + 3*x + 1)
rts = roots(g)
z = map(x^2 + x + 1, rts)
if all([ radiuslttwopower(u, -p) for u in z])
break
else
p’ = 2*p’
end
end
To perform the same task using floating point arithmetic would require a priori error analysis. Arb’s ball arithmetic allows the error analysis to be carried along with the computation. This allows for fast development, while at the same time maintaining guaranteed results.
6.2.2. Torsion units
For an algebraic number field of degree , the set of torsion units is a finite cyclic subgroup of , which plays an important role when investigating the unit group of the ring of integers of .
Given it is important to quickly check if it is a torsion unit. A list of possible integers with can be obtained as follows: If is a torsion unit, then is a primitive -th root of unity for some . In particular contains the -th cyclotomic field and divides . Since there are only finitely many with the property that divides , for every such we can test and in this way decide whether is a torsion unit. While this works well for small , for large this quickly becomes inefficient.
A second approach rests on the fact that torsion units are characterized by their conjugates: An element is a torsion unit if and only if for . Although we can compute approximations of conjugates with arbitrary precision, since conjugates are in general irrational, it is not possible test whether they (or their absolute value) are exactly equal to .
We make use of the following result of Dobrowolski (Dobrowolski1978, ), which bounds the modulus of conjugates of non-torsion units.
Lemma 6.6.
If is not a torsion unit, then there exists some such that
We can rephrase this using approximation as follows.
Lemma 6.7.
Let , , be sequences of real balls with and for .
-
(1)
If the element is torsion, there exists such that for some .
-
(2)
If the element is non-torsion, there exists such that for all .
It is straightforward to turn this into an algorithm to test whether is torsion: Approximate the conjugates of using balls as in 6.2.1 for some starting precision and check if one of the statements of Lemma 6.7 hold. If not, increase the precision and start over. Since the radii of the balls tend to , by Lemma 6.7 the algorithm will eventually terminate.
6.2.3. Residues of Dedekind zeta functions
For a number field and , , the Dedekind zeta function of is defined as
where the sum is over all nonzero ideals of the ring of integers of . This function has an analytic continuation to the whole complex plane with a simple pole at . The analytic class number formula (Cohen1993, ) states that the residue at that pole encodes important arithmetic data of :
where is the class number, is the regulator and is another (easy to determine) constant depending on .
The analytic class number formula is an important tool during class group computations. By approximating the residue, it allows one to certify that tentative class and unit groups are in fact correct (see (Biasse2014, )).
We describe the approximation under GRH using an algorithm of Belabas and Friedmann (Belabas2015, ), but it is also possible with results from Schoof (Schoof1982, ) or Bach (Bach1995, ). Since the aim is to illustrate the use of ball arithmetic, we will not give detailed formulas for the approximation or the error.
Theorem 6.8 (Belabas-Friedmann).
There exist functions , , with
for all . The evaluation of involves only prime powers and prime ideal powers with . Moreover the function is strictly decreasing and depends only on the degree and the discriminant of .
Assume that and we want to find such that
We first compute an such that . Note that since is strictly decreasing, this can be done using ordinary floating point arithmetic with appropriate rounding modes. Once we have this value we compute a real ball with and (as usual we progressively increase precision until the radius of the ball is small enough). By the choice of , the midpoint of is an approximation to the logarithm of the residue with error at most . Again this yields a guaranteed result, but avoids the tedious error analysis due to the form of .
7. Acknowledgments
This work was supported by DFG priority project SPP 1489, DFG SFB-TRR 195 and ERC Starting Grant ANTICS 278537.
References
- (1) E. Bach, Improved approximations for Euler products, Number theory (Halifax, NS, 1994), vol. 15, CMS Conference Proceedings, pages 13–28. Amer. Math. Soc., Providence, RI, 1995.
- (2) K. Belabas, Topics in computational algebraic number theory, J. Théor. Nombres Bordeaux, 16(1):19–63, 2004.
- (3) K. Belabas, E. Friedman. Computing the residue of the Dedekind zeta function, Math. Comp., 84(291):357–369, 2015.
- (4) J. Bezanson, A. Edelman, S. Karpinski, V. B. Shah, Julia: A fresh approach to numerical computing, https://arxiv.org/abs/1411.1607
- (5) J.-F. Biasse, C. Fieker, Subexponential class group and unit group computation in large degree number fields, LMS J. Comput. Math., 17(suppl. A):385–403, 2014.
- (6) W. Bosma, J. J. Cannon, C. Fieker, A. Steel (Eds.), Handbook of Magma Functions, Edition 2.22 (2016).
- (7) W. Brown, Null ideals and spanning ranks of matrices, Comm. Algebra 26, (1998), pp. 2401–2417.
- (8) H. Cohen, A course in computational algebraic number theory, Graduate Texts in Mathematics, vol. 138, Springer-Verlag, Berlin, 1993.
- (9) A. Danilevsky, The numerical solution of the secular equation, (Russian), Matem. Sbornik, 44(2), 1937. pp. 169–171.
- (10) W. Decker, G. M. Greuel, G. Pfister and H. Schönemann, Singular – A computer algebra system for polynomial computations, http://www.singular.uni-kl.de
- (11) E. Dobrowolski, On the maximal modulus of conjugates of an algebraic integer, Bull. Acad. Polon. Sci. Sér. Sci. Math. Astronom. Phys., 26(4):291–292, 1978.
- (12) L. Fousse, G. Hanrot, V. Lefèvre, P. Pélissier, P. Zimmermann, MPFR: A multiple-precision binary floating-point library with correct rounding, ACM Trans. Math. Soft., vol. 33, (2), 13, (2007), pp. 1–15.
- (13) J. von zur Gathen, J. Gerhard, Modern Computer Algebra, Cambridge University Press, 1999.
- (14) M. Giesbrecht, A. Storjohann, Computing rational forms of integer matrices. Journal of Symbolic Computation, 2002, v. 34(3), pp. 157–172.
- (15) T. Granlund and the GMP development team, The GNU Multi Precision Arithmetic Library, http://gmplib.org/
- (16) W. Hart, ANTIC: Algebraic Number Theory in C, Computeralgebra Rundbrief 56, Fachgruppe Computeralgebra, 2015, http://www.fachgruppe-computeralgebra.de/data/CA-Rundbrief/car56.pdf
- (17) W. Hart, F. Johansson, S. Pancratz, FLINT: Fast Library for Number Theory, http://www.flintlib.org
- (18) F. Johansson, Arb: A C library for ball arithmetic, http://arblib.org
- (19) M. Monagan, R. Pearce, Sparse polynomial division using a heap, Journal of Symbolic Computation, vol. 46, (7), July 2011, pp. 807–822.
- (20) M. Monagan, R. Pearce, Parallel sparse polynomial multiplication using heaps, ISSAC’09, ACM Press (2009), pp. 263–269.
- (21) M. Monagan, R. Pearce, Sparse polynomial powering using heaps, Gerdt V.P., Koepf W., Mayr E.W., Vorozhtsov E.V. (eds) Computer Algebra in Scientific Computing. CASC 2012. Lecture Notes in Computer Science, vol 7442. Springer, Berlin, Heidelberg (2012), pp. 236–247.
- (22) PARI Group, PARI/GP version 2.9.0, Univ. Bordeaux, 2016, http://pari.math.u-bordeaux.fr/
- (23) B. Parisse, R. De Graeve, Giac/Xcas version 1.2.2, 2016, http://www-fourier.ujf-grenoble.fr/~parisse/giac.html
- (24) M. Pohst, H. Zassenhaus, Algorithmic algebraic number theory, Cambridge University Press, Cambridge, 1997.
- (25) Sage Developers, SageMath, the Sage Mathematics Software System (Version 7.4), 2016, http://www.sagemath.org
- (26) R. J. Schoof, Quadratic fields and factorization, In Computational methods in number theory, Part II, volume 155 of Math. Centre Tracts, pages 235–286. Math. Centrum, Amsterdam, 1982.
- (27) M. Soltys, Berkowitz’s algorithm and clow sequences, The Electronic Journal of Linear Algebra, Int. Linear Algebra Society, vol 9, Apr. 2002, pp. 42–54.
- (28) A. Steel, A new algorithm for the computation of canonical forms of matrices over fields, J. Symbolic Computation (1997) 24, pp. 409–432.
- (29) E. Vinberg, A Course in Algebra, American Mathematical Society, 2003, pp. 229.