Network Coding Capacity: A Functional Dependence Bound

Satyajit Thakor, Alex Grant and Terence Chan satyajitsinh.thakor@postgrads.unisa.edu.au Institute for Telecommunications Research
University of South Australia

Abstract

Explicit characterization and computation of the multi-source network coding capacity region (or even bounds) is long standing open problem. In fact, finding the capacity region requires determination of the set of all entropic vectors $\Gamma^{*}$ , which is known to be an extremely hard problem. On the other hand, calculating the explicitly known linear programming bound is very hard in practice due to an exponential growth in complexity as a function of network size. We give a new, easily computable outer bound, based on characterization of all functional dependencies in networks. We also show that the proposed bound is tighter than some known bounds.

I Introduction

The network coding approach introduced in [1, 2] generalizes routing by allowing intermediate nodes to forward packets that are coded combinations of all received data packets. This yields many benefits that are by now well documented in the literature [3, 4, 5, 6]. One fundamental open problem is to characterize the capacity region and the classes of codes that achieve capacity. The single session multicast problem is well understood. In this case, the capacity region is characterized by max-flow/min-cut bounds and linear network codes maximize throughput [2].

Significant complications arise in more general scenarios, involving more than one session. Linear network codes are not sufficient for the multi-source problem [7, 8]. Furthermore, a computable characterization of the capacity region is still unknown. One approach is to bound the capacity region by the intersection of a set of hyperplanes (specified by the network topology and sink demands) and the set of entropy functions $\Gamma^{*}$ (inner bound), or its closure $\bar{\Gamma}^{*}$ (outer bound) [9, 10, 3]. An exact expression for the capacity region does exist, again in terms of $\Gamma^{*}$ [11]. Unfortunately, this expression, or even the bounds [9, 10, 3] cannot be computed in practice, due to the lack of an explicit characterization of the set of entropy functions for more than three random variables. In fact, it is now known that $\Gamma^{*}$ cannot be described as the intersection of finitely many half-spaces [12]. The difficulties arising from the structure of $\Gamma^{*}$ are not simply an artifact of the way the capacity region and bounds are written. In fact it has been shown that the problem of determining the capacity region for multi-source network coding is completely equivalent to characterization of $\Gamma^{*}$ [8].

One way to resolve this difficulty is via relaxation of the bound, replacing the set of entropy functions with the set of polymatroids $\Gamma$ (which has a finite characterization). In practice however, the number of variables and constraints increase exponentially with the number of links in the network, and this prevents practical computation for any meaningful case of interest.

In this paper, we provide an easily computable relaxation of the LP bound. The main idea is to find sets of edges which are determined by the source constraints and sink demands such that the total capacity of these sets bounds the total throughput. The resulting bound is tighter than the network sharing bound [13] and the bounds based on information dominance [14].

Section II provides some background on pseudo-variables and pseudo entropy functions (which generalize entropy functions) [8]. These pseudo variables are used to describe a family of linear programming bounds on the capacity region for network coding. In Section III we give an abstract definition of a functional dependence graph, which expresses a set of local dependencies between pseudo variables (in fact a set of constraints on the pseudo entropy). Our definition extends that introduced by Kramer [15] to accommodate cycles. This section also provides the main technical ingredients for our new bound. In particular, we describe a test for functional dependence, and give a basic result relating local and global dependence. The main result is presented in Section IV.

Notation: Sets will be denoted with calligraphic typeface, e.g. $\mathcal{X}$ . Set complement is denoted by the superscript $\mathcal{X}^{c}$ (where the universal set will be clear from context). Set subscripts identify the set of objects indexed by the subscript: $X_{\mathcal{A}}=\{X_{a},a\in\mathcal{A}\}$ . The power set $2^{\mathcal{X}}=\{\mathcal{A},\mathcal{A}\subseteq\mathcal{X}\}$ is the collection of all subsets of $\mathcal{X}$ . Where no confusion will arise, set union will be denoted by juxtaposition, $\mathcal{A}\cup\mathcal{B}=\mathcal{A}\mathcal{B}$ , and singletons will be written without braces.

II Background

II-A Pseudo Variables

We give a brief revision of the concept of pseudo-variables, introduced in [8]. Let $\mathcal{N}=\{1,2,\dots,N\}$ be a finite set, and let $X_{\mathcal{N}}=\{X_{1},X_{2},\dots,X_{N}\}$ be a ground set associated with a real-valued function $g:2^{X_{\mathcal{N}}}\mapsto{\mathbb{R}}$ defined on subsets of $X_{\mathcal{N}}$ , with $g(\emptyset)=0$ . We refer to the elements of $X_{\mathcal{N}}$ as pseudo-variables and the function $g$ as a pseudo-entropy function. Pseudo-variables and pseudo-entropy generalize the familiar concepts of random variables and entropy. Pseudo-variables do not necessarily take values, and there may be no associated joint probability distribution. A pseudo-entropy function may assign values to subsets of $X_{\mathcal{N}}$ in a way that is not consistent with any distribution on a set of $N$ random variables. A pseudo-entropy function $g$ can be viewed as a point in a $2^{N}$ dimensional Euclidean space, where each coordinate of the space is indexed by a subset of $X_{\mathcal{N}}$ .

A function $g$ is called polymatroidal if it satisfies the polymatroid axioms.

$\displaystyle g(\emptyset)$	$\displaystyle=0$		(1)
$\displaystyle g(X_{\mathcal{A}})$	$\displaystyle\geq g(X_{\mathcal{B}}),\quad\text{if}\ \mathcal{B}\subseteq\mathcal{A}$	non-decreasing	(2)
$\displaystyle g(X_{\mathcal{A}})+g(X_{\mathcal{B}})$	$\displaystyle\geq g({X_{\mathcal{A}\cup\mathcal{B}}})+g({X_{\mathcal{A}\cap\mathcal{B}}})$	submodular	(3)

It is called Ingletonian if it satisfies Ingleton’s inequalities (note that Ingletonian $g$ are also polymatroids) [16]. A function $g$ is entropic if it corresponds to a valid assignment of joint entropies on $N$ random variables, i.e. there exists a joint distribution on $N$ discrete finite random variables $Y_{1},\dots,Y_{N}$ with $g(X_{\mathcal{A}})=H(Y_{\mathcal{A}}),\mathcal{A}\subseteq\mathcal{N}$ . Finally, $g$ is almost entropic if there exists a sequence of entropic functions $h^{(k)}$ such that $\lim_{k\to\infty}h^{(k)}=g$ . Let $\Gamma^{*}\subset\bar{\Gamma}^{*}\subset\Gamma^{\text{In}}\subset\Gamma$ respectively denote the sets of all entropic, almost entropic, Ingletonian and polymatroidal, functions.

Both $\Gamma$ and $\Gamma^{\text{In}}$ are polyhedra. They can be expressed as the intersection of a finite number of half-spaces in ${\mathbb{R}}^{N}$ . In particular, every $g\in\Gamma$ satisfies, (1)-(3), which can be expressed minimally in terms of

N+\binom{N}{2}2^{N-2}

linear inequalities involving $2^{N}-1$ variables [9]. Each $g\in\Gamma^{\text{In}}$ satisfies an additional

\frac{1}{4}6^{N}-5^{N}+\frac{3}{2}4^{N}-3^{N}+\frac{1}{4}2^{N}

linear inequalities [16].

Definition 1

Let $\mathcal{A},\mathcal{B}\subseteq\mathcal{X}$ be subsets of a set of pseudo-variables $\mathcal{X}$ with pseudo-entropy $g$ . Define¹¹1Note that this yields the chain rule for pseudo-entropies to be true by definition.

g\left(\mathcal{B}\mid\mathcal{A}\right)\triangleq g\left(\mathcal{A}\mathcal{B}\right)-g(\mathcal{A}).

(4)

A pseudo-variable $X\in\mathcal{X}$ is said to be a function of a set of pseudo-variables $\mathcal{A}\subseteq\mathcal{X}$ if $g\left(X\mid\mathcal{A}\right)=0$ .

Definition 2

Two subsets of pseudo-variables $\mathcal{A}$ and $\mathcal{B}$ are called independent if $g\left(\mathcal{A}\mathcal{B}\right)=g(\mathcal{A})+g(\mathcal{B})$ , denoted by $\mathcal{A}\operatorname{\perp}\mathcal{B}$ .

II-B Network Coding and Capacity Bounds

Let the directed acyclic graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ serve as a simplified model of a communication network with error-free point-to-point communication links. Edges $e\in\mathcal{E}$ have capacity $C_{e}>0$ . For edges $e,f\in\mathcal{E}$ , write $f\to e$ as shorthand for $\mathrm{head}(f)=\mathrm{tail}(e)$ . Similarly, for an edge $f\in\mathcal{E}$ and a node $u\in\mathcal{V}$ , the notations $f\to u$ and $u\rightarrow f$ respectively denote $\mathrm{head}(f)=u$ and $\mathrm{tail}(f)=u$ .

Let $\mathcal{S}$ be an index set for a number of multicast sessions, and let $\{Y_{s}:s\in\mathcal{S}\}$ be the set of source variables. These sources are available at the nodes identified by the mapping $a:\mathcal{S}\mapsto\mathcal{V}$ . Each source may be demanded by multiple sink nodes, identified by the mapping $b:\mathcal{S}\mapsto 2^{\mathcal{V}}$ . Each edge $e\in\mathcal{E}$ carries a variable $U_{e}$ which is a function of incident edge variables and source variables.

Definition 3

Given a network $\mathcal{G}=(\mathcal{V},\mathcal{E})$ , with sessions $\mathcal{S}$ , source locations $a$ and sink demands $b$ , and a subset of pseudo-entropy functions $\Delta\subset{\mathbb{R}}^{2^{|\mathcal{S}|+|\mathcal{E}|}}$ on pseudo-variables $Y_{\mathcal{S}},U_{\mathcal{E}}$ , let $\mathcal{R}(\Delta)=\{(R_{s},s\in\mathcal{S})\}$ be the set of source rate tuples for which there exists a $g\in\Delta$ satisfying

$\displaystyle\operatorname{\perp}_{s\in\mathcal{S}}$	$\displaystyle\;Y_{s}$	( $\mathcal{C}_{1}$ )
$\displaystyle g\left(U_{e}\mid\{Y_{s}:{a(s)\to e}\},\{U_{f}:f\to e\}\right)$	$\displaystyle=0,e\in\mathcal{E}$	( $\mathcal{C}_{2}$ )
$\displaystyle g\left(Y_{s}\mid U_{e}:{e\to u}\right)$	$\displaystyle=0,u\in b(s)$	( $\mathcal{C}_{3}$ )
$\displaystyle g(U_{e})$	$\displaystyle\leq C_{e},e\in\mathcal{E}$	( $\mathcal{C}_{4}$ )
$\displaystyle g(Y_{s})$	$\displaystyle\geq R_{s},s\in\mathcal{S}$

It is known that $\mathcal{R}({\Gamma^{*})}$ and $\mathcal{R}({\bar{\Gamma}^{*})}$ are inner and outer bounds for the set of achievable rates (i.e. rates for which there exist network codes with arbitrarily small probability of decoding error).

It is known that $\mathcal{R}(\Gamma)$ is an outer bound for the set of achievable rates [9]. Similarly, $\mathcal{R}(\Gamma^{\text{In}})$ is an outer bound for the set of rates achievable with linear network codes [8]. Clearly $\mathcal{R}(\Gamma^{\text{In}})\subset\mathcal{R}(\Gamma)$ . The sum-rate bounds induced by $\mathcal{R}(\Gamma^{\text{In}})$ and $\mathcal{R}(\Gamma)$ can in principle be computed using linear programming, since they may be reformulated as

\begin{split}\max\sum_{s\in\mathcal{S}}g(Y_{s})\quad\text{subject to}\\ g\in\mathcal{C}_{1}\cap\mathcal{C}_{2}\cap\mathcal{C}_{3}\cap\mathcal{C}_{4}\cap\Delta\end{split}

(5)

where $\Delta$ is either $\Gamma$ or $\Gamma^{\text{In}}$ , and $\mathcal{C}_{1},\mathcal{C}_{2},\mathcal{C}_{3},\mathcal{C}_{4}$ are the subsets of pseudo-entropy functions satisfying the so-labeled constraints above. Clearly the constraint set $\mathcal{C}_{1}\cap\mathcal{C}_{2}\cap\mathcal{C}_{3}\cap\mathcal{C}_{4}\cap\Delta$ is linear.

One practical difficulty with computation of (5) is the number of variables and the number of constraints due to $\Gamma$ (or $\Gamma^{\text{In}}$ ), both of which increase exponentially with $|\mathcal{E}|$ . The aim of this paper is to find a simpler outer bound. One approach is to use the functional dependence structure induced by the network topology to eliminate variables or constraints from $\Gamma$ [17]. Here we will take a related approach, that directly delivers an easily computable bound.

III Functional Dependence Graphs

Definition 4 (Functional Dependence Graph)

Let $\mathcal{X}=\{X_{1},\dots,X_{N}\}$ be a set of pseudo-variables with pseudo-entropy function $g$ . A directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ with $|\mathcal{V}|=N$ is called a functional dependence graph for $\mathcal{X}$ if and only if for all $i=1,2,\dots,N$

g\left(X_{i}\mid\{X_{j}:(j,i)\in\mathcal{E}\}\right)=0.

(6)

With an identification of $X_{i}$ and node $i\in\mathcal{V}$ , this Definition requires that each pseudo-variable $X_{i}$ is a function (in the sense of Definition 1) of the pseudo-variables associated with its parent nodes. To this end, define

\pi(i)=\{j\in\mathcal{V}:(j,i)\in\mathcal{E}\}.

Where it does not cause confusion, we will abuse notation and identify pseudo-variables and nodes in the FDG, e.g. (6) will be written $g\left(i\mid\pi(i)\right)=0$ .

Definition 4 is more general than the functional dependence graph of [15, Chapter 2]. Firstly, in our definition there is no distinction between source and non-source random variables. The graph simply characterizes functional dependence between variables. In fact, our definition admits cyclic directed graphs, and there may be no nodes with in-degree zero (which are source nodes in [15]). We also do not require independence between sources (when they exist), which is implied by the acyclic constraint in [15]. Our definition of an FDG admits pseduo-entropy functions $g$ with additional functional dependence relationships that are not represented by the graph. It only specifies a certain set of conditional pseudo-entropies which must be zero. Finally, our definition holds for a wide class of objects, namely pseudo-variables, rather than just random variables.

Clearly a functional dependence graph in the sense of [15] satisfies the conditions of Definition 4, but the converse is not true. Henceforth when we refer to a functional dependence graph (FDG), we mean in the sense of Definition 4. Furthermore, an FDG is acyclic if $\mathcal{G}$ has no directed cycles. A graph will be called cyclic if every node is a member of a directed cycle.²²2In this paper we do not consider graphs that are neither cyclic or acyclic.

Definition 4 specifies an FDG in terms of local dependence structure. Given such local dependence constraints, it is of great interest to determine all implied functional dependence relations. In other words, we wish to find all sets $\mathcal{A}$ and $\mathcal{B}$ such that $g(\mathcal{A}\mathcal{B})=g(\mathcal{A})$ .

Definition 5

For disjoint sets $\mathcal{A},\mathcal{B}\subset\mathcal{V}$ we say $\mathcal{A}$ determines $\mathcal{B}$ in the directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ , denoted $\mathcal{A}\rightarrow\mathcal{B}$ , if there are no elements of $\mathcal{B}$ remaining after the following procedure:

Remove all edges outgoing from nodes in $\mathcal{A}$ and subsequently remove all nodes and edges with no incoming edges and nodes respectively.

For a given set $\mathcal{A}$ , let $\phi(\mathcal{A})\subseteq\mathcal{V}$ be the set of nodes deleted by the procedure of Definition 5. Clearly $\phi(\mathcal{A})$ is the largest set of nodes with $\mathcal{A}\rightarrow\phi(\mathcal{A})$ .

Lemma 1 (Grandparent lemma)

Let $\mathcal{G}=(\mathcal{V},\mathcal{E})$ be a functional dependence graph for a polymatroidal pseudo-entropy function $g\in\Gamma$ . For any $j\in\mathcal{V}$ with $i\in\pi(j)\neq\emptyset$

g\left(j\mid\pi(i),\pi(j)\setminus i\right)=0.

Proof:

By hypothesis, $g(k\mid\pi(k))=0$ for any $k\in\mathcal{V}$ . Furthermore, note that for any $g\in\Gamma$ , conditioning cannot increase pseudo-entropy³³3This is a direct consequence of submodularity, (3). and hence $g(k\mid\pi(k),\mathcal{A})=0$ for any $\mathcal{A}\subseteq\mathcal{V}$ . Now using this property, and the chain rule

	$\displaystyle 0$	$\displaystyle=g(j\mid\pi(j))$
		$\displaystyle=g(j\mid\pi(j),\pi(i))$
		$\displaystyle=g(j,\pi(j),\pi(i))-g(\pi(j),\pi(i))$
		$\displaystyle=g(j,\pi(j)\setminus i,\pi(i))-g(\pi(j),\pi(i))$
		$\displaystyle=g(j,\pi(j)\setminus i,\pi(i))-g(\pi(j)\setminus i,\pi(i))$
		$\displaystyle=g(j\mid\pi(i),\pi(j)\setminus i).$

∎

We emphasize that in the proof of Lemma 1 we have only used the submodular property of polymatroids, together with the hypothesized local dependence structure specified by the FDG.

Clearly the lemma is recursive in nature. For example, it is valid for $g(j\mid\pi(j)\setminus i,\pi(i)\setminus k,\pi(k))=0$ and so on. The implication of the lemma is that a pseudo-variable $X_{j}$ in an FDG is a function of $X_{\mathcal{A}}$ for any $\mathcal{A}\subset\mathcal{V}$ with $\mathcal{A}\rightarrow j$ .

Theorem 1

Let $\mathcal{G}$ be a functional dependence graph on the pseudo-variables $\mathcal{X}$ with polymatroidal pseudo-entropy function $g$ . Then for disjoint subsets $\mathcal{A},\mathcal{B}\subset\mathcal{V}$ ,

\mathcal{A}\rightarrow\mathcal{B}\implies g(\mathcal{B}\mid\mathcal{A})=0.

Proof:

Let $\mathcal{A}\rightarrow\mathcal{B}$ in the FDG $\mathcal{G}$ . Then, by Definition 5 there must exist directed paths from some nodes in $\mathcal{A}$ to a every node in $\mathcal{B}$ , and there must not exist any directed path intersecting $\mathcal{B}$ that does not also intersect $\mathcal{A}$ . Recursively invoking Lemma 1, the theorem is proved. ∎

Definition 5 describes an efficient graphical procedure to find implied functional dependencies for pseudo-variables with local dependence specified by a functional dependence graph $\mathcal{G}$ . It captures the essence of the chain rule (4) for pseudo-entropies and the fact that pseudo-entropy is non-increasing with respect to conditioning (3), which are the main arguments necessary for manual proof of functional dependencies.

One application of Definition 5 is to find a reduction of a given set $\mathcal{C}$ , i.e. to find a disjoint partition of $\mathcal{C}$ into $\mathcal{A}$ and $\mathcal{B}$ with $\mathcal{A}\rightarrow\mathcal{B}$ , which implies $g(\mathcal{C})=g(\mathcal{A}\mathcal{B})=g(\mathcal{A})$ . On the other hand, it also tells which sets are irreducible.

Definition 6 (Irreducible set)

A set of nodes $\mathcal{B}$ in a functional dependence graph is irreducible if there is no $\mathcal{A}\subset\mathcal{B}$ with $\mathcal{A}\rightarrow\mathcal{B}$ .

Clearly, every singleton is irreducible. In addition, in an acyclic FDG, irreducible sets are basic entropy sets in the sense of [17]. In fact, irreducible sets generalize the idea of basic entropy sets to the more general (and possibly cyclic) functional dependence graphs on pseudo-variables.

III-A Acyclic Graphs

In an acyclic graph, let $\operatorname{An}(\mathcal{A})$ denote the set of ancestral nodes, i.e. for every node $a\in\operatorname{An}(\mathcal{A})$ , there is a directed path from $a$ to some $b\in\mathcal{A}$ .

Of particular interest are the maximal irreducible sets:

Definition 7

An irreducible set $\mathcal{A}$ is maximal in an acyclic FDG $\mathcal{G}=(\mathcal{V},\mathcal{E})$ if $\mathcal{V}\setminus\phi(\mathcal{A})\setminus\operatorname{An}(\mathcal{A})\triangleq(\mathcal{V}\setminus\phi(\mathcal{A}))\setminus\operatorname{An}(\mathcal{A})=\emptyset$ , and no proper subset of $\mathcal{A}$ has the same property.

Note that for acyclic graphs, every subset of a maximal irreducible set is irreducible. Conversely, every irreducible set is a subset of some maximal irreducible set [17]. Irreducible sets can be augmented in the following way.

Lemma 2 (Augmentation)

Let $A\subset\mathcal{V}$ in an acyclic FDG $\mathcal{G}=(\mathcal{V},\mathcal{E})$ . Let $\mathcal{B}=\mathcal{V}\setminus\phi(\mathcal{A})\setminus\operatorname{An}(\mathcal{A})$ . Then $\mathcal{A}\cup\{b\}$ is irreducible for every $b\in\mathcal{B}$ .

This suggests a process of recursive augmentation to find all maximal irreducible sets in an acyclic FDG (a similar process of augmentation was used in [17]). Let $\mathcal{G}$ be a topologically sorted⁴⁴4I.e. Order nodes such that if there is a directed edge from node $i$ to $j$ then $i\prec j$ [9, Proposition 11.5]. acyclic functional dependence graph $\mathcal{G}=(\{0,1,2,\dots\},\mathcal{E})$ . Its maximal irreducible sets can be found recursively via $\textbf{AllMaxSetsA}(\mathcal{G},\{\})$ in Algorithm 1. In fact, $\textbf{AllMaxSetsA}(\mathcal{G},\mathcal{A})$ finds all maximal irreducible sets containing $\mathcal{A}$ .

Algorithm 1 AllMaxSetsA(

\mathcal{G},\mathcal{A}

)

\mathcal{G}=(\mathcal{V},\mathcal{E}),\mathcal{A}\subset\mathcal{V}

\mathcal{B}\leftarrow\mathcal{V}\setminus\phi(\mathcal{A})\setminus\operatorname{An}(\mathcal{A})

\mathcal{B}\neq\emptyset

then

Output

\{\textbf{AllMaxSetsA}(\mathcal{G},\mathcal{A}\cup\{b\}):b\in\mathcal{B}\}

else

Output

\mathcal{A}

end if

III-B Cyclic Graphs

In cyclic graphs, the notion of a maximal irreducible set is modified as follows:

Definition 8

An irreducible set $\mathcal{A}$ is maximal in a cyclic FDG $\mathcal{G}=(\mathcal{V},\mathcal{E})$ if $\mathcal{V}\setminus\phi(\mathcal{A})=\emptyset$ , and no proper subset of $\mathcal{A}$ has the same property.

For cyclic graphs, every subset of a maximal irreducible set is irreducible. In contrast to acyclic graphs, the converse is not true. In fact there can be irreducible sets that are not maximal, and are not subsets of any maximal irreducible set. It is easy to show that

Lemma 3

All maximal irreducible sets have the same pseudo-entropy.

This fact will be used in development of our capacity bound for network coding in Section IV below. We are interested in finding every maximal irreducible set for cyclic graphs. This may be accomplished recursively via $\textbf{AllMaxSetsC}(\mathcal{G},\{\})$ in Algorithm 2. Note that in contrast to Algorithm 1, $\textbf{AllMaxSetsC}(\mathcal{G},\mathcal{A})$ finds all maximal irreducible sets that do not contain any node in $\mathcal{A}$ .

Algorithm 2 AllMaxSetsC(

\mathcal{G},\mathcal{A}

)

\mathcal{G}=(\mathcal{V},\mathcal{E}),\mathcal{A}\subset\mathcal{V}

v\not\in\phi\left(\mathcal{A}^{c}\setminus\{v\}\right),\forall v\in\mathcal{A}^{c}

then

Output

\mathcal{A}^{c}

else

for all

v\in\mathcal{A}^{c}

v\in\phi\left(\mathcal{A}^{c}\setminus\{v\}\right)

then

Output

\textbf{AllMaxSetsC}(\mathcal{G},\mathcal{A}\cup\{v\})

end if

end for

end if

Example 1 (Butterfly network)

Figure 1 shows the well-known butterfly network and Figure 2 shows the corresponding functional dependence graph. Nodes are labeled with node numbers and pseudo-variables (The sources variables are $Y_{1}$ and $Y_{2}$ . The $U_{i}$ are the edge variables, carried on links with capacity $C_{i}$ ). Edges in the FDG represent the functional dependency due to encoding and decoding requirements.

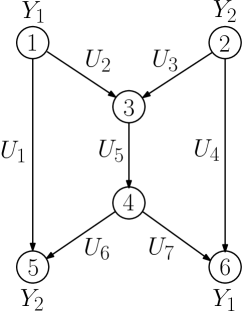
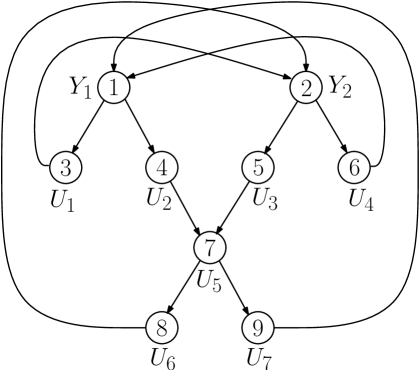
Refer to caption — Figure 1: The butterfly network.

The maximal irreducible sets of the cyclic FDG shown in Figure 2 are

\{1,2\},\{1,5\},\{1,7\},\{1,8\},\{2,4\},\{2,7\},\{2,9\},\{3,4,5\},\\ \{3,4,8\},\{3,7\},\{3,8,9\},\{4,5,6\},\{5,6,9\},\{6,7\},\{6,8,9\}.

IV Functional Dependence Bound

We now give an easily computable outer bound for the total capacity of a network coding system.

Theorem 2 (Functional Dependence Bound)

Let $\mathcal{C}_{1},\mathcal{C}_{2},\mathcal{C}_{3},\mathcal{C}_{4}$ be given network coding constraint sets. Let $\mathcal{G}=(\mathcal{V},\mathcal{E})$ be a functional dependence graph⁵⁵5This FDG will be cyclic due to the sink demands $\mathcal{C}_{3}$ on the (source and edge) pseudo-variables $Y_{\mathcal{S}},U_{\mathcal{E}}$ with pseudo-entropy function $g\in\mathcal{C}_{1}\cap\mathcal{C}_{2}\cap\mathcal{C}_{3}\cap\mathcal{C}_{4}\cap\Gamma$ . Let $\mathcal{B}_{M}$ be the collection of all maximal irreducible sets not containing source variables. Then

\sum_{s\in\mathcal{S}}g(Y_{s})\leq\min_{\mathcal{B}\in\mathcal{B}_{M}}\sum_{e:U_{e}\in\mathcal{B}}C_{e}.

Proof:

Let $\mathcal{B}\in\mathcal{B}_{M}$ , then

$\displaystyle\sum_{s\in\mathcal{S}}g(Y_{s})$	$\displaystyle{=}g(Y_{\mathcal{S}})$	$\displaystyle\mathcal{C}_{1}$
	$\displaystyle{=}g(U_{e}:U_{e}\in\mathcal{B})$	Lemma 3
	$\displaystyle{\leq}\sum_{U_{e}\in\mathcal{B}}g(U_{e})$	Subadditivity of $g\in\Gamma$
	$\displaystyle{\leq}\sum_{e:U_{e}\in{\mathcal{B}}}C_{e}.$	$\displaystyle\mathcal{C}_{4}$

∎

Maximal irreducible sets which do not contain source variables are “information blockers” from sources to corresponding sinks. They can be interpreted as information theoretic cuts in in the network. Note that an improved bound can in principle be obtained by using additional properties of $\Gamma$ (rather than just subadditivity). Similarly, bounds for linear network codes could be obtained by using $\Gamma^{\text{In}}$ .

Corollary 1

For single source multicast networks, Theorem 2 becomes the max-flow bound [9, Theorem 11.3] and hence is tight.

Example 2 (Butterfly network)

The functional dependence bound for the butterfly network of Figure 2 is

R_{1}+R_{2}\leq\min\{C_{3}+C_{7},C_{6}+C_{7},C_{3}+C_{4}+C_{5},\\ C_{3}+C_{4}+C_{8},C_{3}+C_{8}+C_{9},C_{4}+C_{5}+C_{6},\\ C_{5}+C_{6}+C_{9},C_{6}+C_{8}+C_{9}\}.

To the best of our knowledge, Theorem 2 is the tightest bound expression for general multi-source multi-sink network coding (apart from the computationally infeasible LP bound). Other bounds like the network sharing bound [13] and bounds based on information dominance [14] use certain functional dependencies as their main ingredient. In contrast, Theorem 2 uses all the functional dependencies due to network encoding and decoding constraints.

V Conclusion

Explicit characterization and computation of the multi-source network coding capacity region requires determination of the set of all entropic vectors $\Gamma^{*}$ , which is known to be an extremely hard problem. The best known outer bound can in principle be computed using a linear programming approach. In practice this is infeasible due to an exponential growth in the number of constraints and variables with the network size.

We gave an abstract definition of a functional dependence graph, which extends previous notions to accommodate not only cyclic graphs, but more abstract notions of dependence. In particular we considered polymatroidal pseudo-entropy functions, and demonstrated an efficient and systematic method to find all functional dependencies implied by the given local dependencies.

This led to our main result, which was a new, easily computable outer bound, based on characterization of all functional dependencies in networks. We also show that the proposed bound is tighter than some known bounds.

References

[1] R. Ahlswede, N. Cai, S.-Y. R. Li, and R. W. Yeung, “Network information flow,” IEEE Trans. Inform. Theory, vol. 46, pp. 1204–1216, July 2000.
[2] S.-Y. R. Li, R. Yeung, and N. Cai, “Linear network coding,” IEEE Trans. Inform. Theory, vol. 49, pp. 371–381, Feb. 2003.
[3] R. W. Yeung, S.-Y. Li, N. Cai, and Z. Zhang, Network Coding Theory. now Publishers, 2006.
[4] C. Fragouli and E. Soljanin, Network Coding Fundamentals. now Publishers, 2007.
[5] C. Fragouli and E. Soljanin, Network Coding Applications. now Publishers, 2008.
[6] T. Ho and D. S. Lun, Network Coding: An Introduction. Cambridge University Press, 2008.
[7] R. Dougherty, C. Freiling, and K. Zeger, “Insufficiency of linear coding in network information flow,” IEEE Trans. Inform. Theory, vol. 51, Aug. 2005. To appear.
[8] T. H. Chan and A. Grant, “Dualities between entropy functions and network codes,” IEEE Trans. Inform. Theory, vol. 54, pp. 4470–4487, Oct. 2008.
[9] R. W. Yeung, A First Course in Information Theory. Information Technology: Transmission, Processing and Storage, New York: Kluwer Academic/Plenum Publishers, 2002.
[10] L. Song, R. W. Yeung, and N. Cai, “Zero-error network coding for acyclic networks,” IEEE Trans. Inform. Theory, vol. 49, pp. 3129–3139, Dec. 2003.
[11] X. Yan, R. W. Yeung, and Z. Zhang, “The capacity region for multi-source multi-sink network coding,” in IEEE Int. Symp. Inform. Theory, (Nice, France), pp. 116–120, Jun. 2007.
[12] F. Matúš, “Infinitely many information inequalities,” in IEEE Int. Symp. Inform. Theory, 2007.
[13] X. Yan, J. Yang, and Z. Zhang, “An outer bound for multisource multisink network coding with minimum cost consideration,” IEEE Trans. Inform. Theory, vol. 52, pp. 2373–2385, June 2006.
[14] N. Harvey, R. Kleinberg, and A. Lehman, “On the capacity of information networks,” IEEE Trans. Inform. Theory, vol. 52, pp. 2345–2364, June 2006.
[15] G. Kramer, Directed Information for Channels with Feedback. PhD thesis, Swiss Federal Institute of Technology, Zurich, 1998.
[16] L. Guille, T. Chan, and A. Grant, “The minimal set of Ingleton inequalities,” in IEEE Int. Symp. Inform. Theory, pp. 2121–2125, July 2008.
[17] I. Grivell, A. Grant, and T. Chan, “Basic entropy sets,” in Fourth Workshop on Network Coding, Theory and Applications, pp. 1–6, Jan. 2008.