This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

††thanks: These authors contributed equally††thanks: These authors contributed equally

Neutron scattering and muon-spin spectroscopy studies of the magnetic triangular-lattice compounds A2A_{2}La2NiW2O12 (AA = Sr, Ba)

B. C. Yu Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China    J. Y. Yang Institute of High Energy Physics, Chinese Academy of Sciences (CAS), Beijing 100049, China Spallation Neutron Source Science Center (SNSSC), Dongguan 523803, China    D. J. Gawryluk Laboratory for Multiscale Materials Experiments, Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland    Y. Xu Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China    Q. F. Zhan Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China    T. Shiroka Laboratory for Muon-Spin Spectroscopy, Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland Laboratorium für Festkörperphysik, ETH Zürich, CH-8093 Zürich, Switzerland    T. Shang tshang@phy.ecnu.edu.cn Key Laboratory of Polar Materials and Devices (MOE), School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China Chongqing Key Laboratory of Precision Optics, Chongqing Institute of East China Normal University, Chongqing 401120, China
Abstract

We report on the geometrically frustrated two-dimensional triangular-lattice magnets A2A_{2}La2NiW2O12 (AA = Sr, Ba) studied mostly by means of neutron powder diffraction (NPD) and muon-spin rotation and relaxation (µSR) techniques. The chemical pressure induced by the Ba-for-Sr substitution suppresses the ferromagnetic (FM) transition from 6.3 K in the Ba-compound to 4.8 K in the Sr-compound. We find that the R​3¯R\bar{3} space group reproduces the NPD patterns better than the previously reported R​3¯​mR\bar{3}m space group. Both compounds adopt the same magnetic structure with a propagation vector 𝒌=(0,0,0)\boldsymbol{k}=(0,0,0), in which the Ni2+ magnetic moments are aligned ferromagnetically along the cc-axis. The zero-field µSR results reveal two distinct internal fields (0.31 and 0.10 T), caused by the long-range ferromagnetic order. The small transverse muon-spin relaxation rates reflect the homogeneous internal field distribution in the ordered phase and, thus, further support the simple FM arrangement of the Ni2+ moments. The small longitudinal muon-spin relaxation rates, in both the ferromagnetic- and paramagnetic states of A2La2NiW2O12, indicate that spin fluctuations are rather weak. Our results demonstrate that chemical pressure indeed changes the superexchange interactions in A2A_{2}La2NiW2O12 compounds, with the FM interactions being dominant.

††preprint: Preprint: , 9:50

I Introduction

Geometric frustration occurs when a system of interacting spins is unable to find its lowest energy state because of how the spins are arranged. This property plays an important role at microscopic scales in solids. In particular, in certain cases, such as in spin glasses, spin ice, and spin liquids [1, 2, 3, 4], the localized magnetic moments interact through competing exchange interactions that cannot be simultaneously satisfied, thus giving rise to a highly degenerate magnetic ground state. For instance, in a spin-liquid system, the constituent spins are highly correlated, but still strongly fluctuating down to zero temperature [1, 5, 6, 7, 4, 8]. Such fluctuations lead to remarkable collective phenomena such as emergent gauge fields and fractional excitations [9, 10, 4, 8]. Most of the magnetic frustrations have a simple geometric origin [2, 11, 12], usually occurring in materials with a 2D triangular- or kagome lattice, or a 3D pyrochlore lattice, etc., with the nearest-neighbor interactions being antiferromagnetic (AFM) [13, 14].

A two-dimensional triangular lattice with antiferromagnetic interactions provides one of the prototypes of magnetic frustration [13, 14]. The perovskite-derived compounds A4A_{4}BB’B2B_{2}O12 (AA = Sr, Ba, La; BB’ = Mn, Co, Ni; BB = Sb, Te, W, Re) represent one such system [15, 16, 17, 18]. Depending on the valence states of the BB’ and BB atoms, the AA site can be occupied by either a Sr2+ (Ba2+) or La3+ ion, or by their combinations. Here, the magnetic BB’ ions form a layered structure with a 3-fold site symmetry [see Fig. I(a) for the BB’ = Ni2+ case]. Since the magnetic BB’ layers are well separated by the nonmagnetic AA- and BBO6 layers, the former give rise to a magnetic quasi-2D triangular lattice, which can potentially host magnetic frustrations.

To date, different magnetic ground states have been found to occur in the A4A_{4}BB’B2B_{2}O12 family [16, 17, 18], whose magnetic properties are thought to be determined mostly by the competition between the ferromagnetic (FM-) BB’-O-BB-O-BB’ and antiferromagnetic BB’-O-O-BB’ superexchange interactions, shown by solid- and dashed lines in Fig. I(c) [16]. The spin state of the magnetic BB’ ions plays a decisive role in the competition between the two superexchange interactions. As a consequence, A4A_{4}CoB2B_{2}O12 (effective spin S=1/2S=1/2 for Co2+) and Ba2La2NiW2O12 (SS = 1 for Ni2+) are reported to be ferromagnetic, while Ba2La2MnW2O12 (SS = 5/2 for Mn2+) is reported to be antiferromagnetic [16, 19]. Similar superexchange interactions and their competitions have been observed in other triangular-lattice magnets, e.g., Ba3BB’Nb2O9 [20, 21, 22, 23] and AAAg2BB’(VO4)2 [24, 25]. Unsurprisingly, such closely competing interactions can be tuned by either external pressure or by chemical substitution, each of which able to introduce lattice distortions and to modify the bond lengths and angles [24, 25, 26, 27, 28, 29], thus, tuning the magnetic order and frustration. For example, in A4A_{4}CoB2B_{2}O12, the chemical pressure (i.e., the substitution of Ba with Sr and/or La, or W with Re) can tune the FM transition temperature [16]. However, the effects of chemical pressure on the magnetic properties of A4A_{4}NiB2B_{2}O12 have not been investigated in detail.

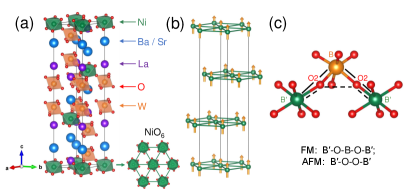
Refer to caption
Figure 1. : (a) Crystal structure of A2A_{2}La2NiW2O12 (AA = Sr, Ba). The Ni layers form triangular lattices. (b) Sublattice of Ni2+ ions showing that the magnetic moments (indicated by arrows) point along the cc-axis. (c) Pathways of the FM BB’-O-BB-O-BB’ (black solid line) and AFM BB’-O-O-BB’ (black dashed line) superexchange interactions.

To clarify the above issues, in this paper, we synthesized polycrystalline samples of A2A_{2}La2NiW2O12 (AA = Sr, Ba) and studied their magnetic properties by means of magnetization-, specific heat-, neutron scattering-, and muon-spin rotation and relaxation (µSR) measurements. The chemical pressure is introduced by substituting Ba with Sr, which suppresses the FM transition temperature from 6.3 down to 4.8 K, while the magnetic moments of the Ni2+ ions are ferromagnetically aligned along the cc-axis in both compounds. Our results suggest that the chemical pressure indeed changes the superexchange interactions in A2A_{2}La2NiW2O12, with the BB’-O-BB-O-BB’ superexchange path dominating the competition between the FM and AFM interactions. External pressure on Sr2La2NiW2O12 or chemical substitution on the Ni site may further tune the magnetic interactions and lead to magnetic frustration.

II Experimental details

The A2A_{2}La2NiW2O12 (AA = Sr, Ba) polycrystalline samples were prepared by the solid-state reaction method. Stoichiometric amounts of La2O3, BaCO3, SrCO3, NiO, and WO3 powders were used to prepare the materials. The La2O3 rare-earth oxide was annealed for 15 hours in atmosphere to remove moisture. The powders were then mixed, ground, and sintered at 1200∘C for 24 hours. After grinding the samples again, the powders were pressed into pellets and sintered at 1200∘C for extra 48 hours. The magnetic-susceptibility and heat-capacity measurements were performed on a Quantum Design magnetic property measurement system (MPMS) and physical property measurement system (PPMS), respectively.

Neutron powder diffraction (NPD) measurements were carried out at the Swiss Neutron Source SINQ of the Paul Scherrer Institute in Villigen, Switzerland. The A2A_{2}La2NiW2O12 powder samples were introduced in cylindrical vanadium cans (8 mm in diameter and 50 mm high) and mounted on a helium cryostat stick (2–300 K). High-resolution room-temperature NPD patterns were recorded at the powder diffractometer HRPT [Ge (822), λ=1.154\lambda=1.154 Å]. To discern the magnetic diffraction peaks, high-intensity NPD patterns were collected at 1.7 K on the DMC diffractometer using a longer wavelength [pyrolitic graphite (002), λ=2.458\lambda=2.458 Å]. The collected NPD patterns were analyzed using the Rietveld package of the FullProf suite [30].

The bulk µSR measurements were carried out at the general-purpose surface-muon instrument (GPS) of the Swiss muon source at Paul Scherrer Institut, Villigen, Switzerland. In this study, we performed two types of experiments: zero-field (ZF)-, and longitudinal-field (LF) µSR measurements. In both cases, we aimed at studying the temperature evolution of the magnetically ordered phase and the spin fluctuations. The µSR spectra were collected upon sample heating and then analyzed by the musrfit software package [31].

Refer to caption
Figure 2. : (a) Temperature-dependent dc magnetic susceptibility χ​(T)\chi(T) of Ba2La2NiW2O12 collected in a field of 0.1 T. The inset shows the inverse susceptibility χ​(T)−1\chi(T)^{-1}, with the solid line being a fit to the Curie-Weiss law. (b) Temperature-dependent magnetic susceptibility of Ba2La2NiW2O12 measured in various magnetic fields up to 6 T. The inset enlarges the χ​(T)\chi(T) curves collected at µH0=0.5{}_{0}H=0.5, 1, and 6 T. Their derivatives with respect to temperature are shown in panel (c). The temperatures where dχ\chi/dTT exhibits a minimum define the Curie temperature TcT_{c} and are indicated by an arrow. The analogous results for Sr2La2NiW2O12 are shown in the panels (d)-(f), respectively.

III Results and discussion

III.1 Magnetic susceptibility

Refer to caption
Figure 3. : Field-dependent magnetization M​(H)M(H) in both the ferromagnetic- and paramagnetic states of Ba2La2NiW2O12 (a) and Sr2La2NiW2O12 (b). Insets highlight the low-field region of M​(H)M(H) for Ba2La2NiW2O12 (at 2.5 K) and Sr2La2NiW2O12 (at 2 K), clearly showing the hysteresis loops.
Refer to caption
Figure 4. : (a) Temperature-dependent heat capacity of Ba2La2NiW2O12 measured in zero-field condition from 2 to 300 K. The inset shows the specific heat C/TC/T versus T2T^{2} below 20 K. The solid line is a fit to C/TC/T = γ\gamma + β\betaT2T^{2} in the paramagnetic state, with γ\gamma ≡\equiv 0 reflecting the compound’s insulating nature. (b) Temperature dependence of the magnetic contribution to the specific heat Cm/TC_{\mathrm{m}}/T for Ba2La2NiW2O12 in various magnetic fields up to 9 T. (c) The zero-field magnetic entropy Sm​(T)S_{\mathrm{m}}(T) obtained from the integration of Cm​(T)/TC_{\mathrm{m}}(T)/T for Ba2La2NiW2O12. The dashed lines mark the entropy values R​ln⁡(2​S+1)R\ln(2S+1), with S=1/2S=1/2 and 1, respectively. The analogous results for Sr2La2NiW2O12 are shown in panels (d), (e) and (f), respectively.

The A2A_{2}La2NiW2O12 samples were first characterized by magnetic-susceptibility measurements. Figures II(a) and (d) show the temperature-dependent magnetic susceptibility χ​(T)\chi(T) collected in an applied magnetic field of 0.1 T using a zero-field-cooling (ZFC) protocol. χ​(T)\chi(T) shows a sharp increase close to TcT_{c}, the temperature where the Ni2+ moments give rise to a FM order. The Curie temperatures TcT_{c} can be determined from the derivative of susceptibility with respect to temperature dχ\chi/dTT [see Fig. II(c) and (f)] which, in a 0.1-T applied field, provides a TcT_{c} of 6.3 and 4.8 K for Ba2La2NiW2O12 and Sr2La2NiW2O12, respectively. The magnetic susceptibility was also measured under various magnetic fields up to 6 T. As shown in Fig. II(b) and (e), as the magnetic field increases, the transition becomes broader and TcT_{c} moves to higher temperatures, both features typical of ferromagnetic materials. The insets in Fig. II(a) and (d) show the Curie-Weiss fits to the inverse susceptibility (solid lines), which yield a Weiss temperature θp=7.4\theta_{\mathrm{p}}=7.4 K for Ba2La2NiW2O12 and θp=8.4\theta_{\mathrm{p}}=8.4 K for Sr2La2NiW2O12. The positive θp\theta_{\mathrm{p}} values indicate that FM interactions are dominant in both compounds. The estimated effective moments are μeff\mu_{\mathrm{eff}} = 3.17 μB\mu_{\mathrm{B}} and 3.13 μB\mu_{\mathrm{B}} for Ba2La2NiW2O12 and Sr2La2NiW2O12, respectively. Both are close to the theoretical value of spin-only Ni2+ ions (2.83 μB\mu_{\mathrm{B}}), i.e., assuming a quenching of the orbital moment, typical of octahedral complexes [32] — such as the NiO6 units in Fig. I(a).

The FM ground state was further confirmed by field-dependent magnetization measurements (see Fig. III.1). For T<TcT<T_{c}, a small yet clear magnetic hysteresis loop is observed. For both materials, the magnetization starts to saturate for μ0​H>5\mu_{0}H>5 T. After substituting the Ba with Sr, the magnetism becomes softer. The coercive field of Ba2La2NiW2O12 is about 67 mT, while, in Sr2La2NiW2O12, it decreases to 4 mT. Thus, in A2A_{2}La2NiW2O12, the chemical pressure suppresses both the magnetization and the TcT_{c}, hence suggesting an enhancement of the magnetic competition. Nevertheless, the FM interactions remain dominant also in Sr2La2NiW2O12.

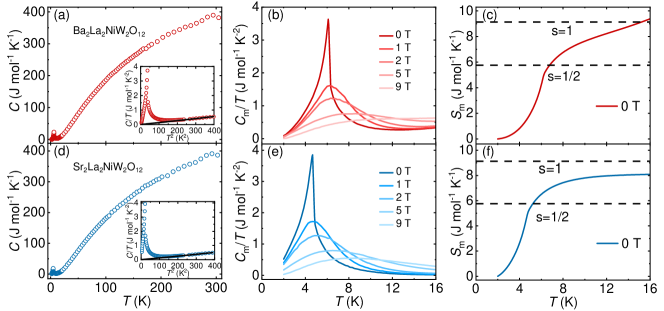
III.2 Heat capacity

We measured the zero-field heat-capacity of A2A_{2}La2NiW2O12 from 2 to 300 K. The low-TT heat-capacity data were also collected under various external fields, up to 9 T. As shown in Fig. III.1, in both compounds, there is a sharp λ\lambda-like transition at low temperatures, typical of long-range magnetic order. The C​(T)C(T) data show a distinct peak at Tc=6.1T_{c}=6.1 and 4.7 K for Ba2La2NiW2O12 and Sr2La2NiW2O12, which are consistent with the TcT_{c} values determined from magnetization data (see Fig. II). To extract the magnetic contribution, the normal-state (i.e., TT ≫\gg TcT_{c}) specific-heat data were fitted to C/TC/T = γ\gamma + β\betaT2T^{2}, where γ≡0\gamma\equiv 0, due to the insulating nature of both compounds [see solid lines in Fig. III.1(a) and (d)]. The derived β\beta values are 0.0013 and 0.0012 J/mol-K4 for Ba2La2NiW2O12 and Sr2La2NiW2O12, which yield a Debye temperature θD=142\theta_{\mathrm{D}}=142 and 145 K, respectively. After subtracting the phonon contribution (i.e, the β\betaT2T^{2} term), the magnetic specific heat Cm/TC_{\mathrm{m}}/T vs. temperature is plotted in Fig. III.1(b) and (e) for Ba2La2NiW2O12 and Sr2La2NiW2O12, respectively. Upon increasing the magnetic field, the peak at TcT_{c} becomes broader and moves to higher temperatures, once more confirming the FM nature of the magnetic transition in both materials. The zero-field magnetic entropy Sm​(T)S_{\mathrm{m}}(T) obtained by integrating Cm​(T)/TC_{\mathrm{m}}(T)/T is shown in Fig. III.1(c) and (f) for Ba2La2NiW2O12 and Sr2La2NiW2O12, respectively. In both compounds, at temperatures close to TcT_{c}, SmS_{\mathrm{m}} reaches R​ln⁡(2)R\ln(2) (corresponding to S=1/2S=1/2). In Ba2La2NiW2O12, at temperatures above TcT_{c}, SmS_{\mathrm{m}} reaches R​ln⁡(3)R\ln(3) (corresponding to S=1S=1), while in Sr2La2NiW2O12, SmS_{\mathrm{m}} is slightly smaller than R​ln⁡(3)R\ln(3). Such a deviation is most likely due to an over-subtraction of the phonon contribution from the specific-heat data. To properly subtract the phonon contribution and estimate the magnetic entropy, heat-capacity measurements on the non-magnetic counterparts, as e.g., AA2La2ZnW2O12, are highly desirable.

Refer to caption
Figure 5. : Rietveld fits of the NPD patterns of Ba2La2NiW2O12 collected in the paramagnetic state (300 K) (a) and in the magnetically-ordered state (1.7 K) (c). The analogous results for Sr2La2NiW2O12 are shown in panels (b) and (d), respectively. Red symbols show the experimental data, while black lines are the refined profiles. Blue lines at the bottom show the residuals, i.e., the difference between the calculated and the experimental data. The black and green ticks under the patterns indicate the positions of nuclear and magnetic reflections, respectively.

III.3 Neutron diffraction

Table 1.: Room-temperature lattice parameters, atomic positions, bond lengths/angles, and goodness of fits for A2A_{2}La2NiW2O12 (A=A= Ba/Sr).
Space group R​3¯R\bar{3}
ZZ 19
aa(Å) 5.66126(9)/5.59654(5)
cc(Å) 27.35363(3)/26.58389(1)
Rp=5.53/5.90R_{\mathrm{p}}=5.53/5.90 %,  Rwp=7.13/6.42R_{\mathrm{wp}}=7.13/6.42 %,  χr2=2.53/1.97\chi^{2}_{r}=2.53/1.97
Atom Wyckoff xx yy zz
Ba/Sr 6​c6c 0 0 0.1329(7)/0.1340(2)
La 6​c6c 0 0 0.2931(1)/0.2913(2)
Ni 3​a3a 0 0 0
W 6​c6c 0 0 0.4182(5) / 0.4215(4)
O1 18​f18f 0.4647(5)/0.4445(1) 0.4715(8)/0.4472(9) 0.1180(3)/0.1216(1)
O2 18​f18f 0.4316(1)/0.4312(6) 0.4537(9)/0.4508(6) 0.2947(2)/0.2926(2)
Bond length: Ni-O2: 2.064(4) Å/2.051(2) Å Bond length: W-O2: 2.009(6) Å/2.004(2) Å
Bond angle: ∠\angleNi-O2-O2: 121.50(5)∘/120.62(4)∘ Bond angle: ∠\angleO2-W-O2: 84.51(3)∘/84.53(2)∘

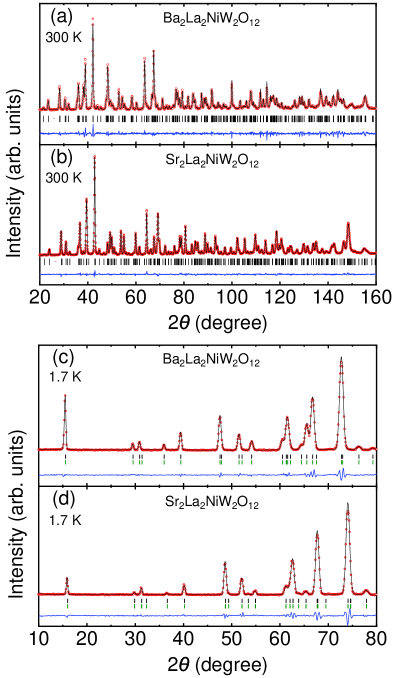
To determine the crystal- and magnetic structures of A2A_{2}La2NiW2O12, neutron powder diffraction patterns were collected at both the paramagnetic (300 K)- and ferromagnetic states (1.7 K). The room-temperature patterns were first analyzed by using the space group R​3¯​mR\bar{3}m (No. 166), as reported in previous studies [16]. With this model, the powder x-ray diffraction (XRD) patterns could be fitted reasonably well with a goodness of fit χr2\chi_{r}^{2} ∼\sim 7. However, in case of the NPD patterns, although the Bragg peaks were located at the right positions, the R​3¯​mR\bar{3}m space group yielded a fairly large χr2\chi_{r}^{2} ∼\sim 18, as evinced also from the clear discrepancy between the observed- and calculated intensities. This indicates that the space group R​3¯​mR\bar{3}m does not describe the crystal structure of A2A_{2}La2NiW2O12 compounds accurately and, thus, further corrections to the structural model are required. Considering that neutron diffraction is more sensitive to the oxygen atoms than x-ray diffraction [33], the oxygen positions are most likely to require corrections. We found that the space group R​3¯R\bar{3} (No. 148) reproduces the NPD patterns quite well. In fact, both R​3¯​mR\bar{3}m and R​3¯R\bar{3} groups belong to the trigonal system, with the latter exhibiting slightly different oxygen positions. Figures III.2(a) and (b) show the Rietveld refinements of NPD at 300 K using the R​3¯R\bar{3} space group for both compounds. These refinements yield a significantly reduced χr2∼2\chi_{r}^{2}\sim 2, thus confirming that, in both cases, the R​3¯R\bar{3} space group is more appropriate than R​3¯​mR\bar{3}m. With R​3¯R\bar{3}, the NiO6 and WO6 octahedra rotate in opposite directions around the cc-axis, which breaks the mirror symmetry. A similar symmetry breaking has been observed also in the Ba2La2NiTe2O12 compound [17]. The refined lattice parameters, atomic positions, and bond lengths/angles, together with the goodness of fits are summarized in Table III.3 for A2A_{2}La2NiW2O12 compounds.

To clarify the magnetic structure of Ba2La2NiW2O12 and Sr2La2NiW2O12, the NPD patterns were also collected in the magnetically ordered state (i.e., 1.7 K) using long wavelength neutrons (λ=2.458\lambda=2.458 Å). The LeBail fits of the magnetic diffraction patterns reveal a commensurate magnetic structure with a propagation vector 𝒌=(0,0,0)\boldsymbol{k}=(0,0,0) for A2A_{2}La2NiW2O12 compounds. For such a magnetic vector, the little group GkG_{k} is identical to the space group R​3¯R\bar{3} and it includes the symmetry elements 1, 3+, 3-, 1¯\bar{1}, 3¯+\bar{3}^{+}, and 3¯−\bar{3}^{-} [34]. The magnetic unit cell of A2A_{2}La2NiW2O12 possesses a single orbit with only one site located at the Ni (0,0,0)(0,0,0) position. For 𝒌=(0,0,0)\boldsymbol{k}=(0,0,0), GkG_{k} has six different irreducible representations (irreps) τ\tau1, τ\tau2, τ\tau3, τ\tau4, τ\tau5, and τ\tau6, among which only τ\tau1, τ\tau3, and τ\tau5 allow for a long-range magnetic order at the Ni site. Table III.3 summarizes the basis vectors of τ\tau1, τ\tau3, and τ\tau5 irreps calculated with BasIreps. For the R​3¯R\bar{3} space group, the Ni atoms are located at the 3aa site (0,0,0)(0,0,0), invariant under all the symmetry operations. As a consequence, all the allowed irreps generate a FM coupling with the spins aligned along the cc-axis for τ\tau1, or lying within the a​bab-plane for τ\tau3 and τ\tau5 (see details in Table III.3). According to the Rietveld refinements of the 1.7-K NPD pattern [see Fig. III.2(c) and (d)], the best fits were obtained by using the τ\tau1 irrep, yielding the smallest χr2\chi_{r}^{2} = 1.93 and 2.77 for Ba2La2NiW2O12 and Sr2La2NiW2O12, respectively. The refined magnetic structure is shown in Fig. I(b). The magnetic moments of Ni atoms obtained from the refinements are 1.94(2) and 1.84(3) μB\mu_{\mathrm{B}} for Ba2La2NiW2O12 and Sr2La2NiW2O12, consistent with their saturation magnetization (see Fig. III.1).

Table 2.: Basis vectors of irreps τ\tau1, τ\tau3, and τ\tau5, as calculated by BasIreps.
Site τ\tau1 τ\tau3 τ\tau5
Ni (0, 0, 1) (1, 0, 0) (1, 0, 0)
(0, 0, 0) (−0.58-0.58, −-1.15, 0) (0.58, 1.15, 0)

III.4 ZF- and LF-µSR

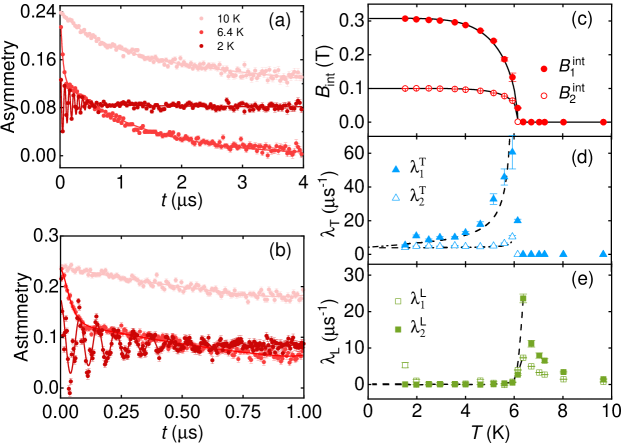
Refer to caption
Figure 6. : (a) Representative zero-field µSR spectra of Ba2La2NiW2O12, collected at various temperatures covering both the paramagnetic- and ferromagnetic states. The short-time spectra, illustrating the coherent oscillations caused by the long-range FM order, are displayed in panel (b). Solid lines through the data are fits to Eq. (1) and (2) (see text for details). Temperature dependence of the internal field Biint​(T)B_{i}^{\mathrm{int}}(T) (c), transverse muon-spin relaxation rate (also known as damping rate) λiT\lambda_{i}^{\mathrm{T}} (d), and longitudinal muon-spin relaxation rate λiL\lambda_{i}^{\mathrm{L}} (e) for Ba2La2NiW2O12, as derived from the ZF-µSR data analysis. Solid lines in (c) are fits to Eq. (3); dash lines in (d) and (e) are guides to the eyes. For clarity reasons, in panel (e), λ1L\lambda_{1}^{\mathrm{L}} was multiplied by a factor 10.

The large gyromagnetic ratio of muons, combined with their availability as 100%\% spin-polarized beams, makes ZF-µSR a very sensitive probe for investigating magnetic materials. Here, to study the magnetic properties of A2A_{2}La2NiW2O12 at a local level, we collected a series of ZF-µSR spectra at temperatures covering both the paramagnetic- and ferromagnetic states. Since neutron diffraction data suggest FM ground states for both Ba2La2NiW2O12 and Sr2La2NiW2O12 (with the Ni2+ moments aligned along the cc-axis), for our µSR measurements we focused on Ba2La2NiW2O12 due to its slightly higher TcT_{c} value. In a magnetic material with a long-range order, the time evolution of ZF-µSR asymmetry, AZF​(t)A_{\mathrm{ZF}}(t), encodes both the intrinsic magnetic fields and their distribution at the muon-stopping site [35]. The ZF-µSR spectra of Ba2La2NiW2O12 collected at different temperatures are shown in Fig. III.4(a). In the paramagnetic state (T>TcT>T_{c}), the ZF-µSR spectra exhibit a relatively slow muon-spin depolarization (∼\sim0.5–1 µs-1 at 10 K), indicating rather weak spin fluctuations. Considering the two muon-stopping sites in Ba2La2NiW2O12, attributed to two distinct oxygen sites (see Table III.3), the ZF-µSR spectra in the paramagnetic state were analyzed using the following model:

AZF​(t)=∑i=12Ai​e−λiL​t.A_{\mathrm{ZF}}(t)=\sum\limits_{i=1}^{2}A_{i}e^{-\lambda^{\mathrm{L}}_{i}t}. (1)

Here, λiL\lambda^{\mathrm{L}}_{i} represent the longitudinal muon-spin relaxation rates, while AiA_{i} are the asymmetries of the two nonequivalent muon-stopping sites.

In the FM state (T<TcT<T_{c}), the ZF-µSR spectra are characterized by highly-damped oscillations, typical of long-range magnetic order. These are clearly visible in Fig. III.4(b), where short-time oscillations are superimposed on a long-time slow relaxation. The ZF-µSR spectra in the FM state were, hence, analyzed using the following model:

AZF​(t)=∑i=12Ai​[α​cos⁡(ωi​t+ϕ)​e−λiT​t+(1−α)​e−λiL​t].A_{\mathrm{ZF}}(t)=\sum\limits_{i=1}^{2}A_{i}[\alpha\cos(\omega_{i}t+\phi)e^{-\lambda^{\mathrm{T}}_{i}t}+(1-\alpha)e^{-\lambda^{\mathrm{L}}_{i}t}]. (2)

Here, α\alpha and 1–α\alpha are the oscillating (i.e., transverse) and nonoscillating (i.e., longitudinal) fractions of the µSR signal, respectively, whose initial total asymmetry is equal to A1A_{1} and A2A_{2}. In polycrystalline materials with a long-range magnetic order, one expects α=2/3\alpha=2/3, since statistically one third of the muon spins are aligned parallel to the local field direction (i.e., Sμ∥BintS_{\mu}\parallel B_{\mathrm{int}}) and, hence, do not precess; ωi\omega_{i} (=γμ​Biint=\gamma_{\mu}B_{i}^{\mathrm{int}}) represents the muon-spin precession frequency, with γμ=2​π×135.5\gamma_{\mu}=2\pi\times 135.5 MHz/T the muon gyromagnetic ratio and BiintB_{i}^{\mathrm{int}} the local field sensed by muons; λiT\lambda^{\mathrm{T}}_{i} are the transverse muon-spin relaxation rates, reflecting the internal field distributions; ϕ\phi is a shared initial phase.

The derived fitting parameters are summarized in Fig. III.4(c)-(e). The BiintB_{i}^{\mathrm{int}}, λiT\lambda^{\mathrm{T}}_{i}, and λiL\lambda^{\mathrm{L}}_{i} all show a distinct anomaly at TcT_{c}. The TcT_{c} determined from ZF-µSR is consistent with the value determined from magnetic susceptibility and heat capacity (see Figs. II and III.1). As shown in Fig. III.4(c), below TcT_{c}, there are two distinct internal fields, here reflecting the two different muon-stopping sites. In the FM state, the temperature evolution of Biint​(T)B^{\mathrm{int}}_{i}(T) resembles the typical mean-field curve. To estimate the zero-temperature internal field, Biint​(T)B^{\mathrm{int}}_{i}(T) was analyzed by means of a phenomenological model:

Biint​(T)=Biint​(0)​[1−(TTc)γ]δ,B^{\mathrm{int}}_{i}(T)=B^{\mathrm{int}}_{i}(0)\left[1-\left(\frac{T}{T_{c}}\right)^{\gamma}\right]^{\delta}, (3)

where Biint​(0)B^{\mathrm{int}}_{i}(0) is the zero-temperature internal field, while γ\gamma and δ\delta represent two empirical parameters. As shown by solid lines in Fig. III.4(c), the above model describes the data reasonably well, yielding B1int​(0)B^{\mathrm{int}}_{1}(0) = 0.30 T and B2int​(0)B^{\mathrm{int}}_{2}(0) = 0.10 T for Ba2La2NiW2O12. The resulting power exponents are γ\gamma = 5.5(2) and δ\delta = 0.54(2) for B1int​(T)B_{1}^{\mathrm{int}}(T), and γ\gamma = 4.6(2) and δ\delta = 0.26(1) for B2int​(T)B_{2}^{\mathrm{int}}(T), respectively. The lack of any anomalies in Biint​(T)B^{\mathrm{int}}_{i}(T) below TcT_{c} is consistent with the simple FM structure of Ba2La2NiW2O12 (see Fig. I). In fact, in some complex magnetic materials with multiple transitions, one observes a more complex Bint​(T)B^{\mathrm{int}}(T), since changes in magnetic structure are reflected in the local-field distribution [36].

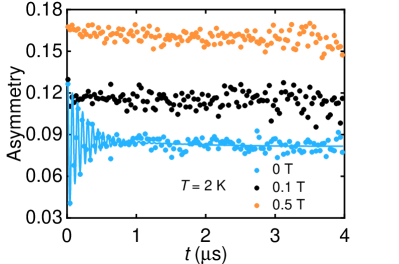
The transverse muon-spin relaxation rate λT\lambda^{\mathrm{T}} reflects the static magnetic field distribution at the muon-stopping site and is also affected by dynamical effects such as spin fluctuations, while its longitudinal counterpart λT\lambda^{\mathrm{T}} is solely determined by spin fluctuations. The λiT​(T)\lambda_{i}^{\mathrm{T}}(T) of Ba2La2NiW2O12 exhibits the typical behavior of magnetic materials with a long-range order [37, 36], i.e., diverging at TcT_{c} and continuously decreasing well inside the magnetic state [see Fig. III.4(d)]. In the paramagnetic state, λiT\lambda_{i}^{\mathrm{T}} is zero, due to the lack of a magnetic moment in the absence of an external field. The λiL​(T)\lambda_{i}^{\mathrm{L}}(T) in Fig. III.4(e) shows a similar behavior to the λiT​(T)\lambda_{i}^{\mathrm{T}}(T), i.e., λiL​(T)\lambda_{i}^{\mathrm{L}}(T) diverges near TcT_{c}, followed by a significant drop at T<TcT<T_{c}, indicating that spin fluctuations are the strongest close to the onset of the FM order. Note that, the absolute values of longitudinal relaxation are much smaller than the transverse ones. Thus, at 1.5 K, λL\lambda^{\mathrm{L}}/λT∼0.097\lambda^{\mathrm{T}}\sim 0.097 and 0.002 for the two different muon-stopping sites. In the paramagnetic state (i.e., T>8T>8 K), λiL\lambda_{i}^{\mathrm{L}} is also very small, suggesting weak spin fluctuations in both the ferromagnetic and paramagnetic states of Ba2La2NiW2O12. Such weak spin fluctuations are further supported by LF-µSR measurements. Figure III.4 shows the 2-K LF-µSR spectra collected in a longitudinal field of 0.1 and 0.5 T. Once the external field exceeds the internal field (here, ∼0.3\sim 0.3 T), the µSR spectra become almost flat. This suggests that, in Ba2La2NiW2O12, muon spins are fully decoupled from the electronic magnetic moments in a field of 0.5 T.

Refer to caption
Figure 7. : LF-µSR spectra of Ba2La2NiW2O12 collected at 2 K in a magnetic field of 0, 0.1, and 0.5 T. Here, we use a longitudinal muon-spin configuration, i.e., pμ∥Sμp_{\mu}\parallel S_{\mu}, with the applied field being parallel to the muon-spin direction. Muon spins are fully decoupled once the external field overcomes the internal field.

IV Discussion

Although our comprehensive set of measurements suggest that both Ba2La2NiW2O12 and Sr2La2NiW2O12 have FM ground states, the magnetic susceptibility and neutron diffraction results indicate that the competition between FM- and AFM couplings is indeed tuned by the chemical pressure induced by the substitution of Ba- with the smaller Sr ions. To understand this, we examine the crystal-structure parameters of A2A_{2}La2NiW2O12 (see details in Table III.3), including the bond lengths and angles. The latter are directly related to the magnetic superexchange interactions and, thus, control the magnetic properties. In A4A_{4}BB’B2B_{2}O12, the BB’O6 octahedra share their corners with the BBO6 octahedra via oxygen atoms, thus leading to two superexchange interaction paths, i.e., BB’-O-BB-O-BB’ and BB’-O-O-BB’ [see details in Fig. I(c)]. According to the Goodenough-Kanamori rule, which provides the signs of the competitive interactions that are responsible for non-collinear spin ordering [38, 39, 40], the BB’-O-BB-O-BB’ superexchange interaction (with ∠\angleO-B-O ∼\sim 90∘) favors a FM coupling, while the BB’-O-O-BB’ path (with ∠\angleBB’-O-O ∼\sim 120-180∘) allows for an AFM coupling. Although the R​3¯R\bar{3} space group implies reduced O-B-O and BB’-O-O bond angles with respect to the previously reported R​3¯​mR\bar{3}m space group [16], the change is such that the FM or AFM character of the superexchange interactions is maintained. For instance, in Ba2La2NiW2O12, R​3¯​mR\bar{3}m gives ∠\angleNi-O2-O2 = 137.2∘ and ∠\angleO2-W-O2 = 86.7∘; while in R​3¯R\bar{3}, these bond angles become 121.5∘ and 84.5∘. Consequently, the BB’-O-BB-O-BB’ and BB’-O-O-BB’ superexchange interaction paths remain valid also in the R​3¯R\bar{3} space group.

The competition between these FM and AFM interactions eventually determines the magnetic ground state of A4A_{4}BB’B2B_{2}O12. Since Sr has a smaller atomic radius than Ba, by replacing Ba with Sr, the lattice constants along both the aa- and cc-axis are reduced by a factor of 1.14 and 2.81%, the Ni-O bond length decreases from 2.064 Å to 2.051 Å, while the Ni-O2-O2 bond angle increases from 121.50∘ to 120.62∘. By contrast, the W-O bond length and the O2-W-O2 bond angle are less affected, most likely because the W-O2 layer is further away from the Ba- or Sr-layers [see Fig. I(a)]. The O2-W-O2 bond angle increases slightly from 84.51∘ to 84.53∘. The changes of Ni-O2-O2 and O2-W-O2 bond angles induced by chemical pressure (i.e., the substitution of Ba by Sr) tune the competition between FM- and AFM superexchange interactions in A2A_{2}La2NiW2O12. The physical pressure might further tune the competition between the FM- and AFM interactions, and yield magnetic frustration. Previous studies reveal that the magnetic ground states of A4A_{4}BB’B2B_{2}O12 can also be tuned by chemical substitution on the BB sites [16]. The substitution on the BB’-site of Ni may enhance the BB’-O-O-BB’ AFM interactions and stabilize the AFM ground state. For instance, Ba2La2MnW2O12 shows an AFM order below 1.7 K [16]. The Ni2+ ions can also be substituted by Cu2+ ions, but the latter case is not yet studied, although it may represent another interesting compound to exhibit magnetic frustration. Finally, the introduction of magnetic ions on the AA site (e.g., the substitution of Ba2+ or Sr2+ with Eu2+), whose magnetic interactions can compete with the above superexchange interactions, may lead to exotic magnetic properties.

V Conclusion

To summarize, we studied the effects of chemical pressure on the magnetic triangular-lattice compounds A2A_{2}La2NiW2O12 (AA = Sr, Ba). Their magnetic properties (due to the Ni2+ ions) were investigated by means of magnetic susceptibility, specific heat, neutron diffraction, and µSR spectroscopy. When replacing Ba with Sr, chemical pressure is introduced which can tune the competition between the FM- and AFM superexchange interactions. While the Curie temperature TcT_{c} is suppressed from 6.3 K to 4.8 K, the FM interactions still persist in Sr2La2NiW2O12. According to the refinements of neutron diffraction patterns, in both compounds, the magnetic moments of Ni atoms are aligned along the cc-axis, with a propagation vector 𝒌=(0,0,0)\boldsymbol{k}=(0,0,0). By using ZF-µSR measurements, we could follow the temperature evolution of the spin fluctuations and of the local magnetic fields. The estimated internal fields at zero temperature for the two different muon-stopping sites are 0.31 and 0.1 T. The smooth transverse muon-spin relaxation rates λT\lambda_{\mathrm{T}} in the ordered phase confirm the simple FM structure of A2A_{2}La2NiW2O12. In both materials, spin fluctuations are rather weak, reflected in a small longitudinal muon-spin relaxation rate in both the ferromagnetic- and paramagnetic states. In the future, it could be interesting to check if the combined physical pressure and chemical substitution on the AA and BB’ sites can further tune the magnetic competitions in Sr2La2NiW2O12, and eventually lead to magnetic frustration or to a quantum spin-liquid state.

Acknowledgements.
This work was supported by the Natural Science Foundation of Shanghai (Grants No. 21ZR1420500 and 21JC1402300), Natural Science Foundation of Chongqing (Grant No. 2022NSCQ-MSX1468), and the Schweizerische Nationalfonds zur Förderung der Wissenschaftlichen Forschung (SNF) (Grants No. 200021_188706 and 206021_139082). Y.X. acknowledges support from the Shanghai Pujiang Program (Grant No. 21PJ1403100) and the Natural Science Foundation of China (Grant No. 12274125).

References

  • Binder and Young [1986] K. Binder and A. P. Young, Spin glasses: experimental facts, theoretical concepts, and open questions, Rev. Mod. Phys. 58, 801 (1986).
  • Collins and Petrenko [1997] M. F. Collins and O. A. Petrenko, Triangular antiferromagnets, Can. J. Phys. 75, 605 (1997).
  • Moessner and Ramirez [2006] R. Moessner and A. P. Ramirez, Geometrical frustration, Phys. Today 59, 24 (2006).
  • Balents [2010] L. Balents, Spin liquids in frustrated magnets, Nature 464, 199 (2010).
  • Ma et al. [2018] Z. Ma, J. Wang, Z.-Y. Dong, J. Zhang, S. Li, S.-H. Zheng, Y. Yu, W. Wang, L. Che, K. Ran, S. Bao, Z. Cai, P. Čermák, A. Schneidewind, S. Yano, J. S. Gardner, X. Lu, S.-L. Yu, J.-M. Liu, S. Li, J.-X. Li, and J. Wen, Spin-glass ground state in a triangular-lattice compound YbZnGaO4, Phys. Rev. Lett. 120, 087201 (2018).
  • Ramirez et al. [1999] A. P. Ramirez, A. Hayashi, R. J. Cava, R. Siddharthan, and B. S. Shastry, Zero-point entropy in ‘spin ice’, Nature 399, 333 (1999).
  • Khatua et al. [2022] J. Khatua, M. Gomilšek, J. C. Orain, A. M. Strydom, Z. Jagličić, C. V. Colin, S. Petit, A. Ozarowski, L. Mangin-Thro, K. Sethupathi, M. S. R. Rao, A. Zorko, and P. Khuntia, Signature of a randomness-driven spin-liquid state in a frustrated magnet, Commun. Phys. 5, 99 (2022).
  • Shen et al. [2018] Y. Shen, Y.-D. Li, H. C. Walker, P. Steffens, M. Boehm, X. Zhang, S. Shen, H. Wo, G. Chen, and J. Zhao, Fractionalized excitations in the partially magnetized spin liquid candidate YbMgGaO4\mathrm{YbMgGaO}_{4}, Nat. Commun. 9, 4138 (2018).
  • Ramirez [1994] A. P. Ramirez, Strongly geometrically frustrated magnets, Annu. Rev. Mater. Sci. 24, 453 (1994).
  • Greedan [2001] J. E. Greedan, Geometrically frustrated magnetic materials, J. Mater. Chem. 11, 37 (2001).
  • Kawamura [1998] H. Kawamura, Universality of phase transitions of frustrated antiferromagnets, J. Phys.: Condens. Matter 10, 4707 (1998).
  • Jaklič and Prelovšek [2000] J. Jaklič and P. Prelovšek, Finite-temperature properties of doped antiferromagnets, Adv. Phys. 49, 1 (2000).
  • Wannier [1950] G. H. Wannier, Antiferromagnetism. The triangular Ising net, Phys. Rev. 79, 357 (1950).
  • Lv et al. [2015] H. Y. Lv, W. J. Lu, D. F. Shao, Y. Liu, and Y. P. Sun, Strain-controlled switch between ferromagnetism and antiferromagnetism in 1T{T}−{-}CrX2{X}_{2} (X{X} = Se, Te) monolayers, Phys. Rev. B 92, 214419 (2015).
  • Longo et al. [1965] J. M. Longo, L. Katz, and R. Ward, Rhenium-containing complex metal oxides of the formula type A\mathrm{A}4Re\mathrm{Re}2MO\mathrm{MO}12, Inorg. Chem. 4, 235 (1965).
  • Rawl et al. [2017] R. Rawl, M. Lee, E. S. Choi, G. Li, K. W. Chen, R. Baumbach, C. R. dela Cruz, J. Ma, and H. D. Zhou, Magnetic properties of the triangular lattice magnets A\mathrm{A}4B\mathrm{B}′{}^{{}^{\prime}}B\mathrm{B}2O\mathrm{O}12 (A\mathrm{A} = Ba\mathrm{Ba}, Sr\mathrm{Sr}, La\mathrm{La}; B\mathrm{B}′{}^{{}^{\prime}} = Co\mathrm{Co}, Ni\mathrm{Ni}, Mn\mathrm{Mn}; B\mathrm{B} = W\mathrm{W}, Re\mathrm{Re}), Phys. Rev. B 95, 174438 (2017).
  • Saito et al. [2019] M. Saito, M. Watanabe, N. Kurita, A. Matsuo, K. Kindo, M. Avdeev, H. O. Jeschke, and H. Tanaka, Successive phase transitions and magnetization plateau in the spin-1 triangular-lattice antiferromagnet Ba\mathrm{Ba}2La\mathrm{La}2NiTe\mathrm{NiTe}2O\mathrm{O}12 with small easy-axis anisotropy, Phys. Rev. B 100, 064417 (2019).
  • Kojima et al. [2018] Y. Kojima, M. Watanabe, N. Kurita, H. Tanaka, A. Matsuo, K. Kindo, and M. Avdeev, Quantum magnetic properties of the spin-12\frac{1}{2} triangular-lattice antiferromagnet Ba\mathrm{Ba}2La\mathrm{La}2CoTe\mathrm{CoTe}2O\mathrm{O}12, Phys. Rev. B 98, 174406 (2018).
  • Doi et al. [2017] Y. Doi, M. Wakeshima, K. Tezuka, Y. J. Shan, K. Ohoyama, S. Lee, S. Torii, T. Kamiyama, and Y. Hinatsu, Crystal structures, magnetic properties, and DFT\mathrm{DFT} calculation of B−\mathrm{B}-site defected 12L−\mathrm{L}-perovskites Ba2La2MW2O12 (M = Mn, Co, Ni, Zn), J. Phys. Condens. Matter 29, 365802 (2017).
  • Lee et al. [2014a] M. Lee, J. Hwang, E. S. Choi, J. Ma, C. R. Dela Cruz, M. Zhu, X. Ke, Z. L. Dun, and H. D. Zhou, Series of phase transitions and multiferroicity in the quasi-two-dimensional spin-12\frac{1}{2} triangular-lattice antiferromagnet Ba\mathrm{Ba}3CoNb\mathrm{CoNb}2O\mathrm{O}9, Phys. Rev. B 89, 104420 (2014a).
  • Yokota et al. [2014] K. Yokota, N. Kurita, and H. Tanaka, Magnetic phase diagram of the S=12{S}=\frac{1}{2} triangular-lattice Heisenberg antiferromagnet Ba\mathrm{Ba}3Co\mathrm{Co}Nb\mathrm{Nb}2O\mathrm{O}9, Phys. Rev. B 90, 014403 (2014).
  • Hwang et al. [2012] J. Hwang, E. S. Choi, F. Ye, C. R. Dela Cruz, Y. Xin, H. D. Zhou, and P. Schlottmann, Successive magnetic phase transitions and multiferroicity in the spin-one triangular-lattice antiferromagnet Ba\mathrm{Ba}3NiNb\mathrm{NiNb}2O\mathrm{O}9, Phys. Rev. Lett. 109, 257205 (2012).
  • Lee et al. [2014b] M. Lee, E. S. Choi, X. Huang, J. Ma, C. R. Dela Cruz, M. Matsuda, W. Tian, Z. L. Dun, S. Dong, and H. D. Zhou, Magnetic phase diagram and multiferroicity of Ba\mathrm{Ba}3Mn\mathrm{Mn}Nb\mathrm{Nb}2O\mathrm{O}9: A spin-52\frac{5}{2} triangular lattice antiferromagnet with weak easy-axis anisotropy, Phys. Rev. B 90, 224402 (2014b).
  • Möller et al. [2012] A. Möller, N. E. Amuneke, P. Daniel, B. Lorenz, C. R. de la Cruz, M. Gooch, and P. C. W. Chu, A{A}Ag2M{M}[VO4]2 (A{A} = Ba, Sr; M{M} = Co, Ni): A series of ferromagnetic insulators, Phys. Rev. B 85, 214422 (2012).
  • Tsirlin et al. [2012] A. A. Tsirlin, A. Möller, B. Lorenz, Y. Skourski, and H. Rosner, Superposition of ferromagnetic and antiferromagnetic spin chains in the quantum magnet Ba\mathrm{Ba}Ag\mathrm{Ag}2Cu\mathrm{Cu}[V\mathrm{V}O\mathrm{O}4]2, Phys. Rev. B 85, 014401 (2012).
  • Sun et al. [2019] Y. Sun, Z. Liu, W. Zhang, X. Chu, Y. Cong, K. Huang, and S. Feng, Unfolding B–O–B bonds for an enhanced ORR performance in ABO3-type perovskites, Small 15, 1803513 (2019).
  • Sengupta et al. [2010] K. Sengupta, M. K. Forthaus, H. Kubo, K. Katoh, K. Umeo, T. Takabatake, and M. M. Abd-Elmeguid, Geometrical frustration versus magnetic order in the heavy-fermion antiferromagnet YbAgGe under high pressure, Phys. Rev. B 81, 125129 (2010).
  • Jiao et al. [2020] Y. Jiao, Y.-W. Fang, J. Sun, P. Shan, Z. Yu, H. L. Feng, B. Wang, H. Ma, Y. Uwatoko, K. Yamaura, Y. Guo, H. Chen, and J. Cheng, Coupled magnetic and structural phase transitions in the antiferromagnetic polar metal Pb2CoOsO6 under pressure, Phys. Rev. B 102, 144418 (2020).
  • Gebauer et al. [2000] R. Gebauer, S. Serra, G. L. Chiarotti, S. Scandolo, S. Baroni, and E. Tosatti, Noncolinear spin polarization from frustrated antiferromagnetism: A possible scenario for molecular oxygen at high pressure, Phys. Rev. B 61, 6145 (2000).
  • Rodríguez-Carvajal [1993] J. Rodríguez-Carvajal, Recent advances in magnetic structure determination by neutron powder diffraction, Phys. B: Condens. Matter. 192, 55 (1993).
  • A. Suter and Wojek [2012] A. A. Suter and B. M. Wojek, Musrfit: A free platform-independent framework for μ\muSR data analysis, Phys. Procedia 30, 69 (2012).
  • Orchard [2003] A. F. Orchard, Magnetochemistry, Oxford Chemistry Primers (Oxford University Press, Oxford, 2003).
  • Furrer [2000] A. Furrer, Neutron Scattering in Novel Materials (World Scientific, Singapore, 2000).
  • Rodríguez-Carvajal [2010] J. Rodríguez-Carvajal, BASIREPS: A program for calculating irreducible representation of little groups and basis functions of polar and axial vector properties (2010), part of FullProf suite, ILL.
  • Yaouanc and de Réotier [2011] A. Yaouanc and P. D. de Réotier, Muon Spin Rotation, Relaxation, and Resonance: Applications to Condensed Matter (Oxford University Press, Oxford, 2011).
  • Zhu et al. [2022] X. Y. Zhu, H. Zhang, D. J. Gawryluk, Z. X. Zhen, B. C. Yu, S. L. Ju, W. Xie, D. M. Jiang, W. J. Cheng, Y. Xu, M. Shi, E. Pomjakushina, Q. F. Zhan, T. Shiroka, and T. Shang, Spin order and fluctuations in the EuAl4 and EuGa4 topological antiferromagnets: A μ\muSR study, Phys. Rev. B 105, 014423 (2022).
  • Tran et al. [2018] L. M. Tran, M. Babij, L. Korosec, T. Shang, Z. Bukowski, and T. Shiroka, Magnetic phase diagram of Ca-substituted EuFe2As2, Phys. Rev. B 98, 104412 (2018).
  • Goodenough [1955] J. B. Goodenough, Theory of the role of covalence in the perovskite-type manganites [La, MM(II)]MnO3, Phys. Rev. 100, 564 (1955).
  • Kanamori [1959] J. Kanamori, Superexchange interaction and symmetry properties of electron orbitals, J. Phys. Chem. Solids 10, 87 (1959).
  • Coey [2010] J. M. D. Coey, Magnetism and Magnetic Materials (Cambridge University Press, Cambridge, 2010).