∎
e1e-mail: ruben@lip.pt
New methods to reconstruct and the energy of gamma-ray air showers with high accuracy in large wide-field observatories
Abstract
Novel methods to reconstruct the slant depth of the maximum of the longitudinal profile () of high-energy showers initiated by gamma-rays as well as their energy () are presented. The methods were developed for gamma rays with energies ranging from a few hundred GeV to TeV. An estimator of is obtained, event-by-event, from its correlation with the distribution of the arrival time of the particles at the ground, or the signal at the ground for lower energies. An estimator of is obtained, event-by-event, using a parametrization that has as inputs the total measured energy at the ground, the amount of energy contained in a region near to the shower core and the estimated .
Resolutions about and about for, respectively, and at energies are obtained, considering vertical showers. The obtained results are auspicious and can lead to the opening of new physics avenues for large wide field-of-view gamma-ray observatories. The dependence of the resolutions with experimental conditions is discussed.
Keywords:
High Energy gamma raysWide field observatories Depth of the shower maximum energy distribution at the ground Primary energy reconstruction resolution1 Introduction
High energy cosmic and gamma rays entering the Earth atmosphere originate Extensive Air Showers (EAS) which may be characterised by the distributions of the number of shower particles as a function of the traversed atmospheric slant depth (longitudinal profiles) and/or by the distributions of the particles arriving at the ground level as a function of the distance to the shower core (Lateral Density Function - LDF).
The longitudinal development of gamma-ray initiated showers was historically described by Rossi and Greisen diffusion equations Rossi-Greisen being the well known Greisen Greisen and Gaisser-Hillas Gaisser-Hillas functions approximate solutions. It can be demonstrated that these functions lead to a quasi-universal shape Longi_profiles . This universality can be shown by representing the shower longitudinal profile in the plane ( , ), where is the slant depth of the maximum of the profile and is the number of the shower particles at that depth. In this reference frame, the profile may be seen as a slightly asymmetric Gaussian with variable width and is essentially insensitive to variations induced by the depth of the first interaction RL . However, at TeV energies or below, the fraction of events where the longitudinal profile do not follow the quasi Gaussian shape may not be negligible. A few of the profiles will have a slower decrease after or even having a double peak structure. These anomalous shower profile structures are associated with interactions where particles travel several radiation/interaction lengths before interacting, or when one of the sub-products of the interaction takes nearly all of the available energy.
Imaging Air Cherenkov Telescopes (IACTs) collect Cherenkov light produced by the EAS and are able, due to their size, intensity, and orientation of the projected image in the camera focal plane, to reconstruct the energy and the direction of the primary gamma-ray. Typical energy resolution of are often quoted for TeV gammas and zenith angles of about , for instance, the resolution of MAGIC-II was measured to be 15% MAGIC .
Ground-based gamma-ray observatories sample the particles (mainly electrons and photons) arriving at the ground level and from their time and position distributions can determine, with reasonable accuracy, the shower core position and the direction of the primary gamma-ray. The determination of the shower energy has, however, a large uncertainty. Indeed, energy resolutions of the order of several tens of percent are often quoted. For instance, in Vikas using a Likelihood fit with Monte Carlo template distributions, the energy reconstruction resolution at TeV is and the HAWC collaboration has recently reported an improved energy resolution of at the same energy using a neural network analysis HAWC_energy .
One of the main limiting factors in the reconstruction of the primary energy for ground arrays is the uncertainty on the position of the first interaction in the atmosphere. Contrary to IACT arrays, there is no direct measurement for ground arrays of the contents of the EAS in the region of the shower maximum, and therefore the shower development stage is unknown. In fact, for showers induced by gamma-rays, with the same energy and zenith angle, the number of particles at the ground is expected to increase with . The previous statement is not absolute as the width of the longitudinal profile is also an important factor to determine not only the total energy at the ground but also the fraction of this energy present in the region of the shower core. A larger shower profile width will, for the same , have larger energy at the ground and a more substantial fraction of energy in the region near the core. Indeed, it is possible to establish, at fixed primary energy, a correlation between the fraction of the energy in the region near the core and the total energy carried by electromagnetic particles (photons, electrons and positrons) that reach the ground ().
The energy measured by a detector array with electromagnetic calorimetric capabilities, like Water Cherenkov Detectors, is by definition highly correlated with . Such correlation is explored to built an estimator of (section 2).
is not easily estimated at ground gamma-ray observatories. However, at very high energies in cosmic rays experiments, correlations between and the distribution of the arrival times of the particles at the ground in each event, have been established SD_XMAX . Such correlations are exploited to build an estimator of (section 3).
An innovative method for the reconstruction of the primary energy of each event, having as inputs the total measured energy at the ground, the fraction of this energy measured in the region near the shower core and the estimated , is then presented (section 4).
Finally, the applicability of such method in realhistogrammed large wide-field gamma-ray observatories is discussed (section 5).
All the present results were obtained using CORSIKA (version 7.5600) CORSIKA to simulate vertical gamma-ray showers assuming an observatory at an altitude of 5200 m a.s.l. The primaries, with energies between GeV and TeV, were injected following an energy spectrum of , which guarantees high enough statistics over the whole simulated energy range. It was used as hadronic interaction model for low and high energy, FLUKA and QGSJET-II.04, respectively, although the choice of these models has little impact on the simulation of electromagnetic showers. The total energy of electromagnetic shower particles was recorded at the observation level and histogrammed in radial bins of 4 meters. This would mimic a calorimeter detector compact array, where the station unit covers an area of . A full study including different zenith angles, detailed simulations of realistic detectors, a wider energy range and also its application to hadronic induced showers, is out of the scope of this work. The main focus of this article is the explanation of the newly proposed method to achieve an accurate energy reconstruction of gamma-ray air showers between several hundreds of GeV and a few TeV. This is the most challenging energy region for this kind of experiments. In addition to the uncertainty on the shower stage, the number of secondary shower particles that reach the ground is reduced when comparing with energies of the order of tens of TeV, undermining the capability to reconstruct the shower quantities. A first glance on its potential is given.
2 Energy distribution at the ground
The density of the shower particles arriving at the ground, as a function of the distance to the shower core, is steeper in the region near the core and flatter at larger distances. This distribution is usually parametrized using the NKG (Nishimura-Kamata-Greisen) formula NKG . The particle density at a given distance from the air shower axis is often used to obtain an estimator of the primary energy, trying to find a region less sensitive to the fluctuations in the shower development, to the primary nature and to array sampling effects. For instance, in the Tibet Air Shower Array, this distance was found to be 50 m tibet .
The energy distribution at the ground as a function of the distance to the core position and its cumulative function, , are shown in figure 1 for an event with GeV, GeV and .
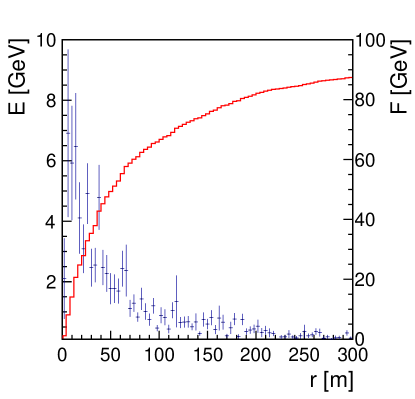
.
The strategy followed in this article is different from one usually employed by shower array experiments HAWC_energy ; LHAASO_energy . Instead of using the shower particle density at the ground at some optimized distance from the shower core, the aim is to characterize the shower development through two variables that will be then used to predict, event by event, the calibration factor between the gamma-ray energy () and the electromagnetic energy arriving at the ground ().
, whose estimator will be discussed in the next section, is naturally one of these variables. The other, , is defined as the ratio between the energy at the ground collected at a distance less than m from the shower core and the total energy at the ground. This parameter will be the main responsible for the improvement of the energy resolution reached in this article. The rationale of this second variable was already introduced in the previous section. For a given and , the development of the shower between the region and the ground level will strongly determine .
An estimator of , designated as , may be obtained using the correlation between and , being a reference distance. In any case, should be greater than m to ensure a good correlation, and lower than some tens of meters to ensure a high number of events where the event footprint, with , is fully contained within the compact array region of the observatory. For the purpose of this article, in the following m is used.
The correlation between and is shown in figure 2 and is parametrized as:
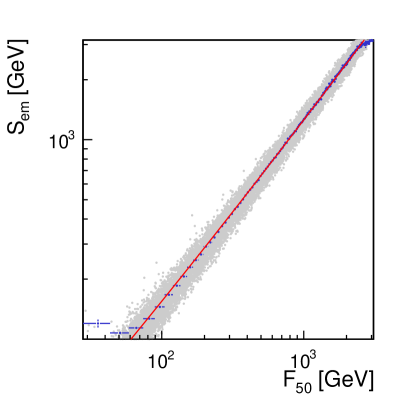
| (1) |
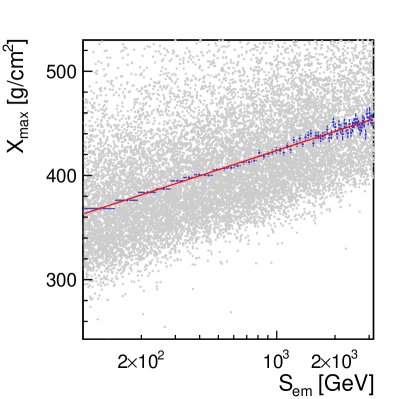
where and are free positive parameters. This parametrization ensures, by construction, that is always greater then . With and in GeV, the best values found to be for and . The result is shown as a red curve in figure 2.
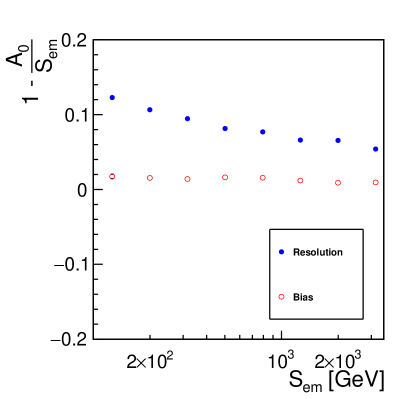
The obtained resolutions and bias111In this work, the bias and resolutions of the estimator, , of variable, , are taken fitting a gaussian function to the residuals, (). The bias and the resolution corresponds to the mean and the sigma parameter of the fitted gaussian, respectively. of are summarized in figure 3, as a function of . As a reference a primary energy of TeV and TeV corresponds to a mean value of of GeV and TeV, respectively (see figure 10). Thus, resolutions of about and are found at primaries energies of TeV and TeV, respectively, while the bias is consistently in the order of a few percent.
In principle, a better estimator of can be obtained using a continuously measured distribution of and not just a single measurement at . With this purpose, , which is a smooth and continuous function, was parametrized as:
| (2) |
The parameter is the estimator while the terms describe the steepness of the function, being and .
In the limits and this parametrization becomes,
| (3) |
and,
| (4) |
which have the form of Weibull cumulative distribution functions Weibull .
Indeed, as an example, it is shown in figure 4 that, in the plane (, ) and assuming , the cumulative distribution function of the event shown in figure 1 (blue points) is well described by the above parametrization.
In this plane a pure Weibull function is just a straight line while to describe this event two straight lines are needed due the transition between the two regimes in the region ( 3 - 3.5). This transition region matches the known behaviour of the energy distribution at the ground with a higher concentration of energy in the core region. Similar fits to a large number of events and whose cumulative functions correspond to quite different steepness in the core region are equally very good.
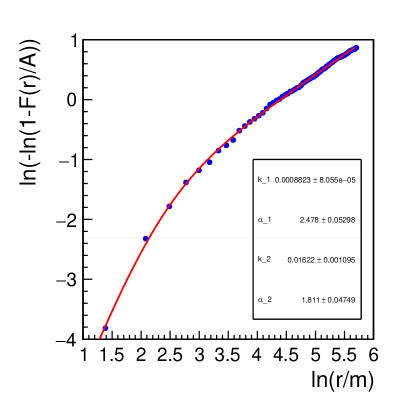
.
In a real event is not known and the parameter , as well as the parameters , , and , have to be fitted. However, it was found that the convergence of this fit is not trivial, as is highly correlated with combinations of the other parameters, and thus elaborated fit strategies will have to be defined, which is beyond the scope of the present article. In these terms will be the estimator used hereafter.
The variable is then defined as . The choice of 20 m for the definition of this variable is a compromise which should be optimized for each specific experiment. Nevertheless, its value should be typically between 15 m and 30 m. Lower values will conflict with the possible experimental resolutions on the shower core, higher values will enter in the region where the cumulative function has a slower increase and also where, for events with the core nearer to the border of the compact region of the array, there will be no direct measurement of the cumulative function.
3 reconstruction and resolution
A first order estimation of may be obtained observing that the mean value of increases with the increase of the electromagnetic energy arriving at the ground (), reflecting the increase of the shower size with the primary energy. This correlation is demonstrated in figure 5 where is represented as a function of . It is then possible to parametrize as a function of as:
| (5) |
with and parameters tuned to describe the mean behaviour. The best achieved parameterization is shown in figure 5 as a red filled curve (corresponding to and ).
A more precise estimate of may be obtained exploring the fact that the shower front at the ground is a curved surface showerCurvature . Ideally, if the shower particles were produced in a single point located along the shower axis, for instance at the , this surface will be spherical, assuming that all the particles travel approximately with the speed of light. The arrival time in each surface station would then change accordingly as a function of the distance to the shower core and with the primary particle direction. Using a simple geometrical fit, the position would be reconstructed straightforwardly, with an accuracy that would mainly depend on the time resolution of the stations.
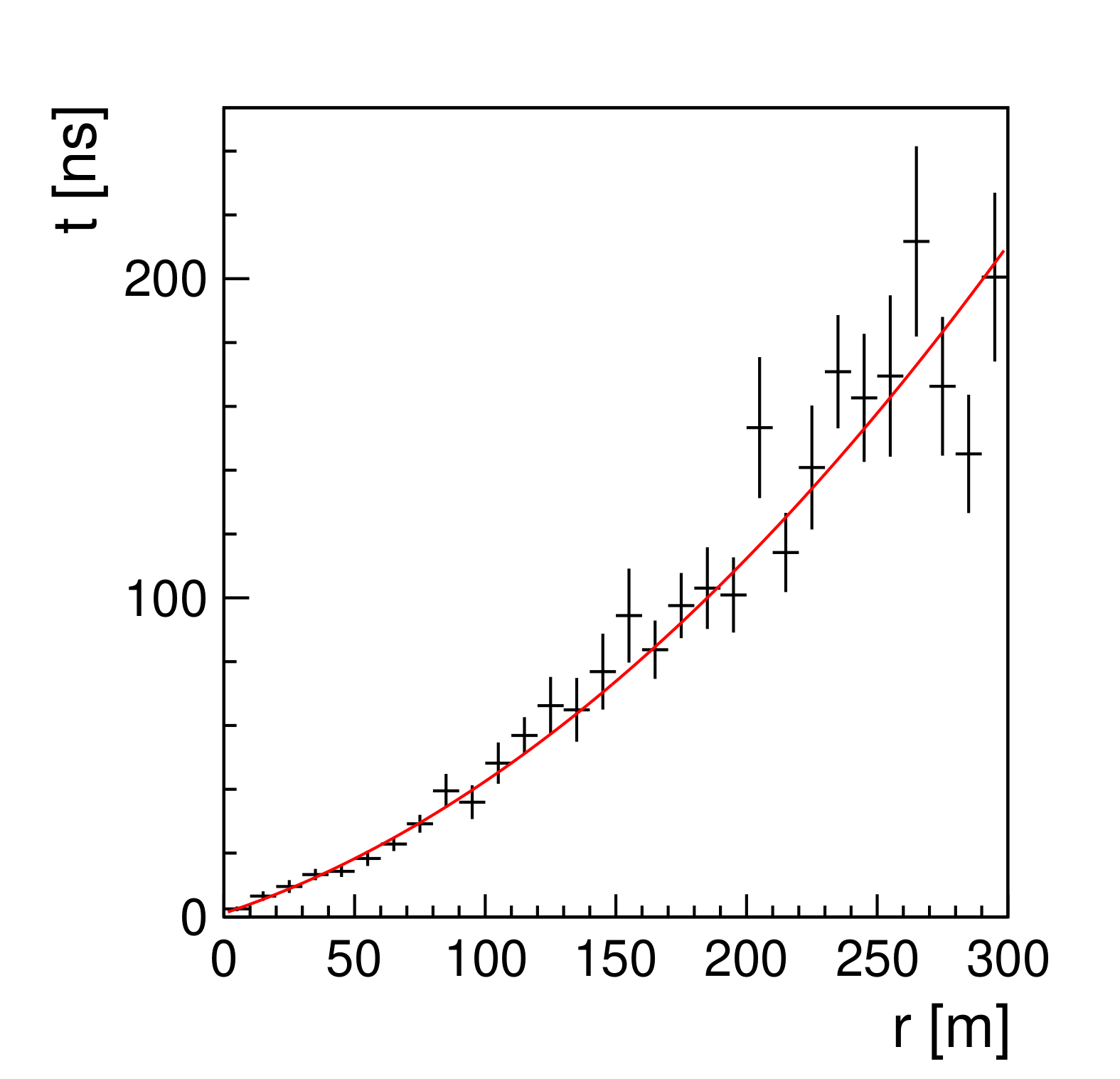
In reality, the geometry is more complex, but nevertheless, it is possible to establish a clear correlation between and the arrival time distribution of particles at the ground. As an example in figure 6 this correlation is shown for an event with and TeV. It was found that most of the events can be described by a quadratic polynomial of the form,
| (6) |
In fact, the application of the above equation to the time profiles as a function of the distance to the shower core leads to a well behaved distribution with the distribution maximum peaking at .
.
The parameter of the quadratic term of the polynomial, , is strongly correlated with (figure 7). The parameter is nearly independent of , and is associated with the event initial time, , usually set to zero when the shower front reaches the shower core position. The dependence of with can be understood if one assumes that most of the particles produced in a shower come from and the shower particles propagate as spherical front. This is of course an approximation but figure 7 supports it and it helps to build some intuition.
Hence, it is possible to parametrize as a function of using:
| (7) |
and are parameters tuned to describe the profile shown in figure 7. The best achieved parametrization is shown by the red curve, with and .
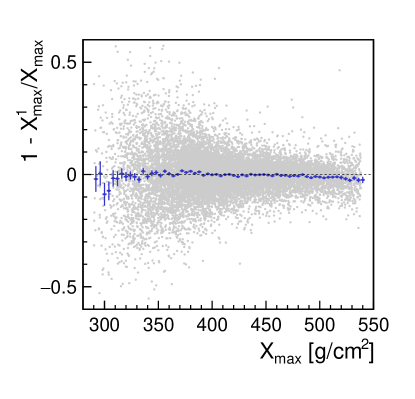
does not show any relevant bias even for low , as shown in figure 8. Nevertheless, in a few cases, particularly at lower energies where the number of particles arriving at the ground is small, the fit may converge to values leading to non-physical values of . In practice, whenever the estimation of from the fit indicates values lower than , the first order estimation is used.
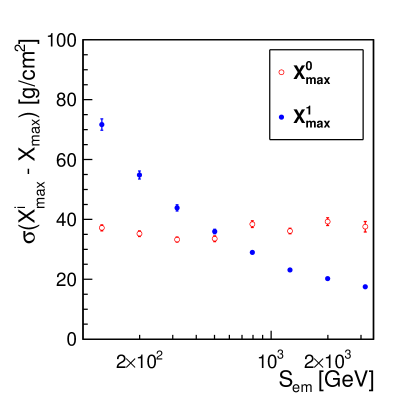
The obtained resolutions as a function of , both for and , are summarized in figure 9. Resolutions of about and were found for primaries energies of TeV and TeV, respectively.
The two resolutions are similar in the region GeV. To be on the safe side, avoiding possible tail effects, we set GeV. Therefore, the estimator of , designated as is defined as:
| (8) |
4 Energy reconstruction and resolution
In electromagnetic showers, the production of muons, either via the photo-production of mesons or by the direct creation of muon pairs is quite small muonproduction and can thus be neglected in the global accounting of the shower energy.
On the other hand, the logarithm of the electromagnetic energy deposited in the atmosphere is linearly correlated with the logarithm of the energy deposited at the Earth surface (), as shown in figure 10.
It is then possible to parametrize as a function of as:
| (9) |
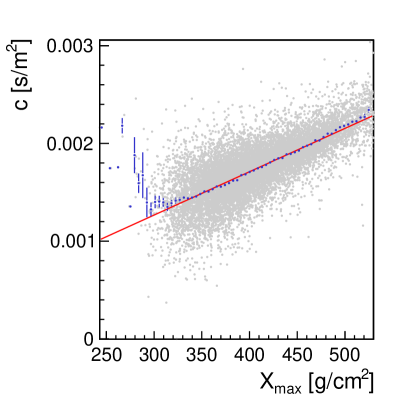
where and are free positive parameters. This parametrization ensures, by construction, that is always greater then . The best values found for and are and , respectively. The result is shown as a red curve in figure 10.
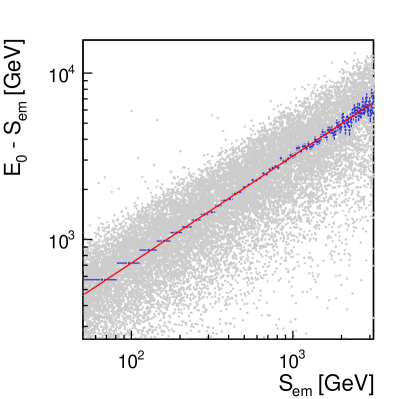
Using the above parametrization and (see section 2) as the estimator of , it is possible to make a first energy reconstruction considering an ideal detector222By ideal detector it is assumed a detector able to accurately collects all the energy of electromagnetic particles reaching the station. The impact of having a real calorimetric detector such as a water Cherenkov detector is addressed in section 5.. An energy resolution of about is obtained at TeV.
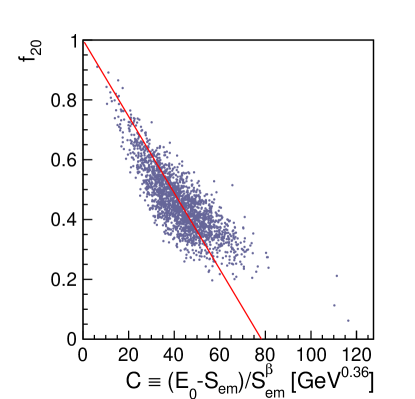
The coefficient , in this first calibration attempt, is a constant. However, can be shown to be correlated with , and . Indeed, it is shown in figure 11 a striking correlation between and , for events with GeV and . The line in the figure is the best linear parameterization imposing that for (no energy deposited in the atmosphere), (all the deposited at the ground is at a distance lower than 20 m from the shower core position).
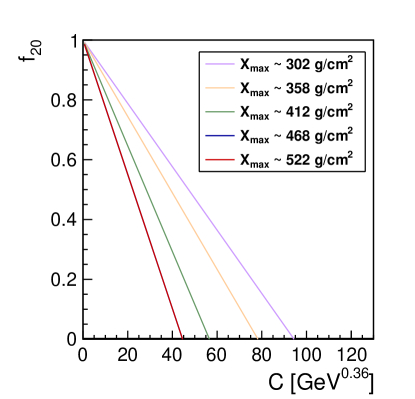
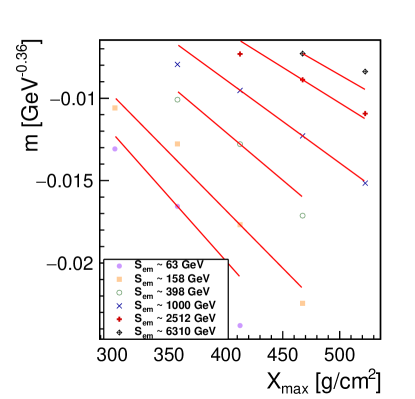
The set of the correlation lines () for several ranges and GeV , are shown in figure 12. There is a linear monotonous decrease of the slope of these lines with the increase of . In figure 13 the obtained are represented as a function of for different bins of together with the best linear parametrization for each bin.
The extrapolation of these lines for points to a non-physical small positive value of (), which means that this linear model is no longer valid for ,which is far below the relevant region for this article333For the energies considered in this article, most shower events have values around . A shower with would have its buried in the ground while a shower with would only reach the ground if it strongly fluctuates.. So we will keep the linear approximation using for all .
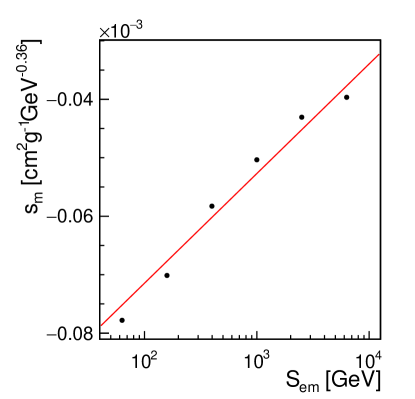
Finally, the slope of the lines represented in figure 13 are shown in figure 14 as a function of . A linear correlation is found between and . As such, one can write,
| (10) |
and,
| (11) |
The best achieved parametrization with the above equation is shown in figure 14, with parameters and .
Finally,
| (12) |
and,
| (13) |
which is our best estimator for the primary energy.
Using in the above parametrization, (see section 2) as the estimator of and (see section 3) as the estimator of , an energy resolution below and were obtained at TeV and TeV, respectively.
Using instead the real and , these energy resolutions improve to about and . These results may be considered as the ultimate resolutions. The difference between the estimated resolutions and the ultimate resolutions are driven, in the TeV region, mainly by the resolution of the estimator. Indeed, a resolution of on the parameter , the estimator, even considering the simulated value, would translate into a resolution on of .
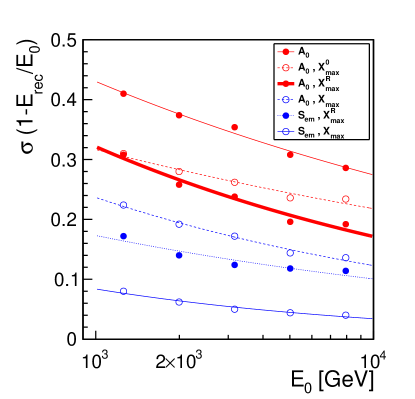
In figure 15 are shown (full red thick line) the estimated energy () resolution as a function of the primary energy. For comparison, the equivalent resolutions obtained applying the constant calibration (), full red thin line, defined by equation 9, or using systematically the estimator (dashed red thin line) are also shown. It is also shown the resolutions that would be obtained using the simulated value of (dashed blue line), or the simulated value of (pointed blue line) or finally using both simulated values (blue thin line).
These results are obtained considering an ideal detector. The degradation factors due to the detector effects are briefly discussed in the next section.
5 Discussion and Conclusions
In this article, new and innovative methods for the determination of the total electromagnetic energy at the ground, of the slant depth of the maximum of the longitudinal profile and, of the primary energy were proposed. In particular, as much as we know, it is the first time that the steepness in the core region of the cumulative function of the energy arriving at the ground is used as a determinant factor to obtain the energy calibration constants.
The obtained results are very promising and can open new physics avenues. The improvement on the energy resolution has, as a direct consequence, a meaningful increase of the sensitivity of the observatories. The obtained resolutions on , yet to be confirmed for cosmic ray shower, would allow very interesting studies on the development of the shower, namely on the characterization of the mass composition of hadronic cosmic rays. This shall be focus of a future publication.
These results, even if obtained considering an ideal detector, are quite robust as they rely only on the estimation of the electromagnetic energy at the ground, and, of the slant depth of the maximum of the longitudinal profile, , which may be, in a first-order approximation, also obtained from the . Typically, a region of a few tens of meters around the core and an energy at the ground of several tens of GeV have to be measured to be able to efficiently apply the proposed algorithms.
The estimation of is thus the critical factor to be able to achieve a good resolution on the reconstruction of the primary gamma-ray energy. Further progress may be envisaged using more sophisticated estimators, like the one suggested by the cumulative function parametrization described in equation 2, or applying, for instance, machine learning techniques.
All the present results were obtained using vertical showers. Inclined showers would imply lower energies at the ground. For instance, at TeV an inclined shower would deposit at the ground around 20% less than a vertical shower of the same energy (see, for instance HAWC_GRB ). Therefore, at lower energies, the energy resolutions will be worse, scaling with . Taking LHAASO LHAASO_energy , as an example, it was shown that for TeV gamma induced showers, there is a degradation in the reconstructed energy resolution of when moving from showers with zenith angle to . It should be noted that the ability to measure higher energies may improve as the probability of the depth of shower maximum to be above the ground surface increases.
A detailed study of the performance of the new reconstruction methods for a specific Wide Field of View Gamma Ray Observatory is out of the scope of this work. Nevertheless, it is important to discuss briefly possible factors that would contribute to the degradation of the results obtained in the previous sections. Most of these effects are mainly critical for primary energies below a few hundreds of GeV, corresponding to energies at the ground of a few tens of GeV, where a detailed design and simulation of the detectors would be mandatory.
The following factors need to be considered:
-
•
The amount of signal (p.e.) generated in each station
The electromagnetic energy deposited in each station may be converted into photoelectrons (p.e.) using as conversion factors where is, following WH_private , a scale factor. corresponds to the existing performance at HAWC. Much higher values of were found in LATTES end-to-end simulations LATTES . Fluctuations may then be generated using a Poisson distribution.
Anyway, for energies at TeV or above the total signal per event is above several thousands of p.e., even for the more conservative scale factors. The uncertainty in the measurements of and is then, at lower energies of the order of just a few % and at higher energies negligible, which in any case will be translated at most in a minor increase of the obtained energies resolutions.
-
•
The precision on the location of the shower core
The reconstructed shower core position should, for each event, be smeared by a few meters following the resolutions quoted in LATTES (m at TeV, m at TeV). This would introduce distortions in the cumulative functions which would correspond to an increase of at most a few % in the value of the resolution of the () estimator.
-
•
The finite dimension of the compact array region of the observatory
The distance of the core position to the border of the compact array region of the observatory will determine the fraction of the event footprint at the ground that would be measured. However, it is possible to imagine more sophisticated methods, using, for instance, neural networks, to make a reasonably accurate estimation of the even in the case where there is only a partial containment of the shower footprint in the required region around the core.
-
•
The time resolution at each detector station Time resolutions better than ns are crucial for good angular resolutions WH_angular . Assuming that the detectors would comply with a ns time resolution, the particle arrival times should be smeared and the estimator (see section 3) re-computed. Once again, this effect should be mainly important for lower energies; at higher energies, above a few TeV, there will be a high number of hit stations and the curvature fit will be more robust. Nevertheless, giving up the possibility to compute, for each event, the curvature of the shower front, the systematic use of the estimator would have only impact at energies above a few TeV degrading the energy resolutions at TeV from to , as shown by the dashed red line in figure 15.
The results obtained, representing such a considerable improvement concerning the presently quoted energy resolutions of the existing or planned Wide Field of View Gamma-Ray Observatories, clearly will encourage detailed simulations and studies on the applicability of the proposed methods.
Acknowledgements.
We would like to thank to A. Bueno, A. De Angelis and J. Vicha for all the useful discussions and carefully reading the manuscript. The authors thank also for the financial support by OE - Portugal, FCT, I. P., under project PTDC/FIS-PAR/29158/2017. R. C. is grateful for the financial support by OE - Portugal, FCT, I. P., under DL57/2016/cP1330/cT0002.References
- (1) B. Rossi, K. Greisen, Revs. Mod. Phys. 13, 240 (1941). DOI 10.1103/RevModPhys.13.240
- (2) K. Greisen, Progr.Cosmic Ray Physics 3, 1 (1956)
- (3) T.K. Gaisser, A.M. Hillas. Reliability of the method of constant intensity cuts for reconstructing the average development of vertical showers. Proc. 15th International Cosmic Ray Conference Plovdiv, Vol 8 353 (1977)
- (4) J. Montanus. Intermediate models for longitudinal profiles of cosmic showers. arXiv:1106.1073 [astro-ph.HE],(2011)
- (5) S. Andringa, R. Conceição, M. Pimenta, Astroparticle Physics 34, 360 (2011). DOI 10.1016/j.astropartphys.2010.10.002
- (6) J. Aleksic, et al. (MAGIC Collaboration), Astroparticle Physics 72, 76 (2016). DOI 10.1016/j.astropartphys.2015.02.005
- (7) V. Joshi, J. Hinton, H. Schoorlemmer, R. López-Coto, R. Parsons, JCAP 01, 012 (2019). DOI 10.1088/1475-7516/2019/01/012
- (8) A. Abeysekara, et al., The Astrophysical Journal 881, 134 (2019). DOI 10.3847/1538-4357/ab2f7d
- (9) A. Aab, et al., Phys. Rev. D 96(12), 122003 (2017). DOI 10.1103/PhysRevD.96.122003
- (10) D. Heck, J.N. Capdevielle, G. Schatz, T. Thouw, F.K. Gmbh. Corsika: A monte carlo code to simulate extensive air showers,” report fzka 6019, forschungszentrum karlsruhe (1998)
- (11) J. Kamata, K.and Nishimura, Progress of Theoretical Physics Supplement 6, 93 (1958). DOI 10.1143/PTPS.6.93
- (12) K. Kawata, T. Sako, M. Ohnishi, M. Takita, Y. Nakamura, K. Munakata, Experimental Astronomy 44 (2017). DOI 10.1007/s10686-017-9530-9
- (13) F. Aharonian, et al., (2020). ArXiv:2010.06205
- (14) W. Weibull, Journal of Applied Mechanics 18, 293 (1951)
- (15) A. Calabrese Melcarne, G. Marsella, D. Martello, L. Perrone, S. Sbano, in 32nd International Cosmic Ray Conference, vol. 1 (2011), vol. 1, pp. 66–69. DOI 10.7529/ICRC2011/V01/0402
- (16) T. Stanev, C.P. Vankov, F. Halzen. Muons in gamma showers. In NASA. Goddard Space Flight Center 19th Intern. Cosmic Ray Conf., Vol. 7 p 219-222 ,(1985)
- (17) A. Abeysekara, et al., Astropart. Phys. 35, 641 (2012). DOI 10.1016/j.astropartphys.2012.02.001
- (18) W. Hofmann. Impact of altitude and Cherenkov photon detection efficiency on the energy threshold of SWGO-like arrays. HAP-20-003
- (19) P. Assis, et. al., Astropart.Phys. 99, 34 (2018). DOI 10.1016/j.astropartphys.2018.02.004
- (20) W. Hofmann, Astropart. Phys. 123, 102479 (2020). DOI 10.1016/j.astropartphys.2020.102479