Newtonian coalescence in colloidal and non-colloidal suspensions
Abstract
Coalescence event in pendant and sessile drop is distinguished by the formation and evolution of the liquid bridge created upon singular contact. The bridge radius, , is known to evolve as , with power-law exponent, , signifying the dominant governing forces. In this work, we experimentally explore the phenomenon in sub-classes of complex fluids namely, colloidal and non-colloidal suspensions that have particle hydrodynamic interactions as origin of viscoelasticity. Our observations suggest that such fluids have flow dependent thinning response with finite elasticity in shear flows but negligible in extensional flows. Based on these, the study extends the Newtonian universality of to these thinning fluids. Further we fortify these observations through a theoretical model developed by employing Ostwald-de Waele constitutive law. Finally, we utilize this theoretical model to inspect the existence of arrested coalescence in generalized Newtonian fluids.
keywords:
American Chemical Society, LaTeX†Department of Mechanical Engineering, Indian Institute of Science, Bangalore, India \alsoaffiliation†Department of Mechanical Engineering, Indian Institute of Science, Bangalore, India \alsoaffiliation†Department of Mechanical Engineering, Indian Institute of Science, Bangalore, India \abbreviationsIR,NMR,UV
1 Introduction
Droplet coalescence is a thermodynamic equilibration process driven by surface energy minimization1. The physics of this phenomenon is characterized by the temporal evolution of a liquid bridge formed upon the proximate approach of two droplets2. This phenomenon is ubiquitous, manifesting in processes linked to life like those in raindrop formation3, 4, growth of tumor cells5, and industrial processes like those in combustion6, spray paintings7, and coatings8. Despite these universal occurrences, studies on the coalescence of complex fluid droplets remain scarce in the literature. Unlike Newtonian fluids, complex fluids have signature micro-structures that can result in a wide range of responses depending on external perturbations making a unified model elusive9. Such diversity in micro-structures and flow behaviors have resulted in classifying these in sub-classes ranging from polymers to suspensions. But there has been a recent surge in studies investigating coalescence dynamics in macromolecular-based micro-structure fluids, i.e., polymeric fluids10, 11, 12, 13, 14. However, coalescence in other complex fluid sub-classes like those in suspensions where micro-structures are comprised of particles having hard-sphere interactions remains unknown.
Depending on the geometry of the problem, literature classifies coalescence primarily in three distinct configurations: pendant-sessile10, 12, 14, sessile-sessile11, 13, and pendant-pendant15, 16, 17. For pendant-sessile and pendant-pendant geometries, the merging kinematics is identified by the liquid bridge of semi-width, , and radius, . Previous studies on Newtonian droplets15, 16, 18, 19 have demonstrated the bridge radius to evolve in time, , as through an interplay of the capillary, viscous and inertial forces. The power-law exponent, , assumes regime dependent universal values of and in viscous15, 16 and inertial18 dominant regimes respectively. However, recent studies on a particular subclass of complex fluids, i.e., gels20 and polymers10, 12, 14, have reported a deviation from Newtonian behavior due to the presence of an additional elastic force during coalescence. Our recent studies on macromolecular fluids10, 12, 14 have demonstrated that the power-law exponent is not always universal; instead, it has a regime-dependent behavior that is classified based on concentration ratio, . The power-law exponent, , assumes a universal value of in inertio/viscoelastic regimes while it monotonically decreases in the elasticity-dominated regime. However, the results proposed by these studies cannot be generalized to other sub-classes of complex fluids owing to differences in micro-structures that give rise to non-Newtonian behaviors. In particular, for colloidal and non-colloidal suspensions, the dispersed phases can comprise of rigid particles that only contribute to dissipation, unlike macromolecular phases with both storage and dissipative characteristics.
In this study, we probe the coalescence paradigm in colloidal and non-colloidal suspensions through experiments and theoretical modeling. Based on rheological characterisation, we classify these as power-law fluids, (where, is viscosity, is shear rate, the flow consistency index and the degree of non-Newtonian behaviour) with exponent , and representing thinning, Newtonian and thickening fluids, respectively, and utilize Ostwald-de Waele constitutive law for developing the theoretical framework. Our experimental results demonstrate the sustenance of Newtonian universality of in thinning fluids (both shear21 and elongational21), which is the signature of the difference in the microstructure of the two subclasses, colloidal and non-colloidal suspensions and macromolecular fluids. In macromolecular fluids, chain relaxation designated by the relaxation time is the signature of viscoelasticity. However, for colloidal and non-colloidal suspensions, viscoelasticity originates via hydrodynamic interactions among particles that are induced through external flow fields. Although such fluids also have finite relaxation time arising from particle self-diffusion22 or inertial relaxation23, the two relaxation mechanisms are different, resulting in shear/extensional elasticity in the former and shear elasticity alone in the latter. These observations are fortified by our theoretical model that generalizes the Newtonian universality of power-law exponent to thinning fluids with zero extensional elasticity. Further, we employ the framework to investigate the existence of arrested coalescence in generalized Newtonian fluids. The study also provides insights into the merging dynamics of thickening fluids where the coalescence appears to be delayed.
2 Materials and methods
Colloidal suspensions of various volume fractions, , are prepared by adding sufficient quantity of silica fumed powder in DI Water. Similarly, the non-colloidal suspensions of different volume fractions are prepared by adding silica glass spheres of corresponding quantities in glycerol. Further, all colloidal and non-colloidal suspensions are agitated in a shaker at 130 RPM for atleast 6 hrs followed by a sonication for 10 mins to ensure homogeneity.The details of particle diameter, , particle density, , and the manufacturer for the dispersed phase is mentioned in Table-I. The volume fraction, , is calculated as stated in Eq(1) with and being mass of dispersed phase and volume of solvent respectively. Values of are given in Table-II. Polymer solution of concentration, , of g/ml is prepared by adding g of Poly(ethylene oxide) g/mol in ml of DI water and stirring the solution at 300 rpm for atleast hrs.
| (1) |
| Suspension | Dispersed Phase | m | g/ml | Manufacturer |
|---|---|---|---|---|
| Colloidal | Silica fumed | 2.2 | Sigma-Aldrich | |
| Non-colloidal | Silica glass spheres | 1.1 | Sigma-Aldrich |
Preceding the experiments PDMS substrates are prepared by cleaning the glass slides with detergent and sonicating them in acetone and water for 20 mins each. These cleansed slides are then dried in a hot air oven at 90∘C for at least 30 mins. Parallelly, PDMS is prepared by mixing it with curing agent (Syl Gard 184 Silicone Elastomer Kit, Dow Corning) in the ratio of 10:1. The mixture is then desiccated for 30 minutes until all visible gas bubbles are removed. Finally, the slides are coated with PDMS using a spin coater by spinning at 5000 rpm for 60 s followed by curing in a hot air oven at 60∘C for at least 8 hrs.
To perform capillary breakup extensional rheometry dripping on a substrate (CABER-DOS)24 experiments a glass substrate (Blue Star, India) of dimensions mm is used. Substrates are cleansed with detergent and then sonicated with acetone and water for 20 minutes each. Subsequently, they are placed in the oven at 95∘C for 30 minutes.
| Colloidal suspension | Non-colloidal suspension | ||
|---|---|---|---|
| (mPas) | (mPas) | ||
| DI Water | 1 | Glycerol | 760 |
| 0.00045 | 1 | 0.0009 | 788 |
| 0.0009 | 1 | 0.009 | 793 |
| 0.0018 | 1 | 0.017 | 830 |
| 0.0045 | 1 | 0.035 | 887 |
| 0.0090 | 1.6 | 0.068 | 875 |
| 0.018 | 3.4 | 0.083 | 955 |
| 0.038 | 16 | 0.15 | 1359 |
| 0.043 | 34 | 0.27 | 2176 |
| 0.051 | 68 | 0.31 | 2676 |
| - | - | 0.35 | 3300 |
3 Rheology
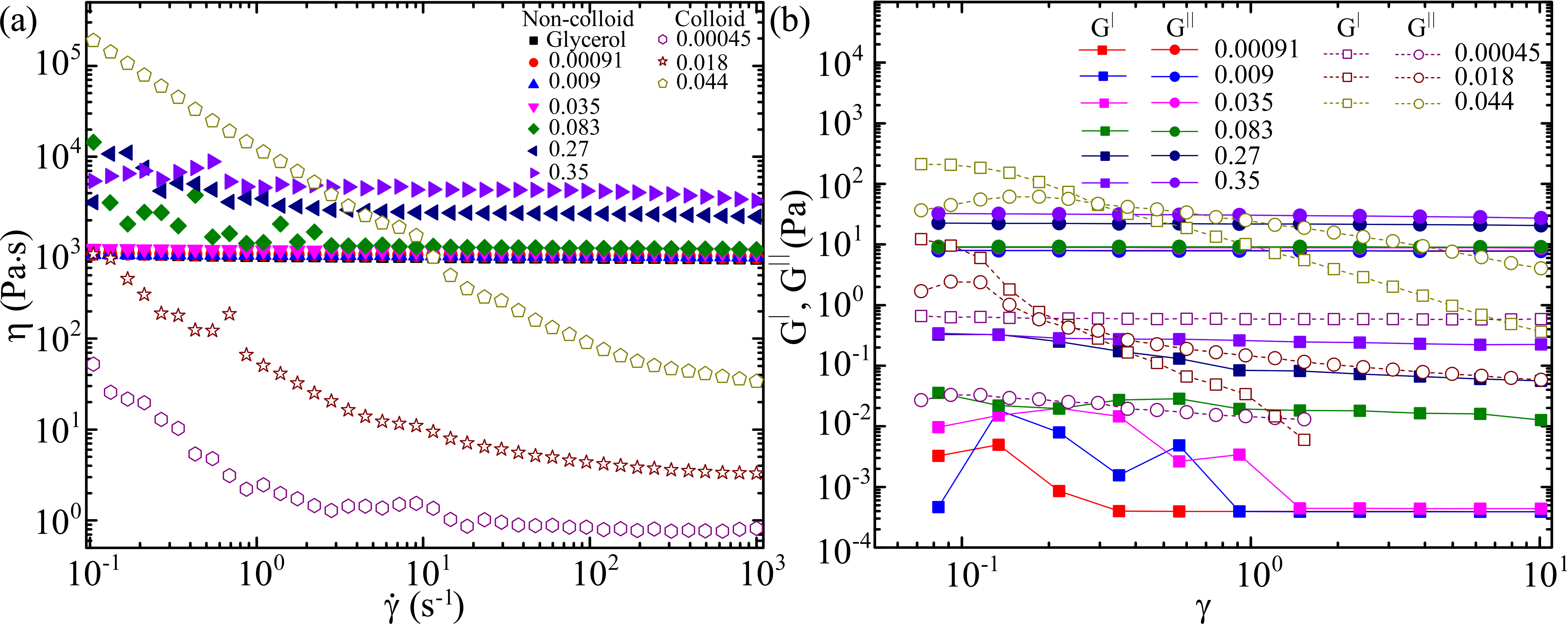
Viscoelastic characterization of colloidal and non-colloidal suspensions are done by performing rheological experiments on cone-plate mm, 1∘ geometry of Anton Paar MCR 302 rheometer. The dependence of viscosity on shear rates for different volume fractions of colloidal and non-colloidal suspensions are given in Fig. 1a. Colloidal suspensions have shown strong shear-thinning behaviour with approaching close to sol-gel25 transition while non-colloidal suspensions have weaker shear-thinning with far from the sol-gel transition. The values of for all the volume fractions are given in Table-II. Fig. 1b represent dependence of loss modulus and storage modulus on shear strain obtained from amplitude sweep experiments for various of colloidal and non-colloidal suspensions.
4 Experiments
A sessile drop is obtained by dispensing a droplet of volume on a substrate. Coalescence is achieved by bringing a sessile drop of same volume towards the pendant drop at an approach velocity of m/s. The schematic of the experimental setup is shown in Fig. 2a. Bridge radius and semi-width are captured at 1,70,000 fps using high-speed camera (Photron Fastcam mini) along with a Navitar lens attachment. Temporal data on bridge shapes is tracked by a custom written edge detection algorithm with sub-pixel accuracy on MATLAB platform. Firstly, the background noise is removed using suitable thresholding intensity. The binary image so obtained gives the row coordinate of the contact point for the two droplets. Along this row, pixel intensities are investigated to find jumps in intensities which gives the location of relevant columns highlighting the bridge location. Further these coordinate points are used to obtain the neighbouring grey intensities from the original image. Based on these, sub-pixel coordinates for bridge location are obtained through five-point weighted averaging. These coordinates are then used to obtain the bridge radius . Similarly at each time step, corresponding image is processed to obtain the temporal evolution data on bridge radius .
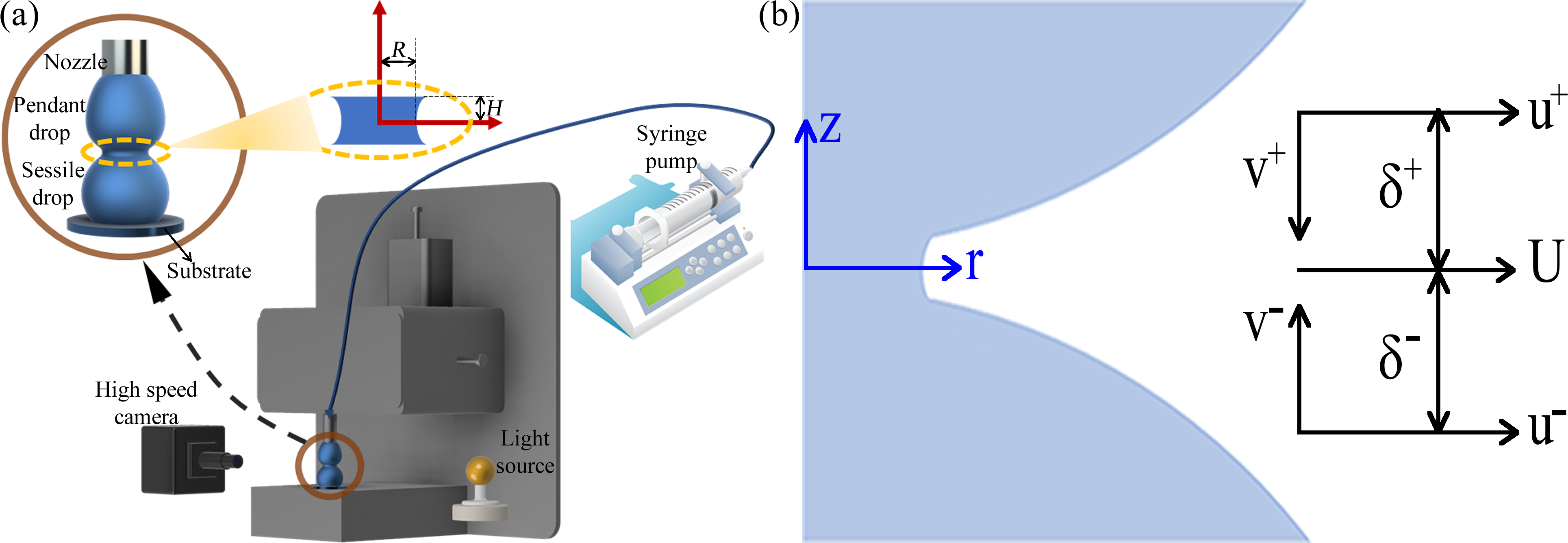
Capillary breakup extensional rheometry dripping on a substrate (CABER-DOS) experimental setup and procedure is adapted from Dinic et. al.24. A pendant drop is created at the tip of a nozzle of radius mm by pumping at a flow rate of mL/min. The pendant drop so obtained is deposited on a glass substrate placed below the nozzle tip at a distance of . Upon contact with substrate the droplet spreads creating a capillary between the nozzle tip and spreading fluid which is captured using high-speed camera. The temporal evolution data of capillary radius is obtained similarly as in coalescence with marked by the formation of the capillary bridge between the nozzle tip and spreading droplet.
5 Theory
In order to develop a theoretical framework for power-law fluids, we employed the symmetry of sessile-pendant geometry for explicating the kinematics of flow field. The analysis is formulated in axis symmetric cylindrical coordinates under quasi-steady and quasi-radial assumptions as shown in Fig. 2b. Based on these the flow field can be simplified at the neck region as and . While for the small neighbourhood region of span on both sides, flow field can be simplified as and respectively. As a consequence of these, terms in velocity gradient tensor at line can be simplified as and .
For the coalescence geometry, conservation laws of mass and momentum can be simplified along the line as written in Eq(2) and Eq(3) respectively. The terms corresponding to stress tensor are obtained by employing the Ostwald-de Waele power-law model constitutive behavior9 represented in Eq(4).
| (2) |
| (3) |
| (4) |
By definition with being the second invariant of the strain-rate tensor, the flow consistency index and the degree of non-Newtonian behaviour with representing shear thinning fluids and , representing the Newtonian and shear thickening behaviour respectively. Owing to the quasi-steady and quasi-radial assumptions, in Eq (4) can be reduced at line as resulting in individual components of stress tensor as:
| (5a) | |||
| (5b) | |||
For obtaining the semi-analytical evolution equation of bridge radius , the -direction momentum equation Eq (3) is further simplified to Eq (6) through scaling arguments , , , along with the components of stress tensor in Eq (3) as and ( is droplet radius and is the surface tension). Here, Eq (6) is a polynomial equation with non-integral power of the form given in Eq (7) with and and , being the scaling constants. The roots of such equation are obtained by using the Newton-Raphson method with initial guesses coming from the special case of where the roots are trivially obtained through quadratic formula. The final evolution equation for bridge radius is of the form given in Eq (8) where .
| (6) |
| (7) |
| (8) |
First order finite difference scheme is used to obtain bridge radius from Eq (8). Time step sec is taken sufficiently small to ensure numerical stability.
6 Results and Discussion
Coalescence in sessile-pendant configuration starts with the formation of liquid bridge of radius, , and width, , that is formed on proximate approach of the two droplets as depicted in Fig. 2a. The evolution of this bridge is driven by the interplay between capillary, viscous and inertial force to reach a thermodynamically stable state of single daughter droplet. Among these forces, capillary force assist the evolution dynamics while the other two oppose the process.
The temporal evolution of dimensionless liquid bridge radius with dimensionless time ( is the inertial time scale), for various volume fractions of colloidal and non-colloidal suspensions, are represented in Fig. 3a and Fig. 3b respectively. The data shown for different volume fractions are an average of 4 trials. The error in the neck radius is %. It is observed from Fig. 3a and b that the bridge radius evolves as . For colloidal suspensions, it can be observed from Fig. 3a that the evolution dynamics is independent of concentration and the power-law exponent, , is equal to the universal Newtonian value . However, for non-colloidal suspensions, the evolution is partially dependent on the concentration . As observed from Fig. 3b, the prefactor, , decreases on increasing concentration but the remains . For all the concentration represented in Fig. 3a and b, the error in the measurement of is and the value of the same are presented in Fig. 3c.
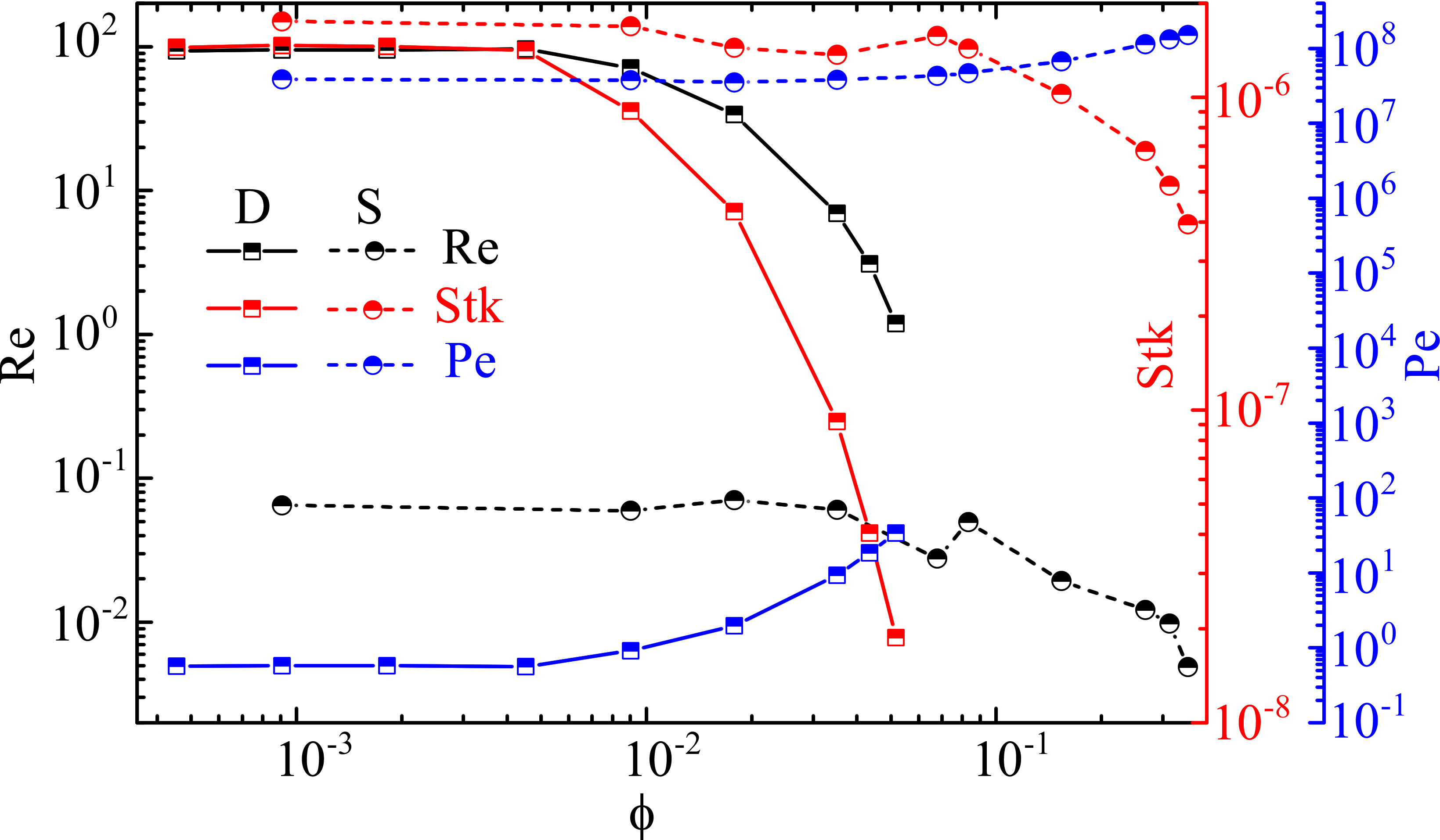
To expound the bridge evolution further, it is important to look at the relative magnitudes of the dominant governing forces in the continuum. For coalescence, these forces are capillary force, , that drives the bridge growth, inertial force, , and viscous force, , that oppose the evolution dynamics. For colloidal and non-colloidal suspensions, Brownian force, , can also play a crucial role. The relative interplay of these forces is elucidated through Reynolds number, , Stokes number, , and Peclet number, where, and are the characteristic length and velocity scale associated with the flow respectively, is the Boltzmann constant, is infinite shear viscosity, and K is the absolute Temperature. The variation of , , and with concentration is represented in Fig. 4. It is observed from the figure that the for colloidal suspensions is of order greater than indicating that coalescence is in the inertial regime. While for non-colloidal suspensions, is of implying viscous as the dominant force. However, the flow is in the inertial dominant region owing to the experimental time, which is in the range of inertial time scale ms. Further observation from Fig. 4 suggests that the Stokes number is of order less than for all the volume fractions for colloidal and non-colloidal suspensions suggesting that the particle relaxation time is much smaller than the characteristic time of the flow field. Therefore, for all the experiments particles were relaxed to the external flow field and were not creating extra resistance through slipping and local agglomeration in flow field which could potentially demonstrate shift from Newtonian coalescence. The relative magnitude of the Brownian forces represented by Pe is highlighted in Fig. 4. The Peclet number for colloidal suspensions is more than and for non-colloidal suspensions it is of signifying that inertial forces are always greater than the Brownian forces and therefore the effect of thermal forces can be neglected in the time scale of experiments.
In order to develop a theoretical framework for understanding coalescence in colloidal and non-colloidal suspensions it is important to look at the rheological properties of these fluids. Fig. 1a and b represent the viscosity and amplitude sweep plots for the volume fractions used in the experiments. It can be observed from Fig. 1a that the colloidal suspensions are strongly shear thinning with their viscosity’s changing significantly in orders as we move to higher volume fractions indicating an approach to a sol-gel transition. However, the non-colloidal suspensions are weakly shear thinning, and their viscosity doesn’t change drastically with concentration indicating a higher concentration for sol-gel transition. Fig. 1b probes the visco-elasticity of respective fluids. As observed all volume fractions of colloidal suspensions have storage modulus more than the loss modulus implying they have significant elasticity to be classified as visco-elastic fluids. But non-colloidal suspensions have loss modulus more than the storage modulus implying that they are weakly viscoelastic and their behavior is much closer to Newtonian fluids. However, it is important to note that the viscosity and amplitude data are obtained through shear rheology therefore they may not be adequate to understand coalescence which is an extensional dominant flow. CABER-(DoS) experiments are performed to get insights into the extensional rheology of colloidal and non-colloidal suspensions. Fig. 5a represents the temporal evolution of dimensionless capillary bridge radius (Here and are the capillary bridge and nozzle radius respectively) for DI Water, non-colloidal suspension , colloidal suspension and Polyethylene oxide g/ml. It is observed that the in colloidal and non-colloidal suspensions have similar evolution characteristics as DI water. The capillary abruptly breaks after initial universal thinning, implying negligible extensional elasticity. However, for polymer, the initial bridge thinning is followed by the formation of a filament that diminishes in time with characteristic relaxation time implying finite extensional elasticity. Snapshots of such evolution of capillary bridge for different time instances is shown in Fig. 5b. Utilizing the above observations, we can identically claim that all volume fractions of colloidal and non-colloidal suspensions explored in the current study have negligible elasticity in extensional flows similar to Newtonian fluids.
Owing to this, the value of power-law exponent across volume fractions was found to be equal to the Newtonian exponent as illustrated by Fig. 3c. Although these fluids have significant elasticity, unlike macromolecular fluids this elasticity is not reflected in the value of exponent . This contrast in behaviour is the signature of difference in the micro-structures of the two subclass of complex fluids. As represented in Fig. 6c and d, Macromolecuar fluids have large molecular chains that contribute to stresses in extensional and shear deformations. However, colloidal and non-colloidal suspensions as represented in Fig. 6a have hard particles that only contribute to shear deformation through agglomerations. In extensional deformations Fig. 6b, these particles are not able to interact as they are pulled apart from each other resulting in negligible extensional elasticity. This behaviour can be further understood from energy perspective. Coalescence in macromolecular fluids have a storage/dissipative dynamics with molecular chains absorbing part of the capillary energy while in suspensions it is dissipative alone with particles contributing to energy dissipation alone.
The rheological behaviour indicates that these dissipative fluids belong to the broader class of power law fluids and the theoretical framework developed above can be effectively used for understanding their coalescence. For the closure of the analytical solution, it is essential to study the physical behaviour of scaling parameters ,and represented in Eq (8). Among these scaling parameters, is the coefficient of capillary force that assists in bridge evolution while is the coefficient of axial stress that resists the same. Owing to this nature, the coefficient will have a negative value while will have a positive value. The magnitudes of these scaling parameters are found by solving the equation for the special case of as this represents the special case of Newtonian fluids for which bridge radius is known to follow the universal dynamics of in the inertial dominant regime. The value obtained for and is and respectively. It is important to note that our bridge evolution equation reduces to a similar form as was obtained by Xia et al.26 However, the two equations have different scaling constants owing to differences in characteristic length assumption.
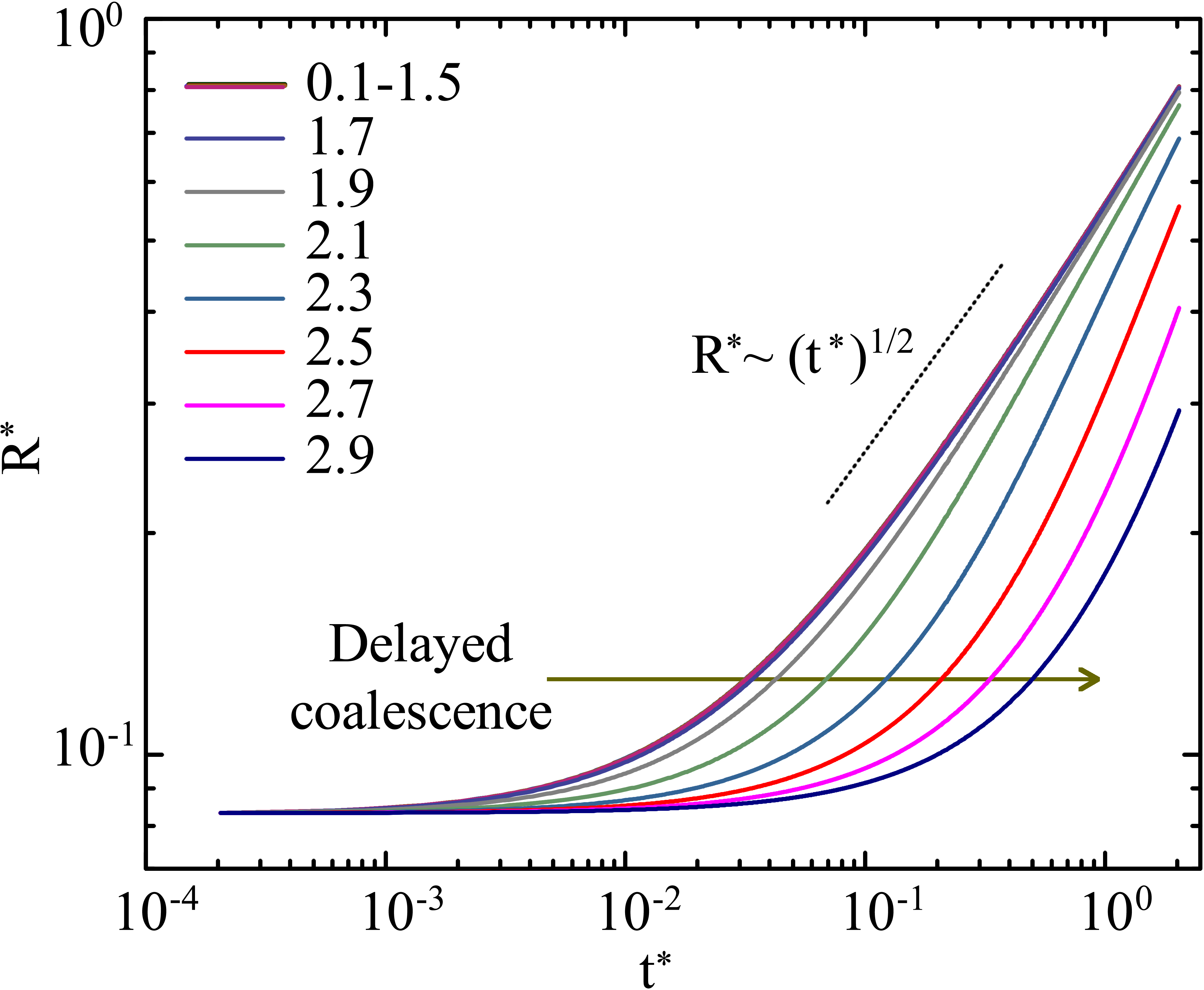
Physically the terms in Eq (6) corresponding to and are the dissipative terms representing inertia and viscous components respectively. The term corresponding to represents the capillary component and is the driving force in coalescence dynamics. The dimensionless solution obtained on solving Eq (8) for different degrees of non-Newtonian behaviours at an interval of in is represented in Fig. 7. It is observed that for thinning fluids the value of the power-law exponent is universal and equal to that of Newtonian fluids . This is evident as in Eq (6), the term representing viscous contribution has degree making it lesser significant when compared with the inertial component having degree . As a consequence inertial forces are the dominant governing force leading to the universal value of . However for thickening fluids it is observed that the bridge radius starts to deviate from the Newtonian behaviour as increases. Such deviation in coalescence from Newtonian and thinning fluids is explained by the nature of Eq (6). As increases for thickening fluids, the viscous component starts to gain significance and at it becomes the dominant term with the degree of Eq (6) being equal to . However, it is important to note that this deviation is different from the sub-Newtonian deviation that occurs in macromolecular fluids. Unlike the latter, the coalescence in thickening fluid is delayed due to greater resistance offered by the viscous stresses instead of additional elastic stresses. Although Eq (6) captures the dynamics of thickening fluids qualitatively, experiments are required to validate the applicability of the model for them.
Further investigating Eq (6) we can look at a special case of arrested coalescence . Eq (6) reduces to a quadratic polynomial of the form at . This polynomial always has real and at least one positive solution as its discriminant implying that for Newtonian fluids, coalescence is never arrested unlike those in macromolecular fluids. The following result can be simply extended to thickening and thinning fluids as the general function with will always have at least one real positive root as long as satisfies the above conditions. The result is significant as it illustrates that arrested coalescence is the signature of elastic droplets. Therefore, if the microstructure of complex fluid droplets doesn’t have a storage mechanism, they are always going to coalesce.
Overall our analysis highlights the importance of storage-based micro-structure for the existence of arrested coalescence via a sub-Newtonian transition regime. The experimental and theoretical observations have generalised the Newtonian universality of to complex fluids of subclass colloidal and non-colloidal suspensions that have thinning and zero extensional elasticity. The analysis has also explored thickening fluids where the coalescence appears to be delayed due to large resistive forces.
7 Conclusion
In this work, we experimentally probe coalescence in colloidal and non-colloidal suspensions. Our observations have extended the Newtonian universality of power-law exponent to these complex fluid. The results are strengthened by the theoretical framework developed based on the Ostwald-de Waele constitutive law. The study highlights the importance of extensional elasticity for the existence of sub-Newtonian regime. colloidal and non-colloidal suspensions have micro-structures that are dissipative with non-zero shear elasticity but zero extensional elasticity resulting in Newtonian type coalescence. Further the theoretical framework is utilized to propose the non-existence of arrested coalescence in generalized Newtonian fluids with zero extensional elasticity. However, the current experiments and analysis neglect the effect of surrounding fluids and higher approach velocities between droplets by assuming air as the outer fluid and low approach velocity respectively. Further studies are required to understand the effect of surrounding fluids and higher approach velocities. The volume fractions explored in this study are thinning and far from sol-gel transition. Therefore future works are required to investigate highly concentrated colloidal and non-colloidal suspensions that have thickening and finite extensional elasticity.
A.K. acknowledges partial support from DST-SERB, A.S.R., and S.C.V. acknowledge partial support from the MHRD.
References
- Frenkel 1945 Frenkel, J. Viscous flow of crystalline bodies under the action of surface tension. J. phys. 1945, 9, 385
- Eggers et al. 1999 Eggers, J.; Lister, J. R.; Stone, H. A. Coalescence of liquid drops. Journal of Fluid Mechanics 1999, 401, 293–310
- Villermaux and Bossa 2009 Villermaux, E.; Bossa, B. Single-drop fragmentation determines size distribution of raindrops. Nature Physics 2009, 5, 697
- Pruppacher and Klett 2010 Pruppacher, H. R.; Klett, J. D. Microphysics of Clouds and Precipitation; Springer, 2010; pp 10–73
- Ambrose et al. 2015 Ambrose, J.; Livitz, M.; Wessels, D.; Kuhl, S.; Lusche, D. F.; Scherer, A.; Voss, E.; Soll, D. R. Mediated coalescence: a possible mechanism for tumor cellular heterogeneity. American journal of cancer research 2015, 5, 3485
- Orme 1997 Orme, M. Experiments on droplet collisions, bounce, coalescence and disruption. Progress in Energy and Combustion Science 1997, 23, 65–79
- Ashgriz and Poo 1990 Ashgriz, N.; Poo, J. Coalescence and separation in binary collisions of liquid drops. Journal of Fluid Mechanics 1990, 221, 183–204
- Djohari et al. 2009 Djohari, H.; Martínez-Herrera, J. I.; Derby, J. J. Transport mechanisms and densification during sintering: I. Viscous flow versus vacancy diffusion. Chemical Engineering Science 2009, 64, 3799–3809
- Bird et al. 1987 Bird, R. B.; Armstrong, R. C.; Hassager, O. Dynamics of polymeric liquids. Vol. 1, 2nd Ed. : Fluid mechanics; Wiley, 1987
- Varma et al. 2020 Varma, S. C.; Saha, A.; Mukherjee, S.; Bandopadhyay, A.; Kumar, A.; Chakraborty, S. Universality in coalescence of polymeric fluids. Soft Matter 2020, 16, 10921–10927
- Varma et al. 2021 Varma, S. C.; Saha, A.; Kumar, A. Coalescence of polymeric sessile drops on a partially wettable substrate. Physics of Fluids 2021, 33, 123101
- Varma et al. 2022 Varma, S. C.; Rajput, A. S.; Kumar, A. Rheocoalescence: Relaxation time through coalescence of droplets. Macromolecules 2022,
- Varma et al. 2022 Varma, S. C.; Dasgupta, D.; Kumar, A. Elasticity can affect droplet coalescence. Physics of Fluids 2022,
- Rajput et al. 2022 Rajput, A. S.; Varma, S. C.; Kumar, A. Sub-Newtonian coalescence in polymeric fluids. arXiv preprint arXiv:2208.09718 2022,
- Paulsen et al. 2011 Paulsen, J. D.; Burton, J. C.; Nagel, S. R. Viscous to inertial crossover in liquid drop coalescence. Physical Review Letters 2011, 106, 114501
- Aarts et al. 2005 Aarts, D. G.; Lekkerkerker, H. N.; Guo, H.; Wegdam, G. H.; Bonn, D. Hydrodynamics of droplet coalescence. Physical Review Letters 2005, 95, 164503
- Wu et al. 2004 Wu, M.; Cubaud, T.; Ho, C.-M. Scaling law in liquid drop coalescence driven by surface tension. Physics of Fluids 2004, 16, L51–L54
- Case and Nagel 2008 Case, S. C.; Nagel, S. R. Coalescence in low-viscosity liquids. Physical Review Letters 2008, 100, 084503
- Paulsen et al. 2012 Paulsen, J. D.; Burton, J. C.; Nagel, S. R.; Appathurai, S.; Harris, M. T.; Basaran, O. A. The inexorable resistance of inertia determines the initial regime of drop coalescence. Proceedings of the National Academy of Sciences 2012, 109, 6857–6861
- Chen et al. 2022 Chen, S.; Pirhadi, E.; Yong, X. Viscoelastic necking dynamics between attractive microgels. Journal of Colloid and Interface Science 2022, 618, 283–289
- Tanner 2020 Tanner, R. I. Computation and experiment in non-colloidal suspension rheology. Journal of Non-Newtonian Fluid Mechanics 2020, 281, 104282
- Shikata and Pearson 1994 Shikata, T.; Pearson, D. S. Viscoelastic behavior of concentrated spherical suspensions. Journal of Rheology 1994, 38, 601–616
- Shaw 2003 Shaw, R. A. Particle-turbulence interactions in atmospheric clouds. Annual Review of Fluid Mechanics 2003, 35, 183–227
- Dinic et al. 2017 Dinic, J.; Biagioli, M.; Sharma, V. Pinch-off dynamics and extensional relaxation times of intrinsically semi-dilute polymer solutions characterized by dripping-onto-substrate rheometry. Journal of Polymer Science Part B: Polymer Physics 2017, 55, 1692–1704
- Kawaguchi 2020 Kawaguchi, M. Dispersion stability and rheological properties of silica suspensions in aqueous solutions. Advances in Colloid and Interface Science 2020, 284, 102248
- Xia et al. 2019 Xia, X.; He, C.; Zhang, P. Universality in the viscous-to-inertial coalescence of liquid droplets. Proceedings of the National Academy of Sciences 2019, 116, 23467–23472