2021
[1,3]\fnmYueyang \surTeng
1]\orgdivCollege of Medicine and Biological Information Engineering, \orgnameNortheastern University, \cityShenyang \postcode110169, \stateChina
2]\orgdivDepartment of Electrical and Computer Engineering, \orgnameStevens Institute of Technology, \orgaddress\streetHoboken, \cityNJ \postcode07030, \stateUSA
3]\orgdivKey Laboratory of Intelligent Computing in Medicine, \orgnameMinistry of Education, \cityShenyang \postcode110169, \stateChina
NL-CS Net: Deep Learning with Non-Local Pior for Image Compressive Sensing
Abstract
Deep learning has been applied to compressive sensing (CS) of images successfully in recent years. However, existing network-based methods are often trained as the black box, in which the lack of prior knowledge is often the bottleneck for further performance improvement. To overcome this drawback, this paper proposes a novel CS method using non-local prior which combines the interpretability of the traditional optimization methods with the speed of network-based methods, called NL-CS Net. We unroll each phase from iteration of the augmented Lagrangian method solving non-local and sparse regularized optimization problem by a network. NL-CS Net is composed of the up-sampling module and the recovery module. In the up-sampling module, we use learnable up-sampling matrix instead of a predefined one. In the recovery module, patch-wise non-local network is employed to capture long-range feature correspondences. Important parameters involved (e.g. sampling matrix, nonlinear transforms, shrinkage thresholds, step size, ) are learned end-to-end, rather than hand-crafted. Furthermore, to facilitate practical implementation, orthogonal and binary constraints on the sampling matrix are simultaneously adopted. Extensive experiments on natural images and magnetic resonance imaging (MRI) demonstrate that the proposed method outperforms the state-of-the-art methods while maintaining great interpretability and speed.
keywords:
compressive sensing, image reconstruction, neural network, non-local prior1 Introduction
Compressed sensing (CS) theory has received a lot of attention in recent years. CS proves that when a signal is sparse in a certain domain, it can be recovered with high probability from much fewer measurements than the Nyquist sampling theorem ref1 ; ref2 ; ref3 ; ref4 ; ref5 . The potential reduction in measurements is attractive for diverse practical applications, including but not limited to magnetic resonance imaging (MRI) ref6 , radar imaging ref7 and sensor networks ref8 .
Over the past decades, a great deal of image CS reconstruction methods have been developed based on sparse representation model ref9 , which operates on the assumption that many images can be sparsely represented by a dictionary. The majority of those traditional methods use some structured sparsity as an image prior and then solve a sparsity-regularized optimization problem in an iterative fashion ref10 ; ref11 . Some elaborate structures were introduced into CS, like Gaussian scale mixtures model in wavelet domain ref12 . In addition, non-local self-similarity of image is also introduced to enhance the CS performance ref13 ; ref14 ; ref15 . For example, Metzler . ref16 combined a Block Matching 3D (BM3D) denoiser into approximate message passing (AMP) framework to perform CS reconstruction. Zhang . ref13 proposed the method combining sparse prior with non-local regularizers achieved well performance. Recently, some optimization-based methods have implemented adaptive sampling using alternating optimization techniques to jointly optimize the sampling matrix and CS recovery algorithms ref9 . Despite the excellent interpretability of the above methods, they all require hundreds of iterations to produce decent results, which inevitably entails a heavy computational burden, in addition to the challenges posed by hand-craft transformations and associated hyper-parameters.
Inspired by the successful applications of deep learning, several network-based CS reconstruction methods were developed to learn the inverse mapping from the CS measurement domain to original signal domain ref17 ; ref18 ; ref19 . Mousavi . ref20 applied a stacked denoising auto-encoder (SDA) to learn the statistical relationship from training data. However, the fully connected network used in SDA results in high computation cost. Kulkarni . ref21 developed a method based on convolutional neural networks, called Recon-Net, to reconstruct the original image from the CS sampled image blocks. Yao . ref22 used residual learning to further improve CS reconstruction. Sun . ref23 propose a novel sub-pixel convolutional generative adversarial network (GAN) to learn compressed sensing reconstruction of images. To mitigate block effect in reconstruction, some models make use of full image areas for reconstruction ref24 ; ref25 . Meanwhile, for further improving the CS performance, some models are proposed to train the non-linear recovery operator to learn the optimal sampling pattern with recovery model ref26 ; ref27 ; ref28 . The main advantage of the network-based methods is the reconstruction speed, as opposed to their optimization-based counterparts. However, the barrier to future performance improvement is their lack of the CS domain-specific insights intrinsic to optimization-based approaches.
To overcome above shortcomings, researchers link optimization methods to networks, which make them interpretable. Specifically, these methods embed the solving process of traditional optimization-based methods into the forward operator of deep learning. For instance, Zhang ref29 proposed a deep network called ISTA-Net, which maps the popular Iterative Shrinkage Thresholding (ISTA) algorithm to network. It learns the sparse transform and soft threshold function via network. Based on ISTA-Net, Zhang . ref30 proposes Opine-Net, which combines an efficient sampling module with ISTA-Net to achieve adaptive sampling and recovery. More recently, You . ref31 improved ISTA-Net, which enables a single model to adapt for multiple sampling rates. Xiang . ref32 proposed FISTA-Net for solving inverse problem, which is an accelerated version of ISTA. The Alternating Direction Method of Multipliers (ADMM) is proposed for the saddle point problem containing Lagrange multipliers that can not be solved directly by the ISTA algorithm. Drawing on the same idea, Yang . ref33 proposed the ADMM-Net, which unfolds ADMM into network and applies it to CS-MRI. It employs a learnable transformation and the corresponding hyper-parameters in ADMM are learned from the network. Zhang . ref34 extended the well-known AMP algorithm to propose AMP-Net. These models enjoy the interpretability with speed and tuning-free advantage. But the existing those approaches make little use of the non-local self-similarity pior which plays an important role in image reconstruction.
There have been many previous methods for image reconstruction based on non-local prior. The non-local means (NLM) filter ref35 is highly successful in the image denoising, where it produces a denoised image by calculating the weighted value of the current pixel and its neighbouring pixels. Inspired by NLM, several inverse problem frameworks incorporating non-local regularizer have been proposed ref13 ; ref14 ; ref15 . For instance, Zhang . ref13 combines the TV regularizer with the non-local regularizer, which is solved using the augmented Lagrangian method and captures non-local features of the image during the iterative process. However, the use of time-consuming NLM filters in the iterations undoubtedly introduces a costly computational complexity. Inspired by deep learning, some recent network-based approaches exploit non-local self-similarity. Liu . ref36 proposed a network incorporated non-local operations into a recurrent neural network (RNN) for image restoration. Although non-local prior has been widely exploited by both optimization-based and network-based methods, few interpretable deep learning models have introduced this important prior.
This paper combines merit of CS and non-local prior to propose a novel interpretable network, dubbed NL-CS Net. It composed of two parts: the up-sampling module and the recovery module. In the up-sampling phase, we adopted fully connection matrix to stimulate block-wise sampling and initial process. In the recovery phase, we maps the augmented Lagrangian method solving non-local regularized CS reconstruction model into the network, where the network consists of fixed number of phases, each of which corresponds to the one iteration. Rather than the traditional time-consuming NLM operation, the patch-wise non-local network is used to exploit global features. The hyper-parameters involved in NL-CS Net (e.g. sampling matrix, step size, ) are learned end-to-end, rather than being hand-crafted. Experimented results on natrual images dataset and MRI dataset shows the feasibility and effectiveness of the proposed method compared with the existing methods.
2 Related work
The goal of CS is to reconstruct image from its CS measurement with high quality. Mathematically, given the original image , its CS measurements can be obtained by , where denotes the sampling matrix and () is commonly regarded as the CS sampling rate. Reconstructing from is typically ill-posed. Proposed NL-CS Net combines merit of CS and non-local prior, thus, we first review the traditional optimization-based algorithm to solve the non-local regularized model for CS.
The traditional methods use a preset sampling matrix to recover from the measured image , which is formulated as solving the following optimization problem:
| (1) |
where denotes the transform matrix and is a regularizer, that imposes prior knowledge, such as sparsity and non-local self-similarity.
More effective in suppressing staircase artifact and restoring the detail, optimization-based approaches, combined traditional sparse priors with non-local regularizer, have been proven to achieve superior performance ref13 .
| (2) |
The is of the following form:
| (5) |
where is the set containing the neighbor of the pixel ; () represents the matrix form of NLM; is a hyper-parameter; is a controlling factor; the superscript indicates the number of iterations. In brief, for a given pixel, the NLM filter can be obtined by calculating a weighted average of the surrounding pixels within a search window.
In order to solve Eq. (2), we equivalently transform Eq. (2) into the following problem through variable splitting technique.
| (6) |
where and are auxiliary variables. Thus, the corresponding augmented Lagrangian function for Eq. (4) is expressed as:
| (7) |
where , and are regularization hyper-parameters; , and are the Lagrangian multipliers. In this case, the augmented Lagrangian method solves Eq. (5) by the folloing update rule:
| (8) |
| (9) |
By applying the alternating direction method, Eq. (6) can be decomposed into three sub-problems in the following form:
| (10) | ||||
| (11) | ||||
| (12) |
where .
is a nonlinear shrinkage function with the hyper-parameter , where .
And is the step size of the gradient descent method. The overall algorithm flow is shown in Algorithm 1.
This algorithm uses time-consuming NLM operations in each iteration. It typically requires hundreds of iterations to achieve a satisfactory result, which suffers from a large amount of computation. The transform , sampling matrix and step size are pre-defined, which is very challenging to detain hyper-parameter.
| Algorithm 1 Non-local Regularized CS Algorithm |
| Input:The sampled signal and sampling matrix and , given. |
| Output: |
| Initialization:, , |
| While (Outer stop conditions not satisfied) do |
| While (Inner stop conditions not satisfied) do |
| Solve sub-problem by computing Eq. (8). |
| Solve sub-problem by computing Eq. (9). |
| Solve sub-problem by computing Eq. (10). |
| End while |
| upate multipliers by computing Eq. (7). |
| End while |
| \botrule |
3 Proposed NL-CS Net for CS
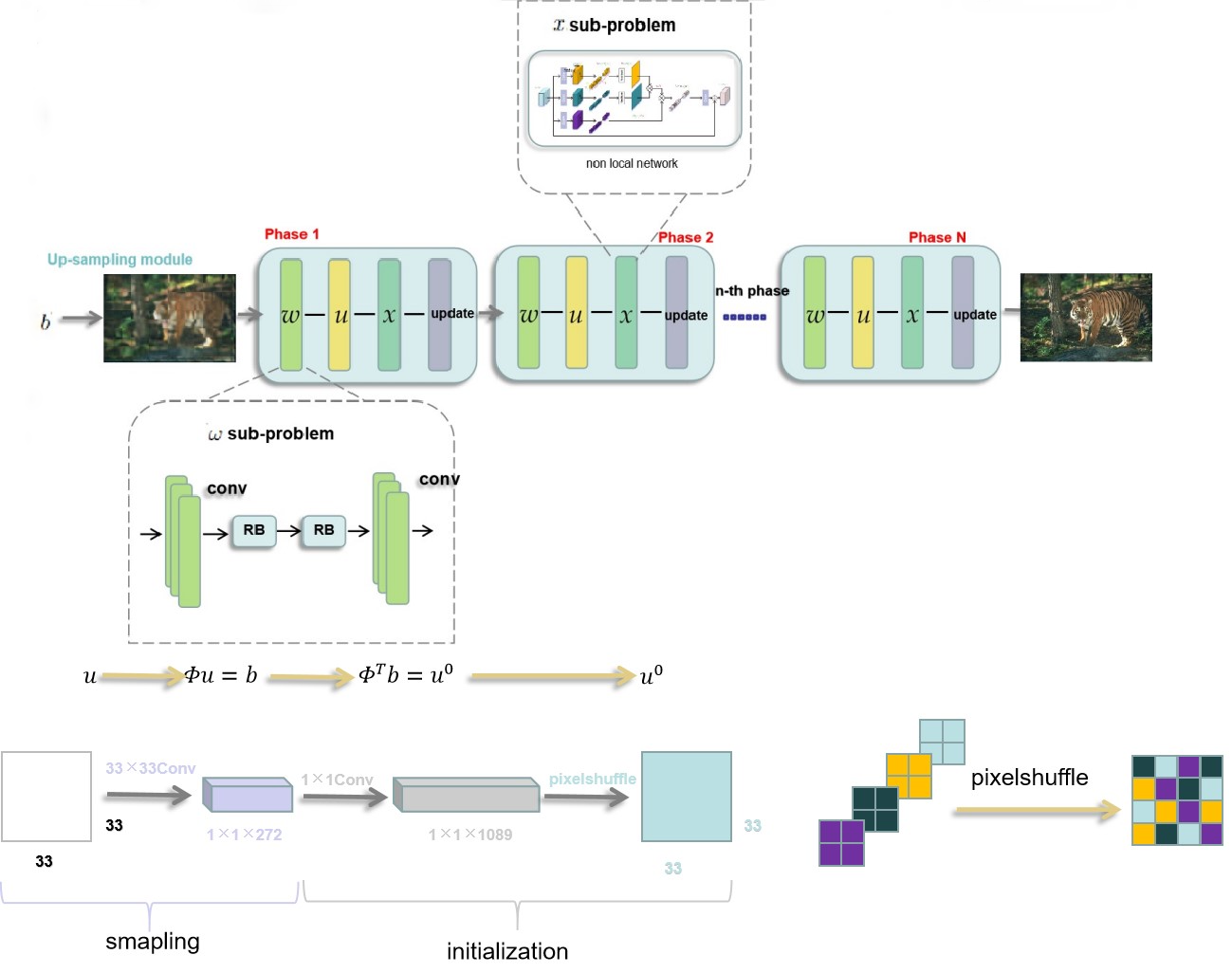
On the basis of Algorithm 1, by combining the merits of optimization-based and network-based approaches, the main idea of this paper is to unfold the solution process of Algorithm 1 into network. The structure of NL-CS Net is shown in Figure 1. For jointly optimizing the sampling matrix and the recovery algorithm, our proposed NL-CS Net consists of a up-sampling module and a recovery module. In the up-sampling phase, we adopted a fully connection matrix to stimulate block-wise sampling and initial process. In the recovery phase, its backbone is designed by mapping the augmented Lagrangian method solving non-local regularized CS reconstruction model into network. The network consists of fixed number of phases, each of which corresponds to the one iteration. Hence, NL-CS Net is composed of , and modules and update Lagrange multiplier module corresponding to four sub-problem Eqs. (8) , (9) , (10) and (7) sequentially in the -th iteration. We designed a novel model to replace soft-shrinkage function and allowed step size and transform matrix to be learned. The learnable patch-wise non-local method is used to exploit global features, rather than the traditional non-local means operation. The parameters involved in NL-CS Net (e.g. sampling matrix, step size, ) are learned end-to-end, rather than being hand-crafted.
3.1 Up-sampling module in NL-CS Net
A warm start often leads to better result. The measured image is compressive from the original image . We obviously use the sampling matrix to obtain from as . Notice that, in this section, we indiscriminately use as one- or two-dimensional tensor according to actual demand. For example, in the formulation , and are one-dimensional, however, in a network, they are two-dimensional. Meanwhile, we can also obtain an approximate from as . In this module, will be leanable instead of pre-defined.
It is well known that the linear transformation can be performed by a series of convolutional operators. Thus, we implement this operation by a convolutional layer and a PixelShuffle layer ref37 , specifically, adjusting the transpose of the sampling matrix to filters with the same size . With those filters, is implemented through a convolutional layer. PixelShuffle layer expands feature maps by reorganization between multiple channels, and we apply it to transform the tensor shape N output into .
| (13) |
Obviously, is one-dimensional and is two-dimensional, and can be inputed into an image-targeted network.
3.2 , and module in NL-CS Net
In the following, we consider that the above three sub-problem Eqs. (8) , (9) and (10) in the -th iteration, and we unfold them into three separate modules in -th phase of NL-CS Net: module, module and module.
The module corresponds to the Eq. (8) and is used to produce the output . The transform matrix of traditional approach is to use a set of pre-trained filters. Here, we adopt a set of learnable filters to transform the image into the transform domain instead of the hand-crafted strategy. Note that it is hard to tune a well-designed threshold in Eq. (8) which is necessary to recover the details of the image. Hence, we set as learnable parameter. For efficiently solve the Eq. (8), we propose a flexible model for solve nonlinear transformation. In detail, the deep learning solution of the sub-problem can be described as follows:
| (14) |
Here, consists of size convolutional layer, which corresponds to 32 filters and Rectified Linear Unit (ReLU). To extract the features of the image and reconstruction, Eq. (12) is composed of two convolutional layers ( and ) and two residual blocks ( and ) . and denote size convolutional layer which corresponds to 32 filters and the residual blocks contain two convolutional layers which correspond to 32 filters and ReLU with skip connection from input to output.
Corresponding to gradient descent-based Eq. (9) in the module. We allow the step size to be learned in the network which is very different from the fixed step size of traditional methods. The module is finally defined as:
| (15) |
where composed of convolutional layer which corresponds to 32 filters and RELU.
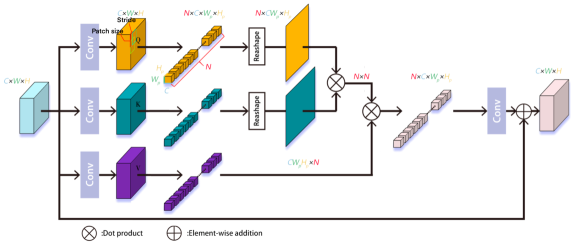
We use the module to compute according to Eq. (10) with input . For more efficient extraction of global features from images, the patch-wise non-local neural networks ref38 is used. It constructed the long-range dependence between image patches and applied a learnable embedding function to make the matching process adaptive. We use the learnable non-local method instead of traditional NLM, as shown in Figure 2. In , given the input feature map , we use three independently learnable weight matrices , and as the embedding functions which is implemented as convolution operation corresponds to 32 filters on the entire feature map. Instead of performing pixel-wise similarity computation in the embedded feature map directly like ref39 , a sliding window with a size of and a step size of 4 is used to select the overlapping patches in the embedded feature map. After the patch extraction operation, we have three sets of patches with size , so that our weight update strategy is to calculate the similarity between those patches. Next, we reshape the patch under the and to a one-dimensional patch. denoted the temporary results, which can be calculated as follows:
| (16) |
In the next step, we calculate the dot product of and . Then, we recover these patches into the feature map of size with using averaging to process the overlapping areas. Finally, we place the output tensor through a convolutional layer and set up a skip connection between it and the input. Combining the with Eq.(10) yields the module as follows:
| (17) |
Finally, we update the Lagrangian multiplier at each phase, which is the same with Eq. (7).
3.3 Total loss function
We will show how to incorporate the two constraints with regarded to into NL-CS Net simultaneously, including the orthogonality constraint and the binary constraint ref30 . For the orthogonal constraint , where is the identity matrix, the orthogonal loss term is defined as , where stands for the Frobenius norm, and we add this directly into the loss function.
To facilitate practical application, we restrict the value of the sampling matrix to 1 or 0. Binary() performs the following operation on each element.
| (18) |
As previously described, we have successfully mapped the process of solving Eq. (2) to our NL-CS Net. The learnable parameters in NL-CS Net are defined in Table 1.
| Leanable parameters | ||||||
| modulee | ,, and | |||||
| module | ,, and | |||||
| module | , and | |||||
| Others | ,,, and | |||||
| \botrule | ||||||
Note that all those parameters are learned end-to-end rather than handcraft. Recovery module are not shared parameter across phase by default, which is a significant difference from traditional optimization-based algorithms.
Given a dataset where is the number of image blocks and represents the original image block, the output of the network through phase is denoted as . Our aim is to minimize the discrepancy between the network output and the original image while satisfying the orthogonal constraint and the binary constraint. Hence the loss function of NL-CS Net is defined as follows:
| (19) |
where is set to be 0.001 by experience.
4 Experimental results
We validate the proposed model on two tasks: the CS reconstruction of natrual images and MRI images. People are most often in contact with natural images, which is very important. MRI is a non-invasive and widely used imaging technique providing both functional and anatomical information for clinical diagnosis. But long scanning and waiting times may lead to motion artefacts and patient discomfort. MRI acceleration is one of the most successful applications of CS (CS-MRI), which can reconstructs high quality MR images from a few sampling data in k-space. To give quantitative criteria, Peak Signal to Noise Ratio (PSNR) is introduced to analyze the reconstruction performance. We use the Adam optimizer with the default learning rate set to 0.0001 and the batch size to 64. All the network were trained on a workstation configured with Intel Core i7-9700 CPU and RTX2080 GPU, and tested on a workstation configured with Intel Core i7-7820 CPU and GTX1060 GPU.
4.1 Experiment on natural image
The training set was standardized using train90 ref21 , which contains 90 natural images. They are constructed by 88,912 randomly cropped image blocks (each of size ). The corresponding measurement matrix is obtained from the training as opposed to fix it. The widely used benchmark datasets: Set11 ref21 and BSD68 ref40 , which have 11 and 68 natural images, respective, were applied for testing. The reconstruction results are presented as the average PSNR of the test images.
4.1.1 Hyper-parameter selection: phase and epoch numbers
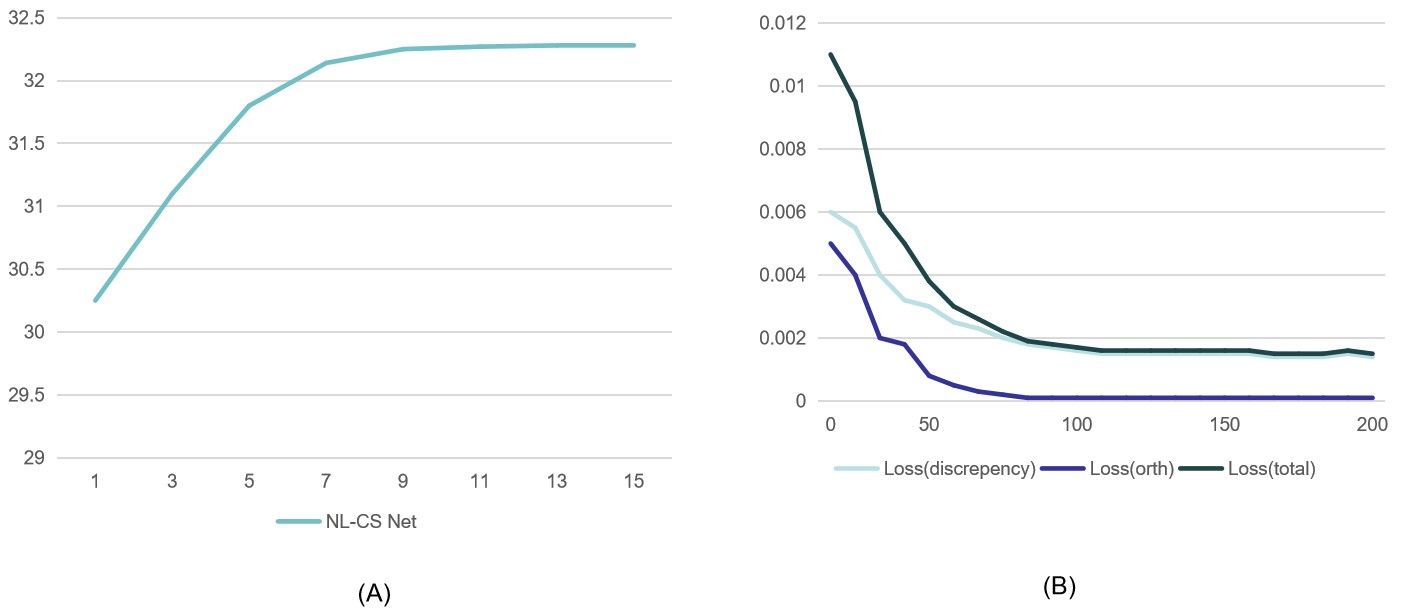
To probe the appropriate number phase for NL-CS Net, we set the phase number from 1 to 15 to observe its performance, in the cases of 25% CS sampling rate reconstruction on Set11. As can be seen in Figure 3a, PSNR rises gradually with the phase number. The curve is almost flat when . To achieve a balance between performance and computational cost, in the following experiments, we set . Figure 3b further demonstrates the convergence process for three types of losses (i.e , and ). We experimented with at the sampling rate of 25% on Set11. The orthogonal constraint term gradually converges to zero which proves its suitability for NL-CS Net. Total loss achieves an acceptable result at about 120 epochs and converges at about 200 epochs. As below, we set epoch number to be 200 for an enough convergence.
4.1.2 Ablation studies
| CS sampling rate (BSD68) | ||||||
|---|---|---|---|---|---|---|
| Algorithm | ||||||
| 50 % | 25 % | 10 % | 4 % | 1 % | Avg | |
| ISTA-Net | 34.04 | 29.36 | 25.32 | 22.17 | 19.14 | 26.01 |
| NL-CS Net(fixed ) | 34.01 | 29.80 | 25.87 | 22.53 | 19.86 | 26.41 |
| NL-CS Net | 34.69 | 29.97 | 26.72 | 24.21 | 21.63 | 27.44 |
| \botrule | ||||||
To adequately demonstrate the advantage of combining non-local regularized terms, we designed ablation experiments. ISTA-NET provides a network form soultion for the norm regularized optimization problem without the non-local regularized terms. For a fair comparison, we trained NL-CS Net with the Gaussian random sampling matrix as ISTA-NET, using the same training set, and tested its performance on BSD68 and the CS sampling rate varies in . As expected from Table 2, NL-CS Net with both fixed and varible sampling matrix outperforms ISTA-net, which further demonstrates the reasonableness of our method. In addition, we observe that joint optimized sampling matrix and recovery operator in our method improves performance by 1.4 over the fixed sampling matrix.
| Different combinations of constraints of NL-CS Net | |||||||
| Binary constraint | ✓ | X | X | ✓ | |||
| Orthogonality constraint | X | ✓ | X | ✓ | |||
| PSNR | 29.92 | 29.95 | 29.85 | 29.97 | |||
| \botrule | |||||||
NL-CS Net introduces two types of constraints including orthogonality constraint and binary constraint. We observe the effect of these two constraints on the reconstruction performance in the case of CS sampling rate = 25% on BSD68. It can be seen in Table 3 that orthogonality constraint and binary constraint acts as network regularization, which enhance the reconstruction performance.
In
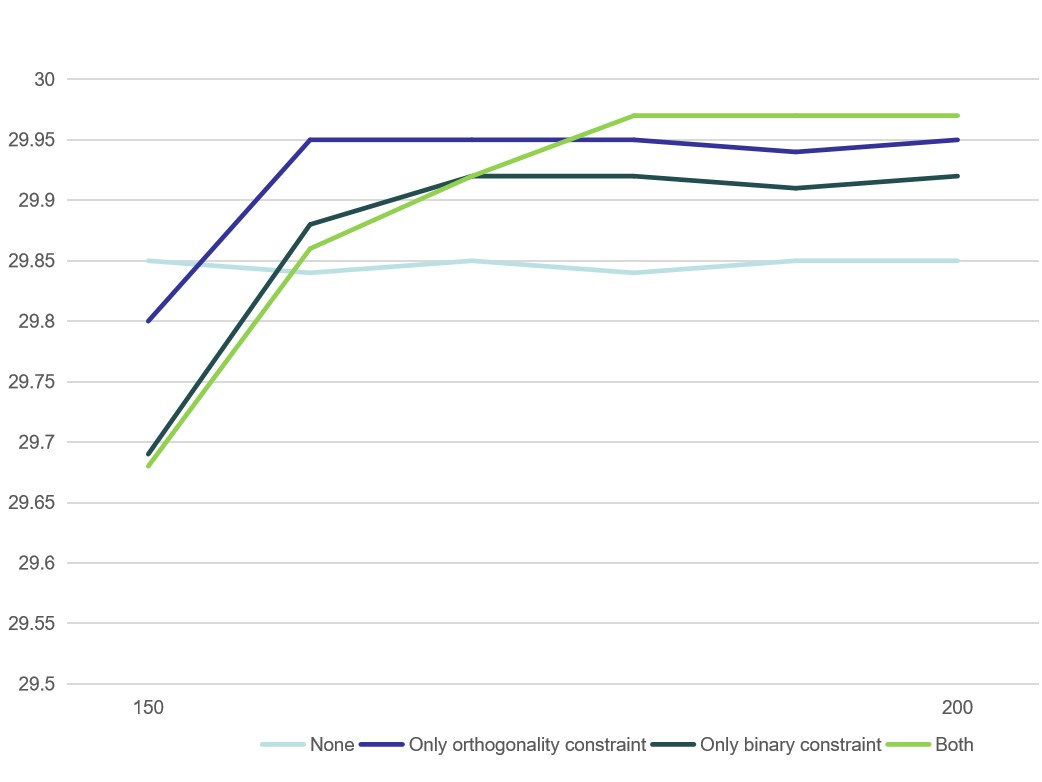
Figure 4, we verify the effect of different constrain combinations on the convergence process, and it can be observed that all combinations converge to similar values at 200 epochs and the combination of orthogonality constraint and binary constraint achieves the best results.
| CS sampling rate (Set11) | Time | ||||||
|---|---|---|---|---|---|---|---|
| Algorithm | Cpu/GPU | ||||||
| 50 % | 25 % | 10 % | 4 % | 1 % | Avg | ||
| TVAL3 | 33.56 | 27.92 | 23.00 | 18.75 | 16.43 | 23.93 | 3.150 s/ |
| D-AMP | 35.93 | 28.47 | 22.64 | 18.40 | 5.20 | 22.13 | 51.21 s/ |
| IR-CNN | 36.23 | 30.07 | 24.02 | 17.56 | 7.78 | 23.13 | / 68.42 s |
| SDA | 28.95 | 25.34 | 22.65 | 20.12 | 17.29 | 22.87 | / 0.003 s |
| ReconNet | 31.50 | 25.60 | 24.28 | 20.63 | 17.29 | 23.86 | / 0.016 s |
| ISTA-Net | 37.74 | 31.53 | 25.80 | 21.23 | 17.30 | 26.72 | / 0.093 s |
| FISTA-Net | 37.85 | 31.66 | 25.98 | 21.20 | 17.34 | 26.81 | / 0.052 s |
| BCS | 34.61 | 29.98 | 26.04 | 23.19 | 19.15 | 26.59 | / 0.002 s |
| NL-CS Net | 37.29 | 32.25 | 27.53 | 24.04 | 19.60 | 28.13 | / 0.326 s |
| \botrule | |||||||
4.1.3 Comparison with state-of-the-art methods
We compare the proposed NL-CS Net with eight representative models, including TVAL3 ref41 , D-AMP ref16 , IR-CNN ref42 , SDA ref20 , Recon-Net ref21 , ISTA-Net ref29 , FISTA-Net ref32 and BCS ref26 . TVAL3, D-AMP and IR-CNN are the optimization-based methods; Recon-net, SDA and BCS are the network-based methods. ISTA-Net and FISTA-Net are interpretable Network. In particular, IR-CNN inserts the trained CNN denoiser into the Half Quadratic Splitting (HQS) optimization method, which is used to solve the inverse problem. Recon-Net use convolutional method to learning the inverse problem map and reconstruction. BCS learns the sampling matrix through the network. ISTA-Net and FISTA-Net are constructed by unfolding traditional optimization-based algorithms into deep learning.

Table 4 shows the quantitative results of various CS algorithms on Set11. For the optimization-based methods including TVAL3, D-AMP and IR-CNN, we observe that they perform badly at extremely low CS sampling rates of 1%-4%, which has a large gap in performance with the other two categories of algorithms. Meanwhile, the proposed NL-CS Net outperforms the optimization-based methods at all the sampling rates. Specifically, NL-CS Net achieves on average 4.2 gain against the best-performing optimization-based method (TVAL3). In particular, the proposed NL-CS Net achieves a gain of 3.17, 11.82, 14.4, over TVAL3, D-AMP and IR-CNN respectively at extremely low 1% sampling rate. The network-based methods, including Recon-net, SDA and BCS, perform well at all sampling rates compared with the traditional methods. Still, at most sampling rates, NL-CS Net achieved the best results except that ISTA-Net and FISTA-Net obtain a minor advantage only with 50% of CS sampling rate. Compared to the two state-of-the-art interpretable networks ISTA-Net and FISTA-Net, the proposed NL-CS Net obtained a gain of 1.32 and 1.35 respectively on the average. In addition, compared to the optimization-based approaches, the proposed NL-CS Net substantially reduces the computation time. The reconstruction speed is approximately more than 10 times faster than that of D-AMP and IR-CNN. Compared to network-based approaches, NL-CS Net achieves decent speed with best performance.
| CS sampling rate (BSD68) | ||||||
|---|---|---|---|---|---|---|
| Algorithm | ||||||
| 50 % | 25 % | 10 % | 4 % | 1 % | Avg | |
| ISTA-Net | 34.04 | 29.36 | 25.32 | 22.17 | 19.14 | 26.01 |
| FISTA-Net | 34.28 | 29.45 | 25.38 | 22.31 | 19.35 | 26.16 |
| BCS | 33.18 | 29.18 | 26.07 | 23.94 | 21.24 | 26.72 |
| NL-CS Net | 34.69 | 29.97 | 26.72 | 24.21 | 21.63 | 27.44 |
| \botrule | ||||||
To further validate the generalizability of our NL-CS Net, we experimented several models that performed well on Set11, including ISTA-Net, FISTA-Net, BCS and ours on a larger dataset BSD68. In Table 5, it can be clearly observed that NL-CS Net outperforms the other algorithms at all sampling rates. It outperforms the second best algorithm by 0.72 in average PSNR, and by 0.39, 0.27, 0.52, 0.61 and 0.41 for different sampling rates from 1% to 50%, respectively.
Figure 5 shows a visual comparison. As can be seen, NL-CS Net is capable of preserving more texture information and recovering richer structural detail due to the effective incorporation of the non-local prior.
| MRI | ||||||
|---|---|---|---|---|---|---|
| Algorithm | ||||||
| 50 % | 40 % | 30 % | 20 % | 10 % | ||
| Zero-filling | 36.73 | 34.76 | 32.59 | 29.96 | 26.35 | |
| TV | 41.69 | 40.00 | 37.99 | 35.20 | 30.90 | |
| RecPF | 41.71 | 40.03 | 38.06 | 35.32 | 30.99 | |
| PBDW | 41.81 | 40.21 | 38.60 | 36.08 | 31.45 | |
| UNet | 42.20 | 40.29 | 37.53 | 35.25 | 31.86 | |
| NL-CS Net | 42.38 | 40.32 | 38.63 | 36.12 | 32.09 | |
| \botrule | ||||||
4.2 CS-MRI
We train and test on the brain and chest MRI images ref33 , in which the size of images is . For each dataset, we randomly take 100 images for training and 50 images for testing. In our experiments, we take , where is Fourier transform and is down sampling matrix. Our proposed NL-CS Net can be directly applied to CS-MRI reconstruction. Here we compare NL-CS Net with four classical CS-MRI methods: Zero-filling, TV ref6 , RecPF ref43 , PBDW ref44 and UNet ref45 .
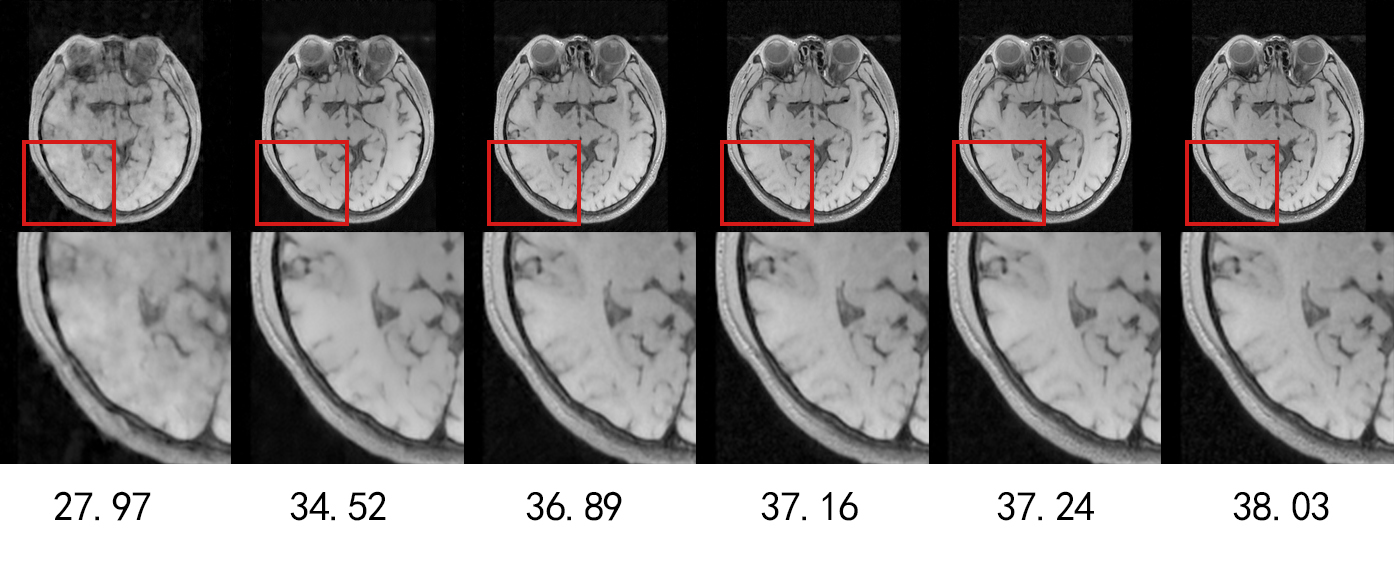
It can be clearly observed in Table 6 that NL-CS Net outperforms the other algorithms at all sampling rates. It outperforms the second best algorithm by 0.64, 0.04, 0.03, 0.11 and 0.57 for different sampling rates from 10% to 50%, respectively. The visualization results are shown in Figure 6, it can be seen that NL-CS Net reconstructs the brain image better than other methods. More details of the brain texture are preserved and the edges are more clearly.
5 Conclusion
Inspired by traditional optimization, we proposed a novel CS framework, dubbed NL-CS Net, with the incorporated learnable sampling matrix and non-local piror. The proposed NL-CS Net possesses well-defined interpretability, and make full use of the merits of both optimization-based and network-based CS methods. Extensive experiments show that NL-CS Net have state-of-art performance while maintaining great interpretability. For future work, one direction is to extend our proposed model to other image inverse problems, such as deconvolution and inpainting. Another one is to combine other iterative algorithms with deep learning.
Acknowledgments
This work was supported by the Natural Science Foundation of Liaoning Province (2022-MS-114).
Declarations
-
•
Funding: Natural Science Foundation of Liaoning Province (2022-MS-114)
-
•
Conflict of interest/Competing interests: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
-
•
Availability of data and materials: We hereby declare that all data and materials used in this study are publicly available with no restrictions. The data used in this research has been made publicly available and can be accessed directly via https://github.com/bianshuai001/NL-CS-Net.
-
•
Code availability: We declare that the code used in this study is open-source and publicly available for unrestricted use. The code used in this research can be accessed via the link https://github.com/bianshuai001/NL-CS-Net. Anyone can retrieve, download, and use the code for non-commercial purposes, subject to appropriate attribution of the source.
References
- (1) E. J. Candes and T. Tao, Near-optimal signal recovery from random projections: universal encoding strategies, IEEE Transactions on Information Theory, 52(12) (2006) 5406-5425.
- (2) M. F. Duarte, M. A. Davenport, D. Takhar and J. N. Laska, Single-pixel imaging via compressive sampling, IEEE Signal Processing Magazine, 25(2) (2008) 83-91.
- (3) J. Haupt, W. U. Bajwa, G. Raz and R. Nowak, Toeplitz compressed sensing matrices with applications to sparse channel estimation, IEEE Transactions on Information Theory, 56(11) (2010)5862-5875.
- (4) K. Q. Dinh, H. J. Shim and B. Jeon, Measurement coding for compressive imaging using a structural measuremnet matrix, 2013 IEEE International Conference on Image Processing. IEEE, (2014) 10-13.
- (5) X. Gao, J. Zhang, W. Che, X. Fan and D. Zhao, Block-based compressive sensing coding of natural images by local structural measurement matrix, 2015 Data Compression Conference. IEEE Computer Society, (2015) 133-142.
- (6) M. Lustig, D. L. Donoho, J. M. Santos and J. M. Pauly, Compressed sensing MRI, IEEE Signal Processing Magazine 25(2) (2008) 72-82.
- (7) J. H. Ender, On compressive sensing applied to radar, SIGNAL PROCESSING -AMSTERDAM- 90(5) (2010) 1402-1414.
- (8) S. Li, L. D. Xu and X. Wang, Compressed sensing signal and data acquisition in wireless sensor networks and internet of things, IEEE Transactions on Industrial Informatics 9(4) (2013)2177-2186.
- (9) M. Elad and M. Aharon, Image denoising via sparse and redundant representations over learned dictionaries, IEEE Transactions on Image Processing, 15(12) (2006) 3736-3745.
- (10) J. M. Duarte-Carvajalino and G. Sapiro, Learning to sense sparse signals: simultaneous sensing matrix and sparsifying dictionary optimization, IEEE Transactions on Image Processing, 18(7) (2009) 1395-1408.
- (11) C. Lu, H. Li and Z. Lin, Optimized projections for compressed sensing via direct mutual coherence minimization, Signal Processing, 151 (2018) 45-55.
- (12) Y. Kim, M. S. Nadar and A. Bilgin, Compressed sensing using a Gaussian Scale Mixtures model in wavelet domain, 2010 IEEE International Conference on Image Processing, (2010) 3365-3368.
- (13) J. Zhang, S. Liu, R. Xiong, S. Ma and D. Zhao, Improved total variation based image Compressive Sensing Recovery by nonlocal regularization,2013 IEEE International Symposium on Circuits and Systems (ISCAS), (2013) 2836-2839.
- (14) J. Zhang, D. Zhao, C. Zhao, R. Xiong, S. Ma and W. Gao, Image compressive sensing recovery via collaborative sparsity, IEEE Journal on Emerging & Selected Topics in Circuits & Systems, 2(3) (2012) 380-391.
- (15) W. Dong, G. Shi, X. Li, Y. Ma and F. Huang, Compressive sensing via nonlocal low-rank regularization, IEEE Transactions on Image Processing, 23(8) (2014) 3618-32.
- (16) C. A. Metzler, A. Maleki and R. G. Baraniuk, From denoising to compressed sensing, IEEE Transactions on Information Theory, 62(9) (2016) 5117-5144.
- (17) A. Adler, D. Boublil, M. Elad and M. Zibulevsky, A deep learning approach to block-based compressed sensing of images, Computer Vision and Pattern Recognition, (2016) 1-6.
- (18) W. Li, F. Liu, L. Jiao and F. Hu, Multi-Scale residual reconstruction neural network With non-local constraint, IEEE Access 7 (2019) 70910-70918.
- (19) K. He, X. Zhang, S. Ren and J. Sun, Deep residual learning for image recognition, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016) 770-778.
- (20) A. Mousavi, A. B. Patel and R. G. Baraniuk, A deep learning approach to structured signal recovery, 2015 53rd Annual Allerton Conference on Communication, Control, and Computing (Allerton), (2015) 1336-1343.
- (21) K. Kulkarni, S. Lohit, P. Turaga, R. Kerviche and A. Ashok, ReconNet: non-iterative reconstruction of images from compressively sensed measurements, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016) 449-458.
- (22) H. Yao, F. Dai, S. Zhang, Y. Zhang, Q. Tian and C. Xu, DR2-Net: deep residual reconstruction network for image compressive sensing, 359(24) (2017) 483-493.
- (23) Y. Sun, J. Chen, Q. Liu and G. Liu, Learning image compressed sensing with sub-pixel convolutional generative adversarial network, Pattern Recognition, 98(12) (2019) 107051.
- (24) W. Shi, F. Jiang, S. Liu and D. Zhao, Image compressed sensing using convolutional neural network, IEEE Transactions on Circuits and Systems for Video Technology, 29(65) (2020) 375-388.
- (25) W. Shi, F. Jiang, S. Liu and D. Zhao, Scalable convolutional neural network for image compressed sensing, 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), (2019) 12282-12291.
- (26) A. Adler, D. Boublil and M. Zibulevsky, Block-based compressed sensing of images via deep learning, 2017 IEEE 19th International Workshop on Multimedia Signal Processing (MMSP), (2017) 1-6.
- (27) J. Du, X. Xie, C. Wang, G. Shi, X. Xu and Y. Wang, Fully convolutional measurement network for compressive sensing image reconstruction, Neurocomputing 328(7) (2019) 105-112.
- (28) W. Shi, F. Jiang, S. Zhang and D. Zhao, Deep networks for compressed image sensing, 2017 IEEE International Conference on Multimedia and Expo (ICME), (2017) 877-882.
- (29) J. Zhang and B. Ghanem, ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing, CVPR, (2018) 1828-1837.
- (30) J. Zhang, C. Zhao and W. Gao, Optimization-Inspired compact deep compressive sensing, IEEE Journal of Selected Topics in Signal Processing 14(4) (2020) 765-774.
- (31) D. You, J. Xie, and J. Zhang, ISTA-Net++: flexible deep unfolding network for compressive sensing, IEEE International Conference on Multimedia and Expo (ICME), (2021) 1-6.
- (32) J. Xiang, Y. Dong and Y. Yang, FISTA-Net: Learning a fast iterative shrinkage thresholding network for inverse problems in imaging, IEEE Transactions on Medical Imaging, 40(5) (2021) 1329-1339.
- (33) Y. Yan, S. Jian, L. Huibin and X. Zongben, Deep ADMM-Net for compressive sensing MRI, Advances in Neural Information Processing Systems, (2016) 10-18.
- (34) Z. Zhang, Y. Liu, J. Liu, F. Wen and C. Zhu, AMP-Net: Denoising-Based Deep Unfolding for Compressive Image Sensing, IEEE Transactions on Image Processing, 30 (2021) 1487-1500.
- (35) A. Buades, B. Coll and J.Morel, A non-local algorithm for image denoising, 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), 2 (2005) 60-65.
- (36) Liu, Ding and Wen, Bihan and Fan, Yuchen and Loy, Chen Change and Huang, Non-Local recurrent network for image restoration, Conference and Workshop on Neural Information Processing Systems(NIPS), (2018) 1680–1689.
- (37) W. Shi, J Caballero, F Huszár, J Totz and Z Wang, Real-Time single image and video super-resolution using an efficient sub-pixel convolutional neural network, 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2016) 1874-1883.
- (38) C. Mou, J. Zhang, X. Fan, H. Liu and R. Wang, COLA-Net: collaborative attention network for image restoration, IEEE Transactions on Multimedia, 24 (2022) 1366-1377.
- (39) X. Wang, R. Girshick, A. Gupta and K. He, Non-local neural networks, 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, (2018) 7794-7803.
- (40) D. Martin, C. Fowlkes, D. Tal and J. Malik, A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics, Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001, 2 (2001) 416-423.
- (41) C, Li, W. Yin and H. Jiang, An efficient augmented Lagrangian method with applications to total variation minimization, Computational Optimization & Applications, 56(3) (2013) 507-530.
- (42) K. Zhang, W. Zuo, S. Gu and L. Zhang, Learning deep CNN denoiser prior for image restoration, 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), (2017) 2808-2817.
- (43) J. Yang, Y. Zhang and W. Yin, A fast alternating direction method for TVL1-L2 signal reconstruction from partial fourier data, IEEE Journal of Selected Topics in Signal Processing 4(2) (2010) 288-297.
- (44) X. Qu, Undersampled MRI reconstruction with patch-based directional wavelets, Magnetic Resonance Imaging 30(7) (2012) 964-977.
- (45) Chang Min Hyun, Hwa Pyung Kim, Sung Min Lee, Sungchul Lee and Jin Keun Seo, Deep learning for undersampled MRI reconstruction, Physics in Medicine and Biology, 63(13) (2018) 135007.