$n$-photon blockade with an $n$-photon parametric drive

In a nonlinear cavity driven by a classical light field, the single-photon existence in the cavity blocks the creation of a second photon r1 ; xu000 ; xu001 , which is known as the single-photon blockade (1PB). Due to its potential applications in information and communication technology, 1PB has been extensively studied in the past years r21 ; r22 ; r23 ; r24 ; r25 ; r26 ; shi01 ; shi02 ; r812 ; t01 . For example, the PB has been predicted in cavity quantum electrodynamics n03 ; n04 ; A01 , quantum optomechanical system n01 ; r30 ; rr00 ; guang1 , and second order nonlinear system zhou01 ; zhou02 ; zhou03 ; zhou04 ; zhou05 .

Traditionally, realizing 1PB requires a large nonlinearity to change the energy-level structure of the system, and 1PB can be used to create a single-photon source r31 . The 1PB effect was first observed in an optical cavity coupled to a single trapped atom r3 . Since then, many experimental groups have observed this strong antibunching behavior in different systems, including a photonic crystal r4 and a superconducting circuit r5 . In addition, the 1PB can also enable by another mechanism, i.e., the quantum interference h022 ; h023 ; h024 ; h241 ; h242 ; r94 , which has been recently observed experimentally h025 ; h026 . In this paper, we are only concerned with the photon blockade based on energy level splitting due to the large nonlinearity.

The $n$-photon blockade ($n$PB) was proposed with the development of 1PB. In analogy to 1PB, $n$PB ($n\geq 2$) is defined by the existence of $n$ photons in a nonlinear cavity suppressing the creation of subsequent photons. The $2$PB ($n$PB with $n=2$) was studied in a Kerr-type system driven by a laser r7 , in a strong-coupling qubit-cavity system r71 , and in a cascaded cavity QED system r11 . The 2PB can also be generated by squeezing dc1 . Experimentally, 2PB was realized in an optical cavity strongly coupled to a single atom r8 , where driving the atom gives a larger optical nonlinearity than driving the cavity. $n$PB with $n>2$ has been studied in a cavity strongly coupled to two atoms r9 , in a cavity with two cascade three-level atoms r10 , and in a Kerr-type system driven by a laser r811 ; r81 . Meanwhile, in analogy to photon blockades, the phonon blockades have been widely studied sheng01 ; sheng02 ; sheng03 ; sheng04 ; sheng05 .

In this paper, we theoretically propose that $n$PB can be triggered in a nonlinear cavity with $n$-photon parametric drive. For convenience, we denote “$n$-photon parametric drive” as $n$PD. We first give a brief introduction to this proposal and then confirm its validity by considering three examples, i.e., an atom-cavity system, a single mode Kerr-nonlinearity system, and a two-coupled-cavities Kerr-nonlinearity system. This proposal is quite general and can be extended to other nonlinear systems for studying $n$PB via $n$PD. The study of the $n$PB in recent decades has mainly focused on a coherent (i.e., single-photon) driving. Comparing with a proposal using a coherent driving, the use of a $n$PD has the following advantages: (i) The nonlinear systems like atom-cavity system will not exist $n$PB with a coherent driving to the cavity due to the bosonic enhancement of photon r8 , while we find that the $n$PB will exist in these system with a $n$PD, so the proposal with the $n$PD is more general to realize a $n$PB. (ii) In the same nonlinear system, the $n$PD approach has a stronger ($n+1$)-photon bunching than the coherent driving approach, so the $n$PD approach has a better $n$PB effect.

The remainder of this paper is organized as follows. In Sec. II, we introduce the Proposal for $n$PB with $n$PD. In Sec. III, we illustrate the $nPB$ in an atom-cavity system. In Sec. IV, we show the $nPB$ in single-mode Kerr-nonlinearity system. In Sec. V, we study the $2PB$ in two-coupled-cavities Kerr-nonlinearity system. Conclusion are given in Sec. VI.

The $n$PD with $n=2$ has many applications, such as in the realization of quantum metrology r92 and cooling of a micromechanical mirror r93 . In the following, we will present our basic idea for studing the $n$PB via $n$PD on a nonlinear cavity.

$n$PD involved in our proposal is described by $\hat{H}_{d}=\lambda(\hat{a}^{{\dagger}n}e^{-i\omega_{p}t}+\hat{a}^{n}e^{i\omega_{p}t})$, where $\hat{a}$ is the cavity annihilation operator, $\lambda$ is the parametric driving amplitude, and $\omega_{p}$ is the driving frequency. Apart from the cavity on which $n$PD is applied, an auxiliary nonlinear system (e.g., an atom, a Kerr-nonlinearity medium, or an auxiliary cavity) is required to realize $n$PB. The Hamiltonian of the auxiliary nonlinear system and the cavity is denoted by $\hat{H}_{0}$. The form of $\hat{H}_{0}$ is not unique, and it depends on the type of the nonlinear system. Generally speaking, the Hamiltonian $\hat{H}_{0}$ can be diagonalized and expressed as

where $\omega_{n}^{j}$ is the $j$th eigenfrequency of $\hat{H}_{0}$ for the photon excitation number $n$, and we have assumed that the ground state energy is zero. The corresponding eigenstate $|\psi_{n}^{j}\rangle$ is constructed by the $k_{n}$ basis for $n$-photon excitation, where the basis forms a closed space. The set of eigenfrequencies $\{\omega_{1}^{j}\},\{\omega_{2}^{j}\}\cdots,\{\omega_{n}^{j}\},\cdots$ are anharmonic due to the strong nonlinear interaction. Among these eigenfrequencies, {$\omega_{n}^{j}$} (where $j$ is from $1$ to $k_{n}$) is crucial to $n$PB because the corresponding eigenstate {$|\psi\rangle_{n}^{j}$} includes a $n$-photon state. When the parametric drive frequency $\omega_{p}$ is tuned to the {$\omega_{n}^{j}$}, the parametric drive resonantly excites $n$ photons in the cavity. As a result, the system occupies the state {$|\psi\rangle_{n}^{j}$} via the nonlinear interaction. This gives rise to an important result for $n$PB. The corresponding conditions for $n$PB are

The $n$-photon resonance excitation by $n$PD ensures that the $n$-photon blockade is triggered in the nonlinear cavity.

To verify the validity of the above proposal, we will study three examples to study $n$PB, in: an atom-cavity system, a single-mode Kerr-nonlinearity system, and a two-coupled-cavities Kerr-nonlinearity system. In these systems, the analytical conditions for $n$PB and the accurate numerical results are studied, which conform that $n$PB can be triggered in a nonlinear cavity with $n$PD if the Hamiltonian $\hat{H}_{0}$ can be diagonalized.

The numerical confirmation of $n$PB adopts an equal-time correlation function, the equal-time $n$-order correlation function is defined as $g^{(n)}(0)=\langle\hat{a}^{{\dagger}n}\hat{a}^{n}\rangle/\langle\hat{a}^{{\dagger}}\hat{a}\rangle^{n}$. The correlation function is calculated by numerically solving the master equation in the steady state. In order to prove $n$PB, it is sufficient to fulfill the conditions $g^{(n)}(0)\geq 0$ and $g^{(n+1)}(0)<0$ simultaneously r8 .

The atom-cavity system is described by the Jaynes-Cummings Hamiltonian, where the cavity is driven by a $n$PD. In a frame rotating at the parametric drive frequency $\omega_{p}/n$, the Hamiltonian is (assuming $\hbar=1$ hereafter)

where $\hat{a}$ is the cavity annihilation operator, $\hat{\sigma}_{\pm}$ are the atom raising and lowering operators, $g$ is the coupling strength of the atom and the cavity mode, $\lambda$ is the amplitude of $n$PD, and $\Delta_{a}=\omega_{a}-\omega_{p}/n$ ($\Delta_{e}=\omega_{e}-\omega_{p}/n$) is the detuning between the cavity frequency $\omega_{a}$ (the atom frequency $\omega_{e}$) and the $1/n$ driving frequency. Here and below, we study the case of $\omega_{a}=\omega_{e}$ for convenience, resulting in $\Delta_{a}=\Delta_{e}$. The Hamiltonian (3) with $n=2$ can be used to exponentially enhance the light-matter coupling in a generic cavity QED p0 ; p1 ; p2 .

In the absence of the $n$PD, the atom-cavity Hamiltonian $\hat{H}_{0}$ (the first three terms of Eq. (3) without driving) is diagonalized as

The energy eigenstates of the system are $|\psi_{n}^{1,2}\rangle=1/\sqrt{2}(|n-1,e\rangle\mp|n,g\rangle)$, where $|g\rangle$ ($|e\rangle$) is the ground (excited) state of the atom, $n$ denotes the photon excitation number. For a $n$-photon excitation, the basis {$|n,g\rangle$, $|n-1,e\rangle$} forms a closed space. The corresponding eigenfrequencies with the $n$-photon excitation are $\omega_{n}^{1,2}=n\omega_{a}\mp\sqrt{n}g$. The energy-level diagram of the system is shown in Fig. 1(a). The optimal conditions for $n$PB are calculated according to Eq. (2), which are simplified as

where $\Delta=\Delta_{a}=\Delta_{e}$. There is one path for the system to reach the state $|\psi_{n}^{1,2}\rangle$: the system first arrives at a $n$-photon state by $n$PD, then goes to the state of $|\psi_{n}^{1,2}\rangle$ via the coupling $g$, i.e., $|0g\rangle\stackrel{{\scriptstyle\lambda}}{{\longrightarrow}}|ng\rangle\stackrel{{\scriptstyle g}}{{\longrightarrow}}|\psi_{n}^{1,2}\rangle$, the $n$PD and the $n$-photon resonance excitation make that the $n$PB is triggered.

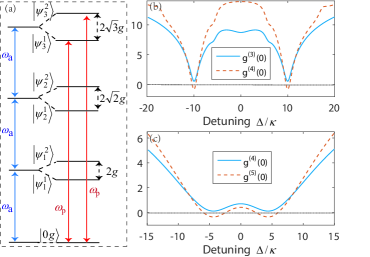
Next, we numerically study the $n$PB effect. The system dynamics is governed by the master equation $\partial\hat{\rho}/\partial t=-i[\hat{H},\hat{\rho}]+\kappa\ell(\hat{a})\rho+\gamma\ell(\hat{\sigma_{-}})\rho$, where $\kappa$ denotes the decay rate of the cavity and $\gamma$ is the atomic spontaneous emission rate. The superoperators are defined by $\ell(\hat{o})\hat{\rho}=\hat{o}\hat{\rho}\hat{o}^{{\dagger}}-\frac{1}{2}\hat{o}^{{\dagger}}\hat{o}\hat{\rho}-\frac{1}{2}\hat{\rho}\hat{o}^{{\dagger}}\hat{o}$. The numerical solutions of $g^{(n)}(0)$ and $g^{(n+1)}(0)$ are calculated by solving the master equation in the steady state. In Fig. 1(b), we study a 3PB by plotting $g^{(3)}(0)$ and $g^{(4)}(0)$ versus $\Delta/\kappa$ with $g/\kappa=10\sqrt{3}$. We note that the 3PB appears on $\Delta/\kappa=\pm 10$ ($g^{(3)}(0)\geq 0$ and $g^{(4)}(0)<0$ simultaneously), which agrees well with the conditions for $n$PB in Eq. (5) with $n=3$. The 4PB is studied in Fig. 1(c) with $g/\kappa=10$, and 4PB appears on $\Delta/\kappa=\pm 5$, which also agrees with Eq. (5) with $n=4$. The numerical results confirm the analytic conditions and the corresponding analysis. In the above atom-cavity system, it was proved that the $n$PB will not exist with a coherent driving (driving the cavity) due to a consequence of the bosonic enhancement of photon r8 , while the $n$PB will exist for this system with a $n$PD. So the proposal with the $n$PD is more general and the $n$PB will occur as long as the analytical eigenvalues of the nonlinear Hamiltonian $\{\omega_{n}^{j}\}$ is solvable.

The system of a single-mode cavity with a Kerr nonlinearity, driven by $n$PD with $n=2$, has been extensively studied due to its rich physics p4 ; p5 ; p6 ; p7 ; p8 . Here we investigate $n$PB utilizing this system. The Hamiltonian of this model in a rotating frame is written as p5

where $\Delta_{a}=\omega_{a}-\omega_{p}/n$ is the cavity detuning from the $1/n$ driving eigenfrequency, $U$ is the Kerr nonlinear strength, and $\lambda$ is the amplitude of the $n$PD.

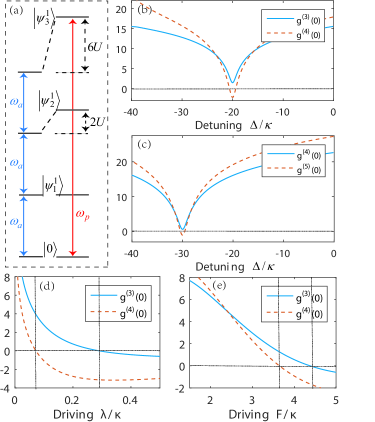
The undriven part of the Hamiltonian (6) is diagonalized as

where the eigenstate is written as the Fock-state basis $|\psi_{n}^{1}\rangle=|n\rangle$ (with $n$ photons in the cavity), the corresponding eigenfrequency is $\omega_{n}^{1}=\omega_{a}n+U(n^{2}-n)$. The $n$PB can be triggered by the $n$-photon-excitation resonance, and the $|0\rangle\rightarrow|n\rangle$ transition is enhanced. The condition for $n$PB is obtained according to Eq. (2), which is given by

Because of the $n$PD and the $n$-photon-excitation resonance, the $n$ photon probability will increase when the condition (8) is satisfied, and the $n$PB is triggered.

The master equation for the system is given by $\partial\hat{\rho}/\partial t=-i[\hat{H},\hat{\rho}]+\kappa\ell(\hat{a})\rho$. The energy-level diagram for 3PB is shown in Fig. 2(a), and the corresponding numerical simulation is shown in Fig. 2(b), where we plot $g^{(3)}(0)$ and $g^{(4)}(0)$ as a function of $\Delta/\kappa$ with $g/\kappa=10$. These results show that 3PB can be obtained at $\Delta/\kappa=-20$, as predicted in Eq. (8) for $n=3$. The 4PB is studied in Fig. 2(c) and the 4PB appears on $\Delta/\kappa=-30$, which also agrees with Eq. (8) with $n=4$.

We note that the studies to date on the $n$PB are mainly focused on a coherent driving $F(\hat{a}^{\dagger}+\hat{a})$, where $F$ is the coherent driving strength. So we compare the 3PB based on the $3$PD with that based on the coherent driving. To this end, we plot $g^{(3)}(0)$ and $g^{(4)}(0)$ versus the $3$PD strength and coherent driving strength in Fig. 2(d, e) under the blockade condition of Eq. (8) ($g/\kappa=10$, $\Delta/\kappa=-20$), respectively. The 3PB with the $3$PD is obtained in a region of small $\lambda$, while the implementation of 3PB with coherent driving needs a larger $F$. The most striking feature is that the 3PB with the $3$PD has a stronger four-photon antibunching and three-photon bunching.

Two coupled cavities with Kerr nonlinearity were considered to study 1PB p9 . We define the two cavities as cavities $a$ and $b$. The Hamiltonian in a rotating frame is

where $\hat{a}$ ($\hat{b}$) is the photon annihilation operator for cavity $a$ ($b$) with frequency $\omega_{a}$ ($\omega_{b}$), $\Delta=\omega_{a}-\omega_{p}/n=\omega_{b}-\omega_{p}/n$, $J$ is the coupling strength of the two cavities, $U$ is the Kerr nonlinear strength, and $\lambda$ is the $n$PD strength.

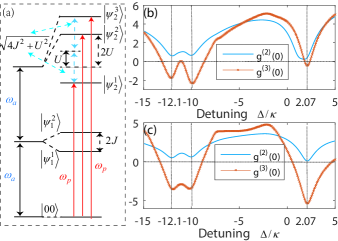
The Hamiltonian for the two cavities with the Kerr nonlinearity (the first four terms in Eq. (9) without driving) is diagonalized as

We find that our approach comes with its own limitations in this system. The eigenfrequencies $\{\omega_{n}^{j}\}$ are more and more difficult to analytically solve with the increase of $n$, so we only study the case of $n=2$, the corresponding energy-level diagram is shown in Fig. 3(a). Now we derive the eigenfrequencies $\{\omega_{2}^{j}\}$ and the eigenstates $\{|\psi_{2}^{j}\rangle\}$. To obtain these, the Hamiltonian will be expanded with the two-cavity states $|20\rangle$, $|02\rangle$ and $|11\rangle$ for the two-photon excitation, where $|\alpha\beta\rangle$ is the Fock-state basis of the system with the number $\alpha$ ($\beta$) denoting the photon number in cavity $a$ ($b$). The two-cavity states satisfy the two-photon excitation condition $\alpha+\beta=2$, and the states $|20\rangle$, $|02\rangle$ and $|11\rangle$ form a closed space. Under these basis states, the Hamiltonian with two-photon excitation can be described as

The three eigenfrequencies are $\omega_{2}^{2}=2(U+\omega_{a})$, and $\omega_{2}^{1,3}=2\omega_{a}+U\mp\sqrt{4J^{2}+U^{2}}$. The corresponding unnormalized eigenstates are $|\psi_{2}^{2}\rangle=-|20\rangle+|02\rangle$, and $|\psi_{2}^{1,3}\rangle=|20\rangle-[\sqrt{2}U\mp\sqrt{2(4J^{2}+U^{2})}]/(2J)|11\rangle+|02\rangle$. The conditions for 2PB, obtained from Eq. (2), are given by

Under these resonance conditions, 2PB can be triggered, which enhances the transition $|00\rangle\rightarrow\{|\psi_{2}^{2}\rangle,|\psi_{2}^{1,3}\rangle\}$. The two cavities occupy the two-photon states $|20\rangle$ and $|02\rangle$, which ensures that 2PB is simultaneously realized in the two cavities when the conditions (12) are satisfied.

The numerical study of 2PB is the same as before. In Fig. 3(b, c), we plot $g^{(2)}(0)$ and $g^{(3)}(0)$ as a function of $\Delta/\kappa$ for cavity $a$ and cavity $b$, respectively. The results indicate that 2PB occurs for $\Delta/\kappa=-12.7$, $\Delta/\kappa=-10$ and $\Delta/\kappa=2.07$, which are predicted by the three $n$PB conditions given in Eq. (12) with $n=2$. The anharmonic distribution of the blockade points are determined by the anharmonic splitting of the energy levels $\omega_{2}^{1}$, $\omega_{2}^{2}$, and $\omega_{2}^{3}$. The distance of the two blockade points on the left is calculated as $d=\sqrt{4J^{2}+U^{2}}-U$, and the distance of the two points on the right is $d=\sqrt{4J^{2}+U^{2}}+U$. Thus, it can be concluded that 2PB is simultaneously realized in both cavity $a$ and cavity $b$ due to the feature of the system and the $N$PD.

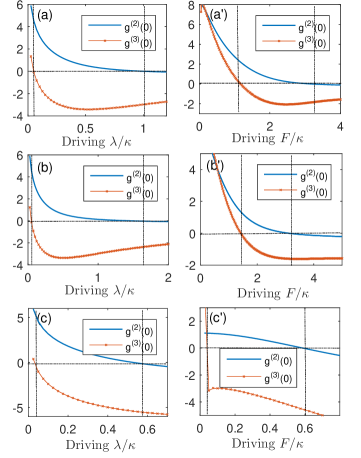
The undriven cavity $b$ has a better 2PB effect than cavity $a$ for a smaller $g^{(3)}(0)$ shown in Fig. 3(b, c), so we compare the $2$PD approach with the coherent driving approach for cavity $b$. The results are presented in Fig. 4, where we plot of $g^{(2)}(0)$ and $g^{(3)}(0)$ as a function of $\lambda/\kappa$ ($F/\kappa$) under the three blockade conditions, respectively. We find that the two approaches have different blockade regions. And the same conclusion is arrived as the single-mode Kerr-nonlinearity system that the 2PB with the $2$PD has a stronger three-photon antibunching and two-photon bunching.

We have proposed that $n$-photon blockade can be realized in a nonlinear cavity with a $n$-photon parametric drive. The validity of this proposal is confirmed by three examples, i.e., $n$-photon blockade in an atom-cavity system, in a single-mode Kerr nonlinear device, and in a two-coupled-cavities Kerr-nonlinear system. By solving the master equation in the steady-state limit and computing the correlation functions $g^{(n)}(0)$ and $g^{(n+1)}(0)$, we have shown that $n$PB can be realized, and the optimal conditions for $n$PB are in good agreement with the numerical simulations, which clearly illustrates the validity of our proposal. This proposal can be extended to other nonlinear systems, as long as the $n$-photon-excitation analytical eigenvalues of the nonlinear Hamiltonian is solvable.

This work is supported by the Key R&D Program of Guangdong province (Grant No. 2018B0303326001), the NKRDP of china (Grants Number 2016YFA0301802), the National Natural Science Foundation of China (NSFC) under Grants No. 11965017, 11705025,11804228, 11774076, the Jiangxi Natural Science Foundation under Grant No. 20192ACBL20051, the Jiangxi Education Department Fund under Grant No. GJJ180873. This work is also supported by the NTT Research, Army Research Office (ARO) (Grant No. W911NF-18-1-0358), the Japan Science and Technology Agency (JST) (via the CREST Grant No. JPMJCR1676), the Japan Society for the Promotion of Science (JSPS) (via the KAKENHI Grant Number JP20H00134, JSPS-RFBR Grant No. 17-52-50023), the Grant No. FQXi-IAF19-06 from the Foundational Questions Institute Fund (FQXi), and a donor advised fund of the Silicon Valley Community Foundation.