states with hidden charm and a three-body nature
Abstract
In this work we study the formation of ’s as a consequence of the dynamics involved in the system when the subsystem generates in isospin 0 and in isospin 1. States with isospin and mass in the energy region MeV are found to arise with spin-parity and , leading to predictions in this way of the existence of resonances with hidden charm and a three-body nature. We also discuss the possibility of the existence of states, i.e., ’s with hidden charm.
1 Introduction
Recently, the LHCb collaboration announced the existence of possible hidden charm pentaquarks in the invariant mass distribution of the process Aaij:2015tga ; Aaij:2016phn ; Aaij:2019vzc . The observation of such states, denoted as , and , constitutes a turning point in the experimental search for signals related to exotic baryons, which had gradually reduced after the lack of evidence for the existence of was reported in higher statistics experiments Battaglieri:2005er ; Miwa:2006if ; Moritsu:2014bht ; Shen:2016csu 111See also Refs. Torres:2010jh ; MartinezTorres:2010zzb for a possible theoretical explanation of the signal observed by the LEPS collaboration for .. Indeed, continuing with the hunting of exotic baryons, more recently, the LHCb collaboration has claimed the existence of yet another pentaquark with hidden charm, similar to the above mentioned states, but with nonzero strangeness, whose mass is around 4459 MeV wang . Coming back to the discussion on the ’s, we must recall that two states were initially claimed in Ref. Aaij:2015tga , the so called , with a width of MeV, and , with a width of . Out of the two states, the existence of the former was based more on a requirement for a good description of the data than on a direct observation Aaij:2015tga . The best fit to the data in Ref. Aaij:2015tga was obtained by considering spin-parity for and for , although acceptable solutions were also obtained for the combinations and and and , respectively. The updated analysis of the same processes as in Ref. Aaij:2015tga , but with much larger statistical significance, was made in Ref. Aaij:2019vzc , which revealed the presence of two states, (mass MeV, width MeV) and ( MeV, MeV), instead of , and a narrow peak at 4312 MeV, ( MeV, ), though no definite spin-parity is assigned to the three states yet. The fits performed in Ref. Aaij:2019vzc with and without describe well the data, and its existence could not be ascertained. Several theoretical descriptions, as well as different spin-parity assignments, have been proposed for the nature of these states, like pentaquarks Maiani:2015vwa ; Lebed:2015tna ; Ghosh:2015ksa ; Weng:2019ynv ; Wang:2019got , meson-baryon states Roca:2015dva ; Xiao:2019aya ; Liu:2019tjn ; Burns:2019iih ; He:2019ify ; Xiao:2019mst ; Guo:2019kdc ; Du:2019pij ; Xu:2020gjl , peaks arising from triangle singularities Guo:2015umn ; Liu:2015fea ; Nakamura:2021qvy (which seems to be more plausible for , although further investigations are necessary Aaij:2019vzc ) or a virtual state for Fernandez-Ramirez:2019koa . In case of the meson-baryon molecular attribution, the predominant interpretation is to consider the ’s as states arising from the , and coupled channel dynamics in s-wave. Within such a description, the states, although there is no consensus on the spin assignment, would have negative parity. However, in Ref. Burns:2019iih , by introducing coupled to , the authors determined a positive parity assignment for .
With all the experimental and theoretical efforts being made to understand the properties of the states claimed in Ref. Aaij:2019vzc , and with the debate on their spin-parity assignments still under way, it is important to investigate the possible formation of states with hidden charm and positive parity. Such states may naturally arise as a consequence of the dynamics involved in the three-body systems and since the interactions between the different subsystems are attractive in s-wave, forming states like , , Braaten:2003he ; AlFiky:2005jd ; Gamermann:2007fi ; Gamermann:2010zz ; Aceti:2014uea ; Ortega:2018cnm ; He:2017lhy ; Hofmann:2005sw ; Mizutani:2006vq ; GarciaRecio:2008dp ; Romanets:2012hm ; Liang:2014kra ; Nieves:2019nol . Further, the () threshold lies around 4814 MeV, and due to the strong attraction present in the and coupled channel system in s-wave, where (among other and states) has been found to get generated around 210 (352) MeV below the () threshold, we can expect large binding energies in the three-body system considered, of the order of 200-300 MeV. In this way, there exists a possibility of finding positive parity state(s) in the energy region 4400-4600 MeV, precisely where the ’s have been observed in Refs. Aaij:2015tga ; Aaij:2019vzc .
Motivated by this reasoning, in this work, we study the coupled configurations of the system. To do this, we solve the Faddeev equations within the fixed center approximation (FCA) Foldy:1945zz ; Brueckner:1953zz ; Deloff:1999gc ; MartinezTorres:2020hus assuming that clusters as . As we will show, states with hidden charm, spin-parity , and masses in the energy region 4400-4600 MeV are found to arise due to the underlying three-body dynamics. We discuss different processes where such positive parity ’s can be studied experimentally. We also investigate the possible existence of isospin 3/2 states with hidden charm. Finally we test the applicability of FCA to the current system by calculating diagrams beyond the approximation and show that such contributions are negligible.
2 Formalism
In the FCA to the Faddeev equations, the scattering between the three particles forming the system is described in terms of a particle interacting with a scattering center. Such a treatment is relevant when two of the particles cluster as a state whose mass is heavier than the third one, which rescatters with those forming the cluster through a series of interactions (for a review on the topic see Ref. MartinezTorres:2020hus ). In this way, the cluster plays the role of the scattering center, which stays unaltered in the scattering process. In this work we study the configurations of the system. We consider then that the system clusters as [] in isospin () and the nucleon rescatters, successively, off the () and () mesons. Since,
when adding a nucleon, we can write the three-body state as,
| (1) |
where represents the cluster, whose isospin is , and () is the isospin (and its third component) of the three-body system. In this way, to describe the interaction between a and the cluster we need to calculate the scattering -matrix
| (2) |
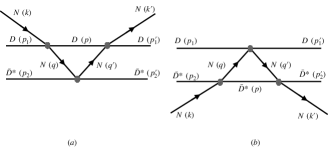
Note that the transition
requires that the scattering of the nucleon on converts the cluster to or in the intermediate states (see Fig. 1). Since our purpose is to identify the cluster with or in all intermediate states, both of which are understood as “molecules”, other intermediate processes are expected to be small and are not considered in the formalism.
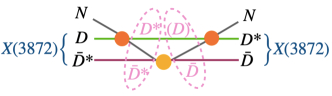
Indeed it was shown in Refs. MartinezTorres:2010ax ; MartinezTorres:2020hus that such considerations lead to small contributions to the dominant process for center of mass energies below the threshold. We thus limit ourselves to investigating the formation of three-body states below the threshold. Besides, to test the validity of the formalism, we have made explicit evaluation of the diagrams beyond FCA and confirm that such contributions are indeed negligible for the system considered in this work, at least for energies below the threshold (consistently with the findings of Ref. MartinezTorres:2010ax ). Details of these calculations are given in a subsequent section.
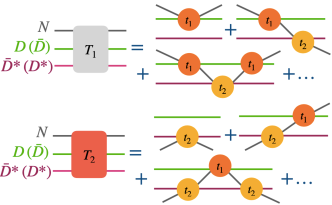
Continuing here with the discussions on the formalism, we can say that we need to study the and systems where () clusters either as or . Note that the interactions in the two kind of three-body systems are different. While one case involves a series of and interactions, the other consists of and interactions. Within the FCA to the Faddeev equations, the -matrix for the () system is obtained from the resummation of two series which consider the rescattering of the nucleon on () and (), as shown in Fig. 2. In this way,
| (3) |
where the partitions and are obtained by solving the coupled equations
| (4) |
for a given isospin and angular momentum of the three-body system. Since we consider s-wave interactions, the value of for the () system is given by the spin of the () subsystem. The and in Eq. (4) are two-body -matrices related to the () and () systems, respectively, and represents the propagator of a nucleon in the cluster formed. For total isospin of the () system, we treat and [ and ] as coupled channels, since both configurations can lead to isospin 1/2.
We must emphasize here that both and are interpreted as quasi-bound states with the same mass, although a different isospin and width Gamermann:2007fi ; Aceti:2014uea ; Gamermann:2009uq . Thus, FCA can be used to take into account transitions between the two systems as in the study of Xie:2010ig . In case a reader is interested in an analysis of the effects of considering FCA for coupled channels with the clusters having different masses, we refer the reader to Ref. Roca:2011br , where effective systems like, and have been studied.
In this way, , and are matrices in the coupled channel space,
| (9) | ||||
| (12) |
where for a given isospin
| (13) |
with , , and , being the two particles forming a cluster with a defined isospin. To see how the elements of Eq. (13) can be determined, let us consider, for example, the system. We can write,
| (14) |
Since () is related to the () interaction, to evaluate from Eq. (13) it is convenient to write Eq. (14) in terms of the isospin of the system, while to determine it is useful to express Eq. (14) in terms of the isospin of the system. For the former case, using Clebsch-Gordan coefficients, we get
| (15) |
and using now Eq. (13),
| (16) |
In Eq. (16), () corresponds to the two-body -matrix for the transition in isospin 0 (isospin 1). This process has been investigated within different models by solving the Bethe-Salpeter equation in a coupled channel approach (see, for example, Refs. Hofmann:2005sw ; Mizutani:2006vq ; GarciaRecio:2008dp ; Romanets:2012hm ; Liang:2014kra ). All studies point to a common finding: the , and coupled channel dynamics is attractive and gives rise to the formation of (). In Refs. Hofmann:2005sw ; Mizutani:2006vq , the pseudoscalar-nucleon interactions with charm are deduced from a Lagrangian based on the SU(4) symmetry. In Refs. GarciaRecio:2008dp ; Romanets:2012hm , by using a model based on the SU(8) spin-flavor symmetry, which is compatible with the heavy-quark symmetry, pseudoscalar-baryon as well as vector-baryon channels are considered as coupled systems and generation of several , and states is reported. In the latter references, is found to have large couplings to the as well as to the channel. The studies in Refs. GarciaRecio:2008dp ; Romanets:2012hm have been updated more recently in Ref. Nieves:2019nol for the sector and it is again concluded that has a predominant molecular nature. However, it is suggested that () should be viewed mostly as a dressed three-quark state. In Ref. Liang:2014kra , within a different formalism based on arguments of heavy-quark and SU(4) symmetries, the , and other coupled pseudoscalar-baryon channels and the , , and other coupled vector-baryon channels systems are studied. In this latter work, box diagrams are considered to construct a transition amplitude for the process . Several and states with and , including , are found. A large coupling of to and is also obtained as in Refs. GarciaRecio:2008dp ; Romanets:2012hm . In the present work, we have considered the models of Refs. GarciaRecio:2008dp ; Liang:2014kra , since in both cases the and channels are coupled, which is compatible with the heavy-quark symmetry. However, since the and states obtained in Refs. GarciaRecio:2008dp ; Liang:2014kra are not all same, and many of them have not been observed experimentally yet, when investigating the () system, we focus mainly on the energy region in which is generated, since all models find similar properties and attribute a molecular nature to it.
Coming back to the discussions on the three-body formalism, proceeding in a similar way as in Eq. (16), we can get the rest of the elements in Eq. (12), for which we need the two-body -matrices for the and systems in isospins 0 and 1. Within the SU(8) model of Refs. GarciaRecio:2008dp ; Romanets:2012hm , in Ref. Gamermann:2010zz the and coupled system has been studied and several and with and have been claimed to get generated with masses in the energy region MeV. But, so far, no clear experimental evidence on the existence of such states is available, although the existence of an anticharm baryon with mass around 3000 MeV was claimed in Ref. Aktas:2004qf . However, subsequent experimental investigations have failed to confirm the former finding Aubert:2006qu . Within the model of Ref. Mizutani:2006vq , where and are not considered as coupled channels, we do not find formation of any state since the interaction is repulsive for the charm sector. If we extend the model of Ref. Liang:2014kra to the charm sector, we find formation of a with a mass around 2950 MeV. Due to the different predictions within the models of Refs. Mizutani:2006vq ; Liang:2014kra ; Gamermann:2010zz , and the absence of conclusive experimental evidences in favor of the existence of any states with charm , we adopt the same strategy as in the charm sector. We thus consider and as coupled channels within the models of Refs. Gamermann:2010zz ; Liang:2014kra and restrict ourselves to an energy region in which the findings of the models, including the one of Ref. Mizutani:2006vq , are compatible. In this way, our predictions for three-body states would be consistent with different input two-body amplitudes.
Proceeding further with the discussion of the FCA, in Eq. (12), the propagator is given by Xie:2010ig
| (17) |
with being the mass of the cluster formed by (), [] represents the mass (energy) of the nucleon which rescatters off the components of the cluster and is the nucleon on-shell energy in the nucleon-cluster rest frame, i.e.,
| (18) |
where is the center-of-mass energy of the three-body system. The function in Eq. (17) is a form factor related to the wave function of the particles of the cluster and it is given by MartinezTorres:2020hus ; MartinezTorres:2010ax
| (19) |
where are the energies of the particles in the cluster and is a normalization factor, . The upper limit of the integration in Eq. (19) is related to the cut-off used when regularizing the two-body loops in the Bethe-Salpeter equation to generate or from the coupled channel interactions. We consider a value for MeV as in Refs. Aceti:2014uea ; Gamermann:2006nm ; Aceti:2012cb and vary it in a reasonable region to determine the uncertainties involved in the results. The unstable character of is implemented in the formalism by substituting in Eq. (19) (a width of 28 MeV is considered in this case). Note that the present in Eq. (17) is a normalization factor whose origin lies in the normalization of the fields when comparing the scattering matrix for a process in which a particle, in this case, a nucleon, rescatters off particles and of a cluster and the -matrix for an effective two-body particle-cluster scattering MartinezTorres:2020hus ; Ren:2018pcd . As a consequence of the normalization of those -matrices,
| (20) |
and a normalization factor needs to be included in the two-body -matrices and too,
| (21) | |||
| (22) |
With these ingredients we first solve Eq. (4) and determine the -matrix from Eq. (3) as a function of the center-of-mass energy for the and systems. We then construct the -matrix of Eq. (2) and search for peaks in , which are identified with three-body states generated from the coupled channel dynamics.
3 Results
3.1 Isospin 1/2
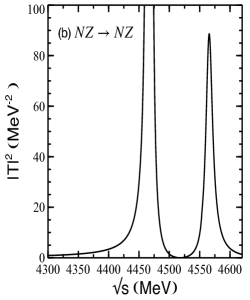
In Fig. 3 we show the for isospin and for the (a) and (b) transitions obtained by using the two-body amplitudes determined from the model based on the heavy-quark and SU(4) symmetries Liang:2014kra . As can be seen, the three-body dynamics generates two states at MeV and MeV, respectively, where and represent the mass and width found. The results shown in Fig. 3 correspond to a value of MeV in Eq. (19). We find that changing in a reasonable range, 700-770 MeV, produces small shifts in the masses of the states, MeV. Similar results are found if we determine the two-body amplitudes from the SU(8) Lagrangian of Ref. GarciaRecio:2008dp , with the corresponding peak positions being MeV and MeV. The results obtained from different two-body interactions and different cut-offs used in the form factor provide us with an estimate of the uncertainties present in the model.
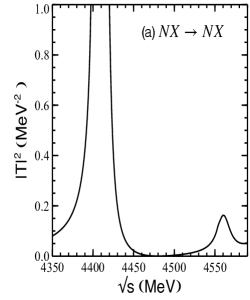
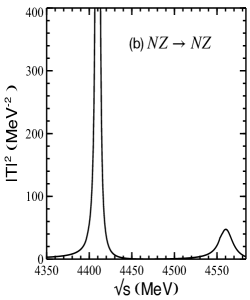
The states obtained correspond to ’s with hidden charm and are generated when the subsystem forms while clusters as or (see Fig. 4). In this sense, the corresponding wave functions would have an overlap with molecular components, besides .
The formation of states from the interaction of a and a has been suggested in Refs. Burns:2019iih ; Burns:2015dwa ; Geng:2017hxc . In particular, the possibility of interpreting the states observed in Refs. Aaij:2015tga ; Aaij:2016phn ; Aaij:2019vzc as molecules was discussed in the former works. In Ref. Burns:2015dwa , such a possibility was claimed based on an analogy between the mass difference of and , with being formed in the system, and the mass difference of and . In this way, according to Ref. Burns:2015dwa , the system could generate a bound state in analogy with formed in . In Ref. Geng:2017hxc , by using scale invariance and arguments of heavy quark symmetry, the potential was obtained by means of pion exchange. It was found that for , the attraction in the system is strong enough to generate bound states, pointing in this way to the existence of molecules, but no detailed calculation of the expected mass of such states was presented. Since the nominal mass of is close to the thresholds, the former could be a candidate for such a kind of molecular state. This suggestion was further considered in Ref. Burns:2019iih , where the potentials for the inelastic as well as for the elastic channels were obtained by using arguments of heavy quark symmetry in the former case, as in Ref. Geng:2017hxc , and the quark model in the latter. By varying the parameters of the model, the authors of Ref. Burns:2019iih find bound states with and , with the former having a larger mass than the latter. In view of the proximity of to the and thresholds, the parameters of the model were adjusted to set the mass of the state to the nominal mass of and the state found was identified with .
In our formalism, although the wave function of the states obtained have an overlap with , the dynamics considered is different to that studied in Refs. Burns:2019iih ; Geng:2017hxc . In our case, is generated from the interaction of , and other coupled channels, and are treated as clusters of the system. In this way, we explicitly consider the three-body dynamics involved in the system, instead of treating it as an effective two-body system. We also consider all the interactions in s-wave. We must mention that since the cut-offs present in the calculation of the input two-body -matrices, which are also used to set the value of in Eq. (19), are fixed to reproduce the properties of and , respectively, there are no parameters in our model which could produce a significant shift of the masses obtained for the states.
Considering only the formation of in the input two-body -matrices, no state is obtained with . However, meson-baryon interactions with charm are found to be attractive at higher energies as well, within different approaches, leading to generation of further states. For example, in Refs. GarciaRecio:2008dp ; Liang:2014kra a with and another with , both with molecular nature and masses in the energy region MeV, are found, although the masses and widths obtained within the two approaches do not coincide and no experimental evidence for these states has been found yet. Nevertheless, if we consider the generation of these ’s in the input two-body -matrices, three-body states with can be obtained. In Fig. 5 we show the modulus squared of the -matrix for the (a) and (b) transitions in isospin and determined following the model of Ref. Liang:2014kra . As can be seen, formation of two states, one at MeV and another at MeV, is found. In case of using the SU(8) model of Ref. GarciaRecio:2008dp for the two-body amplitudes, the corresponding peak positions are MeV and MeV.
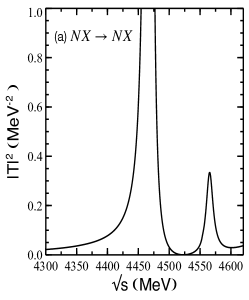
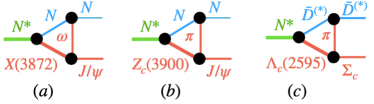
The states generated from the interactions, due to their three-body nature, can decay to three-body channels like and . Due to the formation of states in the subsystems when generating the states, decay channels like can also be useful to study the properties of these states. Note that two-body decay channels like , can also exist, involving in this case triangular loops (see Fig. 6). Although the strength of the signal in such two-body invariant masses might not be large enough for a clear detection of the states. Indeed, the invariant mass distribution reconstructed in Ref. Aaij:2019vzc shows fluctuations around 4400 MeV and 4550 MeV which could correspond to some of the states obtained in this work, and data with higher statistics would be necessary for confirming it. Interestingly, the state obtained at MeV is compatible with the mass and width of the claimed in Ref. Aaij:2019vzc .
Further, we would like to add that the available data on weak decay processes like Aaij:2019zkm and Aaij:2016wxd can be analyzed to investigate the states found in our work. In the former case, the invariant mass spectrum of has been reconstructed and it shows the signal of . The reconstruction of the invariant mass can be useful in finding the nucleon states predicted in our work. The reconstruction of the invariant mass spectrum of using data from Ref. Aaij:2016wxd can also show hidden charm states with positive parities. The states predicted in this work can also be studied at FAIR, in processes like , , , etc.
3.2 Isospin 3/2
So far we have restricted the discussions to the formation of ’s, where the dominant two-body interactions form well known resonances and different models agree on the description of such interactions. For example, there exists a general agreement on the strong coupling or association of the isospin 0 and 1 interactions with and , respectively Braaten:2003he ; AlFiky:2005jd ; Gamermann:2007fi ; Gamermann:2010zz ; Aceti:2014uea ; Ortega:2018cnm ; He:2017lhy . Similarly the isoscalar interaction is known to be attractive in nature, leading to the formation of in various models Hofmann:2005sw ; Mizutani:2006vq ; GarciaRecio:2008dp ; Romanets:2012hm ; Liang:2014kra ; Nieves:2019nol . There exists enough experimental data to define the properties of , and . The reliability of the description of the isovector interaction within different models, however, is difficult to judge at this moment since states are not yet well known experimentally. For example, only three states are listed in Ref. pdg by the Particle Data Group, out of which the quantum numbers of only two are known. Additionally, different theoretical models predict a different spectra. For example, as mentioned earlier, we have considered the theoretical works of Refs. GarciaRecio:2008dp ; Liang:2014kra to describe the interactions. In the former work, relatively narrow ’s with were found with mass around 2600 MeV (which is within the range of invariant masses considered in our study). Such states have not been observed experimentally yet. In Ref. Liang:2014kra , the isospin one and coupled channel interactions are found to be attractive, but only a very broad state (width MeV) is obtained around 2600 MeV. Still, it can be worth exploring the formation of three-body states with isospin 3/2, which requires all the two-body subsystems to interact in isospin 1. Such states will be like ’s with hidden charm, which must also, presumably, exist in nature.
In Fig. 7, we show the isospin 3/2 three-body modulus squared amplitude for total spin 1/2. The amplitude depicted in Fig. 7 is computed with the interactions which give rise to formation of some ’s in the energy region around MeV GarciaRecio:2008dp .
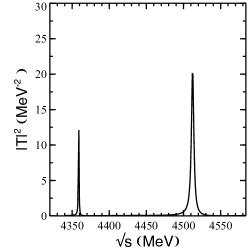
It can be seen that two states arise from the interactions, one with mass around 4359 MeV and a width of about 1.5 MeV, another around 4512 MeV and width 4 MeV. Similar results are obtained for total spin 3/2. We thus find almost spin degenerate states, which we denote as .
We must add that within the model of Ref. Liang:2014kra , no such isospin 3/2 states are found. Thus, the existence of the ’s shown in Fig. 7 is conditioned to the existence of narrow negative-parity state(s) with mass similar to .
4 Contributions from diagrams beyond the fixed center approximation
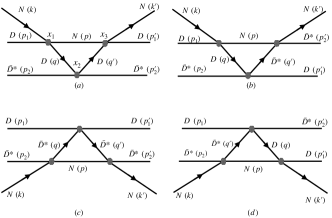
Before ending the discussions, we would like to analyze the uncertainties involved in our findings from additional diagrams beyond those involved in the FCA. In the current study, we consider that and form a cluster which stays unperturbed during the scattering. The meaning of such a consideration is that the third hadrons scatters off the constituents of the cluster which act like static sources. Within such an approximation, at the level of one loop, the diagrams besides those shown in Fig. 8 are considered to be suppressed.
In the present case, where the mass of the nucleon is about half of the mass of /, one might wonder if the additional diagrams shown in Fig. 9 can be neglected and if the fixed center approximation is appropriate for the current system. To test the applicability of the approximation, we make explicit calculations of the diagrams in Fig. 9 in this section and show that the resulting contributions turn out to be negligible. We also discuss the reason behind such findings.
Before going to the details of the calculations, we would like to remind the reader that the fixed center or the static approximation has been applied to studies of anti-kaon deuteron scattering in Refs. Kamalov:2000iy ; Chand:1962ec , where the kaon is about half as heavy as the nucleon. Still, results on the scattering length were obtained in good agreement with the experimental data. Indeed contributions from recoil effects were scrutinized in detail in Ref. Baru:2009tx by considering a perturbative expansion in terms of the ratio of the masses and corrections of the order of 10-15 were found. Such a small correction was attributed to cancellations among different terms in the perturbative series. The mentioned cancellations were attributed, in Ref.Baru:2009tx , to the Pauli principle, or to the orthogonality of the deuteron wave function and the continuum, depending on the isospin of the interactions. Similar conclusions were obtained in a later study in Ref. Mai:2014uma too. It should be mentioned that besides the anti-kaon deuteron case, cancellations have been found in the case of the scattering too Faldt:1974sm , where even though the static approximation may be expected to work well, corrections (from binding energy) turn out to be large when considering each term of the scattering series separately. However, corrections to the different terms end up canceling with each other when the series is summed Faldt:1974sm , rendering the FCA applicable to the system. Interestingly, validity of the FCA was also discussed in Ref. MartinezTorres:2010ax in case of the system. It was found that the FCA amplitude is not reliable in the former case, as expected, except for energies below the cluster-particle threshold, thereby limiting the prospects of the excitation of the constituents of the cluster. Thus, the static approximation has been found to work in a series of unexpected systems due to different reasons.
It might also be useful to cite examples of some three-hadron systems which have been studied by solving the Faddeev equations with and without the consideration of the static approximation for one of the subsystems. For example, the system and coupled channels were studied in Refs. MartinezTorres:2008kh ; MartinezTorres:2010zv by solving the Faddeev equations without invoking the static approximation for any of the pairs. In this case a state, with mass around 1924 MeV, was found with the width ranging between 20-30 MeV. Similar results have been reported in Ref. Jia:2011zzd , where Faddeev equations were solved using an effective potential for each of the pairs. A state with a mass around MeV is obtained in the former work. Further, the same system was studied by treating and as fixed scattering centers in Ref. Xie:2010ig and results compatible with those of Refs. MartinezTorres:2008kh ; MartinezTorres:2010zv ; Jia:2011zzd (mass MeV, width MeV) were found. As shown in Ref. MartinezTorres:2010ax , the condition in which FCA seems to works well is when a three-body system is studied at energies below the threshold, besides having a two-body cluster which is heavier than the third one. Yet another system, , was studied by solving full Faddeev equations MartinezTorres:2012jr as well as by introducing the FCA Debastiani:2017vhv . A -meson with spin parity , mass around 2900 MeV and with of 55 MeV was found to arise from the three-body interactions in Ref. MartinezTorres:2012jr , whose decay to two mesons has been studied in Ref. Malabarba:2021gyq . Indeed a state with same quantum numbers was found in Ref. Debastiani:2017vhv but with the values of mass (and, consequently, width) about 50 MeV lower than those determined with full Faddeev calculations MartinezTorres:2012jr . However, it must be mentioned that the state found in Ref. MartinezTorres:2012jr appeared in the configuration, while a clear signal was not found in the arrangement of the three-body system. The latter is precisely the configuration studied in Ref. Debastiani:2017vhv in order to use the FCA (although the authors of Ref. Debastiani:2017vhv arrive to the conclusion that is the dominant configuration). From the above discussion one can see that, as far as the energy region studied is below the three-body threshold, the order of uncertainties in the results obtained by using FCA is similar to that found within other methods for solving the Faddeev equations where no static approximations are considered.
Let us now discuss the case of the system by evaluating the amplitudes for the diagrams shown in Fig. 9, where the and can propagate as free particles in the loop. Following the same normalization as in Ref. MartinezTorres:2010ax , we can write the contribution to the matrix, to start with, for the diagram in Fig. 9a as
| (23) |
where represent the wave functions of the particles of the cluster in the initial/final state. We refer the reader to Fig. 9a to identify the momenta assigned to each particle. The invariant mass of the system, in Eq. (23), depends on a loop variable through
| (24) |
Integrating on the zero component of the six variables in Eq. (23) and defining
| (25) | |||
we can write
| (26) |
Such change of variables allows us to write
| (27) |
and
| (28) |
where denotes the momentum of the cluster in the initial (final) state. Finally, integrating on , and we get
| (29) |
where represents the total four momentum of the three body system in the initial (final) state and , are calculated following Ref. Gamermann:2009uq . It must be emphasized here that the different two-body amplitudes get contributions from different isospin with different weights (as explained in section 2). Following the same procedure, we can obtain the amplitudes for the remaining diagrams in Fig. 9 as
| (30) |
and
| (31) | |||
| (32) |
Let us call the amplitude of the diagrams shown in Fig. 8, which contribute to the FCA series [Eqs. (4)], as and . To study the effect of the considerations of the diagrams in Fig. 9, which go beyond the FCA, we show in Fig. 10 the ratio
| (33) |

It can be seen that the ratio stays very close to unity, showing that the contribution from the diagrams beyond the FCA provide a very small correction, and, hence, indicating the approximation to be indeed reliable in the present case.
To understand the reason behind such a small correction, we compare the different amplitudes in Fig. 11. Firstly, it can be noticed that the sum of the amplitudes of the one-loop diagrams in the FCA series (see the real and imaginary parts represented as solid and dashed lines in Fig. 11) is much bigger than the amplitudes corresponding to the diagrams beyond the static approximation (see the caption of Fig. 11 for more details).
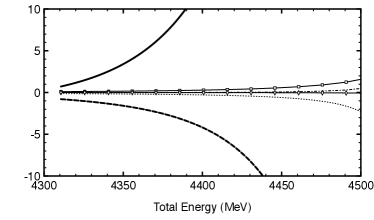
It should be mentioned that the limits on the vertical axis, in Fig. 11, have been kept as shown in the figure to facilitate a comparison of the different amplitudes. Besides the small contributions from the diagrams in Fig. 9, to which we will come back in a moment, it should be noticed that the sum of the amplitudes and have opposite signs, leading to cancellations among the two. The real part of is shown as a dotted line, which should be compared with the real part of , shown as a line with boxes. The imaginary parts of and are shown as a dash-dotted line and a line with diamonds, respectively. The imaginary parts are much smaller, which should be expected at energies below the threshold, though nonzero since there exist lighter (and, hence, open) coupled channels in the two-body subsystems. For example, and are open below the threshold. In any case, we can question why the amplitudes for the diagrams in Fig. 9 turn out to be much smaller. To understand this one must recall that: (1) We have more number of heavier particles (/) propagating in the intermediate state in Fig. 9, when compared to the diagrams shown in Fig. 8. (2) The energies of interest, where we find the states, are below the three-body threshold, where the contributions from the excitation of the particles in the cluster are expected to be small (as found in Ref. MartinezTorres:2010ax ). Finally, we add that the opposite signs in the amplitudes shown in Fig. 11 arise from the dynamics involved in the different subsystems.
From the discussions made in this section, we can conclude that for the present system contributions from diagrams beyond those summed in the FCA series are negligible. Hence, we can conclude that the results obtained in the present work do not get significant corrections from the diagrams beyond FCA.
5 Conclusions
In this work we have investigated the formation of states as a consequence of the dynamics involved in the system. To do this, we solve the Faddeev equations treating the open charm mesons as a cluster. We find that the generation of in the system together with the clustering of () and () as or produces enough attraction to form isospin , states with masses in the energy region MeV and positive parity as summarized in Table 1, where the uncertainties are related to different models considered when determining the two-body interactions. The certainty of the results on isospin 3/2 states depends on the strength of the isovector interactions, which are not well known yet.
| Isospin | Spin-parity | Mass (MeV) | Width (MeV) |
|---|---|---|---|
| 2 | |||
| , | |||
In this way, we can conclude that and states with hidden charm and positive parity arise from three-hadron dynamics. We have discussed that data from decays are available on final states which can confirm the existence of such positive-parity states.
6 Acknowledgements
This work is supported by the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP), processos n∘ 2019/17149-3, 2019/16924-3 and 2020/00676-8, and by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), grant n∘ 305526/2019-7 and 303945/2019-2.
References
- [1] Roel Aaij et al. Observation of Resonances Consistent with Pentaquark States in Decays. Phys. Rev. Lett., 115:072001, 2015.
- [2] Roel Aaij et al. Model-independent evidence for contributions to decays. Phys. Rev. Lett., 117(8):082002, 2016.
- [3] Roel Aaij et al. Observation of a narrow pentaquark state, , and of two-peak structure of the . Phys. Rev. Lett., 122(22):222001, 2019.
- [4] M. Battaglieri et al. Search for pentaquark in high statistics measurement of at CLAS. Phys. Rev. Lett., 96:042001, 2006.
- [5] K. Miwa et al. Search for via reaction near production threshold. Phys. Lett., B635:72–79, 2006.
- [6] M. Moritsu et al. High-resolution search for the pentaquark via a pion-induced reaction at J-PARC. Phys. Rev., C90(3):035205, 2014.
- [7] C. P. Shen et al. First observation of and search for exotic baryons in systems. Phys. Rev., D93(11):112017, 2016.
- [8] A. Martinez Torres and E. Oset. Study of the reaction and an alternative explanation for the ’ pentaquark’ peak. Phys. Rev., C81:055202, 2010.
- [9] A. Martinez Torres and E. Oset. A novel interpretation of the ’ pentaquark’ peak. Phys. Rev. Lett., 105:092001, 2010.
- [10] M. Wang. “recent results on exotic hadrons at lhcb,” (2020), presented on behalf of the lhcb collaboration at implications workshop 2020.
- [11] L. Maiani, A. D. Polosa, and V. Riquer. The New Pentaquarks in the Diquark Model. Phys. Lett., B749:289–291, 2015.
- [12] Richard F. Lebed. The Pentaquark Candidates in the Dynamical Diquark Picture. Phys. Lett., B749:454–457, 2015.
- [13] R. Ghosh, A. Bhattacharya, and B. Chakrabarti. A study on P (4380) and P in the quasi particle diquark model. 2015. [Phys. Part. Nucl. Lett.14,no.4,550(2017)].
- [14] Xin-Zhen Weng, Xiao-Lin Chen, Wei-Zhen Deng, and Shi-Lin Zhu. Hidden-charm pentaquarks and states. Phys. Rev., D100(1):016014, 2019.
- [15] Zhi-Gang Wang. Analysis of the , , and related hidden-charm pentaquark states with QCD sum rules. Int. J. Mod. Phys., A35(01):2050003, 2020.
- [16] L. Roca, J. Nieves, and E. Oset. LHCb pentaquark as a molecular state. Phys. Rev., D92(9):094003, 2015.
- [17] C. W. Xiao, J. Nieves, and E. Oset. Heavy quark spin symmetric molecular states from and other coupled channels in the light of the recent LHCb pentaquarks. Phys. Rev., D100(1):014021, 2019.
- [18] Ming-Zhu Liu, Ya-Wen Pan, Fang-Zheng Peng, Mario Sánchez Sánchez, Li-Sheng Geng, Atsushi Hosaka, and Manuel Pavon Valderrama. Emergence of a complete heavy-quark spin symmetry multiplet: seven molecular pentaquarks in light of the latest LHCb analysis. Phys. Rev. Lett., 122(24):242001, 2019.
- [19] T. J. Burns and E. S. Swanson. Molecular interpretation of the (4440) and (4457) states. Phys. Rev., D100(11):114033, 2019.
- [20] Jun He. Study of , , and in a quasipotential Bethe-Salpeter equation approach. Eur. Phys. J., C79(5):393, 2019.
- [21] Cheng-Jian Xiao, Yin Huang, Yu-Bing Dong, Li-Sheng Geng, and Dian-Yong Chen. Exploring the molecular scenario of Pc(4312) , Pc(4440) , and Pc(4457). Phys. Rev., D100(1):014022, 2019.
- [22] Zhi-Hui Guo and J. A. Oller. Anatomy of the newly observed hidden-charm pentaquark states: , and . Phys. Lett., B793:144–149, 2019.
- [23] Meng-Lin Du, Vadim Baru, Feng-Kun Guo, Christoph Hanhart, Ulf-G Meißner, José A. Oller, and Qian Wang. Interpretation of the LHCb States as Hadronic Molecules and Hints of a Narrow . Phys. Rev. Lett., 124(7):072001, 2020.
- [24] Hao Xu, Qiang Li, Chao-Hsi Chang, and Guo-Li Wang. Recently observed as molecular states and possible mixture of . Phys. Rev., D101(5):054037, 2020.
- [25] Feng-Kun Guo, Ulf-G. Meißner, Wei Wang, and Zhi Yang. How to reveal the exotic nature of the Pc(4450). Phys. Rev., D92(7):071502, 2015.
- [26] Xiao-Hai Liu, Qian Wang, and Qiang Zhao. Understanding the newly observed heavy pentaquark candidates. Phys. Lett., B757:231–236, 2016.
- [27] Satoshi X. Nakamura. , , and as double triangle cusps. 2021.
- [28] C. Fernández-Ramírez, A. Pilloni, M. Albaladejo, A. Jackura, V. Mathieu, M. Mikhasenko, J. A. Silva-Castro, and A. P. Szczepaniak. Interpretation of the LHCb (4312)+ Signal. Phys. Rev. Lett., 123(9):092001, 2019.
- [29] Eric Braaten and Masaoki Kusunoki. Low-energy universality and the new charmonium resonance at 3870-MeV. Phys. Rev., D69:074005, 2004.
- [30] Mohammad T. AlFiky, Fabrizio Gabbiani, and Alexey A. Petrov. X(3872): Hadronic molecules in effective field theory. Phys. Lett., B640:238–245, 2006.
- [31] D. Gamermann and E. Oset. Axial resonances in the open and hidden charm sectors. Eur. Phys. J., A33:119–131, 2007.
- [32] D. Gamermann, C. Garcia-Recio, J. Nieves, L. L. Salcedo, and L. Tolos. Exotic dynamically generated baryons with negative charm quantum number. Phys. Rev., D81:094016, 2010.
- [33] F. Aceti, M. Bayar, E. Oset, A. Martinez Torres, K. P. Khemchandani, Jorgivan Morais Dias, F. S. Navarra, and M. Nielsen. Prediction of an state and relationship to the claimed , . Phys. Rev., D90(1):016003, 2014.
- [34] Pablo G. Ortega, Jorge Segovia, David R. Entem, and Francisco Fernández. The structures in a coupled-channels model. Eur. Phys. J., C79(1):78, 2019.
- [35] Jun He and Dian-Yong Chen. as a virtual state from interaction. Eur. Phys. J., C78(2):94, 2018.
- [36] J. Hofmann and M. F. M. Lutz. Coupled-channel study of crypto-exotic baryons with charm. Nucl. Phys., A763:90–139, 2005.
- [37] T. Mizutani and A. Ramos. D mesons in nuclear matter: A DN coupled-channel equations approach. Phys. Rev., C74:065201, 2006.
- [38] C. Garcia-Recio, V. K. Magas, T. Mizutani, J. Nieves, A. Ramos, L. L. Salcedo, and L. Tolos. The s-wave charmed baryon resonances from a coupled-channel approach with heavy quark symmetry. Phys. Rev., D79:054004, 2009.
- [39] O. Romanets, L. Tolos, C. Garcia-Recio, J. Nieves, L. L. Salcedo, and R. G. E. Timmermans. Charmed and strange baryon resonances with heavy-quark spin symmetry. Phys. Rev., D85:114032, 2012.
- [40] W. H. Liang, T. Uchino, C. W. Xiao, and E. Oset. Baryon states with open charm in the extended local hidden gauge approach. Eur. Phys. J., A51(2):16, 2015.
- [41] Juan Nieves and Rafael Pavao. Nature of the lowest-lying odd parity charmed baryon and resonances. Phys. Rev., D101(1):014018, 2020.
- [42] Leslie L. Foldy. The Multiple Scattering of Waves. 1. General Theory of Isotropic Scattering by Randomly Distributed Scatterers. Phys. Rev., 67:107–119, 1945.
- [43] K. A. Brueckner. Multiple Scattering Corrections to the Impulse Approximation in the Two-Body System. Phys. Rev., 89:834–838, 1953.
- [44] A. Deloff. Eta d and K- d zero energy scattering: A Faddeev approach. Phys. Rev., C61:024004, 2000.
- [45] A. Martinez Torres, K. P. Khemchandani, L. Roca, and E. Oset. Few-body systems consisting of mesons. Few Body Syst., 61(4):35, 2020.
- [46] A. Martinez Torres, E. J. Garzon, E. Oset, and L. R. Dai. Limits to the Fixed Center Approximation to Faddeev equations: the case of the . Phys. Rev., D83:116002, 2011.
- [47] D. Gamermann, J. Nieves, E. Oset, and E. Ruiz Arriola. Couplings in coupled channels versus wave functions: application to the X(3872) resonance. Phys. Rev., D81:014029, 2010.
- [48] Ju-Jun Xie, A. Martinez Torres, and E. Oset. Faddeev fixed center approximation to the system and the signature of a state. Phys. Rev., C83:065207, 2011.
- [49] L. Roca. Pseudotensor mesons as three-body resonances. Phys. Rev. D, 84:094006, 2011.
- [50] A. Aktas et al. Evidence for a narrow anti-charmed baryon state. Phys. Lett., B588:17, 2004.
- [51] Bernard Aubert et al. Search for the charmed pentaquark candidate Theta(c)(3100)0 in e+ e- annihilations at s**(1/2) = 10.58-GeV. Phys. Rev., D73:091101, 2006.
- [52] D. Gamermann, E. Oset, D. Strottman, and M. J. Vicente Vacas. Dynamically generated open and hidden charm meson systems. Phys. Rev., D76:074016, 2007.
- [53] F. Aceti, R. Molina, and E. Oset. The decay in the molecular picture. Phys. Rev., D86:113007, 2012.
- [54] Xiu-Lei Ren, Brenda B. Malabarba, Li-Sheng Geng, K. P. Khemchandani, and A. Martínez Torres. mesons with hidden charm arising from and dynamics. Phys. Lett., B785:112–117, 2018.
- [55] T. J. Burns. Phenomenology of Pc(4380)+, Pc(4450)+ and related states. Eur. Phys. J., A51(11):152, 2015.
- [56] Lisheng Geng, Junxu Lu, and Manuel Pavon Valderrama. Scale Invariance in Heavy Hadron Molecules. Phys. Rev., D97(9):094036, 2018.
- [57] Roel Aaij et al. Observation of the decay. JHEP, 09:028, 2019.
- [58] Roel Aaij et al. Observation of and decays and a measurement of the baryon mass. JHEP, 05:132, 2016.
- [59] P. A. Zyla et al. Review of Particle Physics. PTEP, 2020(8):083C01, 2020.
- [60] S. S. Kamalov, E. Oset, and A. Ramos. Chiral unitary approach to the K- deuteron scattering length. Nucl. Phys. A, 690:494–508, 2001.
- [61] R. Chand and R. H. Dalitz. Charge-independence in K- -deuterium capture reactions. Annals Phys., 20:1–19, 1962.
- [62] V. Baru, E. Epelbaum, and A. Rusetsky. The Role of nucleon recoil in low-energy antikaon-deuteron scattering. Eur. Phys. J. A, 42:111–120, 2009.
- [63] Maxim Mai, Vadim Baru, Evgeny Epelbaum, and Akaki Rusetsky. Recoil corrections in antikaon-deuteron scattering. Phys. Rev. D, 91(5):054016, 2015.
- [64] Goran Faldt. Binding Corrections and the Pion - Deuteron Scattering Length. Phys. Scripta, 16:81–86, 1977.
- [65] A. Martinez Torres, K. P. Khemchandani, and E. Oset. Solution to Faddeev equations with two-body experimental amplitudes as input and application to J**P = 1/2+, S = 0 baryon resonances. Phys. Rev. C, 79:065207, 2009.
- [66] A. Martinez Torres and D. Jido. configuration of the system. Phys. Rev. C, 82:038202, 2010.
- [67] Er-Wei Jia and Hou-Rong Pang. K anti-K N and anti-K anti-K N molecular states with I = 1/2, 3/2 and J**P = 1/2+ studied with three-body Faddeev calculations. Chin. Phys. Lett., 28:061401, 2011.
- [68] A. Martinez Torres, K. P. Khemchandani, M. Nielsen, and F. S. Navarra. Predicting the Existence of a 2.9 GeV Molecular State. Phys. Rev. D, 87(3):034025, 2013.
- [69] V. R. Debastiani, J. M. Dias, and E. Oset. Study of the and systems. Phys. Rev. D, 96(1):016014, 2017.
- [70] Brenda B. Malabarba, K. P. Khemchandani, and A. Martinez Torres. Decay processes of a pseudoscalar D(2900). Phys. Rev. D, 104(11):116002, 2021.
- [71] R Aaij et al. Study of meson decays to , and final states in pp collision. JHEP, 09:145, 2013.