Non-Abelian nonsymmorphic chiral symmetries

The quantum Hall Cage et al. (2012) and quantum anomalous Hall Haldane (1988); Chang et al. (2013) effects represent the earliest examples of topological phases of matter. However, such phases with robust chiral edge modes are only realizable under stringent conditions, like a strong breaking of time-reversal symmetry, either though external magnetic fields or suitable intrinsic magnetic order. The topological landscape changed completely with the advent of topological insulators Hasan and Kane (2010); Qi and Zhang (2011). A key insight from the early studies was how time-reversal symmetry could protect new forms of nontrivial topology and this greatly enlarges the physical setups in which topological phases could emerge. Along with the particle-hole and chiral symmetries, the time-reversal symmetry represents one of the three internal symmetries relevant for the classification of topological phases, and general classification results were soon obtained under the ten-fold way Kitaev (2009); Chiu et al. (2016). The classification was then further refined in the presence of symmorphic  Fu (2011); Hsieh et al. (2012); Tanaka et al. (2012); Dziawa et al. (2012); Ando and Fu (2015) and nonsymmorphic Fang and Fu (2015); Liu et al. (2014); Shiozaki et al. (2015); Parameswaran et al. (2013); Varjas et al. (2015); Shiozaki et al. (2016); Liang et al. (2017); Chang et al. (2017); Ma et al. (2017); Schoop et al. (2016, 2018); Wieder et al. (2016, 2018); Wang et al. (2016); Armitage et al. (2018) spatial symmetries. Such successive extension of the symmetry setting has led to a comprehensive understanding of the diverse set of phases protected by the 230 spatial symmetry groups Kruthoff et al. (2017); Po et al. (2017); Bradlyn et al. (2017); Zhang et al. (2019); Vergniory et al. (2019); Tang et al. (2019), and the results were further extended to magnetic materials Watanabe et al. (2018); Elcoro et al. (2021); Xu et al. (2020) in which time-reversal can also combine nontrivially with partial translation into a symmetry of the magnetic order.

Exhaustive as it may seem, the systematic treatment of (magnetic) spatial symmetries has thus far focused on symmetries that are relevant to electronic materials. Engineered physical platforms Aidelsburger et al. (2018), like cold-atomic, photonic, and acoustic systems, could inherently feature synthetic symmetries that would have been unnatural or fine-tuned for electronic problems El-Ganainy et al. (2018); Peng et al. (2016); Miri et al. (2013); Zhao et al. (2020); Li et al. (2014); Xue et al. (2022); Arkinstall et al. (2017); Kremer et al. (2020). Here we show that a non-Abelian Hofstadter model with ${\rm SU}(2)$ gauge fields, potentially realizable in engineered systems, calls for a further extension of symmetry analysis. A key new ingredient is the coexistence of multiple nonsymmorphic chiral symmetries, which combine site-dependent, local phase factors with fractional translation. As the nonsymmorphic chiral symmetry is not generally respected in electronic materials, it is not included as part of the comprehensive (magnetic) space-group symmetry analysis on electronic topological band theory. Yet its presence has been recognized in the study of specific models, including a minimal two-band model for nonsymmorphic topological crystalline insulators Shiozaki et al. (2015), certain antiferromagnetic semimetals Brzezicki and Cuoco (2017), the low-energy states in the SnTe material class Brzezicki et al. (2019), and, as a theoretical construction via the square-root operation from parent Hamiltonians Arkinstall et al. (2017). So far, efforts have been mostly dedicated to systems that obey a single nonsymmorphic chiral symmetry.

In this work, we show multiple coexisting nonsymmorphic chiral symmetries could be non-Abelian, lead to intriguing symmetry algebras, and, consequently, protect unusual band degeneracy and topology, as illustrated in the non-Abelian Hofstadter model. More concretely, we analyze the associated algebras of the multiple nonsymmorphic chiral symmetries and reveal their dependence on the parity of the two non-Abelian gauge fields that are assumed rational. In particular, when both of the rational gauge fields have even denominators, and one and only one of the denominators is an integer multiple of four, their algebra becomes non-Abelian and gives rise to generic Kramer quartets, i.e. four-fold degeneracy at all momenta, which are jointly protected by inversion and time-reversal. The nonsymmorphic chiral symmetries turn the magnetic Brillouin torus into a real projective plane, and therein protect double Dirac semimetals at half filling. For relatively small systems relevant to engineered physical platforms, we further show that the semimetals get gapped and become an insulator upon the introduction of a boundary, which necessarily breaks some of the nonsymmorphic chiral symmetries. The resulting insulator can be tuned to be either trivial or topological, depending on the parity of the system size.

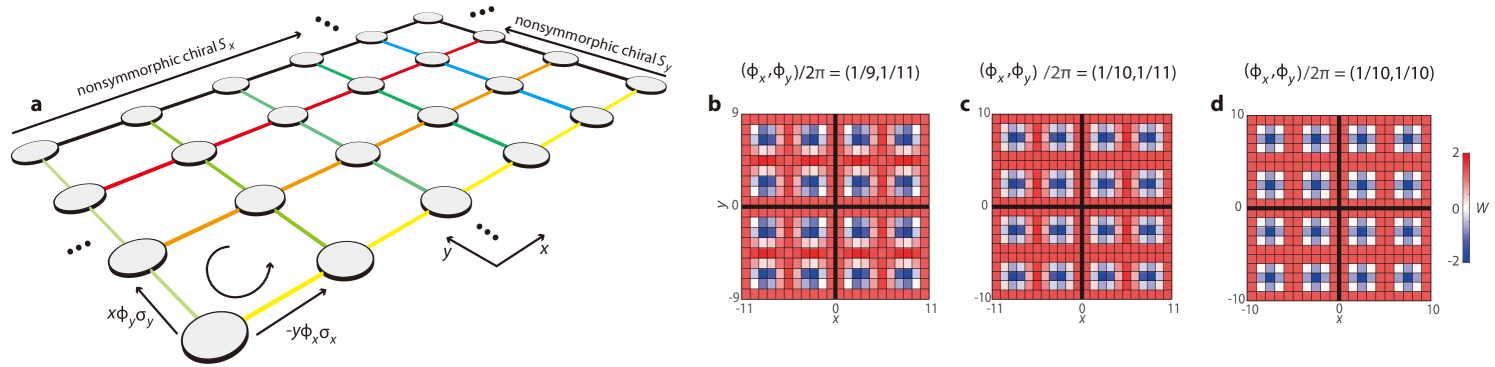
Non-Abelian Hofstadter problem. A less-known fact about the well-known Abelian Hofstadter model, featuring U(1) gauge fields, is that it obeys chiral symmetries that are nonsymmorphic (see Sec. LABEL:sec:abelian). Nevertheless, its nonsymmorphic chiral operators can always be transformed into a local basis and their algebra is always trivial (see Sec. LABEL:sec:abelian), which relates to the equivalence between its formulations in the Landau and the symmetric gauges. However, these conditions can get modified in non-Abelian Hofstadter models Yang et al. (2020). Let us consider a Hofstader–Harper-like, SU(2) gauge fields

The associated Hamiltonian $H(\phi_{x}/2\pi,\phi_{y}/2\pi)$ on a square lattice is given by

Here $t_{x}$ and $t_{y}$ are the real hopping terms in the $x$ and $y$ directions and we restrict ourselves to $t_{x}=t_{y}=t$. $c_{x,y}$ and $c^{\dagger}_{x,y}$ are the annihilation and creation operators at site $(x,y)$. $\phi_{x}$ and $\phi_{y}$ are the SU(2) Peierls phases. The Hamiltonian has a spin-rotation symmetry and stays invariant for arbitrary choices of distinct Pauli matrices in Eq. (1). If $\phi_{x}$ and $\phi_{y}$ are both rational, i.e. they can be written as $\phi_{x}=2\pi p_{x}/q_{x}$ and $\phi_{y}=2\pi p_{y}/q_{y}$ for integers $p_{x}$, $q_{x}$, $p_{y}$, and $q_{y}$. The Hamiltonian can be solved in the $q_{y}\times q_{x}$ super-cell with the magnetic Brillouin zone (MBZ) defined as $k_{x}\in[0,2\pi/q_{y})$ and $k_{y}\in[0,2\pi/q_{x})$.

This model is reminiscent of but distinct from the symmetric-gauge, Abelian Hofstadter problem. Evidently, $H$ reduces to two decoupled Abelian counterparts with opposite homogeneous magnetic fluxes when either $\phi_{x}$ or $\phi_{y}$ vanishes. In contrast, under gauge fields that meet the genuine non-Abelian condition Yang et al. (2020), the associated magnetic fields become spatially inhomogeneous, as characterized by the real-space Wilson loop $W=\mathrm{Tr}\exp\left(\mathrm{i}\oint\boldsymbol{A}\mathop{}\mathrm{d}{l}\right)$ (see Fig. 1).

Symmetry algebra. For $\left\{\mu,\nu\right\}=\left\{x,y\right\}$, a chiral symmetry $S_{\mu}$ appears when $q_{\nu}\in 2\mathbb{Z}$. Its explicit form is given by

where $\mathbf{r}=(x,y)$ and $\sigma_{0}$ operates on the spin degree of freedom. This chiral operator contains site-dependent phase factors and a half translation along a single dimension in the magnetic unit cell (see Fig. 2a and b), satisfies $S_{\mu}^{2}(\mathbf{k})=\exp(\mathrm{i}k_{\mu}q_{\nu})$ that restores a full translation, and thus is an order-two nonsymmorphic symmetry with $d_{\parallel}=0$ Shiozaki et al. (2016) for the associated Bloch Hamiltonian.

If $\left(q_{x}\in 2\mathbb{Z},q_{y}\in 2\mathbb{Z}\right)$, multiple chiral symmetries appear. First, two nonsymmorphic chiral operators $S_{x}$ and $S_{y}$ emerge because we can apply Eq. (3) to both $x$ and $y$ directions (see Fig. 2a and b). It is noted that they have no counterparts in the Landau-gauge non-Abelian Hofstadter model Yang et al. (2020), where gauge fields are arranged along a single spatial dimension. Second, because the magnetic unit cell becomes bipartite under the same condition, the conventional local chiral symmetry $S_{0}$ exists:

After we quotient away the translational part in $S_{x}$ and $S_{y}$, $\mathbf{S}\equiv\left\{S_{0},S_{x},S_{y}\right\}$ becomes the generator of a finite unitary group $\mathbf{G}$. There always exists a proper index-2 subgroup $\mathbf{U}\subset\mathbf{G}$ such that $\mathbf{U}$ only contains unitary symmetries of the hamiltonian, i.e. $\mathbf{U}\equiv S_{\mu}S_{\nu}$. $\mathbf{U}$ contains symmetries that are reminiscent of the projective translational symmetry Zhao et al. (2020), which are shown to protect doubly-degenerate bands and Dirac points at single momenta Zhao et al. (2020), as recently demonstrated in acoustic lattices Li et al. (2022); Xue et al. (2022).

The parity of the gauge field, in particular the denominators, strongly affects the symmetry algebra and thereby the classification of this non-Abelian model (see Table 1), even in the continuum limit with weak fields (i.e. $\phi_{x},\phi_{y}\to 0$). If $\left(q_{x}\in 2\mathbb{Z}+1,q_{y}\in 2\mathbb{Z}+1\right)$, no other internal symmetry beside time reversal $T_{0}=\mathrm{i}\sigma_{y}K$ exists, $\mathbf{U}$ is empty, and $H$ belongs to class AII in Table 1. If $\left(q_{\mu}=2\mathbb{Z}+1,q_{\nu}=2\mathbb{Z}\right)$, a nonsymmorphic chiral symmetry $S_{\mu}$ exists. Although $T_{0}^{2}=-1$ and $S_{\mu}^{2}=1$ are ensured, the square of their associated nonsymmorphic particle-hole symmetry $C_{\mu}=T_{0}^{-1}S_{\mu}$ is uncertain—$C_{\mu}^{2}=1$ if $q_{\nu}=4\mathbb{Z}+2$ and $C_{\mu}^{2}=-1$ if $q_{\nu}=4\mathbb{Z}$, which corresponds to class DIII and CII in Table 1, respectively. For both of the DIII and CII classes, $\mathbf{G}=\{S_{\mu},1\}$ is $\mathbb{Z}_{2}$ and $\mathbf{U}=\{1\}$ is the trivial group $\mathbb{Z}_{1}$.

Richer symmetry algebra appears for $\left(q_{x}\in 2\mathbb{Z},q_{y}\in 2\mathbb{Z}\right)$. In this case, $T_{0}$ and $S_{0}$ enable a local particle-hole symmetry $C_{0}=T_{0}^{-1}S_{0}$ that satisfies $C_{0}^{2}=-1$. Although $\commutator{S_{x}}{S_{y}}=0$ is ensured, $S_{0}$ and $S_{\mu}$ may commute or anticommute. Specifically, $\commutator{S_{0}}{S_{\mu}}=0$ when $q_{\nu}=4\mathbb{Z}$ and $\anticommutator{S_{0}}{S_{\mu}}=0$ when $q_{\nu}=4\mathbb{Z}+2$. There are three resulting scenarios. First, when $\left(q_{x}\in 4\mathbb{Z},q_{y}\in 4\mathbb{Z}\right)$, $\mathbf{S}$ is an Abelian generator. $\mathbf{G}$ is an elementary Abelian group $\mathbb{Z}_{2}\times\mathbb{Z}_{2}\times\mathbb{Z}_{2}$ and $\mathbf{U}=\left\{1,S_{0}S_{x},S_{0}S_{y},S_{x}S_{y}\right\}$ is the Klein four-group $\mathbb{K}_{4}$. $H$ is consequently diagosed as $\mathrm{CII}\oplus\mathrm{CII}\oplus\mathrm{CII}\oplus\mathrm{CII}$, with each subspace chiral symmetric. Second, when $\left(q_{x}\in 4\mathbb{Z}+2,q_{y}\in 4\mathbb{Z}+2\right)$, $\mathbf{G}=\mathbb{D}_{8}\times\mathbb{Z}_{2}$ becomes non-Abelian. However, its subgroup $\mathbf{U}=\mathbb{Z}_{4}\times\mathbb{Z}_{2}$ is still Abelian, which diagnoses $H$ as $\mathrm{AII}\oplus\mathrm{AII}\oplus\mathrm{AII}\oplus\mathrm{AII}$, forming two pairs of chiral partners. Third, when $\left(q_{\mu}\in 4\mathbb{Z}+2,q_{\nu}\in 4\mathbb{Z}\right)$, $\mathbf{G}=\mathbb{D}_{8}\times\mathbb{Z}_{2}$ is the same as that in the previous scenario. However, they differ in their detailed symmetry algebra (Sec. LABEL:sec:sym_diff); accordingly, the only non-Abelian subgroup of $\mathbf{U}=\mathbb{D}_{8}$ appears in Table 1, which leads to a classification of $\mathrm{CII}\oplus\mathrm{CII}$ and the appearance of the Kramer quartet states, as we describe below.

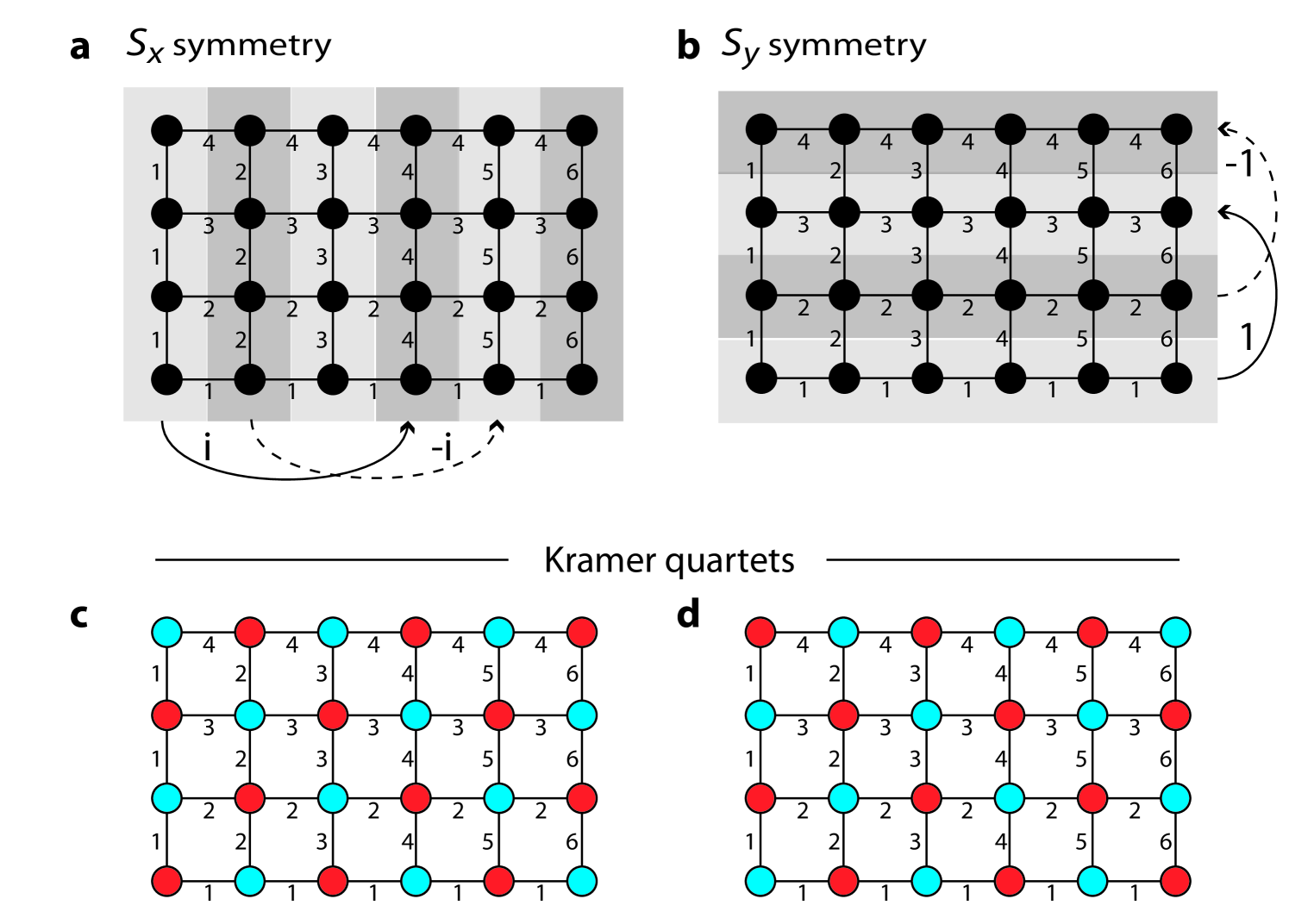
Kramer quartets. A consequence of the non-Abelian symmetry algebra is the existence of generic Kramer quartet states, i.e. a global four-fold degeneracy in the entire MBZ for the case of $\left(q_{\mu}\in 4\mathbb{Z}+2,q_{\nu}\in 4\mathbb{Z}\right)$. Here, time reversal (can be nonsymmorphic, as constructed from the nonsymmorphic chiral symmetries) and inversion protect the conventional Kramer doublets, while the non-Abelian chiral symmetry group ensures that they are degenerate Mobius partners. Without loss of generality, we can decompose $H$ into two CII subspaces, $H_{\mathrm{a}}$ and $H_{\mathrm{b}}$, by diagonalizing the unitary symmetry $U_{xy}=S_{x}S_{y}$ such that both $H_{\mathrm{a}}$ and $H_{\mathrm{b}}$ also obey inversion and a nonsymmorphic time-reversal symmetry $T_{\mu}\equiv S_{\mu}C_{0}^{-1}$ (see Sec. LABEL:sec:kramer), meaning that spins at one site need to perform fractional translation to find their time-reversal partners. Therefore, both $H_{\mathrm{a}}$ and $H_{\mathrm{b}}$ are Kramer doublets.

Mathematically, the anticommutation relation in the non-Abelian group $\mathbf{U}$ enforces the degeneracy between the two CII subsystems $H_{\mathrm{a}}$ and $H_{\mathrm{b}}$ Zhao et al. (2020). Physically, we explicitly construct their wavefunctions by considering the transformation:

where $u$ is the wavefunction in the original basis, $\tau_{x}$ acts on the lattice sites, and we drop the spin index $\sigma$ since the transformation does not act on the spin. $\alpha^{\pm}_{mn}$ are eigenstates of $U_{xy}$ with eigenvalues $\pm 1$ because $U_{xy}\alpha^{\pm}_{mn}=(-1)^{m+n}\mathrm{i}^{(q_{x}+q_{y})/2\mp 1}\alpha^{\pm}_{mn}.$ Since $(q_{x}+q_{y})/2=2\mathbb{Z}+1$, the eigenstate of $H_{\mathrm{a}}$ ($H_{\mathrm{b}}$) occupies each bipartite sublattice with $\alpha^{\pm}$ ($\alpha^{\mp}$), respectively (see Fig. 2c and d). The two subspaces must be similar because $U_{xy}$ consists of two half translation operations, each along $x$ and $y$ directions, which map between the two sublattices (see Fig. 2a and b). Taken together, the non-Abelian subgroup $\mathbf{U}$, inversion, and nonsymmorphic time-reversal symmetry jointly protect the generic Kramer quartet states at arbitrary momenta.

Quantum confinement effects on the real projective plane. When $\left(q_{x}\in 2\mathbb{Z},q_{y}\in 2\mathbb{Z}\right)$ (shaded entries in Table 1), the multiple NCS symmetries $\mathbf{S}$ render the MBZ of the full system a real projective plane, i.e. a 2D generalization of the non-orientable Mobius strip. For the subspaces of the system, there are two sets of momentum labels $\left[\pm\exp\left(\mathrm{i}k_{x}q_{y}/2\right),\pm\exp\left(\mathrm{i}k_{y}q_{x}/2\right)\right]$, independent of each other (except for the the Kramer-quartet case, as proved earlier). As a result, the subspaces are defined on an enlarged MBZ (doubled size in both dimensions) and they exchange these momentum labels at the original MBZ boundary of the full system.

The chiral symmetries $\mathbf{S}$ are also essential for stabilizing the degeneracies at half filling. It is established that the existence of a chiral and a spatial symmetry leads to a lower bound $N_{S}(\mathbf{k})$ on the number of chiral zero modes at momentum $\mathbf{k}$ Koshino et al. (2014) (also see Sec. LABEL:sec:index). In our case, the spatial symmetry is inversion, which always commutes with all chiral symmetries (see Sec. LABEL:sec:kramer). In the presence of multiple chiral symmetries, the lower bound can be calculated for each of them, i.e. $\boldsymbol{N_{S}}(\mathbf{k})\equiv\left(N_{S_{0}}(\mathbf{k}),N_{S_{x}}(\mathbf{k}),N_{S_{y}}(\mathbf{k})\right)$. As we will show below, $\boldsymbol{N_{S}}(\mathbf{k})$ depends on the choice of gauge fields.

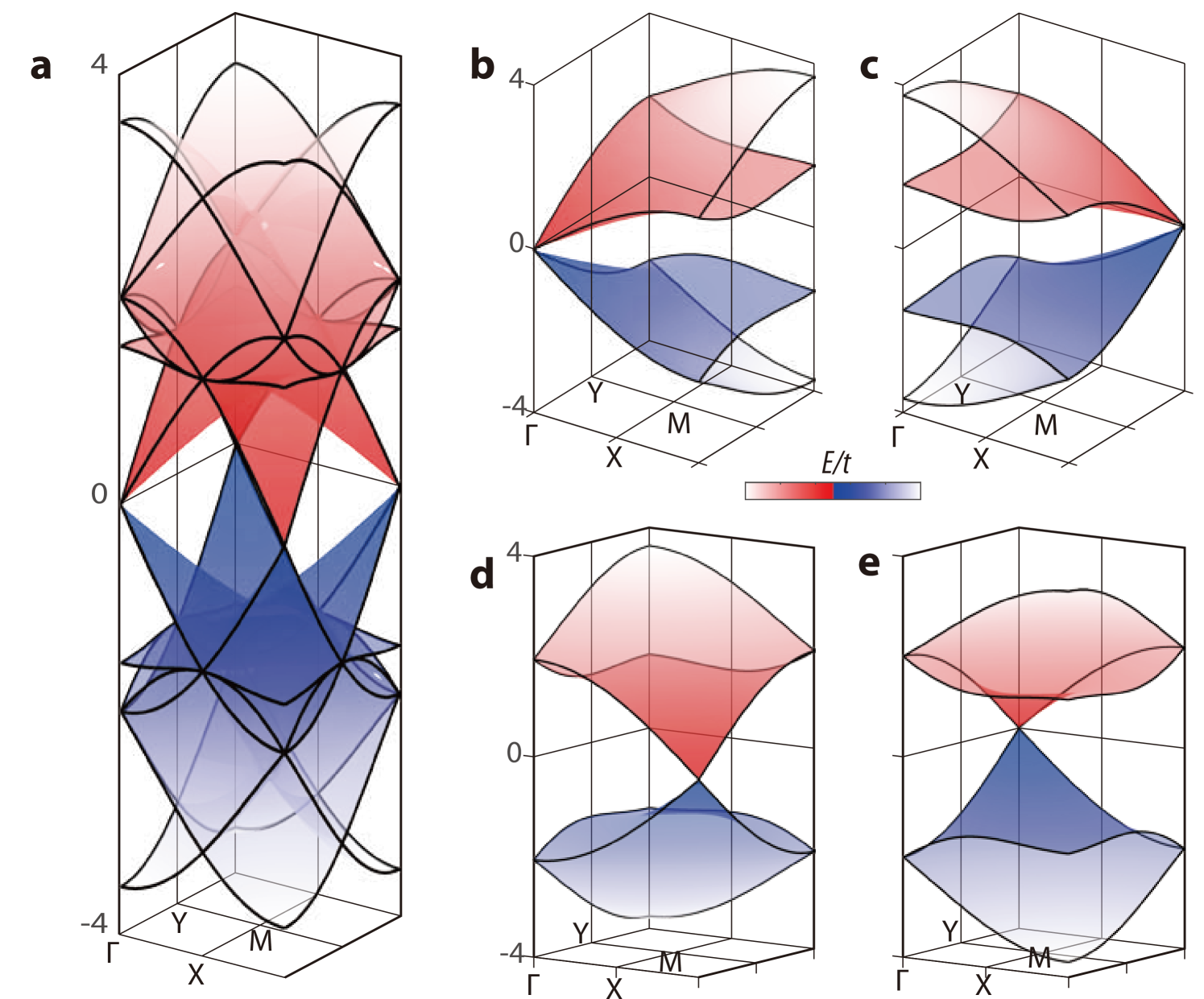
In the case of $H(1/4,1/4)$ (Fig. 3), the full system can be decomposed into four chiral-symmetric subspaces that display pairwise Mobius-type band connections along both the $x$ and $y$ directions at the zone boundary. Notably, its double Dirac point (eight-fold degenerate; Fig. 3a) at $\Gamma$ is, in fact, shared by its four subspaces at the four quadrants. Each of them hosts a double Dirac point at $\Gamma$, $2X$, $2Y$, and $2M$ (Fig. 3b-e and also see Fig. LABEL:fig:1414), respectively. The chiral zero mode indices at the $\Gamma$ point are $\boldsymbol{N_{S}}(\Gamma)=\left(8,8,8\right)$, which indicates that inversion, and both of the local and the nonsymmorphic chiral symmetries jointly protect the double Dirac points at $\Gamma$. This protection is confirmed by an $x$-periodic inversion-symmetric cylinder calculation in Fig. LABEL:smfig:edge1414, which breaks $S_{y}$ but preserves $S_{0}$ and $S_{x}$. Therein, the double Dirac point in the bulk bands reduces to a single Dirac point in the edge spectra at the cost of the reduced symmetries.

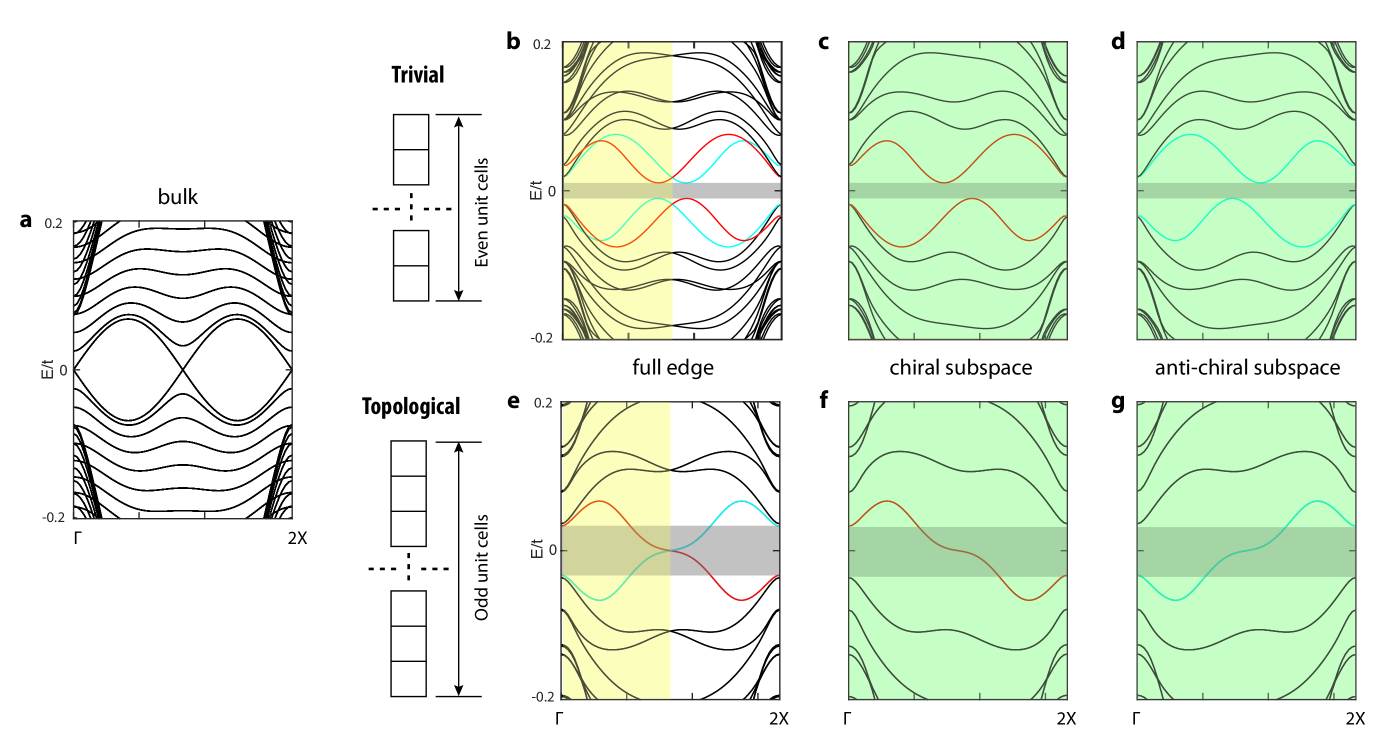
There are situations when components of $\boldsymbol{N_{S}}$ are not identical, which cause consequences of quantum confinement. We again use $H(1/4,1/6)$ as an example. Its chiral zero mode indices are $\boldsymbol{N_{S}}(\mathbf{k})=(0,0,8)$, which indicates $S_{y}$ being crucial in stabilizing the double Dirac points in the bulk bands (Fig. 4a). Thus, an inversion-symmetric cylinder geometry, which is open in $x$ but periodic in $y$, still preserves $S_{y}$ and remains gapless (an example shown in Fig. LABEL:smfig:edge1416). In contrast, a cylinder geometry open in $y$, even if inversion-symmetric, can be gapped because the nonsymmorphic chiral symmetry $S_{y}$ is unavoidably broken. This is confirmed in Fig. 4 with the appearance of a band gap (shaded gray) and edge states (red and blue). Introducing the boundary also lifts the degeneracy of the Kramer quartets because the violation of $S_{y}$ alters the symmetry algebra. Specifically, $\mathbf{U}\subset\mathbf{G}$ is modified as $\mathbb{Z}_{4}\subset\mathbb{D}_{8}$ for this edge Hamiltonian (cf. $\mathbb{D}_{8}\subset\mathbb{D}_{8}\times\mathbb{Z}_{2}$ for the bulk in Table 1). Evidently, bulk boundary correspondence is violated, a typical feature of topological crystalline phases but in this case originating from chiral symmetries: the bulk phase in Fig. 4a is a double Dirac semimetal protected by inversion and nonsymmorphic chiral symmetries, while an edge that violates $S_{y}$ renders it a quantum-confined insulator with a vanishingly small band gap in the thermodynamic limit.

Moreover, this quantum-confined, insulating phase can be either trivial or topological, depending on the parity of the number of unit cells in the cylinder geometry, as illustrated in Fig. 4b-g. Because the cylinder still respects $S_{0}$ and $S_{x}$, we can still decompose the full manifold into two $4X$-periodic, chiral and anti-chiral subspaces that are Mobius partners to each other. Although chiral symmetry does not hold for each subspace, there remains a sublattice symmetry that maps $E(k_{x})\to-E(k_{x}+2X)$, typical in Hofstadter problems. For an even (odd) number of unit cells in the open direction, each subspace contains an even (odd) number of Kramer partners. Taken together, there must be an even (odd) number of crossings at zero energy for each subspace. Therefore, the entire manifold and its two subspaces are simultaneously $\mathbb{Z}_{2}$-even or $\mathbb{Z}_{2}$-odd depending on the parity of the unit cells along the open boundary direction. For other gapped phases at non-half fillings, there is no such dependence. Instead, $\mathbb{Z}_{2}$ time-reversal-invariant insulating phases with a Mobius structure can appear for the edge spectra (Fig. LABEL:fig:gapped1416), where chiral-partnered edge states exchange their nonsymmorphic symmetry labels at the original MBZ boundary.

Conclusion. We have shown that multiple nonsymmorphic chiral symmetries naturally emerge in a non-Abelian generalization of the Hofstadter model with ${\rm SU}(2)$ gauge fields. The nontrivial commutation relations between these symmetries lead to several topological consequences: the Kramer quartet states, semimetals at half filling, and quantum-confined insulators whose topology depends on the system parity. Richer non-Abelian algebras and topology are expected in higher dimensions, e.g. the three-dimensional non-Abelian Hofstadter model where each dimension hosts a unique nonsymmorphic chiral symmetry Liu et al. (2021) (see Sec. LABEL:sec:3d). In particular, our results showcase the diverse possibilities in which internal symmetries, classified according to the ten-fold way, could be combined with spatial symmetries in physical systems beyond electronic band theory. A particularly interesting question concerns whether similar effective symmetries could be relevant to the parton description of spin liquid candidates with an emergent ${\rm SU}(2)$ gauge field.

The proposed non-Abelian Hofstadter system could be simulated with photons and cold atoms. In optics, relevant candidate platforms are anisotropic or bianisotropic materials with electromagnetic duality Liu and Li (2015); He et al. (2016); Cheng et al. (2016); Chen et al. (2019), and $\mathcal{PTD}$-symmetric systems Silveirinha (2017). In cold atoms, the two spatially-dependent gauge potentials could be realized by existing methods—such as laser-assisted tunneling Aidelsburger et al. (2013); Miyake et al. (2013), lattice shading Hauke et al. (2012), or magnetic wires with spatially-modulated currents Goldman et al. (2010); Anderson et al. (2013)—along the two spatial dimensions.