Non-asymptotic convergence bounds for
Wasserstein approximation using point clouds

Given two probability distributions $\rho,\mu$ on $\mathbb{R}^{d}$, the Wasserstein distance of exponent $p$ between $\rho$ and $\mu$ is a way to measure the total cost of moving mass distribution described by $\rho$ to $\mu$, knowing that moving a unit mass from $x$ to $y$ costs $\|x-y\|^{p}$. Formally, it is defined as the value of an optimal transport problem between $\rho$ and $\mu$:

where we minimize of the set $\Pi(\rho,\mu)$ of transport plans between $\rho$ and $\mu$, i.e. probability distributions over $\mathbb{R}^{d}\times\mathbb{R}^{d}$ with marginals $\rho$ and $\mu$. Standard references on the theory of optimal transport include books by Villani and by Santambrogio [19, 20, 18], while the computational and statistical aspects are discussed in a survey of Cuturi and Peyré [16].

In this article, we consider regression problems with respect to the Wasserstein metric, which can be put in the following form

where $\mu$ is the reference distribution, a probability measure on $[0,1]^{\ell}$, $\rho$ is the model distribution, a probability measure on $\mathbb{R}^{d}$, and where $T_{\theta}:[0,1]^{\ell}\to\mathbb{R}^{d}$ is a family of maps indexed by a parameter $\theta\in\Theta$. In the previous formula, we also denoted $T_{\theta}\#\mu$ the image of the measure $\mu$ under the map $T_{\theta}$, also called pushforward of $\mu$ under $T_{\theta}$. This image measure is defined by $T_{\theta\#}\mu(B):=\mu(T_{\theta}^{-1}(B))$ for any measurable set $B$ in the codomain of $T_{\theta}$. In this work, we will concentrate on the quadratic Wasserstein distance $W_{2}$. Several problems related to the design of generative models can be put under the form (2), see for instance [8, 2]. Solving (2) numerically is challenging for several reasons, but in this article we will concentrate on one of them: the non-convexity of the Wasserstein distance under displacement of the measures.

It is well known that the Wasserstein distance is convex for the standard (linear) structure of the space of probability measures, meaning that if $\nu_{0}$ and $\nu_{1}$ are two probability measures and $\nu_{t}=(1-t)\nu_{0}+t\nu_{1}$, then the map $t\in[0,1]\mapsto\mathrm{W}_{p}^{p}(\nu_{t},\rho)$ is convex. Using a terminology from physics, we may say that the Wasserstein distance is convex for the Eulerian structure of the space of probability measures, e.g. when one interpolates linearly between the densities. However, in the regression problem (2), the perturbations are Lagrangian rather than Eulerian, in the sense that modifications of the parameter $\theta$ leads to a displacement of the support of the measure $T_{\theta\#}\mu$. This appears very clearly in particular when $\mu$ is the uniform measure over a set $X=(x_{1},\ldots,x_{N})$ of $N$ point in $[0,1]^{d}$, i.e. $\mu=\delta_{X}$ with

In this case $T_{\theta\#}\mu$ is the uniform measure over the set $T_{\theta}(X)=(T_{\theta}(x_{1}),\ldots,T_{\theta}(x_{n}))$, i.e. $T_{\theta\#}\mu=\delta_{T_{\theta}(X)}$. In this article, we will therefore be interested by the function

This function $F_{N}$ is not convex, and actually exhibits (semi-)concavity properties. This has been observed first in [1] (Theorem 7.3.2), and is related to the positive curvature of the Wasserstein space. A precise statement in the context considered here may also be found as Proposition 21 in [14]. A practical consequence of the lack of convexity of $F_{N}$ is that critical points of $F_{N}$ are not necessarily global minimizers. It is actually easy to construct examples families of critical points $Y_{N}$ of $F_{N}$ such that $F_{N}(Y_{N})$ is bounded from below by a positive constant, while $\lim_{N\to\infty}\min F_{N}=0$, so that the ratio between $F_{N}(Y_{N})$ and $\min F_{N}$ is arbitrarily large as $N\to+\infty$. This can be done by concentrating the points $Y_{N}$ on lower-dimensional subspaces of $\mathbb{R}^{d}$, as in Remarks 2 and 3.

When applying gradient descent to the nonconvex optimization problem (2), it is in principle possible to end up on local minima corresponding to a high energy critical points of the Wasserstein distance, regardless of the non-linearity of the map $\theta\mapsto T_{\theta\#\sigma}$. Our main theorem, or rather its Corollary 6 shows that if the points of $Y$ are at distance at least $\varepsilon>0$ from one another, then

In the previous equation $\|\nabla F_{N}(Y)\|$ denotes the Euclidean norm of the vector in $\mathbb{R}^{Nd}$ obtained by putting one after the other the gradients of $F_{N}$ w.r.t. the positions of the atoms $y_{i}$. We note that due to the weights $1/N$ in the atomic measure $\delta_{Y}$, the components of this vector are in general of the order of $1/N$, see Proposition 1. This inequality resembles the Polyak-Łojasiewicz inequality, and shows in particular that if the quantization error $F_{N}(Y)=\mathrm{W}_{2}^{2}(\rho,\delta_{Y})$ is large, i.e. larger than $\varepsilon^{1-d}/N$, then the point cloud $Y$ is not critical for $F_{N}$. From this, we deduce in 7 that if the points in the initial cloud are not too close to each other at the initialization, then the iterates of fixed step gradient descent converge to points with low energy $F_{N}$, despite the non-convexity of $F_{N}$.

Our main result also has implications in terms of the uniform optimal quantization problem, where one seeks a point cloud $Y=(y_{1},\ldots,y_{N})$ in $(\mathbb{R}^{d})^{N}$ such that the uniform measure supported over $Y$, denoted $\delta_{Y}$, is as close as possible to the model distribution $\rho$ with respect to the $2$-Wasserstein distance:

The uniform optimal quantization problem (4) is a very natural variant of the (standard) optimal quantization problem, where one does not impose that the measure supported on $Y$ is uniform:

and where $\Delta_{N}\subseteq\mathbb{R}^{N}$ is the probability simplex. This standard optimal quantization problem is a cornerstone of sampling theory, and we refer the reader to the book of Graf and Luschgy [10] and to the survey by Pagès [15]. The uniform quantization problem (4) is less common, but also very natural. It has been used in imaging to produce stipplings of an image [4, 3] or for meshing purposes [9]. A common difficulty for solving (5) and (4) numerically is that the minimized functionals $F_{N}$ and $G_{N}$ are non-convex and have many critical points with high energy. However, in practice, simple fixed-point or gradient descent stategies behave well when the initial point cloud is not chosen adversely. Our second contribution is a quantitative explanation for this good behaviour in the case of the uniform optimal quantization problem.

Lloyd’s algorithm [12] is a fixed point algorithm for solving approximately the standard optimal quantization problem (5). Starting from a point cloud $Y^{k}=(y^{k}_{1},\ldots,y^{k}_{N})\in(\mathbb{R}^{d})^{N}$ with distinct points, one defines the next iterate $Y^{k+1}$ in two steps. First, one computes the Voronoi diagram of $Y$, a tessellation of the space into convex polyhedra $(V_{i}(Y^{k}))_{1\leq i\leq N}$, where

In the second step, one moves every point $y^{k}_{i}$ towards the barycenter, with respect to $\rho$, of the corresponding cell $V_{i}(Y^{k})$. This algorithm can also be interpreted as a fixed point algorithm for solving the first-order optimality condition for (5), i.e. $\nabla G_{N}(Y)=0$. One can show that the energy $(G_{N}(Y^{k}))_{k\geq 0}$ decreases in $k$. The convergence of $Y^{k}$ towards a critical point of $F_{N}$ as $k\to+\infty$ has been studied in [5], but the energy of this limit critical point is not guaranteed to be small.

In the case of the uniform quantization problem (4), one can try to minimize the energy $F_{N}$ by gradient descent, defining the iterates

where $\tau>0$ is the time step. The factor $N$ in front of $\nabla F_{N}$ is set as a compensation for the fact that we have, in general, $\nabla F_{N}(Y)=O(1/N)$. When $\tau=1$, one recovers a version of Lloyd’s algorithm for the uniform quantization problem, involving barycenters $B_{N}(Y)$ of Power cells, rather than Voronoi cells, associated to $Y$. More precisely, Proposition 1 proves that $\nabla F_{N}(Y)=(Y-B_{N}(Y))/N$ so that $Y^{k+1}=B_{N}(Y^{k})$ when $\tau=1$. Quite surprisingly, we prove in Corollary 4 that if the points in the initial cloud $Y^{0}$ are not too close to each other, then the uniform measure over the point cloud $Y^{1}=Y^{0}-N\nabla F_{N}(Y^{0})$ obtained after only one step of Lloyd’s algorithm is close to $\rho$. This is illustrated in Figure 1. We prove in particular the following statement.

In Section 2, we start by a short review of background material on optimal transport and optimal uniform quantization. We then establish our main result (3) on the approximation of a measure $\rho$ by barycenters of Power cells. This theorem yields error estimates for one step of Lloyd’s algorithm in deterministic and probabilistic settings (Corollaries 4 and 5). In Section 3, we establish a Polyak-Łojasiewicz-type inequality (Corollary 6) for the function $F_{N}=\frac{1}{2}\mathrm{W}_{2}^{2}(\rho,\delta_{Y})$ introduced in (3), and we study the convergence of a gradient descent algorithm for $F_{N}$ (Theorem 7). Finally, in Section 4, we report numerical results on optimal uniform quantization in dimension $d=2$.

In this section we briefly review Kantorovich duality and its relation to semidiscrete optimal transport. The cost is fixed to $c(x,y)=\|x-y\|^{2}$, and we assume that $\rho$ is a probability density over a compact convex domain $\Omega$. In this setting, Brenier’s theorem implies that given any probability measure $\mu$ supported on $\Omega$, the optimal transport plan between $\rho$ and $\mu$, i.e. the minimizer $\pi$ in the definition of the Wasserstein distance (1) with $p=2$, is induced by a transport map $T_{\mu}:\Omega\to\Omega$, meaning $\pi=(T_{\mu},Id)_{\#}\rho$. One can derive an alternative expression for the Wasserstein distance using Kantorovich duality, which leads to a more precise description of the optimal transport map [18, Theorem 1.39]:

where $\phi^{c}(x)=\min_{i}c(x,y_{i})-\phi_{i}$. When $\mu=\delta_{Y}$ is the uniform probability measure over a point cloud $Y=(y_{1},\ldots,y_{N})$ containing $N$ distinct points, we set $\phi_{i}=\phi(y_{i})$ and we define the $i$th Power cell associated to the couple $(Y,\phi)$ as

Then, the Kantorovich dual (8) of the optimal transport problem between $\rho$ and $\delta_{Y}$ turns into a finite-dimensional concave maximization problem

By Corollary 1.2 in [11], a vector $\phi\in\mathbb{R}^{N}$ is optimal for this maximization problem if and only if the potential $\phi$ is such that each Power cell contain the same amount of mass, i.e. if

From now on, we denote $P_{i}(Y)=\mathrm{Pow}_{i}(Y,\phi)\cap\Omega$, where $\phi\in\mathbb{R}^{N}$ satisfies (10). The optimal transport map $T_{Y}$ between $\rho$ and $\delta_{Y}$ sends every Power cell $P_{i}(Y)$ to the point $y_{i}$, i.e. it is defined $\rho$-almost everywhere by $\left.{T_{Y}}\right|_{P_{i}(Y)}=y_{i}$. We refer again to the introduction of [11] for more details.

In this article, we study the behaviour of the squared Wasserstein distance between the (fixed) probability density $\rho$ and a uniform finitely supported measure $\delta_{Y}$ where $Y=(y_{1},\ldots,y_{N})$ is a cloud of $N$ points, in terms of variations of $Y$. As in equation (3), we denote $F_{N}=\frac{1}{2}\mathrm{W}_{2}^{2}(\rho,\cdot)$. Proposition 21 in [14] gives an expression for the gradient of $F$, and proves its semiconcavity. We recall that $F$ is called $\alpha$–semiconcave, with $\alpha\geq 0$, if the function $F-\frac{\alpha}{2}\|\cdot\|^{2}$ is concave. We denote $\mathbb{D}_{N}$ the generalized diagonal

It is not difficult to prove that $F_{N}$ admits at least one minimizer, and that this minimizer $Y$ satisfies the first-order optimality condition $Y=B_{N}(Y)$. A point cloud that satisfies this condition is called critical.

One can find a critical point of $F_{N}$ by following the discrete gradient flow of $F_{N}$, defined in (7), starting from an initial position $Y^{0}\in(\mathbb{R}^{d})^{N}\setminus\mathbb{D}_{N}$. Thanks to the expression of $\nabla F_{N}$ given in Proposition 1, the discrete gradient flow may be written as

where $\tau_{N}$ is a fixed time step. For $\tau_{N}=1$, one recovers a variant of Lloyd’s algorithm, where one moves every point to the barycenter of its Power cell $P_{i}(Y^{k})$ at each iteration:

We can state the following result about Lloyd’s algorithm for the uniform quantization problem, whose proof is postponed to the appendix.

Experiments suggest that following the discrete gradient flow of $F_{N}$ does not bring us to high energy critical points of $F_{N}$, such as those described in Remark 2, unless we started from an adversely chosen point cloud. The following theorem and its corollaries, the main results of this article, backs up this experimental evidence. It shows that if the point cloud $Y$ is not too concentrated, then the uniform measure over the barycenters of the power cells, $\delta_{B_{N}(Y)}$, is a good quantization of the probability density $\rho$, i.e. it bounds the quantization error after one step of Lloyd’s algorithm (14).

We will use the following notation for $\varepsilon>0$:

Note that $\mathbb{D}_{N,\varepsilon}$ is an $\varepsilon$-neighborhood around the generalized diagonal $\mathbb{D}_{N}$.

The proof relies on arguments from convex geometry. In particular, we denote $A\oplus B$ the Minkowski sum of sets: $A\oplus B=\{a+b\mid(a,b)\in A\times B\}$.

This theorem could be extended mutatis mutandis to the case where $\rho$ is a general probability measure (i.e. not a density). However, this would imply some technical complications in the definition of the barycenters $b_{i}$ by introducing a disintegration of $\rho$ with respect to the transport plan $\pi$.

In the next corollary, we assume that any pair of distinct points in $Y_{N}\in(\mathbb{R}^{d})^{N}$ is bounded from below by $\varepsilon_{N}\geq CN^{-\beta}$, implying that $I_{\varepsilon_{N}}(Y_{N})=N$. This corresponds to the value one could expect for a point set uniformly sampled from a set with Minkowski dimension $\beta$. When $\beta>d-1$, the corollary asserts that one step of Lloyd’s algorithm is enough to approximate $\rho$, in the sense that the uniform measure $\delta_{B_{N}(Y_{N})}$ over the barycenters converges towards $\rho$ as $N\to+\infty$.

The next corollary is a probabilistic analogue of Corollary 4, assuming that the initial point cloud $Y$ is drawn from a probability density $\sigma$ on $\Omega$. Note that $\sigma$ can be distinct from $\rho$. The proof of this corollary relies on McDiarmid’s inequality to quantify the proportion of $\varepsilon$-isolated points in a point cloud that is drawn randomly and independently from $\sigma$. The proof of this result is in Appendix B.

The modified Polyak-Łojasiewicz inequality (20) suggests that the discrete gradient flow 13 will bring us close to a point cloud with low Wasserstein distance to $\rho$, provided that can guarantee that the the points clouds $Y^{k}$ remain far for generalized diagonal during the iterations. We prove in Lemma 3 in Appendix D that if $Y^{k+1}=Y^{k}-\tau_{N}\nabla F_{N}(Y^{k})$ and $\tau_{N}\in(0,1)$, then

We note that this inequality ensures that $Y^{k}$ never touches the generalized diagonal $\mathbb{D}_{N}$, so that the gradient $\nabla F_{N}(Y^{k})$ is well-defined at each step. Combining this inequality with 3, one can actually prove that if the points in the initial cloud $Y^{0}_{N}$ are not too close to each other, then a few steps of gradient discrete gradient descent leads to a discrete measure $Y^{k}_{N}$ that is close to the target $\rho$. Precisely, we arrive at the following theorem, proved in Appendix D.

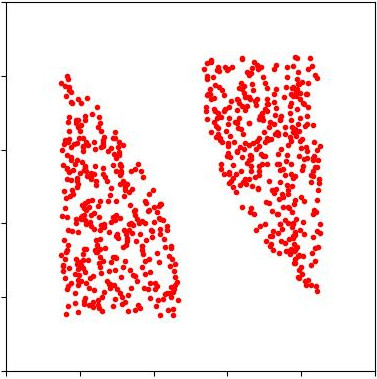
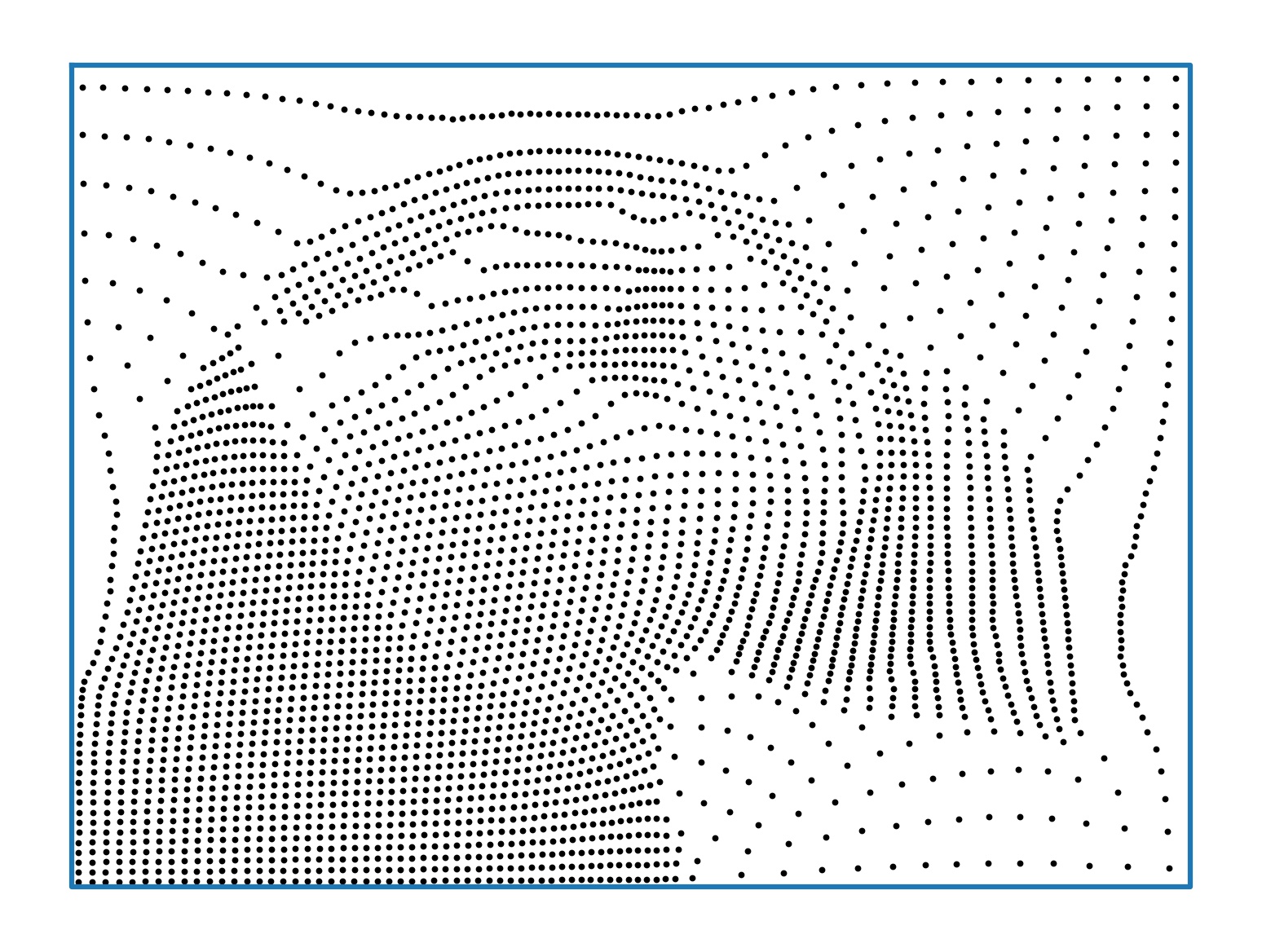
As we mentioned in the introduction, uniform optimal quantization allows to sparsely represent a (gray scale) image via points, clustered more closely in areas where the image is darker [4, 3]. On figure 3, we ploted the point clouds obtained after a single Lloyd step toward the density representing the image on the left (Puffin), starting from regular grids. The observed rate of convergence, $N^{-1.00}$, is coherent with the theoretical estimate $\log(N)/N$ of 1.

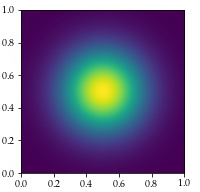
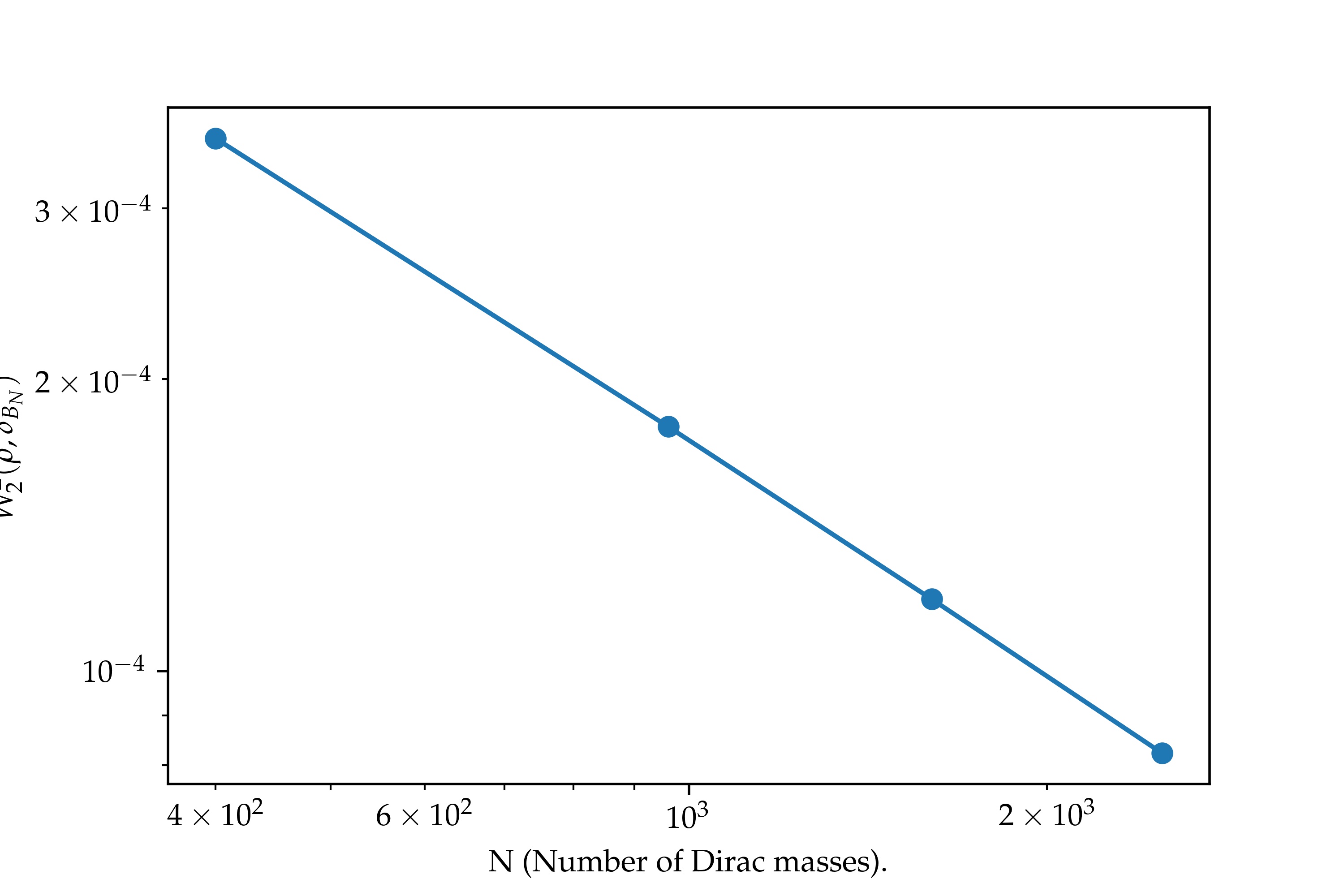
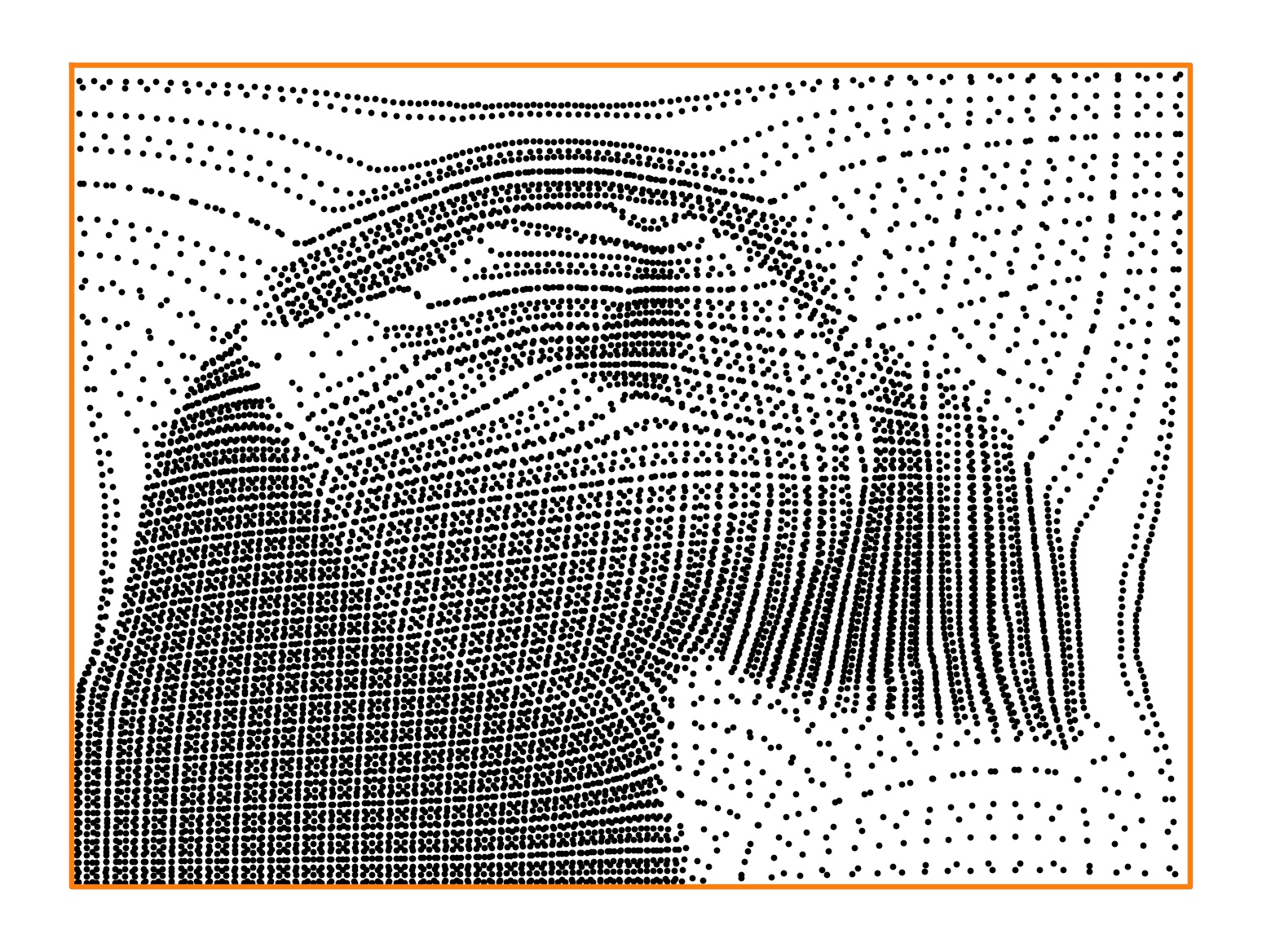
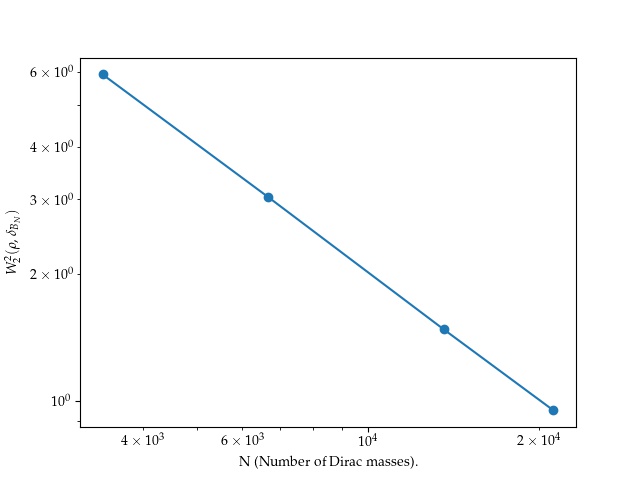
We now consider a toy model where we approximate a gaussian density truncated to the unit square $\Omega=[0,1]^{2}$, $\rho(x,y)=\frac{1}{Z}e^{-8((x-\frac{1}{2})^{2}+(y-\frac{1}{2})^{2})}$ where $Z$ is a normalization constant. On the left column of this figure, the initial point clouds $Y_{N}^{0}$ are randomly distributed in $[0,1]^{2}$. The three point clouds represented above are obtained after one step of Lloyd’s algorithm (14). The red curve displays in a log-log scale the mean values of $F_{N}(B_{N}(Y_{N}))$ over a hundred random point clouds, for $N\in\{400,961,1600,2500\}$. In this case, we observe a decrease rate $N^{-0.95}$ with respect to the number of points, similar to the case of the gray scale picture.

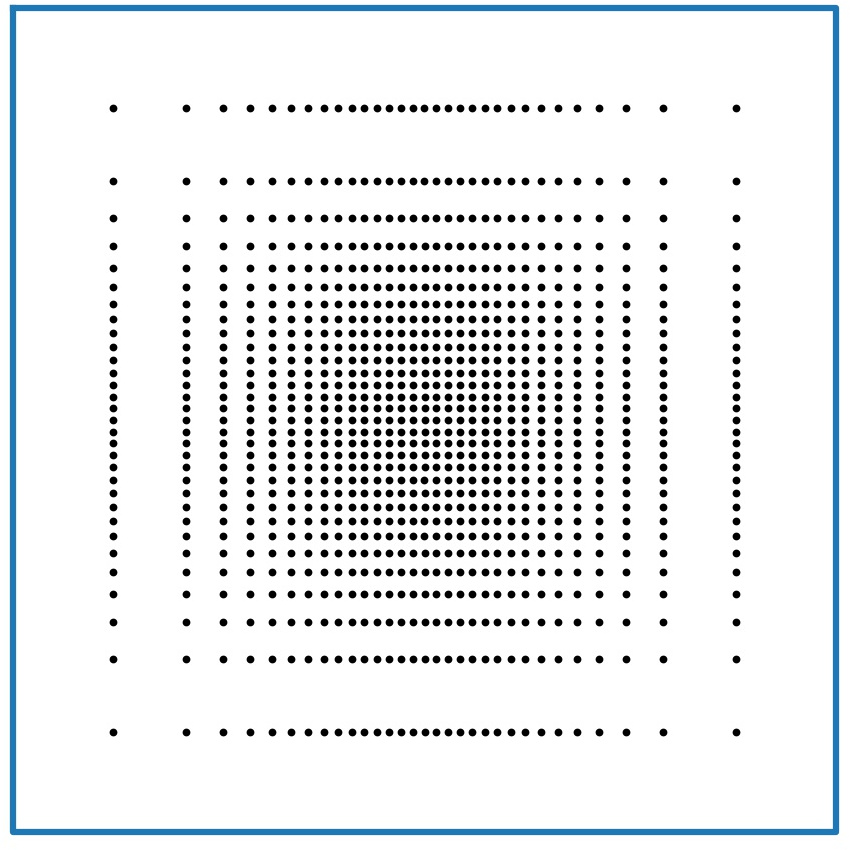
However, an interesting phenomena occurs when the initial point cloud $Y_{N}^{0}$ is aligned on a axis-aligned grid. The pictures in the right column of Fig. 2 where computed starting from such a grid with $N\in\{400,961,1600,2500\}$ points. As in the randomly initialized case, we represented the values of $F_{N}(B_{N}(Y_{N}))$ in log-log scale. The corresponding discrete probability measure $\delta_{B_{N}(Y_{N})}$ seems to converge to $\rho$ as $N\to\infty$, but with a much worse rate for these "low" values of $N$: $F_{N}(B_{N}(Y_{N}))\simeq N^{-0.8}$. In this specific setting, with a separable density and an axis-aligned grid $Y_{0}$, the power cells are rectangles and a single Lloyd step brings us to a critical point of $F_{N}$. Thanks to this remark, it is possible to estimate the approximation error from the one-dimensional case. In fact, Appendix E shows that for any $\delta\in(0,1)$, there exists variances $\sigma_{N}=\sigma_{N}(\delta)$ such that the approximation error $W_{2}^{2}(\rho_{\sigma_{N}},\delta_{B_{N}})$ is of order $N^{-\frac{2-\delta}{2}}$. On the other hand, for a fixed $\sigma$, the approximation error is of order $N^{-1}$, to be compared with the bound $\log(N)/N$ for general measures.