Non-degenerate surfaces of revolution in Minkowski space that satisfy the relation $aH+bK=c$

Consider the three-dimensional Minkowski space $\hbox{\bf E}_{1}^{3}$, that is, the real vector space $\hbox{\bb R}^{3}$ endowed with the Lorentzian metric $\langle,\rangle=(dx)^{2}+(dy)^{2}-(dz)^{2}$, where $(x,y,z)$ stand for the usual coordinates of $\hbox{\bb R}^{3}$. A vector $v\in\hbox{\bf E}_{1}^{3}$ is said spacelike if $\langle v,v\rangle>0$ or $v=0$, timelike if $\langle v,v\rangle<0$ and lightlike if $\langle v,v\rangle=0$ and $v\not=0$. A submanifold $S\subset\hbox{\bf E}_{1}^{3}$ is said spacelike, timelike or lightlike if the induced metric on $S$ is a Riemannian metric (positive definite), a Lorentzian metric (a metric of index $1$) or a degenerated metric, respectively. In the case that $S$ is a straight-line $L=<v>$, this means that $v$ is spacelike, timelike or lightlike, respectively. If $S$ is a plane $P$, this is equivalent that any orthogonal vector to $P$ is timelike, spacelike or lightlike respectively.

An immersion $x:M\rightarrow\hbox{\bf E}_{1}^{3}$ of a surface $M$ is said non-degenerated if the induced metric $x^{*}(\langle,\rangle)$ on $M$ is non-degenerate. In this setting, there is only two possibilities: if $x^{*}(\langle,\rangle)$ is positive definite , that is, it is a Riemmannian metric and the immersion is called spacelike or $x^{*}(\langle,\rangle)$ is a Lorentzian metric, that is, a metric of index $1$, and the immersion is called timelike. For spacelike surfaces, the tangent planes are spacelike everywhere, and for timelike surfaces, they are timelike.

We consider spacelike or timelike surfaces in $\hbox{\bf E}_{1}^{3}$ that satisfy the relation

$$aH+bK=c,$$

(1)

where $H$ and $K$ are the mean curvature and the Gauss curvature of the surface, and $a$, $b$ and $c$ are constants. We say that the surface is a linear Weingarten surface of $\hbox{\bf E}_{1}^{3}$. In general, a Weingarten surface is a surface that satisfies a certain smooth relation $W=W(H,K)=0$ and our case, that is, surfaces that satisfy (1) is the simplest case of $W$, that is, that $W$ is a linear function in its variables. The family of linear Weingarten surfaces include the surfaces with constant mean curvature ($b=0$) and the surfaces with constant Gauss curvature ($a=0$).

In this work we study linear Weingarten surfaces that are rotational, that is, invariant by a group of motions of $\hbox{\bf E}_{1}^{3}$ that pointwised fixed a straight-line. In such case, Equation (1) is a second ordinary differential equation that describes the shape of the generating curve of the surface. One can not expect to integrate this equation, because even in the trivial cases that $a=0$ or $b=0$, this integration is not possible. We are going to discard the cases that $H$ is constant of $K$ is constant, which are known: see for example [1, 2, 3]. We will obtain a first integration of (1). For the particular case that $a^{2}-4bc\epsilon=0$, we describe all solutions, exactly, we have

In this section we describe the surfaces of revolution of $\hbox{\bf E}_{1}^{3}$ and we recall the concepts of mean curvature and Gauss curvature for a non-degenerate surface. We consider the rigid motions of the ambient space that leave a straight-line pointwised fixed, called, the axis of the surface. Let $L$ be the axis of the surface. Depending on $L$, there are three types of rotational motions. After an isometry of $\hbox{\bf E}_{1}^{3}$, the expressions of rotational motions with respect to the canonical basis $\{e_{1},e_{2},e_{3}\}$ are as follows:

$$R_{v}:\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right)\longmapsto\left(\begin{array}[]{ccc}\cos{v}&\sin{v}&0\\ -\sin{v}&\cos{v}&0\\ 0&0&1\end{array}\right)\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right).$$

$$R_{v}:\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right)\longmapsto\left(\begin{array}[]{ccc}1&0&0\\ 0&\cosh{v}&\sinh{v}\\ 0&\sinh{v}&\cosh{v}\end{array}\right)\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right).$$

$$R_{v}:\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right)\longmapsto\left(\begin{array}[]{ccc}1&-v&v\\ v&1-\frac{v^{2}}{2}&\frac{v^{2}}{2}\\ v&-\frac{v^{2}}{2}&1+\frac{v^{2}}{2}\end{array}\right)\left(\begin{array}[]{c}x_{1}\\ x_{2}\\ x_{3}\end{array}\right).$$

See [4, 5] for more details.

In particular, there exists a planar curve $\alpha=\alpha(u)$ that generates the surface, that is, $M$ is the set of points given by $\{R_{v}(\alpha(u));u\in I,v\in\hbox{\bb R}\}$. We now describe the parametrizations of a rotational surface.

1. 1.

   Case $L$ is a timelike axis. Consider that $L$ is the $x_{3}$-axis. If $p=(x_{0},y_{0},z_{0})\not\in L$, then $\{R_{v}(p);v\in\hbox{\bb R}\}$ is an Euclidean circle of radius $\sqrt{x_{0}^{2}+y_{0}^{2}}$ in the plane $z=z_{0}$. If $\alpha(u)=(u,0,z(u))$ is a planar curve in the plane $y=0$, then the surface of revolution generated by $\alpha$ writes as

   $$X(u,v)=(u\cos(v),u\sin(v),z(u)),\ u\not=0.$$

   (2)

2. 2.

   Case $L$ is a spacelike axis. Consider that $L$ is the $x_{1}$-axis. If $p=(x_{0},y_{0},z_{0})$ does not belong to $L$, then $\{R_{v}(p);v\in\hbox{\bb R}\}$ is an Euclidean hyperbola in the plane $x=x_{0}$ and with equation $y^{2}-z^{2}=y_{0}^{2}-z_{0}^{2}$. For this kind of rotational surfaces, we have two type of surfaces:

   1. (a)

      If $\alpha(u)=(u,0,z(u))$ is a planar curve in the plane $y=0$, then the surface of revolution generated by $\alpha$ writes as

      $$X(u,v)=(u,z(u)\sinh(v),z(u)\cosh(v)),\ u\not=0.$$

      (3)

   2. (b)

      If $\alpha(u)=(u,z(u),0)$ is a planar curve in the plane $z=0$, then the surface is given by

      $$X(u,v)=(u,z(u)\cosh(v),z(u)\sinh(v)),\ u\not=0.$$

      (4)

3. 3.

   Case $L$ is a lightlike axis. Consider that $L$ is the straight-line $v_{1}=<(0,1,1)>$. If $p=(x_{0},y_{0},z_{0})$ does not belong to the plane $<e_{1},v_{1}>$, the orbit $\{R_{v}(p);v\in\hbox{\bb R}\}$ is the curve

   $$\beta(v)=(x-(y-z)v,xv+y-(y-z)\frac{v^{2}}{2},xv+z-(y-z)\frac{v^{2}}{2}).$$

   The curve $\beta$ lies in the plane $y-z=y_{0}-z_{0}$ and describes a parabola in this plane, namely,

   $$\beta(v)=(x,y,z)+v(-(y-z)e_{1}+xv_{1})-\frac{y-z}{2}v^{2}v_{1}.$$

   Consider $\alpha(u)$ a planar curve in the plane $<(0,1,1),(0,1,-1)>$ given as a graph on the straight-line $<(0,1,-1)>$, that is, $\alpha(u)=(0,u+z(u),-u+z(u))$. The surface of revolution generated by $\alpha$ is

   $$X(u,v)=(-2uv,z(u)+u-uv^{2},z(u)-u-uv^{2}),\ u\not=0.$$

   (5)

Let $M$ be surface and $x:M\rightarrow\hbox{\bf E}_{1}^{3}$ a non-degenerate immersion and we simply say that $M$ is non-degenerate. The surface could be not orientable, but if the immersion is spacelike, then $M$ is necessarily orientable. This is due to the following fact. At each point $p\in M$ there is two possible choices of a unit normal vector to the tangent plane $T_{p}M$ of $M$ at $p$. The normal vector to $M$ is a timelike vector, and in Minkowski space, two any timelike vectors are not orthogonal. Thus, if $E_{3}=(0,0,1)$, at each point $p\in M$, we take that unit normal vector $N(p)$ such that $\langle N(p),E_{3}\rangle<0$. This allows to define an global orientation on $M$, proving that $M$ is orientable. With this choice of $N$, we say that $N$ is future directed. In the case that the immersion is timelike, we will assume that $M$ is orientable.

Let $x:M\rightarrow\hbox{\bf E}_{1}^{3}$ be a non-degenerate immersion of a surface $M$ and let $N$ be a Gauss map. Let $U,V$ be vector fields to $M$ and we denote by $\nabla^{0}$ and $\nabla$ the Levi-Civitta connections of $\hbox{\bf E}_{1}^{3}$ and $M$ respectively. The Gauss formula says $\nabla_{U}^{0}V=\nabla_{U}V+\mbox{II}(U,V),$ where II is the second fundamental form of the immersion. The Weingarten endomorphism is $A_{p}:T_{p}M\rightarrow T_{p}M$ defined as $A_{p}(U)=-(\nabla_{U}^{0}N)_{p}^{\top}=(-dN)_{p}(U)$. We have then $\mbox{II}(U,V)=-\epsilon\langle\mbox{II}(U,V),N\rangle N=-\epsilon\langle AU,V\rangle N$, where $\epsilon=1$ if $M$ is spacelike and $\epsilon=-1$ if $M$ is timelike. The mean curvature vector $\vec{H}$ is defined as $\vec{H}=(1/2)\mbox{trace}(\mbox{II})$ and the Gauss curvature $K$ as the determinant of II computed in both cases with respect to an orthonomal basis. The mean curvature $H$ is the function given by $\vec{H}=HN$, that is, $H=-\epsilon\langle\vec{H},N\rangle$. If $\{e_{1},e_{2}\}$ is an orthonormal basis at each tangent plane, with $\langle e_{1},e_{1}\rangle=1$, $\langle e_{2},e_{2}\rangle=\epsilon$, then

	$\displaystyle\vec{H}$	$\displaystyle=$	$\displaystyle\frac{1}{2}\mbox{(}\mbox{II}(e_{1},e_{1})+\mbox{II}(e_{2},e_{2}))=-\epsilon\frac{1}{2}(\langle Ae_{1},e_{1}\rangle+\epsilon\langle Ae_{2},e_{2}\rangle)N=-\epsilon(\frac{1}{2}\mbox{trace}(A))N$
	$\displaystyle K$	$\displaystyle=$	$\displaystyle-\epsilon\mbox{det}(A).$

In this work we need to compute $H$ and $K$ using a parametrization of the surface. Let $X:D\subset\hbox{\bb R}^{2}\rightarrow\hbox{\bf E}_{1}^{3}$ be a parametrization of the surface, $X=X(u,v)$. Then $A=\mbox{II}(\mbox{I})^{-1}$, $\mbox{I}=\langle,\rangle$ and we have the known formulae ([5]):

$$H=-\epsilon\frac{1}{2}\frac{eG-2fF+gE}{EG-F^{2}},\hskip 28.45274ptK=-\epsilon\frac{eg-f^{2}}{EG-F^{2}},$$

(6)

where $\{E,F,G\}$ and $\{e,f,g\}$ are the coefficients of I and II, respectively:

$$E=\langle X_{u},X_{u}\rangle,\ F=\langle X_{u},X_{v}\rangle,\ G=\langle X_{v},x_{v}\rangle,$$

$$e=-\langle N_{u},X_{u}\rangle,\ f=-\langle N_{u},X_{v}\rangle,\ g=-\langle N_{v},X_{v}\rangle,$$

where the subscripts denote the corresponding derivatives. Here $N$ is

$$N=\frac{X_{u}\times X_{v}}{\sqrt{\epsilon(EG-F^{2})}}.$$

We recall that

$$W:=EG-F^{2}=\epsilon|X_{u}\times X_{v}|^{2}\ \left\{\begin{array}[]{l}\mbox{is positive if $M$ is spacelike}\\ \mbox{is negative if $M$ is timelike}\end{array}\right.$$

Finally, in order to the computations for $H$ and $K$, we recall that the cross-product $\times$ satisfies that for any vectors $u,v,w\in\hbox{\bf E}_{1}^{3}$, $\langle u\times v,w\rangle=\mbox{det}(u,v,w)$. Then (6) writes as

$$H=-\frac{\epsilon}{2}\frac{G\mbox{det}(X_{u},X_{v},X_{uu})-2F\mbox{det}(X_{u},X_{v},X_{uv})+E\mbox{det}(X_{u},X_{v},X_{vv})}{(\epsilon(EG-F^{2}))^{3/2}}:=\frac{H_{1}}{2W^{3/2}}.$$

(7)

$$K=-\frac{\mbox{det}(X_{u},X_{v},X_{uu})\mbox{det}(X_{u},X_{v},X_{vv})-\mbox{det}(X_{u},X_{v},X_{uv})^{2}}{(EG-F^{2})^{2}}:=\frac{K_{1}}{W^{2}}.$$

(8)

In Minkowski ambient space, the role of spheres is played by pseudohyperbolic surfaces and pseudospheres [4]. If $p_{0}\in\hbox{\bf E}_{1}^{3}$ and $r>0$ the pseudohyperbolic surface centered at $p_{0}$ with radius $r>0$ is $\hbox{\bf H}^{2,1}(r;p_{0})=\{p\in\hbox{\bf E}_{1}^{3};\langle p-p_{0},p-p_{0}\rangle=-r^{2}\}$ and the pseudosphere centered at $p_{0}$ and radius $r>0$ is $\hbox{\bf S}^{2,1}(r;p_{0})=\{p\in\hbox{\bf E}_{1}^{3};\langle p-p_{0},p-p_{0}\rangle=r^{2}\}$. If $M$ is spacelike (resp. timelike) then $N$ is timelike (resp. spacelike) and $N:M\rightarrow\hbox{\bf H}^{2,1}(1)$ (resp. $N:M\rightarrow\hbox{\bf S}^{2,1}(1)$), where $\hbox{\bf H}^{2,1}(1)=\hbox{\bf H}^{2,1}(1;O)$ (resp. $\hbox{\bf S}^{2,1}(1)=\hbox{\bf S}^{2,1}(r;O)$, being $O$ the origin of coordinates of $\hbox{\bb R}^{3}$. For both kind of surfaces, we can take $N(p)=(p-p_{0})/r$ and $A=-\frac{1}{r}I$. Then $H=\epsilon/r$ and $K=-\epsilon/r^{2}$.

We assume that the generating curve $\alpha$ lies in the $xz$-plane and we parametrize $\alpha$ as the graph of a function $z=z(u)$, that is, $\alpha(u)=(u,0,z(u))$, $u>0$. Then the surface is parametrized as in (2) and $W=u^{2}(1-z^{2})$. Thus $z^{\prime 2}<1$ if the surface is spacelike and $z^{\prime 2}>1$ if $M$ is timelike. Using (7) and (8), the expressions of $H$ and $K$ are:

$$H=-\frac{1}{2}\Bigg{(}\frac{\epsilon z^{\prime}}{u\sqrt{\epsilon(1-z^{\prime 2})}}+\frac{z^{\prime\prime}}{(\epsilon(1-z^{\prime 2}))^{3/2}}\Bigg{)},\ \ K=-\frac{z^{\prime}z^{\prime\prime}}{u(1-z^{\prime 2})^{2}}.$$

Then the relation (1) writes as

$$\frac{a}{2}\Bigg{(}\frac{\epsilon z^{\prime}}{u\sqrt{\epsilon(1-z^{\prime 2})}}+\frac{z^{\prime\prime}}{(\epsilon(1-z^{\prime 2}))^{3/2}}\Bigg{)}+b\frac{z^{\prime}z^{\prime\prime}}{u(1-z^{\prime 2})^{2}}=-c.$$

Multiplying by $u$ we obtain a first integral. Exactly, we have

$$a\Bigg{(}u\frac{\epsilon z^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}\Bigg{)}^{\prime}+b\Bigg{(}\frac{1}{1-z^{\prime 2}}\Bigg{)}^{\prime}=-2cu.$$

Then there exists a integration constant $\lambda\in\hbox{\bb R}$ such that

$$\epsilon\frac{auz^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}+\frac{b}{1-z^{\prime 2}}=-cu^{2}+\lambda.$$

(9)

Let

$$\phi=\frac{z^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}.$$

Then $1+\epsilon\phi^{2}=1/(1-z^{\prime 2})$ and Equation (9) writes as $b\phi^{2}+au\phi+\epsilon(b+cu^{2}-\lambda)=0$. Hence, we obtain $\phi$:

$$\frac{z^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-au\pm\sqrt{(a^{2}-4bc\epsilon)u^{2}+4b\epsilon(-b+\lambda)}}{2b}.$$

(10)

We completely solve this differential equation in two particular cases:

1. 1.

   Consider $\lambda=b$. Then we have

   $$\frac{z^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-a\pm\sqrt{a^{2}-4bc\epsilon}}{2b}u=Cu,\ \ C=\frac{-a\pm\sqrt{a^{2}-4bc\epsilon}}{2b}.$$

   Then

   $$z(u)=\pm\frac{\sqrt{\epsilon+C^{2}u^{2}}}{C}+\mu,\ \mu\in\hbox{\bb R}.$$

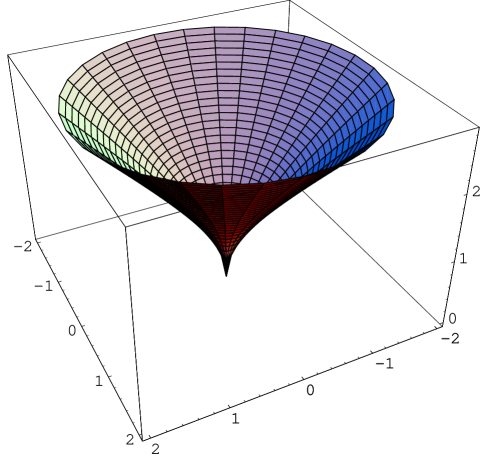
   From the parametrization (2) of the surface, one concludes that $M$ satisfies the equation $x^{2}+y^{2}-(z-\mu)^{2}=-\frac{\epsilon}{C^{2}}$. Letting $p_{0}=(0,0,\mu)$, if $\epsilon=1$, the surface $M$ is the pseudohyperbolic surface $\hbox{\bf H}^{2,1}(1/|C|;p_{0})$ and when $\epsilon=-1$, $M$ is a pseudosphere $\hbox{\bf S}^{2,1}(1/|C|;p_{0})$.

2. 2.

   Assume $a^{2}-4bc\epsilon=0$. Then

   $$\frac{z^{\prime}}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-au\pm C}{2b},\ \ C=2\sqrt{b\epsilon(-b+\lambda)}.$$

   The integration of this equation is

   $$z(u)=\pm\sqrt{\frac{4\epsilon b^{2}}{a^{2}}+(\frac{C}{a}\pm u)^{2}}+\mu,\ \mu\in\hbox{\bb R}.$$

We distinguish two cases according the two possible parametrizations.

1. 1.

   Case I. Assume that the parametrization is given by (3). The relation (1) writes as

   $$\frac{a}{2}\Bigg{(}\frac{\epsilon}{z\sqrt{\epsilon(1-z^{\prime 2})}}+\frac{z^{\prime\prime}}{(\epsilon(1-z^{\prime 2}))^{3/2}}\Bigg{)}+b\frac{z^{\prime\prime}}{z(1-z^{\prime 2})^{2}}=-c.$$

   Multiplying by $zz^{\prime}$, we obtain a first integral. Exactly, we have

   $$a\Bigg{(}\frac{\epsilon z}{\sqrt{\epsilon(1-z^{\prime 2})}}\Bigg{)}^{\prime}+b\Bigg{(}\frac{1}{1-z^{\prime 2}}\Bigg{)}^{\prime}=-c(z^{2})^{\prime}.$$

   Then there exists an integration constant $\lambda\in\hbox{\bb R}$ such that

   $$\epsilon\frac{az}{\sqrt{\epsilon(1-z^{\prime 2})}}+\frac{b}{1-z^{\prime 2}}=-cz^{2}+\lambda.$$

   (11)

   Now we take $\phi=1/\sqrt{\epsilon(1-z^{\prime 2})}$. Then Equation (11) writes as

   $$b\phi^{2}+az\phi+\epsilon(cz^{2}-\lambda)=0.$$

   Then

   $$\frac{1}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-az\pm\sqrt{(a^{2}-4bc\epsilon)z^{2}+4b\epsilon\lambda}}{2b}.$$

   (12)

   We completely solve this differential equation in two particular cases:

   1. (a)

      Consider $\lambda=0$. Then we have

      $$\frac{1}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-a\pm\sqrt{a^{2}-4bc\epsilon}}{2b}z=Cz,\ \ C=\frac{-a\pm\sqrt{a^{2}-4bc\epsilon}}{2b}.$$

      The solution of this differential equation is

      $$z(u)=\pm\sqrt{\frac{\epsilon}{C^{2}}\pm(u\pm C\mu)^{2}},\ \mu\in\hbox{\bb R}\}.$$

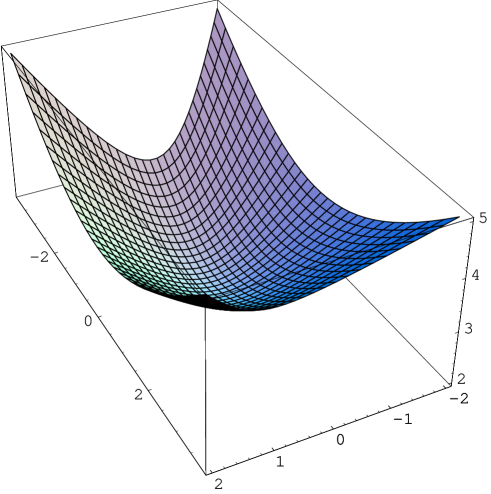
      From the parametrization (3) of the surface, one concludes that $M$ satisfies the equation $(x-C\mu)^{2}+y^{2}-z^{2}=-\frac{\epsilon}{C^{2}}$. Thus, if we set $p_{0}=(\pm C\mu,0,0)$, for $\epsilon=1$ we obtain that $M$ is the pseudohyperbolic surface $\hbox{\bf H}^{2,1}(1/|C|;p_{0})$ and for $\epsilon=-1$, $M$ is the pseudosphere $\hbox{\bf S}^{2,1}(1/|C|;p_{0})$.

   2. (b)

      Assume $a^{2}-4bc\epsilon=0$. Then

      $$\frac{1}{\sqrt{\epsilon(1-z^{\prime 2})}}=\frac{-az\pm C}{2b},\ \ C=2\sqrt{b\epsilon\lambda}.$$

      The integration of this equation is

      $$z(u)=\pm\frac{C}{a}\pm\sqrt{\frac{4\epsilon b^{2}}{a^{2}}\pm(u\pm\mu)^{2}},\ \mu\in\hbox{\bb R}.$$

2. 2.

   Case II. The expression of the parametrization is written in (4). In this case, the surface is timelike, since $EG-F^{2}=-z^{2}(1+z^{\prime 2})$. The Weingarten relation (1) is

   $$\frac{a}{2}\Bigg{(}\frac{-1}{z\sqrt{1+z^{\prime 2}}}+\frac{z^{\prime\prime}}{(1+z^{\prime 2})^{3/2}}\Bigg{)}-b\frac{z^{\prime\prime}}{z(1+z^{\prime 2})^{2}}=c.$$

   Multiplying by $zz^{\prime}$ again, we have

   $$-a\Bigg{(}\frac{z}{\sqrt{1+z^{\prime 2}}}\Bigg{)}^{\prime}+b\Bigg{(}\frac{1}{1+z^{\prime 2}}\Bigg{)}^{\prime}=c(z^{2})^{\prime}.$$

   It follows the existence of an integration constant $\lambda\in\hbox{\bb R}$ such that

   $$-\frac{az}{\sqrt{1+z^{\prime 2}}}+\frac{b}{1+z^{\prime 2}}=cz^{2}+\lambda.$$

   (13)

   If we set $\phi=1/\sqrt{1+z^{\prime 2}}$, Equation (13) is $b\phi^{2}-az\phi-cz^{2}-\lambda=0$, obtaining

   $$\frac{1}{1+z^{\prime 2}}=\frac{az\pm\sqrt{(a^{2}+4bc)z^{2}+4b\lambda}}{2b}.$$

   (14)

   As in the previous case, we solve this equation in the next two cases:

   1. (a)

      If $\lambda=0$, then

      $$\frac{1}{\sqrt{1+z^{\prime 2}}}=\frac{-a\pm\sqrt{a^{2}+4bc}}{2b}z=Cz,\ \ C=\frac{a\pm\sqrt{a^{2}+4bc}}{2b}.$$

      The solution of this equation is

      $$z(u)=\pm\sqrt{\frac{1}{C^{2}}-(u\pm C\mu)^{2}},\ \mu\in\hbox{\bb R}\}.$$

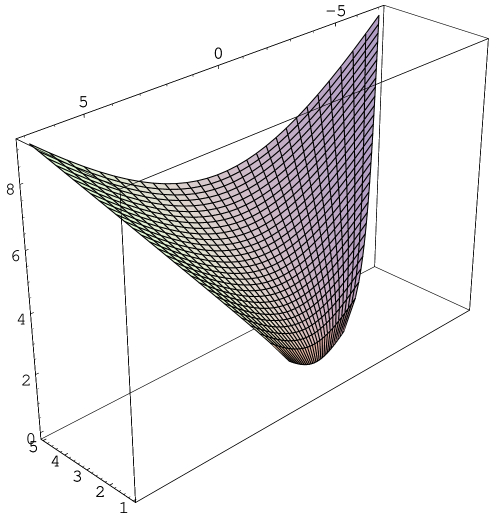
      This surface is the pseudosphere $\hbox{\bf S}^{2,1}(1/|C|;p_{0})$, with $p_{0}=(\pm C\mu,0,0)$ since by the expression of the parametrization (4), the coordinates of $M$ satisfies $(x\pm C\mu)^{2}+y^{2}-z^{2}=1/C^{2}$.

   2. (b)

      If $a^{2}+4bc=0$, then

      $$\frac{1}{\sqrt{1+z^{\prime 2}}}=\frac{az\pm C}{2b},\ \ C=2\sqrt{b\lambda}.$$

      The solution of this equation is

      $$z(u)=\frac{-C}{a}\pm\sqrt{\frac{4b^{2}}{a^{2}}\pm(u\pm\mu)^{2}},\ \mu\in\hbox{\bb R}.$$

Consider the parametrization given in (5). Then $EG-F^{2}=16u^{2}z^{\prime}$ and the relation (1) writes as

$$\frac{a}{2}\Bigg{(}\frac{1}{2u\sqrt{\epsilon z^{\prime}}}-\frac{\epsilon z^{\prime\prime}}{4(\epsilon z^{\prime})^{3/2}}\Bigg{)}+b\frac{z^{\prime\prime}}{8uz^{\prime 2}}=c.$$

Multiplying by $u$ we obtain a first integral. Exactly, we have

$$\frac{a}{4}\Bigg{(}\frac{u}{\sqrt{\epsilon z^{\prime}}}\Bigg{)}^{\prime}-\frac{b}{8}\Bigg{(}\frac{1}{z^{\prime}}\Bigg{)}^{\prime}=cu.$$

Then there exists a integration constant $\lambda\in\hbox{\bb R}$ such that

$$\frac{a}{4}\frac{u}{\sqrt{\epsilon z^{\prime}}}-\frac{b}{8z^{\prime}}=\frac{c}{2}u^{2}+\lambda.$$

(15)

From (15), we obtain the value of $\sqrt{\epsilon z^{\prime}}$:

$$\sqrt{\epsilon z^{\prime}}=\frac{a\epsilon u\pm\sqrt{(a^{2}-4bc\epsilon)u^{2}-8b\epsilon\lambda}}{4\epsilon(cu^{2}+2\lambda)}.$$

As in the two previous cases, we distinguish two special cases:

1. 1.

   If $\lambda=0$, then

   $$\sqrt{\epsilon z^{\prime}}=\frac{a\pm\epsilon\sqrt{a^{2}-4bc\epsilon}}{4c}\frac{1}{u}:=\frac{C}{u},\ \ C=\frac{a\pm\epsilon\sqrt{a^{2}-4bc\epsilon}}{4c}.$$

   We solve this equation obtaining

   $$z(u)=-\frac{\epsilon C^{2}}{u}+\mu,\ \ \mu\in\hbox{\bb R}.$$

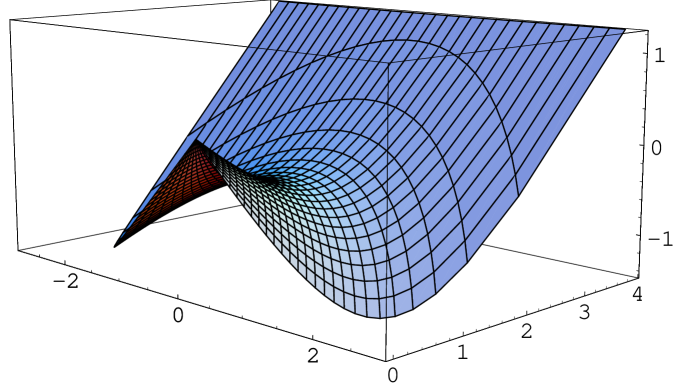
   From the parametrization (5), we see that $M$ satisfies the equation $x^{2}+y^{2}-(z-\mu)^{2}=-4\epsilon C^{2}$. Thus, if $p_{0}=(0,0,\mu)$, we have that $M=\hbox{\bf H}^{2,1}(2|C|;p_{0})$ if $\epsilon=1$, and $M=\hbox{\bf S}^{2,1}(2|C|;p_{0})$ if $\epsilon=-1$.

2. 2.

   Assume $a^{2}-4bc\epsilon=0$. Then

   $$\sqrt{\epsilon z^{\prime}}=\frac{a\epsilon u\pm C}{4\epsilon(cu^{2}+2\lambda)},\ \ C=\sqrt{-8b\epsilon\lambda}.$$

   We point out that $-8b\epsilon\lambda>0$ and that combining with $a^{2}-4bc\epsilon=0$, we have $c\lambda\leq 0$. The solution is

   $$z(u)=\frac{1}{64}\Big{(}\frac{\mp 4aC\lambda\pm\epsilon(cC^{2}-2a^{2}\lambda)u}{\epsilon c\lambda(2\lambda+cu^{2})}+\epsilon\frac{cC^{2}+2a^{2}\lambda}{\sqrt{-2c^{3}\lambda^{3}}}\mathrm{arc}\tanh(\sqrt{-\frac{c}{2\lambda}}\ u)\Big{)}+\mu,\ \ \mu,\lambda\in\hbox{\bb R}.$$