Non-Hermitian Chiral Edge Modes With Complex Fermi Velocity
Abstract
Recently, much attention has been paid to uncovering the influence of dissipation on a quantum system, particularly on how the non-Hermitian (NH) terms modify the band topology of topological materials and reshape the profile of the wavefunctions of a system (or the NH skin effect). In this paper, a specific NH skin effect that induced by local dissipation is studied for chiral edge modes, in which the NH term corresponds to the local imaginary Fermi velocity of the chiral edge modes. By solving the NH Schrödinger equation of the non-Hermitian chiral edge modes (nhCEs) with complex Fermi velocity, we uncovered the remarkable complex spectra and the wavefunctions of the nhCEs. We find that the complex spectra of these modes is a straight line in the topological materials, and its chirality can separates the modes with positive energy from those with negative energy, in which they are localized at different positions. We also studied the nhCEs at the boundary of 2-dimensional (2D) topological materials, the 2D -wave superconductor and the Qi-Wu-Zhang model, in which the general law of nhCEs was verified. We expect that our findings will pave the way for researching the transport properties of the chiral edge modes in the non-equilibrium context.
pacs:
11.30. Er, 75.10. Jm, 64.70. Tg, 03.65.-WI Introduction
The physics of non-Hermitian (NH) systems have attracted much attention in recent years NH_system1 ; NH_system2 , not only because of its remarkable topological property NH_topology1 ; NH_topology2 , but also because of many interesting phenomena that do not have Hermite counterpart, such as -physics NH_PT1 ; NH_PT2 ; NH_PT3 and NH skin effectNH_skin0 ; NH_skin1 ; NH_skin2 ; NH_skin3 ; NH_skin4 . The NH Hamiltonian is an effective description of some open quantum systems open_system_NH or the system that composed of quansi-particles finite_lifetime . Many remarkable phenomena has been uncovered by studying the effective NH Hamiltonian, such as unidirectional invisibility uni_directional1 ; uni_directional2 , single-mode lasing sigle_mode_pt1 ; single_mode_pt2 , and enhanced sensitivity enhenced_apply1_pt ; enhenced_apply2_pt ; enhenced_apply3_pt ; enhenced_apply4_pt . In a NH system, the main problem is to figure out how the dissipation (or the NH terms) affects the property of the system, which are determined both by its complex spectra and its wavefunctions NH_spectra_vector ; NH_BBC4 . Fortunately, most of problems have been settled thanks to the non-Bloch band theory NH_skin3 ; NH_skin4 ; non_bloch , which only takes into account the global dissipation in the bulk. However, dissipation that only occurs in certain part of system is more common and easier to control in real experiments nonequilibrium_boundary ; open_system_local , which makes the problem that how the local dissipation affects the property of a system becomes an urgent issue needs to be addressed. Many interesting phenomena induced by local dissipation have been revealed local_NH1 ; local_NH2 ; local_NH3 , such as scale-free localization scale_free_local ; imputiry_nonreciprocal and the -physics local_nh_PT . The influence of local dissipation on the anomalous chiral edge modes is also an interesting topic, not only because of its amazing transport property, but also because it would gives insights to the problem of hybrid skin-topological effect chiral_localization ; high_order_skin1 .
The anomalous chiral edge modes can only be found at the edge of topological materials because of the Nielsen-Ninomiya theorem NN_theorem1 ; NN_theorem2 . In solid state materials, these anomalous edge modes serve as perfectly robust transport channels that produce quantised Hall conductance. Due to the topological protection of the bulk band structure, they are robust against localization, meaning that it remains extended even though there is defect or disorder edge_localization1 ; edge_localization2 ; edge_localization3 ; edge_localization4 . Incredibly, the inclusion of dissipation would make it possible to localize these chiral edge modes, which is related to the hybrid skin-topological effect chiral_localization . However, we find that previous studies of the non-Hermitian chiral edge modes (nhCEs) experiencing imaginary potential chiral_localization can not be generalized to the chiral Majorana edge modes in the two-dimensional (2D) topological supercondutors (SC), that the chiral Majorana edge modes remained as the extended states due to the intrinsic particle-hole symmetry. Fortunately, this problem is solved by considering the nhCEs with complex Fermi velocity, that the non-hermitian Majorana chiral edge modes become the localized states.
In this paper, the general properties of nhCEs with complex Fermi velocity is revealed by solving the NH Schrödinger equation of nhCEs. We find that the interplay between dissipation and the underlying low energy physics gives rise to non-trivial energy spectra and distinct localization rules, in which the chirality of edge modes is essential in determining the position where they are localized. We find that the complex spectra of nhCEs with local complex Fermi velocity is a straight line, and the chirality can tells the difference between the modes with positive energy and the those with negative energy, in which they are localized at different positions. Moreover, general properties of the nhCEs are verified in the 2-dimensional (2D) topological materials , the 2D -wave SC and Qi-Wu-Zhang (QWZ) model.
The structure of this paper is as follows. In Sec. II, we formulate the Shrödinger equation of the nhCEs with local complex Fermi velocity, in which the influences of the dissipation to its wavefunction and its energies are revealed. We find that its localization rules are related to the chirality of the edge modes, so called the chiral localization. In Sec. III, we study the nhCEs at the boundary of 2D -wave SC. It is find that the only NH term that would results in localized chiral Majorana edge modes is the imaginary Fermi velocity. In Sec. IV, the nhCEs in the 2D QWZ model are studied. Main findings and future directions are summarized in Sec. V.
II the non-Hermitian anomalous chiral edge modes
The anomalous chiral edge modes can only exist at the boundary of topological materials due to the Nielsen-Ninomiya theorem NN_theorem1 ; NN_theorem2 , these long-wave-length excitations are restricted to propagate only in one direction and are protected by the non-trivial topology of bulk. And the dispersion relation of those modes are linear in , i. e. , they are correspond to the robust edge channels in the Quantum Hall Liquids, that
| (1) |
where is the Fermi velocity that defined as . And in the topological materials, the Fermi energy and Fermi wave-vector is set to zero for simplicity. Furthermore, we need to set the upper bound of wave-vector to the anomalous edge modes in the actual topological system, in which the modes that wave-vector above is no longer the anomalous edge modes, in other words, the anomalous edge modes are those satisfy .
Now, we want to know what the consequences would be if these topological modes are dissipative. The physical meaning of dissipation is that the lifetime of edge excitations is finite, which is usually corresponds to the situations that either there is particle gain/loss at the boundary of system, or the boundary potential has a non-zero imaginary part. Given that the bulk topology of system is unaffected by the local dissipation which only exist at the boundaries, then it is expected that only the anomalous chiral edge modes would experience dissipation, and become the nhCES we want to study. For the nhCEs, it is natural that the eigenenergys might have non-zero imaginary parts, which the effective low-energy description is a non-Hermitian Hamiltonian
| (2) |
where the eigenenergy’s imaginary part is depend on how is varied. Furthermore, because the low energy physics is linear in , then there would have two kinds of dissipation, one is -dependent (that is linear in ), another one is -independent. The -independent dissipation corresponds to the gain/loss of particles and has been studied in Ref. chiral_localization , we will study the -dependent dissipation in this paper, which the dissipation is the non-reciprocal hopping at the boundary of system and corresponds to the imaginary fermi velocity of the anomalous chiral edge modes.
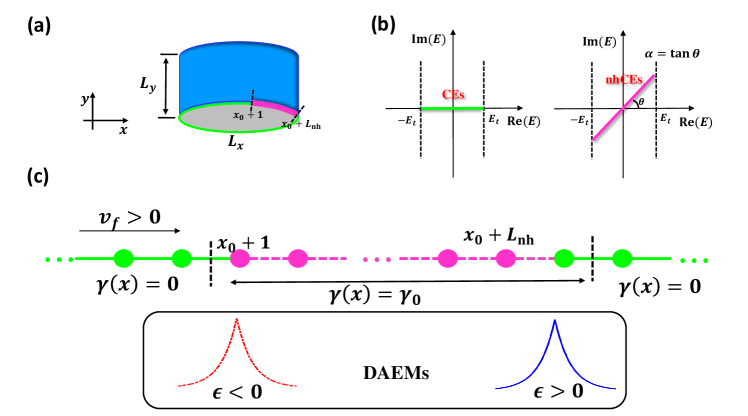
Before we continue our discussion, let’s clarify the configuration of topological materials which host the nhCEs. The system is in cylinder geometry that periodic in the -direction and open in the -direction, and the dissipation is introduced locally to the lower boundary of system to make its edge modes become dissipative, as present in Fig. 1 (a), where the height and the circumference of cylinder are and correspondingly.
For the -dependent dissipation, and the Schrödinger equation of the nhCEs reads
| (3) |
where and are real valued, and corresponds to the imaginary part of the eigenenergy. The solution of Eq. (3) is
| (4) | |||||
where is the normalization factor. Because the edge of topological materials is a periodic chain in our configuration, then the principle of continuous condition of the wavefunctions implies that should be satisfied. Then, we have
| (5) |
where . Consequently, the following equations should be satisfied
| (6) | |||
| (7) |
where is the average value of which the weight function is . Given that is a constant when is fixed, then the real part and the imaginary part of eienenergy is proportional to each other, which means that the complex spectra of these nhCEs is a straight line.
Interestingly, acquires an exponential factor, which implies that the anomalous edge modes might become the localized states. However, if the sign of factor remains the same along the edge of system, then the edge modes will still be the extended state. Take and as an example, one can find that is exponentially increase when , where , which means that there is no site where can localize at. As the results, the edge modes can only localize at the position where changes sign. For example, if , can localize at the position that and , in which is exponentially decay at the both sides of ; and if , can only localize at the position that and .
More specifically, let’s consider the distribution of dissipation as a Heaviside function at the boundary of system, that
| (8) |
where is the total links at the boundary of system which have non-reciprocal hopping, or the Fermi velocity of edge modes in these space is a complex number. For the dissipation in Eq. (8), its easy to find that
| (9) |
It says that is fixed when , and are given, which implies that the shape of complex spectra is a straight line. Owing to continuous condition of the wavefunction, the distribution of would completely determine the profile of the nhCEs. That the modes with the positive sign of and those with negative sign of are localized at different positions, one is at , another one is at . Suppose and , then the modes that are localized at ; while the modes that are localized at , as seen in Fig. 1 (b). While the situation that (for the edge modes at another boundary) and is the other way around, the modes which are localized at ; while the modes which are localized at .
Interestingly, the shape of the nhCEs in the space where is exponentially like for the dissipation is a Heaviside function in Eq. (8), i.e. , and the localization strength , where the first factor is because for the low-energy excitations. In results, the localization behavior of nhCEs with complex Fermi velocity is scale-relevant.
In the following sections, we will examine the general law of nhCEs with local complex Fermi velocity in the 2D -wave SC and the Chern insulators, in which the remarkable complex spectra and the wavefunctions’ profile of nhCES are investigated.
III non-Hermitian chiral majorana edge modes in the 2D -wave SC
Owing to the superconducting gap, a SC is similar to an insulator, while one thing that distinguishes SC from an insulator is that the former has intrinsic particle-hole symmetry (PHS). The SC is usually described with a Bogoliubov-de Genes Hamiltonian
| (10) |
where is a Nambu vector that , which is an annihilation operator of both the particles and the holes, and is a Bloch Hamiltonian. Because of the PHS, the eigenvector of is symmetric, that if is the eigenvector with eigenvalue , then is the eigenvector with eigenvalue . Meanwhile, the excitations of the system are the Bogoliubov quasiparticles
| (11) |
which is composed of both particles and holes. Similar to topological insulators (TIs), non-trivial bulk topology of will results in gapless Majorana edge modes, which are the equal superposition of particles and holes ( or for the Majorana chiral edge modes). In the 2D -wave SC, the Bloch Hamiltonian is topo_mat_ref1 ; topo_mat_ref2
| (12) | |||||
where the PHS is: . The topology of 2D -wave SC is captured by the Chern number of the ground state manifold in Eq. (12), that the Chern number is non-zero when , and we had set for simplicity. Amazingly, due to the PHS, the in gap low-energy excitations of a SC are the Majorana fermions, which are their own anti-particles. These Majorana fermions which have unusual braiding statistical property are key for the topological quantum computation topo_comp_ref1 ; topo_comp_ref2 .
When the system is in a cylinder geometry, that the boundary condition along -direction is periodic while the boundary condition along -direction is open. Then there are Majorana chiral edge modes at the boundaries and , which is two-component vector
| (13) |
where the internal degrees of freedom in each unit cell are the particles and the holes, that the edge modes are the equal superposition of the particles and the holes, so become the Majorana fermions of the system. The energy dispersion of the edge modes is
| (14) |
where ”” specify different boundaries, and the fermi velocity of chiral Majorana edge modes is . Then, we want to figure out how to have the localized Majornan modes by introducing the dissipations, that both the imaginary Fermi velocity and the imaginary potential are discussed.
III.1 Two-body gain/loss at the boundary 2D -wave SC
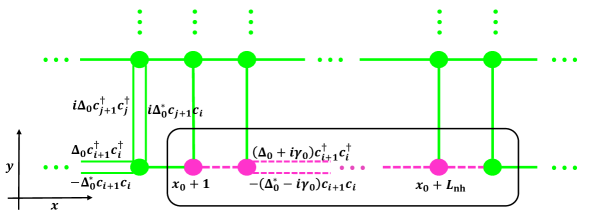
In the 2D -wave SC, the momentum part in the corresponding Dirac Hamiltonian is . The Fermi velocity of the Majorana edge mode is the pairing term along -direction, and the complex Fermi velocity corresponds to the pairing amplitude being a complex number . This can be realized with the two-body gain (loss) along the boundary, which is usually caused by the inelastic collisions two_body_loss1 ; two_body_loss2 . Then, suppose that the dissipation is a Heaviside function in Eq. (8), that the links among the lattices that range from site to site experiencing the two-body gain, as presented in Fig. 2.
The complex spectra of 2D -wave SC which its boundary experiencing two-body gain is presented in Fig. 3 (a), which the complex spectra of nhCEs is a straight line. Moreover, if the dissipation corresponds to the imaginary Fermi velocity of anomalous edge modes, then the edge modes are localized at and , see Fig. 3 (b), that the modes with are localized at , while the modes with are localized at .
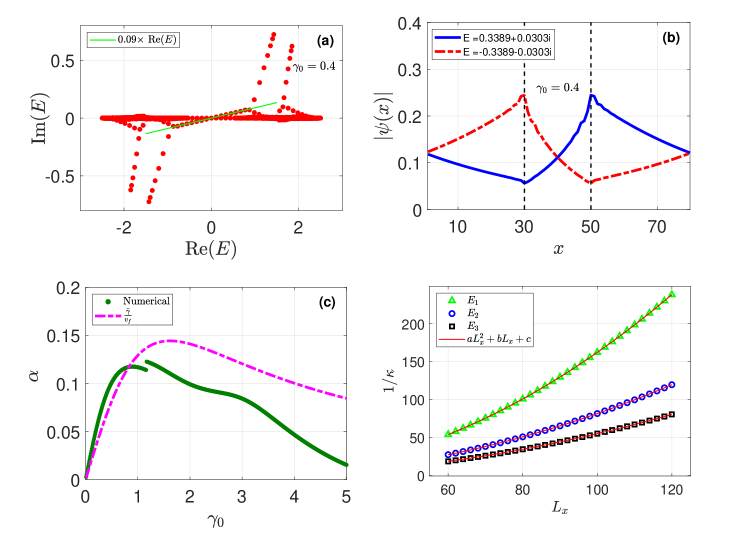
Moreover, in Fig. 3 (c), the numerical value of is obtained by fitting the complex spectra of nhCEs in the region and , this is because that the bulk gap of 2D -wave SC in Eq. (12) is when . We find that is well described with , however it is much smaller than when is sufficient high, see the situation that in Fig. 3 (c). This is attribute to the bound state, that the effective dissipation that the edge modes felt is smaller than if there is bound state, such that is smaller than .
Furthermore, the scaling behavior of the nhCEs with complex Fermi velocity is checked in Fig. 3 (d), that the inverse localization strength in the space where for different values of is well described by . The scaling behavior of the wavefunctions is originates from two parts, one is that , another one is that , such that .
III.2 gain/loss of particles at the boundary of 2D -wave SC
It is proposed in Ref. chiral_localization that the nhCEs with local imaginary potential become the localized sates, which the dissipation corresponds to the local gain/loss of particles. However, local gain/loss of particles is not as usual as we expected in SC, the localized Majornana edge modes was not observed by introducing an on-site imaginary potential at the boundary of a 2D -wave SC. Instead the nhCEs remain extended, as presented in Fig. 4 (b). And the in-gap Majornana edge modes acquire a tiny imaginary part, see Fig. 4 (a), this is because that the on-site imaginary potential can still perturb its eigenenergy.
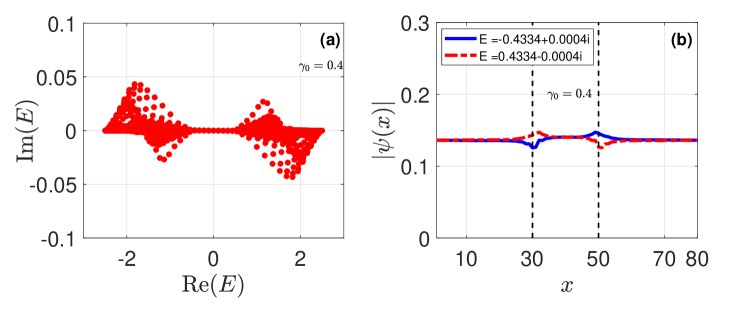
The reason why nhCEs remain extended for such occasion is because that the on-site imaginary potential keeps the PHS of SC NH_majorana . Because the Majornana chiral edge modes are the equal superposition of particles and holes, and the gain of particles is also the loss of holes, so the net contribution of imaginary potential to the Majornana chiral edge modes is zero as long as the PHS is maintained. In other words, the gain/loss of particles is not the imaginary potential to anomalous edge modes of the topological SC, therefore the nhCEs remain extended. If the PHS is broken, that the dissipation corresponds to the gain/loss of particles only or the gain/loss of holes only, then the chiral localization of the dissipative Majornana edge modes would be possible. However, it is impossible to break the PHS of SC because it is an intrinsic symmetry, so we conclude that the nhCEs remain extended in 2D -wave SC when the dissipation is the local gain/loss of particles.
IV Non-Hermitian chiral edge modes in the Chern insulators
The anomalous chiral edge modes in a Chern insulator are act as dissipationless channel that transports current along the boundary of system, and it is restricted to moving in a single direction. These modes are protected by the bulk topology of system and are robust against the disorder and the impurity. However, it is not known what will happen to these chiral edge modes when the dissipation corresponds to the imaginary Fermi velocity is introduced.
Take the 2D QWZ model as an example, in which the Bloch Hamiltonian is topo_mat_ref1 ; topo_mat_ref2
| (15) | |||||
where the Pauli matrices represent the internal degrees of freedom in each lattice site, which denote as and , () is the hopping amplitude along the ()-direction, and is the on-site potential which determines the band-gap of system. For QWZ model, edge long-wave-length excitations exist when the Chern number of its ground state manifold is non-zero. This is satisfied when , where we had set for simplicity. When the QWZ model is in a cylinder geometry as illustrated in Fig. 1 (a), there are two chiral edge modes at the boundaries and that propagate in opposite directions along the boundaries (the -direction). The edge modes are the two-component wavefunctions, referred to as
| (16) |
where the basis is the internal degrees of freedom and . The energy dispersion of the edge modes is
| (17) |
where the sign ”” depends on different boundaries, that the Fermi velocity of chiral edge modes is , i.e. .
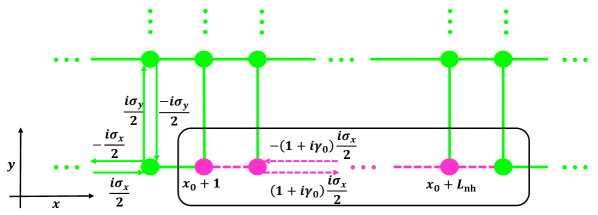
Now, we introduce the dissipation to the boundary of 2D QWZ model to make the Fermi velocity of edge modes becomes a complex number, that there are () links that stretches from site to site which the hopping amplitude is . Given that the momentum part is in the context of Dirac Hamiltonian in Eq. 15, then to meet with our expectation, it is necessary that the hopping between and and the hopping between to is a complex number , as presented in Fig. 5.
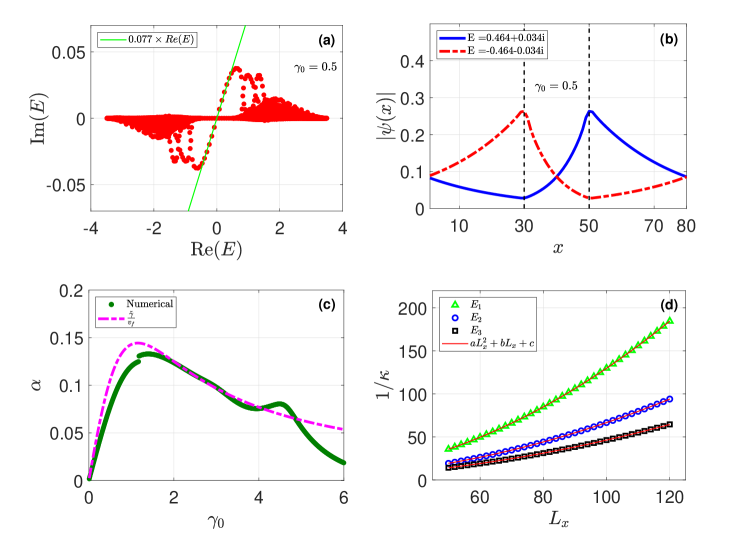
The complex spectra of 2D QWZ model that has non-reciprocal hopping at its lower boundary is presented in Fig. 6 (a), which the complex spectra of nhCEs is a straight line, i.e. is satisfied for the nhCEs, this is because that is fixed when , and are given. And the profile of the wavefunctions for the nhCEs at the boundary are presented in Fig. 6 (b), that the modes which are localized at site ; while the modes which are localized at site .
Moreover, in Fig. 6 (c), the numerical value of is obtained by fitting the complex spectra of nhCEs in the region and , this is because that the bulk gap of QWZ model in Eq. (15) is when . We find that is well described with . And the scaling behavior of the nhCEs with complex Fermi velocity in the QWZ model is checked in Fig. 6 (d), that the inverse localization strength in the space where for different values of is well described by .
V conclusion and discussion
In this paper, we investigated the properties of NH anomalous chiral edge modes that has local complex Fermi velocity. By solving the NH Schrödinger equation, we find that these dissipative modes that reside on the boundary of topological materials become the localized states. We find that the complex spectra of these nhCEs is a straight line. Surprisingly, the chirality of edge modes will determine the position where the nhCEs are localized, that the positive energy modes and the negative energy modes are localized at different positions. Different from the scale-free localization that induced by the local non-reciprocal hopping in the 1-dimension chain local_nh_PT , the localization of nhCEs with complex Fermi velocity is scale-relevant, which is the key property of low-energy physics. Furthermore, the general properties of these nhCEs have been tested in the 2D topological materials, the 2D -wave SC and the QWZ model, which is consistent with our theoretical prediction.
Significantly, previous studies on the nhCEs with local imaginary potential chiral_localization cannot be generalized to the 2D -wave SC, as there are no localized edge modes when the dissipation is local gain/loss of particles. This is because that the intrinsic PHS is maintained if there is on-site imaginary potential for topological SC NH_majorana . The Majorana edge modes in the 2D -wave SC are equal superposition of particles and holes, while the gain of particles is also loss of holes, so the net contribution of imaginary potential to the Majorana chiral edge modes in the 2D -wave SC is zero. As a results, it is impossible to introduce an imaginary potential to the chiral Majorana edge modes, then we can’t localize Majorana edge modes by introducing a local gain/loss of particles. This means that the only way to have localized Majorana edge modes in the dissipative context is for the dissipation to play the role of an imaginary Fermi velocity for the chiral Majorana edge modes.
In the NH system, The localization of the wavefunction is related to a unique phenomena called the NH skin effect. The physical implications of the NH skin effect have been extensively studied, such as chiral damping in open quantum system chiral_damping . It is expected that the localization of nhCEs would have its counterpart in the corresponding dynamic process, which would alter the transport property of the anomalous chiral edge modes. This is worth of researching and is a potential future direction.
VI acknowledgment
This work is supported by NSFC Grant No. 11974053 and No. 12174030.
References
- (1) Y. Ashida, Z. Gong, and M. Ueda, Non-hermitian physics, Advances in Physics 69, 249 (2020).
- (2) M. Sternheim and J. F. Walker, Non-hermitian hamiltonians, decaying states, and perturbation theory, Phys.Rev. C 6, 114 (1972).
- (3) Z. Gong, Y. Ashida, K. Kawabata, K. Takasan, S. Higashikawa, and M. Ueda, Topological Phases of Non-Hermitian Systems, Phys. Rev. X 8, 031079 (2018).
- (4) K. Kawabata, K. Shiozaki, M. Ueda, and Masatoshi Sato, Symmetry and Topology in Non-Hermitian Physics, Phys. Rev. X 9, 041015 (2019).
- (5) C. M. Bender and S. Boettcher, Real spectra in nonhermitian hamiltonians having pt symmetry, Phys. Rev. Lett. 80, 5243 (1998).
- (6) C. M. Bender, Making sense of non-hermitian hamiltonians, Reports on Progress in Physics 70, 947 (2007).
- (7) A. Mostafazadeh, Pseudo-Hermiticity versus PT symmetry: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian, J. Math. Phys. 43, 205 (2002); A. Mostafazadeh, Pseudo-Hermiticity versus PT symmetry II: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian, J. Math. Phys. 43, 2814 (2002); A. Mostafazadeh, Pseudo-Hermiticity versus PT symmetry III: The necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian, J. Math. Phys. 43, 3944 (2002);
- (8) V. M. Martinez Alvarez, J. E. Barrios Vargas, and L. E. F. Foa Torres, Non-Hermitian robust edge states in one dimension: Anomalous localization and eigenspace condensation at exceptional points, Phys. Rev. B 97, 121401(R) (2018).
- (9) Ching Hua Lee, and Ronny Thomale, Anatomy of skin modes and topology in non-Hermitian systems, Phys. Rev. B 99, 201103(R) (2018).
- (10) Stefano Longhi, Probing non-Hermitian skin effect and non-Bloch phase transitions, Phys. Rev. Research 1, 023013 (2019).
- (11) Shun-Yu Yao, and Zhong Wang, Edge States and Topological Invariants of Non-Hermitian Systems, Phys. Rev. Lett. 121, 086803 (2018).
- (12) Shun-Yu Yao, Fei Song, and Zhong Wang, Non-Hermitian Chern Bands, Phys. Rev. Lett. 121, 136802 (2018).
- (13) F. Roccati, G. Massimo Palma, F. Ciccarello, F. Bagarello, Non-Hermitian Physics and Master Equations, Open Systems & Information Dynamics 29, 1 (2022).
- (14) V. Kozii and L. Fu, Non-Hermitian Topological Theory of Finite-Lifetime Quasiparticles: Prediction of Bulk Fermi Arc Due to Exceptional Point, arxiv: 1708.05841v1, (2017).
- (15) Z. Lin, H. Ramezani, T. Eichelkraut, T. Kottos, H. Cao, and D. N. Christodoulides, Unidirectional invisibility induced by PT -symmetric periodic structures, Phys. Rev. Lett. 106, 213901 (2011)
- (16) L. Feng, Y.-L. Xu, W. S. Fegadolli, M.-H. Lu, J. E. B.Oliveira, V. R. Almeida, Y.-F. Chen, and A. Scherer, Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies, Nature Materials 12, 108 (2013).
- (17) H. Hodaei, M.-A. Miri, M. Heinrich, D. N. Christodoulides, and M. Khajavikhan, Parity-time–symmetric microring lasers, Science 346, 975 (2014).
- (18) L. Feng, Z. J. Wong, R.-M. Ma, Y. Wang, and X. Zhang, Single-mode laser by parity-time symmetry breaking, Science 346, 972 (2014).
- (19) H. Hodaei, A. U. Hassan, S. Wittek, H. Garcia-Gracia, R. El-Ganainy, D. N. Christodoulides, and M. Khajavikhan, Enhanced sensitivity at higher-order exceptional points, Nature 548, 187 (2017).
- (20) P.-Y. Chen and J. Jung, PT symmetry and singularity enhanced sensing based on photoexcited graphene meta surfaces, Phys. Rev. Applied 5, 064018 (2016).
- (21) Z.-P. Liu, J. Zhang, i. m. c. K. Ozdemir, B. Peng, H. Jing, X.-Y. Lü, C.-W. Li, L. Yang, F. Nori, and Y.-x. Liu, Metrology with PT -symmetric cavities: Enhanced sensitivity near the PT -phase transition, Phys. Rev. Lett. 117, 110802 (2016).
- (22) P.-Y. Chen, M. Sakhdari, M. Hajizadegan, Q. Cui, M. M.-C. Cheng, R. El-Ganainy, and A. Alú, Generalized parity–time symmetry condition for enhanced sensortelemetry, Nature Electronics 1, 297 (2018).
- (23) N. Matsumoto, K. Kawabata, Y. Ashida, S. Furukawa, and M. Ueda, Continuous Phase Transition without Gap Closing in Non-Hermitian Quantum Many-Body Systems, Phys. Rev. Lett. 125, 260601 (2020).
- (24) Xiao-Ran Wang, Cui-xian Guo, and Su-Peng Kou, Defective edge states and number-anomalous bulk-boundary correspondence in non-Hermitian topological systems, Phys. Rev. B. 101, 121116(R) (2020).
- (25) K. Yokomizo and S. Murakami, Non-Bloch Band Theory of Non-Hermitian Systems, Phys. Rev. Lett. 123, 066404 (2019).
- (26) G. T. Landi, D. Poletti, and G. Schaller, Nonequilibrium boundary-driven quantum systems: Models, methods, and properties, Rev. Mod. Phys. 94, 045006 (2022).
- (27) G. Barontini, R. Labouvie, F. Stubenrauch, A. Vogler, V. Guarrera, and H. Ott, Controlling the Dynamics of an Open Many-Body Quantum System with Localized Dissipation, Phys. Rev. Lett. 110, 035302 (2013).
- (28) J. Wiersig, Role of nonorthogonality of energy eigenstates in quantum systems with localized losses, Phys. Rev. A 98, 052105 (2018).
- (29) H. Fröml, C. Muckel, C. Kollath, A. Chiocchetta, and S. Diehl, Ultracold quantum wires with localized losses: Many-body quantum zeno effect, Phys. Rev. B 101, 144301 (2020).
- (30) V. Alba and F. Carollo, Noninteracting fermionic systems with localized losses: Exact results in the hydrodynamic limit, Phys. Rev. B 105, 054303 (2022).
- (31) L. Li, C. H. Lee, and J. Gong, Impurity induced scale-free localization, Communications Physics 4, 42 (2021).
- (32) Y. Liu, Y. Zeng, L. Li and S. Chen, Exact solution of the single impurity problem in nonreciprocal lattices: Impurity-induced size-dependent non-Hermitian skin effect, Phys. Rev. B 104, 085401 (2021).
- (33) C.-X. Guo, X. Wang, H Hu, and S. Chen, Accumulation of scale-free localized states induced by local non-Hermiticity, Phys. Rev. B 107, 134121 (2023).
- (34) X.-R. Ma, K. Cao, X.-R. Wang, Z. Wei, and S.-P. Kou, chiral skin effect, arxiv: 2304.01422v1, (2023)
- (35) Y. Li, C. Liang, C. Wang, C. Lu and Y. C. Liu, Gain/Loss-Induced Hybrid Skin-Topological Effect, Phys. Rev. Lett. 128, 223903 (2022).
- (36) H. B. Nielsen and M. Ninomiya, Nucl. Phys. B 193, 173 (1981).
- (37) H. B. Nielsen and M. Ninomiya, Phys. Lett. B 105, 219 (1981).
- (38) Z. Wang, Y. Chong, J. D. Joannopoulos and M. Soljačić, Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).
- (39) M. Hafezi, S. Mittal, J. Fan, A. Migdall and J. M. Taylor, Imaging topological edge states in silicon photonics. Nat. Photonics 7, 1001–1005 (2013).
- (40) Z. Yang, F. Gao, X. Shi, X. Lin, Z. Gao, Y. Chong and B. Zhang, Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
- (41) Y. Ding, and et al. Experimental demonstration of acoustic Chern insulators. Phys. Rev. Lett. 122, 014302 (2019).
- (42) János K. Asbóth, László Oroszlány, and András Pályi, A Short Course on Topological Insulators, Springer Press, Switzerland, 2016.
- (43) B. Andrei Bernevig, Taylor L. Hughes, and András Pályi, Topological Insulators and topological superconductors, Princeton University Press, Princeton and Oxford, 2013.
- (44) J. K. Pachos, Introduction to topological quantum computation, Cambridge university press, The Edinburgh building, Cambridge, 2012.
- (45) R. Moessner and J. E. Moore, Topological phases of matter, Cambridge university press, Cambridge CB2 8BS, 2021.
- (46) K. Yamamoto, M. Nakagawa, K. Adachi, K. Takasan, M. Ueda, and N. Kawakami, Theory of Non-Hermitian Fermionic Superfluidity with a Complex-Valued Interaction, Phys. Rev. Lett. 123, 123601 (2019).
- (47) G. Pagano, M. Mancini, G. Cappellini, L. Livi, C. Sias, J. Catani, M. Inguscio, and L. Fallani, Strongly Interacting Gas of Two-Electron Fermions at an Orbital Feshbach Resonance, Phys. Rev. Lett. 115, 265301 (2015).
- (48) S. Lieu, Non-Hermitian Majorana modes protect degenerate steady states, Phys. Rev. B 100, 085110 (2019).
- (49) F. Song, S. Yao, and Z. Wang, Non-Hermitian Skin Effect and Chiral Damping in Open Quantum Systems, Phys. Rev. Lett. 123, 170401 (2019).