Nonlinear hydrodynamic response confronts LHC data
Abstract
Higher order harmonic flow (with ) in heavy-ion collisions can be measured either with respect to their own plane, or with respect to a plane constructed using lower-order harmonics. By assuming that higher flow harmonics are the superposition of medium nonlinear and linear responses to initial anisotropies, we propose a set of nonlinear response coefficients ’s, which are independent of initial state by construction. In experiments, ’s can be extracted as the ratio between higher order harmonic flow measured in the plane constructed by and , and moments of lower order harmonic flow. Simulations with single-shot hydrodynamics and AMPT model lead to results of these nonlinear response coefficients in good agreement with the experimental data at the LHC energy. Predictions for and measured with respect to plane of lower order harmonics are given accordingly.
keywords:
Harmonic flow, nonlinear hydrodynamics response, heavy-ion collisions1 Introduction
The observed flow phenomena in high energy heavy-ion collisions carried out at RHIC and the LHC provides great opportunities in analyzing the collective dynamics of the strongly-coupled Quark-Gluon Plasma (QGP) (for a recent review, cf. [1]). To a quantitative level, the analysis of harmonic flow , which is defined through a Fourier decomposition of the observed particle spectrum,
| (1) |
has led to strong constraints on the dissipative properties of the QGP medium in various aspects. For instance, correlations among flow harmonics have been studied in terms of the correlations between event-plane [2], which present non-trivial patterns depending on the shear viscosity over entropy ratio of the medium. Recent measurements of harmonic flow have achieved results with high precisions, which extends the studies of harmonic flow to flow fluctuations [3] and higher order harmonic flow () [4]. In particular, higher order flow harmonics have been measured with respect to their own event-plane, and plane constructed by lower order flow harmonics, from which nonlinear medium response to initial eccentricities can be studied. In this work, we focus on the nonlinear generation of higher order flow harmonics in heavy-ion collisions. By assuming that higher harmonics are the superposition of medium nonlinear and linear responses, a new set of nonlinear response coefficients are formulated.
2 Nonlinear hydrodynamic response and
We expand harmonic flow in a series of initial eccentricities , accounting for the fact that magnitudes of initial eccentricities are small. Note that in this work, , as well as defined in Eq. (1) are taken as complex quantities. For higher order flow harmonics, it has been shown that nonlinear hydro response to initial eccentricities result in significant contributions [5, 6]. Taking the fourth order harmonic flow as an example, in addition to the component which is linearly proportional to , there exists a large fraction induced by hydro response to . Therefore, one can write as,
| (2) |
has been absorbed into in the second term on the right hand side of Eq. (2), accordingly the coefficient is found independent of initial eccentricities by construction. Similar strategy can be applied to other higher order harmonic flow as well. For , and , the corresponding expansion leads to
| (3a) | ||||
| (3b) | ||||
| (3c) | ||||
The nonlinear terms in the right-hand side are the lowest-order terms involving and which are compatible with rotational symmetry. For , there exists a non-negligible component from cubic order hydro response to , which has already been noticed through the observed event-plane correlation between and [2], thus one must expand to cubic order, with an extra cubic order coefficient . For , there is no contributions of quadratic order, thus the coefficient is defined regarding the cubic order hydro response to .
In the hydro response formalism, ’s are interpreted as ratios between nonlinear and linear flow response coefficients, which are independent of the initial density profile for a given centrality class. Each can be readily evaluated in a single-shot hydrodynamic simulation [6] by choosing an initial density profile such that only the term involving is nonvanishing in the expansion of Eqs. (2) and (3). If one analyses a set of events in a centrality class, where the flow fluctuates event to event, as in actual heavy-ion experiments and AMPT simulations [7], ’s can be isolated using Eqs. (2) and (3) under the assumption that the terms in the right-hand side are mutually uncorrelated [8]:
| (4a) | ||||
| (4b) | ||||
| (4c) | ||||
| (4d) | ||||
The expressions on the right hand side of Eqs. (4) involve the higher order harmonic flow measured in the plane of lower order harmonics. For example, can be measured in experiments in its own event-plane which is defined in Eq. (1), as well as the event-plane which is determined by . More explicitly, measured with respect to is
| (5) |
It is worth mentioning that measuring higher order flow harmonics in the event plane of and/or is equivalent to the corresponding measurement of event plane correlations [2], as demonstrated by the second identity in Eq. (5). The denominators in Eqs. (4) involve various moments of the distributions of and . There is no direct measurement of flow moments up to date in experiments, though it can be done in a generalized scalar-product method, with sufficient rapidity gap [9]. In this work, we extract flow moments from flow cumulants [10] which are measured. For instance, the fourth order moment of is related to and by
| (6) |
3 Results and discussions
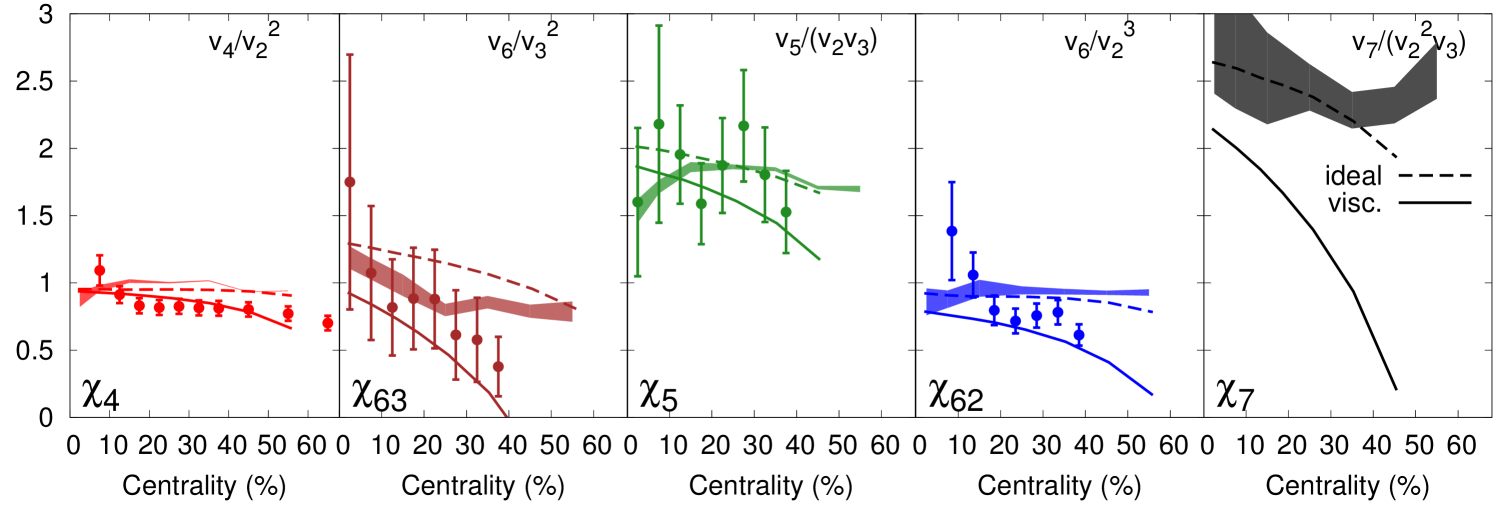
The CMS collaboration has measured , and cumulants of distributions [4]111 Cumulants of distributions from the CMS collaboration have so far been published up to . In this work we approximately take , as being implied from the measurements by the ATLAS collaboration [3]. , therefore we are able to assess and according to Eqs. (4). To evaluate and , we estimate and from the event-plane correlations and measured by the ATLAS collaboration [2], in addition to the cumulants of distributions from the CMS collaboration. ’s from the TeV PbPb at the LHC are shown as symbols in Fig. 1. To make comparisons, we calculate these nonlinear response coefficients from single-shot hydro simulations [6] as well as AMPT [7]. There is no event-by-event fluctuations implemented in our hydro simulations, where the initial condition is taken by perturbing a smooth and azimuthally symmetric Gaussian density profile with specific initial eccentricities. The normalization of the Gaussian profile is adjusted to fit the values of of LHC PbPb in a given centrality class. Results from ideal and viscous (with ) hydro simulations are depicted as dashed and solid lines respectively in Fig. 1, which present an overall agreement comparing with the experimental data. AMPT simulations contain non-trivial event-by-event fluctuations at the nucleonic and partonic levels, and the parton ellastic cross-section is taken to be mb. It is worth mentioning that ideal hydrodynamics predicts quantitative relations among these nonlinear response coefficients due to Cooper-Fyer freeze-out [11]: , and , which are consistent with the experimental data in Fig. 1 as well as the results obtained from AMPT.
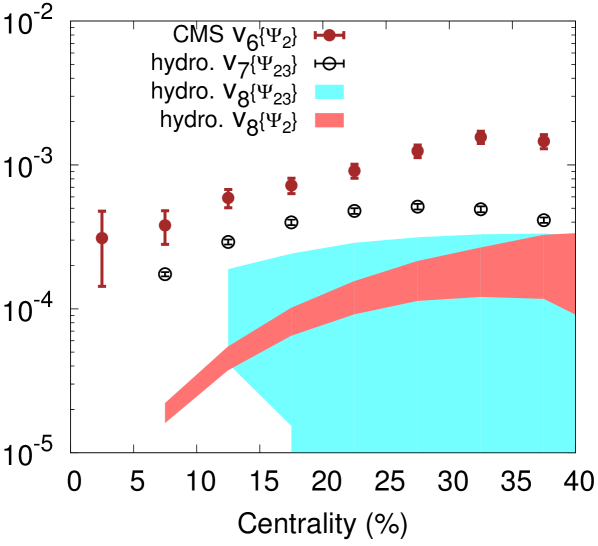
Although there is no experimental data available so far for the extraction of nonlinear response coefficients for the flow harmonics of order , we make predictions in our model simulations for and . For , there exist a cubic order term and a quartic order term allowed by rotational symmetry,
| (7) |
which correspond in experiments to the measurements of in the event-plane constructed by and , and event-plane of respectively,
| (8) |
from our model simulations are presented in Fig. 1. In Fig. 2, and measured in the event-plane consturcted by and are predicted with single-shot hydro simulations according to Eqs. (4d) and (8).
4 Conclusions
Under fairly general assumptions, we have proposed a new set of nonlinear response coefficients based on the measurements of higher order harmonic flow with respect to the event-plane constructed by and . These coefficients are independent of the detailed information of initial state by construction. Model simulations with single-shot hydrodynamics and AMPT give rise to predictions in good agreement with experimental data. We noticed that the relative ratios among these coefficients are consistent with an ideal hydro expectation based on the analysis of freeze-out. Nonlinear response coefficients associated with and are calculated as well in our theoretical models as predictions.
Acknowledgements
LY is funded by the European Research Council under the Advanced Investigator Grant ERC-AD-267258.
References
- [1] Heinz U and Snellings R 2013 Ann. Rev. Nucl. Part. Sci. 63 123–151 (Preprint 1301.2826)
- [2] Aad G et al. (ATLAS) 2014 Phys. Rev. C90 024905 (Preprint 1403.0489)
- [3] Aad G et al. (ATLAS Collaboration) 2013 JHEP 1311 183 (Preprint 1305.2942)
- [4] Chatrchyan S et al. (CMS) 2014 Phys. Rev. C89 044906 (Preprint 1310.8651)
- [5] Gardim F G, Grassi F, Luzum M and Ollitrault J Y 2012 Phys. Rev. C85 024908 (Preprint 1111.6538)
- [6] Teaney D and Yan L 2012 Phys. Rev. C86 044908 (Preprint 1206.1905)
- [7] Lin Z W, Ko C M, Li B A, Zhang B and Pal S 2005 Phys. Rev. C72 064901 (Preprint nucl-th/0411110)
- [8] Yan L and Ollitrault J Y 2015 Phys. Lett. B744 82–87 (Preprint 1502.02502)
- [9] Bhalerao R S, Ollitrault J Y and Pal S 2015 Phys. Lett. B742 94–98 (Preprint 1411.5160)
- [10] Borghini N, Dinh P M and Ollitrault J Y 2001 Phys. Rev. C64 054901 (Preprint nucl-th/0105040)
- [11] Borghini N and Ollitrault J Y 2006 Phys.Lett. B642 227–231