Nonlogarithmic divergence of a deflection angle by a marginally unstable photon sphere of the Damour-Solodukhin wormhole in a strong deflection limit
Abstract
Static, spherically symmetric black holes and compact objects without an event horizon have unstable (stable) circular orbits of a light called photon (antiphoton) sphere. A Damour-Solodukhin wormhole has been suggested as a simple black hole mimicker and the difference of its metric tensors from a black hole is described by a dimensionless parameter . The wormhole with two flat regions has two photon spheres and an antiphoton sphere for and a photon sphere for . When the parameter is , the photon sphere is marginally unstable because of degeneration of the photon spheres and antiphoton sphere. We investigate gravitational lensing by the wormhole in weak and strong gravitational fields. We find that the deflection angle of a light ray reflected by the marginally unstable photon sphere diverges nonlogarithmically in a strong deflection limit for , while the deflection angle reflected by the photon sphere diverges logarithmically for . We extend a strong deflection limit analysis for the nonlogarithmic divergence case. We expect that our method can be applied for gravitational lenses by marginally unstable photon spheres of various compact objects.
I Introduction
Recently, LIGO and VIRGO Collaborations have reported the direct detection of gravitational waves from black holes Abbott:2016blz ; LIGOScientific:2018mvr and Event Horizon Telescope Collaboration has reported the ring image of supermassive black hole candidates at the center of a giant elliptical galaxy M87 Akiyama:2019cqa . The black holes and the other compact objects with a strong gravitational field described by general relativity will be more important to understand our universe.
It is well known that static, spherically symmetric compact objects have unstable (stable) circular photon orbit called photon (antiphoton) sphere Claudel:2000yi ; Perlick_2004_Living_Rev . The upper bound of the radius of the (anti)photon sphere of the static, spherically symmetric black hole under the weak energy condition is given by , where is the mass of the black hole Hod:2017xkz . The (anti)photon sphere has important roles in several phenomena in a strong gravitational field: Light rays emitted by a source and reflected by the photon sphere make infinite number of dim images Hagihara_1931 ; Darwin_1959 ; Atkinson_1965 ; Luminet_1979 ; Ohanian_1987 ; Nemiroff_1993 ; Frittelli_Kling_Newman_2000 ; Virbhadra_Ellis_2000 ; Bozza_Capozziello_Iovane_Scarpetta_2001 ; Bozza:2002zj ; Perlick_2004_Phys_Rev_D ; Bozza_2010 , which are named relativistic images in Ref. Virbhadra_Ellis_2000 , on the both sides of the photon sphere and we can survey the compact object with the photon sphere by the images even if the compact objects themselves do not emit light rays. The photon sphere can be observed during a collapsing star to be a black hole Ames_1968 ; Synge:1966okc ; Yoshino:2019qsh . The photon sphere has strong influence on the high-frequency behavior of the photon absorption cross section Sanchez:1977si ; Decanini:2010fz and the high-frequency spectrum of quasinormal modes of compact objects Press:1971wr ; Goebel_1972 ; Raffaelli:2014ola . An observer moving on the photon sphere feels no centrifugal force and no gyroscopic precession Abramowicz_Prasanna_1990 ; Abramowicz:1990cb ; Allen:1990ci ; Hasse_Perlick_2002 and it is the fastest way to circle a static, spherically symmetric black hole for massless particles Hod:2012nk . The photon sphere is correspond to Bondi’s sonic horizon of a radial fluid Mach:2013gia ; Chaverra:2015bya ; Cvetic:2016bxi ; Koga:2016jjq ; Koga:2018ybs ; Koga:2019teu .
Stability of light rings, i.e., circular photon orbits Koga:2019uqd , of compact objects are an important property of the spacetime. Instability of the compact objects with the stable light rings has been concerned since they cause the slow decay of linear waves Keir:2014oka ; Cardoso:2014sna ; Cunha:2017qtt . The numbers of light rings of stationary, axisymmetic compact objects without an event horizon under energy conditions are two at least, they are even number in general, and the inner light ring is stable Cunha:2017eoe . Hod has shown that spherically symmetric compact objects without an event horizon have odd number light rings because of degeneration Hod:2017zpi . We note that we cannot apply the theorem of the number of the light rings for wormholes since a trivial topology has been assumed in Refs. Cunha:2017eoe ; Hod:2017zpi .
General relativity permits the wormholes which can have nontrivial topological structures Visser_1995 ; Morris_Thorne_1988 . The wormholes have a throat which connects two regions of one universe or two universes. Gravitational lensing Schneider_Ehlers_Falco_1992 ; Schneider_Kochanek_Wambsganss_2006 ; Perlick_2004_Living_Rev is used to find dark gravitating objects like wormholes. However, we cannot distinguish the wormhole with a positive mass from other massive objects such as a black hole under a weak-field approximation. Therefore, we must rely on the observation near the throat or the photon sphere in a strong gravitational field such as gravitational lensing of light rays scatter by the throat or the photon sphere Chetouani_Clement_1984 ; Perlick_2004_Phys_Rev_D ; Nandi:2006ds ; Muller:2008zza ; Tsukamoto_Harada_Yajima_2012 ; Perlick:2014zwa ; Tsukamoto:2016qro ; Tsukamoto:2016zdu ; Nandi:2016uzg ; Tsukamoto:2017edq ; Shaikh:2018oul ; Shaikh:2019jfr ; Shaikh:2019itn , visualizations Muller_2004 ; James:2015ima , shadows in an accretion gas Ohgami:2015nra ; Ohgami:2016iqm ; Kuniyasu:2018cgv , wave optics Nambu:2019sqn , and gravitational waves Cardoso:2016rao to distinguish wormhole from the other compact objects.
A Damour-Solodukhin wormhole Damour:2007ap has been suggested as a black hole mimicker. Its metric was created by making a slight modification to the Schwarzschild metric and it can be the simplest metric among black hole mimickers. The difference of the metric from the Schwarzschild spacetime is described by a positive dimensionless parameter . Lemos and Zaslavskii have pointed out that we can distinguish the wormhole from the black hole by a tidal force acting on a body near the throat even if the difference of the metric tensors of the wormhole from the black hole is small, i.e., Lemos:2008cv . Emissions from its accretion disk Karimov:2019qco , quasinormal modes and gravitational waves Bueno:2017hyj ; Volkel:2018hwb , images of its accretion disks Paul:2019trt , shadow Amir:2018pcu , gravitational lensing Nandi:2018mzm ; Ovgun:2018fnk ; Bhattacharya:2018leh ; Ovgun:2018swe ; Ovgun:2018oxk , and particle collision Tsukamoto:2019ihj in the Damour-Solodukhin wormhole spacetime have been investigated.
Gravitational lensing in a strong deflection limit, which is a semianalytic formalism for gravitational lensing of a light ray reflected by the photon sphere, has been investigated by Bozza Bozza:2002zj . The deflection angle of the light ray in the strong deflection limit has the following form
| (1) | |||||
or
| (2) | |||||
where and are the impact parameter and the critical impact parameter of the light ray, respectively, is an image angle, is the image angle of the photon sphere, where is a distance between an observer and a lens object, and is a positive parameter and is a parameter. We can assume that the impact parameter is non-negative without loss of generality when we treat one light ray in a spherically symmetric spacetime. The analysis in the strong deflection limit has been improved Eiroa:2002mk ; Bozza:2005tg ; Bozza:2006nm ; Bozza:2007gt ; Tsukamoto:2016qro ; Tsukamoto:2016jzh ; Ishihara:2016sfv ; Shaikh:2019itn ; Shaikh:2019jfr and its relations to high-energy absorption cross section Wei:2011zw and to quasinormal modes Stefanov:2010xz have been investigated. Recently, Shaikh et al. have considered the deflection angle of light rays scattered by a photon sphere at the throat of a wormhole Shaikh:2018oul ; Shaikh:2019jfr .
The deflection angle of a light ray scattered by a photon sphere of the Damour-Solodukhin wormhole in the strong deflection limit was obtained by Nandi et al. Nandi:2018mzm , Ovgun Ovgun:2018fnk , and Bhattacharya and Karimov Bhattacharya:2018leh when the wormhole metric is similar to the black hole, i.e., for . In Ref. Bhattacharya:2018leh , Bhattacharya and Karimov have pointed out that by Ovgun Ovgun:2018fnk is in error.
In this paper, firstly we reexamine the deflection angle of the light ray scattered by the photon spheres of the Damour-Solodukhin wormhole for . We recover Bhattacharya and Karimov’s result Bhattacharya:2018leh and we give a small modification for calculation in Nandi:2018mzm . Secondly we extend the analysis for . The deflection angles diverge logarithmically in the strong deflection limit if the dimensionless parameter . Interestingly, we have found that the deflection angle of a light ray scattered by a marginally unstable photon sphere at the throat diverges nonlogarithmically for . We construct the strong deflection limit analysis for the deflection angle with a nonlogarithmic divergence in the Damour-Solodukhin wormhole spacetime.
This paper is organized as follows. In Sec. II, we review the Damour-Solodukhin wormhole spacetime. In Secs. III and IV, we investigate the deflection angle and observables, respectively, in the strong deflection limit. We review the gravitational lensing under a weak-field approximation in Sec. V and we summarize our result in Sec. VI. In Appendixes A and B, the Arnowitt-Deser-Misner (ADM) masses and the violation of energy conditions of the Damour-Solodukhin wormhole are shown, respectively. In this paper we use the units in which a light speed and Newton’s constant are unity.
II Damour-Solodukhin wormhole spacetime
In this section, we review the trajectory of a light ray and its deflection angle in a Damour-Solodukhin wormhole spacetime Damour:2007ap with a line element given by, in coordinates ,
| (3) | |||||
where and are positive parameters and the radial coordinate is defined in a range . A throat exists at . The wormhole spacetime can take different values of the parameters and in two asymptotically flat regions. For simplicity, we assume the equal parameters in the both regions. The line element is the same the one in the Schwarzschild spacetime in a limit and it is the same as the static case of a Kerr-like wormhole Bueno:2017hyj . Bozza has considered the deflection angle of a light ray in the strong deflection limit in a general asymptotically flat, static, and spherically symmetric spacetime with its metric tensor behaving
| (4) | |||
| (5) | |||
| (6) |
where is a time coordinate and is a positive parameter Bozza:2002zj . The Damour-Solodukhin wormhole spacetime is an asymptotically flat, static, and spherically symmetric spacetime but the -component of the metric tensor (3) does not satisfy the assumption (4). We notice that -component of the metric tensor shown in Eq. (3) behaving asymptotically
| (7) |
is not suitable for a variable defined in Sec. III. Thus, we introduce a new time coordinate and a positive parameter which are defined by
| (8) |
and
| (9) |
respectively, to satisfy the assumption (4). By using and , the line element (3) is rewritten in
where , , and are given by
| (11) | |||
| (12) |
and
| (13) |
respectively. 111The metric tensor does not satisfy the condition (5) but it does not give us troubles to define the variable . Notice that is rewritten as . Since the spacetime is a static, spherically symmetric spacetime, there are time-translational and axial Killing vectors and , respectively.
From , where is the wave number of a light ray and where the dot denotes the differentiation with respect to an affine parameter, the trajectory of the light ray is obtained as
| (14) |
Here we have set without loss of generality. Equation (14) can be expressed as
| (15) |
where the effective potential is defined by
| (16) |
where is the impact parameter of the light ray and the conserved energy and the conserved angular momentum of the light ray are constant along the trajectory. Since in spatial infinity , the light ray exists there.
By introducing a proper radial distance from the throat given by
the line element, the equation of trajectory of the light ray, and the effective potential are rewritten in
| (19) |
and
| (20) |
respectively. Note that the proper radial distance is defined in a range and the throat is at .
From , we get the circular light orbits with and at and , respectively. From straightforward calculations, we obtain for and for . Therefore, the throat is a photon (antiphoton) sphere for () and the photon sphere is marginally unstable for . Figure 1 shows the dimensionless effective potential for the (marginally unstable) photon sphere and antiphoton sphere.
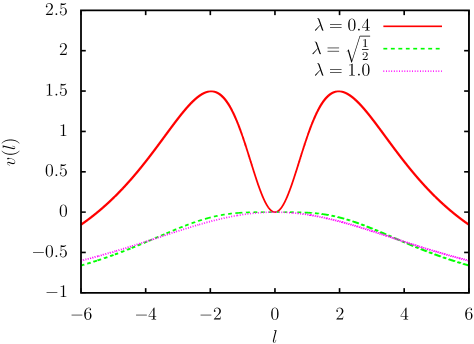
The circular orbit of a light ray with at is unstable for , i.e., it is a photon sphere. Notice that the wormhole has two asymptotically flat regions and it has two photon spheres at for . The photon spheres at and the antiphoton sphere at the throat degenerate to be a marginally unstable photon sphere at the throat just for . The wormhole has only one photon sphere at the throat for .
As shown Fig. 2, we can classify the light ray which coming from a spatial infinity into a falling case with , a critical case with , and a scattered case with . Here the critical impact parameter is defined by
| (21) |
where is the closest distance of the light ray and hereafter subscript denotes quantities of the photon sphere at .
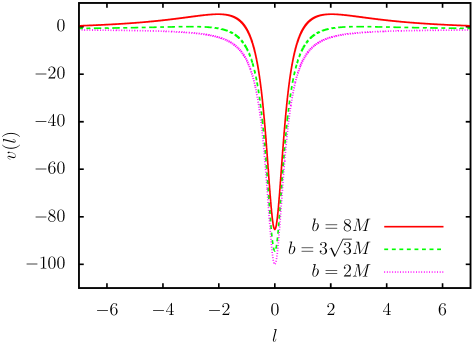
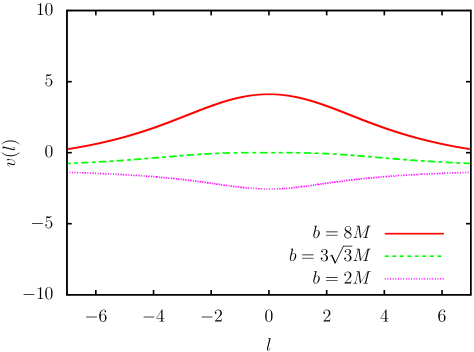
We concentrate on the scattered case. In this case, a light ray comes from a spatial infinity, it is deflected by the wormhole at a reflection point , and it goes back to the same spatial infinity. The reflection point is obtained as the largest positive solution of the equation or . At the reflection point , the equation of the trajectory (14) gives
| (22) |
where the subscript denotes the quantity at . The impact parameter is expressed by
| (23) |
Here we have used Eq. (22).
From Eq. (14), the deflection angle of the light ray as a function of the reflection point is obtained as
| (24) |
where is defined by
| (25) | |||||
where is a dimensionless effective potential in the radial coordinate and where is the position of the reflection point in the radial coordinate .
III Deflection angle in a strong deflection limit
In this section, we investigate the deflection angle in the strong deflection limit or . We treat it in the cases for , , and in this order. In the strong deflection limit , the deflection angle of the light ray in a strong deflection is expressed by a following form Bozza:2002zj : 222The subleading term is in Ref. Bozza:2002zj but we should read it as . See Refs. Tsukamoto:2016jzh ; Tsukamoto:2016qro ; Iyer:2006cn .
| (26) | |||||
We introduce a variable Bozza:2002zj defined by
| (27) |
III.1
In the case for , the photon sphere is at and the critical impact parameter is given by . By using , we rewrite as
| (28) |
where is given by
| (29) | |||||
where ′ is the differentiation with respect to and is given by
and and are defined by
| (31) | |||
| (32) |
is regular but diverges in a limit . We define as
| (33) |
Since and , the integral of diverges in the strong deflection limit . By using , we separate into a divergent part and a regular part :
| (34) |
where
| (35) | |||
| (36) |
where is defined by
| (37) |
The divergent part can be integrated and it becomes
| (38) |
We expand and in powers of :
| (39) | |||
| (40) |
By substituting them into Eq. (38), we obtain
| (41) | |||||
By using the impact parameter expanded in powers of obtained as
| (42) |
we can rewrite as
| (43) | |||||
The regular part can be expanded in powers of and it is expressed by
| (44) |
We are interested in term:
| (45) | |||||
where is given by
| (46) | |||||
Thus, we have obtained the deflection angle of the light ray in the strong deflection limit in the form of Eq. (26) with
| (47) | |||||
| (48) |
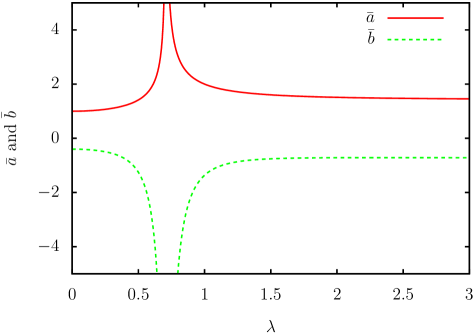
This is the same as the deflection angle obtained by Bhattacharya and Karimov Bhattacharya:2018leh . We plot and for in Fig. 3.
We comment on the details of earlier work on it. First, the deflection angle in the strong deflection limit was calculated by Nandi et al. Nandi:2018mzm . They considered the metric tensor (3) in the coordinates and they defined the variable 333Note that we use , while Nandi et al. have used Nandi:2018mzm .
| (49) |
Note that the integration range of Eq. (2.10) in Ref. Nandi:2018mzm , should be modified to be
| (50) |
The error affects to and the difference is small when is small as shown Table I. Their results in Ref. Nandi:2018mzm will be valid since they discussed in the case of .
The deflection angle was calculated also by Ovgun Ovgun:2018fnk , in the coordinates ,
| (51) |
See Eq. (2.32) in Ref. Ovgun:2018fnk . Bhattacharya and Karimov pointed out that obtained in Ref. Ovgun:2018fnk , i.e., Eq. (51), is in error Bhattacharya:2018leh .
III.2
We consider the case of . In this case, the throat is the photon sphere at and the critical impact parameter is . We notice that the regular factor is given by
| (52) |
and the form of is not suitable for analysis of the strong deflection limit. Thus, we express as
| (53) |
where a new regular factor and a new divergent factor are given by
| (54) |
and
where and are defined as
| (56) | |||
| (57) |
Notice that and in the case of . Since we obtain and , the integral of defined as
| (58) |
gives the divergent part of in the strong deflection limit . We separate into the divergent part and a regular part , i.e.,
| (59) |
where
| (60) | |||
| (61) |
Here, is
| (62) |
The divergent part can be integrated and we obtain
| (63) |
By substituting and expanded in powers of as
| (64) | |||
| (65) |
into Eq. (63), we obtain
| (66) | |||||
From the impact parameter which is expanded in powers of as
we obtain as
| (68) | |||||
The regular part can be expanded in powers of as
| (69) |
and the term of gives
| (70) | |||||
where is given by
Therefore, we have obtained
| (72) | |||||
| (73) |
III.3
In the case of , the throat corresponds with the photon sphere, i.e., . The critical impact parameter is given by . From and , when , the divergent factor gives
| (74) |
and it causes the integral to diverge as
| (75) |
This implies that has the following form, in the strong deflection limit ,
| (76) |
where and are constant.
We separate the integral as
| (77) |
where a divergent part and a regular part are defined by
| (78) | |||
| (79) |
respectively, and where
| (80) |
The regular part can be expanded in powers of as
| (83) |
and the term of gives
| (84) |
where is given by
| (85) |
We obtain in a numerical calculation. Therefore, the deflection angle of the light in the strong deflection limit is obtained as
| (86) |
where and are given by
| (87) |
IV Observables in the strong deflection limit
We consider a small angle lens equation Bozza:2008ev
| (88) |
where and are angular distances between a lens object and a source object and between the observer and the source object, respectively, is an effective deflection angle defined by
| (89) |
is an image angle, and is a source angle as shown Fig. 4.
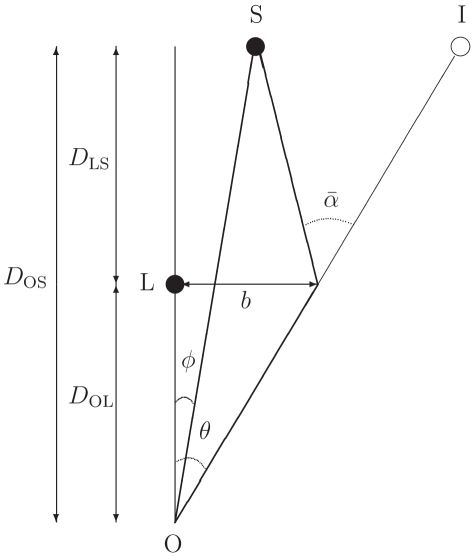
Here, we have assumed that all the angles are small, i.e., , , . Under the assumption, an impact parameter is expressed by , where is an angular distance between the observer and the lens.
We can express the deflection angle of a light ray which rotates around the photon sphere times as
| (90) |
where the winding number is a positive integer in this section and in Sec. V. We define as
| (91) |
We expand the deflection angle around as
| (92) | |||||
IV.1
For , we can rewrite the deflection angle in the strong deflection limit as
| (93) | |||||
where is the image angle of the photon sphere 444 It is known that Eq. (93) is a good approximation in some examples by comparing the exact deflection angle even if the winding number . See Ref. Tsukamoto:2014dta as an example.. In this case, we obtain
| (94) |
| (95) |
We consider the solution of the lens equation (88) for the light ray with the winding number . From Eqs. (90)-(92), (94), and (95), we get
| (96) |
From Eqs. (88) and (96), we obtain the image angle
| (97) |
and its Einstein ring angle as
| (98) |
We get the magnification of the image
| (99) | |||||
the sum of the magnifications of the infinite numbers of images
| (100) |
the magnification without the outermost image
| (101) |
and the ratio of the magnification of the outermost image to the others
| (102) |
The difference of the image angles between the outermost images and the photon sphere is obtained as
| (103) |
IV.2
For , the deflection angle in the strong deflection limit can be expressed by
| (104) |
In this case, we obtain
| (105) |
and, from Eqs. (91) and (104),
| (106) |
Thus, from Eqs. (90)-(92), (105), and (106), the effective deflection angle is obtained by
| (107) |
From Eqs. (88) and (107), we get the image angle with the winding number
| (108) |
and the Einstein ring angle
| (109) |
Therefore, we obtain the magnification of the image
| (110) |
where defined by
| (111) |
can be calculated numerically. We can calculate the magnification of the infinite number of images
| (112) |
and the sum of the magnifications of the images without the outermost image
| (113) |
where
| (114) | |||
| (115) |
Therefore, the ratio of the magnifications of the outermost image to the other images is obtained as
| (116) |
where we have used
| (117) |
The difference of the image angles between the outermost images and the photon sphere is
| (118) |
V Gravitational lens under the weak-field approximation
Under a weak-field approximation , the line element is given by
| (119) | |||||
From Eq. in Ref. Weinberg:1972kfs , the deflection angle of a light ray is obtained as
| (120) |
where is
| (121) |
From Eq. (23), is satisfied. Thus, the deflection angle is rewritten as
| (122) |
This is the same as Eq. in Ref. Ovgun:2018fnk .
VI Discussion and conclusion
From Secs. I to IV, we have concentrated on an infinite number of images with positive impact parameters or positive image angles . The each image has a partner with a negative impact parameter. The image angle and the magnification of the partner of the image with are given by and , respectively. Thus, the diameter of the pair images on a sky is obtained as and the total magnification of the pair images is given by . The observables and the parameters , , , and of the deflection angle in the strong deflection limit are summarized in Table II.
| [as] | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [as] | ||||||||||
| [as] | ||||||||||
As shown in Sec V, the gravitational lensing under the weak-field approximation is not characterized by but . Under an assumption that is constant, the size of the photon sphere monotonically decreases as increases from to and monotonically increases as increases from to . The minimal value of is given by for . 555When is constant, the size of the photon sphere monotonically increases as increases from 0 to and it takes a constant and minimum value for .
We summarize our result. We have shown that the Damour-Solodukhin wormhole with two flat regions has two photon spheres and an antiphoton sphere for and only one photon sphere for and the photon sphere is marginally unstable when . We have reexamined that deflection angle in the strong deflection limit for and we have extent the analysis for and . We have found that the deflection angle of a light ray reflected by the marginally unstable photon sphere diverges nonlogarithmically in the strong deflection limit for , while the deflection angle of the light reflected by the photon sphere diverges logarithmically for . We expect that our method can be applied for gravitational lenses by marginally unstable photon spheres of various compact objects.
Acknowledgements
The author thanks R. Izmailov, K. K. Nandi, A. Övgün, and an anonymous referee for their useful comments.
Appendix A Arnowitt-Deser-Misner masses
Wormholes have two ADM masses since the ADM mass is defined in every asymptotically flat region Poisson . For simplicity, we have assumed the equal ADM masses of the Damour-Solodukhin wormhole. See Visser Visser_1995 for the details of the mass of the wormholes.
We show that is the ADM mass of the wormhole. By using a radial coordinate , which is given by
| (127) |
or
| (128) |
the line element under the weak field approximation is rewritten as
We consider the hypersurfaces , which are surfaces of constant with a unit normal . The induced metric on is obtained as
The induced metric on a two-sphere at with a unit normal is
| (131) |
The extrinsic curvature of embedded in is obtained as , where is the covariant differentiation on . The extrinsic curvature of embedded in flat space is given by . The ADM mass is obtained as
| (132) | |||||
where . Therefore, the ADM mass is not but .
Appendix B Violation of energy conditions
The Ricci tensor and Ricci scalar are given by
| (133) | |||
| (134) | |||
| (135) | |||
| (136) |
and
| (137) |
respectively. The Einstein tensor is given by
| (138) | |||
| (139) | |||
| (140) |
The nonzero components of the stress energy tensor are , , and , where is the energy density, is the radial pressure, and is the tangential pressure.
From the Einstein equation , we obtain
| (141) | |||
| (142) | |||
| (143) |
The weak, null, and strong energy conditions Visser_1995 are violated everywhere because of .
References
- (1) B. P. Abbott et al. [LIGO Scientific and Virgo Collaborations], Phys. Rev. Lett. 116, 061102 (2016).
- (2) B. P. Abbott et al. [LIGO Scientific and Virgo Collaborations], Phys. Rev. X 9, 031040 (2019).
- (3) K. Akiyama et al. [Event Horizon Telescope Collaboration], Astrophys. J. 875, L1 (2019).
- (4) C. M. Claudel, K. S. Virbhadra and G. F. R. Ellis, J. Math. Phys. 42, 818 (2001).
- (5) V. Perlick, Living Rev. Relativity 7, 9 (2004).
- (6) S. Hod, Phys. Lett. B 727, 345 (2013).
- (7) Y. Hagihara, Jpn. J. Astron. Geophys., 8, 67 (1931).
- (8) C. Darwin, Proc. R. Soc. Lond. A 249, 180 (1959).
- (9) R. d’ E. Atkinson, Astron. J. 70, 517 (1965).
- (10) J.-P. Luminet, Astron. Astrophys. 75, 228 (1979).
- (11) H. C. Ohanian, Am. J. Phys. 55, 428 (1987).
- (12) R. J. Nemiroff, Am. J. Phys. 61, 619 (1993).
- (13) S. Frittelli, T. P. Kling, and E. T. Newman, Phys. Rev. D 61, 064021 (2000).
- (14) K. S. Virbhadra and G. F. R. Ellis, Phys. Rev. D 62, 084003 (2000).
- (15) V. Bozza, S. Capozziello, G. Iovane, and G. Scarpetta, Gen. Relativ. Gravit. 33, 1535 (2001).
- (16) V. Bozza, Phys. Rev. D 66, 103001 (2002).
- (17) V. Perlick, Phys. Rev. D 69, 064017 (2004).
- (18) V. Bozza, Gen. Relativ. Gravit. 42, 2269 (2010).
- (19) W. L. Ames and K. S. Thorne, Astrophys. J. 151, 659 (1968).
- (20) J. L. Synge, Mon. Not. Roy. Astron. Soc. 131, no. 3, 463 (1966).
- (21) H. Yoshino, K. Takahashi, and K. i. Nakao, Phys. Rev. D 100, 084062 (2019).
- (22) N. G. Sanchez, Phys. Rev. D 18, 1030 (1978).
- (23) Y. Decanini, A. Folacci, and B. Raffaelli, Phys. Rev. D 81, 104039 (2010).
- (24) W. H. Press, Astrophys. J. 170, L105 (1971).
- (25) C. J. Goebel, Astrophys. J. 172, L95 (1972).
- (26) B. Raffaelli, Gen. Rel. Grav. 48, 16 (2016).
- (27) M. A. Abramowicz and A. R. Prasanna, Mon. Not. Roy. Astr. Soc. 245, 720 (1990).
- (28) M. A. Abramowicz, Mon. Not. Roy. Astr. Soc. 245, 733 (1990).
- (29) B. Allen, Nature 347, 615 (1990).
- (30) W. Hasse and V. Perlick, Gen. Relativ. Gravit. 34, 415 (2002).
- (31) S. Hod, Phys. Rev. D 84, 104024 (2011).
- (32) P. Mach, E. Malec, and J. Karkowski, Phys. Rev. D 88, 084056 (2013)
- (33) E. Chaverra and O. Sarbach, Class. Quant. Grav. 32, 155006 (2015)
- (34) M. Cvetic, G. W. Gibbons, and C. N. Pope, Phys. Rev. D 94, 106005 (2016).
- (35) Y. Koga and T. Harada, Phys. Rev. D 94, 044053 (2016).
- (36) Y. Koga and T. Harada, Phys. Rev. D 98, 024018 (2018).
- (37) Y. Koga, Phys. Rev. D 99, 064034 (2019).
- (38) Y. Koga and T. Harada, Phys. Rev. D 100, 064040 (2019).
- (39) J. Keir, Class. Quant. Grav. 33, 135009 (2016).
- (40) V. Cardoso, L. C. B. Crispino, C. F. B. Macedo, H. Okawa, and P. Pani, Phys. Rev. D 90, 044069 (2014).
- (41) P. V. P. Cunha, E. Berti, and C. A. R. Herdeiro, Phys. Rev. Lett. 119, 251102 (2017).
- (42) P. V. P. Cunha, C. A. R. Herdeiro, and E. Radu, Phys. Rev. D 96, 024039 (2017).
- (43) S. Hod, Phys. Lett. B 776, 1 (2018).
- (44) M. Visser, Lorentzian Wormholes: From Einstein to Hawking (American Institute of Physics, Woodbury, NY, 1995).
- (45) M. S. Morris and K. S. Thorne, Am. J. Phys. 56, 395 (1988).
- (46) P. Schneider, J. Ehlers, and E. E. Falco, Gravitational Lenses (Springer-Verlag, Berlin, 1992).
- (47) P. Schneider, C. S. Kochanek, and J. Wambsganss, Gravitational Lensing: Strong, Weak and Micro, Lecture Notes of the 33rd Saas-Fee Advanced Course, edited by G. Meylan, P. Jetzer, and P. North (Springer-Verlag, Berlin, 2006).
- (48) L. Chetouani and G. Clément, Gen. Relativ. Gravit. 16, 111 (1984).
- (49) K. K. Nandi, Y. Z. Zhang, and A. V. Zakharov, Phys. Rev. D 74, 024020 (2006).
- (50) T. Muller, Phys. Rev. D 77, 044043 (2008).
- (51) N. Tsukamoto and T. Harada, Phys. Rev. D 95, 024030 (2017).
- (52) N. Tsukamoto, T. Harada, and K. Yajima, Phys. Rev. D 86, 104062 (2012).
- (53) V. Perlick, AIP Conf. Proc. 1577, 94 (2015).
- (54) N. Tsukamoto, Phys. Rev. D 94, 124001 (2016).
- (55) K. K. Nandi, R. N. Izmailov, A. A. Yanbekov, and A. A. Shayakhmetov, Phys. Rev. D 95, 104011 (2017).
- (56) N. Tsukamoto, Phys. Rev. D 95, 084021 (2017).
- (57) R. Shaikh, P. Banerjee, S. Paul, and T. Sarkar, Phys. Rev. D 99, 104040 (2019).
- (58) R. Shaikh, P. Banerjee, S. Paul, and T. Sarkar, JCAP 1907, 028 (2019).
- (59) R. Shaikh, P. Banerjee, S. Paul, and T. Sarkar, Phys. Lett. B 789, 270 (2019) Erratum: [Phys. Lett. B 791, 422 (2019)].
- (60) T. Muller, Am. J. Phys. 72, 1045,(2004).
- (61) O. James, E. von Tunzelmann, P. Franklin, and K. S. Thorne, Am. J. Phys. 83, 486 (2015).
- (62) T. Ohgami and N. Sakai, Phys. Rev. D 91, 124020 (2015).
- (63) T. Ohgami and N. Sakai, Phys. Rev. D 94, 064071 (2016).
- (64) M. Kuniyasu, K. Nanri, N. Sakai, T. Ohgami, R. Fukushige, and S. Komura, Phys. Rev. D 97, 104063 (2018).
- (65) Y. Nambu, S. Noda, and Y. Sakai, Phys. Rev. D 100, 064037 (2019).
- (66) V. Cardoso, E. Franzin and P. Pani, Phys. Rev. Lett. 116, no. 17, 171101 (2016) Erratum: [Phys. Rev. Lett. 117, 089902 (2016)].
- (67) T. Damour and S. N. Solodukhin, Phys. Rev. D 76, 024016 (2007)
- (68) J. P. S. Lemos and O. B. Zaslavskii, Phys. Rev. D 78, 024040 (2008).
- (69) R. K. Karimov, R. N. Izmailov, and K. K. Nandi, Eur. Phys. J. C 79, 952 (2019).
- (70) P. Bueno, P. A. Cano, F. Goelen, T. Hertog, and B. Vercnocke, Phys. Rev. D 97, 024040 (2018).
- (71) S. H. Volkel and K. D. Kokkotas, Class. Quant. Grav. 35, 105018 (2018).
- (72) S. Paul, R. Shaikh, P. Banerjee, and T. Sarkar, JCAP 03, 055 (2020).
- (73) M. Amir, K. Jusufi, A. Banerjee, and S. Hansraj, Class. Quant. Grav. 36, no. 21, 215007 (2019).
- (74) K. K. Nandi, R. N. Izmailov, E. R. Zhdanov, and A. Bhattacharya, JCAP 1807, 027 (2018).
- (75) A. Ovgun, Phys. Rev. D 98, 044033 (2018).
- (76) A. Bhattacharya and R. K. Karimov, arXiv:1811.00768 [gr-qc].
- (77) A. Ovgun, arXiv:1811.06870 [gr-qc].
- (78) A. Ovgun, Universe 5, 115 (2019).
- (79) N. Tsukamoto and T. Kokubu, Phys. Rev. D 101, 044030 (2020).
- (80) N. Tsukamoto, Phys. Rev. D 95, 064035 (2017).
- (81) E. F. Eiroa, G. E. Romero, and D. F. Torres, Phys. Rev. D 66, 024010 (2002).
- (82) V. Bozza, F. De Luca, G. Scarpetta, and M. Sereno, Phys. Rev. D 72, 083003 (2005). [gr-qc/0507137].
- (83) V. Bozza, F. De Luca, and G. Scarpetta, Phys. Rev. D 74, 063001 (2006).
- (84) V. Bozza and G. Scarpetta, Phys. Rev. D 76, 083008 (2007).
- (85) A. Ishihara, Y. Suzuki, T. Ono, and H. Asada, Phys. Rev. D 95, 044017 (2017).
- (86) S. W. Wei, Y. X. Liu, and H. Guo, Phys. Rev. D 84, 041501 (2011).
- (87) I. Z. Stefanov, S. S. Yazadjiev, and G. G. Gyulchev, Phys. Rev. Lett. 104, 251103 (2010).
- (88) S. V. Iyer and A. O. Petters, Gen. Rel. Grav. 39, 1563 (2007).
- (89) V. Bozza, Phys. Rev. D 78, 103005 (2008).
- (90) N. Tsukamoto, T. Kitamura, K. Nakajima, and H. Asada, Phys. Rev. D 90, 064043 (2014).
- (91) S. Weinberg, “Gravitation and Cosmology : Principles and Applications of the General Theory of Relativity,” John Wiley & Sons, New York, USA, 1972.
- (92) E. Poisson, A Relativist’s Toolkit: The Mathematics of Black-Hole Mechanics, (Cambridge University Press, Cambridge, 2004).