Non–static fluid spheres admitting a conformal Killing vector: Exact solutions

L. Herrera lherrera@usal.es Departament de Física, Universitat Illes Balears, E-07122 Palma de Mallorca, Spain and Instituto Universitario de Física Fundamental y Matemáticas, Universidad de Salamanca, Salamanca 37007, Spain. A. Di Prisco adiprisco56@gmail.com Escuela de Física, Facultad de Ciencias, Universidad Central de Venezuela, Caracas 1050, Venezuela. J. Ospino Departamento de Matemática Aplicada and Instituto Universitario de Física Fundamental y Matemáticas, Universidad de Salamanca, Salamanca 37007, Spain. j.ospino@usal.es

Abstract

We carry on a general study on non–static spherically symmetric fluids admitting a conformal Killing vector (CKV). Several families of exact analytical solutions are found for different choices of the CKV, in both, the dissipative and the adiabatic regime. To specify the solutions, besides the fulfillment of the junction conditions on the boundary of the fluid distribution, different conditions are imposed, such as vanishing complexity factor and quasi–homologous evolution. A detailed analysis of the obtained solutions, its prospective applications to astrophysical scenarios, as well as alternative approaches to obtain new solutions, are discussed.

Relativistic Fluids, spherical sources, self–similarity, interior solutions.

pacs:

04.40.-b, 04.40.Nr, 04.40.Dg

I Introduction

The purpose of this work is twofold. On the one hand we want to delve deeper into the physical consequences derived from the assumption that a given space–time admits a CKV. This interest in its turn is motivated by the relevance of such kind of symmetry in hydrodynamics.

Indeed, in general relativity, self–similar solutions are related to the existence of a homothetic Killing vector field (HKV), a generalization of which is a conformal Killing vector field (CKV). The physical interest of systems admitting a CKV is then suggested by the important role played by self-similarity in classical hydrodynamics.

Thus, in Newtonian hydrodynamics, self–similar solutions are those described by means of physical quantities which are functions depending on dimensionless variables $x/l(t)$ , where $x$ and $t$ are independent space and time variables and $l$ is a time dependent scale. Therefore the spatial distribution of the characteristics of motion remains similar to itself at all times 1 . In other words, self–similarity is to be expected whenever the system under consideration possesses no characteristic length scale.

The above comments suggest that self–similarity plays an important role in the study of systems close to the critical point, where the correlation length becomes infinite, in which case different phases of the fluid (e.g. liquid–vapor) may coexist, the phase boundaries vanish and density fluctuations occur at all length scales. This process may be observed in the critical opalescence.

Besides, examples of self–similar fluids may be found in the study of strong explosions and thermal waves 2 ; 3 ; 4 ; 5 .

Motivated by the above arguments many authors, since the pioneering work by Cahill and Taub 6 , have focused their interest in the problem of self–similarity in self–gravitating systems. Some of them are restricted to general relativity, with especial emphasis on the ensuing consequences from the existence of HKV or CKV, and possible solutions to the Einstein equations (see for example 7 ; 8co ; 9co ; 10co ; 11co ; 12co ; 13co ; 14 ; 15 ; 16 ; 17 ; 18 ; 19 ; 20 ; 21 ; 22 ; 23 ; 24 ; 25 ; 26 ; 27 ; 28 ; 29 ; 30 ; 31 ; 32 ; 33 ; 33b ; 34 ; 35 ; 36 ; 37 ; 38 ; 39 ; 40 ; 40bis ; 41 ; 42 ; 43 ; 44 ; sherif ; matondo and references therein). Also, a great deal of work has been done in the context of other theories of gravitation (see for example rej ; RS ; MH2 ; HM2 ; SIF ; SHS ; Bhar2 ; TD ; DRGR2 ; OS ; ZSRA ; DRGR ; SNN and references therein). Finally, it is worth mentioning the interest of this kind of symmetry related to the modeling of wormholes (see BHL1 ; BHL ; RRKKK ; K ; SIF2 ; kar ; sahoo and references therein).

On the other hand, the problem of general relativistic gravitational collapse has attracted the attention of researchers since the seminal paper by Oppenheimer and Snyder. The origin of such interest resides in the fact that the gravitational collapse of massive stars represents one of the few observable phenomena where general relativity is expected to play a relevant role. To tackle such a problem there are two different approaches: Numerical methods or analytical exact solutions to Einstein equations. Numerical methods enable researchers to investigate systems that are extremely difficult to handle analytically. However, purely numerical solutions usually hinder the investigation of general, qualitative, aspects of the process. On the other hand, analytical solutions although are generally found either for too simplistic equations of state and/or under additional heuristic assumptions whose justification is usually uncertain, are more suitable for a general discussion and seem to be useful to study non–static models which are relatively simple to analyze but still contain some of the essential features of a realistic situation.

In this manuscript we endeavor to find exact, analytical, non–static solutions admitting a CKV, including dissipative processes. The source will be represented by an anisotropic fluid dissipating energy in the diffusion approximation. In order to find the solutions we shall specialize the CKV to be either space–like (orthogonal to the four–velocity), or time–like (parallel to the four–velocity). In each case we shall consider separately the dissipative and non–dissipative regime. Also, in order to specify the models, we will assume specific restrictions on the mode of the evolution, (e.g. the quasi–homologous condition), and on the complexity factor, among other conditions. A fundamental role in finding our models is played by the equations ensuing from the junction conditions on the boundary of the fluid distribution, whose integration provides one of the functions defining the metric tensor.

Several families of solutions are found and discussed in detail. A summary of the obtained results and a discussion on the physical relevance of these solutions are presented in last section. Finally several appendices are included containing useful formulae.

II The metric, the source and relevant equations and variables

In what follows we shall briefly summarize the definitions and main equations required for describing spherically symmetric dissipative fluids. We shall heavily rely on epjc , therefore we shall omit many steps in the calculations, details of which the reader may find in epjc .

We consider a spherically symmetric distribution of collapsing fluid, bounded by a spherical surface $\Sigma$ . The fluid is assumed to be locally anisotropic (principal stresses unequal) and undergoing dissipation in the form of heat flow (diffusion approximation).

The justification to consider anisotropic fluids is provided by the fact that pressure anisotropy is produced by many different physical phenomena of the kind expected in gravitational collapse scenario (see report and references therein). Furthermore we expect that the final stages of stellar evolution should be accompanied by intense dissipative processes, which, as shown in ps , should produce pressure anisotropy.

Choosing comoving coordinates, the general interior metric can be written as

ds^{2}=-A^{2}dt^{2}+B^{2}dr^{2}+R^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2}),

(1)

where $A$ , $B$ and $R$ are functions of $t$ and $r$ and are assumed positive. We number the coordinates $x^{0}=t$ , $x^{1}=r$ , $x^{2}=\theta$ and $x^{3}=\phi$ . Observe that $A$ and $B$ are dimensionless, whereas $R$ has the same dimension as $r$ .

The energy momentum tensor in the canonical form, reads

T_{\alpha\beta}={\mu}V_{\alpha}V_{\beta}+Ph_{\alpha\beta}+\Pi_{\alpha\beta}+q\left(V_{\alpha}K_{\beta}+K_{\alpha}V_{\beta}\right),

(2)

with

P=\frac{P_{r}+2P_{\bot}}{3},\qquad h_{\alpha\beta}=g_{\alpha\beta}+V_{\alpha}V_{\beta},

\Pi_{\alpha\beta}=\Pi\left(K_{\alpha}K_{\beta}-\frac{1}{3}h_{\alpha\beta}\right),\qquad\Pi=P_{r}-P_{\bot}

where $\mu$ is the energy density, $P_{r}$ the radial pressure, $P_{\perp}$ the tangential pressure, $q^{\alpha}=qK^{\alpha}$ the heat flux, $V^{\alpha}$ the four–velocity of the fluid, and $K^{\alpha}$ a unit four–vector along the radial direction. Since we are considering comoving observers, we have

\displaystyle V^{\alpha}

\displaystyle=

\displaystyle A^{-1}\delta_{0}^{\alpha},\;\;q^{\alpha}=qK^{\alpha},\;\;K^{\alpha}=B^{-1}\delta^{\alpha}_{1}.

(3)

These quantities satisfy

\displaystyle V^{\alpha}V_{\alpha}=-1,\;\;V^{\alpha}q_{\alpha}=0,\;\;K^{\alpha}K_{\alpha}=1,\;\;K^{\alpha}V_{\alpha}=0.

(4)

It is worth noticing that we do not explicitly add bulk or shear viscosity to the system because they can be trivially absorbed into the radial and tangential pressures, $P_{r}$ and $P_{\perp}$ , of the collapsing fluid (in $\Pi$ ). Also we do not explicitly introduce dissipation in the free streaming approximation since it can be absorbed in $\mu,P_{r}$ and $q$ .

The Einstein equations for (1) and (2), are explicitly written in Appendix A.

The acceleration $a_{\alpha}$ and the expansion $\Theta$ of the fluid are given by

a_{\alpha}=V_{\alpha;\beta}V^{\beta},\;\;\Theta={V^{\alpha}}_{;\alpha},

(5)

and its shear $\sigma_{\alpha\beta}$ by

\sigma_{\alpha\beta}=V_{(\alpha;\beta)}+a_{(\alpha}V_{\beta)}-\frac{1}{3}\Theta h_{\alpha\beta}.

(6)

From (5) we have for the four–acceleration and its scalar $a$ ,

a_{\alpha}=aK_{\alpha},\;\;a=\frac{A^{\prime}}{AB},

(7)

and for the expansion

\Theta=\frac{1}{A}\left(\frac{\dot{B}}{B}+2\frac{\dot{R}}{R}\right),

(8)

where the prime stands for $r$ differentiation and the dot stands for differentiation with respect to $t$ .

We obtain for the shear (6) its non zero components

\sigma_{11}=\frac{2}{3}B^{2}\sigma,\;\;\sigma_{22}=\frac{\sigma_{33}}{\sin^{2}\theta}=-\frac{1}{3}R^{2}\sigma,

(9)

and its scalar

\sigma^{\alpha\beta}\sigma_{\alpha\beta}=\frac{2}{3}\sigma^{2},

(10)

where

\sigma=\frac{1}{A}\left(\frac{\dot{B}}{B}-\frac{\dot{R}}{R}\right).

(11)

Next, the mass function $m(t,r)$ reads

m=\frac{R^{3}}{2}{R_{23}}^{23}=\frac{R}{2}\left[\left(\frac{\dot{R}}{A}\right)^{2}-\left(\frac{R^{\prime}}{B}\right)^{2}+1\right].

(12)

Introducing the proper time derivative $D_{T}$ given by

D_{T}=\frac{1}{A}\frac{\partial}{\partial t},

(13)

we can define the velocity $U$ of the collapsing fluid as the variation of the areal radius with respect to proper time, i.e.

U=D_{T}R\;\;\mbox{(negative in the case of collapse)},

(14)

where $R$ defines the areal radius of a spherical surface inside the fluid distribution (as measured from its area).

Then (12) can be rewritten as

E\equiv\frac{R^{\prime}}{B}=\left(1+U^{2}-\frac{2m}{R}\right)^{1/2}.

(15)

Using (15) we can express (229) as

4\pi q=E\left[\frac{1}{3}D_{R}(\Theta-\sigma)-\frac{\sigma}{R}\right],

(16)

where $D_{R}$ denotes the proper radial derivative,

D_{R}=\frac{1}{R^{\prime}}\frac{\partial}{\partial r}.

(17)

Using (225)-(227) with (13) and (17) we obtain from (12)

\displaystyle D_{T}m=-4\pi\left(P_{r}U+qE\right)R^{2},

(18)

and

\displaystyle D_{R}m=4\pi\left(\mu+q\frac{U}{E}\right)R^{2},

(19)

which implies

m=4\pi\int^{r}_{0}\left(\mu+q\frac{U}{E}\right)R^{2}R^{\prime}dr,

(20)

satisfying the regular condition $m(t,0)=0$ .

Integrating (20) we find

\frac{3m}{R^{3}}=4\pi{\mu}-\frac{4\pi}{R^{3}}\int^{r}_{0}{R^{3}\left(D_{R}{\mu}-3q\frac{U}{RE}\right)R^{\prime}dr}.

(21)

II.1 The Weyl tensor and the complexity factor

Some of the solutions exhibited in the next section are obtained from the condition of vanishing complexity factor. This is a scalar function intended to measure the degree of complexity of a given fluid distribution ps1 ; ps2 , and is related to the so called structure scalars sc .

In the spherically symmetric case the magnetic part of the Weyl tensor ( $C^{\rho}_{\alpha\beta\mu}$ ) vanishes, accordingly it is defined by its “electric” part $E_{\gamma\nu}$ , defined by

E_{\alpha\beta}=C_{\alpha\mu\beta\nu}V^{\mu}V^{\nu},

(22)

whose non trivial components are

$\displaystyle E_{11}$	$\displaystyle=$	$\displaystyle\frac{2}{3}B^{2}{\cal E},$
$\displaystyle E_{22}$	$\displaystyle=$	$\displaystyle-\frac{1}{3}R^{2}{\cal E},$
$\displaystyle E_{33}$	$\displaystyle=$	$\displaystyle E_{22}\sin^{2}{\theta},$	(23)

where

\displaystyle{\cal E}=\frac{1}{2A^{2}}\left[\frac{\ddot{R}}{R}-\frac{\ddot{B}}{B}-\left(\frac{\dot{R}}{R}-\frac{\dot{B}}{B}\right)\left(\frac{\dot{A}}{A}+\frac{\dot{R}}{R}\right)\right]+\frac{1}{2B^{2}}\left[\frac{A^{\prime\prime}}{A}-\frac{R^{\prime\prime}}{R}+\left(\frac{B^{\prime}}{B}+\frac{R^{\prime}}{R}\right)\left(\frac{R^{\prime}}{R}-\frac{A^{\prime}}{A}\right)\right]-\frac{1}{2R^{2}}.

(24)

Observe that the electric part of the Weyl tensor, may be written as

E_{\alpha\beta}={\cal E}\left(K_{\alpha}K_{\beta}-\frac{1}{3}h_{\alpha\beta}\right).

(25)

As shown in ps1 ; ps2 the complexity factor is identified with the scalar function $Y_{TF}$ which defines the trace–free part of the electric Riemann tensor (see sc for details).

Thus, let us define tensor $Y_{\alpha\beta}$ by

Y_{\alpha\beta}=R_{\alpha\gamma\beta\delta}V^{\gamma}V^{\delta},

(26)

which may be expressed in terms of two scalar functions $Y_{T},Y_{TF}$ , as

\displaystyle Y_{\alpha\beta}=\frac{1}{3}Y_{T}h_{\alpha\beta}+Y_{TF}\left(K_{\alpha}K_{\beta}-\frac{1}{3}h_{\alpha\beta}\right).

(27)

Then after lengthy but simple calculations, using field equations, we obtain (see 1B for details)

\displaystyle Y_{T}=4\pi(\mu+3P_{r}-2\Pi),\qquad Y_{TF}={\cal E}-4\pi\Pi.

(28)

Next, using (225), (227), (228) with (12) and (24) we obtain

\frac{3m}{R^{3}}=4\pi\left({\mu}-\Pi\right)-\cal{E},

(29)

which combined with (21) and (28) produces

Y_{TF}=-8\pi\Pi+\frac{4\pi}{R^{3}}\int^{r}_{0}{R^{3}\left(D_{R}{\mu}-3{q}\frac{U}{RE}\right)R^{\prime}dr}.

(30)

It is worth noticing that due to a different signature, the sign of $Y_{TF}$ in the above equation differs from the sign of the $Y_{TF}$ used in ps1 for the static case.

Thus the scalar $Y_{TF}$ may be expressed through the Weyl tensor and the anisotropy of pressure or in terms of the anisotropy of pressure, the density inhomogeneity and the dissipative variables.

In terms of the metric functions the scalar $Y_{TF}$ reads

\displaystyle Y_{TF}=\frac{1}{A^{2}}\left[\frac{\ddot{R}}{R}-\frac{\ddot{B}}{B}+\frac{\dot{A}}{A}\left(\frac{\dot{B}}{B}-\frac{\dot{R}}{R}\right)\right]+\frac{1}{B^{2}}\left[\frac{A^{\prime\prime}}{A}-\frac{A^{\prime}}{A}\left(\frac{B^{\prime}}{B}+\frac{R^{\prime}}{R}\right)\right].

(31)

II.2 The exterior spacetime and junction conditions

Since we are considering bounded fluid distributions then we still have to satisfy the junction (Darmois) conditions. Thus, outside $\Sigma$ we assume we have the Vaidya spacetime (i.e. we assume all outgoing radiation is massless), described by

ds^{2}=-\left[1-\frac{2M(v)}{\bf r}\right]dv^{2}-2d{\bf r}dv+{\bf r}^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2}),

(32)

where $M(v)$ denotes the total mass, and $v$ is the retarded time.

The matching of the full nonadiabatic sphere to the Vaidya spacetime, on the surface $r=r_{\Sigma}=$ constant, requires the continuity of the first and second fundamental forms across $\Sigma$ (see chan and references therein for details), which implies

m(t,r)\stackrel{{\scriptstyle\Sigma}}{{=}}M(v),

(33)

and

\displaystyle 2\left(\frac{{\dot{R}}^{\prime}}{R}-\frac{\dot{B}}{B}\frac{R^{\prime}}{R}-\frac{\dot{R}}{R}\frac{A^{\prime}}{A}\right)\stackrel{{\scriptstyle\Sigma}}{{=}}-\frac{B}{A}\left[2\frac{\ddot{R}}{R}-\left(2\frac{\dot{A}}{A}-\frac{\dot{R}}{R}\right)\frac{\dot{R}}{R}\right]+\frac{A}{B}\left[\left(2\frac{A^{\prime}}{A}+\frac{R^{\prime}}{R}\right)\frac{R^{\prime}}{R}-\left(\frac{B}{R}\right)^{2}\right],

(34)

where $\stackrel{{\scriptstyle\Sigma}}{{=}}$ means that both sides of the equation are evaluated on $\Sigma$ .

Comparing (34) with (226) and (227) one obtains

q\stackrel{{\scriptstyle\Sigma}}{{=}}P_{r}.

(35)

Thus the smooth matching of (1) and (32) on $\Sigma$ implies (33) and (35).

Finally, the total luminosity ( $L_{\infty}$ ) for an observer at rest at infinity is defined by

L_{\infty}=4\pi P_{r\Sigma}\left[R^{2}\left(\frac{R^{\prime}}{B}+\frac{\dot{R}}{A}\right)^{2}\right]_{\Sigma}.

(36)

III The transport equation

In the dissipative case we shall need a transport equation in order to find the temperature distribution and evolution. Assuming a causal dissipative theory (e.g.the Israel– Stewart theory 19nt ; 20nt ; 21nt ) the transport equation for the heat flux reads

	$\displaystyle\tau h^{\alpha\beta}V^{\gamma}q_{\beta;\gamma}$	$\displaystyle+$	$\displaystyle q^{\alpha}=-\kappa h^{\alpha\beta}\left(T_{,\beta}+Ta_{\beta}\right)$		(37)
		$\displaystyle-$	$\displaystyle\frac{1}{2}\kappa T^{2}\left(\frac{\tau V^{\beta}}{\kappa T^{2}}\right)_{;\beta}q^{\alpha},$		(37)

where $\kappa$ denotes the thermal conductivity, and $T$ and $\tau$ denote temperature and relaxation time respectively.

In the spherically symmetric case under consideration, the transport equation has only one independent component which may be obtained from (37) by contracting with the unit spacelike vector $K^{\alpha}$ , it reads

\tau V^{\alpha}q_{,\alpha}+q=-\kappa\left(K^{\alpha}T_{,\alpha}+Ta\right)-\frac{1}{2}\kappa T^{2}\left(\frac{\tau V^{\alpha}}{\kappa T^{2}}\right)_{;\alpha}q.

(38)

Sometimes it is possible to simplify the equation above, in the so called truncated transport equation, when the last term in (37) may be neglected t8 , producing

\tau V^{\alpha}q_{,\alpha}+q=-\kappa\left(K^{\alpha}T_{,\alpha}+Ta\right).

(39)

IV The homologous and quasi–homologous conditions

As mentioned before, in order to specify some of our models we shall impose the condition of vanishing complexity factor. However, for time dependent systems, it is not enough to define the complexity of the fluid distribution. We need also to elucidate what is the simplest pattern of evolution of the system.

In ps2 the concept of homologous evolution was introduced, in analogy with the same concept in classical astrophysics, as to represent the simplest mode of evolution of the fluid distribution.

Thus, the field equation (226) written as

D_{R}\left(\frac{U}{R}\right)=\frac{4\pi}{E}q+\frac{\sigma}{R},

(40)

can be easily integrated to obtain

U=\tilde{a}(t)R+R\int^{r}_{0}\left(\frac{4\pi}{E}q+\frac{\sigma}{R}\right)R^{\prime}dr,

(41)

where $\tilde{a}$ is an integration function, or

U=\frac{U_{\Sigma}}{R_{\Sigma}}R-R\int^{r_{\Sigma}}_{r}\left(\frac{4\pi}{E}q+\frac{\sigma}{R}\right)R^{\prime}dr.

(42)

If the integral in the above equations vanishes we have from (41) or (42) that

U=\tilde{a}(t)R.

(43)

This relationship is characteristic of the homologous evolution in Newtonian hydrodynamics 20n ; 21n ; 22n . In our case, this may occur if the fluid is shear–free and non dissipative, or if the two terms in the integral cancel each other.

In ps2 , the term “homologous evolution” was used to characterize relativistic systems satisfying, besides (43), the condition

\frac{R_{1}}{R_{2}}=\mbox{constant},

(44)

where $R_{1}$ and $R_{2}$ denote the areal radii of two concentric shells ( $1,2$ ) described by $r=r_{1}={\rm constant}$ , and $r=r_{2}={\rm constant}$ , respectively.

The important point that we want to stress here is that (43) does not imply (44). Indeed, (43) implies that for the two shells of fluids $1,2$ we have

\frac{U_{1}}{U_{2}}=\frac{A_{2}\dot{R}_{1}}{A_{1}\dot{R}_{2}}=\frac{R_{1}}{R_{2}},

(45)

that implies (44) only if $A=A(t)$ , which by a simple coordinate transformation becomes $A={\rm constant}$ . Thus in the non–relativistic regime, (44) always follows from the condition that the radial velocity is proportional to the radial distance, whereas in the relativistic regime the condition (43) implies (44), only if the fluid is geodesic.

In epjc the homologous condition was relaxed, leading to what was defined as quasi–homologous evolution, restricted only by condition (43), implying

\frac{4\pi}{R^{\prime}}Bq+\frac{\sigma}{R}=0.

(46)

V Conformal motions: exact solutions

We shall consider spacetimes whose line element is defined by (1), admitting a CKV, i.e. satisfying the equation

\mathcal{L}_{\chi}g_{\alpha\beta}=2\psi g_{\alpha\beta}\rightarrow\mathcal{L}_{\chi}g^{\alpha\beta}=-2\psi g^{\alpha\beta},

(47)

where $\mathcal{L}_{\chi}$ denotes the Lie derivative with respect to the vector field ${\mathbb{\chi}}$ , which unless specified otherwise, has the general form

\mathbb{\chi}=\xi(t,r,)\partial_{t}+\lambda(t,r,)\partial_{r},

(48)

and $\psi$ in principle is a function of $t,r$ . The case $\psi=constant$ corresponds to a HKV.

Our goal consists in finding exact solutions admitting a one parameter group of conformal motions, expressed in terms of elementary functions.

Two different families of solutions will be obtained depending on the choice of $\chi^{\alpha}$ . One of these families corresponds to the case with $\chi^{\alpha}$ orthogonal to $V^{\alpha}$ , while the other corresponds to the case with $\chi^{\alpha}$ parallel to $V^{\alpha}$ . For both families we shall consider separately the non–dissipative ( $q=0$ ) and the dissipative ( $q\neq$ ) case.

For the non–dissipative case of the family of solutions with $\chi^{\alpha}$ orthogonal to $V^{\alpha}$ , we shall obtain from the matching conditions and specific values of the relevant parameters, solutions $I,II,III$ , and for the particular case $M=0$ we shall obtain solutions $IV,V$ . For the dissipative case of this family, imposing the vanishing complexity factor condition and the shear–free condition we shall obtain solution $VI$ .

For the non–dissipative case of the family of solutions with $\chi^{\alpha}$ parallel to $V^{\alpha}$ , we shall obtain from the matching conditions and the vanishing complexity factor condition solution $VII$ , whereas from specific values of relevant parameters we shall obtain solution $VIII$ . Also imposing the condition $M=0$ we shall obtain in this case solutions $IX,X$ .

Finally for the dissipative case of this family, imposing the complexity factor condition, we shall obtain solution $XI$ .

Let us start by considering the case $\chi^{\alpha}$ orthogonal to $V^{\alpha}$ and $q=0$ .

V.1 $\chi_{\alpha}V^{\alpha}=q=0$ .

Then from

\mathcal{L}_{\chi}g_{\alpha\beta}=2\psi g_{\alpha\beta}=\chi^{\rho}\partial_{\rho}g_{\alpha\beta}+g_{\alpha\rho}\partial_{\beta}\chi^{\rho}+g_{\beta\rho}\partial_{\alpha}\chi^{\rho},

(49)

we obtain

\psi=\chi^{1}\frac{A^{\prime}}{A},

(50)

\psi=\chi^{1}\frac{B^{\prime}}{B}+(\chi^{1})^{\prime},

(51)

\psi=\chi^{1}\frac{R^{\prime}}{R},

(52)

and

\chi^{1}_{,t}=\chi^{1}_{,\theta}=\chi^{1}_{,\phi}=0.

(53)

From (50) and (52) it follows

A=h(t)R,

(54)

where $h$ is an arbitrary function of $t$ , which without loos of generality may be put equal to $1$ by reparametrizing $t$ .

Thus we may write

A=\alpha R,

(55)

where $\alpha$ is a unit constant with dimensions of $\frac{1}{length}$ .

Next, taking the time derivative of (51) and (52) and using (53) we obtain

\frac{B}{G(r)}=\alpha F_{1}(t)R,

(56)

where $G(r)$ is an arbitrary function of $r$ which may be put equal to $1$ by a a reparametrization of $r$ , and $F_{1}$ is an arbitrary dimensionless function of $t$ .

Thus we have

B=\alpha F_{1}(t)R,

(57)

and

(\chi^{1})^{\prime}=0\Rightarrow\chi^{1}=constant.

(58)

Then, feeding back (55) and (57) into (226) with $q=0$ , one obtains

A=\alpha R=\frac{F(t)}{f(t)+g(r)},\quad B=\frac{1}{f(t)+g(r)},

(59)

where $f$ and $g$ are two arbitrary functions of their arguments and $F(t)\equiv\frac{1}{F_{1}(t)}$ .

So far we see that any model is determined up to three arbitrary functions $F(t),f(t),g(r)$ .

Then the field equations read

8\pi\mu=\frac{(f+g)^{2}}{F^{2}}\left[\frac{\dot{F}^{2}}{F^{2}}-\frac{4\dot{F}\dot{f}}{F(f+g)}+\frac{3\dot{f}^{2}}{(f+g)^{2}}\right]+2g^{\prime\prime}(f+g)-3g^{\prime 2}+\frac{\alpha^{2}(f+g)^{2}}{F^{2}},

(60)

8\pi P_{r}=\frac{(f+g)^{2}}{F^{2}}\left[\frac{\dot{F}^{2}}{F^{2}}+\frac{2\dot{F}\dot{f}}{F(f+g)}-\frac{3\dot{f}^{2}}{(f+g)^{2}}+\frac{2\ddot{f}}{f+g}-\frac{2\ddot{F}}{F}\right]+3g^{\prime 2}-\frac{\alpha^{2}(f+g)^{2}}{F^{2}},

(61)

8\pi P_{\bot}=\frac{(f+g)^{2}}{F^{2}}\left[\frac{\dot{F}^{2}}{F^{2}}-\frac{3\dot{f}^{2}}{(f+g)^{2}}+\frac{2\ddot{f}}{f+g}-\frac{\ddot{F}}{F}\right]+3g^{\prime 2}-2g^{\prime\prime}(f+g).

(62)

Using the results above the matching conditions (33) and (35) on the surface $r=r_{\Sigma}=constant$ read

\dot{R}_{\Sigma}^{2}+\alpha^{2}(R_{\Sigma}^{2}-2MR_{\Sigma}-\omega R_{\Sigma}^{4})=0,

(63)

and

2\ddot{R}_{\Sigma}R_{\Sigma}-\dot{R}^{2}_{\Sigma}-\alpha^{2}(3\omega R_{\Sigma}^{4}-R_{\Sigma}^{2})=0,

(64)

with $\omega\equiv g^{\prime}(r_{\Sigma})^{2}$ .

Refer to caption — Figure 1: $\tilde{V}$ as function of $x$ . The horizontal line corresponds to the value of $\tilde{V}=1/27$

It is a simple matter to check that (63) is just the first integral of (64), therefore we only need to consider the former equation.

It would be useful to write (63) in the form

\dot{R}^{2}_{\Sigma}=\alpha^{2}R^{4}_{\Sigma}\left[\omega-V(R_{\Sigma})\right],

(65)

with

V(R_{\Sigma})=\frac{1}{R_{\Sigma}^{2}}-\frac{2M}{R_{\Sigma}^{3}},

(66)

\tilde{V}(R_{\Sigma})\equiv M^{2}V(R_{\Sigma})=\frac{1}{x^{2}}-\frac{2}{x^{3}},

(67)

with $x\equiv\frac{R_{\Sigma}}{M}$ .

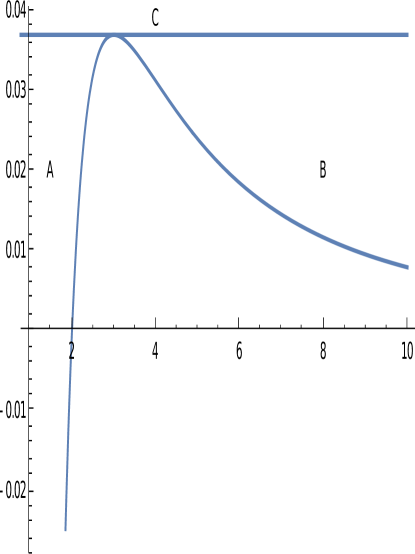
The maximum of $\tilde{V}$ ( $\tilde{V}_{max.}=\frac{1}{27}$ ) occurs at $x=3$ ( $R_{\Sigma}=3M)$ , whereas $\tilde{V}$ vanishes at at $x=2$ ( $R_{\Sigma}=2M)$ .

Obviously all solutions have to satisfy the conditions $\omega>V(R_{\Sigma})$ . Among them we have:

•

Solutions with $\omega<\frac{1}{27M^{2}}$ . In this case we may have solutions evolving between the singularity and some value of $R_{\Sigma}$ in the interval $[2M,3M]$ (region A in figure 1), and solutions with $R_{\Sigma}$ in the interval $[3M,\infty]$ (region B in figure 1).
•

Solutions with $\omega>\frac{1}{27M^{2}}$ in which case $R_{\Sigma}$ is in the interval $[0,\infty]$ (region C in figure 1).
•

Solutions with $\omega=\frac{1}{27M^{2}}$ in which case $R_{\Sigma}$ may be in the interval $[0,3M]$ or in the interval $[3M,\infty]$
•

Solutions with $\omega=0$ . In which case $R_{\Sigma}$ oscillates in the interval $[0,2M]$ .

In general, we may write from (65)

\alpha(t-t_{0})=\pm\int{\frac{dR_{\Sigma}}{R_{\Sigma}^{2}\sqrt{\omega-V(R_{\Sigma})}}},

(68)

from which we may obtain $R_{\Sigma}$ expressed in terms of elliptic functions. However, in some cases analytical solutions may be found in terms of elementary functions. For doing that we shall proceed as follows.

Let us introduce the variable $r=x+b$ in the polynomial

P(r)=a_{0}r^{4}+a_{1}r^{3}+a_{2}r^{2}+a_{3}r+a_{4},

(69)

which allows us to write

	$\displaystyle P(x)$	$\displaystyle=$	$\displaystyle a_{0}x^{4}+(a_{1}+4a_{0}b)x^{3}+(a_{2}+3a_{1}b+6a_{0}b^{2})x^{2}+(a_{3}+2a_{2}b+3a_{1}b^{2}+4a_{0}b^{3})x$		(70)
		$\displaystyle+$	$\displaystyle a_{4}+a_{3}b+a_{2}b^{2}+a_{1}b^{3}+a_{0}b^{4},$		(70)

P(x)=(\sqrt{a_{0}}x+b_{1})^{2}(x+b_{2})(x+b_{3}),

(71)

where $b_{1,2,3}$ and $b$ are solutions of the following equations

a_{4}+a_{3}b+a_{2}b^{2}+a_{1}b^{3}+a_{0}b^{4}=b_{1}^{2}b_{2}b_{3},

(72)

a_{3}+2a_{2}b+3a_{1}b^{2}+4a_{0}b^{3}=b_{1}^{2}(b_{2}+b_{3})+2\sqrt{a_{0}}b_{1}b_{2}b_{3},

(73)

a_{2}+3a_{1}b+6a_{0}b^{2}=b_{1}^{2}+2\sqrt{a_{0}}b_{1}(b_{2}+b_{3})+a_{0}b_{2}b_{3},

(74)

a_{1}+4a_{0}b=2\sqrt{a_{0}}b_{1}+a_{0}(b_{2}+b_{3}).

(75)

Then the integration of (68) produces

\pm\int\frac{dx}{(\sqrt{a_{0}}x+b_{1})\sqrt{(x+b_{2})(x+b_{3})}}=\left\{\beta_{1}\arctan\left(\beta_{2}\sqrt{\frac{b_{2}+x}{b_{3}+x}}\right)\atop\beta_{1}\arctan^{-1}\left(\beta_{2}\sqrt{\frac{b_{2}+x}{b_{3}+x}}\right),\right.

(76)

where

	$\displaystyle\beta_{1}$	$\displaystyle=$	$\displaystyle\frac{2}{\sqrt{(b_{1}-\sqrt{a_{0}}b_{2})(\sqrt{a_{0}}b_{3}-b_{1})}},$		(77)
	$\displaystyle\beta_{2}$	$\displaystyle=$	$\displaystyle\sqrt{\frac{\sqrt{a_{0}}b_{3}-b_{1}}{b_{1}-\sqrt{a_{0}}b_{2}}}.$		(78)

To obtain explicit solutions expressed through elementary functions, we shall assume $b=0$ , thus in our notation we have

$\displaystyle a_{0}$	$\displaystyle=$	$\displaystyle\omega,$	(79)
$\displaystyle a_{1}$	$\displaystyle=$	$\displaystyle a_{4}=0,$	(80)
$\displaystyle a_{2}$	$\displaystyle=$	$\displaystyle-1\qquad a_{3}=2M.$	(81)

Imposing $b=0$ , we are led to two sub-cases, $b_{2}=0$ , or $b_{3}=0$ , in both sub–cases $M=\frac{1}{3\sqrt{3\omega}}$ .

Using (79)–(81) in (76), we obtain for both sub–cases the same solutions, namely

R^{(I)}_{\Sigma}=\frac{6M\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}{3-\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]},

(82)

and

R^{(II)}_{\Sigma}=\frac{6M\coth^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}{3-\coth^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}.

(83)

In the first case, the areal radius of the boundary ( $R^{(I)}_{\Sigma}$ ) expands from $0$ (the singularity) approaching $3M$ asymptotically as $t\rightarrow\infty$ , thereby representing a white hole scenario.

In the second case, the areal radius of the boundary ( $R^{(II)}_{\Sigma}$ ) contracts from $\infty$ (for $\coth^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]=3)$ approaching $3M$ asymptotically as $t\rightarrow\infty$ .

Thus the fulfillment of the matching conditions provides one of the arbitrary functions of time describing our metric. In order to specify further our model we shall impose the quasi–homologous evolution and the vanishing complexity factor condition.

As we can see from (42), in the non–dissipative case the quasi–homologous condition implies that the fluid is shear–free ( $\sigma=0$ ), implying in its turn

\frac{\dot{B}}{B}=\frac{\dot{R}}{R}\,\,\Rightarrow\,\,F(t)=Const.\equiv F_{0}.

(84)

Thus the metric functions become

A=\frac{F_{0}}{f(t)+g(r)},\quad B=\frac{1}{f(t)+g(r)},\quad R=\frac{F_{0}}{\alpha\left[f(t)+g(r)\right]}.

(85)

Therefore our models are now specified up to an arbitrary function of $r$ ( $g(r)$ ). In order to fix this function we shall further impose the vanishing complexity factor condition.

Then feeding back (85) into (31) we obtain

\frac{A^{\prime\prime}}{A}-\frac{A^{\prime}}{A}(\frac{B^{\prime}}{B}+\frac{R^{\prime}}{R})=0.

(86)

Using (85) in (86), it follows at once

g(r)=c_{1}r+c_{2},

(87)

with $c_{1}\equiv\pm\sqrt{\omega}$ , and $c_{2}$ is another integration constant, we shall choose the negative sign in $c_{1}$ in order to ensure that $R^{\prime}>0$ . However it should be noticed that the regularity conditions, necessary to ensure elementary flatness in the vicinity of the axis of symmetry, and in particular at the center (see 1n , 2n , 3n ), are not satisfied.

Therefore after the imposition of the two conditions above (quasi–homologous evolution and vanishing complexity factor) we have all the metric functions completely specified for any of the above solutions to (65).

Thus in the case $b=0$ we obtain from (82)

f^{(I)}(t)=\frac{F_{0}\left\{3-\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]\right\}}{6\alpha M\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}-c_{1}r_{\Sigma}-c_{2},

(88)

from which the physical variables are easily found to be

$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-3c_{1}^{2}+\frac{\left\{-F_{0}-6\alpha c_{1}M(r_{\Sigma}-r)+3F_{0}\coth^{2}[\frac{\alpha}{2}(t-t_{0})]\right\}^{2}}{36F_{0}^{2}M^{2}}+\frac{3\cosh^{2}[\frac{\alpha}{2}(t-t_{0})]}{4M^{2}\sinh^{6}[\frac{\alpha}{2}(t-t_{0})]},$	(89)
$\displaystyle 8\pi P_{r}$	$\displaystyle=$	$\displaystyle\frac{2\alpha c_{1}(r_{\Sigma}-r)}{3F_{0}M}-\frac{\alpha^{2}c_{1}^{2}(r_{\Sigma}-r)^{2}}{F_{0}^{2}}-\frac{3c_{1}\alpha(r_{\Sigma}-r)}{2F_{0}M\sinh^{4}[\frac{\alpha}{2}(t-t_{0})]},$	(90)
$\displaystyle 8\pi P_{\bot}$	$\displaystyle=$	$\displaystyle 3c_{1}^{2}+\frac{\left[F_{0}-3\alpha c_{1}M(r_{\Sigma}-r)\right]}{3F_{0}M^{2}\sinh^{2}[\frac{\alpha}{2}(t-t_{0})]}+\frac{\left[F_{0}-6\alpha c_{1}M(r_{\Sigma}-r)\right]}{4F_{0}M^{2}\sinh^{4}[\frac{\alpha}{2}(t-t_{0})]}.$	(91)

From (90) it follows at once that $(P_{r})_{\Sigma}=0$ .

It is worth noticing that the expansion scalar for this model reads

\Theta=\frac{3\cosh[\frac{\alpha}{2}(t-t_{0})]}{2M\sinh^{3}[\frac{\alpha}{2}(t-t_{0})]}.

(92)

Thus the expansion is homogeneous and positive, diverging at $t=t_{0}$ , and tending to zero as $t\rightarrow\infty$ . The fast braking of the expansion for $t>t_{0}$ is produced by the negative initially large (diverging at $t=t_{0}$ ) value of $D_{T}U$ . This can be checked from (235), where the negative gravitational term proportional to $m/R^{2}$ provides the leading term in the equation ( $\frac{m}{R^{2}}\sim\frac{1}{\sinh^{4}[\frac{\alpha}{2}(t-t_{0})]})$ . As time goes on there is a sharp decreasing in the inertial mass density ( $\mu+P_{r}$ ) which as $t\rightarrow\infty$ becomes arbitrarily small (see (97) below). Now, the striking fact is that the equilibrium is reached asymptotically, but not, as usual, by the balance between the gravitational term (the first term on the right of (235)) and the hydrodynamic terms (the second term on the right of (235)). Instead, both terms cancel independently. Indeed, as $t\rightarrow\infty$ , the gravitational term vanishes due to the fact that the inertial mass density (the “passive gravitational mass density”) $\mu+P_{r}\rightarrow 0$ , and the hydrodynamic term vanishes because, as it can be easily checked, the radial pressure gradient cancels the anisotropic factor, as $t\rightarrow\infty$ .

Next, if we take (83) we obtain for $f(t)$

f^{(II)}(t)=\frac{F_{0}\left\{3-\coth^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]\right\}}{6\alpha M\coth^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}-c_{1}r_{\Sigma}-c_{2},

(93)

whereas the expressions for the physical variables read

$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-3c_{1}^{2}+\frac{3\sinh^{2}[\frac{\alpha}{2}(t-t_{0})]}{4M^{2}\cosh^{6}[(\frac{\alpha}{2}(t-t_{0})]}+\frac{\left\{F_{0}+6\alpha c_{1}M(r_{\Sigma}-r)-3F_{0}\tanh^{2}[\frac{\alpha}{2}(t-t_{0})]\right\}^{2}}{36F_{0}^{2}M^{2}},$	(94)
$\displaystyle 8\pi P_{r}$	$\displaystyle=$	$\displaystyle\frac{2\alpha c_{1}(r_{\Sigma}-r)}{3F_{0}M}-\frac{\alpha^{2}c_{1}^{2}(r_{\Sigma}-r)^{2}}{F_{0}^{2}}-\frac{3c_{1}\alpha(r_{\Sigma}-r)}{2F_{0}M\cosh^{4}[\frac{\alpha}{2}(t-t_{0})]},$	(95)
$\displaystyle 8\pi P_{\bot}$	$\displaystyle=$	$\displaystyle 3c_{1}^{2}-\frac{F_{0}-3\alpha c_{1}M(r_{\Sigma}-r)}{3F_{0}M^{2}\cosh^{2}[\frac{\alpha}{2}(t-t_{0})]}+\frac{F_{0}-6\alpha c_{1}M(r_{\Sigma}-r)}{4F_{0}M^{2}\cosh^{4}[\frac{\alpha}{2}(t-t_{0})]}.$	(96)

In the limit $t\rightarrow\infty$ the two above solutions converge to the same static distribution whose physical variables are

	$\displaystyle 8\pi\mu=\frac{1}{9M^{2}}\left[3+\left(\frac{r}{r_{\Sigma}}\right)^{2}-4\left(\frac{r}{r_{\Sigma}}\right)\right],$		(97)
	$\displaystyle 8\pi P_{r}=\frac{1}{9M^{2}}\left[-3-\left(\frac{r}{r_{\Sigma}}\right)^{2}+4\left(\frac{r}{r_{\Sigma}}\right)\right],$
	$\displaystyle 8\pi P_{\bot}=\frac{1}{9M^{2}},$

where the constant $F_{0}$ has been chosen $F_{0}=\frac{r_{\Sigma}\alpha}{\sqrt{3}}$ . It is worth noticing that the ensuing equation of state for the static limit is the Chaplygin–type equation $\mu=-P_{r}$ .

In the case $\omega=0$ the expression for $R_{\Sigma}$ is given by

R^{(III)}_{\Sigma}=2M\cos^{2}\frac{\alpha}{2}(t-t_{0}),

(98)

and from(87)

\omega=g^{\prime}(r_{\Sigma})^{2}=c_{1}^{2}=0.

(99)

Then the following expressions may be obtained for the metric functions

A=\frac{F_{0}}{f(t)+c_{2}},\qquad B=\frac{1}{f(t)+c_{2}}\qquad R=\frac{F_{0}}{\alpha\left[f(t)+c_{2}\right]},

(100)

with $f(t)\equiv f^{III}(t)$ , given by

f^{(III)}(t)=\frac{F_{0}}{2\alpha M\cos^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}-c_{2},

(101)

and the physical variables read

$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle\frac{\left\{3-2\cos^{2}[\frac{\alpha}{2}(t-t_{0})]\right\}}{4M^{2}\cos^{6}[\frac{\alpha}{2}(t-t_{0})]},$	(102)
$\displaystyle 8\pi P_{r}$	$\displaystyle=$	$\displaystyle 0,$	(103)
$\displaystyle 8\pi P_{\bot}$	$\displaystyle=$	$\displaystyle\frac{1}{4M^{2}\cos^{4}[\frac{\alpha}{2}(t-t_{0})]}.$	(104)

It is worth stressing the presence of important topological pathologies in this solution (e.g. $R^{\prime}=0$ ), implying the appearance of shell crossing singularities.

Before closing this subsection we would like to call the attention to a very peculiar solution that may be obtained by assuming that the space–time outside the boundary surface delimiting the fluid is Minkowski. This implies $M=0$ , and then the solutions to (63) read

R^{(IV)}_{\Sigma}=\frac{1}{\sqrt{\omega}\cos[\alpha(t-t_{0})]},

(105)

and

R^{(V)}_{\Sigma}=\frac{1}{\sqrt{\omega}\sin[\alpha(t-t_{0})]}.

(106)

Assuming further that the evolution is quasi–homologous and the complexity factor vanishes, we obtain for the functions $f(t)$

f^{(IV)}(t)=\frac{1}{\alpha}F_{0}\sqrt{\omega}\cos[\alpha(t-t_{0})]+\sqrt{\omega}r_{\Sigma}-c_{2},

(107)

and

f^{(V)}(t)=\frac{1}{\alpha}F_{0}\sqrt{\omega}\sin[\alpha(t-t_{0})]+\sqrt{\omega}r_{\Sigma}-c_{2}.

(108)

The corresponding physical variables for $f^{(IV)}$ read

	$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-2\omega\cos^{2}[\alpha(t-t_{0})]$		(109)
		$\displaystyle+$	$\displaystyle\omega(1-\frac{r}{r_{\Sigma}})\left[1-\frac{r}{r_{\Sigma}}+2\cos[\alpha(t-t_{0})]\right],$		(109)

8\pi P_{r}=-\omega\left(1-\frac{r}{r_{\Sigma}}\right)\left[4\cos[\alpha(t-t_{0})]+1-\frac{r}{r_{\Sigma}}\right],

(110)

8\pi P_{\bot}=\omega\cos^{2}[\alpha(t-t_{0})]-2\omega\left(1-\frac{r}{r_{\Sigma}}\right)\cos[\alpha(t-t_{0})],

(111)

whereas for $f^{(V)}$ they are

	$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-2\omega\sin^{2}[\alpha(t-t_{0})]$		(112)
		$\displaystyle+$	$\displaystyle\omega(1-\frac{r}{r_{\Sigma}})\left[1-\frac{r}{r_{\Sigma}}+2\sin[\alpha(t-t_{0})]\right],$		(112)

8\pi P_{r}=-\omega\left(1-\frac{r}{r_{\Sigma}}\right)\left[4\sin[\alpha(t-t_{0})]+1-\frac{r}{r_{\Sigma}}\right],

(113)

8\pi P_{\bot}=\omega\sin^{2}[\alpha(t-t_{0})]-2\omega\left(1-\frac{r}{r_{\Sigma}}\right)\sin[\alpha(t-t_{0})].

(114)

In the above the constants $F_{0},\alpha,r_{\Sigma}$ have been chosen such that $\frac{F_{0}}{\alpha r_{\Sigma}}=1$ .

This kind of configurations have been considered in 11co ; zel .

V.2 $\chi_{\alpha}V^{\alpha}=0;q\neq 0$

Let us now consider the general dissipative case when the vector $\chi^{\alpha}$ is orthogonal to the four–velocity.

Then from (49) we obtain, following the same procedure as in the non–dissipative case

A=\alpha R,

(115)

where $\alpha$ is a unit constant with dimensions of $\frac{1}{length}$ ,

F(t)B=\alpha R,

(116)

where $F(t)$ is and arbitrary function of $t$ , and

\chi^{1}_{,1}=0\Rightarrow\chi^{1}=constant.

(117)

Then, feeding back (115) and (116) into (226) with $q\neq 0$ , one obtains

\frac{\dot{B}^{\prime}}{B}-\frac{2\dot{B}B^{\prime}}{B^{2}}=4\pi qAB.

(118)

The equation above may be formally integrated, to obtain

B=\frac{1}{f(t)+g(r)-4\pi\int\int qAdtdr},

(119)

A=\alpha R=\frac{F(t)}{f(t)+g(r)-4\pi\int\int qAdtdr},

(120)

where $f$ and $g$ are two arbitrary functions of their arguments.

In order to find a specific solutions we shall impose next the vanishing complexity factor condition ( $Y_{TF}=0$ ).

Then from the above expressions and (31), the condition $Y_{TF}=0$ reads

\frac{1}{F^{2}}\left(\frac{\ddot{F}}{F}+\frac{\dot{F}\dot{B}}{FB}-\frac{\dot{F}^{2}}{F^{2}}\right)+\frac{B^{\prime\prime}}{B}-2\left(\frac{B^{\prime}}{B}\right)^{2}=0.

(121)

In order to find a solution to the above equation we shall assume that

\left(\frac{\ddot{F}}{F}+\frac{\dot{F}\dot{B}}{FB}-\frac{\dot{F}^{2}}{F^{2}}\right)=0,

(122)

and

\frac{B^{\prime\prime}}{B}-2\left(\frac{B^{\prime}}{B}\right)^{2}=0.

(123)

The integration of (123) produces

B=-\frac{1}{\beta(t)r+\gamma(t)},

(124)

where $\beta,\gamma$ are arbitrary functions of $t$ . It is worth noticing that $\beta$ has dimensions of $\frac{1}{length}$ , and $\gamma$ is dimensionless.

Next, taking the $r$ derivative of (122) we obtain $\gamma=\frac{\beta}{\alpha}$ .

Then we may write

B=-\frac{\alpha}{\beta(t)(\alpha r+1)}.

(125)

Next, combining (122) with (125) we obtain

F(t)=c_{3}e^{c_{4}\int\beta dt},

(126)

where $c_{3},c_{4}$ are arbitrary constants.

From the above expression it follows at once

\frac{\dot{F}}{F}=c_{4}\beta.

(127)

On the other hand, (119) with (125), imply

4\pi\int\int qAdtdr=\beta(t)r,\quad g(r)=g_{1}r+g_{0},

(128)

where $g_{1},g_{0}$ are constant.

We may now write the physical variables in terms of the function $\beta(t)$ , they read

8\pi\mu=\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}e^{2c_{4}\int{\beta dt}}}\left(\alpha^{2}-4c_{4}\dot{\beta}+\frac{3\dot{\beta}^{2}}{\beta^{2}}+c_{4}^{2}\beta^{2}\right)-3\beta^{2},

(129)

4\pi q=-\frac{\beta\dot{\beta}(\alpha r+1)}{\alpha c_{3}e^{c_{4}\int{\beta dt}}},

(130)

8\pi P_{r}=-\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}e^{2c_{4}\int{\beta dt}}}\left(\alpha^{2}-\frac{2\ddot{\beta}}{\beta}+\frac{3\dot{\beta}^{2}}{\beta^{2}}+c_{4}^{2}\beta^{2}\right)+3\beta^{2},

(131)

8\pi P_{\bot}=-\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}e^{2c_{4}\int{\beta dt}}}\left(c_{4}\dot{\beta}-\frac{2\ddot{\beta}}{\beta}+\frac{3\dot{\beta}^{2}}{\beta^{2}}\right)+3\beta^{2}.

(132)

The function $\beta$ may be found, in principle, from the junction condition (35), however since this is in practice quite difficult at this level of generality, we shall first impose further constraints on our fluid distribution in order to obtain a simpler model, and afterwards we shall use the junction conditions.

We shall start by imposing the quasi–homologous condition (46). Then using (119) and (120) in (46) we get

4\pi qA\frac{B^{2}}{B^{\prime}}=\frac{\dot{F}}{F}.

(133)

Using (133) with (125)–(128) one obtains

\beta=-\frac{1}{c_{4}t+c_{5}},

(134)

where $c_{5}$ is a constant with dimensions of $length$ .

So the metric functions may be written as

B=\frac{\alpha(c_{4}t+c_{5})}{(\alpha r+1)},

(135)

A=\alpha R=\frac{c_{3}}{\alpha r+1}.

(136)

It is worth noticing that the areal radius is independent on time ( $U=0$ ), solutions of this kind have been found in epjc

Next, instead of quasi–homologous condition we shall impose the shear–free condition. Then assuming $\sigma=0$ it follows at once that $\dot{F}=0$ implying $c_{4}=0$ . Then the metric functions become

B=-\frac{\alpha}{\beta(\alpha r+1)},\quad A=-\frac{c_{3}\alpha}{\beta(\alpha r+1)},\quad R=-\frac{c_{3}}{\beta(\alpha r+1)},

(137)

from which we can write the physical variables as

8\pi\mu=\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}}\left(\alpha^{2}+\frac{3\dot{\beta}^{2}}{\beta^{2}}\right)-3\beta^{2},

(138)

4\pi q=-\frac{\beta\dot{\beta}(\alpha r+1)}{\alpha c_{3}},

(139)

8\pi P_{r}=-\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}}\left(\alpha^{2}-\frac{2\ddot{\beta}}{\beta}+\frac{3\dot{\beta}^{2}}{\beta^{2}}\right)+3\beta^{2},

(140)

8\pi P_{\bot}=-\frac{\beta^{2}(\alpha r+1)^{2}}{\alpha^{2}c_{3}^{2}}\left(-\frac{2\ddot{\beta}}{\beta}+\frac{3\dot{\beta}^{2}}{\beta^{2}}\right)+3\beta^{2}.

(141)

Now we can find $\beta$ from the junction condition (35), which using (139) and (140) reads

\frac{2\ddot{\beta}}{\beta}-3\left(\frac{\dot{\beta}}{\beta}\right)^{2}+\frac{2\alpha_{1}\dot{\beta}}{\beta}=\alpha^{2}-3\alpha^{2}_{1},

(142)

with

\alpha_{1}\equiv\frac{\alpha c_{3}}{\alpha r_{\Sigma}+1}.

(143)

In order to integrate the above equation, let us introduce the variable $s=\frac{\dot{\beta}}{\beta}$ , which casts (142) into the Ricatti equation

2\dot{s}-s^{2}+2\alpha_{1}s=\alpha^{2}-3\alpha^{2}_{1},

(144)

whose solution is

s=\alpha_{1}+\sqrt{\alpha^{2}-4\alpha^{2}_{1}}\tan\left[\frac{\sqrt{\alpha^{2}-4\alpha^{2}_{1}}}{2}(t-t_{0})\right],

(145)

producing for $\beta$

\beta(t)=\alpha_{2}e^{\alpha_{1}t}\sec^{2}\left[\frac{\sqrt{\alpha^{2}-4\alpha^{2}_{1}}}{2}(t-t_{0})\right],

(146)

where $\alpha_{2}$ is a negative constant of integration with the same dimensions as $\beta$ .

Using the truncated version of the transport equation (39), we obtain for the temperature

T(t,r)=\frac{\alpha r+1}{4\pi c_{3}\kappa\alpha}\left[\frac{\tau r(\dot{\beta}^{2}+\beta\ddot{\beta})}{c_{3}}-\dot{\beta}\ln(\alpha r+1)\right]+T_{0}(t),

(147)

where $c_{3}$ and $T_{0}(t)$ are arbitrary constant and function of integration, respectively. The model described by equations (137)–(141) and (146), (147) will be named as model $VI$ .

V.3 $q=0;\chi^{\alpha}||V^{\alpha}$

We shall next analyze the case when the vector ${\mathbb{\chi}}$ is parallel to the four–velocity vector. We start by considering the non–dissipative case. In this case the equation (49) produces

A=Bh(r),\qquad R=Br,\qquad\chi^{0}=1,\qquad\psi=\frac{\dot{B}}{B},

(148)

where $h(r)$ is an arbitrary function of its argument. It is worth noticing that in this case the fluid is necessarily shear–free.

Thus the line element may be written as

ds^{2}=B^{2}\left[-h^{2}(r)dt^{2}+dr^{2}+r^{2}(d\theta^{2}+\sin^{2}\theta d\phi^{2})\right].

(149)

Next, using (148) in (226), the condition $q=0$ reads

\frac{\dot{R}^{\prime}}{R}-2\frac{\dot{R}}{R}\frac{R^{\prime}}{R}-\frac{\dot{R}}{R}\left(\frac{h^{\prime}}{h}-\frac{1}{r}\right)=0,

(150)

whose solution is

\displaystyle R=\frac{r}{h(r)\left[f(t)+g(r)\right]},

(151)

implying

\displaystyle B=\frac{1}{h(r)\left[f(t)+g(r)\right]},\quad A=\frac{1}{f(t)+g(r)},

(152)

where $g,f$ are two arbitrary functions of their argument.

Thus the metric is defined up to three arbitrary functions ( $g(r),f(t),h(r)$ ).

The function $f(t)$ will be obtained from the junction conditions (33), (35).

Indeed, evaluating the mass function at the boundary surface $\Sigma$ we obtain from (33) and (151)

\dot{R}^{2}_{\Sigma}=\alpha^{2}R^{4}_{\Sigma}\left[\epsilon-V(R_{\Sigma})\right],

(153)

where $\alpha^{2}\equiv\frac{h^{2}_{\Sigma}}{r^{2}_{\Sigma}}$ , $\epsilon\equiv(g^{\prime})^{2}_{\Sigma}h^{2}_{\Sigma}$ , and

V(R_{\Sigma})=\frac{2\sqrt{\epsilon}}{R_{\Sigma}}(1-a_{1})+\frac{a_{1}}{R^{2}_{\Sigma}}(2-a_{1})-\frac{2M}{R^{3}_{\Sigma}},

(154)

with $a_{1}\equiv\frac{h^{\prime}_{\Sigma}r_{\Sigma}}{h_{\Sigma}}$ .

On the other hand, from (35), using (151) we obtain

			$\displaystyle 2\ddot{R}_{\Sigma}R_{\Sigma}-\dot{R}^{2}_{\Sigma}-3\epsilon\alpha^{2}R^{4}_{\Sigma}-4\alpha^{2}\sqrt{\epsilon}R^{3}_{\Sigma}(a_{1}-1)$		(155)
		$\displaystyle-$	$\displaystyle\alpha^{2}R^{2}_{\Sigma}a_{1}(a_{1}-2)=0,$		(155)

To specify a model we have to obtain $f(t)$ from the solution to the above equations.

In the special case $a_{1}=1$ (153) becomes

\dot{R}^{2}_{\Sigma}=\alpha^{2}R^{4}_{\Sigma}\left[\epsilon-\frac{1}{R^{2}_{\Sigma}}+\frac{2M}{R^{3}_{\Sigma}}\right],

(156)

which has exactly the same form as (65) and therefore admits the same kind of solutions, and (155) reads

\displaystyle 2\ddot{R}_{\Sigma}R_{\Sigma}-\dot{R}^{2}_{\Sigma}-3\epsilon\alpha^{2}R^{4}_{\Sigma}+\alpha^{2}R^{2}_{\Sigma}=0,

(157)

a first integral of which, as it can be easily shown, is (156), therefore we only need to satisfy (156).

In order to determine the functions $g(r),h(r)$ we shall assume the vanishing complexity factor condition $Y_{TF}=0$ .

Using (151) in (31) the condition $Y_{TF}=0$ reads

\frac{g^{\prime\prime}}{g^{\prime}}-\frac{1}{r}+\frac{2h^{\prime}}{h}=0,

(158)

\frac{v^{\prime}}{v}-\frac{1}{r}+\frac{2h^{\prime}}{h}=0,

(159)

with $v\equiv g^{\prime}$ , whose formal solution is

v=\frac{c_{4}r}{h^{2}},

(160)

producing

g=c_{4}\int\frac{r}{h^{2}}dr+c_{5},

(161)

where $c_{4},c_{5}$ are arbitrary constants.

If we choose

h(r)=c_{6}r,

(162)

implying $a_{1}=1$ , then we obtain from (161)

g=c_{7}\ln r+c_{5},

(163)

where $c_{6},c_{7}$ are constants.

Thus, let us consider the following model. The time dependence described by $f(t)$ is obtained from the solution to (156) given by

R^{(VII)}_{\Sigma}=\frac{6M\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]}{3-\tanh^{2}\left[\frac{\alpha}{2}(t-t_{0})\right]},

(164)

with $\epsilon=\frac{1}{27M^{2}}$ , and the radial dependence of the model is given by the functions $g(r),h(r)$ given by (162) (163).

The physical variables corresponding to this model read

			$\displaystyle 8\pi\mu=\frac{3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]}{4M^{2}\sinh^{4}[\frac{\alpha}{2}(t-t_{0})]}+\frac{(3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]-1)^{2}}{36M^{2}}$
		$\displaystyle-$	$\displaystyle\frac{1}{9M^{2}}+\ln\left(\frac{r}{r_{\Sigma}}\right)\left[\frac{3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]-1}{9\sqrt{3}M^{2}}+\frac{1}{27M^{2}}\ln\left(\frac{r}{r_{\Sigma}}\right)\right],$

	$\displaystyle 8\pi P_{r}$	$\displaystyle=$	$\displaystyle\ln\left(\frac{r}{r_{\Sigma}}\right)\left[\frac{(3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]-1)(3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]-5)}{18\sqrt{3}M^{2}}-\right.$		(166)
			$\displaystyle\left.\frac{1}{27M^{2}}\ln\left(\frac{r}{r_{\Sigma}}\right)\right],$		(166)

	$\displaystyle 8\pi P_{\bot}=\frac{(3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]+1)}{12M^{2}\sinh^{2}[\frac{\alpha}{2}(t-t_{0})]}+\frac{1}{9M^{2}}$
	$\displaystyle+\ln\left(\frac{r}{r_{\Sigma}}\right)\frac{(3\coth^{2}[\frac{\alpha}{2}(t-t_{0})]-1)}{6\sqrt{3}M^{2}\sinh^{2}[\frac{\alpha}{2}(t-t_{0})},$		(167)

where the following relationships between the constants has been used $\alpha^{2}\equiv c_{6}^{2}$ , $\epsilon\equiv\frac{1}{27M^{2}}\equiv c_{7}^{2}c_{6}^{2}$

In the limit $t\rightarrow\infty$ the above model tends to a static fluid distribution described by

\displaystyle 8\pi\mu=\ln\left(\frac{r}{r_{\Sigma}}\right)\left[\frac{2}{9\sqrt{3}M^{2}}+\frac{1}{27M^{2}}\ln\left(\frac{r}{r_{\Sigma}}\right)\right],

(168)

8\pi P_{r}=-\ln\left(\frac{r}{r_{\Sigma}}\right)\left[\frac{2}{9\sqrt{3}M^{2}}+\frac{1}{27M^{2}}\ln\left(\frac{r}{r_{\Sigma}}\right)\right],

(169)

\displaystyle 8\pi P_{\bot}=\frac{1}{9M^{2}},

(170)

satisfying the equation of state $P_{r}=-\mu$ .

Another case which allows integration in terms of elementary function may be obtained from the conditions $\epsilon=0$ and $a_{1}=1/2$ . Then (153) reads

\dot{R}^{2}_{\Sigma}=\alpha^{2}R^{4}_{\Sigma}\left[\frac{2M}{R^{3}_{\Sigma}}-\frac{3}{4R^{2}_{\Sigma}}\right].

(171)

The above equation may be easily integrated, producing

R^{(VIII)}_{\Sigma}=\frac{4M}{3}\left(1+\sin\tilde{t}\right),

(172)

with $\tilde{t}\equiv\frac{\sqrt{3}\alpha}{2}(t-t_{0})$ .

Next, in order to specify further the model, we shall impose the vanishing complexity factor condition. In this case ( $a_{1}=1/2$ ), the general solution to (159) reads

h=c_{1}\sqrt{r},\qquad g=c_{2}r+c_{3},

(173)

however since $\epsilon=0$ the constant $c_{2}$ must vanish.

The physical variables for this model read

\displaystyle 8\pi\mu=\frac{27}{64M^{2}(1+\sin\tilde{t})^{2}}\left[\frac{3\cos^{2}\tilde{t}}{(1+\sin\tilde{t})^{2}}+\frac{r_{\Sigma}}{r}\right],

(174)

\displaystyle 8\pi P_{r}=\frac{27}{64M^{2}(1+\sin\tilde{t})^{2}}\left(1-\frac{r_{\Sigma}}{r}\right),

(175)

\displaystyle 8\pi P_{\bot}=\frac{27}{64M^{2}(1+\sin\tilde{t})^{2}}.

(176)

This solution represents fluid distribution oscillating between $R_{\Sigma}=0$ and $R_{\Sigma}=\frac{8M}{3}$ . It is worth noticing that the energy density is always positive, whereas the radial pressure is not.

Finally, we shall present two solutions describing a “ghost” compact object, of the kind already discussed in the previous section.

Thus assuming $M=0$ , equation (153) becomes

\dot{R}^{2}_{\Sigma}=\alpha^{2}R^{4}_{\Sigma}\left[\epsilon-\frac{2\sqrt{\epsilon}(1-a_{1})}{R_{\Sigma}}-\frac{a_{1}(2-a_{1})}{R^{2}_{\Sigma}}\right].

(177)

Solutions to the above equation in terms of elementary functions may be obtained by assuming $a_{1}=1$ , in which case the two possible solutions to (177) are

R^{(IX)}_{\Sigma}=\frac{1}{\sqrt{\epsilon}\cos[\alpha(t-t_{0})]},

(178)

and

R^{(X)}_{\Sigma}=\frac{1}{\sqrt{\epsilon}\sin[\alpha(t-t_{0})]}.

(179)

Imposing further the vanishing complexity factor condition, then functions $h(r),g(r)$ are given by (162) and (163). The physical variables corresponding to (178) and (179) read respectively

	$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-2\epsilon\cos^{2}[\alpha(t-t_{0})]+$		(180)
		$\displaystyle+$	$\displaystyle\epsilon\ln\frac{r}{r_{\Sigma}}\left[2\cos[\alpha(t-t_{0})]+\ln\frac{r}{r_{\Sigma}}\right],$		(180)

\displaystyle 8\pi P_{r}=-\epsilon\ln\frac{r}{r_{\Sigma}}\left[4\cos[\alpha(t-t_{0})]+\ln\frac{r}{r_{\Sigma}}\right],

(181)

8\pi P_{\bot}=\epsilon\cos^{2}[\alpha(t-t_{0})]-2\epsilon\ln\frac{r}{r_{\Sigma}}\cos[\alpha(t-t_{0})],

(182)

and

	$\displaystyle 8\pi\mu$	$\displaystyle=$	$\displaystyle-2\epsilon\sin^{2}[\alpha(t-t_{0})]+$		(183)
		$\displaystyle+$	$\displaystyle\epsilon\ln\frac{r}{r_{\Sigma}}\left[2\sin[\alpha(t-t_{0})]+\ln\frac{r}{r_{\Sigma}}\right],$		(183)

\displaystyle 8\pi P_{r}=-\epsilon\ln\frac{r}{r_{\Sigma}}\left[4\sin[\alpha(t-t_{0})]+\ln\frac{r}{r_{\Sigma}}\right],

(184)

8\pi P_{\bot}=\epsilon\sin^{2}[\alpha(t-t_{0})]-2\epsilon\ln\frac{r}{r_{\Sigma}}\sin[\alpha(t-t_{0})].

(185)

V.4 $\chi^{\alpha}||V^{\alpha};q\neq 0$

Finally, we shall consider the case where the CKV is parallel to the four–velocity, and the system is dissipative. As result of the admittance of the CKV the metric functions read as (148). Then, feeding this back into (226) produces

\frac{\dot{B}^{\prime}}{B}-2\frac{\dot{B}}{B}\frac{B^{\prime}}{B}-\frac{\dot{B}}{B}\frac{h^{\prime}}{h}=4\pi qAB,

(186)

which may be formally integrated, to obtain

B=\frac{1}{h(r)\left[f(t)+g(r)-\int\int 4\pi qBdrdt\right]},

(187)

implying

A=\frac{1}{\left[f(t)+g(r)-\int\int 4\pi qBdrdt\right]},

(188)

and

R=\frac{r}{h(r)\left[f(t)+g(r)-\int\int 4\pi qBdrdt\right]},

(189)

where $f(t)$ and $g(r)$ are arbitrary functions of their arguments.

To specify a model we shall impose the vanishing complexity factor condition. Thus, using (187)–(189) in (31) the condition $Y_{TF}=0$ reads

g^{\prime}-\int{4\pi qBdt}=\frac{\gamma(t)r}{h^{2}(r)},

(190)

a formal integration of which produces

g-\int{\int{4\pi qBdtdr}}=\gamma(t)\int{\frac{rdr}{h^{2}(r)}},

(191)

where $\gamma(t)$ is an arbitrary function.

Also, taking the $t$ -derivative of (190) we obtain

4\pi qB=-\frac{\dot{\gamma}(t)r}{h^{2}(r)}.

(192)

Using the above expressions we may write the metric functions (187)–(189) as

B=\frac{1}{h(r)\left[f(t)+\gamma(t)\int{\frac{rdr}{h^{2}(r)}}\right]},

(193)

implying

A=\frac{1}{\left[f(t)+\gamma(t)\int{\frac{rdr}{h^{2}(r)}}\right]},

(194)

and

R=\frac{r}{h(r)\left[f(t)+\gamma(t)\int{\frac{rdr}{h^{2}(r)}}\right]}.

(195)

Further restrictions on functions $f(t),\gamma(t)$ will be obtained from the junction condition $(P_{r}=q)_{\Sigma}$ .

Indeed, using (192)–(195) and (227), the condition $(P_{r}=q)_{\Sigma}$ , reads

			$\displaystyle h^{2}_{\Sigma}X_{\Sigma}\left(\frac{1}{r_{\Sigma}}-\frac{h^{\prime}_{\Sigma}}{h_{\Sigma}}-\frac{X^{\prime}_{\Sigma}}{X_{\Sigma}}\right)\left(\frac{1}{r_{\Sigma}}-\frac{h^{\prime}_{\Sigma}}{h_{\Sigma}}-3\frac{X^{\prime}_{\Sigma}}{X_{\Sigma}}\right)$		(196)
		$\displaystyle-$	$\displaystyle X_{\Sigma}\left(-2\frac{\ddot{X}_{\Sigma}}{X_{\Sigma}}+3\frac{\dot{X}^{2}_{\Sigma}}{X^{2}_{\Sigma}}+\alpha^{2}\right)=-\frac{2\dot{\gamma}}{\alpha},$		(196)

where

X\equiv f(t)+\gamma(t)\int{\frac{rdr}{h^{2}(r)}},\qquad\alpha\equiv\frac{h_{\Sigma}}{r_{\Sigma}}.

(197)

In order to solve the above equation we shall assume

\displaystyle-2\frac{\ddot{X}_{\Sigma}}{X_{\Sigma}}+3\frac{\dot{X}^{2}_{\Sigma}}{X^{2}_{\Sigma}}+\alpha^{2}=\frac{2\dot{\gamma}}{X_{\Sigma}\alpha},

(198)

and

1-a_{1}-\frac{r_{\Sigma}X^{\prime}_{\Sigma}}{X_{\Sigma}}=0,

(199)

where $a_{1}\equiv\frac{h^{\prime}_{\Sigma}r_{\Sigma}}{h_{\Sigma}}$ .

From (199) it follows at once that

1-a_{1}=\frac{\gamma(t)}{\alpha^{2}X_{\Sigma}},

(200)

producing

\frac{\gamma(t)\dot{X}_{\Sigma}}{X^{2}_{\Sigma}}=\frac{\dot{\gamma}(t)}{X_{\Sigma}}.

(201)

Using (200) and (201) in (198), this last equation becomes

\displaystyle 2\frac{\ddot{X}_{\Sigma}}{X_{\Sigma}}-3\frac{\dot{X}^{2}_{\Sigma}}{X^{2}_{\Sigma}}+\frac{2\alpha\dot{X}_{\Sigma}(1-a_{1})}{X_{\Sigma}}-\alpha^{2}=0.

(202)

In order to integrate (202), let us introduce the variable $y=\frac{\dot{X}_{\Sigma}}{X_{\Sigma}}$ , in terms of which (202) reads

\dot{y}-\frac{1}{2}y^{2}+\alpha(1-a_{1})y-\frac{\alpha^{2}}{2}=0.

(203)

This is a Ricatti equation, a particular solution of which is

y_{0}=\alpha(1-a_{1})\pm\alpha\sqrt{a^{2}_{1}-2a_{1}}.

(204)

Then, in order to find the general solution to (203) let us introduce the variable $z=y-y_{0}$ , producing

\dot{z}-\frac{1}{2}z^{2}+\left[\alpha(1-a_{1})-y_{0}\right]z=0,

(205)

whose solution reads

z=\frac{2\delta}{1+be^{\delta t}},

(206)

where $b$ is an arbitrary constant of integration and $\delta\equiv\alpha(1-a_{1})-y_{0}$ .

With this result, we can easily find $X_{\Sigma}$ , whose expression reads

X_{\Sigma}=\frac{ce^{(2\delta+y_{0})t}}{(1+be^{\delta t})^{2}},

(207)

where $c$ is a constant of integration.

Using (207) in (200) we obtain the explicit form of $\gamma(t)$ , and using this expression and (207) in (197) we obtain the explicit from of $f(t)$ . Thus, the model is completely determined up to a single function of $r$ ( $h(r)$ ).

In terms of $X(t,r)$ and $h(r)$ , the physical variables read

	$\displaystyle 8\pi\mu=$		$\displaystyle 3\dot{X}^{2}-h^{2}X^{2}\left[-\frac{2h^{\prime\prime}}{h}+\frac{3(h^{\prime})^{2}}{h^{2}}-\frac{2X^{\prime\prime}}{X}+\frac{3(X^{\prime})^{2}}{X^{2}}\right.$		(208)
			$\displaystyle\left.+\frac{2h^{\prime}X^{\prime}}{hX}-\frac{4h^{\prime}}{rh}-\frac{4X^{\prime}}{rX}\right],$		(208)

	$\displaystyle 8\pi P_{r}=$		$\displaystyle 2\ddot{X}X-3\dot{X}^{2}+h^{2}X^{2}\left[\frac{(h^{\prime})^{2}}{h^{2}}+\frac{3(X^{\prime})^{2}}{X^{2}}+\frac{4h^{\prime}X^{\prime}}{hX}\right.$		(209)
			$\displaystyle\left.-\frac{2h^{\prime}}{rh}-\frac{4X^{\prime}}{rX}\right],$		(209)

	$\displaystyle 8\pi P_{\bot}=$		$\displaystyle 2\ddot{X}X-3\dot{X}^{2}+h^{2}X^{2}\left[-\frac{h^{\prime\prime}}{h}+\frac{(h^{\prime})^{2}}{h^{2}}-\frac{2X^{\prime\prime}}{X}\right.$		(210)
			$\displaystyle\left.+\frac{3(X^{\prime})^{2}}{X^{2}}-\frac{h^{\prime}}{rh}-\frac{2X^{\prime}}{rX}\right],$		(210)

\displaystyle 8\pi q=-2hX\dot{X}^{\prime}.

(211)

In order to obtain a specific model we shall assume $a_{1}=2$ , which implies $y_{0}=-\alpha$ and $\delta=0$ , then feeding back these values in (207), the expression for $X_{\Sigma}$ becomes

X_{\Sigma}=\tilde{c}e^{-\alpha t},

(212)

with $\tilde{c}\equiv\frac{c}{(1+b)^{2}}$ .

Next, we shall assume for $h(r)$ the form

h(r)=c_{2}r^{2},

(213)

where $c_{2}$ is a constant with dimensions $1/[length]^{2}$ , producing

\alpha=c_{2}r_{\Sigma}.

(214)

Using (213) and (214) we obtain for the radial dependence of $X$

\int{\frac{rdr}{h(r)^{2}}}=-\frac{r_{\Sigma}^{2}}{2\alpha^{2}r^{2}}.

(215)

From (200) we obtain at once for $\gamma(t)$

\gamma(t)=-\alpha^{2}\tilde{c}e^{-\alpha t},

(216)

and from (197) and (215) the expression for $f(t)$ reads

f(t)=\frac{\tilde{c}e^{-\alpha t}}{2}.

(217)

Finally the expression for $X(t,r)$ reads

X^{(XI)}(t,r)=\frac{\tilde{c}e^{-\alpha t}}{2}\left[1+\left(\frac{r_{\Sigma}}{r}\right)^{2}\right].

(218)

Thus, the physical variables for this model $XI$ (including the total mass and the temperature) read

8\pi\mu=\frac{3\tilde{c}^{2}\alpha^{2}e^{-2\alpha t}}{4r^{4}}\left(5r^{4}+2r^{2}r^{2}_{\Sigma}+r^{4}_{\Sigma}\right),

(219)

8\pi P_{r}=8\pi P_{\bot}=\frac{\tilde{c}^{2}\alpha^{2}e^{-2\alpha t}}{4r^{4}}\left(2r^{2}r^{2}_{\Sigma}-9r^{4}-r^{4}_{\Sigma}\right),

(220)

8\pi q=-\tilde{c}^{2}\alpha^{2}e^{-2\alpha t}\left(r^{2}+r^{2}_{\Sigma}\right)\frac{r_{\Sigma}}{r^{3}},

(221)

m_{\Sigma}=\frac{e^{\alpha t}}{\tilde{c}\alpha},

(222)

	$\displaystyle T(t,r)=\frac{\tilde{c}e^{-\alpha t}(r^{2}+r^{2}_{\Sigma})}{2r^{2}}\left[\frac{\tau r^{2}_{\Sigma}\tilde{c}\alpha^{2}e^{-\alpha t}}{4\pi\kappa r^{2}}\right.$
	$\displaystyle\left.+\frac{\alpha}{4\pi\kappa}\ln\left(\frac{r^{2}}{r^{2}+r^{2}_{\Sigma}}\right)+T_{0}(t)\right],$		(223)

this last expression was obtained using the truncated transport equation (39).

It is worth noticing that this model is intrinsically isotropic in pressure, the energy density is positive and larger than the pressure, and the matching condition $q\stackrel{{\scriptstyle\Sigma}}{{=}}P_{r}$ is obviously satisfied. However the physical variables are singular at the center.

VI Discussion

We have seen so far that the admittance of CKV leads to a wealth of solutions to the Einstein equations for a general spherically symmetric fluid distributions, which could be applied to a variety of astrophysical problems, or serve as testbeds for discussions about theoretical issues such as wormholes and white holes.

In order to find solutions expressed in terms of elementary functions we have imposed further constrains on the fluid distribution. Some of which are endowed with a distinct physical meaning (e.g. the vanishing complexity factor, or the quasi–homologous condition), while others have been imposed just to produce models described by elementary functions.

We started by considering non–dissipative fluids admitting a CKV orthogonal to the four–velocity. In this case the assumed symmetry reduces the metric variables to three functions (two functions of $t$ and one function of $r$ ). Then, the matching conditions reduce to a single differential equation (65) whose solution provides one of the three functions describing the metric. In order to obtain a solution expressed in terms of elementary functions we have assumed specific values of the parameters entering into the equation.

The first choice ( $\omega=\frac{1}{27M^{2}}$ ) leads to two expressions for the areal radius of the boundary ((82) and (83)). The first one describes a fluid distribution whose boundary areal radius expands from $0$ to $3M$ , while the second one describes a contraction of the boundary areal radius from infinity to $3M$ . To find the remaining two functions to determine the metric we have assumed the quasi–homologous condition and the vanishing complexity factor condition. In this way we are lead to our models $I$ and $II$ , both of which have positive energy densities and the physical variables are singular free, except the model $I$ for $t=t_{0}$ .

As $t\rightarrow\infty$ both solutions tend to the same static solution (97) satisfying a Chaplygin–type equation of state $\mu=-P_{r}$ . The way of reaching this static limit deserves some comments. Usually the hydrostatic equilibrium is reached when the “gravitational force term” (the first term on the right of (235)) cancels the “hydrodynamic force term” (the second term on the right of (235)). However here the situation is different, the equilibrium is reached because as $t\rightarrow\infty$ both terms tend to zero.

In spite of the good behavior of these two models, it should be mentioned that regularity conditions are not satisfied by the resulting function $R$ on the center of the distribution. Accordingly for the modeling of any specific scenario, the central region should be excluded.

Next, we have considered the case $\omega=0$ , which together with the vanishing complexity factor condition produces the model $III$ . In this model the boundary areal radius oscillates between $0$ and $2M$ . The energy density and the tangential pressure of this model are positive and homogeneous, while the radial pressure vanishes identically. As in the previous two models this solution does not satisfy the regularity condition at the center.

As an additional example of analytical solution we have considered the case $M=0$ . The two models for this kind of solution are the models $IV$ and $V$ . They represent a kind of “ghost” stars, formed by a fluid distribution not producing gravitational effects outside the boundary surface. They present pathologies, both physical and topological, and therefore their physical applications are dubious. However since this kind of distributions have been considered in the past (see for example zel ) we present them here.

Next we have considered the subcase where the CKV is orthogonal to the four velocity and the fluid is dissipative. For this case we have found a model satisfying the vanishing complexity factor and the quasi–homologous condition, which together with the fulfillment of the matching conditions determine all the metric functions. This model (model $VI$ ) is described by expressions (137)–(141), and the expression (147) for the temperature, which has been calculated using the truncated version of the transport equation. It contains contribution from the transient regime (proportional to $\tau$ ) as well as from the stationary regime. As previous models, this solution does not satisfy the regularity conditions at the center.

The other family of solutions corresponds to the case when the CKV is parallel to the four–velocity. In the non–dissipative case, as consequence of this symmetry, the metric functions are determined up to three functions (two functions of $r$ and one function of $t$ ). Besides, the fluid is necessarily shear–free, a result which was already known t1 ; t3 . The function of $t$ is obtained from the fulfillment of the matching conditions (Eqs. (153), (155)). These equations have been integrated for different values of the parameters entering into them. Thus, for $a_{1}=1$ and $\epsilon=\frac{1}{27M^{2}}$ , together with the vanishing complexity factor condition and $h(r)=c_{6}r$ , we have found model $VII$ . The boundary areal radius of this model expands from zero to $3M$ , and the physical variables are given by (V.3)–(167). In the limit $t\rightarrow\infty$ the model tends to a static sphere whose equation of state is $P_{r}=-\mu$ . The energy density is positive, and presents a singularity only at $t=t_{0}$ , however regularity conditions are not satisfied at the center.

The integration of the matching conditions for $\epsilon=0$ and $a_{1}=\frac{1}{2}$ together with the vanishing complexity factor, produce the model $VIII$ . The boundary areal radius of this model oscillates between zero and $\frac{8M}{3}$ . The energy density is positive and larger than the radial pressure, but the fluid distribution is singular at $r=0$ .

For $M=0$ and $a_{1}=1$ we obtain models $IX$ and $X$ they describe the kind of “ghost stars” mentioned before. However they are plagued with, both, physical and topological pathologies which renders them unviable for physical modeling. We include them just for sake of completeness.

Finally, we have considered the dissipative case for the CKV parallel to the four–velocity. The metric variables for this case take the form (187)–(189), which after imposing the vanishing complexity factor condition become (193)–(195). Thus the metric is determined up to three functions (two functions of $t$ and one function of $r$ ). The two functions of $t$ will be obtained from the integration of the matching conditions, while the function of $r$ is assumed as (213). The model is further specified with the choice $a_{1}=2$ . This produce the model $XI$ .

As it follows from (218) the boundary areal radius of the model tends to infinity as $t\rightarrow\infty$ , while in the same limit the total mass $m_{\Sigma}$ tends to infinity, whereas both $q$ and $\mu$ tend to zero. The explanation for this strange result comes about from the fact that $R_{\Sigma}$ grows exponentially with $t$ , overcompensating the decreasing of $\mu$ and $q$ in (20). It is also worth noticing the negative sign of $q$ , implying an inward heat flux driving the expansion of the fluid distribution.

Overall, we believe that the eleven models exhibited (or at least some of them) could be useful to describe some stages of some regions of self–gravitating fluid, in the evolution of compact objects. Each specific scenario imposing specific values on the relevant parameters. It should be reminded that in any realistic collapsing scenario we do not expect the same equation of state to be valid all along the evolution and for the whole fluid configuration.

Before concluding, some general comments are in order.

1.

The analytical integration of the equations derived from the matching conditions have been carried out by imposing specific values on the parameters entering into those equations, also the models have been specified by using some conditions such as the quasi–homologous condition. Of course the number of available options is huge. Among them we would like to mention the prescription of the total luminosity measured by an observer at rest at infinity (36). Let us recall that this is one of the few observables in the process of stellar evolution. Equivalently one could propose a specific evolution of the total mass with time.
2.

In some cases, when the topological pathologies are not “severe”, the time interval of viability of the solution may be restricted by the condition that $U\leq 1$ (e.g. for solutions $I$ and $II$ ). In other cases however, due to topological defects, the interpretation of $U$ as a velocity becomes dubious and therefore it is not clear that $U$ should satisfy the above mentioned condition.
3.

Model $XI$ is dissipative and intrinsically isotropic in pressure. However as shown in ps dissipation produces pressure anisotropy, unless a highly unlikely cancellation of the four terms on the right of equation (28) in ps occurs. This happens in model $XI$ , which renders this solution a very remarkable one.
4.

For reasons explained in the Introduction we have focused on the obtention of analytical solutions expressed through elementary functions. However it should be clear that for specific astrophysical scenarios, a numerical approach for solving the matching conditions, could be more appropriate.

Acknowledgements.

This work was partially supported by the Spanish Ministerio de Ciencia e Innovación under Research Projects No. FIS2015-65140-P (MINECO/FEDER). ADP acknowledges hospitality from the Physics Department of the Universitat de les Illes Balears.

Appendix A Einstein equations

Einstein’s field equations for the interior spacetime (1) are given by

G_{\alpha\beta}=8\pi T_{\alpha\beta},

(224)

and its non zero components read

	$\displaystyle 8\pi T_{00}=8\pi\mu A^{2}=\left(2\frac{\dot{B}}{B}+\frac{\dot{R}}{R}\right)\frac{\dot{R}}{R}-\left(\frac{A}{B}\right)^{2}\left[2\frac{R^{\prime\prime}}{R}+\left(\frac{R^{\prime}}{R}\right)^{2}-2\frac{B^{\prime}}{B}\frac{R^{\prime}}{R}-\left(\frac{B}{R}\right)^{2}\right],$		(225)
	$\displaystyle 8\pi T_{01}=-8\pi qAB=-2\left(\frac{{\dot{R}}^{\prime}}{R}-\frac{\dot{B}}{B}\frac{R^{\prime}}{R}-\frac{\dot{R}}{R}\frac{A^{\prime}}{A}\right),$		(226)
	$\displaystyle 8\pi T_{11}=8\pi P_{r}B^{2}=-\left(\frac{B}{A}\right)^{2}\left[2\frac{\ddot{R}}{R}-\left(2\frac{\dot{A}}{A}-\frac{\dot{R}}{R}\right)\frac{\dot{R}}{R}\right]+\left(2\frac{A^{\prime}}{A}+\frac{R^{\prime}}{R}\right)\frac{R^{\prime}}{R}-\left(\frac{B}{R}\right)^{2},$		(227)
	$\displaystyle 8\pi T_{22}=\frac{8\pi}{\sin^{2}\theta}T_{33}=8\pi P_{\perp}R^{2}=-\left(\frac{R}{A}\right)^{2}\left[\frac{\ddot{B}}{B}+\frac{\ddot{R}}{R}-\frac{\dot{A}}{A}\left(\frac{\dot{B}}{B}+\frac{\dot{R}}{R}\right)+\frac{\dot{B}}{B}\frac{\dot{R}}{R}\right]$
	$\displaystyle+\left(\frac{R}{B}\right)^{2}\left[\frac{A^{\prime\prime}}{A}+\frac{R^{\prime\prime}}{R}-\frac{A^{\prime}}{A}\frac{B^{\prime}}{B}+\left(\frac{A^{\prime}}{A}-\frac{B^{\prime}}{B}\right)\frac{R^{\prime}}{R}\right].$		(228)

The component (226) can be rewritten with (8) and (10) as

4\pi qB=\frac{1}{3}(\Theta-\sigma)^{\prime}-\sigma\frac{R^{\prime}}{R}.

(229)

Appendix B Dynamical equations

The non trivial components of the Bianchi identities, $T^{\alpha\beta}_{;\beta}=0$ , from (224) yield

	$\displaystyle T^{\alpha\beta}_{;\beta}V_{\alpha}=-\frac{1}{A}\left[\dot{\mu}+\left(\mu+P_{r}\right)\frac{\dot{B}}{B}+2\left(\mu+P_{\perp}\right)\frac{\dot{R}}{R}\right]-\frac{1}{B}\left[q^{\prime}+2q\frac{(AR)^{\prime}}{AR}\right]=0,$		(230)
	$\displaystyle T^{\alpha\beta}_{;\beta}K_{\alpha}=\frac{1}{A}\left[\dot{q}+2q\left(\frac{\dot{B}}{B}+\frac{\dot{R}}{R}\right)\right]+\frac{1}{B}\left[P_{r}^{\prime}+\left(\mu+P_{r}\right)\frac{A^{\prime}}{A}+2(P_{r}-P_{\perp})\frac{R^{\prime}}{R}\right]=0,$		(231)

or, by using (7), (8), (13), (17) and (15), they become,

\displaystyle D_{T}\mu+\frac{1}{3}\left(3\mu+P_{r}+2P_{\perp}\right)\Theta+\frac{2}{3}(P_{r}-P_{\perp})\sigma+ED_{R}q+2q\left(a+\frac{E}{R}\right)=0,

(232)

\displaystyle D_{T}q+\frac{2}{3}q(2\Theta+\sigma)+ED_{R}P_{r}+\left(\mu+P_{r}\right)a+2(P_{r}-P_{\perp})\frac{E}{R}=0.

(233)

This last equation may be further transformed as follows, the acceleration $D_{T}U$ of an infalling particle can be obtained by using (7), (227), (12) and (15), producing

D_{T}U=-\frac{m}{R^{2}}-4\pi P_{r}R+Ea,

(234)

and then, substituting $a$ from (234) into (233), we obtain

\displaystyle\left(\mu+P_{r}\right)D_{T}U=-\left(\mu+P_{r}\right)\left[\frac{m}{R^{2}}+4\pi P_{r}R\right]-E^{2}\left[D_{R}P_{r}+2(P_{r}-P_{\perp})\frac{1}{R}\right]-E\left[D_{T}q+2q\left(2\frac{U}{R}+\sigma\right)\right].

(235)

References

(1) Barenblatt, G.I.; Zeldovich, Ya.B. Self-Similar Solutions as Intermediate Asymptotics. Ann. Rev. Fluid. Mech. 1972, 4, 285–312.
(2) Sedov, L. I. Propagation of strong shock waves. J. Appl. Math. Mech. 1946, 10, 241–250.
(3) Sedov, L. I. Similarity and Dimensional Methods in Mechanics; Academic. New York, USA, 1967.
(4) Taylor, G.I. The Formation of a Blast Wave by a Very Intense Explosion. II. The Atomic Explosion of 1945. Proc. Roy. Soc. 1950, 201, 175–186.
(5) Zeldovich, Ya.B.; Raizer, Yu.P. Physics of Shock Waves and High Temperature; Academic. New York, USA, 1963.
(6) Cahill, M.E.; Taub, A.H. Spherically symmetric similarity solutions of the Einstein field equations for a perfect fluid. Commun. Math. Phys. 1971, 21, 1–40.
(7) Herrera, L.; Jimenez, J.; Leal, L.; Ponce de Leon, J.; Esculpi, M.; Galina, V. Anisotropic fluids and conformal motions in general relativity. J. Math. Phys. 1984, 25, 3274–3278.
(8) Herrera,L.; Ponce de Leon, J. Isotropic spheres admitting a one parameter group of conformal motions. J. Math. Phys. 1985, 26, 778–784.
(9) Herrera,L.; Ponce de Leon, J. Anisotropic spheres admitting a one parameter group of conformal motions. J. Math. Phys. 1985, 26, 2018–2023.
(10) Herrera,L.; Ponce de Leon, J. Isotropic and anisotropic charged spheres admitting a one parameter group of conformal motions. J. Math. Phys. 1985, 26, 2302–2307.
(11) Herrera,L.; Ponce de Leon, J. Confined gravitational fields produced by anisotropic spheres. J. Math. Phys. 1985, 26, 2847–2849.
(12) Maartens, R.; Mason, P.S.; Tsamparlis, M. Kinematic and dynamic properties of conformal Killing vectors in anisotropic fluids. J. Math. Phys. 1986, 27, 2987–2994.
(13) Duggal, K.L.; Sharma, R. Conformal collineations and anisotropic fluids in general relativity. J. Math. Phys. 1986, 27, 2511–2513.
(14) Esculpi, M.; Herrera, L. Conformally symmetric radiating spheres in general relativity. J. Math. Phys. 1986, 27, 2087–2096.
(15) Duggal, K.L. Relativistic fluids with shear and timelike conformal collineations. J. Math. Phys. 1987, 28, 2700–2704.
(16) Mason, D.P.; Maartens, R. Kinematics and dynamics of conformal collineations in relativity. J. Math. Phys. 1987, 28, 2182–2186.
(17) Di Prisco, A.; Herrera, L.; Jimenez, J.; Galina , V.; Ibanez, J. The Bondi metric and conformal motions. J. Math. Phys. 1987, 28, 2692–2696.
(18) Duggal, K.L. Relativistic fluids and metric symmetries. J. Math. Phys. 1989, 30, 1316–1322.
(19) A.A. Coley.; B.O.J. Tupper. Special conformal Killing vector space-times and symmetry inheritance J. Math. Phys., 1989 30, 261–2625.
(20) A.A. Coley.; B.O.J. Tupper. Spacetimes admitting inheriting conformal Killing vector fields Classical Quantum Grav. 1990, 7, 1961–1981.
(21) A.A. Coley.; B.O.J. Tupper. Spherically symmetric spacetimes admitting inheriting conformal Killing vector fields. Classical Quantum Grav. 1990, 7, 2195–2214.
(22) Maartens, R; Maharaj, M.S. Conformally symmetric static fluid spheres. J. Math. Phys. 1990, 31, 151–155.
(23) Di Prisco, A.; Herrera, L.; Esculpi, M. Self-similar scalar soliton star in the thin wall approximation. Phys. Rev. D 1991, 44, 2286–2294.
(24) Saridakis, E.; Tsamparlis, M. Symmetry inheritance of conformal Killing vectors. J. Math. Phys. 1991, 32, 1541–1551.
(25) Aguirregabiria, J.M.; Di Prisco, A.; Herrera, L.; Ibanez, J. Time evolution of self–similar scalar soliton stars: A general study. Phys. Rev. D 1992, 46, 2723–2725.
(26) Maartens, R.;Maharaj, S.D.; Tupper, B.O.J. General solution and classification of conformal motions in static spherical spacetimes. Classical Quantum Grav. 1995, 12, 2577–2586.
(27) Maharaj, S.D.; Maartens, R.; Maharaj, M.S. Conformal symmetries in static spherically symmetric spacetimes. Int. J. Theor. Phys. 1995, 34, 2285–222901.
(28) Carot , J.; Sintes, A. Homothetic perfect fluid spacetimes. Classical Quantum Grav. 1997, 14, 1183–1205.
(29) Carr, B.J.; Coley, A. A. TOPICAL REVIEW: Self-similarity in general relativity. Classical Quantum Grav. 1999, 16, R31–R71.
(30) Barreto, W.; da Silva, A. Self-similar and charged spheres in the diffusion approximation. Classical Quantum Grav. 1999, 16, 1783–1792.
(31) Yavuz, I. ; Yilmaz, I; Baysal, H. Strange Quark Matter Attached to the String Cloud in the Spherical Symmetric Space-Time Admitting Conformal Motion. Int. J. Mod. Phys. D 2005, 14, 1365–1372 .
(32) Sharif, M.; Sheikh, U. Timelike and Spacelike Matter Inheritance Vectors in Specific Forms of Energy-Momentum Tensor. Int. J. Mod. Phys. A 2006, 21, 3213–3234.
(33) Barreto, W.; Rodriguez, B.; Rosales, L.; Serrano, O. Self–similar and charged radiating spheres: an anisotropic approach. Gen. Relativ. Gravit. 2007, 39, 23–39.
(34) Mak, M.K.; Harko, T. Quark stars admitting a one parameter group of conformal motions. Int. J. Mod. Phys. D. 2004, 13, 149–156.
(35) Moopanar, S.; Maharaj, S.D. Conformal symmetries of spherical spacetimes. Int. J. Theor. Phys. 2010, 49, 1878–1885.
(36) Bhar, P. Vaydya–Tikekar–type superdense star admitting conformal motion in presence of quintessence field. Eur. Phys. J. C 2015, 75, 123.
(37) Apostolopoulos, P.S. Spatially inhomogeneous and irrotational geometries admitting intrinsic conformal symmetries. Phys. Rev. D 2016, 94, 124052.
(38) Shee, D.; Rahaman, F.; Guha, B.K.; Ray, S. Anisotropic stars with non–static conformal symmetry. Astr. Space Sci. 2016, 361, 167.
(39) Majonjo, A.; Maharaj, S.D.; Moopanar, S. Conformal vectors and stellar models. Eur. Phys. J. Plus 2017, 132, 62.
(40) Newton Singh, K.; Murad, M.; Pant, N. A 4D spacetime embedded in a 5D pseudo–Euclidean space describing interior compact stars. Eur. Phys. J. A 2017, 53, 21.
(41) Shee, D.; Deb, D.; Ghosh, S.; Guha, B.K.; Ray, S. On the features of Matese–Whitman mass fucntion. arXiv: 1706.00674 2017.
(42) Herrera, L.; Di Prisco, A. Self–similarity in static axially symmetric relativistic fluid. Int. J. Mod. Phys. D 2018, 27, 1750176.
(43) Ojako, S.; Goswami, R.; Maharaj, S.D. New class of solutions in conformally symmetric massless scalar field collapse. Gen. Relativ. Gravit. 2021, 53, 13.
(44) Shobhane, P.; Deo, S. Spherically symmetric distributions of wet dark fluid admitting conformal motions. Adv. Appl. Math. Sci. 2021, 20, 1591–1598.
(45) Jape, J.; Maharaj, S.D.; Sunzu, J.; Mkenyeleye, J. Generalized compact star models with conformal symmetry. Eur. Phys. J. C 2021, 81, 2150121.
(46) Ivanov, B. Generating solutions for charged stellar models in general relativity. Eur. Phys. J. C 2021, 81, 227.
(47) Sherif, A.; Dunsby, P.; Goswami , R.; Maharaj, S.D. On homothetic Killing vectors in stationary axisymmetric vacuum spacetimes. Int. J. Geom. Meth. Mod. Phys. 2021, 18, 21550121.
(48) Matondo, D.; Maharaj, S.D. A Tolman-like Compact Model with Conformal Geometry. Entropy 2021, 23, 1406.
(49) Bhar, P.; Rej, P. Stable and self–consistent charged gravastar model within the framework of $f(R,T)$ gravity. Eur. Phys. J. C 2021, 81, 763.
(50) Sharma, R. Proper special conformal Killing vectors and the quadratic theory of gravity. J. Math. Phys., 1991, 32, 1854.
(51) Mak, M.K.; Harko, T. Can the galactic rotation curves be explained in brane world models? Phy. Rev. D 2004, 70, 024010.
(52) Harko, T.; Mak, M.K. Conformally symmetric vacuum solutions of the gravitational field equations in the brane world model. Ann. Phys., 2005, 319, 471–492.
(53) Sharif, M.; Ismat Fatima, H. Static spherically symmetric solutions in $f(G)$ gravity. Int. J. Mod. Phys. D 2016, 25, 1650083.
(54) Sefiedgar, A.S.; Haghani, Z.; Sepangi, H.R. Brane $f(R)$ gravity and dark matter. Phy. Rev. D 2012, 85, 064012.
(55) Bhar, P. Higher dimensional charged gravastar admitting conformal motion. Astrophys. Space Sci. 2014, 354, 457–462.
(56) Turkoglu, M.; Dogru, M. Conformal cylindrically symmetric spacetimes in modified gravity. Mod. Phys. Lett. A 2015, 30, 1550202.
(57) Das, A.; Rahaman, F.; Guha, B.K.; Ray, S. Relativistic compact stars in $f(T)$ gravity admitting conformal motion. Astrophys. Space Sci. 2015, 358, 36.
(58) Sert, O. Radiation fluid stars in the non–minimally coupled $Y(R)F^{2}$ gravity. arXiv: 1611.03821v1 2016.
(59) Zubair, M.; Sardar, L.H.; Rahaman, F.; Abbas, G. Interior solutions for fluid spheres in $f(R,T)$ gravity admitting conformal killing vectors. Astrophys. Space Sci. 2016, 361, 238.
(60) Das, A.; Rahaman, F.; Guha, B.K.; Ray, S. Compact stars in $f(R,{\cal T})$ gravity. Eur. Phys. J. C 2016, 76, 654.
(61) Sharif, M.; Naz, S. Stable charged gravastar model in $f(R,T^{2})$ gravity with conformal motion. Eur. Phys. J. P. 2022, 137, 421.
(62) Bohmer, C.G.; Harko , T.; Lobo, F.S.N. Conformally traversable wormholes. Phys. Rev. D 2007, 76, 084014.
(63) Bohmer, C.G.; Harko , T.; Lobo, F.S.N. Wormhole geometries with conformal motions. Classical Quantum Grav. 2008, 25, 075016.
(64) Rahaman, F.; Ray, S.; Khadekar, G.; Kuhfittig, P.; Karakar, I. Int. J. Theor. Phys. 2015, 54, 699.
(65) Kuhfittig, P. Wormholes admitting conformal Killing vectors and supported by generalized Chaplygin gas. Eur. Phys. J. C 2015, 75, 357.
(66) Sharif, M.; Ismat Fatima, H. Conformally symmetric traversable wormhole in $f(G)$ gravity. Gen. Relativ. Gravit. 2016, 48, 148.
(67) Kar, S. Curious variant of the Bronnikov–Ellis spacetime.Phys. Rev. D 2022, 105, 024013.
(68) Mustafa, G.; Hassan, Z.; Sahoo, P.K. Traversable wormhole inspired by non–commutative geometries in $f(Q)$ gravity with conformal symmetry. Ann. Phys. 2022, 437, 168751.
(69) Herrera, L.; Di Prisco , A.; Ospino, J. Quasi–homologous evolution of self–gravitating systems with vanishing complexity factor. Eur. Phys. J. C 2020, 80, 631.
(70) Herrera, L.: Santos, N.O. Local anisotropy in self–gravitating systems. Phys. Rep. 1997, 286, 53–130.
(71) Herrera, L. Stabilty of the isotropic pressure condition. Phys. Rev. D 2020, 101, 104024.
(72) Herrera, L. New definition of complexity for self–gravitating fluid distributions: The spherically symmetric case. Phys. Rev. D 2018, 97, 044010.
(73) Herrera, L.; Di Prisco , A.; Ospino, J. Definition of complexity for dynamical spherically symmetric dissipative self–gravitating fluid distributions. Phys. Rev. D 2018, 98, 104059.
(74) Herrera, L.; Ospino, J.; Di Prisco, A.; Fuenmayor, E.; Troconis, O. Structure and evolution of self–gravitating objects and the orthogonal splitting of the Riemann tensor. Phys. Rev D 2009, 79, 064025.
(75) Herrera, L.; Di Prisco , A.; Ibáñez, J. Tilted Lemaitre–Tolman–Bondi spacetimes: Hydrodynamic and thermodynamic properties. Phys. Rev. D 2011, 84, 064036.
(76) Chan, R.Collapse of a radiating star with shear. Mon. Not. R. Astron. Soc. 1997, 288, 589–595.
(77) Israel, W. Nonstationary irreversible thermodynamics: A causal relativistic theory. Ann. Phys. (NY) 1976, 100, 310–331.
(78) Israel, W.; Stewart, J. Thermodynamic of nonstationary and transient effects in a relativistic gas. Phys. Lett. A 1976, 58, 213–215.
(79) Israel, W.; Stewart, J. Transient relativistic thermodynamics and kinetic theory. Ann. Phys. (NY) 1979, 118, 341–372.
(80) Triginer, J.; Pavon, D. On the thermodynamics of tilted and collisionless gases in Friedmann–Robertson–Walker spacetimes. Class. Quantum Grav. 1995, 12, 199.
(81) Schwarzschild, M. Structure and Evolution of the Stars; Dover: New York, USA, 1958.
(82) Kippenhahn , R.; Weigert, A. Stellar Structure and Evolution; Springer Verlag: Berlin, Germany, 1990.
(83) Hansen, C; Kawaler, S. Stellar Interiors: Physical Principles, Structure and Evolution; Springer Verlag: Berlin, Germany, 1994.
(84) Stephani, H.; Kramer, D.; MacCallum, M.; Honselaers, C.; Herlt, E. Exact Solutions to Einstein Field Equations, 2nd ed; Cambridge University Press: Cambridge, England, 2003.
(85) Carot, J. Some developments on axial symmetry. Class. Quantum Grav. 2000, 17, 2675.
(86) Carlson, Jr., G.T.; Safko, J.L. Canonical forms for axial symmetric space–times. Ann. Phys. (N.Y.) 1980, 128, 131–153.
(87) Zeldovich, Y.B.; Novikov, I.D. Relativistic Astrophysics.; Chicago U. P.: Chicago, USA, 1971.
(88) Oliver Jr., D.R.; Davis, W.R. On certain timelike symmetry properties and the evolution of matter field space–times that admit them. Gen. Rel. Grav. 1977, 8, 905–914.
(89) Herrera, L.; Di Prisco, A.; Ibanez, J. Reversible dissipative processes, conformal motions and Landau damping. Phys. Lett. A 2012, 376, 899–900.

Non–static fluid spheres admitting a conformal Killing vector: Exact solutions

Abstract

pacs:

I Introduction

II The metric, the source and relevant equations and variables

II.1 The Weyl tensor and the complexity factor

II.2 The exterior spacetime and junction conditions

III The transport equation

IV The homologous and quasi–homologous conditions

V Conformal motions: exact solutions

V.1 χα​Vα=q=0\chi_{\alpha}V^{\alpha}=q=0.

V.2 χα​Vα=0;q≠0\chi_{\alpha}V^{\alpha}=0;q\neq 0

V.3 q=0;χα||Vαq=0;\chi^{\alpha}||V^{\alpha}

V.4 χα||Vα;q≠0\chi^{\alpha}||V^{\alpha};q\neq 0

VI Discussion

Acknowledgements.

Appendix A Einstein equations

Appendix B Dynamical equations

References

V.1 $\chi_{\alpha}V^{\alpha}=q=0$ .

V.2 $\chi_{\alpha}V^{\alpha}=0;q\neq 0$

V.3 $q=0;\chi^{\alpha}||V^{\alpha}$

V.4 $\chi^{\alpha}||V^{\alpha};q\neq 0$