Novel echoes from black holes in conformal Weyl gravity
Abstract
We reveal a novel class of echoes from black holes in conformal Weyl gravity and show that they are generated due to the large-scale structure of the cosmos, rather than near-horizon modifications of black holes as well as wormhole spacetimes. To this end, we take into account the evolution of a massive scalar perturbation on the background geometry of conformal Weyl black holes and show that the corresponding effective potential enjoys a double-peak barrier against the incident scalar waves. We perform the calculations for the time evolution profiles of scalar perturbations to understand how the linear term in the metric function and the cosmological constant produce echoes. The Prony method is also employed to calculate the quasinormal frequencies of the early-stage quasinormal ringing phase.
pacs:
04.20.Ex, 04.25.Nx, 04.30.Nk, 04.70.-sI Introduction
After the merger phase of the black hole binaries, the newly formed remnant object settles down to form a new black hole111The formation of black holes could also happen in other channels, such as binary neutron stars and black hole-neutron star binaries under certain conditions. AbbottBBHmerger ; AbbottBBHcoalescence . This new deformed black hole undergoes the ringdown stage VishveshwaraNature ; PressRingdown ; ChandrasekharDetweiler and emits gravitational waves in the form of quasinormal radiation that could be detected through the gravitational wave interferometers Isi ; MaSunChen . Although there is a debate in the literature regarding the existence of the first overtone in the ringdown signal of GW150914 BertiRingdown ; CommentGW150914 ; ReplyGW150914 , such modes would be detectable through space-based gravitational wave detectors in the future GWspectroscopy ; RoadMap . This final signal of merger events is a superposition of damped oscillations with discrete frequencies and decay times that are known as quasinormal modes (QNMs) [see Nollert ; Kokkotas ; BertiR ; KonoplyaR for review papers on QNMs].
In addition to interest in the QNMs from the gravitational wave astronomy point of view, they attracted much attention in different branches of fundamental physics as well. The QNMs spectrum governs the dynamic stability of black holes undergoing the perturbations of various test fields InstabilityKZ ; InstabilityWang ; MomenniaLQBH , the overdamped QN frequencies play a crucial role in the semi-classical approach to quantum gravity Hod and they have been used to fix the Barbero-Immirzi parameter in loop quantum gravity Dreyer . Besides, the eikonal QN frequencies correspond to unstable circular null geodesics that are related to the black hole shadow size CardosoUCNG ; KonoplyaUCNG ; MomenniaPRD ; FurtherClarification and the QN modes in anti-de Sitter (adS) background refer to the decay of perturbations of corresponding thermal state in the conformal field theory Horowitz ; LemosAdS ; KokkotasAdS ; MehrabJHEP ; MomenniaPLB .
Recently, the QN modes of black holes undergoing various test field perturbations have been investigated in modified theories of gravity, such as higher dimensional Einstein gravity coupled to Yang-Mills field YangMills , Einstein-Born-Infeld gravity BornInfeld , loop quantum gravity MomenniaLQBH ; QuantumCorrectedBH ; AxialLQG ; LQBHjcap , quantum corrected black hole metrics GongQuantum ; CaoQuantum ; DubinskyQuantum ; MalikQuantum , deformed Schwarzschild black holes DeformedSchw , spinning C-metric Cmetric , and dirty black holes Dirty . In addition, the QNMs of black holes in Einstein-Gauss-Bonnet-adS spacetime EGB , dark matter halo DMH , and gravity fRgravity have been studied and the anomalous decay rate of QNMs in Reissner-Nordström dS background has been examined YerkoAnomalous . Furthermore, the QNMs of Dilaton-dS black holes DubinskyDilaton , regular black holes Skvortsova ; Skvortsova2025 , and Kaluza–Klein black holes KaluzaPLB ; KaluzaMomennia ; KaluzaPRD have been explored.
Black hole perturbations in conformal Weyl gravity and corresponding QN modes have been investigated in a few articles so far MomenniaPRD ; MomenniaPLB ; MomenniaEPJC ; KonoplyaWeyl ; YerkoWeyl ; Malik ; Konoplya2025 . The QNMs have been studied for perturbations in the scalar MomenniaPRD ; MomenniaPLB ; YerkoWeyl ; Konoplya2025 , electromagnetic MomenniaEPJC ; Konoplya2025 , gravitational MomenniaEPJC , and Dirac fields Malik ; Konoplya2025 . It has been already shown that the quasinormal ringing of conformal black holes undergoing massless scalar perturbations contains dark matter and dS phases KonoplyaWeyl . In this article, we shall show that for the massive test scalar field perturbations, a series of echoes dominates the ringdown profile of the modes.
Although the early-stage quasinormal oscillations of black hole mimickers are indistinguishable from those of the Schwarzschild ringdown, the signal could be modified at later times by a series of echoes. The echoes have been reported for QN modes of wormholes in WormholesEcho for the first time, and then studied for a large number of spacetimes including black hole toy models (for instance, see an incomplete list CardosoEcho ; NatureEcho ; MaselliEcho ; TsangEcho ; WangEcho ; KonoplyaEcho ; YangEcho ; GuoEcho ; SangEcho and references therein). In this scenario, in addition to the photon sphere peak in the effective potential of the wave-like master equation, a second peak appears from various modifications in the background spacetime due to, for example, quantum corrections or the free parameters of the gravitational model under investigation222In the effective potential of some black hole toy models, more than two peaks have been reported as well.. Therefore, a substantial component of the high-frequency initial signal crosses the potential barrier and would be trapped between a double peak potential barrier, which leads to a series of echoes detected by a distant observer.
Generally, the double-peak potentials and echoes appeared in limited cases, like quantum-corrected black holes Abedi , by taking into account different equations of state for the ultra-compact objects StarEcho , and considering matter distribution around the black hole BHshell and wormhole wormshell environment. In this paper, we show that this second peak also appears in the case of conformal Weyl black holes due to the linear term in the metric function, but on the right-hand side of the angular momentum barrier. Even though this is also the case when one adds the matter distribution around compact objects BHshell ; wormshell , we can observe more intense echoes for our black hole case study due to large-scale structure of the Universe as well as the free parameters of the theory purely arising as integration constants.
On one hand, there are still large uncertainties in measuring the background test fields and the black hole parameters, such as angular momentum and electric charge, by taking into account recent electromagnetic and gravitational data from black holes AbbottBBHmerger ; AbbottBBHcoalescence ; M87 ; Sgr . This uncertainty in estimating parameters provides an opportunity to examine the strong field regime and allows the existence of black hole models beyond Einstein gravity or general relativity coupled to various matter sources (see the incomplete list HartleThorne ; EMDA ; LQBH ; Herdeiro ; TopologicalBH ; GausBonBH ; EYM ; Bah ; Rastgoo ; MariaLima and references therein for some black hole metrics). On the other hand, the standard cosmological model of the -cold dark matter successfully explains the current epoch of the Universe. Therefore, one should take into account the contribution of dark energy and dark matter in the context of black hole physics in order to construct a scenario in consistency with the large-scale structure of the cosmos. In this regard, more recently it has been demonstrated that the Hubble law emerges from the frequency-shift considerations of test particles revolving the rotating Kerr black hole in asymptotically dS spacetime MomenniaHubble , confirming that adding a cosmological constant term to the Einstein field equations is indeed inevitable Carroll .
In this direction, one may note that the cosmological constant term arises naturally as an integration constant in the black hole solutions of conformal Weyl gravity Birkoff and this theory of general relativity can explain the galactic rotation curves without the need for any dark matter GRCurves ; DM . Hence, in this paper, we are interested in investigating the black hole solutions in conformal Weyl gravity in order to incorporate the information of the large-scale structure of the Universe into the black hole solutions. Therefore, we take into account gravitational modeling beyond Einstein gravity to study modifications in the ringdown signal of the black holes due to the free parameters of the theory.
The Lagrangian density of Weyl gravity is defined by the square of the Weyl tensor and it is one of the successful and interesting theories in higher derivative gravity scenario Weyl . This theory of gravity is invariant under local scale transformation of the metric , and therefore it is unique up to the choice of the matter source for preserving the conformal invariance property of spacetime.
Recently, different aspects of the conformal gravity have been recently studied, such as self-dual gravitational instantons instantons , black hole shadows shadow , and its ghost problem ghost . The role of the linear term, appearing in the metric function of conformal Weyl black holes, has been explored from the geometrical and astrophysical perspectives LRterm . In addition, the Nöther currents, black hole entropy universality, and conformal field theory duality in conformal Weyl gravity have been investigated CFTduality .
This paper is organized as follows. The next section is devoted to a brief review of black hole solutions in conformal Weyl gravity and the free parameters of the spacetime. In Sec. III, we consider the perturbations of a test massive scalar field minimally coupled to the gravitational theory and investigate criteria for having double-peak potential barriers. Then, we briefly explain the time-domain integration and the Prony method that are used to study the QN modes throughout the paper. In Sec. IV, the dependence of the early-stage quasinormal ringing and subsequent echoes on the free parameter of conformal Weyl gravity is investigated and the results are discussed. Finally, we finished our paper with some concluding remarks through the last Sec. V.
II Black hole solutions in conformal Weyl gravity
In order to give a brief overview of conformal Weyl black holes, we start with the unique conformally invariant action of Riemannian spacetime in four dimensions as follows
| (1) |
which is a dimensionless parameter, is the determinant of the spacetime metric, and is the conformal Weyl tensor with the following explicit form Weyl
| (2) | |||||
where is the Riemann curvature tensor, is the Ricci tensor, and is the Ricci curvature scalar corresponding to the background metric . One can show that the Weyl tensor transforms covariantly as under conformal transformation, and thus the gravitational action (1) remains invariant. We also note that Birkoff’s theorem holds in the conformal Weyl gravity Birkoff .
By taking the variation of the action (1) with respect to the metric tensor , one can obtain the field equations of the theory as follows Bach
| (3) |
in which is the Bach tensor and refers to the standard covariant derivative compatible with the metric tensor . The Bach tensor has been linearized by Riegert and it was demonstrated that there is a massless spin- ghost particle arising from the fourth-order gravitational wave equations RiegertGhost . Recently, a couple of suggestions have been proposed to circumvent this ghost instability in the linearized equations YangGW as well as take advantage of the conformal symmetry of Weyl spacetime in the metric MomenniaEPJC .
The static and spherically symmetric vacuum solutions of the Weyl gravity describing black holes in this theory were first shown by Riegert Birkoff and later obtained in MannheimKazanas . It was shown that the following spherically symmetric line element
| (4) |
with the metric function
| (5) |
satisfies all components of the Bach tensor (3) where , , and are three integration constants. In order to compare our results with the Schwarzschild black holes as well as in consistency with the previous studies on the quasinormal modes of Weyl solutions MomenniaPRD ; MomenniaEPJC ; MomenniaPLB , we found that it is convenient to introduce the constants in terms of the integration constants as below
| (6) |
By considering these new definitions for the integration constants, the metric function (5) converts to
| (7) |
that reduces to the standard Schwarzschild-dS solutions for . In this way, the constant parameter characterizes deviations from the Schwarzschild-dS black holes in a similar manner as in MomenniaPRD ; MomenniaEPJC ; MomenniaPLB . Therefore, we have a spectrum of conformal solutions depending on the values of the free dimensionless parameter obeying the condition in the nearly extreme regime MomenniaPRD . Generally, the metric function (7) has at most three real roots located at (the event horizon), (the cosmological horizon), and (a negative root) so that . In this paper, we shall study the perturbations in the range .
It is notable to mention that in contrast with Einstein gravity that the cosmological constant is added in the action by hand, it arises purely as an integration constant in the Weyl gravity solutions (7). Initially, it has been advocated that the linear -term in the metric function can explain the flat galaxy rotation curves without the need for dark matter GRCurves ; DM ; MannheimKazanas and there is still a debate in the literature regarding this matter Horne ; Hobson ; Mannheim2022 . But, here, we are going to show that this term can be responsible for observing echoes in the ringdown signal of black holes in Weyl gravity.
III Perturbation equations and time-domain integration
III.1 Massive scalar field perturbations
The wave equation and the effective potential of a massive scalar perturbation minimally coupled to the background spacetime of the Weyl solutions (7) are given by MomenniaPLB
| (8) |
| (9) |
where is the test field mass, are the multipole numbers, and is the tortoise coordinate with the following definition
| (10) |
In this coordinate, the whole accessible space for the observer lies between two infinities corresponding to the event horizon () and the cosmological horizon ().
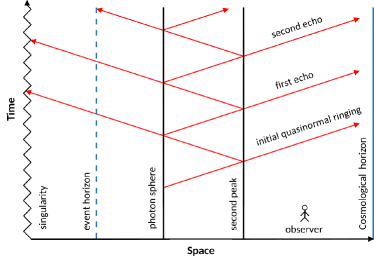
The QN modes of conformal Weyl black holes are solutions to the wave equation (8) when satisfying the boundary conditions of purely ingoing waves at the event horizon and purely outgoing waves at the cosmological horizon . Therefore, no waves are allowed to come from either left or right infinity, and thus the distant observer only detects the outgoing waves (see Fig. 5 and related discussion). Imposing these conditions on the wave equation (8) lead to a discrete set of eigenvalues with a real part representing the actual oscillations of the test field and an imaginary part giving its damping rate.
In order to see how the constant parameter produces the second peak in the effective potential as well as affects the angular momentum peak, we substitute the metric function (7) into (9) to get the explicit form of the potential in terms of the black hole parameters as below
| (11) | |||||
From this relation, we can see that the last two terms can produce the second peak in the effective potential if we choose suitable values for the parameters , , and . We need the effective potential vanishes at the cosmological horizon (that is also located on the right side of the second peak), hence we impose the condition on the potential since the last -term dominates for very large distances. On the other hand, the only term that can raise the effective potential after the angular momentum peak (and before being suppressed by the last -term) is the linear -term which dominates at intermediate distances. Therefore, by considering the linear term, in order for the effective potential grows and make the second peak, one should impose the following restrictions
| (12) |
on the parameter space. With these conditions at hand and for , from Eq. (11) we see that the combination of the set of terms raises the potential starting from zero value at the event horizon and suppress it to form the first peak similar to the standard Schwarzschild case, whereas the linear -term raises the effective potential again at intermediate distances and -term suppresses it at large distances to form the second peak.
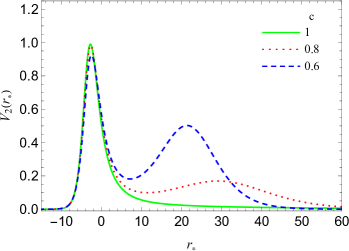
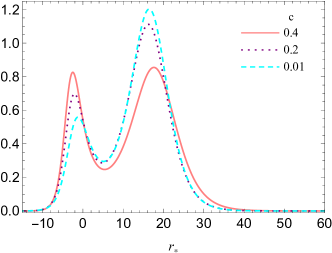
The effective potential enjoys the second peak for as for the case and figure 1 illustrates the behavior of the effective potential (9) versus the tortoise coordinates for different values of the constant parameter . We find that this figure confirms our discussion regarding the effective potential and shows a double-peak barrier in the potential profile while the conditions (12) are satisfied.
In this scenario, the role of the test field mass is helping the -term to suppress the effective potential and generate the second peak. Otherwise, this term would be positive, and hence the potential would grow in the asymptotic region. Therefore, we see that the first peak is produced by the black hole itself while the second peak is produced due to the large-scale structure of the Universe characterized by non-vanishing integration constants (responsible for dark matter) and (responsible for dark energy).
With this design at hand, we can observe echoes in the background spacetime of Weyl solutions as well. In this case, the main burst is generated at the photon sphere (left peak), but the frequency is not of the same order as the Schwarzschild-dS black hole QNMs for . Then, a substantial component of this high-frequency initial signal crosses the potential barrier and would be trapped between the double peak barrier, which leads to a series of echoes detected by a distant observer. These echoes occur in a transient regime and each echo has a smaller amplitude and lower frequency in comparison with previous ones.
The effects of the cosmological constant and the test scalar mass on the QNMs of black holes have been studied thoroughly so far. In this study, we need to understand the dependence of the quasinormal ringing on the constant parameter that characterizes deviations from the Schwarzschild- black hole. Hence, we fix the free parameters as , , , and in order to concentrate our attention on the variation of in ringdown profiles.
III.2 Ringing waveform
We obtain the time-domain profile of modes by taking the integration of the wave-like equation (8). In order to obtain the time evolution of modes, we follow the discretization scheme described in Pullin and rewrite the wave equation in terms of the light-cone coordinates and as below
| (13) |
that takes into account the contribution of all the modes and determines the behavior of the asymptotic tails at late times. By applying the time evolution operator for small on and considering Eq. (13), we get
| (14) |
where is the step size of the grids. This relation allows us to obtain the values of starting from the two null surfaces and as initial data. In this paper, we consider at , and use the Gaussian wave packet
| (15) |
centered on and having width at as the initial pulse. Then, we choose the observer to be located between the secondary peak and the cosmological horizon corresponding to to generate the quasinormal ringing waveforms. Although the waveforms for various multipole numbers are qualitatively similar, we choose the case in our analysis in order to have a better illustration of the situation. This is because the case shows the echoes after the ringdown phase more obvious in comparison with .
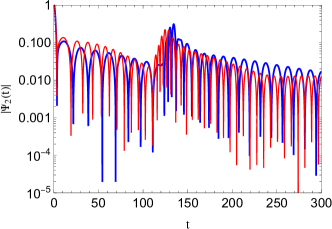
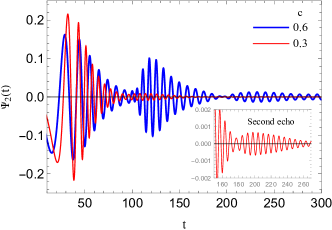
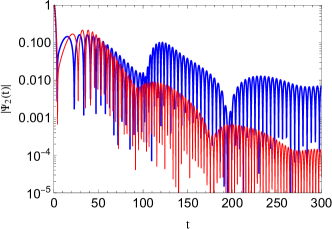
| initial outburst, , echoes | |||
| initial outburst, , echoes | |||
| initial outburst, , echoes | |||
| initial outburst, , echoes | |||
| initial outburst, , echoes | |||
| initial outburst, , echoes | |||
| , echoes | |||
| , echoes | |||
| initial outburst, |
III.3 The Prony method
In order to find the QN frequencies of the ringdown before the echo stage emerges, we follow the procedure described in Marple ; PronyBerti and apply the Prony method to the generated signal. This method can be employed for mining information from (damped) sinusoidal signals. Here, the main idea is to express the ringing waveform as a superposition of complex exponentials with arbitrary amplitudes and phases as follows
| (16) |
where are the QN frequencies with the real part and the imaginary part . To utilize the Prony method, and since the time is discretized by , it is convenient to rewrite this expression in the following slightly different form PronyBerti
| (17) |
where is the value of at the th step and the new unknown complex parameters are given by
| (18) |
| (19) |
Indeed, this method allows us to obtain ’s, and since and are known, we can calculate the QN frequencies from Eq. (18) as below
| (20) |
In order to find ’s, as the first step, one can introduce in Eq. (17) to obtain a new summation as follows
| (21) | |||||
Now, by taking into account the following polynomial function
| (22) |
one finds that the second summation in the last equality of Eq. (21) is zero, hence from its left-hand side, we have
| (23) |
that can be used to find the series coefficients presented in the polynomial function (22). To do so, we assume the ringdown waveform starts at and finishes at some time . Therefore, by substituting in Eq. (23), we can find linear equations for unknown series coefficients . Once the coefficients are found by solving these equations, we numerically solve the polynomial function (22) for the roots . Finally, Eq. (20) can be used to calculate the quasinormal frequencies.
IV Echoes from Weyl black hole solutions
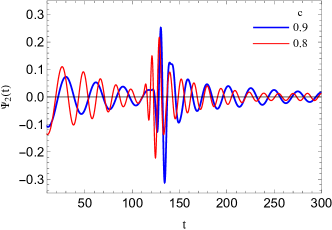
Here, we investigate the dependence of the quasinormal ringing in the background of Weyl solutions on the constant parameter by employing the time-domain integration approach described in the previous section. We recall that the integration constant measures deviations from the Schwarzschild-dS black holes for . The time-domain profile of the modes is illustrated in Figs. 2-4 for various values of the constant parameter while the other free parameters are fixed to , , , and . Generally, according to the time evolution of the modes, we can observe that the echoes appear after the period of initial quasinormal oscillations and dominate the signal.
Besides, the fundamental QN frequencies of the initial ringdown stage and their corresponding quality factor have been calculated and the results are given in Table 1. However, note that the accuracy of quasinormal frequencies extracted from the ringdown waveform data is sensitive to the temporal range of considered early-stage quasinormal ringing. Furthermore, from the quality factor of the QN frequencies, we find that the signal of the conformal Weyl black hole has higher quality compared to the Schwarzschild-dS one. Hence, the Weyl solutions are better oscillators and their signal is more likely to be detected.
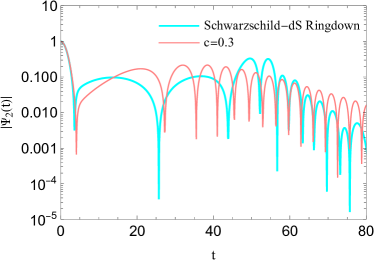
Fig. 2 illustrates a comparison between the initial quasinormal ringdown of the conformal Weyl black holes and the Schwarzschild-dS solutions before a series of echoes appear. This figure indicates that the initial quasinormal ringing of conformal Weyl black holes does not follow the standard Schwarzschild-dS ringdown. For the special case and from this figure, we see that the real part of the QN frequencies for the Weyl solutions is close to the Schwarzschild-dS black holes, but the perturbations live longer in the former background (also see Table 1 for quantified QN frequencies of this early-stage ringing phase and compare row with row).
However, the situation would change if the constant parameter varies. As one can see from Table 1 and Figs. 3-4, both the real and imaginary parts of the QN frequencies decrease with an increase in the constant parameter . Hence, the perturbations live longer with lower frequency as the constant parameter increases. Furthermore, these figures show that a distinctive picture of echoes appears after the initial oscillatory ringing and dominates the time evolution of the modes. This behavior can be observed for the range of the constant parameter subject to choosing suitable values for the rest of the free parameters. These echoes disappear for .
Strictly speaking, one must obey the conditions (12) on the set of parameters in order to observe echoes raising immediately after the quasinormal ringdown period. But if we violate one of these constraints on the free parameters, we would see that quasinormal oscillations dominate the signal and echoes disappear. Besides, in the cases studied here, we see that the effective potential is positive definite and the perturbations decay with the time that guarantees the dynamical stability of the spacetime undergoing massive scalar perturbations.
It is worthwhile to recall that, unlike the well-known echoes produced due to near-horizon modifications, such as horizon-corrected black holes and wormholes, from our analysis, we see that the echoes in conformal Weyl spacetime are generated because of the large-scale structure of the Universe. This new class of echoes emerges due to trapped modes between the photon sphere peak and the second barrier generated by the dark matter and dark energy contents of the cosmos, rather than trapped signals between the angular momentum peak and the near-horizon area (see Fig. 5 for a schematic illustration of the situation and compare with Fig. of Ref. Abedi for corrections near the horizon).
As the final remark, we should note that the large-scale terms presented in the spacetime (4) that are responsible for observing these echoes, i.e., the linear -term (responsible for dark matter) and the cosmological constant -term (responsible for dark energy), arose quite naturally as integration constants in the conformal Weyl gravity theory. Therefore, these novel echoes emerged due to the large-scale structure of the universe and differ from the ones that appeared in black holes due to near-horizon modifications Abedi , the compact stars because of discontinuity in their effective potential discontinuityPotential , wormhole spacetimes WormholesEcho , and considering massive thin shells in the black hole BHshell and wormhole wormshell environment.
V Outlook and Conclusions
We have employed the time-domain integration in order to analyze the quasinormal ringing of black hole solutions in conformal Weyl gravity and used the Prony method to extract the quasinormal frequencies of the early-stage oscillations. The metric under consideration depends on an integration constant, which is denoted by throughout the paper, and characterizes deviations from the standard Schwarzschild-dS metric; The conformal Weyl black holes deviate from the Schwarzschild-dS black holes if the free parameter deviates from one, hence the former solutions reduce to the latter ones provided .
We have shown that the deviations from the Schwarzschild-dS black holes are characterized by echoes such that the first stage signal is dominated by a series of echoes at later times. The echoes could be observed for the range of the constant parameter for our black hole case study. In addition, one may consider the possibility that if this class of echoes could be produced after the merger phase and exist in nature, their contribution to the recent pulsar timing array observations PTA ; NANOGrav might be inevitable. This is because each echo that propagates through the cosmos has a smaller amplitude and lower frequency in comparison with previous ones, hence finally, leads to Nano-Hertz gravitational waves. However, this impact is not clear yet and it requires more investigations which we leave here as a proposal.
We have seen that this phenomenon emerged due to the large-scale structure of the Universe, unlike wormholes and horizon-corrected black holes, because the echoes are induced due to the appearance of the second peak on the right side of the photon sphere peak; This second peak basically appeared because of the presence of the linear -term (responsible for dark matter) and the quadratic -term (responsible for dark energy) in the metric function that encode the large-scale information of the cosmos and arose quite naturally as integration constants in the conformal Weyl gravity theory. Therefore, we have seen that the echoes emerge when one assigns conformal symmetry to the astrophysical black hole spacetimes. Furthermore, even after conformal symmetry breaking, the echoes are present if nature chooses the constant parameter value in the interval .
VI acknowledgments
The author acknowledges SNII and was supported by the National Council of Humanities, Sciences, and Technologies of Mexico (CONAHCyT) through Estancias Posdoctorales por México Convocatoria 2023(1) under the postdoctoral Grant No. 1242413.
References
- (1) B. P. Abbott et al. [LIGO Scientific and Virgo Collaborations], Observation of Gravitational Waves from a Binary Black Hole Merger, Phys. Rev. Lett. 116 (2016) 061102.
- (2) B. P. Abbott et al. [LIGO Scientific and Virgo Collaborations], GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence, Phys. Rev. Lett. 116 (2016) 241103.
- (3) C. V. Vishveshwara, Scattering of Gravitational Radiation by a Schwarzschild Black-hole, Nature 227 (1970) 936.
- (4) W. H. Press, Long wave trains of gravitational waves from a vibrating black hole, Astrophys. J. Lett. 170 (1971) L105.
- (5) S. Chandrasekhar and S. L. Detweiler, The quasi-normal modes of the Schwarzschild black hole, Proc. Roy. Soc. Lond. A 344 (1975) 441.
- (6) M. Isi, M. Giesler, W. M. Farr, M. A. Scheel and S. A. Teukolsky, Testing the no-hair theorem with GW150914, Phys. Rev. Lett. 123 (2019) 111102.
- (7) S. Ma, L. Sun and Y. Chen, Using rational filters to uncover the first ringdown overtone in GW150914, Phys. Rev. D 107 (2023) 084010.
- (8) R. Cotesta, G. Carullo, E. Berti and V. Cardoso, Analysis of Ringdown Overtones in GW150914, Phys. Rev. Lett. 129 (2022) 111102.
- (9) M. Isi and W. M. Farr, Comment on “Analysis of Ringdown Overtones in GW150914”, Phys. Rev. Lett. 131 (2023) 169001.
- (10) G. Carullo, R. Cotesta, E. Berti and V. Cardoso, Reply to Comment on “Analysis of Ringdown Overtones in GW150914”, Phys. Rev. Lett. 131 (2023) 169002.
- (11) E. Berti, V. Cardoso and C. M. Will, Gravitational-wave spectroscopy of massive black holes with the space interferometer LISA, Phys. Rev. D 73 (2006) 064030.
- (12) L. Barack et al., Black holes, gravitational waves and fundamental physics: a roadmap, Class. Quant. Grav. 36 (2019) 143001.
- (13) H. P. Nollert, Topical review. Quasinormal modes: the characteristic ‘sound’ of black holes and neutron stars, Class. Quant. Grav. 16 (1999) R159.
- (14) K. D. Kokkotas and B. G. Schmidt, Quasinormal modes of stars and black holes, Living Rev. Rel. 2 (1999) 2.
- (15) E. Berti, V. Cardoso and A. O. Starinets, Quasinormal modes of black holes and black branes, Class. Quant. Grav. 26 (2009) 163001.
- (16) R. A. Konoplya and A. Zhidenko, Quasinormal modes of black holes: from astrophysics to string theory, Rev. Mod. Phys. 83 (2011) 793.
- (17) R. A. Konoplya and A. Zhidenko, Instability of higher-dimensional charged black holes in the de Sitter world, Phys. Rev. Lett. 103 (2009) 161101.
- (18) Z. Zhu, S. J. Zhang, C. E. Pellicer, B. Wang and E. Abdalla, Stability of Reissner-Nordström black hole in de Sitter background under charged scalar perturbation, Phys. Rev. D 90 (2014) 049904.
- (19) M. Momennia, Quasinormal modes of self-dual black holes in loop quantum gravity, Phys. Rev. D 106 (2022) 024052.
- (20) S. Hod, Bohr’s Correspondence Principle and the Area Spectrum of Quantum Black Holes, Phys. Rev. Lett. 81 (1998) 4293.
- (21) O. Dreyer, Quasinormal Modes, the Area Spectrum, and Black Hole Entropy, Phys. Rev. Lett. 90 (2003) 081301.
- (22) V. Cardoso, A. S. Miranda, E. Berti, H. Witek and V. T. Zanchin, Geodesic stability, Lyapunov exponents, and quasinormal modes, Phys. Rev. D 79 (2009) 064016.
- (23) R. A. Konoplya, Z. Stuchlik and A. Zhidenko, Massive nonminimally coupled scalar field in Reissner-Nordström spacetime: Long-lived quasinormal modes and instability, Phys. Rev. D 98 (2018) 104033.
- (24) M. Momennia and S. H. Hendi, Near-extremal black holes in Weyl gravity: Quasinormal modes and geodesic instability, Phys. Rev. D 99 (2019) 124025.
- (25) R. A. Konoplya, Further clarification on quasinormal modes/circular null geodesics correspondence, Phys. Lett. B 838 (2023) 137674.
- (26) G. T. Horowitz and V. E. Hubeny, Quasinormal modes of AdS black holes and the approach to thermal equilibrium, Phys. Rev. D 62 (2000) 024027.
- (27) V. Cardoso and J. P. S. Lemos, Quasinormal modes of Schwarzschild–anti-de Sitter black holes: Electromagnetic and gravitational perturbations, Phys. Rev. D 64 (2001) 084017.
- (28) E. Berti and K. D. Kokkotas, Quasinormal modes of Reissner–Nordström–anti-de Sitter black holes: Scalar, electromagnetic, and gravitational perturbations, Phys. Rev. D 67 (2003) 064020.
- (29) S. H. Hendi and M. Momennia, Thermodynamic description and quasinormal modes of adS black holes in Born-lnfeld massive gravity with a non-abelian hair, JHEP 10 (2019) 207.
- (30) M. Momennia, S. H. Hendi and F. Soltani Bidgoli, Stability and quasinormal modes of black holes in conformal Weyl gravity, Phys. Lett. B 813 (2021) 136028.
- (31) Y. Guo and Y. G. Miao, Null geodesics, quasinormal modes, and the correspondence with shadows in high-dimensional Einstein-Yang-Mills spacetimes, Phys. Rev. D 102 (2020) 084057.
- (32) H. Ma and J. Li, Dirac quasinormal modes of Born-Infeld black hole spacetimes, Chin. Phys. C 44 (2020) 095102.
- (33) J. Yang, C. Zhang and Y. Ma, Shadow and stability of quantum-corrected black holes, Eur. Phys. J. C 83 (2023) 619.
- (34) S. Yang, W. D. Guo, Q. Tan and Y. X. Liu, Axial gravitational quasinormal modes of a self-dual black hole in loop quantum gravity, Phys.Rev.D 108 (2023) 024055.
- (35) E. R. Livine, C. Montagnon, N. Oshita and H. Roussille, Scalar Quasi-Normal Modes of a Loop Quantum Black Hole, JCAP 10 (2024) 037.
- (36) H. Gong, S. Li, D. Zhang, G. Fu and J. P. Wu, Quasinormal modes of quantum-corrected black holes, Phys. Rev. D 110 (2024) 044040.
- (37) L. M. Cao, J. N. Chen, L. B. Wu, L. Xie and Y. S. Zhou, The pseudospectrum and spectrum (in) stability of quantum corrected Schwarzschild black hole, Sci. China Phys. Mech. Astron. 67 (2024) 100412.
- (38) A. Dubinsky, Quantum gravitational corrections to the Schwarzschild spacetime and quasinormal frequencies, [arXiv:2405.13552].
- (39) Z. Malik, Perturbations and quasinormal modes of the dirac field in effective quantum gravity, [arXiv:2409.01561].
- (40) C. Y. Chen, H. W. Chiang and J. S. Tsao, Eikonal quasinormal modes and photon orbits of deformed Schwarzschild black holes, Phys. Rev. D 106 (2022) 044068.
- (41) B. Gwak, Quasinormal modes in near-extremal spinning C-metric, Eur. Phys. J. Plus 138 (2023) 582.
- (42) J. Matyjasek, Quasinormal modes of dirty black holes in the effective theory of gravity with a third order curvature term, Phys. Rev. D 102 (2020) 124046.
- (43) Y. Myrzakulov, K. Myrzakulov, S. Upadhyay and D. V. Singh, Quasinormal modes and phase structure of regular AdS Einstein-Gauss-Bonnet black holes, Int. J. Geom. Meth. Mod. Phys. 20 (2023) 2350121.
- (44) D. Liu, Y. Yang, S. Wu, Y. Xing, Z. Xu and Z. W. Long, Ringing of a black hole in a dark matter halo, Phys. Rev. D 104 (2021) 104042.
- (45) M. Khodadi and J. T. Firouzjaee, A survey of strong cosmic censorship conjecture beyond Einstein’s gravity, Phys. Dark Univ. 37 (2022) 101084.
- (46) P. A. Gonzalez, E. Papantonopoulos, J. Saavedra and Y. Vasquez, Quasinormal modes for massive charged scalar fields in Reissner-Nordström dS black holes: anomalous decay rate, JHEP 06 (2022) 150.
- (47) A. Dubinsky and A. Zinhailo, Asymptotic decay and quasinormal frequencies of scalar and Dirac fields around dilaton-de Sitter black holes, Eur. Phys. J. C 84 (2024) 847.
- (48) M. Skvortsova, Ringing of Extreme Regular Black Holes, Gravit. Cosmol. 30 (2024) 279.
- (49) M. Skvortsova, Long lived quasinormal modes of regular and extreme black holes, [DOI:10.1209/0295-5075/adaee2].
- (50) X. He, B. Wang, S. Chen, R. G. Cai and C. Y. Lin, Quasinormal modes in the background of charged Kaluza–Klein black hole with squashed horizons, Phys. Lett. B 665 (2008) 392.
- (51) S. H. Hendi, S. Hajkhalili, M. Jamil and M. Momennia, Stability and phase transition of rotating Kaluza-Klein black holes, Eur. Phys. J. C 81 (2021) 1112.
- (52) L. M. Cao, L. B. Wu, Y. Zhao and Y. S. Zhou, Quasinormal modes of tensor perturbations of Kaluza-Klein black holes in Einstein-Gauss-Bonnet gravity, Phys. Rev. D 108 (2023) 124023.
- (53) M. Momennia and S. H. Hendi, Quasinormal modes of black holes in Weyl gravity: Electromagnetic and gravitational perturbations, Eur. Phys. J. C 80 (2020) 505.
- (54) R. A. Konoplya, Conformal Weyl gravity via two stages of quasinormal ringing and late-time behavior, Phys. Rev. D 103 (2021) 044033.
- (55) R. Becar, P. A. Gonzalez, F. Moncada and Y. Vasquez, Massive scalar field perturbations in Weyl black holes, Eur. Phys. J. C 83 (2023) 942.
- (56) Z. Malik, Quasinormal modes of the Mannheim–Kazanas black holes, Z. Naturforsch. A 79, 1063 (2024).
- (57) R. A. Konoplya, A. Khrabustovskyi, J. Kriz and A. Zhidenko, Quasinormal Ringing and Shadows of Black Holes and Wormholes in Dark Matter-Inspired Weyl Gravity, [arXiv:2501.16134].
- (58) V. Cardoso, E. Franzin and P. Pani, Is the Gravitational-Wave Ringdown a Probe of the Event Horizon?, Phys. Rev. Lett. 116 (2016) 171101; ibid, 117 (2016) 089902(E).
- (59) V. Cardoso, S. Hopper, C. F. B. Macedo, C. Palenzuela and P. Pani, Gravitational-wave signatures of exotic compact objects and of quantum corrections at the horizon scale, Phys. Rev. D 94 (2016) 084031.
- (60) V. Cardoso and P. Pani, Tests for the existence of black holes through gravitational wave echoes, Nat. Astron. 1 (2017) 586.
- (61) A. Maselli, S. H. Volkel and K. D. Kokkotas, Parameter estimation of gravitational wave echoes from exotic compact objects, Phys. Rev. D 96 (2017) 064045.
- (62) K. W. Tsang, M. Rollier, A. Ghosh, A. Samajdar, M. Agathos, K. Chatziioannou, V. Cardoso, G. Khanna and C. V. D. Broeck, A morphology-independent data analysis method for detecting and characterizing gravitational wave echoes, Phys. Rev. D 98 (2018) 024023.
- (63) Y. T. Wang, J. Zhang, S. Y. Zhou and Y. S. Piao, On echo intervals in gravitational wave echo analysis, Eur. Phys. J. C 79 (2019) 726.
- (64) K. A. Bronnikov and R. A. Konoplya, Echoes in brane worlds: Ringing at a black hole-wormhole transition, Phys. Rev. D 101 (2020) 064004.
- (65) Y. Yang, D. Liu, Z. Xu, Y. Xing, S. Wu and Z. W. Long, Echoes of novel black-bounce spacetimes, Phys. Rev. D 104 (2021) 104021.
- (66) G. Guo, P. Wang, H. Wu and H. Yang, Echoes from hairy black holes, JHEP 06 (2022) 073.
- (67) A. Sang, M. Zhang, S. W. Wei and J. Jiang, Echoes of black holes in Einstein-nonlinear electrodynamic theories, Eur. Phys. J. C 83 (2023) 291.
- (68) J. Abedi, H. Dykaar and N. Afshordi, Echoes from the abyss: Tentative evidence for Planck-scale structure at black hole horizons, Phys. Rev. D 96 (2017) 082004.
- (69) P. Pani and V. Ferrari, On gravitational-wave echoes from neutron-star binary coalescences, Class. Quant. Grav. 35 (2018) 15LT01.
- (70) E. Barausse, V. Cardoso and P. Pani, Can environmental effects spoil precision gravitational-wave astrophysics?, Phys. Rev. D 89 (2014) 104059.
- (71) R. A. Konoplya, Z. Stuchlik and A. Zhidenko, Echoes of compact objects: New physics near the surface and matter at a distance, Phys. Rev. D 99 (2019) 024007.
- (72) K. Akiyama et al. [Event Horizon Telescope Collaboration], First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole, Astrophys. J. Lett. 875 (2019) L1.
- (73) K. Akiyama et al. [Event Horizon Telescope Collaboration], First Sagittarius A* Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole in the Center of the Milky Way, Astrophys. J. Lett. 930 (2022) L12.
- (74) J. B. Hartle and K. S. Thorne, Slowly Rotating Relativistic Stars. II. Models for Neutron Stars and Supermassive Stars, Astrophys. J. 153 (1968) 807.
- (75) A. Garcia, D. Galtsov and O. Kechkin, Class of stationary axisymmetric solutions of the Einstein-Maxwell-Dilaton-Axion field equations, Phys. Rev. Lett. 74 (1995) 1276.
- (76) L. Modesto, Semiclassical loop quantum black hole, Int. J. Theor. Phys. 49 (2010) 1649.
- (77) C. A. R. Herdeiro and E. Radu, Kerr Black Holes with Scalar Hair, Phys. Rev. Lett. 112 (2014) 221101.
- (78) S. H. Hendi and M. Momennia, Thermodynamic instability of topological black holes with nonlinear source, Eur. Phys. J. C 75 (2015) 54.
- (79) S. H. Hendi, S. Panahiyan, B. Eslam Panah, M. Faizal and M. Momennia, Critical behavior of charged black holes in Gauss-Bonnet gravity’s rainbow, Phys. Rev. D 94 (2016) 024028.
- (80) S. H. Hendi and M. Momennia, AdS charged black holes in Einstein-Yang-Mills gravity’s rainbow: Thermal stability and P-V criticality, Phys. Lett. B 777 (2018) 222.
- (81) I. Bah and P. Heidmann, Topological stars and black holes, Phys. Rev. Lett. 126 (2021) 151101.
- (82) S. Hergott, V. Husain and S. Rastgoo, Model metrics for quantum black hole evolution: Gravitational collapse, singularity resolution, and transient horizons, Phys. Rev. D 106 (2022) 046012.
- (83) M. M. Lima and C. Gomes, Black Hole Solutions in Non-Minimally Coupled Weyl Connection Gravity, Universe 10 (2024) 433.
- (84) M. Momennia, A. Herrera-Aguilar and U. Nucamendi, Kerr black hole in de Sitter spacetime and observational redshift: Toward a new method to measure the Hubble constant, Phys. Rev. D 107 (2023) 104041.
- (85) S. M. Carroll, The Cosmological Constant, Living Rev. Rel. 4 (2001) 1.
- (86) R. J. Riegert, Birkhoff’s Theorem in Conformal Gravity, Phys. Rev. Lett. 53 (1984) 315.
- (87) P. D. Mannheim and J. G. O’Brien, Impact of a Global Quadratic Potential on Galactic Rotation Curves, Phys. Rev. Lett. 106 (2011) 121101.
- (88) P. D. Mannheim, Making the Case for Conformal Gravity, Found. Phys. 42 (2012) 388.
- (89) H. Weyl, Republication of: Purely infinitesimal geometry by Hermann Weyl, Gen. Rel. Grav. 54 (2022) 51.
- (90) C. Corral, G. Giribet and R. Olea, Self-dual gravitational instantons in conformal gravity: Conserved charges and thermodynamics, Phys. Rev. D 104 (2021) 064026.
- (91) M. Fathi, M. Olivares and J. R. Villanueva, Ergosphere, Photon Region Structure, and the Shadow of a Rotating Charged Weyl Black Hole, Galaxies 9 (2021) 43.
- (92) A. Hell, D. Lust and G. Zoupanos, On the Ghost Problem of Conformal Gravity, JHEP 08 (2023) 168.
- (93) D. Gregoris, Y. C. Ong and B. Wang, A critical assessment of black hole solutions with a linear term in their redshift function, Eur. Phys. J. C 81 (2021) 684.
- (94) D. Aggarwal, D. Chang, Q. D. Helmers, N. Sivrioglu, L. R. Ram-Mohan, L. Rodriguez, S. Rodriguez and R. Suleiman, Nöther currents, black hole entropy universality and CFT duality in conformal Weyl gravity, Int. J. Mod. Phys. D 32 (2023) 2350017.
- (95) R. Bach, Zur Weylschen Relativitätstheorie und der Weylschen Erweiterung des Krümmungstensorbegriffs, Math. Z. 9 (1921) 110.
- (96) R. J. Riegert, The particle content of linearized conformal gravity, Phys. Lett. A 105 (1984) 110.
- (97) R. Yang, Gravitational waves in conformal gravity, Phys. Lett. B 784 (2018) 212.
- (98) P. D. Mannheim and D. Kazanas, Exact Vacuum Solution to Conformal Weyl Gravity and Galactic Rotation Curves, Astrophys. J. 342 (1989) 635.
- (99) K. Horne, Conformal Gravity rotation curves with a conformal Higgs halo, MNRAS 458 (2016) 4122.
- (100) M. Hobson and A. Lasenby, Conformal gravity does not predict flat galaxy rotation curves, Phys. Rev. D 104 (2021) 064014.
- (101) P. D. Mannheim, Structure of conformal gravity in the presence of a scale breaking scalar field, Gen. Relativ. Gravit. 54 (2022) 99.
- (102) C. Gundlach, R. H. Price and J. Pullin, Late-time behavior of stellar collapse and explosions. I. Linearized perturbations, Phys. Rev. D 49 (1994) 883.
- (103) S. L. Marple, Digital spectral analysis with applications, (Prentice-Hall, New Jersey, 1987).
- (104) E. Berti, V. Cardoso, J. A. Gonzalez and U. Sperhake, Mining information from binary black hole mergers: A comparison of estimation methods for complex exponentials in noise, Phys. Rev. D 75 (2007) 124017.
- (105) S. F. Shen, K. Lin, T. Zhu, Y. P. Yan, C. G. Shao and W. L. Qian, Two distinct types of echoes in compact objects, Phys. Rev. D 110 (2024) 084022.
- (106) G. Agazie et al. [NANOGrav Collaboration], The NANOGrav 15 yr Data Set: Evidence for a Gravitational-wave Background, Astrophys. J. Lett. 951 (2023) L8.
- (107) A. Afzal et al. [NANOGrav Collaboration], The NANOGrav 15 yr Data Set: Search for Signals from New Physics, Astrophys. J. Lett. 951 (2023) L11.