Nuclear spin-wave quantum register for a solid state qubit

Andrei Ruskuc Thomas J. Watson, Sr, Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA, USA Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA, USA Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA Chun-Ju Wu Thomas J. Watson, Sr, Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA, USA Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA, USA Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA, USA Jake Rochman Thomas J. Watson, Sr, Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA, USA Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA, USA Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA Joonhee Choi joonhee@caltech.edu Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA Division of Physics, Mathematics and Astronomy, California Institute of Technology, Pasadena, CA, USA Andrei Faraon faraon@caltech.edu Thomas J. Watson, Sr, Laboratory of Applied Physics, California Institute of Technology, Pasadena, CA, USA Kavli Nanoscience Institute, California Institute of Technology, Pasadena, CA, USA Institute for Quantum Information and Matter, California Institute of Technology, Pasadena, CA, USA

Solid-state nuclear spins surrounding individual, optically addressable qubits Awschalom2018 ; Chatterjee2021 provide a crucial resource for quantum networks Briegel1998 ; Hensen2015 ; Bhaskar2020 ; Pompili2021 , computation Waldherr2014 ; Taminiau2014 ; Zhong2019 ; Bradley2019a ; Kinos2021 and simulation Randall2021 . While hosts with sparse nuclear spin baths are typically chosen to mitigate qubit decoherence Wolfowicz2021 , developing coherent quantum systems in nuclear spin-rich hosts enables exploration of a much broader range of materials for quantum information applications. The collective modes of these dense nuclear spin ensembles provide a natural basis for quantum storage Taylor2003 , however, utilizing them as a resource for single spin qubits has thus far remained elusive. Here, by using a highly coherent, optically addressed ¹⁷¹Yb³⁺ qubit doped into a nuclear spin-rich yttrium orthovanadate crystal Kindem2020 , we develop a robust quantum control protocol to manipulate the multi-level nuclear spin states of neighbouring ⁵¹V⁵⁺ lattice ions. Via a dynamically-engineered spin exchange interaction, we polarise this nuclear spin ensemble, generate collective spin excitations, and subsequently use them to implement a long-lived quantum memory. We additionally demonstrate preparation and measurement of maximally entangled ¹⁷¹Yb–⁵¹V Bell states. Unlike conventional, disordered nuclear spin based quantum memories GurudevDutt2007 ; Kolkowitz2012 ; Taminiau2012 ; Zhao2012 ; Metsch2019 ; Bourassa2020a ; Hensen2020 ; Kornher2020 ; Wolfowicz2016 , our platform is deterministic and reproducible, ensuring identical quantum registers for all ¹⁷¹Yb³⁺ qubits. Our approach provides a framework for utilising the complex structure of dense nuclear spin baths, paving the way for building large-scale quantum networks using single rare-earth ion qubits Utikal2014 ; Siyushev2014 ; Zhong2018 ; Chen2020 ; Kindem2020 .

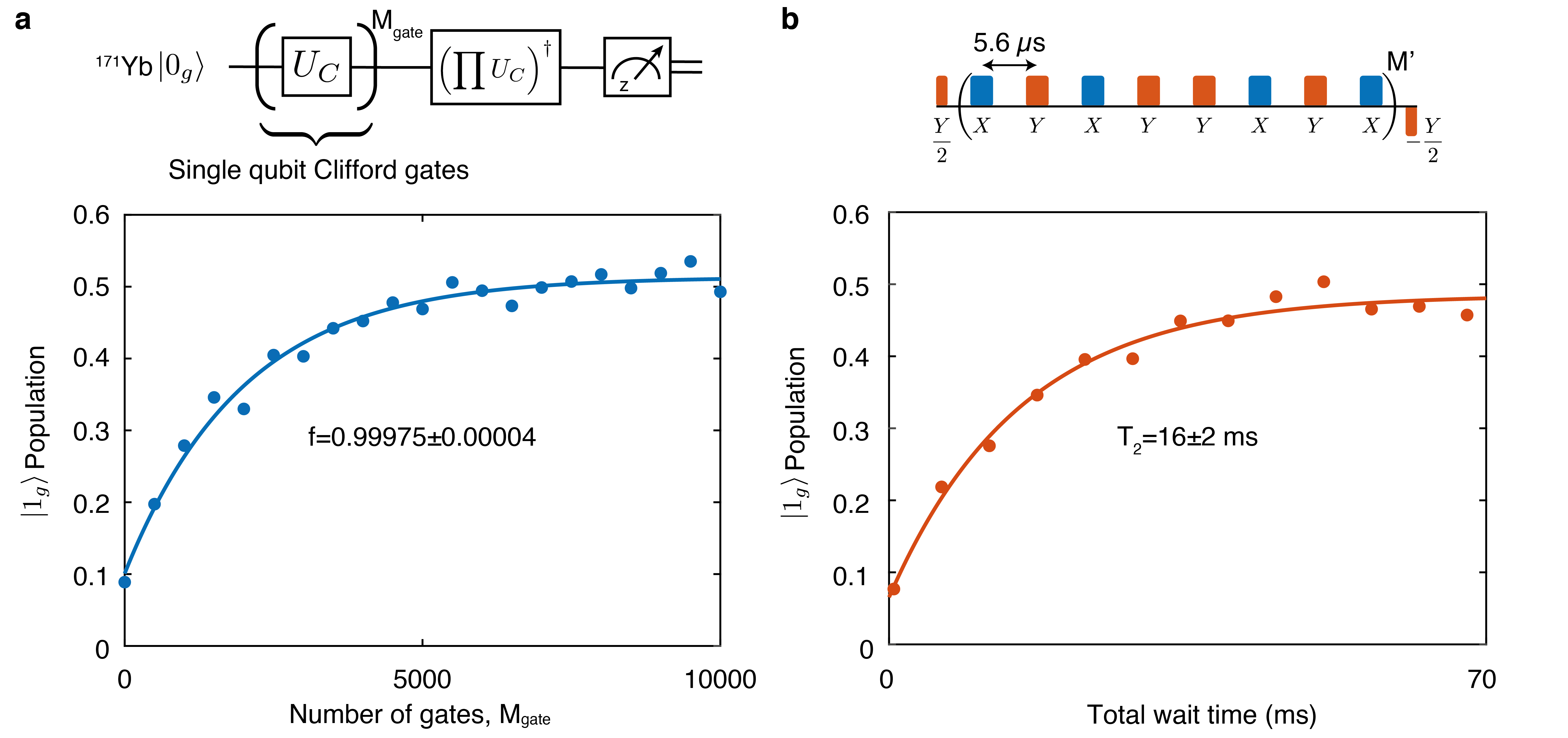
We recently demonstrated that at zero magnetic field, the hyperfine levels of single ¹⁷¹Yb³⁺ ions doped into yttrium orthovanadate (YVO₄), coupled to nanophotonic cavities, form high-quality optically addressable qubits Kindem2020 (Fig. 1a). The surrounding ⁵¹V⁵⁺ lattice ion nuclear spins generate a noisy magnetic field environment due to their large magnetic moment and high spin (I=7/2). Coherent ¹⁷¹Yb qubit operation is enabled by magnetically-insensitive transitions, leading to long coherence times (16 ms) and high gate fidelities (0.99975) (Extended Data Fig. 2). Whilst decoupling from sources of magnetic noise achieves an excellent operating regime for the ¹⁷¹Yb qubit, the ⁵¹V nuclear spins also provide a readily accessible, local resource for quantum information storage due to their inherently weak interactions with the environment. To date, most research regarding host nuclear spin utilisation has focused on several spectrally distinguishable impurity nuclear spins coupled to a localised electronic spin, e.g. ¹³C coupled to colour centres in diamond or ²⁹Si coupled to defects in silicon carbide, rare-earth ions, quantum dots or donor qubits in silicon GurudevDutt2007 ; Kolkowitz2012 ; Taminiau2012 ; Zhao2012 ; Bradley2019a ; Metsch2019 ; Bourassa2020a ; Hensen2020 ; Kornher2020 ; Wolfowicz2016 . Recently, a regime consisting of a large number of indistinguishable nuclear spins coupled to the delocalised electronic spin in a quantum dot has also been explored Gangloff2019 ; Gangloff2020 . In contrast, our system addresses a new regime where a small, deterministic cluster of spectrally indistinguishable nuclear spins are coupled to a single localized electronic spin. Specifically, the ¹⁷¹Yb electronic wavefunction is confined to the lattice site, and the YVO₄ crystal consists of highly isotopically pure nuclear spins (99.8% ⁵¹V). This confined, dense nuclear spin ensemble could be used as a deterministic local quantum processor by creating and manipulating entangled states, such as collective spin wave-like excitations, for near-term quantum applications. Critically, interfacing with these nuclear spins whilst preserving high qubit coherence necessitates the development of novel quantum control protocols using magnetically insensitive transitions that are robust against environmental noise.

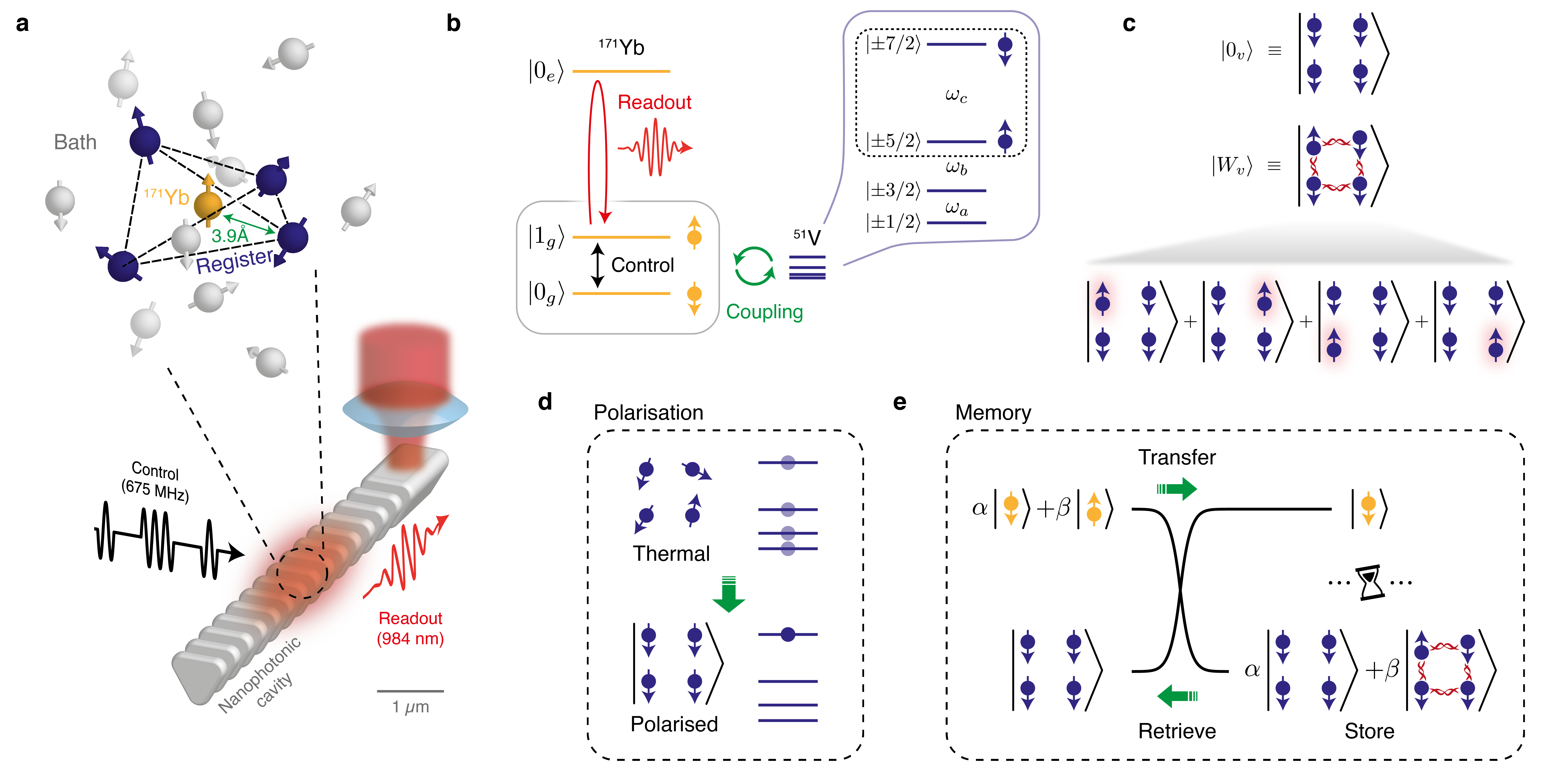
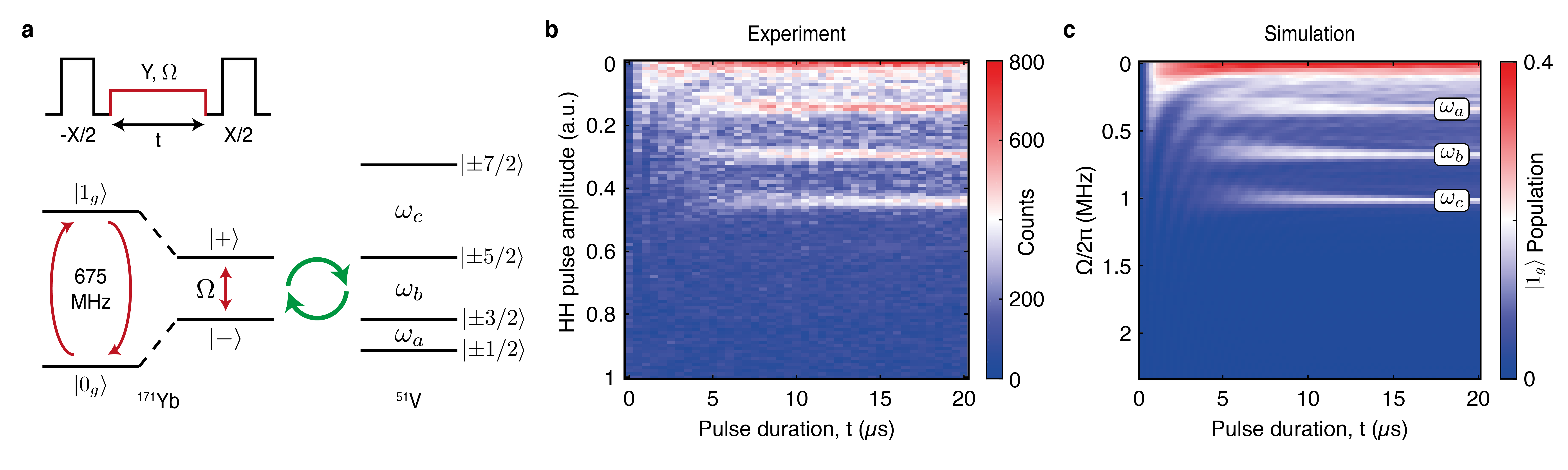
Refer to caption — Fig. 1: Schematic of a many-body nuclear spin register for optically-coupled ¹⁷¹Yb qubits in nanophotonic cavities. a, Optically addressable ¹⁷¹Yb ion (yellow) surrounded by a local ensemble of nuclear spins from lattice ⁵¹V ions. The register (blue) consists of four ⁵¹V spins equidistantly spaced by $3.9~{}\AA$ from the central ¹⁷¹Yb. The nuclear spin bath (grey) creates random magnetic noise termed the nuclear Overhauser field. A nanophotonic cavity enables optical initialisation and readout of the ¹⁷¹Yb ion via single-photon detection at 984 nm Kindem2020 . 675 MHz microwave pulses provide high-fidelity control of the ¹⁷¹Yb spin state. b, Energy level structure of ¹⁷¹Yb and ⁵¹V ions. Pulse-based control of the ¹⁷¹Yb ground-state transition ( $\ket{0_{g}}\leftrightarrow\ket{1_{g}}$ ) enables engineered spin-exchange interactions with neighbouring ⁵¹V ions. The energy level structure of the spin-7/2 ⁵¹V consists of four quadratically-spaced, doubly degenerate energy levels, $\{\ket{\pm m_{I}}\}=\{\ket{\pm 1/2}$ , $\ket{\pm 3/2}$ , $\ket{\pm 5/2}$ , $\ket{\pm 7/2}\}$ , resulting in three distinct transitions, $\omega_{a,b,c}/2\pi=$ 330 kHz, 660 kHz, and 991 kHz, respectively. The $\omega_{c}$ transition (dotted box) is used to implement the local nuclear spin register for quantum information storage. c, Effective qubit states of the nuclear spin register. The $\ket{0_{v}}$ and $\ket{W_{v}}$ states consist of all four ⁵¹V ions prepared in the $\ket{\downarrow}=\ket{\pm 7/2}$ state and a single spin excitation equally delocalised in the $\ket{\uparrow}=\ket{\pm 5/2}$ state, respectively. d, Initialisation of the nuclear spins from a thermal state into the polarised $\ket{\downarrow\downarrow\downarrow\downarrow}$ state. e, Transfer of a quantum state from ¹⁷¹Yb to the ⁵¹V register, storage and subsequent retrieval. Both the state initialization and transfer are enabled by robust, dynamically engineered interactions between ¹⁷¹Yb and ⁵¹V ions.

At zero-magnetic field the ¹⁷¹Yb ground state contains a pair of levels, $\ket{0_{g}}$ and $\ket{1_{g}}$ , separated by 675 MHz, which form our qubit Kindem2018a (Fig. 1b). We can optically read out the $\ket{1_{g}}$ population via a series of $\pi$ pulses at 984 nm, each followed by time-resolved detection of resonant photon emission (Extended Data Fig. 1). This is enabled by coupling the ¹⁷¹Yb ion to a nanophotonic cavity leading to high transition cyclicity, reduced optical lifetime and high photon collection efficiency Kindem2020 . The local crystalline environment consists of ⁸⁹Y, ⁵¹V and ¹⁶O ions. Of these, ⁵¹V with nuclear spin 7/2 has the largest magnetic dipole moment and zero-field structure due to a quadrupole interaction with the lattice electric field Bleaney1982 . This leads to four quadratically-spaced, doubly degenerate energy levels, $\{\ket{\pm m_{I}}\}=$ { $\ket{\pm 1/2}$ , $\ket{\pm 3/2}$ , $\ket{\pm 5/2}$ , $\ket{\pm 7/2}$ }, and three magnetic-dipole allowed transitions between these levels $\omega_{a}$ , $\omega_{b}$ , $\omega_{c}$ (Fig. 1b).

Local ⁵¹V ions are categorised into two complementary ensembles: the register and the bath. The register spins fulfil two conditions: (1) they are constituents of the frozen core: a set of ⁵¹V ions spectrally distinguished from the bath due to proximity to ¹⁷¹Yb; (2) the ¹⁷¹Yb–⁵¹V interaction Hamiltonian can drive transitions between their quadrupole levels. As shown later, experimental evidence suggests that the register consists of four ⁵¹V spins, equidistant from the central ¹⁷¹Yb (Fig. 1a). At zero field, the ¹⁷¹Yb $\ket{0_{g}}$ , $\ket{1_{g}}$ states have no intrinsic magnetic dipole moment and thus interactions with ⁵¹V register spins are forbidden to first order. However, a weak ¹⁷¹Yb dipole moment is induced by a random magnetic field originating from the bath (the nuclear Overhauser field, with $z$ component $B^{\text{OH}}_{z}$ ), giving rise to an effective ¹⁷¹Yb–⁵¹V register interaction. Specifically, a second-order perturbation analysis yields the following Hamiltonian:

\hat{H}_{\text{int}}=\hat{\tilde{S}}_{z}B^{\text{OH}}_{z}\sum_{i\in\text{register}}\left(a_{x}\hat{I}_{x}^{(i)}+a_{z}\hat{I}_{z}^{(i)}\right),

(1)

where $\hat{\tilde{S}}_{z}$ is the ¹⁷¹Yb qubit operator along the $z$ axis in a weakly perturbed basis, $\hat{I}_{x,z}^{(i)}$ are the nuclear spin-7/2 operators along the $x,z$ axes, and $a_{x,z}$ are the coupling coefficients (Supplementary Information). Note that $B^{\text{OH}}_{z}$ varies randomly in time as the bath changes state in a stochastic fashion, rendering this interaction Hamiltonian unreliable for register quantum state manipulation. To this end, we develop a protocol to generate a deterministic ¹⁷¹Yb–⁵¹V interaction via Hamiltonian engineering, which will be elaborated later.

An additional challenge is presented by the spectral indistinguishability of the register spins, necessitating storage in collective states. As originally proposed for quantum dots Taylor2003 , single spin excitations of a polarised nuclear spin ensemble can be used for quantum information storage. These states are often termed spin waves or nuclear magnons and are generated by spin-preserving exchange dynamics. Specifically, preparing these collective nuclear spin states relies firstly on initialising the thermal register ensemble into a pure state, $\ket{0_{v}}=\ket{\downarrow\downarrow\downarrow\downarrow}$ , where $\{\ket{\uparrow},\ket{\downarrow}\}=\{\ket{\pm 5/2},\ket{\pm 7/2}\}$ is a two-level sub-manifold of the nuclear spin-7/2 ⁵¹V ion (Fig. 1c,d). Next, with access to exchange dynamics and ¹⁷¹Yb initialised in $\ket{1_{g}}$ , we can transfer a single excitation from the ¹⁷¹Yb to the register. We note that the excitation is delocalised equally across the four register spins due to coupling homogeneity as determined by the lattice geometry, thus naturally realising the entangled four-body W-state $\ket{W_{v}}$ Weimer2013 given by

\displaystyle\ket{W_{v}}=\frac{\ket{\uparrow\downarrow\downarrow\downarrow}+\ket{\downarrow\uparrow\downarrow\downarrow}+\ket{\downarrow\downarrow\uparrow\downarrow}+\ket{\downarrow\downarrow\downarrow\uparrow}}{2}

(2)

(Fig. 1c). If the ¹⁷¹Yb qubit is initialised into $\ket{0_{g}}$ there are no spin excitations in the system and the ⁵¹V register remains in $\ket{0_{v}}$ . Crucially, these dynamics realise a quantum swap gate between a target state prepared by the ¹⁷¹Yb qubit, $\ket{\psi}=\alpha\ket{0_{g}}+\beta\ket{1_{g}}$ , and the $\ket{0_{v}}$ state of the ⁵¹V register, leading to

\left(\alpha\ket{0_{g}}+\beta\ket{1_{g}}\right)\ket{0_{v}}\rightarrow\ket{0_{g}}\left(\alpha\ket{0_{v}}+\beta\ket{W_{v}}\right).

(3)

After waiting for a certain period of time, the stored quantum state can be retrieved from the ⁵¹V register by applying a second swap gate (Fig. 1e). Note that the spin-wave like state $\ket{W_{v}}$ of the nuclear ensemble is being utilized as a constituent of the quantum memory basis.

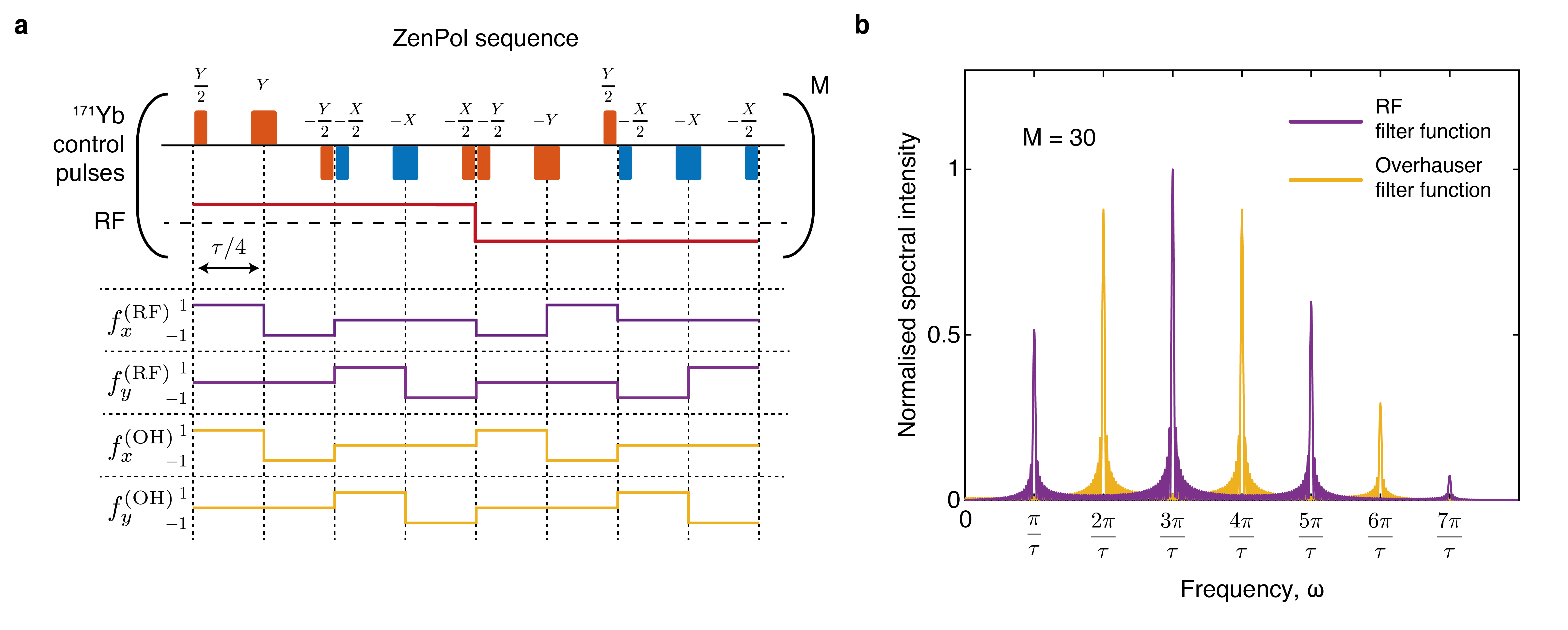
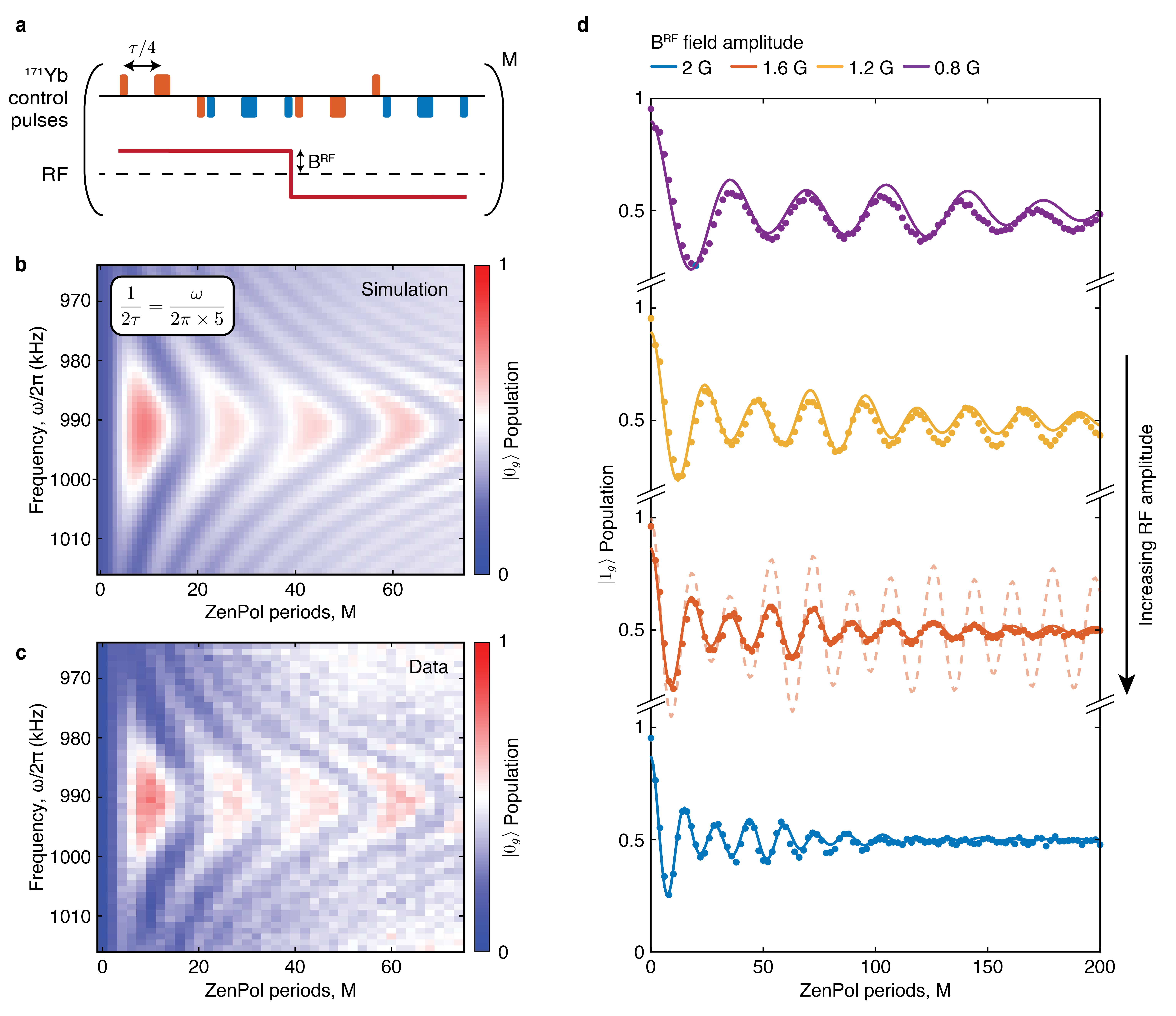
To realise this storage protocol we require ¹⁷¹Yb–⁵¹V spin-exchange interactions that are independent from the random, bath-induced dipole moment (equation (1)). We note that established pulse-based methods used to generate such interactions, e.g. Hartmann Hahn Hartmann1962 and PulsePol Schwartz2018 , do not suit our requirements as they are susceptible to random noise from the bath (Extended Data Fig. 3 and Supplementary Information). To this end, we employ a framework for robust dynamic Hamiltonian engineering Choi2019 to design a new sequence tailored for qubits with no intrinsic magnetic moment (subsequently referred to as ZenPol for ‘zero first-order Zeeman nuclear-spin polarisation’). ZenPol comprises equidistant $\pi/2$ and $\pi$ pulses combined with a synchronous, $z$ -directed, square-wave RF magnetic field with tuneable amplitude, $B^{\text{RF}}$ , and period $2\tau$ (Fig. 2a). The sequence is repeated $M$ times leading to a total interrogation duration of $t_{M}=2\tau M$ . The RF field induces an alternating ¹⁷¹Yb magnetic dipole moment, thereby generating a similar ¹⁷¹Yb–⁵¹V interaction as $B^{\text{OH}}_{z}$ in equation (1) but in a controlled manner. The sequence is synchronised with the ⁵¹V precession at one of the nuclear spin transition frequencies, $\omega_{j}$ , by satisfying

\frac{1}{2\tau}=\frac{\omega_{j}}{2\pi k},

(4)

with $k$ an odd integer (Extended Data Fig. 4). At this resonance condition the leading-order dynamics are understood by considering the temporal interference between time-varying ¹⁷¹Yb spin operators and ⁵¹V precession in the interaction picture (Methods). The ZenPol sequence is designed such that RF-induced spin-preserving dynamics interfere constructively, while all other dynamics, including the bath-induced incoherent interactions, undergo destructive interference. As a result, the ¹⁷¹Yb–⁵¹V interaction is governed by the following time-averaged effective Hamiltonian

\hat{H}_{\text{avg}}=b_{(k,\omega_{j})}B^{\text{RF}}\sum_{i\in\text{register}}\left(\hat{\tilde{S}}_{+}\hat{\tilde{I}}^{(i)}_{-}+\hat{\tilde{S}}_{-}\hat{\tilde{I}}^{(i)}_{+}\right),

(5)

where $b_{(k,\omega_{j})}$ is a $k$ -dependent prefactor for the $\omega_{j}$ transition, $\hat{\tilde{I}}_{+}=\ket{\uparrow}\bra{\downarrow},\hat{\tilde{I}}_{-}=\ket{\downarrow}\bra{\uparrow}$ are the raising and lowering operators in an effective nuclear two-level manifold and $\hat{\tilde{S}}_{\pm}$ are similarly defined for the ¹⁷¹Yb qubit (Methods). We note that while the nuclear spin can stochastically occupy either the $\{\ket{+m_{I}}\}$ or $\{\ket{-m_{I}}\}$ manifold of states, our protocol is insensitive to this sign. We emphasize that the ZenPol sequence operates at zero magnetic field where a long ¹⁷¹Yb coherence time can be maintained; it is insensitive to the presence of random noise from the bath; and is also robust to experimental imperfections, e.g. pulse rotation errors (Methods).

We use the ZenPol sequence to perform spectroscopy of the ¹⁷¹Yb nuclear spin environment. Figure 2b shows a ZenPol spectrum obtained by initialising the ¹⁷¹Yb into $\ket{0_{g}}$ , applying an $M=30$ period ZenPol sequence with variable inter-pulse spacing ( $\tau/4$ ) and reading out the ¹⁷¹Yb population. As a result of the engineered exchange interaction, we find that the $\ket{0_{g}}$ population decreases significantly at expected $\tau$ values corresponding to the odd- $k$ ⁵¹V resonances (red line, Fig. 2b). Even- $k$ resonances are also observed even in the absence of the RF field, which are attributed to the incoherent interaction dominated by the random nuclear Overhauser field (blue line, Fig. 2b).

In particular, we note that all the odd- $k$ resonances are split near each isolated ⁵¹V transition (dotted boxes, Fig. 2b). For example, resonance frequencies of $\{$ 660 kHz, 685 kHz $\}$ and $\{$ 991 kHz, 1028 kHz $\}$ are identified around the $\omega_{b}~{}(k=3)$ and $\omega_{c}~{}(k=5)$ transitions, respectively. In both cases, the higher-frequency resonance agrees well with literature values extracted from NMR on YVO₄ crystals (685 kHz, 1027 kHz) Bleaney1982 . We therefore postulate the presence of two nuclear spin ensembles: a distant large ensemble with unperturbed frequency (constituents of the bath) and a local small ensemble with a frequency shift due to crystalline strain in the vicinity of the ¹⁷¹Yb ion (the register).

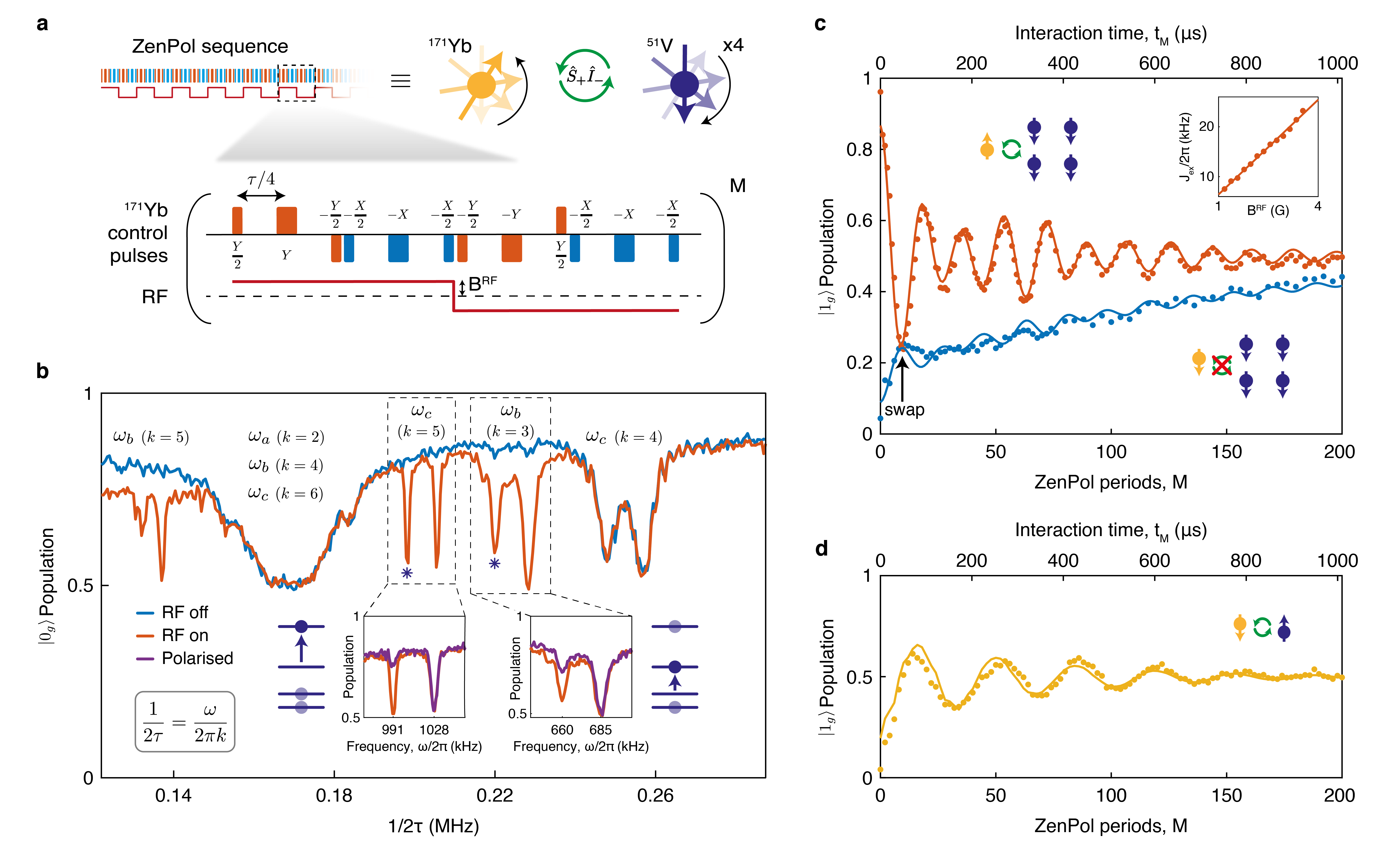
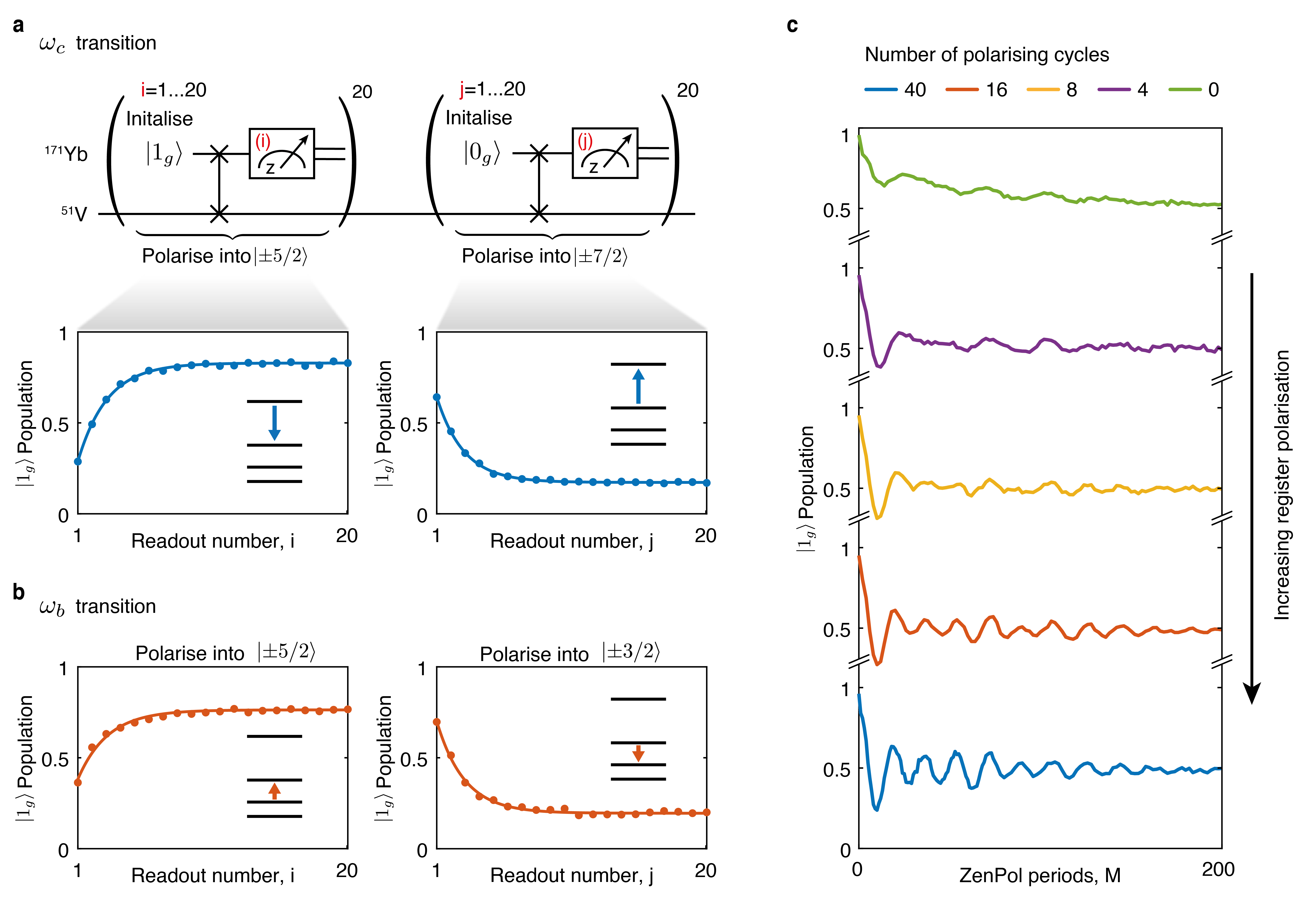
Polarisation of the entire nuclear spin register relies on repeated application of the ZenPol sequence, resonant with a targeted transition, interleaved with reinitialisation of the ¹⁷¹Yb qubit leading to unidirectional transfer of ⁵¹V population (Extended Data Fig. 1c). Since the spin-7/2 ⁵¹V ions have four doubly-degenerate energy levels, we achieve high fidelity initialisation by independently polarising different transitions with different values of $\tau$ . For example, to prepare the register spins in $\ket{\pm 7/2}=\ket{\downarrow}$ , we repeatedly apply a pair of ZenPol sequences which first polarise into $\ket{\pm 5/2}$ using the $\omega_{b}$ transition, and then subsequently into $\ket{\pm 7/2}$ using the $\omega_{c}$ transition (Extended Data Fig. 5). We confirm that both $\omega_{b}$ and $\omega_{c}$ transitions of the ⁵¹V register are successfully polarised as indicated by the near-complete disappearance of the initial resonances (insets, Fig. 2b). Note that the resonances at 685 kHz and 1028 kHz are unaffected, corroborating our speculation on the existence of two distinct ⁵¹V ensembles discussed above. The $\omega_{a}$ transition is not directly addressed by the ZenPol sequence due to spectral overlap with other resonances, however, this does not limit our polarisation fidelity, estimated to be $\approx 84\%$ , as discussed in Supplementary Information.

After initialising all four register ⁵¹V spins into a polarized state $\ket{0_{v}}=\ket{\downarrow\downarrow\downarrow\downarrow}$ , the ZenPol sequence can also induce coherent oscillations of a single spin excitation between the ¹⁷¹Yb ion and the polarised ⁵¹V ensemble. Figure 2c shows the ¹⁷¹Yb population as a function of sequence period, $M$ , when the single-spin exchange is targeted at the $\omega_{c}$ transition. With ¹⁷¹Yb initialised in $\ket{1_{g}}$ , the quantum state evolves according to:

\ket{\psi(t_{M})}=\ket{1_{g}}\ket{0_{v}}\cos(J_{\text{ex}}t_{M}/2)\\ -i\ket{0_{g}}\ket{W_{v}}\sin(J_{\text{ex}}t_{M}/2)

(6)

with spin-exchange rate $J_{\text{ex}}=4b_{(5,\omega_{c})}B^{\text{RF}}$ (red, Fig. 2c). Note that when $J_{\text{ex}}t_{M}=\pi$ , the sequence realises a swap gate (black arrow, Fig. 2c), whereby a single-spin excitation is completely transferred to the register, i.e., $\ket{1_{g}}\ket{0_{v}}\rightarrow\ket{0_{g}}\ket{W_{v}}$ . Furthermore, we emphasize that $J_{\text{ex}}$ can be accurately controlled by varying $B^{\text{RF}}$ , allowing for fidelity optimisation of the swap gate (inset, Fig. 2c). By contrast, with ¹⁷¹Yb initialised in $\ket{0_{g}}$ , exchange interactions are forbidden and thus oscillations are suppressed (blue, Fig. 2c).

We note that the spin-exchange rate is collectively enhanced by a factor of $\sqrt{N}$ , where $N$ is the number of indistinguishable spins forming the register. We verify this by controlling the number of spins in the $\omega_{c}$ transition manifold and measuring the effect on $J_{\text{ex}}$ . This is implemented by first emptying the $\omega_{c}$ manifold via the application of downward-polarising ZenPol sequences, thereby pumping all four spins to $\ket{\pm 3/2}$ and $\ket{\pm 1/2}$ . Subsequently, a single excitation is performed on the $\omega_{b}$ transition to flip one spin from $\ket{\pm 3/2}$ to $\ket{\uparrow}(=\ket{\pm 5/2})$ , leading to $N=1$ spins in the $\omega_{c}$ manifold (Supplementary Information). Applying a ZenPol sequence resonant with the $\omega_{c}$ transition, we find that the resulting exchange frequency is reduced by a factor of $\approx\sqrt{4}$ (Fig. 2d); according to the YVO₄ lattice structure, the register likely consists of the second-nearest shell of four equidistant ⁵¹V ions (Supplementary Information). This assumption is supported by close agreement between experiment and numerical simulation in all cases (Extended Data Fig. 6).

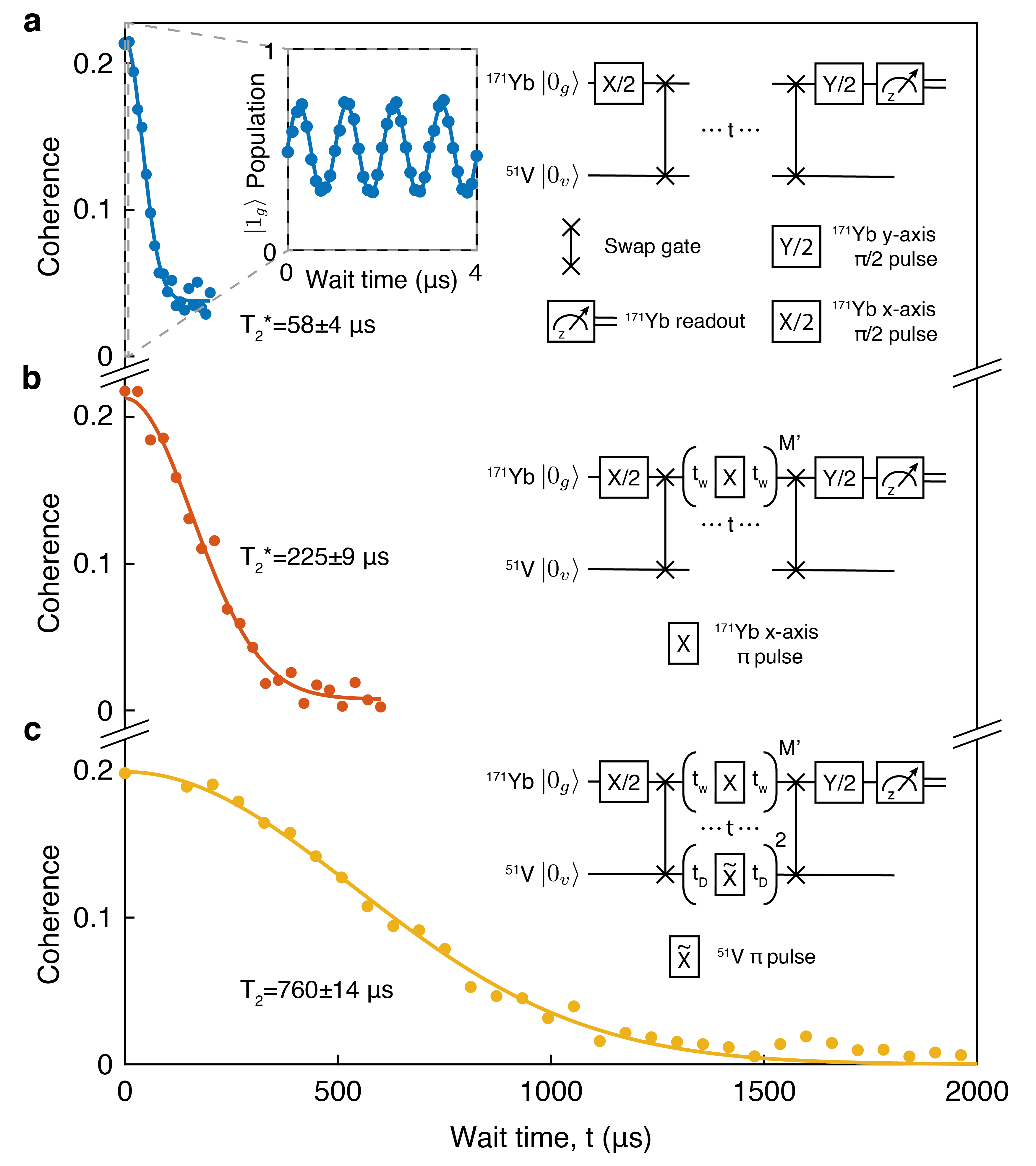
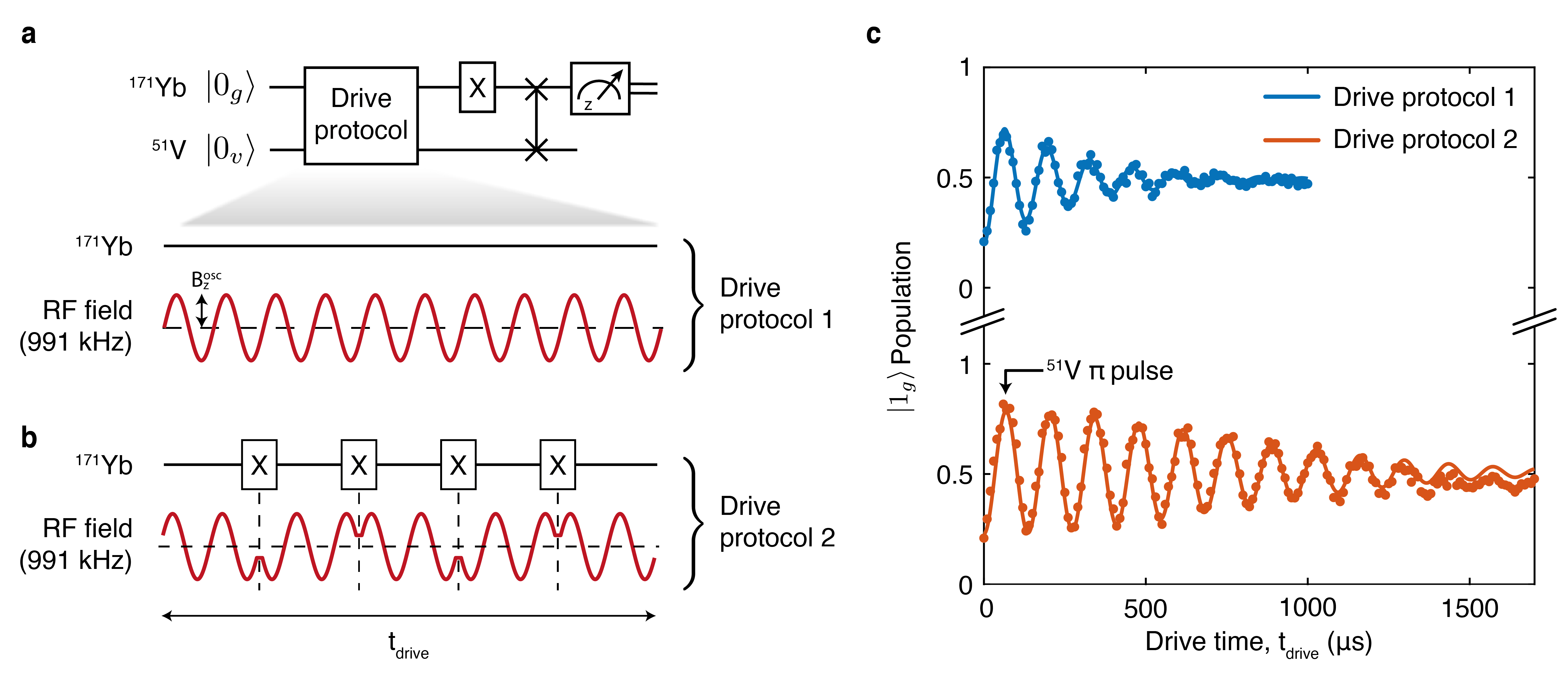
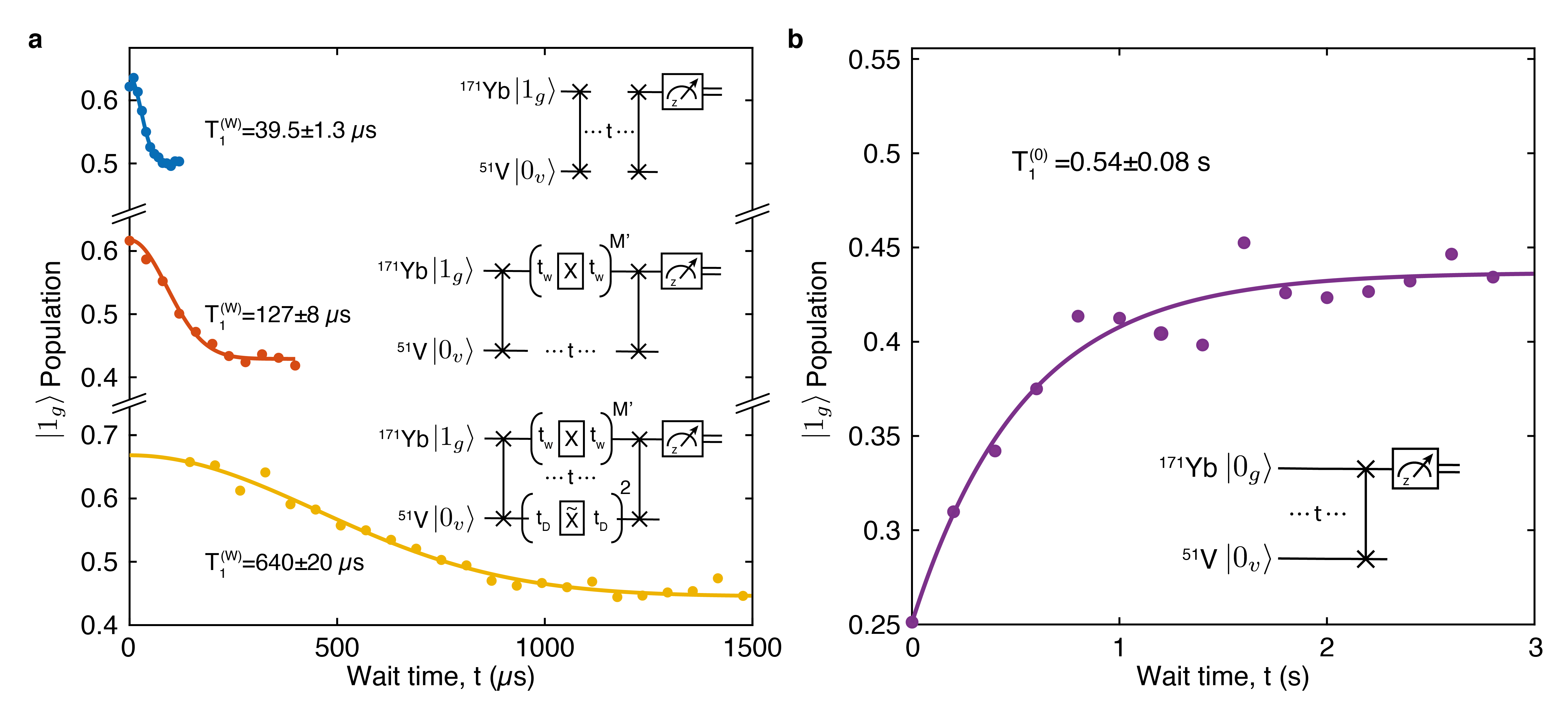
To evaluate the performance of the ⁵¹V register as a quantum memory, we characterize its information storage times under various conditions. Specifically, we first transfer a superposition state from the ¹⁷¹Yb qubit, $\frac{1}{\sqrt{2}}\left(\ket{0_{g}}+i\ket{1_{g}}\right)$ , to the ⁵¹V register via the ZenPol-based swap gate. Subsequently, the transferred state $\frac{1}{\sqrt{2}}\left(\ket{0_{v}}+\ket{W_{v}}\right)$ is stored for a variable wait time, $t$ , before being swapped back to the ¹⁷¹Yb and measured along the $x$ -axis, thereby probing the coherence of the final state. As shown in Fig. 3a, we observe a sinusoidal oscillation of the ¹⁷¹Yb population, modulated by a Gaussian coherence decay, whose contrast vanishes with a $1/e$ time of $T_{2}^{*}=58\pm 4~{}\mu$ s. This oscillation has a frequency of $\omega_{c}/2\pi=991~{}$ kHz, originating from relative phase accumulation between $\ket{0_{v}}$ and $\ket{W_{v}}$ during the wait time. The coherence time of the ⁵¹V register is predominantly limited by local magnetic field noise from two sources: a fluctuating ¹⁷¹Yb dipole moment (¹⁷¹Yb Knight field) and the nuclear Overhauser field (Supplementary Information). As shown in Fig. 3b, the noise created by ¹⁷¹Yb can be effectively decoupled from the register by periodically flipping the ¹⁷¹Yb magnetic dipole orientation via a series of $\pi$ pulses. Similar to the motional narrowing effect Bauch2018 , the neutralization of the dipole moment arrests undesired phase diffusion of the register, leading to an increased $1/e$ coherence time of $T_{2}^{*}=225\pm 9~{}\mu$ s. We further extend the coherence time by performing dynamical decoupling on the ⁵¹V register to mitigate the decoherence effect of the nuclear spin bath. This relies on applying ⁵¹V $\pi$ pulses resonant with the $\omega_{c}$ transition whilst leaving the bath unperturbed (Extended Data Fig. 7 and Methods). In Fig. 3c, we apply two ⁵¹V $\pi$ pulses with variable inter-pulse delay, combined with periodic $\pi$ pulses applied to the ¹⁷¹Yb qubit, significantly extending the $1/e$ coherence time to $T_{2}=760\pm 14~{}\mu$ s.

We also characterise the population relaxation times of the $\ket{0_{v}}$ and $\ket{W_{v}}$ states with measured lifetimes of $T_{1}^{(0)}=0.54\pm 0.08$ s and $T_{1}^{(W)}=39.5\pm 1.3~{}\mu$ s, respectively. Due to the entangled nature of the $\ket{W_{v}}$ state, $T_{1}^{(W)}$ is limited by dephasing and is extended to $127\pm 8~{}\mu$ s and $640\pm 20~{}\mu$ s by applying the same decoupling sequences as in Fig. 3b,c respectively (Extended Data Fig. 8). We note that these dephasing processes can be sensitive to the the stochastic occupation of the $\ket{+m_{I}}$ and $\ket{-m_{I}}$ states, depending on the degree of noise correlation between the four register spins (Supplementary Information).

Finally, we benchmark our multi-spin register by characterizing fidelities of ¹⁷¹Yb–⁵¹V Bell state generation and detection, serving as a vital component of the quantum repeater protocol Briegel1998 . In particular, the maximally entangled Bell state $\ket{\Psi^{+}}=\frac{1}{\sqrt{2}}\left(\ket{1_{g}}\ket{0_{v}}-i\ket{0_{g}}\ket{W_{v}}\right)$ can be prepared by initialising the system in $\ket{1_{g}}\ket{0_{v}}$ and applying a $\sqrt{\text{swap}}$ gate based on the ZenPol sequence satisfying $J_{\text{ex}}t_{M}=\pi/2$ (equation (6)). The Bell state coherence is evaluated by monitoring the contrast of oscillation between a given Bell state and its parity conjugate Levine2018 . In our system, the free evolution of $\ket{\Psi^{+}}$ gives rise to a parity oscillation at frequency $\omega_{c}$ with $\ket{\Psi^{-}}=\frac{1}{\sqrt{2}}\left(\ket{1_{g}}\ket{0_{v}}+i\ket{0_{g}}\ket{W_{v}}\right)$ (Supplementary Information). We read out this oscillation by applying a second $\sqrt{\text{swap}}$ gate to the system, encoding the parity into ¹⁷¹Yb population. Figure 4a shows the measured parity oscillations decaying with a $1/e$ time of $T^{*}_{\text{2,Bell}}=8.5\pm 0.5~{}\mu$ s, limited by the $T_{2}^{*}$ dephasing time of the ¹⁷¹Yb qubit Kindem2020 . To improve the coherence, we apply an XY-8 decoupling sequence Gullion1990 to the ¹⁷¹Yb, leading to an enhanced value of $T^{*}_{\text{2,Bell}}=239\pm 6~{}\mu$ s (Fig. 4b); this timescale is similar to that in Fig. 3b, indicating that the Bell state coherence is likely limited by the $T_{2}^{*}$ dephasing time of the ⁵¹V register.

In order to estimate the Bell state preparation fidelity, defined as $\mathcal{F}=\langle\Psi^{+}|\rho|\Psi^{+}\rangle$ , we perform a sequential tomography protocol Kalb2017 to reconstruct the system density matrix $\rho$ in the effective manifold spanned by four states { $\ket{0_{g}0_{v}},\ket{0_{g}W_{v}},\ket{1_{g}0_{v}},\ket{1_{g}W_{v}}$ } (Extended Data Fig. 9 and Methods). Taking into account errors in state readout, we obtain a corrected Bell state fidelity of 0.76 $\pm$ 0.01, as summarized in Fig. 4c (the uncorrected fidelity is measured to be 0.61 $\pm$ 0.01). We speculate that this is limited by a combination of incomplete register initialisation, imperfect Hamiltonian engineering and detrimental dephasing of the register during Bell state generation. See Methods and Supplementary Information for detailed discussions including error analysis.

In this work we have demonstrated a noise-robust control protocol to coherently manipulate the local ⁵¹V nuclear ensemble surrounding a single optically-addressed ¹⁷¹Yb spin, enabling the polarisation of the high spin ( $I=7/2$ ) nuclear register, the creation of collective spin-wave excitations, and the preparation of maximally entangled Bell states. Based on these capabilities, we show that the local nuclear spins realise an ensemble-based quantum memory exhibiting long coherence times. Crucially, this memory is deterministic and reproducible in that every ¹⁷¹Yb ion doped into a YVO₄ crystal accesses a near-identical nuclear register in its local environment (Extended Data Fig. 10). We envisage that this resource will enable the implementation of multi-node quantum network architectures using rare-earth ions with both enhanced connectivity and large-scale entanglement Briegel1998 . Furthermore, realising coherent quantum systems using dense lattice nuclear spins will open the door to exploration of new materials for quantum information applications Wolfowicz2021 . Finally, these multi-level nuclear spin ensembles offer an attractive, highly controllable platform to investigate the many-body dynamics of a much larger Hilbert space, paving the way for application of solid-state, noisy intermediate-scale quantum (NISQ) devices in the context of quantum simulation Gangloff2020 ; Randall2021 .

References

(1) Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photonics 12, 516–527 (2018).
(2) Chatterjee, A. et al. Semiconductor qubits in practice. Nat. Rev. Phys. 3, 157–177 (2021).
(3) Briegel, H. J., Dür, W., Cirac, J. I. & Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 81, 5932–5935 (1998).
(4) Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
(5) Bhaskar, M. K. et al. Experimental demonstration of memory-enhanced quantum communication. Nature 580, 60–64 (2020).
(6) Pompili, M. et al. Realization of a multi-node quantum network of remote solid-state qubits. Science 372, 259–264 (2021).
(7) Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
(8) Taminiau, T. H., Cramer, J., Van Der Sar, T., Dobrovitski, V. V. & Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 9, 171–176 (2014).
(9) Zhong, M., Ahlefeldt, R. L. & Sellars, M. J. Quantum information processing using frozen core Y3+ spins in Eu3+:Y2SiO5. New J. Phys. 21 (2019).
(10) Bradley, C. E. et al. A Ten-Qubit Solid-State Spin Register with Quantum Memory up to One Minute. Phys. Rev. X. 9, 31045 (2019).
(11) Kinos, A. et al. Roadmap for Rare-earth Quantum Computing . Preprint at https://arxiv.org/abs/2103.15743 (2021).
(12) Randall, J. et al. Observation of a many-body-localized discrete time crystal with a programmable spin-based quantum simulator. Preprint at http://arxiv.org/abs/2107.00736 (2021).
(13) Wolfowicz, G. et al. Quantum guidelines for solid-state spin defects. Nature Reviews Materials (2021).
(14) Taylor, J. M., Marcus, C. M. & Lukin, M. D. Long-Lived Memory for Mesoscopic Quantum Bits. Phys. Rev. Lett. 90, 4 (2003).
(15) Kindem, J. M. et al. Control and single-shot readout of an ion embedded in a nanophotonic cavity. Nature 580, 201–204 (2020).
(16) Gurudev Dutt, M. V. et al. Quantum Register Based on Individual Electronic and Nuclear Spin Qubits in Diamond. Science 316, 1312–1317 (2007).
(17) Kolkowitz, S., Unterreithmeier, Q. P., Bennett, S. D. & Lukin, M. D. Sensing distant nuclear spins with a single electron spin. Phys. Rev. Lett. 109, 1–5 (2012).
(18) Taminiau, T. H. et al. Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602 (2012).
(19) Zhao, N. et al. Sensing single remote nuclear spins. Nat. Nanotechnol. 7, 657–662 (2012).
(20) Metsch, M. H. et al. Initialization and Readout of Nuclear Spins via negatively charged Silicon-Vacancy Center in Diamond. Phys. Rev. Lett. 122, 190503 (2019).
(21) Bourassa, A. et al. Entanglement and control of single nuclear spins in isotopically engineered silicon carbide. Nat. Mater. 19, 1319–1325 (2020).
(22) Hensen, B. et al. A silicon quantum-dot-coupled nuclear spin qubit. Nat. Nanotechnol. 15, 13–17 (2020).
(23) Kornher, T. et al. Sensing Individual Nuclear Spins with a Single Rare-Earth Electron Spin. Phys. Rev. Lett. 124, 170402 (2020).
(24) Wolfowicz, G. et al. 29Si nuclear spins as a resource for donor spin qubits in silicon. New J. Phys. 18 (2016).
(25) Utikal, T. et al. Spectroscopic detection and state preparation of a single praseodymium ion in a crystal. Nat. Commun. 5, 1–8 (2014).
(26) Siyushev, P. et al. Coherent properties of single rare-earth spin qubits. Nat. Commun. 5, 1–6 (2014).
(27) Zhong, T. et al. Optically Addressing Single Rare-Earth Ions in a Nanophotonic Cavity. Phys. Rev. Lett. 121, 183603 (2018).
(28) Chen, S., Raha, M., Phenicie, C. M., Ourari, S. & Thompson, J. D. Parallel single-shot measurement and coherent control of solid-state spins below the diffraction limit. Science 370, 592–595 (2020).
(29) Gangloff, D. A. et al. Quantum interface of an electron and a nuclear ensemble. Science 364, 62–66 (2019).
(30) Gangloff, D. A. et al. Revealing beyond-mean-field correlations in a nuclear ensemble via a proxy qubit. Preprint at https://arxiv.org/abs/2012.11279 (2020).
(31) Kindem, J. M. et al. Characterization of Yb 3+ 171:YVO4 for photonic quantum technologies. Phys. Rev. B 98, 1–10 (2018).
(32) Bleaney, B., Gregg, J. F., De Oliveira, A. C. & Wells, M. R. Nuclear magnetic resonance of 51V (I=7/2) in lanthanide vanadates: II. The nuclear electric quadrupole interaction. J. Phys. C: Solid State Phys. 15, 5293–5303 (1982).
(33) Weimer, H., Yao, N. Y. & Lukin, M. D. Collectively enhanced interactions in solid-state spin qubits. Phys. Rev. Lett. 110, 1–5 (2013).
(34) Hartmann, S. R. & Hahn, E. L. Nuclear double resonance in the rotating frame. Phys. Rev. 128, 2042–2053 (1962).
(35) Schwartz, I. et al. Robust optical polarization of nuclear spin baths using Hamiltonian engineering of nitrogen-vacancy center quantum dynamics. Sci. Adv. 4, 1–8 (2018).
(36) Choi, J. et al. Robust Dynamic Hamiltonian Engineering of Many-Body Spin Systems. Phys. Rev. X. 10, 31002 (2019).
(37) Bauch, E. et al. Ultralong Dephasing Times in Solid-State Spin Ensembles via Quantum Control. Phys. Rev. X. 8, 031025 (2018).
(38) Gullion, T., Baker, D. B. & Conradi, M. S. New, compensated Carr-Purcell sequences. J. Magn. Reson. 89, 479–484 (1990).
(39) Kalb, N. et al. Entanglement distillation between solid-state quantum network nodes. Science 356, 928–932 (2017).
(40) Levine, H. et al. High-Fidelity Control and Entanglement of Rydberg-Atom Qubits. Phys. Rev. Lett. 121, 123603 (2018).
(41) Zhong, T., Rochman, J., Kindem, J. M., Miyazono, E. & Faraon, A. High quality factor nanophotonic resonators in bulk rare-earth doped crystals. Opt. Express 24, 536 (2016).
(42) Zhong, T. et al. Nanophotonic rare-earth quantum memory with optically controlled retrieval. Science 1395, 1392–1395 (2017).
(43) Drever, R. W. P. et al. Laser Phase and Frequency Stabilization Using an Optical Resonator. Appl. Phys. B 31, 97–105 (1983).
(44) Slichter, C. P. Principles of Magnetic Resonance (Springer-Verlag, New York, 1992), 3rd edn.
(45) Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 1–39 (2017).
(46) Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
(47) Nguyen, C. T. et al. An integrated nanophotonic quantum register based on silicon-vacancy spins in diamond. Phys. Rev. B 100, 1–19 (2019).
(48) Bleaney, B., Gregg, J. F., De Oliveira, A. C. & Wells, M. R. Nuclear magnetic resonance of 51V (I=7/2) in lanthanide vanadates: I. The paramagnetic shifts. J. Phys. C: Solid State Phys. 15, 5293–5303 (1982).
(49) Cohen-Tannoudji, C., Dupont-Roc, J. & Grynberg, G. Atom-Photon Interactions (Wiley-VCH, Weinheim, 2004).
(50) Bermudez, A., Jelezko, F., Plenio, M. B. & Retzker, A. Electron-mediated nuclear-spin interactions between distant nitrogen-vacancy centers. Phys. Rev. Lett. 107, 3–7 (2011).
(51) Knill, E. et al. Randomized benchmarking of quantum gates. Physical Review A - Atomic, Molecular, and Optical Physics 77, 1–7 (2008).
(52) Scheuer, J. et al. Robust techniques for polarization and detection of nuclear spin ensembles. Phys. Rev. B 96, 1–10 (2017).
(53) Urbaszek, B. et al. Nuclear spin physics in quantum dots: An optical investigation. Rev. Mod. Phys. 85, 79–133 (2013).

Extended Data

Methods

Experimental Setup

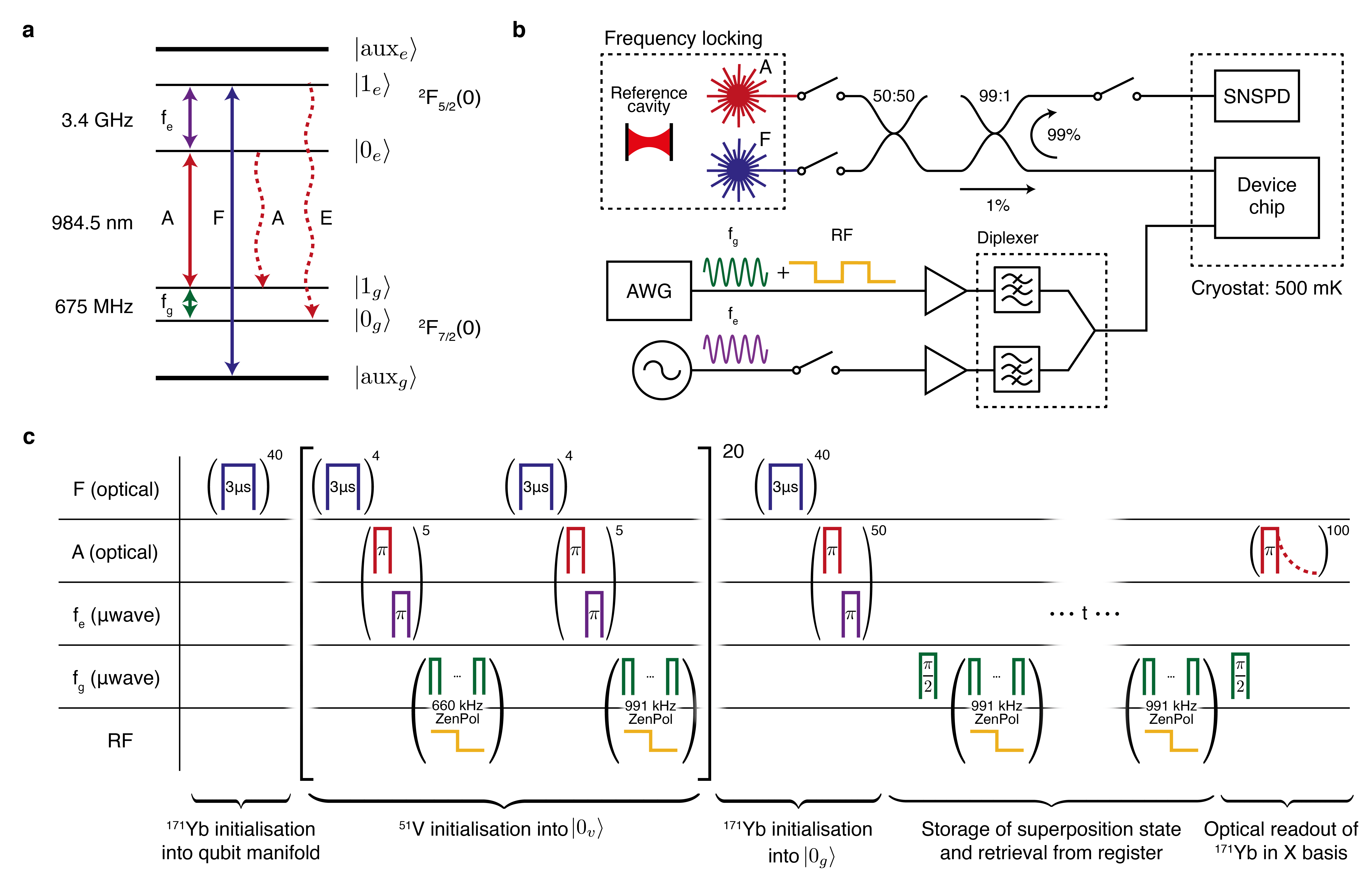
The YVO₄ crystal used in this project was cut and polished from an undoped boule (Gamdan Optics) with a residual total ¹⁷¹Yb concentration of 140 ppb. Nanophotonic cavities were fabricated from this material using focused ion beam milling, see Zhong2016 ; Zhong2017a for more detail on this process. The cavity used in this work has a Q-factor of $\approx 10,000$ leading to Purcell enhancement and consequent reduction of the ¹⁷¹Yb excited state lifetime from 267 $\mu$ s to 2.3 $\mu$ s as described and measured in Kindem2020 and $>99\%$ of ion emission coupling to the cavity mode. The reduced optical lifetime enables detection of single ¹⁷¹Yb ions. The cavity is undercoupled with $\kappa_{\text{in}}/\kappa\approx 0.14$ leading to $14\%$ of emitted light entering the waveguide mode. Waveguide–free-space coupling is achieved via angled couplers with an efficiency of $\approx 25\%$ and the end-to-end system efficiency (probability of detecting an emitted photon) is $\approx 1\%$ .

The device sits on the still-plate of a ³He cryostat (Bluefors LD-He250) with base temperature of 460 mK. Optical signals are fed into the fridge through optical fibre and focused onto the device with an aspheric lens doublet mounted on a stack of $x$ - $y$ - $z$ piezo nano-positioners (Attocube). The device is tuned on-resonance with the ¹⁷¹Yb optical transitions via nitrogen condensation. Residual magnetic fields are cancelled along the crystal $c\equiv z$ axis with a set of home-built superconducting magnet coils.

The various optical transitions of a single ¹⁷¹Yb qubit are employed for state readout and initialisation (Extended Data Fig. 1a). Optical addressing of the A transition for readout is established with a continuous-wave (CW) titanium sapphire (Ti:Sapph) laser (M² Solstis) which is frequency-stabilised to a high-finesse reference cavity (Stable Laser Systems) using Pound-Drever-Hall locking Drever1983 . The laser double-passes through two free-space acousto-optic-modulator (AOM) setups leading to single-photon level extinction of the input beam, and pulse generation with $\approx 10~{}$ ns rise times. A second CW external cavity diode laser (Toptica DL-Pro) is used to address the F transition during initialisation. The laser passes through an identical AOM setup and is frequency stabilised via offset-frequency locking to the Ti:Sapph.

The light output from the cavity is separated from the input with a 99:1 fibre beamsplitter, and passed through a single AOM which provides time-resolved gating of the light to prevent reflected laser pulses from saturating the detector. The light is then sent to a tungsten-silicide superconducting nanowire single photon detector (SNSPD) (Photonspot) which also sits on the still-plate of the cryostat. Photon detection events are subsequently time-tagged and histogrammed (Swabian Timetagger 20).

Microwave pulses to control the ground-state qubit transition (675 MHz) and square-wave RF to generate the ¹⁷¹Yb–⁵¹V interaction (100–300 kHz) are directly synthesised with an arbitrary waveform generator (Tektronix 5204AWG) and amplified (Amplifier Research 10U1000). A second microwave path is used for the excited state microwave control (3.4 GHz) necessary for qubit initialisation. The control pulses are generated by switching the output of a signal generator (SRS SG386) and amplifying (Minicircuits ZHL-16W-43-S+). The two microwave signal paths are combined with a diplexer (Marki DPXN2) and sent into the fridge to the device. A gold coplanar waveguide fabricated on the YVO₄ surface enables microwave driving of the ions.

See Extended Data Fig. 1 for a schematic of the complete experimental setup.

¹⁷¹Yb Initialisation, Readout and Experiment Sequence

At the 500 mK experiment operating temperature and at zero magnetic field, the equilibrium ¹⁷¹Yb population is distributed between the $\ket{\text{aux}_{g}}$ , $\ket{0_{g}}$ and $\ket{1_{g}}$ states (Extended Data Fig. 1a). All experiments start by initialising the single ¹⁷¹Yb ion into $\ket{0_{g}}$ via a two-stage protocol Kindem2020 . Firstly the $\ket{\text{aux}_{g}}$ state is emptied with a series of $3~{}\mu$ s pulses applied to the optical F transition each followed by a $3~{}\mu$ s wait period. When the ¹⁷¹Yb ion is successfully excited from $\ket{\text{aux}_{g}}$ to $\ket{1_{e}}$ , the population in $\ket{1_{e}}$ will preferentially decay to $\ket{0_{g}}$ during the wait time via the cavity-enhanced E transition. Subsequently, the $\ket{1_{g}}$ state is also emptied by applying an optical $\pi$ pulse to the A transition followed by a microwave $\pi$ pulse to the $f_{e}$ transition in rapid succession, which similarly leads to excitation from $\ket{1_{g}}$ to $\ket{1_{e}}$ and decay into $\ket{0_{g}}$ . This process is repeated several times for improved fidelity.

Readout of the ¹⁷¹Yb $\ket{1_{g}}$ state is performed by applying a series of 100 $\pi$ pulses to the A transition, each of which is followed by a $10~{}\mu s$ photon detection window. This process is enabled by the cyclic nature of the A transition. To read out the $\ket{0_{g}}$ population we apply an additional $\pi$ pulse to swap the $\ket{0_{g}}\leftrightarrow\ket{1_{g}}$ populations before performing the same optical readout procedure.

Extended Data Fig. 1c shows an exemplary pulse sequence used to store and retrieve a superposition state from the register consisting of four ⁵¹V lattice ions. The sequence starts with initialisation of the ¹⁷¹Yb qubit into $\ket{0_{g}}$ and the spin-7/2 ⁵¹V register into $\ket{0_{v}}=\ket{\pm 7/2}^{\otimes 4}$ . A series of ZenPol polarisation operations are interleaved with ¹⁷¹Yb re-initialisation sequences and alternate between $\omega_{b}$ and $\omega_{c}$ transition control to sequentially polarize the ⁵¹V register towards the $\ket{\pm 7/2}$ level. After the initialization sequence, a single $\pi/2$ pulse is applied to the ¹⁷¹Yb qubit to prepare a superposition state. Subsequently, the state is transferred to the ⁵¹V register using a swap operation resonant with the $\omega_{c}$ transition as detailed in the main text. After a variable wait time, the superposition state is retrieved with a second swap gate and measured in the $x$ -basis via a $\pi/2$ pulse followed by optical readout on the A transition as detailed above.

ZenPol Sequence

We consider a system of a single ¹⁷¹Yb qubit coupled to four neighbouring nuclear spin-7/2 ⁵¹V ions. This hybrid spin system is described by the effective Hamiltonian (setting $\hbar=1$ ):

\hat{H}=\Delta(t)\hat{\tilde{S}}_{z}+\sum_{i\in\text{register}}Q(\hat{I}_{z}^{(i)})^{2}+\\ \sum_{i\in\text{register}}\hat{\tilde{S}}_{z}\left[B^{\text{OH}}_{z}+B^{\text{RF}}(t)\right]\left[a_{x}\hat{I}^{(i)}_{x}+a_{z}\hat{I}^{(i)}_{z}\right]

(7)

where $\Delta(t)=\gamma_{z}^{2}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))^{2}/2\omega_{01}$ is the effective energy shift due to both $z$ -directed nuclear Overhauser ( $B^{\text{OH}}_{z}$ ) and external RF ( $B^{\text{RF}}(t)$ ) magnetic fields, $\omega_{01}/2\pi=675$ MHz is the ¹⁷¹Yb qubit transition frequency, $\gamma_{z}/2\pi=8.5$ MHz/G is the ¹⁷¹Yb ground-state longitudinal gyromagnetic ratio, $Q/2\pi=165$ kHz is the ⁵¹V register nuclear quadrupole splitting, $\hat{\tilde{S}}_{z}$ is the ¹⁷¹Yb qubit operator along the $z$ -axis, $\hat{I}_{x,z}$ are the ⁵¹V spin-7/2 operators along the $x$ - and $z$ -axis, and $a_{x,z}$ are the effective coupling strengths between ¹⁷¹Yb and ⁵¹V along the $x$ - and $z$ -axes. See Supplementary Information for a detailed derivation of this effective Hamiltonian.

As discussed in the main text, polarisation of the ⁵¹V register and preparation of collective spin-wave states relies on induced polarisation transfer from the ¹⁷¹Yb to ⁵¹V and is achieved via periodic driving of the ¹⁷¹Yb qubit. Specifically, periodic pulsed control can dynamically engineer the original Hamiltonian (equation (7)) to realize effective spin-exchange interaction between ¹⁷¹Yb and ⁵¹V ions of the form, $\hat{\tilde{S}}_{+}\hat{I}_{-}+\hat{\tilde{S}}_{-}\hat{I}_{+}$ , in the average Hamiltonian picture Choi2019 ,Slichter1992 . One example of such a protocol is the recently developed PulsePol sequence Schwartz2018 , however, it relies on states with a constant, non-zero magnetic dipole moment and therefore cannot be used in our system since the ¹⁷¹Yb qubit has no intrinsic magnetic dipole moment. Motivated by this approach, we have developed a variant of the PulsePol sequence that accompanies a square-wave RF field synchronized with the sequence (Extended Data Fig. 4a). The base sequence has a total of 8 free-evolution intervals with equal duration ( $\tau/4$ ) defined by periodically spaced short pulses and is repeatedly applied to ¹⁷¹Yb. Following the sequence design framework presented in Ref. Choi2019 , we judiciously choose the phase and ordering of the constituent $\pi/2$ and $\pi$ pulses such that the resulting effective interaction has spin-exchange form with strength proportional to the RF magnetic field amplitude ( $B^{\text{RF}}$ ), whilst decoupling from interactions induced by the Overhauser field ( $B_{z}^{\text{OH}}$ ). We also design the sequence to cancel detuning induced by both of these fields and to retain robustness against pulse rotation errors to leading order. We term this new sequence ‘ZenPol’ for ‘zero first-order Zeeman nuclear-spin polarisation’.

To understand how the ZenPol sequence works, one can consider a toggling-frame transformation of the ¹⁷¹Yb spin operator along the quantisation axis ( $\hat{\tilde{S}}_{z,\text{tog}}(t)$ ): we keep track of how this operator is transformed after each preceding pulse. For example, the first $\pi/2$ pulse around the $y$ -axis transforms $\hat{\tilde{S}}_{z}$ into $-\hat{\tilde{S}}_{x}$ and the subsequent $\pi$ pulse around the $y$ -axis transforms $-\hat{\tilde{S}}_{x}$ into $+\hat{\tilde{S}}_{x}$ . Over one sequence period, the toggling-frame transformation generates a time-dependent Hamiltonian $\hat{H}_{\text{tog}}(t)$ that is piecewise constant for each of 8 free-evolution intervals, which can be expressed as

\hat{H}_{\text{tog}}(t)=\\ \Delta(t)\left[f_{x}^{\text{OH}}(t)\hat{\tilde{S}}_{x}+f_{y}^{\text{OH}}(t)\hat{\tilde{S}}_{y}\right]+\sum_{i\in\text{register}}Q(\hat{I}_{z}^{(i)})^{2}+\\ \sum_{i\in\text{register}}B^{\text{OH}}_{z}\left[f_{x}^{\text{OH}}(t)\hat{\tilde{S}}_{x}+f_{y}^{\text{OH}}(t)\hat{\tilde{S}}_{y}\right]\left[a_{x}\hat{I}^{(i)}_{x}+a_{z}\hat{I}^{(i)}_{z}\right]+\\ \sum_{i\in\text{register}}B^{\text{RF}}\left[f_{x}^{\text{RF}}(t)\hat{\tilde{S}}_{x}+f_{y}^{\text{RF}}(t)\hat{\tilde{S}}_{y}\right]\left[a_{x}\hat{I}^{(i)}_{x}+a_{z}\hat{I}^{(i)}_{z}\right].

(8)

Here, $f^{\text{OH}}_{x,y}(t)$ describes the time-dependent modulation of the ¹⁷¹Yb qubit operator along the $z$ axis ( $\hat{\tilde{S}}_{z,\text{tog}}(t)=f^{\text{OH}}_{x}(t)\hat{\tilde{S}}_{x}+f^{\text{OH}}_{y}(t)\hat{\tilde{S}}_{y}$ ) (Extended Data Fig. 4a). Note that $f^{\text{OH}}_{z}(t)=0$ for all intervals. Since the externally-applied square-wave RF field is constant for each half-sequence period, we can replace $B^{\text{RF}}(t)$ with the amplitude $B^{\text{RF}}$ and transfer the time dependence to $f_{x,y}^{\text{OH}}$ by applying sign flips, thus leading to redefined modulation functions $f_{x,y}^{\text{RF}}$ (Extended Data Fig. 4a).

The spin-7/2 ⁵¹V ion exhibits three distinct transitions at frequencies $\omega_{a,b,c}$ (Fig. 1b). In the following, we consider an effective spin-1/2 system for the ⁵¹V ions using the $\omega_{c}$ manifold, $\{\ket{\uparrow}=\ket{\pm 5/2}$ , $\ket{\downarrow}=\ket{\pm 7/2}\}$ , with $\hat{\tilde{I_{x}}}=\frac{1}{2}\left(\ket{\uparrow}\bra{\downarrow}+\ket{\downarrow}\bra{\uparrow}\right),\hat{\tilde{I_{y}}}=\frac{1}{2i}\left(\ket{\uparrow}\bra{\downarrow}-\ket{\downarrow}\bra{\uparrow}\right)$ and $\hat{\tilde{I_{z}}}=\frac{1}{2}\left(\ket{\uparrow}\bra{\uparrow}-\ket{\downarrow}\bra{\downarrow}\right)$ . In a rotating frame with respect to the target frequency $\omega_{c}$ , the nuclear spin operators become $\hat{\tilde{I}}_{x}\rightarrow\hat{\tilde{I}}_{x}\cos(\omega_{c}t)+\hat{\tilde{I}}_{y}\sin(\omega_{c}t)$ and $\hat{\tilde{I}}_{z}\rightarrow\hat{\tilde{I}}_{z}$ . Thus, the leading-order average Hamiltonian, $\hat{H}_{\text{avg}}=\frac{1}{2\tau}\int_{0}^{2\tau}dt\;\hat{H}_{\text{tog}}(t)$ , in the rotating frame is given by:

\hat{H}_{\text{avg}}=\sum_{i\in\text{register}}\frac{a_{x}\sqrt{7}}{2\tau}\int_{0}^{2\tau}dt\bigg{\{}\\ B^{\text{OH}}_{z}\!\left[f_{x}^{\text{OH}}(t)\hat{\tilde{S}}_{x}{+}f_{y}^{\text{OH}}(t)\hat{\tilde{S}}_{y}\right]\!\left[\hat{\tilde{I}}^{(i)}_{x}\cos(\omega_{c}t){+}\hat{\tilde{I}}^{(i)}_{y}\sin(\omega_{c}t)\right]{+}\\ B^{\text{RF}}\!\left[f_{x}^{\text{RF}}(t)\hat{\tilde{S}}_{x}{+}f_{y}^{\text{RF}}(t)\hat{\tilde{S}}_{y}\right]\!\left[\hat{\tilde{I}}^{(i)}_{x}\cos(\omega_{c}t){+}\hat{\tilde{I}}^{(i)}_{y}\sin(\omega_{c}t)\right]\bigg{\}}.

(9)

Here, various terms are excluded as they time average to zero (rotating-wave approximation). The $\sqrt{7}$ prefactor comes from mapping the original spin-7/2 operators to the effective spin-1/2 ones. Additionally, the energy shift induced by $B^{\text{OH}}_{z}$ and time-dependent $B^{\text{RF}}$ is cancelled since we are using square-wave RF. The Fourier transforms of the modulation functions $f_{x,y}(t)$ , termed the filter functions Degen2017 , directly reveal resonance frequencies at which equation (9) yields non-zero contributions (Extended Data Fig. 4b). Resonant interactions with strength proportional to the nuclear Overhauser field are achieved at sequence periods $2\tau$ which satisfy $\frac{1}{2\tau}=\frac{\omega_{c}}{2\pi\times 2},\frac{\omega_{c}}{2\pi\times 4},\frac{\omega_{c}}{2\pi\times 6},\cdots$ ; interactions proportional to the RF field occur at sequence periods satisfying $\frac{1}{2\tau}=\frac{\omega_{c}}{2\pi\times 1},\frac{\omega_{c}}{2\pi\times 3},\frac{\omega_{c}}{2\pi\times 5},\cdots$ . Critically, these two sets of resonances occur at different values of $2\tau$ , hence we can preferentially utilise the coherent, RF-induced interactions whilst decoupling from those induced by the randomised Overhauser field. This is experimentally demonstrated in Fig. 2b where the RF-induced resonances are spectrally resolved. In this measurement the linewidth of the register resonances are limited by that of the filter function. We also note that the $\omega_{a}$ transition cannot be independently addressed by the ZenPol sequence due to the multiplicity of the three ⁵¹V transitions determined by the quadratic Hamiltonian ( $\omega_{a}=\omega_{b}/2=\omega_{c}/3$ ).

We use the RF-driven resonance identified at $\frac{1}{2\tau}=\frac{\omega_{c}}{2\pi\times 5}$ by setting the free-evolution interval to $\frac{\tau}{4}=\frac{5\pi}{4\omega_{c}}$ . Under this resonance condition, the average Hamiltonian (equation (9)) is simplified to

$\displaystyle\hat{H}_{\text{avg}}$	$\displaystyle=-\sqrt{7}\left(\frac{1+\sqrt{2}}{5\pi}\right)a_{x}B^{\text{RF}}\times$
	$\displaystyle\qquad\qquad\sum_{i\in\text{register}}\left((\hat{\tilde{S}}_{x}+\hat{\tilde{S}}_{y})\hat{\tilde{I}}^{(i)}_{x}+(-\hat{\tilde{S}}_{x}+\hat{\tilde{S}}_{y})\hat{\tilde{I}}^{(i)}_{y}\right)$
	$\displaystyle=-\sqrt{7}\left(\frac{\sqrt{2}+2}{5\pi}\right)a_{x}B^{\text{RF}}\sum_{i\in\text{register}}\left(\hat{\tilde{S}}_{x}^{\prime}\hat{\tilde{I}}^{(i)}_{x}+\hat{\tilde{S}}_{y}^{\prime}\hat{\tilde{I}}^{(i)}_{y}\right)$
	$\displaystyle=b_{(5,\omega_{c})}B^{\text{RF}}\sum_{i\in\text{register}}\left(\hat{\tilde{S}}_{+}^{\prime}\hat{\tilde{I}}^{(i)}_{-}+\hat{\tilde{S}}_{-}^{\prime}\hat{\tilde{I}}^{(i)}_{+}\right).$	(10)

Here, going from the first to the second line, we change the local ¹⁷¹Yb basis by rotating 45 degrees around the $z$ -axis such that $\hat{\tilde{S}}_{x}^{\prime}=(\hat{\tilde{S}}_{x}+\hat{\tilde{S}}_{y})/\sqrt{2},\hat{\tilde{S}}_{y}^{\prime}=(-\hat{\tilde{S}}_{x}+\hat{\tilde{S}}_{y})/\sqrt{2}$ , and from the second to the third line, $\hat{\tilde{S}}_{\pm}^{\prime}=\hat{\tilde{S}}_{x}^{\prime}\pm i\hat{\tilde{S}}_{y}^{\prime}$ and $\hat{\tilde{I}}_{\pm}=\hat{\tilde{I}}_{x}\pm i\hat{\tilde{I}}_{y}$ are used. We define the coefficient $b_{(k,\omega_{j})}$ which determines the interaction strength for the $k^{\text{th}}$ resonance addressing transition $\omega_{j}$ (for example, $b_{(5,\omega_{c})}=-\sqrt{7}(\sqrt{2}+2)a_{x}/10\pi$ ). In the main text, we omit the primes on the ¹⁷¹Yb qubit operators for the sake of notational simplicity. The same analysis can be performed for other transitions, yielding a similar spin-exchange Hamiltonian, albeit with different interaction strength.

Direct Drive Gates for ⁵¹V Register

Performing dynamical decoupling on the register requires selective driving of the froze-core ⁵¹V nuclear spins without perturbing the bath and is achieved through a two-fold mechanism. Firstly we initialise the ¹⁷¹Yb qubit into $\ket{0_{g}}$ and apply a sinusoidal $z$ -directed RF magnetic field at $\omega_{c}/2\pi=991$ kHz through the coplanar waveguide to induce an oscillating ¹⁷¹Yb magnetic dipole moment (Extended Data Fig. 7a). This generates an $x$ -directed field component at each ⁵¹V spin, where the driving Hamiltonian is given by $\hat{H}_{\text{drive}}=\mu_{N}g_{vx}A_{x}B^{\text{osc}}_{z}\sin(\omega_{c}t)\hat{I}_{x}$ with $A_{x}=-3ln\mu_{0}\gamma_{z}^{2}/8\pi r^{3}\omega_{01}$ . Here, $\mu_{N}$ is the nuclear magneton, $g_{vx}$ is the ⁵¹V $x$ -directed $g$ -factor, $B_{z}^{\text{osc}}$ is the sinusoidal RF magnetic field amplitude, $\hat{I}_{x}$ is the nuclear spin-7/2 operator along the $x$ -axis, $\{l,n\}$ are the $\{x,z\}$ directional cosines of the ¹⁷¹Yb–⁵¹V displacement vector, $\mu_{0}$ is the vacuum permittivity, and $r$ is the ¹⁷¹Yb–⁵¹V ion distance (Supplementary Information). The lattice symmetry of the host leads to equidistant spacing of the four proximal ⁵¹V spins from the central ¹⁷¹Yb qubit allowing homogeneous coherent driving of all register spins.

In this direct driving scheme, we note that the effect of $B_{z}^{\text{osc}}$ is amplified by a factor of $A_{x}\approx 6.7$ for the frozen-core register spins at a distance of r = 3.9 Å (Supplementary Information). Crucially, the amplification factor scales as $A_{x}\propto 1/r^{3}$ with distance $r$ from the ¹⁷¹Yb qubit, leading to a reduced driving strength for distant ⁵¹V bath spins. Moreover, the transition frequency of the bath, $\omega_{c}^{\text{bath}}/2\pi=1028$ kHz, is detuned by 37 kHz from that of the register, $\omega_{c}/2\pi=991$ kHz, further weakening the bath interaction due to off-resonant driving provided that the Rabi frequency is less than the detuning.

In a rotating frame at frequency $\omega_{c}$ , the driving Hamiltonian $\hat{H}_{\text{drive}}$ gives rise to Rabi oscillation dynamics of the register spins within the $\omega_{c}$ manifold, $\{\ket{\uparrow}=\ket{\pm 5/2},\ket{\downarrow}=\ket{\pm 7/2}\}$ . To calibrate ⁵¹V $\pi$ pulse times, we initialise the register into $\ket{0_{v}}=\ket{\downarrow\downarrow\downarrow\downarrow}$ , drive the register for variable time, and read out the $\ket{0_{v}}$ population by preparing the ¹⁷¹Yb qubit in $\ket{1_{g}}$ and applying a swap gate to the $\omega_{c}$ transition. If the final ⁵¹V spin state is in $\ket{\downarrow}$ ( $\ket{\uparrow}$ ) the swap will be successful (unsuccessful) and the ¹⁷¹Yb qubit will end up in $\ket{0_{g}}$ ( $\ket{1_{g}}$ ). Using this method, we induce resonant Rabi oscillations of the register at a Rabi frequency of $2\pi\times(7.65\pm 0.05)$ kHz (blue markers, Extended Data Fig. 7c) which exhibit exponential decay on a $280\pm 30~{}\mu$ s timescale, limited by dephasing caused by the fluctuating ¹⁷¹Yb Knight field. This can be decoupled using motional narrowing techniques whereby we periodically apply $\pi$ pulses to the ¹⁷¹Yb every 6 $\mu s$ during the drive period. In order to drive the ⁵¹V spins in a phase-continuous manner, we compensate for the inversion of the ¹⁷¹Yb magnetic dipole moment after each $\pi$ pulse by applying a $\pi$ phase shift to the sinusoidal driving field (Extended Data Fig. 7b). This leads to an extended $1/e$ Gaussian decay time of $1040\pm 70~{}\mu$ s (red markers, Extended Data Fig. 7c).

The arrow in Extended Data Fig. 7c indicates the 69 $\mu$ s ⁵¹V $\pi$ pulse time used for dynamical decoupling. In contrast to the spin-preserving exchange interaction, this direct drive protocol provides independent, local control of the four ¹⁷¹V spins with no constraints on the number of excitations, thereby coupling the ⁵¹V register to states outside the two-level manifold spanned by $\ket{0_{v}}$ and $\ket{W_{v}}$ . For example, at odd multiple $\pi$ times, we find

	$\displaystyle\ket{0_{v}}\rightarrow\Ket{\uparrow\uparrow\uparrow\uparrow}$
	$\displaystyle\ket{W_{v}}\rightarrow\frac{\left(\Ket{\downarrow\uparrow\uparrow\uparrow}+\Ket{\uparrow\downarrow\uparrow\uparrow}+\Ket{\uparrow\uparrow\downarrow\uparrow}+\Ket{\uparrow\uparrow\uparrow\downarrow}\right)}{2},$

both of which contain more than a single excitation. For this reason, we use an even number of ⁵¹V $\pi$ pulses in our decoupling sequences to always return the ⁵¹V register to the memory manifold prior to state retrieval.

Population Basis Measurements

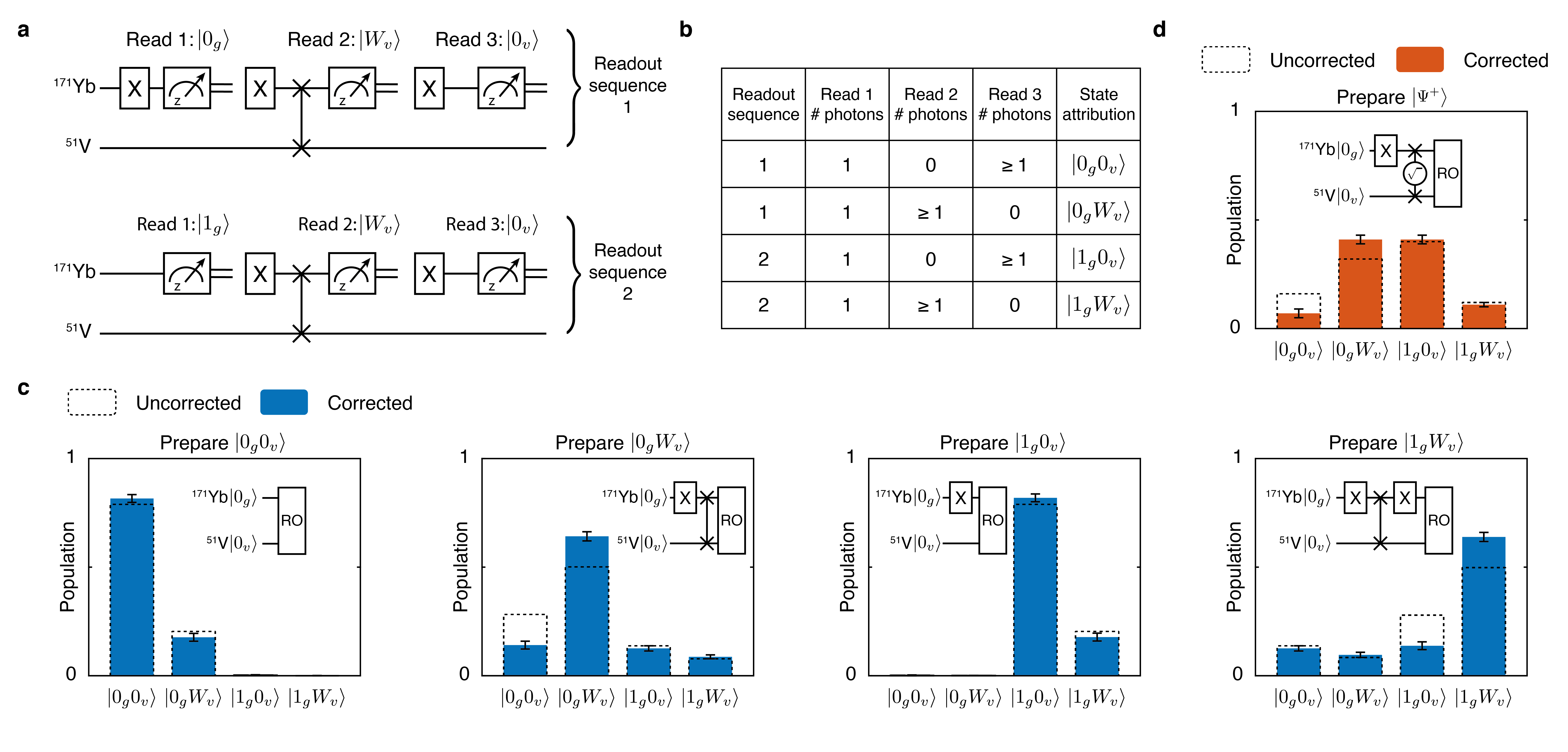
We develop a sequential tomography protocol Kalb2017 to read out the populations of the joint ¹⁷¹Yb–⁵¹V density matrix $\rho$ in the effective four-state basis, $\{\ket{0_{g}0_{v}},\ket{0_{g}W_{v}},\ket{1_{g}0_{v}},\ket{1_{g}W_{v}}\}$ . This is achieved using two separate sequences: Readout sequence 1 and Readout sequence 2, applied alternately, which measure the $\{\ket{0_{g}0_{v}}$ , $\ket{0_{g}W_{v}}\}$ and $\{\ket{1_{g}0_{v}}$ , $\ket{1_{g}W_{v}}\}$ populations respectively. As shown in Extended Data Fig. 9a, these sequences are distinguished by the presence (absence) of a single $\pi$ pulse applied to the ¹⁷¹Yb qubit at the start of the sequence. This is followed by a single optical readout cycle on the A transition; results are post-selected on detection of a single optical photon during this period. Hence the presence (absence) of the first $\pi$ pulse results in $\ket{0_{g}}$ ( $\ket{1_{g}}$ ) state readout after post selection. Furthermore, in all post-selected cases the ¹⁷¹Yb qubit is initialised to $\ket{1_{g}}$ by taking into account this conditional measurement outcome. Subsequently, an unconditional $\pi$ pulse is applied to the ¹⁷¹Yb, preparing it in $\ket{0_{g}}$ and a swap gate is applied, thereby transferring the ⁵¹V state to the ¹⁷¹Yb. Finally, we perform single-shot readout of the ¹⁷¹Yb state according to the protocol developed in Kindem2020 . Specifically, we apply two sets of 100 readout cycles to the A transition separated by a single $\pi$ pulse which inverts the ¹⁷¹Yb qubit population. The ⁵¹V state is ascribed to $\ket{W_{v}}$ ( $\ket{0_{v}}$ ) if $\geq 1$ (0) photons are detected in the second readout period and 0 ( $\geq 1$ ) photons are detected in the third. We summarise the possible photon detection events and state attributions in Extended Data Fig. 9b.

We demonstrate this protocol by characterizing the state preparation fidelities of the four basis states. The measured histograms are presented in Extended Data Fig. 9c alongside the respective gate sequences used for state preparation. The resulting uncorrected (corrected) preparation fidelities for these four basis states are:

	$\displaystyle\mathcal{F}_{\ket{0_{g}0_{v}}}=0.79\pm 0.01\;(0.82\pm 0.02),$
	$\displaystyle\mathcal{F}_{\ket{0_{g}W_{v}}}=0.50\pm 0.02\;(0.64\pm 0.02),$
	$\displaystyle\mathcal{F}_{\ket{1_{g}0_{v}}}=0.79\pm 0.01\;(0.82\pm 0.02),$
	$\displaystyle\mathcal{F}_{\ket{1_{g}W_{v}}}=0.50\pm 0.02\;(0.64\pm 0.02).$

We note that the reduced fidelity of $\ket{0_{g}W_{v}}$ and $\ket{1_{g}W_{v}}$ relative to $\ket{0_{g}0_{v}}$ and $\ket{1_{g}0_{v}}$ arises from the swap gate used for the $\ket{W_{v}}$ state preparation. Finally, we also characterize the fidelity of the maximally entangled ¹⁷¹Yb–⁵¹V Bell state, $\ket{\Psi^{+}}=\frac{1}{\sqrt{2}}\left(\ket{1_{g}0_{v}}-i\ket{0_{g}W_{v}}\right)$ , prepared using a single $\sqrt{\text{swap}}$ gate as described in the main text (Extended Data Fig. 9d). The corresponding uncorrected (corrected) populations for the four basis states, denoted $p_{ij}$ ( $c_{ij}$ ) are:

	$\displaystyle p_{00}\equiv\bra{0_{g}0_{v}}\rho\ket{0_{g}0_{v}}$	$\displaystyle=0.16\pm 0.01\;(c_{00}=0.07\pm 0.02),$
	$\displaystyle p_{01}\equiv\bra{0_{g}W_{v}}\rho\ket{0_{g}W_{v}}$	$\displaystyle=0.32\pm 0.01\;(c_{01}=0.41\pm 0.02),$
	$\displaystyle p_{10}\equiv\bra{1_{g}0_{v}}\rho\ket{1_{g}0_{v}}$	$\displaystyle=0.40\pm 0.02\;(c_{10}=0.41\pm 0.02),$
	$\displaystyle p_{11}\equiv\bra{1_{g}W_{v}}\rho\ket{1_{g}W_{v}}$	$\displaystyle=0.12\pm 0.01\;(c_{11}=0.11\pm 0.01).$

Swap Gate Fidelity Correction

Since ¹⁷¹Yb readout fidelity is $>95\%$ Kindem2020 , the dominant error introduced during the population basis measurements arises from the swap gate. We measure its fidelity in the population basis by preparing either the $\ket{0_{g}0_{v}}$ state (zero spin excitations) or the $\ket{1_{g}0_{v}}$ state (single spin excitation) and applying two consecutive swap gates such that the system is returned to the initial state. By comparing the ¹⁷¹Yb population before ( $p_{\text{pre}}$ ) and after ( $p_{\text{post}}$ ) the two gates are applied, we can extract fidelity estimates independently from the ⁵¹V state initialisation. Assuming the swap and swap-back processes are symmetric, we obtain a gate fidelity $\mathcal{F}_{\text{sw}}=\sqrt{(1-2p_{\text{post}})/(1-2p_{\text{pre}})}$ . This quantity is measured for zero spin excitations leading to $\mathcal{F}_{\text{sw},0}=0.83$ and with a single spin excitation leading to $\mathcal{F}_{\text{sw},1}=0.52$ .

When measuring the joint ¹⁷¹Yb–⁵¹V populations $\{p_{00}$ , $p_{01}$ , $p_{10}$ , $p_{11}\}$ we can use these fidelities to extract a set of corrected populations $\{c_{00},c_{01},c_{10},c_{11}\}$ according to the method described in Bernien2013 ; Nguyen2019a using

\begin{pmatrix}c_{11}\\ c_{10}\\ c_{01}\\ c_{00}\end{pmatrix}=E^{-1}\begin{pmatrix}p_{11}\\ p_{10}\\ p_{01}\\ p_{00}\end{pmatrix},

(11)

where

\displaystyle E{=}\frac{1}{2}\begin{pmatrix}1{+}\mathcal{F}_{\text{sw,1}}&&1{-}\mathcal{F}_{\text{sw,0}}&&0&&0\\ 1{-}\mathcal{F}_{\text{sw,1}}&&1{+}\mathcal{F}_{\text{sw,0}}&&0&&0\\ 0&&0&&1+\mathcal{F}_{\text{sw,1}}&&1{-}\mathcal{F}_{\text{sw,0}}\\ 0&&0&&1-\mathcal{F}_{\text{sw,1}}&&1{+}\mathcal{F}_{\text{sw,0}}\end{pmatrix}.

We use a similar approach to correct the $\sqrt{\text{swap}}$ gate used to read out the Bell state coherence (Supplementary Information).

Supplementary Information

.1 ¹⁷¹Yb–⁵¹V Interactions

.1.1 Ground State ¹⁷¹Yb Hamiltonian

The effective spin-1/2 Hamiltonian for the ${}^{2}\text{F}_{7/2}(0)$ ${}^{171}\text{Yb}^{3+}$ ground state is given by Kindem2018a :

\hat{H}_{\text{eff}}=\mu_{B}\mathbf{B}\cdot\mathbf{g}\cdot\hat{\mathbf{S}}+\hat{\mathbf{I}}_{\text{Yb}}\cdot\mathbf{A}\cdot\hat{\mathbf{S}}

(S1)

where $\mathbf{B}$ is the magnetic field, $\hat{\mathbf{S}}$ and $\hat{\mathbf{I}}_{\text{Yb}}$ are vectors of ¹⁷¹Yb electron and nuclear spin-1/2 operators respectively and we neglect the nuclear Zeeman term. The ground state $\mathbf{g}$ tensor is given by:

\mathbf{g}=\begin{pmatrix}g_{x}&0&0\\ 0&g_{x}&0\\ 0&0&g_{z}\end{pmatrix}=\begin{pmatrix}0.85&0&0\\ 0&0.85&0\\ 0&0&-6.08\end{pmatrix},

(S2)

which is a uniaxial tensor with the extraordinary axis parallel to the $c$ -axis of the crystal and the two ordinary axes aligned with the crystal $a$ -axes. The ground state $\mathbf{A}$ tensor is given by:

\mathbf{A}=2\pi\times\begin{pmatrix}0.675&0&0\\ 0&0.675&0\\ 0&0&-4.82\end{pmatrix}\text{GHz}.

(S3)

Extended Data Fig. 1a shows the zero magnetic field energy level structure with hybridised ¹⁷¹Yb electron-nuclear spin eigenstates. Note that the zero-field ¹⁷¹Yb qubit states, $\ket{0_{g}}$ and $\ket{1_{g}}$ , have no magnetic dipole moment. See Kindem2018a for more details. Throughout this work we adopt an $\hbar=1$ convention.

.1.2 Local Nuclear Spin Environment

The ¹⁷¹Yb³⁺ ion substitutes for yttrium in a single site of the YVO₄ crystal, furthermore naturally abundant V and Y contain 99.8% ⁵¹V and 100% ⁸⁹Y isotopes, respectively. Hence each ¹⁷¹Yb ion experiences a near-identical nuclear spin environment. The ⁵¹V ions have nuclear spin-7/2 leading to electric quadrupole interactions that cause a zero-field splitting. The resulting zero-field energy level structure of the ⁵¹V spins is given by:

\hat{H}_{\text{V}}=Q\hat{I}_{z}^{2}

(S4)

where $Q/2\pi=171~{}\text{kHz}$ measured using nuclear magnetic resonance (NMR) on bulk YVO₄ crystals Bleaney1982 and $\hat{I}_{z}$ is the ⁵¹V nuclear spin-7/2 spin operator along the $c\equiv z$ axis. Note that the local ⁵¹V register ions surrounding the ¹⁷¹Yb qubit experience a frozen-core detuning as discussed in the main text, leading to a smaller quadrupolar splitting with $Q/2\pi=165~{}\text{kHz}$ . The energy level structure of these register ions is shown in Fig. 1b. The ⁸⁹Y ion, on the other hand, has no zero-field structure.

The positions of the six nearest ⁵¹V ions are tabulated below, where $\mathbf{r}=[x~{}y~{}z]$ is the ¹⁷¹Yb–⁵¹V position vector with magnitude $r$ and direction cosines $\{l,m,n\}$ .

⁵¹V ion #	Shell	$r$ (Å)	$x$ (Å)	$y$ (Å)	$z$ (Å)	$l$	$m$	$n$
1	1^st	3.1	0	0	-3.1	0	0	-1
2	1^st	3.1	0	0	3.1	0	0	1
3	2^nd	3.9	0	-3.6	1.6	0	-0.91	0.40
4	2^nd	3.9	0	3.6	1.6	0	0.91	0.40
5	2^nd	3.9	-3.6	0	-1.6	-0.91	0	-0.40
6	2^nd	3.9	3.6	0	-1.6	0.91	0	-0.40

Note that the two nearest ⁵¹V ions (1 and 2) are located directly above and below the ¹⁷¹Yb qubit along the $z$ -axis, due to their positions they cannot be driven by the induced ¹⁷¹Yb magnetic dipole moment and thus belong to the bath (Supplementary Information Section .1.4). In contrast, ions 3–6 are symmetrically positioned in the lattice with non-zero $x/y$ and $z$ coordinates, forming the frozen-core register spins utilized as a quantum memory.

The ⁵¹V ions have a uniaxial g-tensor with form Bleaney1982a :

\mathbf{g}_{\text{V}}=\begin{pmatrix}g_{vx}&0&0\\ 0&g_{vx}&0\\ 0&0&g_{vz}\end{pmatrix}

(S5)

See Supplementary Information Section .4 for an experimental estimation of these tensor components.

.1.3 ¹⁷¹Yb–⁵¹V Interactions

The magnetic dipole-dipole interaction between the ¹⁷¹Yb qubit and a single ⁵¹V ion can be described by the following Hamiltonian:

\hat{H}_{dd}=\frac{\mu_{0}}{4\pi}\left[\frac{\boldsymbol{\mu}_{\text{Yb}}\cdot\boldsymbol{\mu}_{\text{V}}}{r^{3}}-\frac{3(\boldsymbol{\mu}_{\text{Yb}}\cdot\mathbf{r})(\boldsymbol{\mu}_{\text{V}}\cdot\mathbf{r})}{r^{5}}\right]

(S6)

where $\boldsymbol{\mu}_{\text{Yb}}=-\mu_{B}\mathbf{g}\cdot\hat{\mathbf{S}}$ , $\boldsymbol{\mu}_{\text{V}}=\mu_{N}\mathbf{g}_{\text{V}}\cdot\hat{\mathbf{I}}$ (note that $\hat{\bf S}$ and $\hat{\bf I}$ are vectors of ¹⁷¹Yb and ⁵¹V spin operators, respectively), $\mu_{B}$ is the Bohr magneton, $\mu_{N}$ is the nuclear magneton, $\mu_{0}$ is the vacuum permeability and $\mathbf{r}$ is the ¹⁷¹Yb–⁵¹V displacement vector with magnitude $r$ . Due to the highly off-resonant nature of the ¹⁷¹Yb–⁵¹V interaction, a secular approximation would be appropriate. To first order, however, all secular terms involving the ¹⁷¹Yb qubit basis are zero, i.e., $\bra{0_{g}}\hat{H}_{dd}\ket{0_{g}}=0$ , $\bra{1_{g}}\hat{H}_{dd}\ket{1_{g}}=0$ .

To proceed, we consider second-order effects which generally scale as $\sim$ $g^{2}/\Delta E$ , where $\Delta E$ is the energy separation between a pair of unperturbed eigenstates. By taking into account the fact that $g_{z}$ is roughly 7 times larger than $g_{x},g_{y}$ and $\hat{S_{z}}$ terms in $\hat{H}_{dd}$ mix $\ket{0_{g}}$ and $\ket{1_{g}}$ with small $\Delta E$ whereas $\hat{S_{x}}$ and $\hat{S_{y}}$ mix the ¹⁷¹Yb qubit states and $\ket{\text{aux}_{g}}$ with large $\Delta E$ , we restrict our consideration to the $\hat{S}_{z}$ terms in $\hat{H}_{dd}$ :

\hat{H}_{dd}\approx\frac{\mu_{0}\mu_{B}\mu_{N}g_{z}}{4\pi r^{3}}\hat{S}_{z}\left[3lng_{vx}\hat{I}_{x}+3mng_{vx}\hat{I}_{y}+(3n^{2}-1)g_{vz}\hat{I}_{z}\right]

(S7)

where $\{l,m,n\}$ are direction cosines of the ¹⁷¹Yb–⁵¹V displacement vector. Note that the $\hat{S}_{z}$ operator is the electron spin-1/2 operator defined as $\hat{S}_{z}=1/2(\ket{0_{g}}\bra{1_{g}}+\ket{1_{g}}\bra{0_{g}})$ in the basis of the hybridised eigenstates of the ¹⁷¹Yb qubit.

.1.4 Nuclear Overhauser Field

As discussed in the main text, we can divide the ⁵¹V spins into two ensembles: register spins and bath spins. The bath spins comprise ⁵¹V ions which are not driven by the ¹⁷¹Yb qubit for the following two reasons:

1.

Ions which aren’t driven due to position: certain ions (such as 1 and 2 in the above table) only interact via an Ising-type $\hat{S}_{z}\hat{I}_{z}$ Hamiltonian. Hence the ¹⁷¹Yb qubit cannot be used to drive transitions between the ⁵¹V $z$ -quantised quadrupole levels.
2.

Ions which aren’t driven due to detuning: As observed in the ZenPol spectra (Fig. 2b in the main text), more distant spins are spectrally separated from the nearby ions comprising the register.

We assume that the bath spins are in an infinite-temperature mixed state: $\rho_{\text{V}}=\mathbb{1}_{\text{V}}/Tr\{\mathbb{1}_{\text{V}}\}$ , where $\mathbb{1}_{v}$ is the identity matrix in the Hilbert space for the bath spins. In the mean field picture, their effect on the ¹⁷¹Yb can be approximated as a classical fluctuating magnetic field, commonly termed the nuclear Overhauser field. As mentioned previously, since $g_{z}^{2}\gg g_{x,y}^{2}$ , the $z$ -component of the Overhauser field is dominant, given by

B^{\text{OH}}_{z}=\sum_{\text{i}\in\text{bath}}\frac{\mu_{0}\mu_{N}g_{vz}}{4\pi(r^{(i)})^{3}}(3(n^{(i)})^{2}-1)m_{I}^{(i)},

(S8)

where $r^{(i)}$ and $n^{(i)}$ are the distance and $z$ -direction cosine between the ¹⁷¹Yb and $i$ ^th bath spin, and $m_{I}^{(i)}\in\{-7/2,-5/2,...,5/2,7/2\}$ is the nuclear spin projection at site $i$ . Note that $B_{z}^{\text{OH}}$ is randomly fluctuating due to the stochastic occupation of the 8 possible $\ket{m_{I}}$ states, however, it is quasi-static on the timescale of our control sequences, hence we do not label the time dependence.

Crucially, the nuclear Overhauser field generates some weak mixing between $\ket{0_{g}}$ and $\ket{1_{g}}$ leading to perturbed eigenstates $\ket{\tilde{0}_{g}}$ and $\ket{\tilde{1}_{g}}$ which have a small, induced, $z$ -directed dipole moment. These states have the form

	$\displaystyle\ket{\tilde{0}_{g}}$	$\displaystyle=\ket{0_{g}}-\frac{\gamma_{z}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))}{2\omega_{01}}\ket{1_{g}}$
	$\displaystyle\ket{\tilde{1}_{g}}$	$\displaystyle=\ket{1_{g}}+\frac{\gamma_{z}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))}{2\omega_{01}}\ket{0_{g}}$		(S9)

where $\gamma_{z}=g_{z}\mu_{B}$ is the longitudinal gyromagnetic ratio of the ¹⁷¹Yb qubit and $\omega_{01}/2\pi=675$ MHz is the unperturbed ¹⁷¹Yb $\ket{0_{g}}\leftrightarrow\ket{1_{g}}$ transition frequency. Here we have added the effect of an externally applied, $z$ -directed, square-wave RF magnetic field $B^{\text{RF}}(t)$ with amplitude $B^{\text{RF}}$ used in the ZenPol sequence (see main text for details); note that this field is piecewise constant for each half-sequence period, hence the time dependence corresponds to periodic flips between $\pm B^{\text{RF}}$ . In addition, these fields induce a detuning of the ¹⁷¹Yb $\ket{0_{g}}\leftrightarrow\ket{1_{g}}$ transition, which can be calculated using second-order perturbation theory as $\Delta(t)=\gamma_{z}^{2}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))^{2}/2\omega_{01}$ .

.1.5 Interaction with Register Ions

We postulate that the second nearest shell of four ⁵¹V ions (ions 3–6 in the table above) comprise the register. These four ions are equidistant from the ¹⁷¹Yb and interact via both an $\hat{S}_{z}\hat{I}_{z}$ term and $\hat{S}_{z}\hat{I}_{x}$ or $\hat{S}_{z}\hat{I}_{y}$ terms. To identify an effective interaction Hamiltonian in the perturbed basis $\{\ket{\tilde{0}_{g}},\ket{\tilde{1}_{g}}\}$ , we consider only secular matrix elements of $\hat{H}_{dd}$ (equation (S7)):

\hat{\tilde{H}}_{dd}=\bra{\tilde{0}_{g}}\hat{H}_{dd}\ket{\tilde{0}_{g}}\ket{\tilde{0}_{g}}\bra{\tilde{0}_{g}}+\bra{\tilde{1}_{g}}\hat{H}_{dd}\ket{\tilde{1}}\ket{\tilde{1}_{g}}\bra{\tilde{1}_{g}}

(S10)

where

	$\displaystyle\bra{\tilde{0}_{g}}\hat{H}_{dd}\ket{\tilde{0}_{g}}$	$\displaystyle=-\frac{\mu_{0}\mu_{N}\gamma_{z}^{2}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))}{8\pi r^{3}\omega_{01}}\left[3lng_{vx}\hat{I}_{x}+3mng_{vx}\hat{I}_{y}+(3n^{2}-1)g_{vz}\hat{I}_{z}\right]$
	$\displaystyle\bra{\tilde{1}_{g}}\hat{H}_{dd}\ket{\tilde{1}_{g}}$	$\displaystyle=+\frac{\mu_{0}\mu_{N}\gamma_{z}^{2}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))}{8\pi r^{3}\omega_{01}}\left[3lng_{vx}\hat{I}_{x}+3mng_{vx}\hat{I}_{y}+(3n^{2}-1)g_{vz}\hat{I}_{z}\right].$

Hence the effective interaction between the ¹⁷¹Yb qubit and the four register spins, $\hat{H}_{\text{int}}=\sum_{i\in\text{register}}\hat{\tilde{H}}_{dd}^{\text{(i)}}$ , can be described by

\hat{H}_{\text{int}}=\hat{\tilde{S}}_{z}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))\sum_{i\in\text{register}}\left(J_{x}^{(i)}\hat{I}_{x}^{(i)}+J_{y}^{(i)}\hat{I}_{y}^{(i)}+J_{z}^{(i)}\hat{I}_{z}^{(i)}\right)

(S11)

with

	$\displaystyle J_{x}^{(i)}$	$\displaystyle=\frac{3\mu_{0}\mu_{N}\gamma_{z}^{2}g_{vx}l^{(i)}n^{(i)}}{4\pi(r^{(i)})^{3}\omega_{01}}$
	$\displaystyle J_{y}^{(i)}$	$\displaystyle=\frac{3\mu_{0}\mu_{N}\gamma_{z}^{2}g_{vx}m^{(i)}n^{(i)}}{4\pi(r^{(i)})^{3}\omega_{01}}$
	$\displaystyle J_{z}^{(i)}$	$\displaystyle=\frac{3\mu_{0}\mu_{N}\gamma_{z}^{2}g_{vz}(3(n^{(i)})^{2}-1)}{4\pi(r^{(i)})^{3}\omega_{01}}$

and

\hat{\tilde{S}}_{z}=\frac{1}{2}(\ket{\tilde{1}_{g}}\bra{\tilde{1}_{g}}-\ket{\tilde{0}_{g}}\bra{\tilde{0}_{g}}).

Finally, we perform local basis transformations of each ⁵¹V ion to further simplify the Hamiltonian form. Specifically, we apply the following unitary rotation:

	$\displaystyle\hat{H}_{\text{int}}$	$\displaystyle\rightarrow U\hat{H}_{\text{int}}U^{\dagger}$
	$\displaystyle U$	$\displaystyle=\prod_{j\in\text{register}}\exp[i\theta^{(j)}\hat{I}_{z}^{(j)}],$

where $\theta^{(j)}=\tan^{-1}(m^{(j)}/l^{(j)})$ , which leads to

\hat{H}_{\text{int}}=\hat{\tilde{S}}_{z}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))\sum_{i\in\text{register}}\left[a_{x}\hat{I}_{x}^{(i)}+a_{z}\hat{I}_{z}^{(i)}\right]

(S12)

with $a_{x}=\sqrt{(J_{x}^{(i)})^{2}+(J_{y}^{(i)})^{2}}$ and $a_{z}=J_{z}^{(i)}$ . Note that the coupling coefficients $a_{x}$ and $a_{z}$ are homogeneous (i.e. independent of site index $i$ ) since the four register spins are equidistant from the central ¹⁷¹Yb and have directional cosine factors with equal magnitude.

The same result can also be derived using the Schrieffer-Wolff transformation Tannoudji2004 ; Bermudez2011 , where the interaction Hamiltonian obtained here corresponds to the dominant second-order perturbation terms. Hereafter we simplify our notation and use $\ket{0_{g}}$ and $\ket{1_{g}}$ without tildes to represent the weakly perturbed eigenstates in the presence of any small magnetic field.

.1.6 Full System Hamiltonian

Combining the various energy and interaction terms, the full system Hamiltonian (in a ¹⁷¹Yb frame rotating at $\omega_{01}/2\pi=675$ MHz) becomes:

\hat{H}_{\text{full}}=\frac{\gamma_{z}^{2}\left(B^{\text{OH}}_{z}+B^{\text{RF}}(t)\right)^{2}}{2\omega_{01}}\hat{\tilde{S}}_{z}+\sum_{i\in\text{register}}Q\left(\hat{I}_{z}^{(i)}\right)^{2}+\hat{\tilde{S}}_{z}(B^{\text{OH}}_{z}+B^{\text{RF}}(t))\sum_{i\in\text{register}}\left[a_{x}\hat{I}_{x}^{(i)}+a_{z}\hat{I}_{z}^{(i)}\right].

(S13)

.2 Randomised Benchmarking and ¹⁷¹Yb Qubit Coherence

High fidelity control of the ¹⁷¹Yb $\ket{0_{g}}\leftrightarrow\ket{1_{g}}$ transition is essential for implementing the ZenPol sequence and enabling coherent ¹⁷¹Yb–⁵¹V interactions. For example, a single swap operation realised by the ZenPol sequence contains 120 local ¹⁷¹Yb gates. We characterise our single qubit gate fidelity using randomised benchmarking Knill2008 , which provides a value independent from state preparation or measurement (SPAM) errors. We apply randomly sampled single qubit Clifford gates constructed using $\pi$ and $\pi/2$ rotations around the $x$ and $y$ directions followed by the single-gate inverse operation (Extended Data Fig. 2a). When the number of gates, $M_{\text{gate}}$ , increases, the sequence error accumulates and the probability of returning to the initial $\ket{0_{g}}$ state reduces according to an exponential decay:

P=0.5+P_{0}d^{M_{\text{gate}}}.

(S14)

When ensemble-averaged over a sufficiently large number of random gate sets (in our case 100), $f=\frac{1}{2}(1+d)$ becomes a reliable estimate of the average single-qubit gate fidelity. Measurement results are presented in Extended Data Fig. 2a, leading to an extracted average single qubit gate fidelity of $f=0.99975\pm 0.00004$ .

We also measure the $T_{2}$ coherence time of the qubit transition using an XY-8 dynamical decoupling sequence Gullion1990 . Specifically, we work with a fixed inter-pulse separation of 5.6 $~{}\mu$ s and measure the coherence time by varying the number of decoupling periods, $M^{\prime}$ (Extended Data Fig. 2b). We measure an exponential decay with $1/e$ time constant $T_{2}=16\pm 2$ ms. We note that this measurement uses the same method as in Kindem2020 , however, we observe a factor of three improvement in coherence due to the improved microwave setup leading to correspondingly increased $\pi$ gate fidelities.

.3 Extra Register Detail

In this section we provide additional technical details related to the single excitation states used to store quantum information on the ⁵¹V spins.

The general form for the engineered spin-exchange interaction is:

\hat{H}_{\text{avg}}=B^{\text{RF}}\sum_{i\in\text{register}}b_{(k,\omega_{j})}^{(i)}\left(\hat{\tilde{S}}_{+}\hat{\tilde{I}}^{(i)}_{-}+\hat{\tilde{S}}_{-}\hat{\tilde{I}}^{(i)}_{+}\right),

(S15)

where, $B^{\text{RF}}$ is the square-wave RF magnetic field amplitude, $b_{(k,\omega_{j})}^{(i)}$ is the $k^{\text{th}}$ resonance prefactor for transition $\omega_{j}$ of the $i$ ^th register spin, $\hat{\tilde{I}}_{+}=\ket{\uparrow}\bra{\downarrow}$ , $\hat{\tilde{I}}_{-}=\ket{\downarrow}\bra{\uparrow}$ , are raising and lowering operators in an effective nuclear spin-1/2 manifold and $\hat{\tilde{S}}_{+}=\ket{1_{g}}\bra{0_{g}}$ , $\hat{\tilde{S}}_{-}=\ket{0_{g}}\bra{1_{g}}$ are raising and lowering operators for the ¹⁷¹Yb qubit. Note, unlike the main text, we do not assume homogeneous coupling to the register spins, hence the $b_{(k,\omega_{j})}^{(i)}$ coefficients depend on the register site index $i$ . In addition, we consider an arbitrary number of register spins, $N$ , that are spectrally indistinguishable.

When the ¹⁷¹Yb is initialised in $\ket{1_{g}}$ and the ⁵¹V register spins are polarised in $\ket{0_{v}}=\ket{\downarrow}^{\otimes N}$ , this interaction leads to the following spin-exchange evolution Taylor2003 :

\ket{\psi(t)}=\ket{1_{g}}\ket{0_{v}}\cos(J_{\text{ex}}t/2)-i\ket{0_{g}}\ket{1_{v}}\sin(J_{\text{ex}}t/2)

(S16)

where the spin-exchange frequency is given by:

J_{\text{ex}}=2B^{\text{RF}}\sqrt{\sum_{i\in\text{register}}\left|b_{(k,\omega_{j})}^{(i)}\right|^{2}}

(S17)

and the resulting single-spin excited state generated by this interaction is:

\ket{1_{v}}=\frac{1}{\sqrt{\sum_{i}|b_{(k,\omega_{j})}^{(i)}|^{2}}}\sum_{i\in\text{register}}b_{(k,\omega_{j})}^{(i)}\ket{\downarrow...\uparrow^{(i)}...\downarrow}.

(S18)

Based on the results presented in Fig. 2d and Supplementary Information Section .8 we postulate that for our system the register consists of the second nearest shell of four homogeneously coupled ⁵¹V ions. In this case we recover the expressions presented in the main text, namely, the single-spin excitation in the register realises an entangled four-body W-state, $\ket{W_{v}}$ , as depicted in Fig. 1c:

\ket{1_{v}}=\ket{W_{v}}=\frac{\ket{\uparrow\downarrow\downarrow\downarrow}+\ket{\downarrow\uparrow\downarrow\downarrow}+\ket{\downarrow\downarrow\uparrow\downarrow}+\ket{\downarrow\downarrow\downarrow\uparrow}}{2}

(S19)

and the spin-exchange rate is given by $J_{\text{ex}}=4B^{\text{RF}}b_{(k,\omega_{j})}$ . In general, for $N$ homogeneously coupled register spins, we expect that the spin-exchange rate is enhanced by a factor of $\sqrt{N}$ , leading to faster swap gate operation.

We note that in this protocol it is possible to transfer a second spin excitation to the register. More specifically, the spin-preserving exchange interaction, $\hat{\tilde{S}}_{-}\hat{\tilde{I}}_{+}+\hat{\tilde{S}}_{+}\hat{\tilde{I}}_{-}$ , couples the state $\ket{1_{g}}\ket{W_{v}}$ to $\ket{0_{g}}\ket{2_{v}}$ , where $\ket{2_{v}}$ is a ⁵¹V state with two spins in $\ket{\uparrow}$ . To avoid undesired excitation to states outside of the effective $\{\ket{0_{v}},\ket{W_{v}}\}$ manifold, we always prepare the ¹⁷¹Yb qubit in $\ket{0_{g}}$ before retrieving stored states from the ⁵¹V register. Hence the swap gate realised by this interaction operates on a limited basis of states.

We stress that utilising the dense, lattice nuclear spins ensures near identical registers for all ¹⁷¹Yb ions. Extended Data Figure 10 shows ZenPol spectra near the $\omega_{c}$ transition, collectively enhanced spin-exchange oscillations and motionally-narrowed $T_{2}^{*}$ times for three ⁵¹V registers coupled to three different ¹⁷¹Yb ions. The ¹⁷¹Yb optical and microwave frequencies were re-calibrated for each ion, however, all aspects of the experimental sequences related to register control and readout were identical.

.4 Simulation

We simulate our coupled spin system using the effective Hamiltonian derived in Supplementary Information Section .1.6, however we add three additional terms:

1.

Nuclear Zeeman interactions of the ⁵¹V register spins with the Overhauser field from the bath: Since the energy levels are quantised along the $z$ -axis, magnetic fluctuations along the $z$ -direction dominate, which can be captured by the following Hamiltonian

$\hat{H}_{\text{nz}}=\sum_{i\in\text{register}}\mu_{N}g_{vz}B^{\text{OH}}_{z}\left(\mathbf{r}_{i}\right)\hat{I}_{z}^{(i)}$ (S20)

where $B^{\text{OH}}_{z}\left(\mathbf{r}_{i}\right)$ is the $z$ -component of the Overhauser field evaluated at the position of the $i$ ^th register ion, $\mathbf{r}_{i}$ .

Nuclear magnetic dipole-dipole interactions of the register spins:

\hat{H}_{\text{ndd}}=\sum\limits_{\begin{subarray}{c}i,j\in\text{register}\\ i<j\end{subarray}}\frac{\mu_{0}}{4\pi}\left[\frac{\boldsymbol{\mu}_{V}^{(i)}\cdot\boldsymbol{\mu}_{V}^{(j)}}{r_{ij}^{3}}-\frac{3(\boldsymbol{\mu}_{V}^{(i)}\cdot\mathbf{r}_{ij})(\boldsymbol{\mu}_{V}^{(j)}\cdot\mathbf{r}_{ij})}{r_{ij}^{5}}\right]

(S21)

with $\mathbf{r}_{ij}$ the displacement vector between ⁵¹V register spins at sites $i$ and $j$ .

¹⁷¹Yb-enhanced register spin-spin interactions: These terms are derived by considering second-order perturbations using the Schrieffer-Wolff transformation Tannoudji2004 ; Bermudez2011 . For example, the dominant Ising-type terms take the form

\hat{H}_{\text{edd}}=\sum_{i,j\in\text{register}}\frac{1}{2\omega_{01}}\left[\left(3n^{2}-1\right)\frac{\mu_{0}\mu_{N}\gamma_{z}g_{vz}}{4\pi r^{3}}\right]^{2}\hat{\tilde{S}}_{z}\hat{I}^{(i)}_{z}\hat{I}^{(j)}_{z},

(S22)

where $r$ and $n$ are the magnitude and $z$ -direction cosine of the ¹⁷¹Yb–⁵¹V register ion displacement vector. However, we note that the ZenPol sequence cancels these interactions to first order.

By simulating ¹⁷¹Yb Ramsey coherence times we extract $g_{vz}\approx 1.6$ . We note that estimation of the bare ⁵¹V coherence time indicates a potential discrepancy in this value by up to $25\%$ , discussed further in Supplementary Information Section .9, however, this has a negligible impact on the ZenPol sequence simulations. We obtain an estimate for $g_{vx}\approx 0.6$ by calibrating the RF field amplitude and comparing with the experimental results of direct ⁵¹V spin driving in Extended Data Fig. 7.

We compute the nuclear Overhauser field $B_{z}^{\text{OH}}$ according to equation (S8) by randomly sampling the bath states for each Monte-Carlo simulation repetition. We include a simple model of the bath dynamics by incorporating stochastic jumps of the bath spins on magnetic-dipole allowed transitions.

We simulate the register spin dynamics in a reduced Hilbert space by considering only the $\omega_{c}$ manifold. This enables fast simulation of all four register spins plus the ¹⁷¹Yb qubit transition (Hilbert space with dimension 32). Imperfect polarisation of the ⁵¹V register into $\ket{\downarrow}=\ket{\pm 7/2}$ is categorised into two distinct types:

1.

Imperfect polarisation within the $\omega_{c}$ transition i.e. a small residual population $\epsilon_{1}$ in $\ket{\uparrow}=\ket{\pm 5/2}$ .
2.

Imperfect polarisation outside the $\omega_{c}$ manifold i.e. a small residual population $\epsilon_{2}$ in $\ket{\pm 1/2}$ and $\ket{\pm 3/2}$ .

This leads to a $\ket{\downarrow}$ population of $1-\epsilon_{1}-\epsilon_{2}$ . We incorporate incomplete polarisation by sampling different register initial states for each Monte-Carlo repetition. For case 1, this involves occasionally initialising a given ⁵¹V ion into $\ket{\uparrow}$ , while for case 2 this involves reducing the Hilbert space dimension by removing the ⁵¹V ion from the simulation. We also take into account finite pulse duration effects by modeling the ZenPol sequence using 25 ns $\pi/2$ and 50 ns $\pi$ pulses (Extended Data Fig. 6a).

As shown in Extended Data Fig. 6d, the spin-exchange oscillations from numerical simulation (red dashed line) exhibit slower decay than the measured experimental results (red markers). We add a phenomenological exponential decay envelope, $ce^{-M/\tau_{M}}$ , to the simulation results where $c$ and $\tau_{M}$ are free parameters, and $M$ is the ZenPol sequence period. The additional decay could be caused by heating due to the RF field, excess ¹⁷¹Yb dephasing or additional register spin interactions which we haven’t considered here. We fit this model by optimising multiple parameters: $\epsilon_{1}$ , $\epsilon_{2}$ , $B^{\text{RF}}$ , $c$ and $\tau_{M}$ . The resulting values of $\epsilon_{1}$ and $\epsilon_{2}$ are 0.12 and 0.04, respectively, indicating $\approx 84\%$ polarisation into $\ket{\downarrow}$ ; the RF magnetic field amplitude is $B^{\text{RF}}\approx 1.6$ G and the phenomenological exponential decay parameters are $c=0.8$ and $\tau_{M}=90$ leading to a close fit with the experimental results (red solid line, Fig. 2c and Extended Data Fig. 6d). Additional simulation results following this methodology with varying $B^{\text{RF}}$ and $\tau$ are presented in Extended Data Fig. 6.

Finally, we model the results with a single-spin excitation in the $\omega_{c}$ -manifold by including the $\ket{\pm 3/2}$ level in the simulation (Fig. 2d and Supplementary Information Section .8). The initial state used in this simulation is partially polarised between the $\ket{\pm 3/2}$ level with population $1-\epsilon$ and the $\ket{\pm 1/2}$ level with population $\epsilon$ . We use the same value of $B^{\text{RF}}=1.6$ G as in Fig. 2c, and optimise the polarisation level leading to $1-\epsilon=0.8$ . The close correspondence between the measured and simulated oscillation profiles suggests that the register consists of the second shell of four homogeneously coupled ⁵¹V ions.

.5 Hartmann Hahn Spectroscopy

In addition to the ZenPol spectra discussed in the main text, we use Hartmann-Hahn (HH) double resonance Hartmann1962 to perform spectroscopy of the nuclear spin environment. This method enables spin exchange between two systems with different transition frequencies by resonantly driving a qubit with a Rabi frequency that matches the energy level splitting of the environmental nuclear spins. In our case, we resonantly drive the ¹⁷¹Yb at 675 MHz to generate a pair of dressed states $\ket{\pm}=\frac{1}{\sqrt{2}}\left(\ket{0_{g}}\pm i\ket{1_{g}}\right)$ with splitting $\Omega$ which we sweep over a range $\approx$ $2\pi\times$ (0–2.3) MHz (Extended Data Fig. 3). The ¹⁷¹Yb qubit is initialised into the $\ket{-}$ dressed state by a $\pi/2$ pulse preceding the driving period. If resonant with a nuclear spin transition, the ¹⁷¹Yb qubit undergoes spin exchange at a rate dictated by the interaction strength. Finally we read out the ¹⁷¹Yb $\ket{+}$ dressed state population to determine whether spin exchange has occurred.

Extended Data Fig. 3b shows experimental results of HH spectroscopy where we vary both the HH drive Rabi frequency ( $\Omega$ ) and also the HH pulse duration ( $t$ ). The counts plotted on the colour-bar are proportional to the $\ket{+}$ dressed state population. We find three clear resonances at evenly spaced pulse amplitudes 0.15, 0.30 and 0.45 corresponding to the $\omega_{a}$ , $\omega_{b}$ and $\omega_{c}$ ⁵¹V transitions; notably, unlike ZenPol, the HH sequence only has one harmonic leading to a single resonant interaction per transition. Also note the lack of oscillations when varying the pulse duration, $t$ , on resonance with either of the three transitions: this is because the spin exchange is driven by the randomised, Overhauser field induced ¹⁷¹Yb dipole moment. For this reason, the HH sequence cannot be used to generate the coherent exchange interaction necessary to realise a swap gate for our system. In the case of no driving ( $\Omega=0$ ), the signal rapidly saturates as $t$ increases as a result of Ramsey dephasing of the initial state. However, as $\Omega$ exceeds the ¹⁷¹Yb spin linewidth ( $\sim 50$ kHz Kindem2020 ), this effect diminishes due to the emergence of spin-locking effects and consequently leads to an increased saturation timescale when not resonant with the ⁵¹V transitions. The resolution of this measurement is also limited by the ¹⁷¹Yb spin linewidth, and we therefore cannot resolve the split-resonance structure observed in the ZenPol spectra. The results agree well with simulations (Extended Data Fig. 3c) indicating that interactions with the ⁵¹V quadrupolar structure dominate these measurements.

.6 Polarisation of multi-level register nuclear spins

Polarisation dynamics are explored using the PROPI method (polarisation readout by polarisation inversion) Scheuer2017 . This sequence uses the back-action of the ⁵¹V spins on the ¹⁷¹Yb to measure the register polarisation after successive ZenPol polarisation cycles. For instance, when polarising into $\ket{\uparrow}=\ket{\pm 5/2}$ on the $\omega_{c}$ transition, the ¹⁷¹Yb is initialised into $\ket{1_{g}}$ and undergoes spin exchange with any ⁵¹V population in $\ket{\downarrow}=\ket{\pm 7/2}$ . The ¹⁷¹Yb $\ket{0_{g}}$ population after interaction is therefore related to the residual ⁵¹V $\ket{\downarrow}$ population. As presented in Extended Data Fig. 5a, we measure the ¹⁷¹Yb population after each of 20 consecutive polarisation cycles and observe a saturation after 10 cycles, indicating that the ¹⁷¹Yb polarisation has been transferred to the ⁵¹V register. The high-contrast signal obtained in this measurement is enabled by alternating the ⁵¹V polarisation direction, i.e. periods of polarisation into $\ket{\uparrow}$ are interleaved with periods of polarisation into $\ket{\downarrow}$ . This mitigates the need to wait for slow register thermalisation ( $T_{1}^{(0)}=0.54~{}s$ , see Supplementary Information Section .10) between consecutive experiment repetitions. These measurements are repeated with ZenPol sequences on the $\omega_{b}$ transition, demonstrating similar levels of polarisation saturation after approximately 10 cycles (Extended Data Fig. 5b).

We also demonstrate the effect of incomplete register polarisation on the spin-exchange oscillation by varying the number of polarisation cycles on the $\omega_{b}$ and $\omega_{c}$ transitions before each experiment (Extended Data Fig. 5c). As expected, we see that coherent spin-exchange oscillations emerge as an increasing number of polarisation cycles are applied.

These results inform the design of polarisation sequences used in subsequent single-spin excitation experiments where 40 polarisation cycles interleaved between the $\omega_{b}$ and $\omega_{c}$ transitions are sufficient to polarise the register into $\ket{0_{v}}=\ket{\downarrow\downarrow\downarrow\downarrow}$ . Based on simulations discussed in Supplementary Information Section .4 we estimate this protocol achieves $\approx 84\%$ polarisation into the $\ket{0_{v}}$ state. Note that we don’t use the ZenPol sequence to directly polarise the $\omega_{a}$ transition due to spectral overlap with $\omega_{b}$ and $\omega_{c}$ (Fig. 2b). We postulate that the high degree of polarisation can still be achieved even in the absence of direct $\omega_{a}$ transition control due to two factors:

1.

The thermalisation timescale of the $\omega_{a}$ transition is significantly shorter than the interrogation time. Specifically, our experiments typically run for several minutes whereas the $\omega_{a}$ thermalisation rate is likely similar to $T_{1}^{(0)}=0.54$ s. Thus, undesired population in the $\ket{\pm 1/2}$ level can still pumped to $\ket{\pm 7/2}$ once it relaxes to $\ket{\pm 3/2}$ .
2.

Once successfully initialised into the $\omega_{c}$ manifold the probability of shelving into the $\ket{\pm 1/2}$ level is small as it necessitates two consecutive decays on the $\omega_{b}$ and $\omega_{a}$ transitions, both of which are considerably slower than our experiment/polarisation repetition rate (20 ms).

We tried to improve the polarisation fidelity by incorporating direct driving on the $\omega_{a}$ transition using the method in Extended Data Fig. 7 during the polarisation protocol, thus leading to fast population exchange between $\ket{\pm 1/2}$ and $\ket{\pm 3/2}$ . However, there was no improvement to the contrast of the resulting spin exchange oscillations thereby indicating that shelving into $\ket{\pm 1/2}$ is not a limiting factor in our experiments.

.7 Analysis of Spin Exchange Dynamics

In this section we present an analysis of the spin exchange dynamics on the $\omega_{c}$ register transition. The spin-exchange measurements in Fig. 2c are measured at a fixed ZenPol period of $2\tau=5.048~{}\mu$ s leading to resonant interactions with the 991 kHz $\omega_{c}$ transition. However, analogous to the Rabi oscillations in a two-level system, the oscillation frequency and contrast of these spin transfer oscillations also depend on the detuning of the ZenPol sequence relative to the ⁵¹V transition. Specifically, we expect the following relations:

	$\displaystyle J_{\text{ex}}(\delta)=\sqrt{J_{\text{ex}}(0)^{2}+\delta^{2}}$		(S23)
	$\displaystyle C(\delta)=\frac{J_{\text{ex}}(0)^{2}}{J_{\text{ex}}(0)^{2}+\delta^{2}}$		(S24)

Here $J_{\text{ex}}$ and $C$ are the spin-exchange frequency and oscillation contrast, respectively, and $\delta$ is the detuning of the ZenPol sequence resonance relative to a target nuclear spin transition. We polarise the register into $\ket{0_{v}}$ and measure the frequency detuning dependence of the spin-exchange oscillations in Extended Data Fig. 6c. These results agree well with the corresponding simulations shown in Extended Data Fig. 6b.

We also demonstrate control of the spin exchange frequency by varying the RF magnetic field amplitude ( $B^{\text{RF}}$ ). Extended Data Figure 6d shows the spin-exchange dynamics for four different values of $B^{\text{RF}}$ = 0.8 G, 1.2 G, 1.6 G and 2.0 G. The inset in Fig. 2c plots extracted spin exchange frequencies $J_{\text{ex}}$ for a range of different $B^{\text{RF}}$ demonstrating linear dependence as expected and leading to accurate control of the engineered interaction strength (see main text for details).

.8 Single Excitation in $\omega_{c}$ Manifold

The ability to shelve populations in different quadrupole levels enables the operation of the ⁵¹V register with an alternative set of many-body states: $\ket{0^{\prime}_{v}}$ and $\ket{1^{\prime}_{v}}$ . For this experiment we polarise the ⁵¹V spins down the energy ladder on the $\omega_{b}$ and $\omega_{c}$ transitions leading to polarisation primarily into the $\ket{\pm 3/2}$ level, with a small residual population in $\ket{\pm 1/2}$ . For the purpose of this analysis we will assume perfect polarisation into $\ket{\pm 3/2}$ , however we note that $\omega_{a}$ transition polarisation would be required for this.

We prepare the register $\ket{1^{\prime}_{v}}$ state by injecting a single spin excitation on the $\omega_{b}$ transition (i.e. from $\ket{\pm 3/2}\rightarrow\ket{\uparrow}=\ket{\pm 5/2}$ ), this is achieved using the corresponding ZenPol resonance at $\omega_{b}$ , $k=3$ :

\ket{1^{\prime}_{v}}=\frac{1}{2}\left(\Ket{\uparrow,\frac{3}{2},\frac{3}{2},\frac{3}{2}}+\Ket{\frac{3}{2},\uparrow,\frac{3}{2},\frac{3}{2}}+\Ket{\frac{3}{2},\frac{3}{2},\uparrow,\frac{3}{2}}+\Ket{\frac{3}{2},\frac{3}{2},\frac{3}{2},\uparrow}\right)

(S25)

Here we omit the $\pm$ sign in the state label for simplicity. Subsequently, we prepare the ¹⁷¹Yb in $\ket{0_{g}}$ and induce a spin exchange oscillation between $\ket{\uparrow}$ and $\ket{\downarrow}=\ket{\pm 7/2}$ via a ZenPol sequence resonant with the $\omega_{c}$ transition. The resulting time evolution is given by

\ket{\psi(t)}=\ket{0_{g}}\ket{1^{\prime}_{v}}\cos\left(\frac{J^{\prime}_{\text{ex}}t}{2}\right)-i\ket{1_{g}}\ket{0^{\prime}_{v}}\sin\left(\frac{J^{\prime}_{\text{ex}}t}{2}\right)

(S26)

where

\ket{0^{\prime}_{v}}=\frac{1}{2}\left(\Ket{\downarrow,\frac{3}{2},\frac{3}{2},\frac{3}{2}}+\Ket{\frac{3}{2},\downarrow,\frac{3}{2},\frac{3}{2}}+\Ket{\frac{3}{2},\frac{3}{2},\downarrow,\frac{3}{2}}+\Ket{\frac{3}{2},\frac{3}{2},\frac{3}{2},\downarrow}\right)

(S27)

and $J^{\prime}_{\text{ex}}=2b_{(5,\omega_{c})}B^{\text{RF}}$ . Notice that the spin-exchange oscillation rate, $J^{\prime}_{\text{ex}}$ , no longer has a $\sqrt{N}$ rate enhancement, this is because every ket in the $\ket{1^{\prime}_{v}}$ and $\ket{0^{\prime}_{v}}$ states contains only a single spin in the $\omega_{c}$ -transition manifold. Using this manifold for information storage would have several benefits. For instance, direct microwave driving of the register $\omega_{c}$ transition would lead to Rabi oscillation between $\ket{0^{\prime}_{v}}$ and $\ket{1^{\prime}_{v}}$ and could therefore be used to realise local gates in this basis. Additionally, a second spin excitation is not allowed in this scheme, therefore the ZenPol sequence reproduces a complete two-qubit swap gate regardless of the ¹⁷¹Yb state. For these reasons, we believe that there may be some advantages to working with the $\{\ket{0^{\prime}_{v}}$ , $\ket{1^{\prime}_{v}}\}$ manifold if the state initialisation fidelity into $\ket{\pm 3/2}$ can be improved via direct $\omega_{a}$ transition polarisation. We leave this for future work.

.9 $T_{2}^{*}$ Coherence Discussion

Here we provide detailed discussions regarding the ⁵¹V register coherence decay processes described in the main text. There are two magnetic interactions which limit the $T_{2}^{*}$ dephasing timescale: (1) the direct nuclear Zeeman interaction of each register spin with the Overhauser field (equation (S20)) and (2) a contribution from the ¹⁷¹Yb Knight field Urbaszek2013 . In the latter case, the bath-induced ¹⁷¹Yb dipole moment generates a randomly fluctuating magnetic field at each ⁵¹V ion, the Knight field, which is described by

\hat{H}_{\text{nz,eff}}=\mp g_{vz}\mu_{N}B^{\text{OH}}_{z}A_{z}\hat{I}_{z}

(S28)

with

A_{z}=\frac{\mu_{0}\gamma_{z}^{2}(1-3n^{2})}{8\pi r^{3}\omega_{01}}.

Here, the $-$ and $+$ cases in equation (S28) correspond to ¹⁷¹Yb in $\ket{1_{g}}$ and $\ket{0_{g}}$ , respectively. The constants are defined in Supplementary Information Section .1. We note that $A_{z}$ corresponds to an effective local field amplification factor with value $A_{z}\approx 3.1$ for the register spins. We define the ¹⁷¹Yb Knight field to be $\mp A_{z}B^{\text{OH}}_{z}$ .

By applying periodic $\pi$ pulses to the ¹⁷¹Yb, we flip its state between $\ket{0_{g}}$ and $\ket{1_{g}}$ , thereby switching the sign of the Knight field. This leads to the cancellation of ⁵¹V phase accumulation between successive free evolution periods, resulting in a longer coherence time. We numerically simulate the register coherence times using the method outlined in Supplementary Information Section .4. When limited by the ¹⁷¹Yb Knight field, simulation yields a Gaussian decay with a $1/e$ coherence time of $33~{}\mu$ s (equivalent to experimental results in Fig. 3a). We also predict an upper bound for the coherence time when decoupled from the ¹⁷¹Yb Knight field by turning off Hamiltonian terms associated with equation (S28), yielding an extended Gaussian decay of $417~{}\mu$ s (equivalent to experimental results in Fig. 3b). These simulated values are consistent with the corresponding experimental results ( $58\pm 4~{}\mu$ s and $225\pm 9~{}\mu$ s respectively) to within a factor of two. We note that this could indicate an error in our estimation of $g_{vz}$ by up to $25\%$ , potentially caused by a small discrepancy in the position of the two ⁵¹V bath spins closest to ¹⁷¹Yb. Further analysis of these parameters is left for future work.

.10 $T_{1}$ Lifetime Discussion

We measure the population decay of both the $\ket{0_{v}}$ and $\ket{W_{v}}$ states (timescales $T_{1}^{(0)}$ and $T_{1}^{(W)}$ respectively) by preparing the ⁵¹V register in the appropriate state and waiting for a variable time, $t$ , before swapping to the ¹⁷¹Yb for readout.

The $\ket{0_{v}}$ state exhibits slow exponential decay with $1/e$ time constant $T_{1}^{(0)}=0.54\pm 0.08$ s (Extended Data Fig. 8b). There are two contributions which could be limiting this decay:

1.

Resonant population exchange between the register spins and unpolarised frozen-core ‘dark spins’. For instance, the two nearest ⁵¹V ions (ions 1 and 2 in the table in Supplementary Information Section .1.2) may interact resonantly with the neighbouring register spins. However, we cannot detect or polarise these dark spins since they only interact with the ¹⁷¹Yb via Ising-like $\hat{S}_{z}\hat{I}_{z}$ terms.
2.

Off-resonant population exchange between the register and detuned unpolarised bath spins.

As for the $\ket{W_{v}}$ state, it exhibits a Gaussian decay with a much faster $1/e$ time constant of $T_{1}^{(W)}=39.5\pm 1.3~{}\mu$ s (Extended Data Fig. 8a). This can be explained by considering the effect of dephasing on the register spins. Specifically, the $\ket{W_{v}}$ state which our ¹⁷¹Yb qubit interacts with is given as

\ket{W_{v}}=\frac{1}{2}\left(\Ket{\uparrow\downarrow\downarrow\downarrow}+\Ket{\downarrow\uparrow\downarrow\downarrow}+\Ket{\downarrow\downarrow\uparrow\downarrow}+\Ket{\downarrow\downarrow\downarrow\uparrow}\right).

Crucially, there are three additional orthogonal states required to span the ⁵¹V register single excitation subspace:

	$\displaystyle\ket{\alpha_{v}}$	$\displaystyle=\frac{1}{2}\left(\Ket{\uparrow\downarrow\downarrow\downarrow}+\Ket{\downarrow\uparrow\downarrow\downarrow}-\Ket{\downarrow\downarrow\uparrow\downarrow}-\Ket{\downarrow\downarrow\downarrow\uparrow}\right)$
	$\displaystyle\ket{\beta_{v}}$	$\displaystyle=\frac{1}{2}\left(\Ket{\uparrow\downarrow\downarrow\downarrow}-\Ket{\downarrow\uparrow\downarrow\downarrow}+\Ket{\downarrow\downarrow\uparrow\downarrow}-\Ket{\downarrow\downarrow\downarrow\uparrow}\right)$
	$\displaystyle\ket{\gamma_{v}}$	$\displaystyle=\frac{1}{2}\left(\Ket{\uparrow\downarrow\downarrow\downarrow}-\Ket{\downarrow\uparrow\downarrow\downarrow}-\Ket{\downarrow\downarrow\uparrow\downarrow}+\Ket{\downarrow\downarrow\downarrow\uparrow}\right)$

We assume uncorrelated noise at each of the four ⁵¹V spins and apply a pure-dephasing master equation model. In the single excitation subspace, this becomes:

	$\displaystyle\dot{\rho}=2\Gamma$	$\displaystyle\left[\mathcal{D}\left(\Ket{\uparrow\downarrow\downarrow\downarrow}\Bra{\uparrow\downarrow\downarrow\downarrow}\right)+\mathcal{D}\left(\Ket{\downarrow\uparrow\downarrow\downarrow}\Bra{\downarrow\uparrow\downarrow\downarrow}\right)\right.$		(S29)
		$\displaystyle\left.+\mathcal{D}\left(\Ket{\downarrow\downarrow\uparrow\downarrow}\Bra{\downarrow\downarrow\uparrow\downarrow}\right)+\mathcal{D}\left(\Ket{\downarrow\downarrow\downarrow\uparrow}\Bra{\downarrow\downarrow\downarrow\uparrow}\right)\right]\rho$		(S30)

where the dephasing channel (Lindbladian) is given by

\mathcal{D}\left(\hat{a}\right)\rho=\hat{a}\rho\hat{a}^{\dagger}-\frac{1}{2}\{\hat{a}^{\dagger}\hat{a},\rho\}

(S31)

and $\Gamma$ is the dephasing rate on the $\omega_{c}$ transition of a single ⁵¹V spin. We solve this equation for different initial states $\rho(0)$ . When $\rho(0)=\ket{0_{v}}\bra{0_{v}}$ , dephasing does not contribute to $T_{1}^{(0)}$ , i.e. $\rho(t)=\rho(0)$ . However, when $\rho(0)=\ket{W_{v}}\bra{W_{v}}$ the state evolves according to

\rho(t)=\ket{W_{v}}\bra{W_{v}}e^{-2\Gamma t}+\frac{1}{4}\left(1-e^{-2\Gamma t}\right)\mathbb{1}^{(\text{SEM})}

(S32)

where $\mathbb{1}^{(\text{SEM})}$ is the single excitation manifold identity operator:

\mathbb{1}^{(\text{SEM})}=\ket{W_{v}}\bra{W_{v}}+\ket{\alpha_{v}}\bra{\alpha_{v}}+\ket{\beta_{v}}\bra{\beta_{v}}+\ket{\gamma_{v}}\bra{\gamma_{v}}

i.e. dephasing leads to decay of $\ket{W_{v}}$ into $\mathbb{1}^{(\text{SEM})}$ at rate $2\Gamma$ . For completeness we also consider the decay of the off-diagonal coherence term $\rho_{01}=\bra{0_{v}}\rho\ket{W_{v}}$ and find that

\rho_{01}(t)=\rho_{01}(0)e^{-\Gamma t}.

(S33)

Essentially, the pure dephasing model predicts $T_{2}^{*}=2T_{1}^{(W)}$ for our system.

We verify that dephasing is the main source of $\ket{W_{v}}$ population decay by demonstrating lifetime extension using the same motional narrowing approach employed to improve the coherence time (Supplementary Information Section .9). Specifically, during the wait time, we apply a series of $\pi$ pulses to the ¹⁷¹Yb separated by $6~{}\mu$ s leading to an extended lifetime of $T_{1}^{(W)}=127\pm 8~{}\mu$ s (Extended Data Fig. 8a). We note that both the bare and motionally-narrowed $T_{1}^{(W)}$ and $T_{2}^{*}$ times are close to the $T_{2}^{*}=2T_{1}^{(W)}$ limit identified above. We further extend the $T_{1}^{(W)}$ lifetime to $640\pm 20~{}\mu$ s using two ⁵¹V $\pi$ pulses applied during the wait time, thereby achieving dynamical decoupling from the nuclear Overhauser field (equivalent to the results in Fig. 3c).

Finally we note that if $T_{1}^{(W)}$ is limited by the ¹⁷¹Yb Knight field as a common noise source, there may be some discrepancy in the predictions of this model due to a high degree of noise correlation between the four ⁵¹V register spins arising from lattice symmetry. However, when performing motional narrowing we decouple the ¹⁷¹Yb Knight field and are likely limited by the, considerably less correlated, local Overhauser field. Further exploration of these correlated/uncorrelated fields is left for future work.

.11 Parity Oscillations and Coherence

Here we derive an expression for the ¹⁷¹Yb–⁵¹V Bell-state coherence $\rho_{01}=\bra{1_{g}0_{v}}\rho\ket{0_{g}W_{v}}$ in terms of the parity oscillation contrast with a correction factor. In particular, when reading out this coherence, we apply a $\sqrt{\text{swap}}$ gate which maps $\ket{\Psi^{+}}=\frac{1}{\sqrt{2}}(\ket{1_{g}0_{v}}-i\ket{0_{g}W_{v}})$ to $\ket{0_{g}W_{v}}$ and $\ket{\Psi^{-}}=\frac{1}{\sqrt{2}}(\ket{1_{g}0_{v}}+i\ket{0_{g}W_{v}})$ to $\ket{1_{g}0_{v}}$ . Note that reading out the ¹⁷¹Yb state is sufficient to distinguish the $\ket{\Psi^{+}}$ and $\ket{\Psi^{-}}$ states in this measurement. We can account for the readout fidelity of the $\ket{\Psi^{\pm}}$ states by using a $\sqrt{\mathcal{F}_{\text{sw,1}}}$ factor (Methods), i.e. if the state $\ket{\Psi^{+}}$ ( $\ket{\Psi^{-}}$ ) is perfectly prepared, ¹⁷¹Yb will be measured in state $\ket{0_{g}}$ ( $\ket{1_{g}}$ ) with probability $\frac{1}{2}(1+\sqrt{\mathcal{F}_{\text{sw,1}}})$ . To span the ¹⁷¹Yb–⁵¹V Hilbert space, we also need to consider the effect of the readout $\sqrt{\text{swap}}$ gate when the system is initialised into the other two states: $\ket{1_{g}W_{v}}$ or $\ket{0_{g}0_{v}}$ . To this end, we assign imperfect readout probabilities of $q_{11}$ and $q_{00}$ for $\ket{1_{g}W_{v}}$ and $\ket{0_{g}0_{v}}$ , respectively. Specifically, we can represent the dependence of the parity readout on the input state using the following matrix relation:

\begin{pmatrix}p_{\text{1,Yb}}\\ p_{\text{0,Yb}}\end{pmatrix}=\mathcal{M}_{\text{swap}}\mathcal{M}_{\text{wait}}\begin{pmatrix}p_{11}\\ p_{\Psi^{+}}\\ p_{\Psi^{-}}\\ p_{00}\end{pmatrix}

(S34)

with

	$\displaystyle\mathcal{M}_{\text{swap}}$	$\displaystyle=\begin{pmatrix}q_{11}&&\frac{1}{2}(1-\sqrt{\mathcal{F}_{\text{sw,1}}})&&\frac{1}{2}(1+\sqrt{\mathcal{F}_{\text{sw,1}}})&&1-q_{00}\\ 1-q_{11}&&\frac{1}{2}(1+\sqrt{\mathcal{F}_{\text{sw,1}}})&&\frac{1}{2}(1-\sqrt{\mathcal{F}_{\text{sw,1}}})&&q_{00}\end{pmatrix},$
	$\displaystyle\mathcal{M}_{\text{wait}}$	$\displaystyle=\begin{pmatrix}1&&0&&0&&0\\ 0&&\cos^{2}(\omega_{c}t/2)&&\sin^{2}(\omega_{c}t/2)&&0\\ 0&&\sin^{2}(\omega_{c}t/2)&&\cos^{2}(\omega_{c}t/2)&&0\\ 0&&0&&0&&1\end{pmatrix}.$

Here $p_{\text{1,Yb}}$ and $p_{\text{0,Yb}}$ are the probabilities of measuring the ¹⁷¹Yb qubit in $\ket{1_{g}}$ and $\ket{0_{g}}$ , respectively, and $p_{\Psi^{\pm}}=\bra{\Psi^{\pm}}\rho\ket{\Psi^{\pm}}$ are the probabilities of being in the $\ket{\Psi^{\pm}}$ Bell states. The contrast $C_{\text{parity}}$ of the parity oscillation between $\ket{\Psi^{+}}$ and $\ket{\Psi^{-}}$ is extracted by measuring the difference in the ¹⁷¹Yb $\ket{1_{g}}$ populations measured at $t=0$ and $t=\pi/\omega_{c}$ , allowing us to estimate the Bell state coherence as $|\rho_{01}|=C_{\text{parity}}/2\sqrt{\mathcal{F}_{\text{sw,1}}}$ . This implies that uncorrected and corrected Bell state coherence values differ by a factor of $\sqrt{\mathcal{F}_{\text{sw,1}}}=0.72$ . Using the results presented in Fig. 4b we obtain corrected and uncorrected estimates for $|\rho_{01}|$ of $0.352\pm 0.004$ and $0.254\pm 0.003$ respectively.

.12 Bell State Fidelity Error Analysis

To extract the Bell state fidelity and uncertainty, we perform a maximum likelihood analysis of the population and parity oscillation measurements, adopting a similar approach as in Bernien2013 . The population measurement involves a series of $n$ experiments with outcomes distributed between the four population states: $\{n_{00},n_{01},n_{10},n_{11}\}$ where $n=n_{00}+n_{01}+n_{10}+n_{11}$ . The likelihood function for the uncorrected populations, $\{p_{00},p_{01},p_{10},p_{11}\}$ has multinomial form:

\mathcal{L}\left(\{p_{ij}\}|\{n_{ij}\}\right)=\frac{n!}{n_{00}!n_{01}!n_{10}!n_{11}!}p_{00}^{n_{00}}p_{01}^{n_{01}}p_{10}^{n_{10}}p_{11}^{n_{11}}

(S35)

where we have assumed a prior uniform over the physical values of $\{p_{ij}\}$ , i.e. $0\leq p_{ij}\leq 1$ and $\sum p_{ij}=1$ . The likelihood function for the corrected populations, $\{c_{00},c_{01},c_{10},c_{11}\}$ , is obtained by substituting equation (11) into equation (S35) and assuming a prior uniform over the physical values of $\{c_{ij}\}$ , i.e. $0\leq c_{ij}\leq 1$ and $\sum c_{ij}=1$ . Corrected populations are obtained by maximising this likelihood function. The error for a specific population (say $c_{00}$ ) is obtained by marginalising $\mathcal{L}\left(\{c_{ij}\}|\{n_{ij}\}\right)$ over the other three ( $c_{01},c_{10},c_{11}$ ) and taking a $68\%$ symmetric confidence interval.

We extract a likelihood function for the coherence by considering the following model:

y_{i}=0.5+\sqrt{\mathcal{F}_{\text{sw,1}}}\rho_{01}\cos(\omega_{c}t_{i})+\epsilon_{i}

(S36)

where $\{t_{i},y_{i}\}$ are the parity oscillation data at the $i$ ^th point, $\rho_{01}$ is the corrected coherence, $\mathcal{F}_{\text{sw,1}}$ is the parity oscillation correction factor associated with the swap gate infidelity, and $\epsilon_{i}$ is the experimental error assumed to be normally distributed with $\mu=0$ and unknown $\sigma$ . The likelihood function is given by

\mathcal{L}\left(\rho_{01},\sigma|\{t_{i},y_{i}\}\right)=\prod_{i}\frac{1}{\sqrt{2\pi}\sigma}\exp\left[-\frac{\left(y_{i}-0.5-\sqrt{\mathcal{F}_{\text{sw,1}}}\rho_{01}\cos(\omega_{c}t_{i})\right)^{2}}{2\sigma^{2}}\right].

(S37)

We obtain a likelihood for the corrected coherence, $\mathcal{L}\left(\rho_{01}|\{t_{i},y_{i}\}\right)$ by marginalising over $\sigma$ .

The likelihood function for the fidelity is obtained by taking a product of the likelihood function for the populations with the likelihood function for the coherence and evaluating a contour integral at constant $\mathcal{F}$ , given by

\mathcal{L}\left(\mathcal{F}\right)=\int_{\mathcal{F}}\mathcal{L}\left(\{c_{ij}\}|\{n_{ij}\}\right)\mathcal{L}\left(\rho_{01}|\{t_{i},y_{i}\}\right)d\rho_{01}\prod_{ij}dc_{ij}.

(S38)

The Bell state fidelity is extracted by maximising this likelihood and the error is evaluated as a symmetric $68\%$ confidence interval.

Acknowledgements

This work was funded by the Institute of Quantum Information and Matter, an NSF Physics Frontiers Center (PHY-1733907) with support from the Moore Foundation, NSF 1820790, Office of Naval Research Award No. N00014-19-1-2182, Air Force Office of Scientific Research Grant No. FA9550-18-1-0374 and No. FA9550-21-1-0055, Northrop Grumman, General Atomics, and Weston Havens Foundation. The device nanofabrication was performed in the Kavli Nanoscience Institute at the California Institute of Technology. J.R. acknowledges the support from the Natural Sciences and Engineering Research Council of Canada (NSERC) (PGSD3-502844-2017). A.R. acknowledges the support from the Eddleman Graduate Fellowship. J.C. acknowledges support from the IQIM postdoctoral fellowship. We thank J. Kindem, J. G. Bartholomew, N. Yao, A. Sipahigil, M. Lei and T. Xie for useful discussion, and M. Shaw for help with superconducting photon detectors.

Nuclear spin-wave quantum register for a solid state qubit

References

Extended Data

Methods

Experimental Setup

171Yb Initialisation, Readout and Experiment Sequence

ZenPol Sequence

Direct Drive Gates for 51V Register

Population Basis Measurements

Swap Gate Fidelity Correction

Supplementary Information

.1 171Yb–51V Interactions

.1.1 Ground State 171Yb Hamiltonian

.1.2 Local Nuclear Spin Environment

.1.3 171Yb–51V Interactions

.1.4 Nuclear Overhauser Field

.1.5 Interaction with Register Ions

.1.6 Full System Hamiltonian

.2 Randomised Benchmarking and 171Yb Qubit Coherence

.3 Extra Register Detail

.4 Simulation

.5 Hartmann Hahn Spectroscopy

.6 Polarisation of multi-level register nuclear spins

.7 Analysis of Spin Exchange Dynamics

.8 Single Excitation in ωc\omega_{c} Manifold

.9 T2∗T_{2}^{*} Coherence Discussion

.10 T1T_{1} Lifetime Discussion

.11 Parity Oscillations and Coherence

.12 Bell State Fidelity Error Analysis

Acknowledgements

¹⁷¹Yb Initialisation, Readout and Experiment Sequence

Direct Drive Gates for ⁵¹V Register

.1 ¹⁷¹Yb–⁵¹V Interactions

.1.1 Ground State ¹⁷¹Yb Hamiltonian

.1.3 ¹⁷¹Yb–⁵¹V Interactions

.2 Randomised Benchmarking and ¹⁷¹Yb Qubit Coherence

.8 Single Excitation in $\omega_{c}$ Manifold

.9 $T_{2}^{*}$ Coherence Discussion

.10 $T_{1}$ Lifetime Discussion