PHOBOS Collaboration
Nucleon-Gold Collisions at 200 AGeV Using Tagged d+Au Interactions in PHOBOS
Abstract
Forward calorimetry in the PHOBOS detector has been used to study charged hadron production in +Au, +Au and +Au collisions at . The forward proton calorimeter detectors are described and a procedure for determining collision centrality with these detectors is detailed. The deposition of energy by deuteron spectator nucleons in the forward calorimeters is used to identify +Au and +Au collisions in the data. A weighted combination of the yield of +Au and +Au is constructed to build a reference for Au+Au collisions that better matches the isospin composition of the gold nucleus. The and centrality dependence of the yield of this improved reference system is found to match that of +Au. The shape of the charged particle transverse momentum distribution is observed to extrapolate smoothly from + to central +Au as a function of the charged particle pseudorapidity density. The asymmetry of positively- and negatively-charged hadron production in +Au is compared to that of +Au. No significant asymmetry is observed at mid-rapidity. These studies augment recent results from experiments at the LHC and RHIC facilities to give a more complete description of particle production in +A and +A collisions, essential for the understanding the medium produced in high energy nucleus-nucleus collisions.
PACS numbers: 25.75.Dw, 25.75.Gz
I Introduction
The PHOBOS detector Back et al. (2003a) at the Relativistic Heavy Ion Collider (RHIC) Hahn et al. (2003) is one of several experiments Adamczyk et al. (2003); Adcox et al. (2003a); Ackermann et al. (2003) that have measured the invariant yield of charged hadrons in collisions of deuterons with gold nuclei at a nucleon-nucleon center of mass energy of . In the referenced papers, charged hadron production is studied as a function of both transverse momentum () and collision centrality (a measure correlated with the impact parameter of the deuteron). The particle yields for above about 1.5–2.0 GeV are similar to, or possibly slightly enhanced above, those observed in + collisions at the same energy Back et al. (2003b), somewhat reminiscent of the so-called Cronin effect seen in proton-nucleus collisions Cronin et al. (1975). Previous analyses of the +Au charged hadron spectra by PHOBOS Back et al. (2003b) and the other RHIC experiments Adler et al. (2003a); Adams et al. (2003a); Arsene et al. (2003); Adams et al. (2006); Adler et al. (2006) have demonstrated that this enhancement stands in stark contrast to the observed suppression of high hadrons in the (central) Au+Au collision system at Adcox et al. (2002, 2003b); Adler et al. (2002); Back et al. (2004a). Since no suppression is found in +Au collisions, the effect seen in central Au+Au interactions has been interpreted as evidence of final state effects, in particular parton energy loss. It should be noted that evidence of possible collective effects in systems such has +Au and +Pb have been found recently, but only for events with very high final state particle multiplicity (see, as one example, Ref. Chatrchyan et al. (2013)).
The choice of the reference system used in comparing to Au+Au data, and of the centrality measure, are both of critical importance to the understanding of the observed suppression. The data and Monte Carlo (MC) simulations presented in this paper are used to study the choice of centrality measure, as well as the choice of reference system. Centrality measures based on the multiplicity of particles in the high-pseudorapidity region as well as on the number of spectators in the gold nucleus are examined. To study the chosen reference system, a calorimetry-based technique is used to identify, on an event-by-event basis, the subsets of +Au collisions in which only the proton or only the neutron participated in the collision. Specifically, a calorimeter on the side of the interaction region where the Au beam exits is used as part of the determination of collision centrality while a second calorimeter on the other side is used in the selection of +Au and +Au interactions. Similar tagging of the nucleon+Au component of the +Au data has also been investigated by the PHENIX collaboration Adler et al. (2008); Adare et al. (2014). These nucleon-nucleus collisions are used to construct an ideal reference system for comparison with Au+Au collisions. Further, the charged hadron yields of +Au and +Au are compared in order to study the ability of nucleon-nucleus collisions to transport charge to the mid-rapidity region.
II The PHOBOS Detector
The PHOBOS experiment makes use of multiple detector components to measure particles produced by collisions at RHIC. Silicon pad detectors near the interaction point are used for particle tracking and collision vertex determination, see Sect. IV. Additional silicon pad detectors provide full azimuth and large pseudorapidity coverage, as described in Sect. III. Collision triggering is provided by plastic scintillator arrays at high pseudorapidity, see Sect. III, and by calorimeters measuring the number of neutral spectator nucleons, described below. More detail on these subsystems may be found in Ref. Back et al. (2003a).
To study nucleon-nucleus collisions, two calorimeters were added to the PHOBOS experiment prior to the 2003 +Au physics run at RHIC. These detectors extend the measurement of forward-going nuclear fragments. Complementing the pre-existing zero-degree calorimeters (“ZDCs”) that collect energy from spectator neutrons Adler et al. (2003b), the proton calorimeter (“PCAL”) detectors measure energy from free spectator protons. Each PCAL detector is assembled from lead-scintillator bricks originally constructed for the E864 experiment Armstrong et al. (1998) at the AGS. The bricks are 117 in length with a cross section facing the interaction point. Each brick has an array of scintillating fibers running along its entire length. All of the fibers from a single detector element are read out by a Phillips XP 2262B phototube at the back.
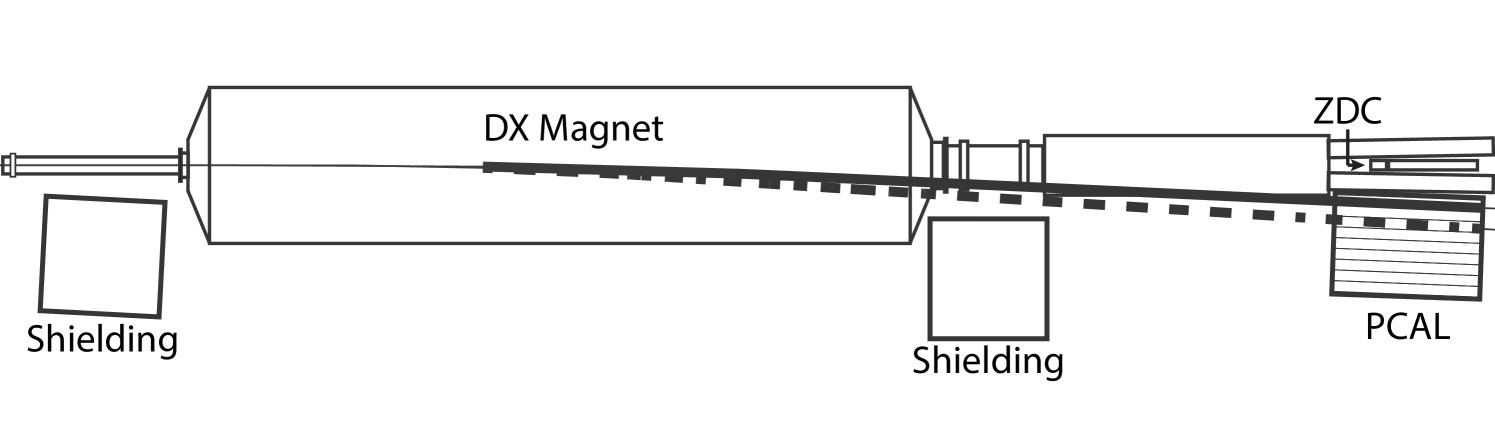
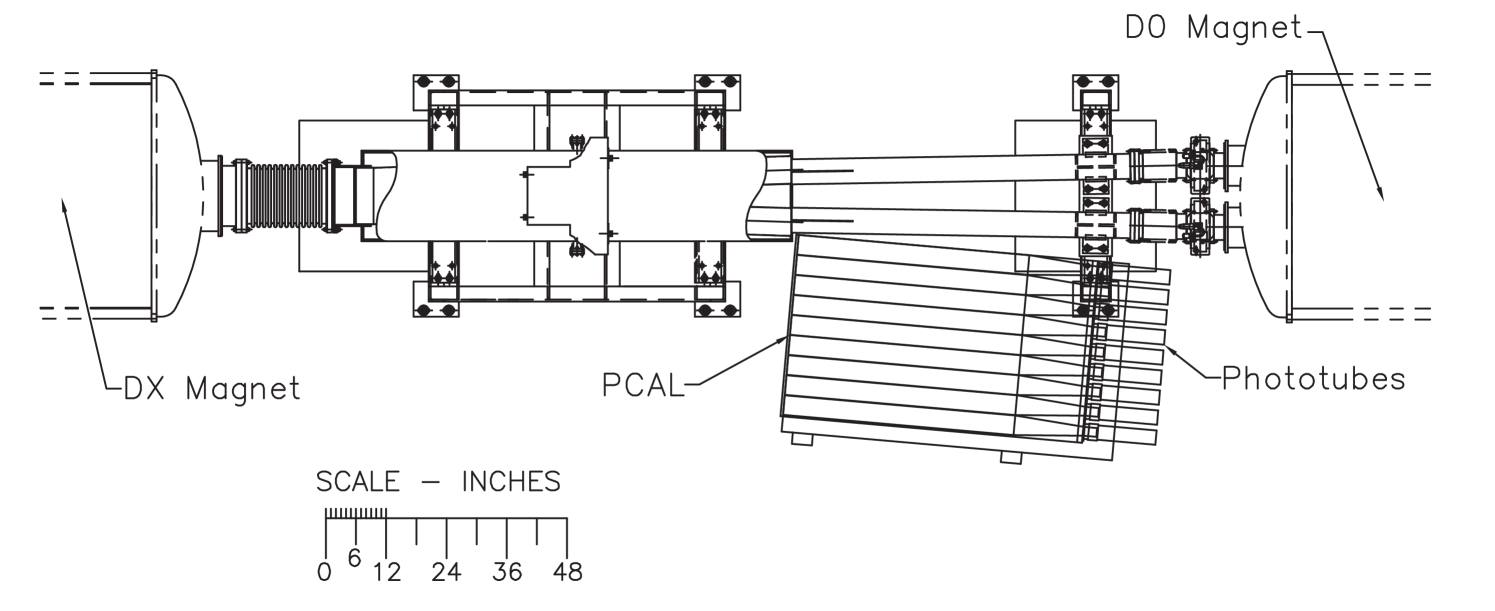
The PCAL detector on the Au-exit side of the collision (see plan view in Fig. 1) consists of an array 8 bricks wide by 10 bricks high. The d-exit side PCAL (not shown in the figure) is a small array. As mentioned above, the former is used for centrality determination while the latter is used, along with the ZDC, for tagging +Au and +Au interactions. Both calorimeters are centered at the beam height and the smaller calorimeter is mounted with its elements at the same location transverse to the beam as the two closest elements shown in Fig. 1.
Because of their higher charge to mass ratio (compared to the deuteron and Au nuclei, as well as nuclear fragments), spectator protons emerging from either side of the interaction are bent out of the beam pipe and into a PCAL detector by the RHIC DX-magnets. The primary purpose of these DX-magnets is to direct the deuteron and gold ion beams into and out of the interaction region.
The larger Au-PCAL covers a pseudorapidity region and therefore could be struck by produced particles in addition to the spectator protons it was designed to detect. In order to prevent this, two shields consisting of 44 thick concrete blocks were installed between the calorimeter and the interaction region.
The energy coming from Au-side spectator protons (EPcal) is calculated using bricks in the the Au-PCAL which are located in the two rows at beam height, as well as the outer four columns away from the beam. The two rows at beam height are found to contain a majority of the hadronic shower energy in simulations of single nucleons having momenta comparable to nuclear thermal and fragmentation emission. The columns away from the beam supplement the shower containment. The remaining bricks, in columns near the beam but above and below beam height, are not included in EPcal. This reduces contamination from particles emitted in the neutron-induced hadronic showers which escape the ZDC.
The Au-PCAL modules have been calibrated relative to each other using energy deposited by cosmic rays. Fast scintillator detectors are installed above and below the Au-PCAL detector to serve as cosmic ray triggers during dedicated calibration data taking. Modules in the d-PCAL have been calibrated relative to each other by minimizing the width of the single-proton peak in the d-PCAL energy distribution.
III Collision Reconstruction
III.1 Collision Selection
Deuteron-gold interactions are identified using a set of selection criteria designed to minimize background (i.e. beam-gas interactions) and enhance the sample of collisions which could produce particles inside the spectrometer acceptance. First, at least one hit is required in both of the 16-scintillator arrays (see Ref. Back et al. (2003a) for more details on this and other detector elements) which cover a pseudorapidity range of . Then, the longitudinal collision vertex, as determined by a single-layer silicon detector covering the beam-pipe in the mid-rapidity range, is required to be within 10 of the nominal interaction point. Further, this vertex is required to be in reasonable agreement (within 25 ) with that found by the simple timing difference of two sets of fast Cherenkov counters, located at and ( being in the deuteron direction). Finally, events that appeared to have signals from either a previous or following collision are removed. If two events occur within 5 , the later event is rejected as containing pile-up signals in the silicon. If two events occur within 500 , as determined using the fast trigger detectors, then both are rejected as pile-up.
III.2 Centrality Determination
Two experimental observables have been used as centrality measures by the analysis presented in this paper. The first variable, “ERing”, is a measure of the total energy recorded in “Rings”, endcap silicon detectors. The rings have nearly coverage in azimuth and cover eta ranges of and . The second variable, EPcal, is described in Sect. II, and measures the energy of Au protons that do not participate in inelastic collisions with the deuteron. Thus, EPcal measures protons near beam rapidity, .
The distribution of each of these variables in the +Au data can be used to determine the fractional cross section centrality bins. Details on this procedure may be found in Refs. Back et al. (2004b, 2005a). The extraction of average values of collision parameters, such as the number of participant nucleons (), as well as the determination of the centrality-dependent efficiency of the collision event selection requires a set of simulations. Models of +Au collisions from both the HIJING Gyulassy and Wang (1994) and AMPT Zhang et al. (2000) packages have been studied. The detector simulation has been performed using the GEANT package Brun et al. (1987). In addition to , other centrality parameters have been studied using these simulations, including and , the number of participants in the gold and deuteron, respectively, , the number of nucleon-nucleon collisions in the interaction, and , the average number of collisions per deuteron participant.
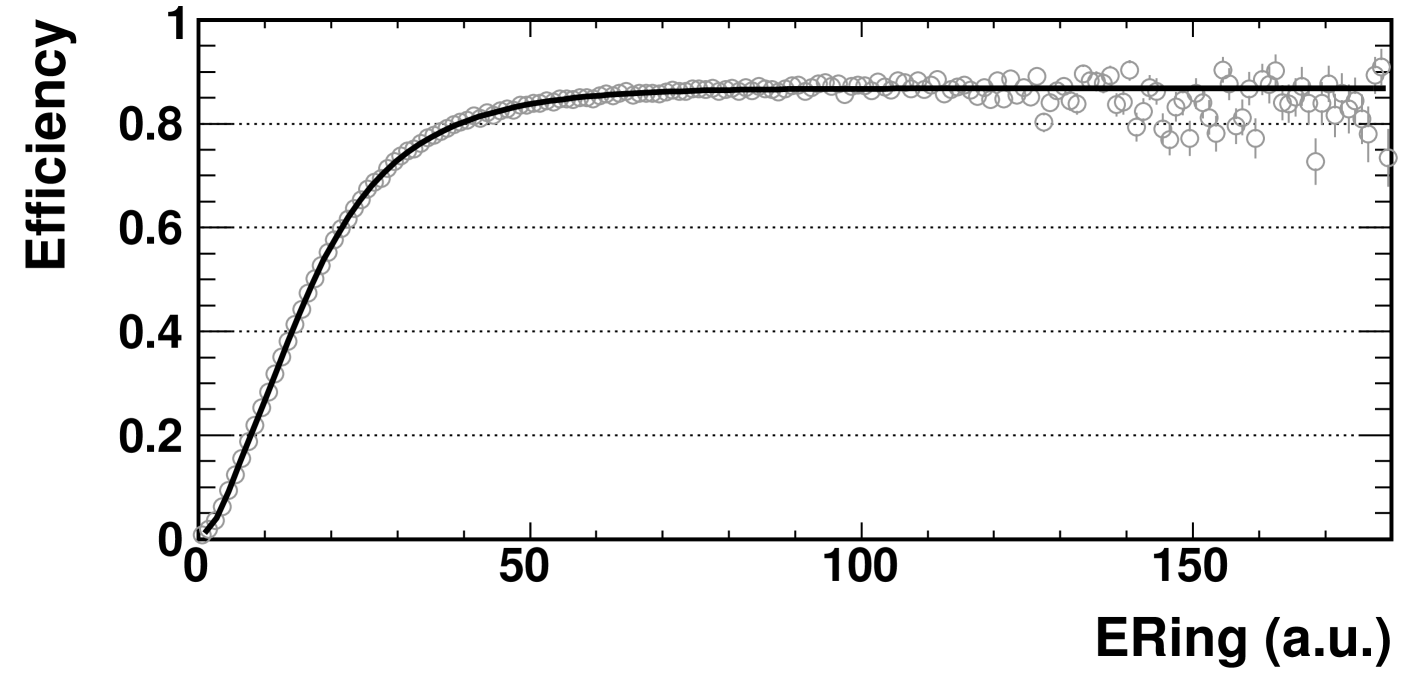
The efficiency of the collision selection can be determined from the simulations as a function of the chosen centrality variable. This is done by counting the fraction of simulated events that pass the event selection as a function of centrality. Because the event selection contains a vertex cut, the fraction is calculated as the number of events passing the event selection divided by the number of events having a true interaction vertex within 10 of the nominal interaction point. The efficiency as a function of the ERing centrality variable, obtained using AMPT simulations, is shown in Fig. 2. Note that the efficiency does not approach unity, even for central events, due to the small acceptance of the detectors that determine the collision vertex as part of the trigger.
This efficiency is used to unbias the centrality variable distribution measured in the data. The unbiased distribution is then divided into fractional cross section bins, using the method described in Ref. Back et al. (2002a).
The efficiency function presented in Fig. 2 is also used to correct, on an event-by-event basis, the measurements of the charged hadron spectra presented in this article. This accounts for the variation of the selection efficiency within a centrality bin, whereas the application of the average efficiency in a centrality bin would not.
For both the HIJING and AMPT collision generators, a Glauber model has been used to determine the average values of centrality parameters, such as , which cannot be measured directly. A Hulthén wave function Hulthén and Sugawara (1957) has been used to model the deuteron profile, while the gold nucleus density has been modeled using a Woods-Saxon distribution. The value of the inelastic nucleon-nucleon cross section used in the Glauber model is 41 . The average value of the chosen centrality parameter can then be determined for each fractional cross section bin; for details on this procedure, see Ref. Back et al. (2002b).
The systematic uncertainties of the various (unbiased) centrality parameters, such as , have been studied. The dependence on simulations has been quantified by varying the centrality efficiency, for example, that shown in Fig. 2 for ERing centrality bins. The amount by which the efficiency can vary is estimated by dividing the simulated events into vertex bins. The dependence on the deuteron wave function has been studied by using both a Hulthén wave function, as well as a Woods-Saxon distribution. The uncertainty of the centrality parameters resulting from the choice of collision simulation model has been studied by comparing to simple Glauber MCs. Uncertainties in using the efficiency function to unbias the centrality parameters have been accounted for by smearing the centrality measure (i.e. ERing) prior to applying the efficiency correction. Finally, the centrality parameters coming from different collision simulation packages are compared.
The centrality parameters determined from ERing centrality bins are presented in Table 1. The values for +Au and +Au tagged events, described in Sect. III.4, are also shown. The systematic uncertainties of and are typically slightly different, with that for usually larger. The table lists the larger of the two uncertainties.
III.3 Proton Calorimeter Centrality Determination
The Au-PCAL detector facilitates the determination of the centrality of +Au collisions using a variable, EPcal, which is independent of the measured multiplicity. As has been shown previously Back et al. (2004b, 2005a), multiplicity measurements in a particular region of pseudorapidity may be biased if the centrality of collisions is determined using (multiplicity based) observables in a similar pseudorapidity region. The ERing observable is measured at high pseudorapidity, allowing measurements at mid-rapidity to be minimally biased by such auto-correlations. Centrality derived from the number of spectator nucleons should be free of such biases. A measurement of the charged hadron spectral shape in centrality bins from both ERing and EPcal is presented in Sect. VI.
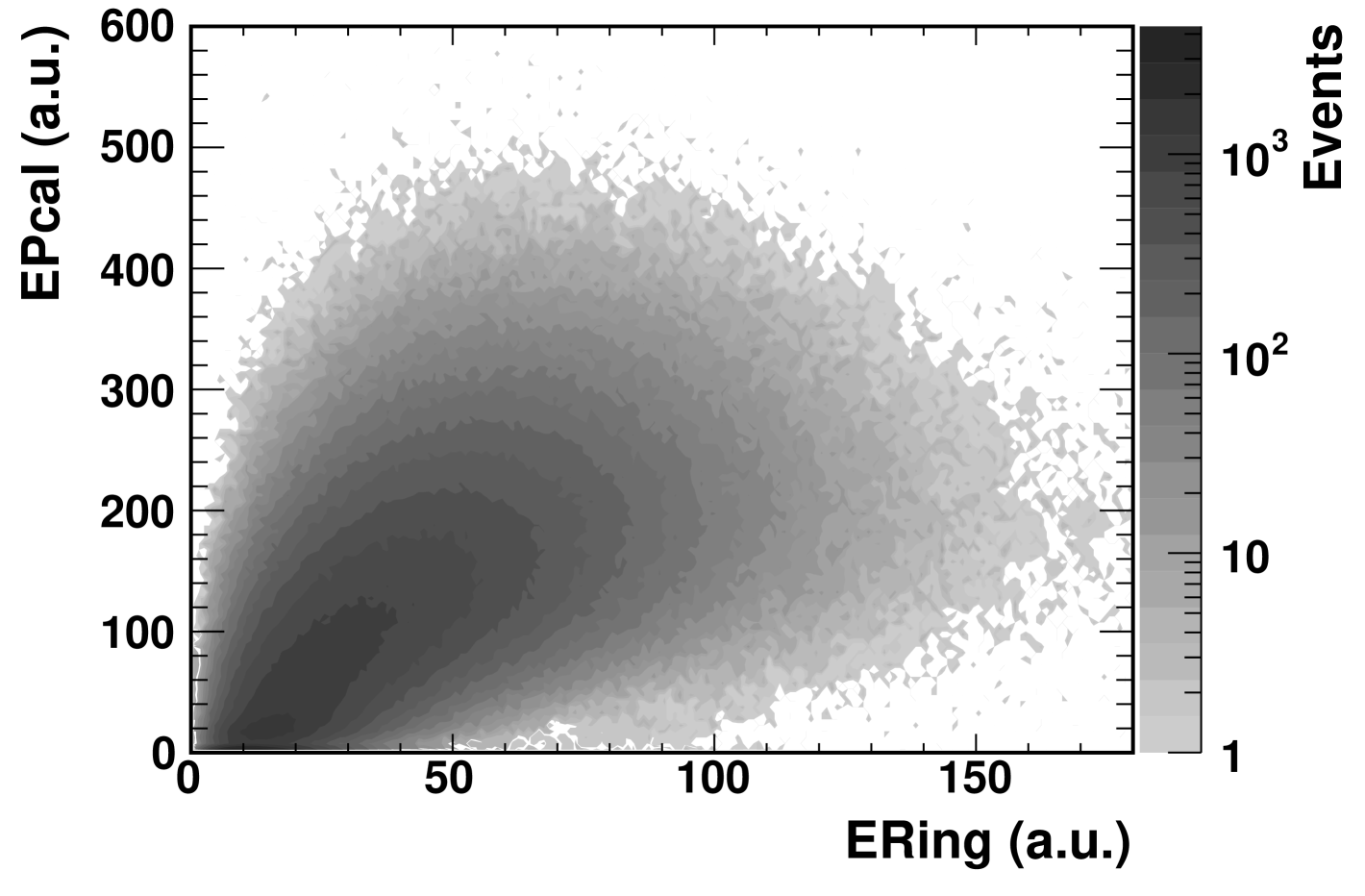
Centrality bins could, in principle, be derived from EPcal signals using the same procedure as for the other observables. However, the breakup of the gold nucleus is not modeled by either the MC event generators, HIJING and AMPT, or the GEANT detector simulation. As a result, an alternative procedure has been developed that exploits the monotonic correlation in the +Au data between the EPcal signal, and the signal of another (well-modeled) detector, ERing. This correlation is shown in Fig. 3.
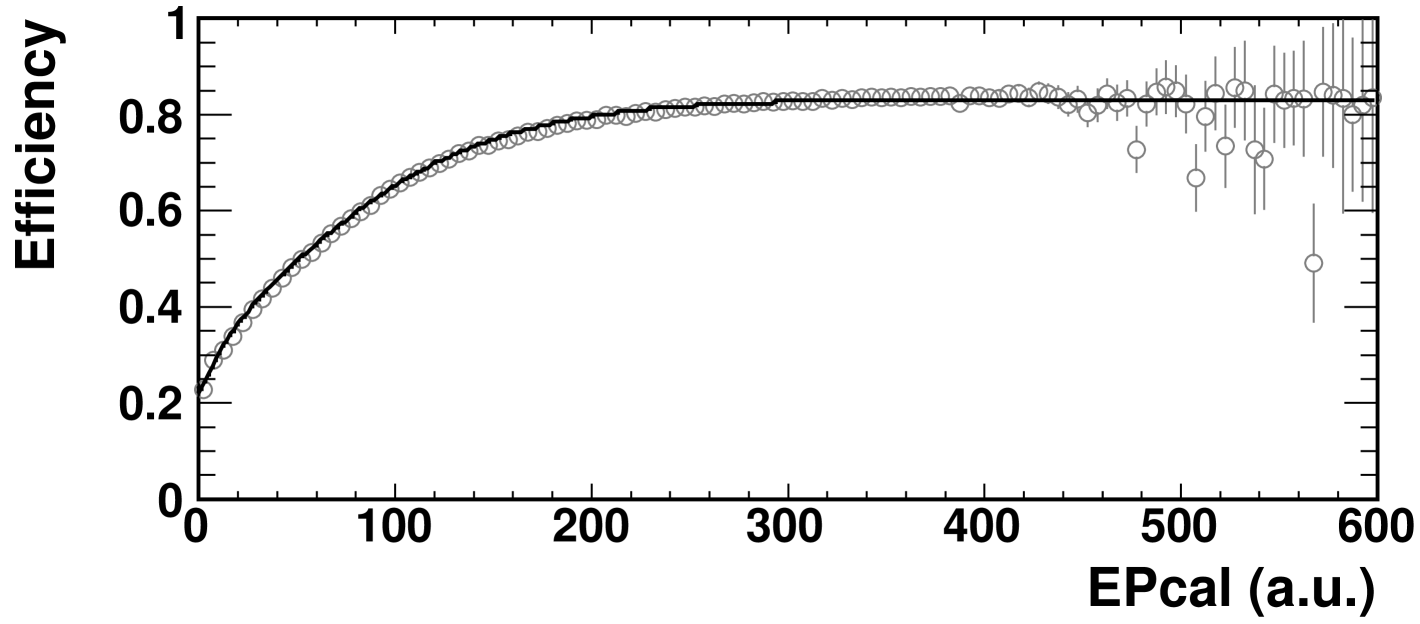
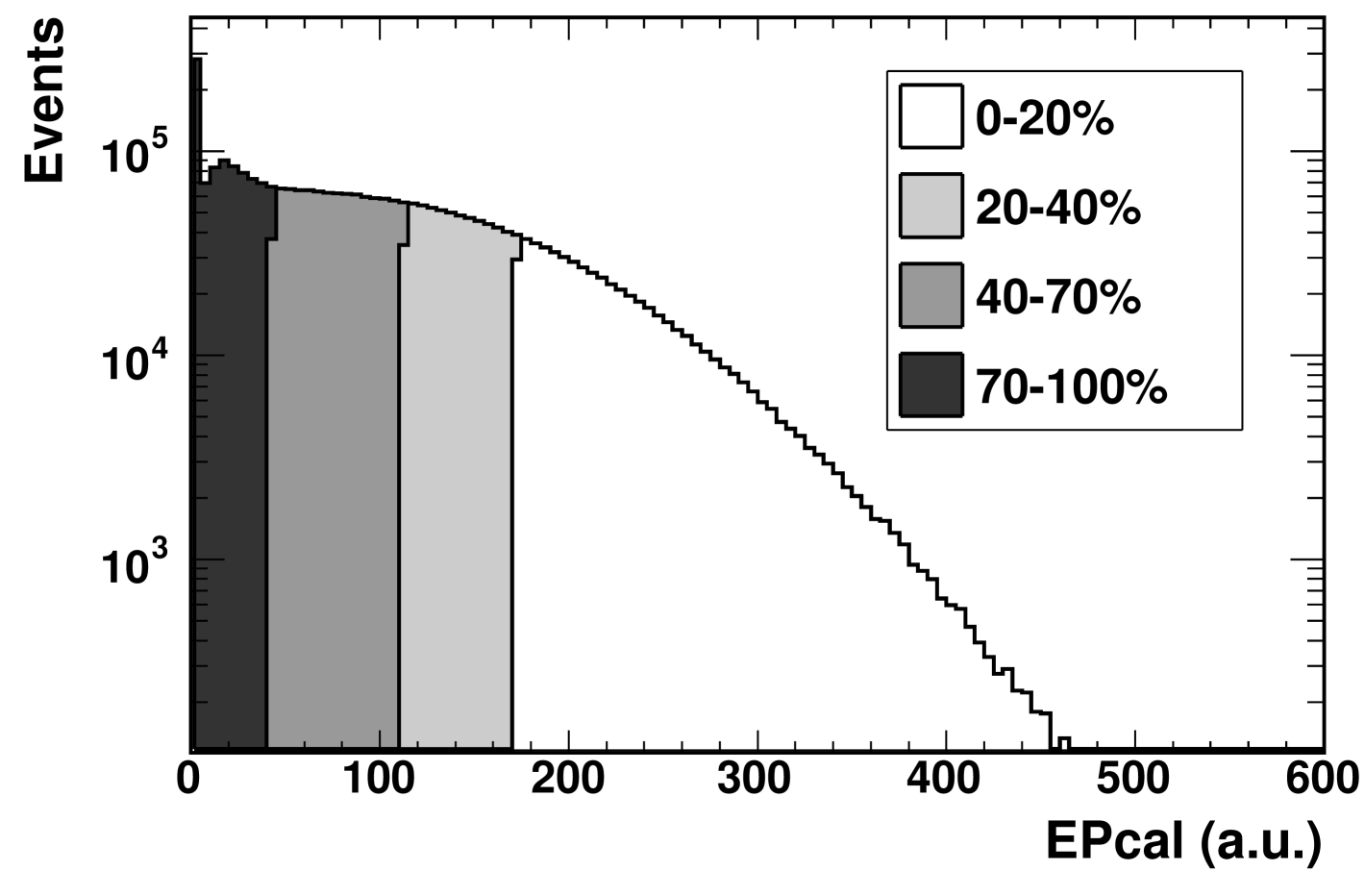
The method for deriving event selection efficiency for a given value of EPcal uses the known efficiency of ERing. Using each event in the data, two distributions of EPcal are generated: one simply counting events and one counting events but weighted by the inverse of the known efficiency of the correlated observable, . The efficiency as a function of EPcal is determined from the ratio of the simple-count distribution divided by that using weighted counts. This efficiency is used in the standard procedure to evaluate EPcal cutoff values for the centrality bins. Figures 4 and 5 show the event selection efficiency as a function of EPcal and the resulting EPcal centrality bins, respectively, obtained by using ERing.
Two different procedures have been developed to estimate the average number of nucleons participating in the inelastic collision, , for a given EPcal centrality bin. Both procedures exploit the correlation of EPcal with ERing and then of ERing with . The same procedures are used to estimate other collision parameters as well, such as the number of nucleon-nucleon collisions, , or the impact parameter, .
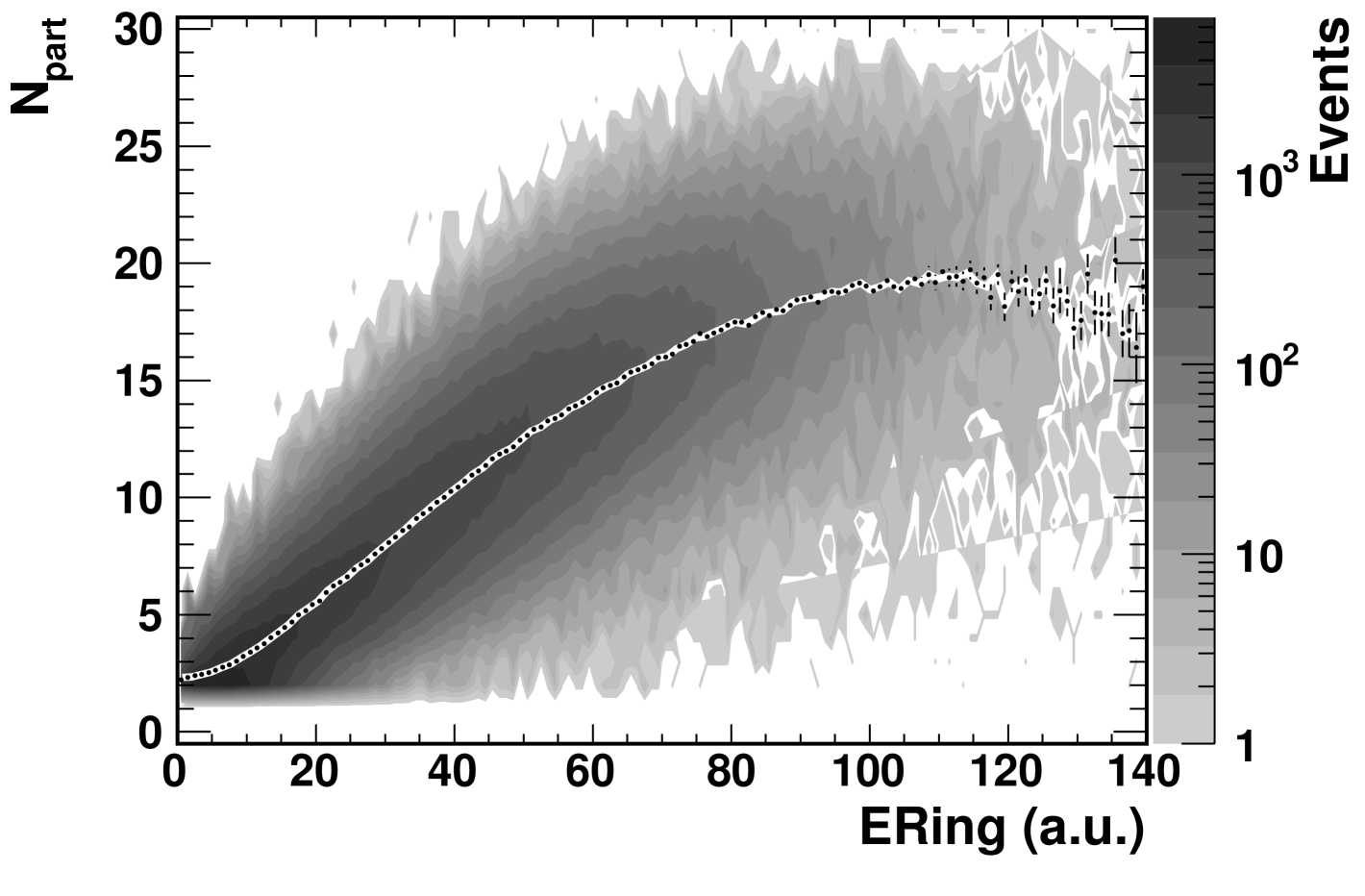
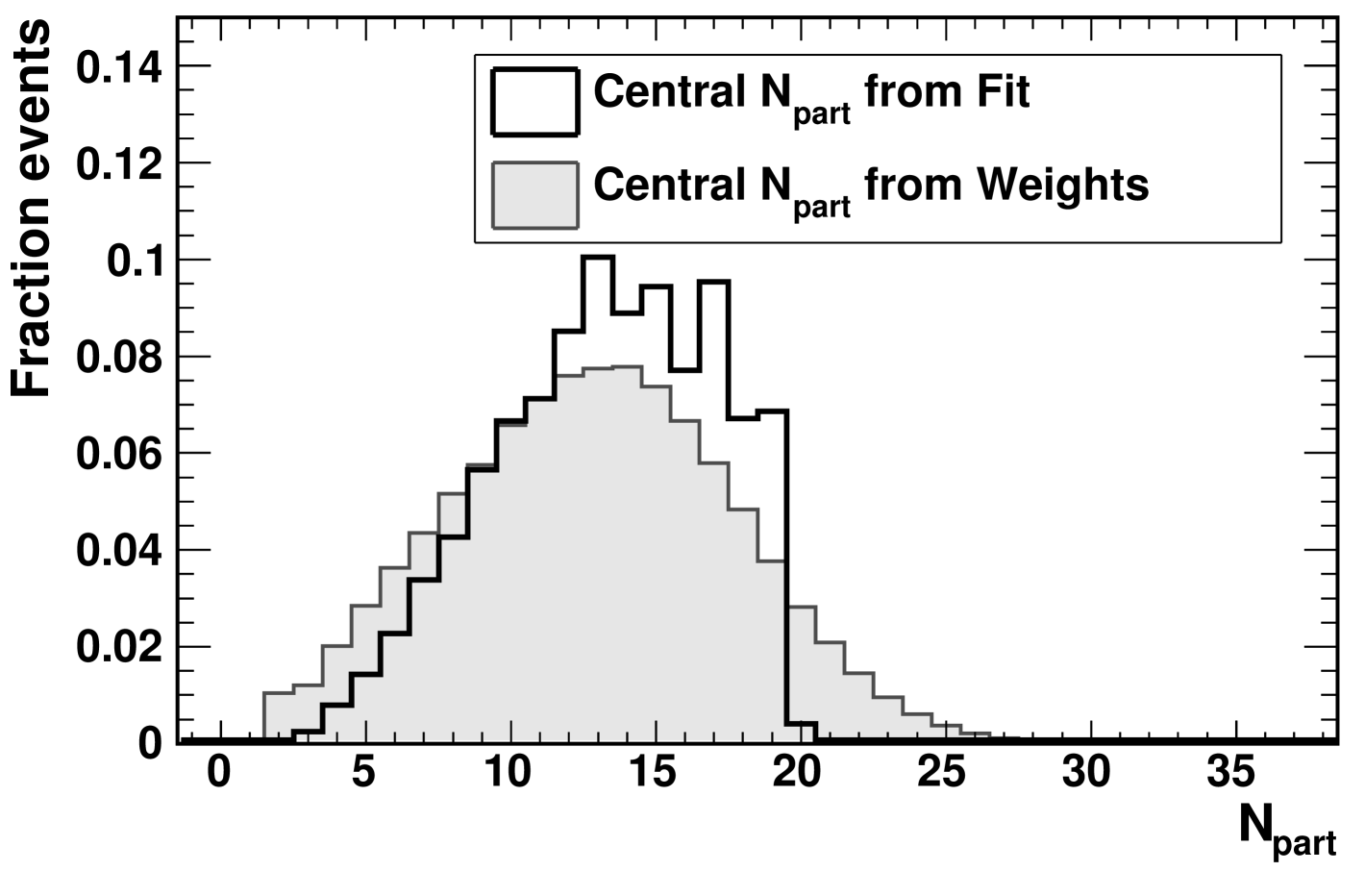
The simpler approach involves fitting the mean in small bins of ERing, as shown in Fig. 6. The fit is used to estimate the average value of given the value of ERing in an event. These values are then used to obtain distributions for each EPcal centrality bin.
The second approach begins by dividing the ERing distribution for events in a given EPcal centrality bin by the distribution for all events in order to determine the probability of any particular value of ERing in that bin. Then, for each centrality bin, all MC events are weighted according to the appropriate probability for their value of ERing and the distribution of is determined with these weights applied.
The results of the two techniques are compared for the most central EPcal bin in Fig. 7. In the first procedure (open histogram), the spread of in the resulting distribution depends only on the width of the correlation of EPcal and ERing, while in the second (grey histogram) it is also affected by the correlation of ERing and . The latter is almost certainly an overestimate of the width of in a given centrality bin, while the former may underestimate the spread. However, in the analysis of spectra and yields, this difference in width is only significant to the degree that it affects the mean value. The differences of the means found using the two techniques are included in the systematic uncertainty estimate for the values of . Analogous systematic uncertainties are determined for the other centrality parameters, such as or . The weighting and fit procedures differ by about 5% in central +Au and about 25% in peripheral +Au.
| Parameter | System(s) | ERing Bins | EPcal (from ERing) Bins | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 0-20% | 20-40% | 40-70% | 70-100% | 0-20% | 20-40% | 40-70% | 70-100% | ||
| () | +Au | ||||||||
| +Au, +Au | |||||||||
| +Au | |||||||||
| +Au, +Au | |||||||||
| +Au | |||||||||
| +Au, +Au | |||||||||
| +Au | |||||||||
| +Au, +Au | |||||||||
| Sys. Error | +Au | 7.5% | 10% | 15% | 30% | 15% | 15% | 20% | 30% |
| +Au, +Au | 10% | 12% | 17% | 31% | 31% | 31% | 31% | 31% | |
The systematic uncertainty inherent in the procedure used to determine centrality from the EPcal variable has been studied. This has been done by applying the indirect procedure described above for EPcal to well modeled detectors at mid-rapidity, for which the direct procedure described in Sect. III.2 can also be used. Discrepancies between centrality parameters obtained via the direct and indirect methods are used to quantify the systematic uncertainties on this procedure. This uncertainty is in addition to those described in Sect. III.2.
III.4 Deuteron-Nucleon Tagging
The low binding energy of the deuteron nucleus (1.11 per nucleon) facilitates the analysis presented in this paper. Because the deuteron is so weakly bound, it is possible for the nucleons to be relatively far apart at the moment the deuteron collides with the gold nucleus. This can result in only one nucleon of the deuteron participating in the (inelastic hadronic) collision. Furthermore, the binding energy is so small compared to the beam energy that the remaining spectator nucleon can emerge from the collision almost completely unperturbed. Thus, such a collision can be treated as an effective collision between a single nucleon and a gold nucleus.
Although the size of a deuteron is relatively large, the proton-neutron separation is typically not larger than the size of the Au target. As a result, the nucleon-gold collisions that form a subset of the deuteron-gold data are not equivalent to minimum bias nucleon-gold data. Rather, they are biased towards more peripheral interactions. Further investigations of this bias and the techniques used to address it in the present analysis are discussed below.
The subset of +Au collisions matching +Au and +Au interactions have been identified through the observation of the spectator nucleon of the deuteron. The deuteron spectators are measured in PHOBOS using both the PCAL and ZDC detectors on the deuteron-exit side of the collision. Qualitatively, a collision in which the d-PCAL registered a spectator and the d-ZDC did not is labeled an +Au interaction (and vice-versa for +Au interactions).
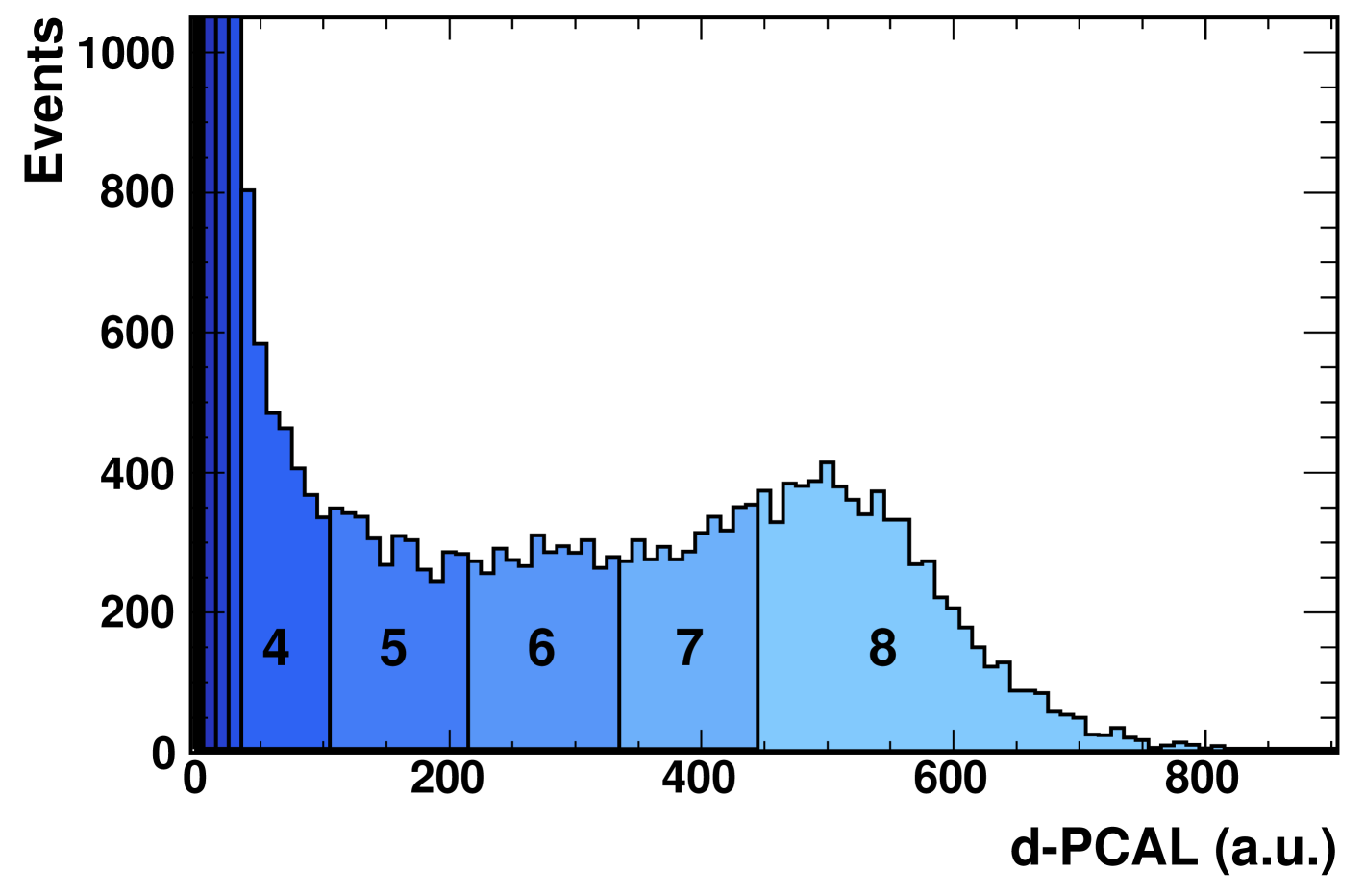
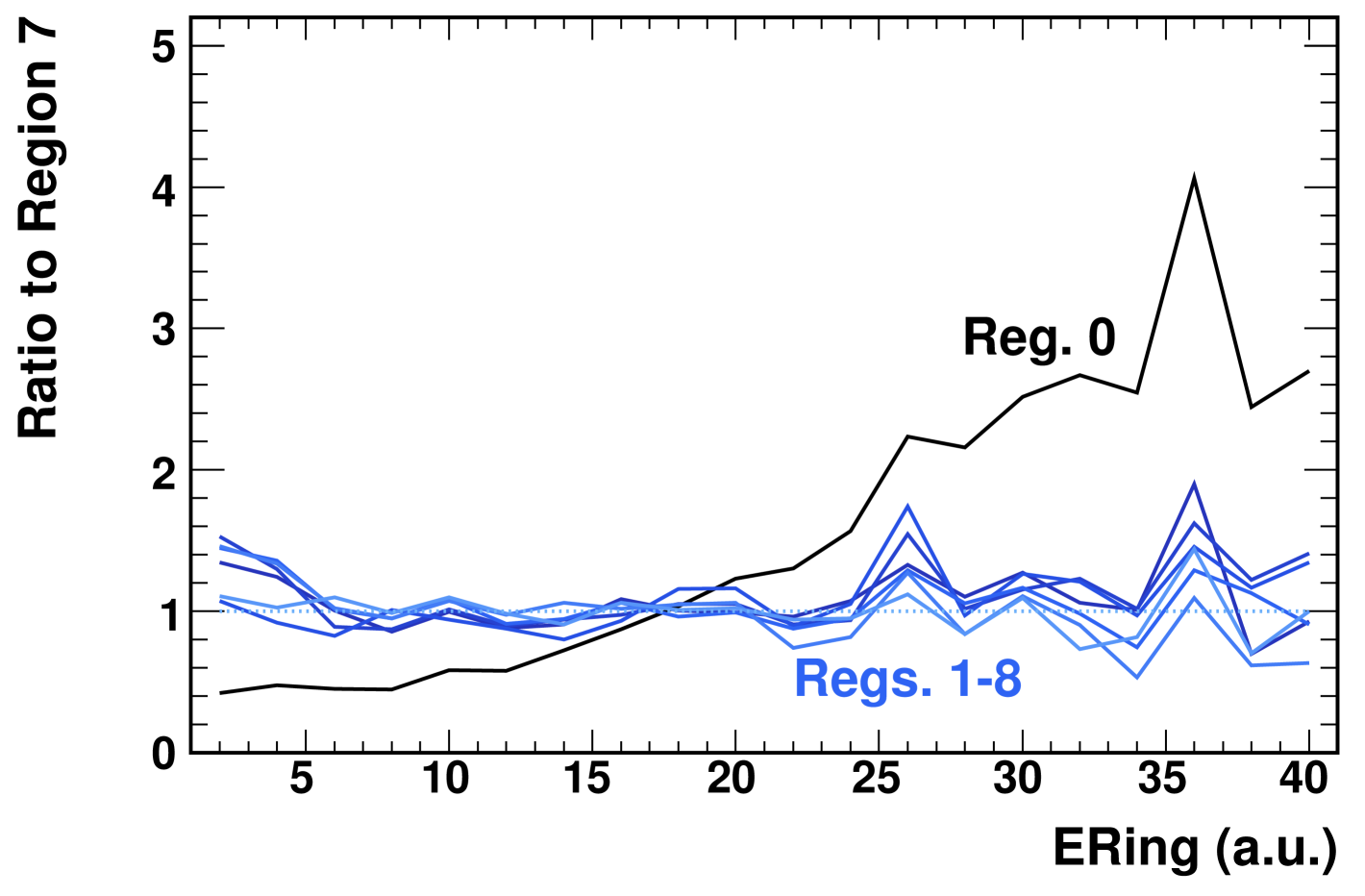
The observation of a spectator by one of the detectors is established from the amount of energy deposited in that calorimeter. Because the response of these calorimeters has not been simulated in the PHOBOS +Au MC, the efficiency and purity of the chosen signal cuts cannot be studied directly. Instead, the effect of the cuts on an independent centrality measure (ERing) has been explored. This alternative method is motivated by the expectation that tagging nucleon-nucleus collisions should produce a data set that is biased toward interactions with larger impact parameters than the full +Au data set.
The distribution of energy deposited in the d-PCAL is shown in Fig. 8 which has been divided into an arbitrary set of regions numbered 0–8. While regions 7 and 8 show evidence of a proton peak in the d-PCAL, events from all regions with non-zero energy deposition (regions 1–8) show similar centrality characteristics, as will be discussed below. Only events in region 0 show a bias toward more central collisions and are therefore assumed to completely lack a proton spectator.
The presence or absence of a centrality bias in the regions displayed in Fig. 8 is seen in Fig. 9, which shows the variation in the shape of the ERing distribution for events depositing different amounts of charge in the d-PCAL. Each line represents the ratio between a particular region of Fig. 8 and region 7. Collisions that deposit no energy into the d-PCAL show a striking bias towards more central (higher ERing) interactions. Collisions in regions 1–8 all show similar ERing distributions. This suggests that any amount of energy deposited into the d-PCAL is due to a proton spectator from the deuteron.
Furthermore, the observation that the shape of the ERing distribution is the same for all collisions which deposit energy in the d-PCAL supports the idea that these collisions are all of the same type, namely +Au. As expected, the centrality of +Au and tagged +Au collisions differ, but the centrality of +Au does not depend on the amount of energy that the spectator proton deposits in the calorimeter.
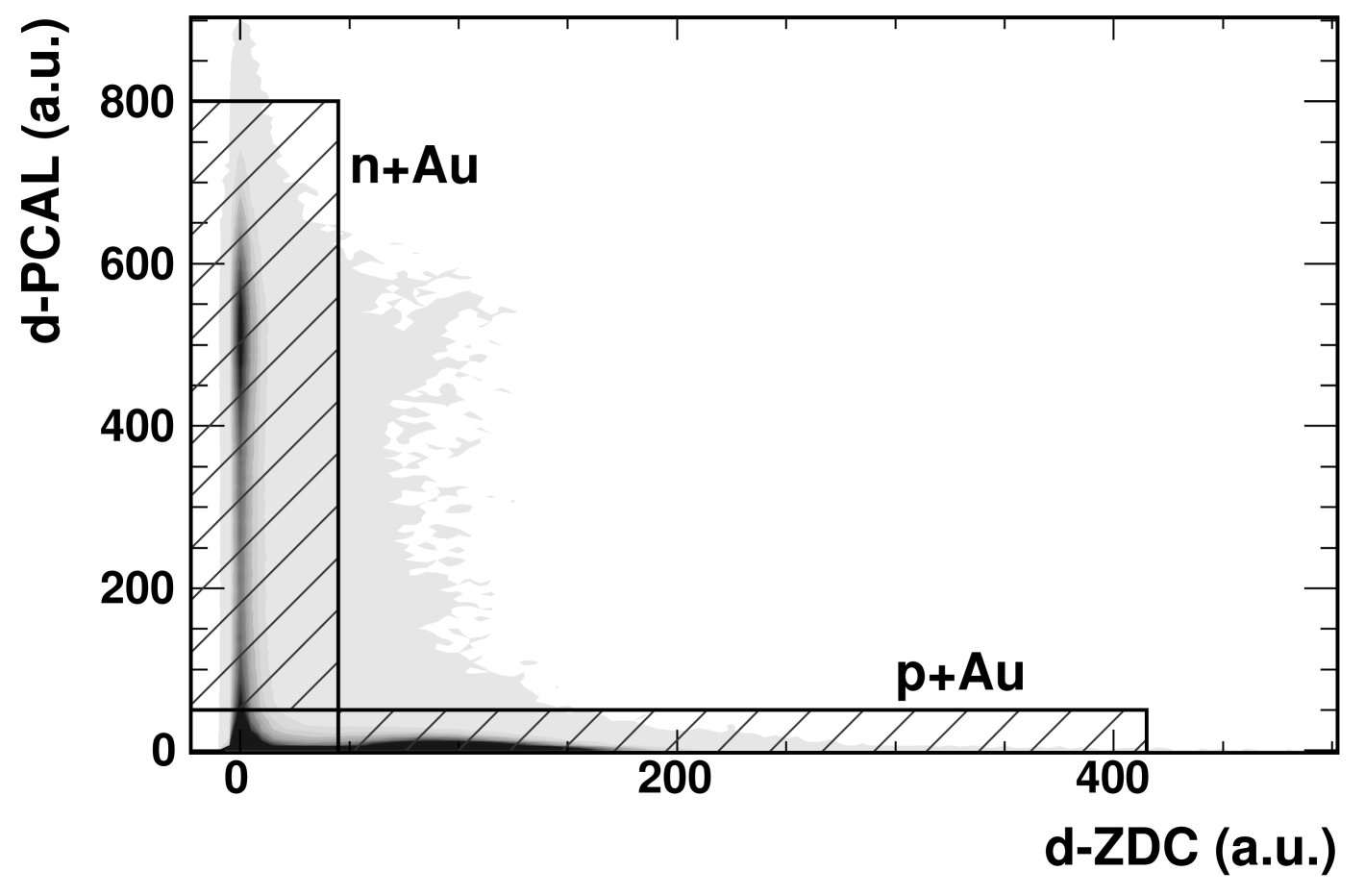
A similar procedure has been followed in order to determine the range of energy deposited in the d-ZDC that corresponds to a neutron spectator. The final regions in which +Au and +Au interactions are identified is shown in Fig. 10. The minimum value of energy deposition in the d-PCAL is well above region 0, but ensures a very clean +Au sample.
III.5 Centrality of Nucleon-Nucleus Collisions
The centrality of the tagged +Au and +Au collision data sets are quantified (by parameters such as ) within the fractional cross section bins determined for +Au. This is necessary because the forward calorimeters are not included in the simulations of the detector response, which precludes an event tagging procedure based on the simulated energy deposition of those detectors.
Within a +Au fractional cross section bin in the MC, the centrality parameters of tagged events, such as in +Au collisions, are obtained using the true subset of simulated +Au events identified as +Au or +Au. These subsets are identified by the presence of a neutron or proton, respectively, emerging from the collision with a longitudinal momentum of 100 GeV.
The use of a tagging procedure based on true simulated momenta is valid under the assumption that the event tagging procedure used in data has an efficiency that does not depend on the centrality of the collision. That is, the average value of in +Au is the same whether the tagging efficiency is 80% or 100%, as long as the tagging procedure does not alter the shape of the distribution (but merely scales its normalization).
The validity of this assumption rests on three reasonable conjectures. First, that it is not possible for a nucleon to both interact inelastically and to still deposit a measurable amount of energy into a forward calorimeter. Note that the Au-PCAL acceptance covers only protons having no transverse momentum and a longitudinal momentum , and that the smaller d-PCAL will observe only protons with even higher momenta. Second, that if a spectator nucleon is present, it will be detected by a forward calorimeter with an efficiency that is independent of the collision centrality. Finally, that the forward calorimeter on the deuteron side detects only deuteron spectators and not produced particles.
These conjectures imply that the tagging efficiency is independent of the centrality of the +Au collisions. This allows nucleon-nucleus collisions to be extracted from the +Au (AMPT) simulations, analogous to the tagging procedure used for data. Simulated nucleons emerging from the interaction at the nucleon beam energy are taken to be spectators. The centrality parameters extracted using this method are presented in Table 1.
The +Au and +Au events from the simulations have been used to obtain a rough estimate of the tagging efficiencies. Taking the ratio of +Au (+Au) to +Au collisions that passed the event selection in the simulation gives the fraction of +Au (+Au) events in the +Au sample that would be tagged with a perfectly efficient detector. Dividing the actual ratio of tagged +Au (+Au) to +Au events found in the data by the fraction expected from simulation gives an estimate of the efficiency. It is found that of +Au interactions and of +Au interactions are tagged using the procedure described above. The lower +Au efficiency may be at least partly due to the relatively large minimum d-PCAL energy required in the tagging procedure (see Sect. III.4).
IV Hadron Spectra Extraction
The transverse momentum spectra of charged hadrons have been extracted from tracks reconstructed using hits in the 16 layers of silicon detectors that make up the two-arm magnetic spectrometer. Hit position information is obtained both inside and outside the 2 T magnetic field. Details of the vertex determination and particle tracking, as used in previous PHOBOS +Au hadron spectra analyses, have been described in Refs. Back et al. (2003b, 2004a). However, the current studies make use of an expanded set of data and an updated reconstruction procedure. As the +Au collision trigger (described in Sect. III.1) does not include a high particle trigger, as employed in Back et al. (2003b), a less biased data sample has been used in the present analysis. To improve the efficiency of the particle reconstruction, the final minimization step of the tracking has been performed multiple times for each track. This helps prevent the reconstruction from falling into a local minimum, which reduces the number of both poor-quality track fits as well as ghost tracks.
In an effort to more accurately apply acceptance and efficiency corrections, several changes have been made to the procedure used to extract the hadron momentum spectra described in Ref. Back et al. (2003b). First, the geometrical acceptance and tracking efficiency correction have been applied separately for each of the two spectrometer arms. To account for acceptance effects as accurately as possible, the correction factors as a function of have been applied as interpolated spline functions of the track-embedding results (described in Ref. Back et al. (2004a)), rather than as smooth analytic functions. Further, the minimum of acceptable tracks has been lowered to correspond to the value at which the acceptance and efficiency corrections are roughly 30% of their maximal value. This leads to a minimum value of 0.3 to 0.4 GeV, depending on the longitudinal collision vertex position, for hadrons bending towards higher- (out of the PHOBOS spectrometer acceptance) and a minimum of about 0.1 GeV for hadrons bending towards negative . Corrections for dead and hot channels in the spectrometer have also been applied independently for each spectrometer arm, to account for discrepancies on the level of 1% in the hot and dead channel fraction of the two arms. The number of ghost and secondary tracks passing the reconstruction cuts are corrected for as a function of . Due to improvements in the reconstruction software since the publication of Ref. Back et al. (2003b), these corrections are on the order of 1%. Finally, corrections have been applied for the momentum resolution of the tracking and the variable bin sizes of the spectra. These corrections are determined using a dedicated simulation of single particles through each spectrometer arm to determine the distribution of reconstructed transverse momentum in each (true) bin.
The efficiency of the event selection described in Sect. III.1 depends on centrality, particularly for peripheral events. Spectra uncorrected for this effect would correspond to an ensemble of events with a biased (higher) number of participants, rather than to a minimum bias selection using the same centrality binning. Instead, the efficiency determined as a function of centrality (see Fig. 2) is used to correct the spectra.
The spectra of charged hadrons for +Au, +Au and +Au collisions are presented in Fig. 11 in four bins of +Au centrality, as determined by the ERing variable. For +Au and +Au, the same ERing cuts were used as for +Au. Therefore, these do not correspond to bins of the listed fractional cross-section for nucleon-gold interactions. Note that the difference in the range between +Au and the nucleon-nucleus spectra is simply due to fewer +Au and +Au collisions being collected compared to +Au.
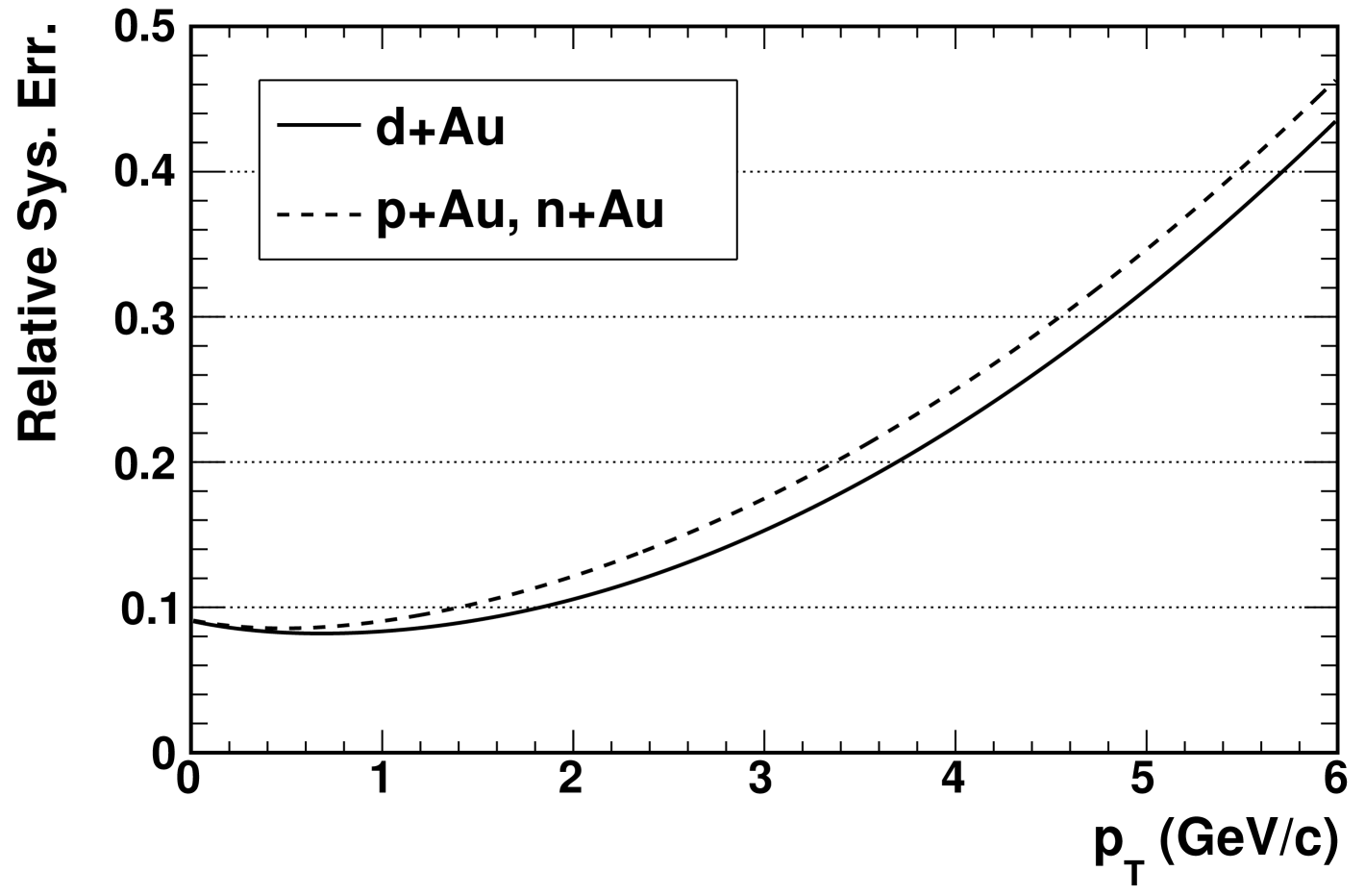
Systematic uncertainties on the measured charged hadron spectra have been quantified using the data. The largest correction, the acceptance and efficiency of the tracking, is the source of the largest systematic error (about 8% at ). This error has been estimated by comparing the yield in different subsets of the data for which the particle spectrum is expected to be the same. For example, the charged hadron yield of data taken with the spectrometer magnet in the positive polarity is compared to that of data taken with the magnet in the negative polarity. Similarly, yields measured separately in each spectrometer arm have been compared in order to derive uncertainties arising from the dead and hot channel correction. With these corrections applied separately to each arm, the systematic uncertainty on this effect is reduced to from in the previous analysis Back et al. (2003b).
For corrections in which such studies are not possible, the uncertainties are taken to be of the same order as the corrections themselves. At , this gives a ghost track uncertainty of 1%, an uncertainty on the effect of secondary tracks of 3% and an uncertainty on the momentum resolution and momentum binning correction (which are applied together) of about 3.5%.
Uncertainty on the yield of nucleon-nucleus collisions due to tagging has been estimated. This is done by varying the d-PCAL and d-ZDC cuts used to tag events, which is expected to impact the number of interactions in the data set, but not the yield of those interactions. The total systematic uncertainties for the charged hadron spectra are shown in Fig. 12.
The charged hadron spectra are used to derive the multiplicity near mid-rapidity for +Au, +Au and +Au. Spectra are modeled with the following functional form
| (1) |
In the actual fit, parameter in Eq. 1 is replaced by its value in terms of the analytically integrated yield and the other four parameters.
| (2) |
This allows both the value of and its statistical uncertainty to be obtained directly from the fit. Systematic uncertainties on the multiplicity are obtained by simultaneously shifting each point in the spectra to the limit of its individual systematic error and extracting . The resulting systematic uncertainty on the integrated yield is about 9%.
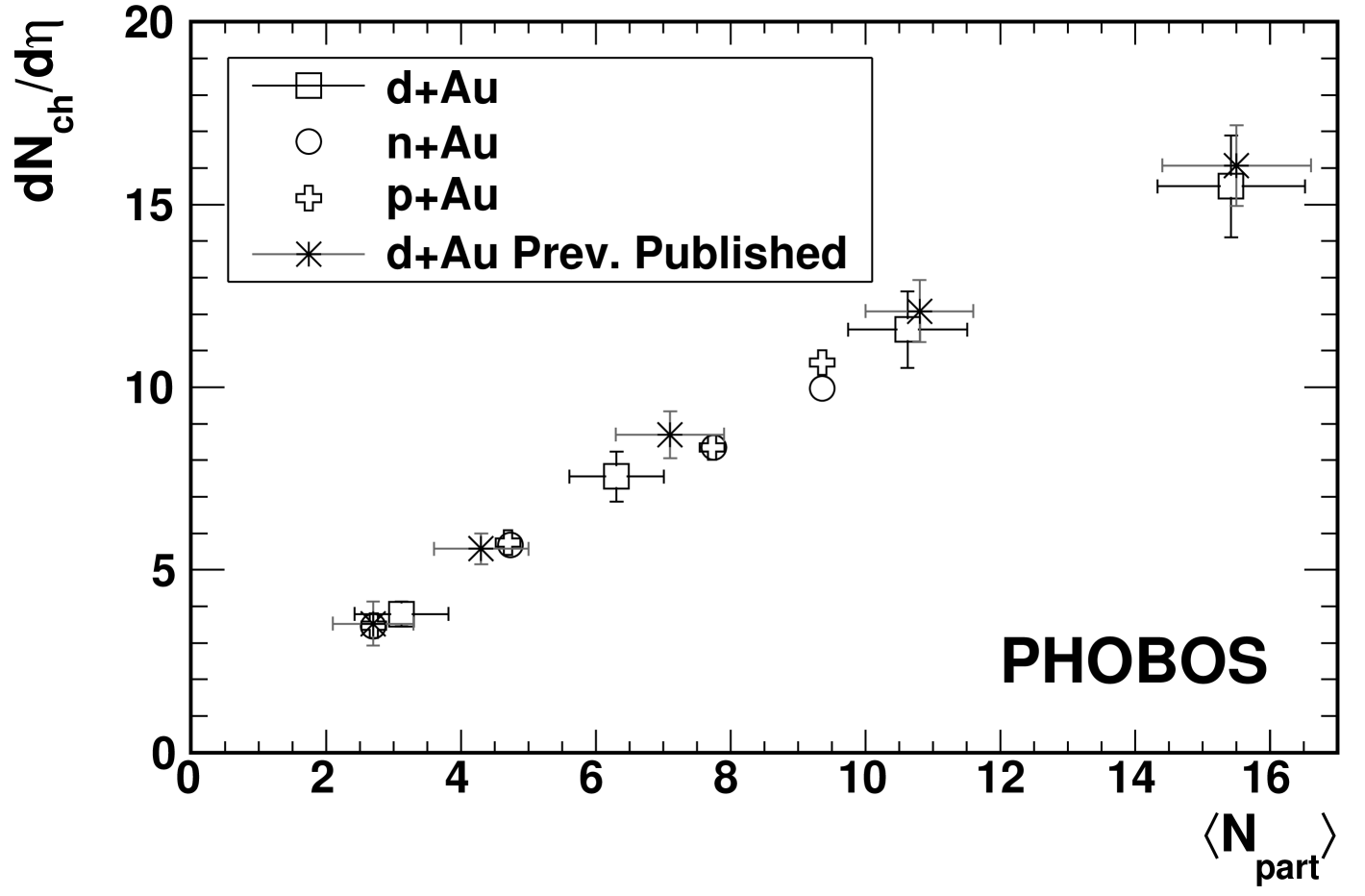
The charged particle multiplicity near mid-rapidity, at , is shown in Fig. 13 for +Au, +Au and +Au as a function of . The number of participants is determined using ERing centrality bins, since the ERing measurement of particles far from mid-rapidity has been shown to introduce at most a minimal bias on the measurement Back et al. (2005b). A consistent dependence of the multiplicity on is observed across all three collision systems.
V An Improved Reference System
The yield of hadrons in +Au collisions has played a vital role in the investigation of particle production in high energy Au+Au collisions. The nuclear modification factor, , of a collision system, , given by
| (3) |
where Au+Au, +Au, etc., has been used to test the scaling of the high- hadron yield with the number of binary nucleon interactions occuring during the collision. The nuclear modification factor of nucleus-nucleus collisions at RHIC has been studied extensively for Au+Au interactions at Adare et al. (2012) Back et al. (2005c); Arsene et al. (2006); Adare et al. (2012), Adcox et al. (2002, 2003b); Adler et al. (2002) and Back et al. (2004a); Adams et al. (2003b); Adler et al. (2003c, 2004); Abelev et al. (2009); Adare et al. (2012), as well as for Cu+Cu interactions at Adare et al. (2008), Adare et al. (2008) and Alver et al. (2006); Adare et al. (2008); Abelev et al. (2010).
One of the fundamental conclusions drawn from examination of the nuclear modification factor is that the production of high- charged hadrons in central Au+Au collisions at is highly suppressed with respect to binary collision scaling Back et al. (2004a). However, it cannot be known from the nucleus-nucleus data alone whether the suppression is due to initial Kharzeev et al. (2003a) or final Baier et al. (1997) state effects. Nucleon-nucleus collisions at the same center of mass energy would provide a control experiment capable of distinguishing between the two possibilities, as such collisions should provide a nucleus in the same initial state but should not produce an extended medium in the final state. At RHIC these studies have been performed using +Au rather than nucleon-nucleus collisions Back et al. (2003b); Adams et al. (2003a); Adler et al. (2003a, 2006); Arsene et al. (2004, 2003). The assumption was made that, due to the small size and weak binding of the deuteron nucleus, +Au collisions would provide as good a control experiment for Au+Au interactions as nucleon-nucleus collisions.
This assumption can be tested using tagged +Au and +Au collisions to construct an improved reference for Au+Au collisions. Previous studies performed by the NA49 collaboration Fischer (2003); Rybicki (2004) have suggested that hadron production of nucleus-nucleus collisions may be better understood through careful consideration of the neutron content of the nucleus. Taking into account the fact that a gold nucleus consists of 60% neutrons and 40% protons, an improved nuclear modification factor for comparison to Au+Au can be defined as:
| (4) |
where is the average number of collisions in +Au, is the average number of collisions in +Au, and is the yield of the reference nucleon-nucleon system.
The nucleon-nucleon reference comes from the UA1 measurement Albajar et al. (1990) of the + inelastic cross section. Note that data for + is used since data for the preferable + system is not available at this energy. As described in Ref. Back et al. (2003b), corrections are applied to the UA1 results to account for (a) the conversion from rapidity to pseudorapidity and (b) the difference between the UA1 acceptance () and the PHOBOS acceptance (). An inelastic + cross section of 41 is used to estimate the yield of + collisions given the differential cross section measurements from UA1.
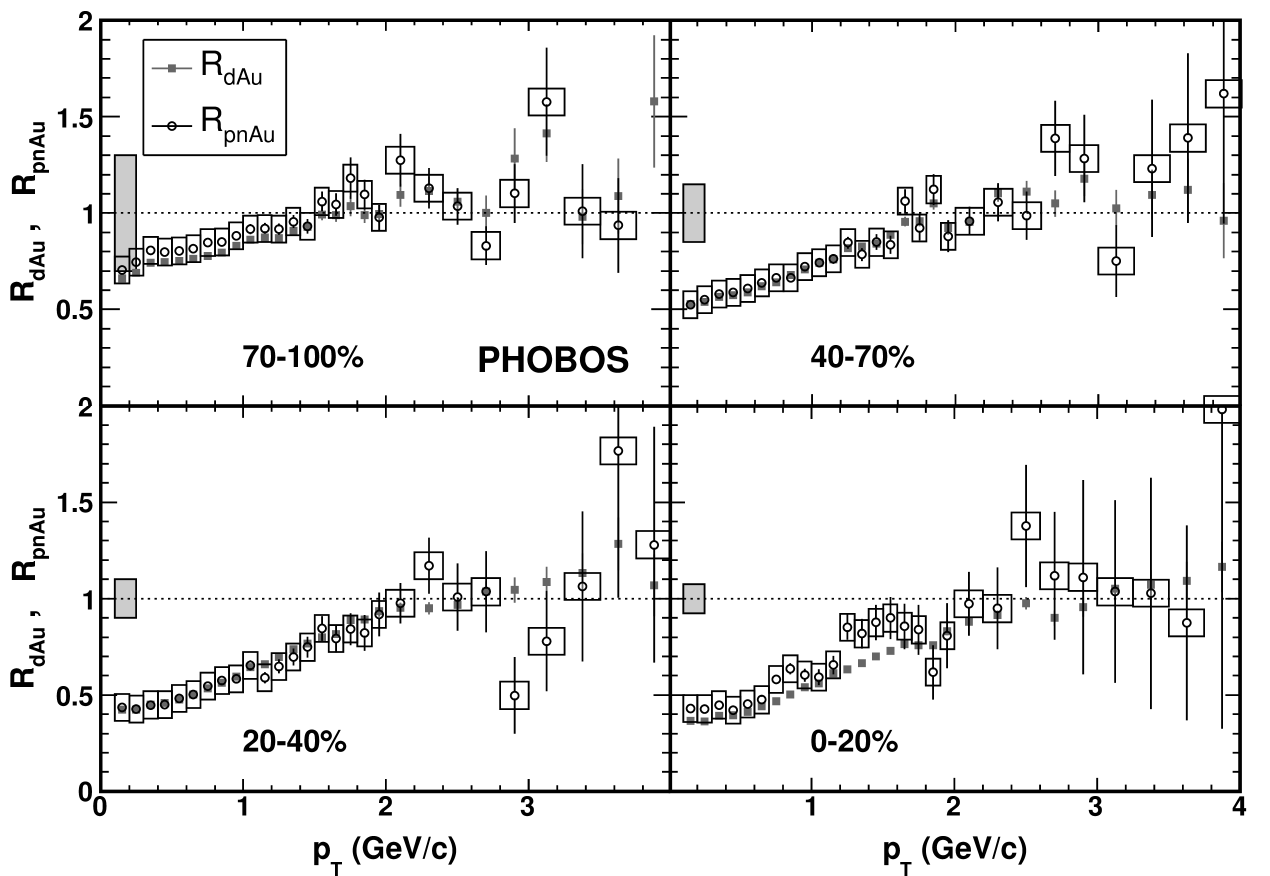
The nuclear modification factor as a function of in the nucleon+Au system, , is compared to that of +Au, , for each centrality bin in Fig. 14. Common systematic errors among the two systems on the determination of affect the overall scale of the ratios, as shown by the height of the grey band. Further systematic errors in the determination of for the tagged nucleon+Au system are shown as boxes around the points.
Qualitatively similar results have been found for a narrower window of pseudorapidity by PHENIX Adler et al. (2008). The presented in that work is a simple average of +Au and +Au, as opposed to the weighted combination shown in Eq. 4. While the shapes of the modification factors are similar in this work and Ref. Adler et al. (2008), the latter appear to be slightly shifted to larger values, most likely due to the use of different reference spectra.
No significant difference between and is observed. This measurement supports the conclusions drawn from the nuclear modification factor measurements of +Au collisions Back et al. (2003b); namely, that high- hadron production in central Au+Au collisions is significantly suppressed with respect to the expectation of binary collision scaling of + Back et al. (2004a), while the production in +Au collisions is not. It should be noted that no claim of binary collision scaling in +Au or nucleon+Au interactions has been made.
It has been observed that the nuclear modification factor in +Au exhibits a dependence on pseudorapidity Back et al. (2004c); Arsene et al. (2003, 2004, 2006). Thus, the apparent tendency of and to take the value of unity at high is likely a consequence of the PHOBOS pseudorapidity acceptance. Further, as will be discussed in Sect. VI, the hadron production of +Au collisions is known to be enhanced with respect to binary collision scaling in a certain range of transverse momentum. Any statement that +Au lacks a suppression of high- hadrons is therefore contingent upon the magnitude of this enhancement; see Ref. Accardi (2005) for a discussion.
Nevertheless, the stark discrepancy observed between nucleon+Au and Au+Au collisions at demonstrate that final state effects play a much stronger role in the high- hadron production of central Au+Au collisions than do initial state effects. While the pseudorapidity dependence of may provide evidence of some initial modification of the gold nucleus Kharzeev et al. (2003b); Jalilian-Marian and Kovchegov (2006), it is clear that interactions with some dense, large volume medium produced only in the nucleus-nucleus system forms the dominant source of high- hadron suppression in Au+Au collisions. The data presented here demonstrate that this conclusion is not biased by the use of deuteron-nucleus rather than nucleon-nucleus interactions as the control experiment for Au+Au.
VI Centrality Dependence of the Spectral Shape
Although no clear evidence for enhancements above unity are seen in the nuclear modification factor shown in Fig. 14, the dependence may be related to the so-called Cronin effect. This effect refers to the larger ratio of hadron production seen at high compared to lower in proton-nucleus collisions Cronin et al. (1975) relative to + collisions scaled by the effective thickness of the nucleus. General aspects of the enhancement of inclusive charged hadron production (that is, unidentified hadrons) in +Au collisions can be described by models in which partons undergo multiple scattering at the initial impact of the +Au collision Accardi (2005). However, the observed difference in the strength of enhancement for mesons and baryons Shao (2006) is not easily explained by initial state partonic scattering models. While other theories, such as those based on the recombination model of hadronization Hwa and Yang (2004), may be better suited to describe the enhancement of individual hadron species, the shape of the +Au spectrum relative to that of + is not a thoroughly understood phenomenon. Of particular importance is the dependence of the spectral shape on the nuclear thickness probed by the projectile (i.e. the deuteron in a +Au collision) Accardi and Gyulassy (2004).
The centrality dependence of the nuclear modification factor in +Au and Au+Au collisions at RHIC has been studied extensively Back et al. (2005b); Adcox et al. (2005); Adams et al. (2005); Arsene et al. (2005). A particularly convenient method for exploring how the shape of the transverse momentum spectra changes relative to + has been suggested in Ref. Back et al. (2003b). This method involves studying the centrality dependence of the charged hadron yield in +Au collisions relative to + at several values of .
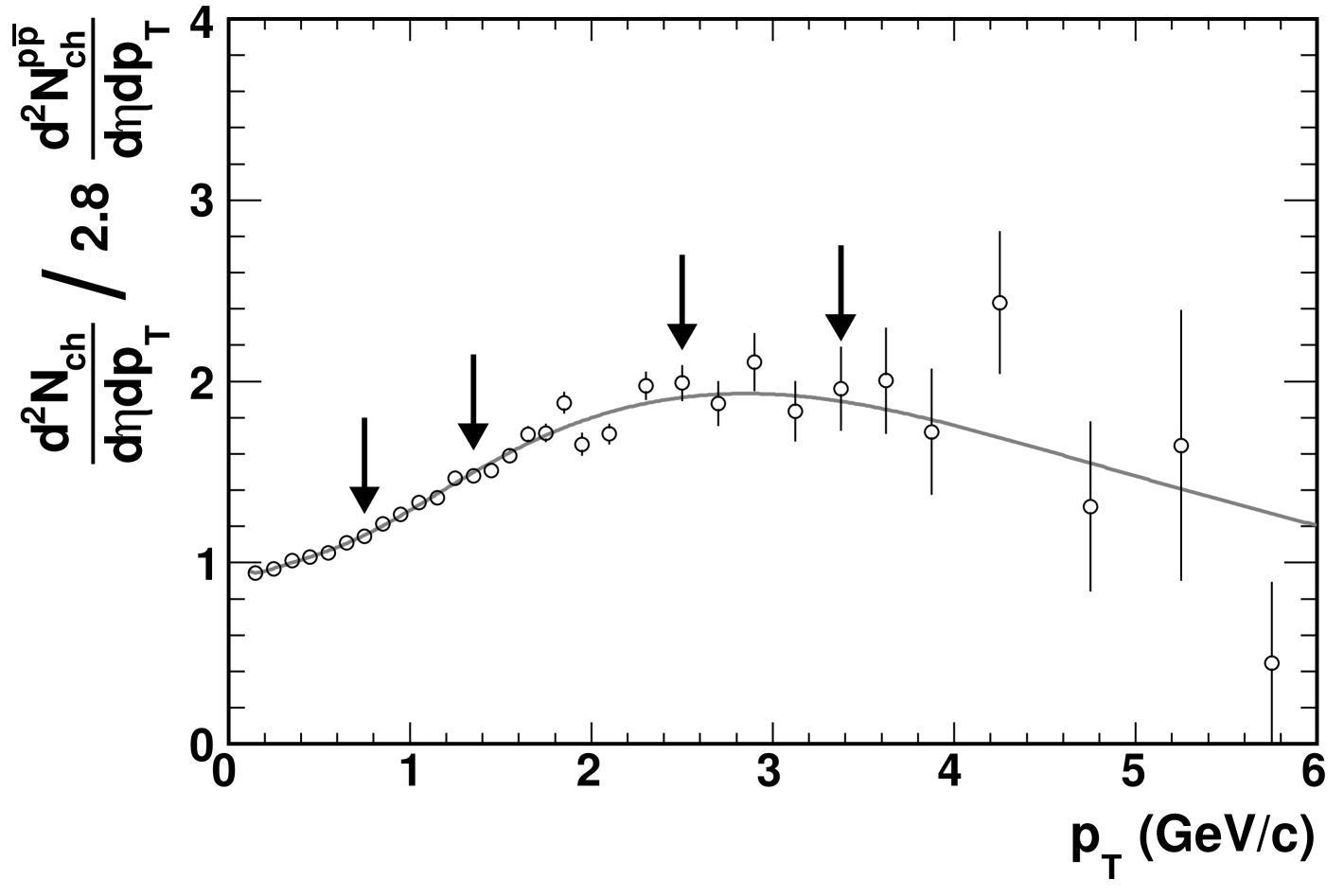
The procedure for determining the so-called relative yield is as follows. First, the transverse momentum spectrum in a particular +Au centrality bin is compared to the spectrum of +. To compare only the shape of the two spectra, they are then normalized such that the spectra match at . While this specific value of is arbitrary, it has been intentionally chosen to be in a region where soft processes drive particle production. Matching the +Au spectra to the + spectra serves to remove any trivial enhancement of hadron production in +Au that is simply due to the larger number of nucleon-nucleon collisions occurring in that system. However, matching in this way does not assume scaling, nor does it have any effect on the relative shape of the spectra.
Next, the ratio of the normalized +Au spectra and the + spectra is determined. The value of this ratio at certain transverse momentum values are selected, as shown in Fig. 15. Finally, the centrality dependence of the normalized ratio, the relative yield, at the chosen values is studied.
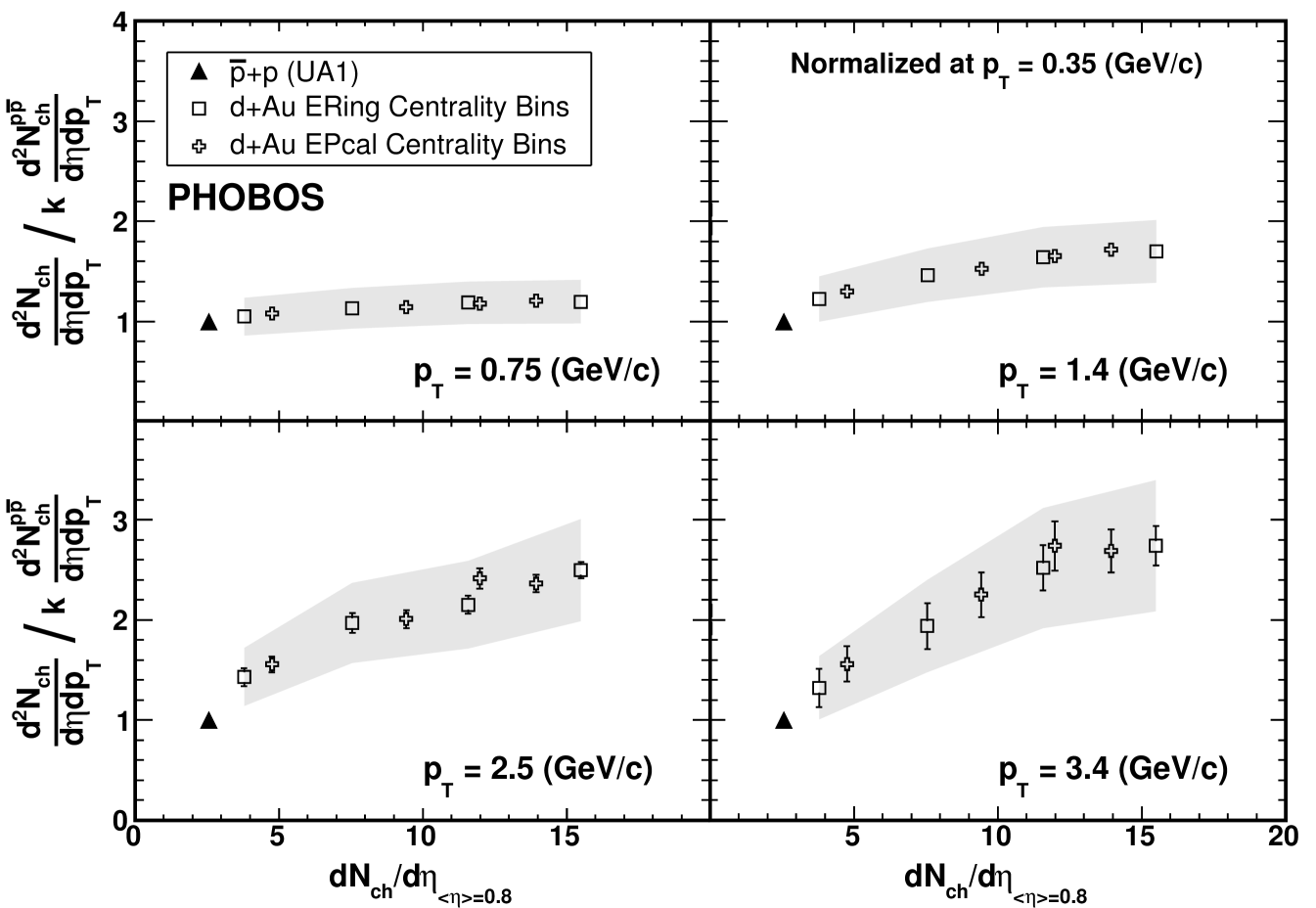
The relative yield of +Au collisions to + is shown in Fig. 16 as a function of , for four different values of transverse momentum. It is expected that systematic effects on the relative yield are highly correlated between the spectra measured with different centrality bins. Thus, shifts in the relative yield will tend to move all points together. See Table 1 for a description of the systematic uncertainties on the centrality variables measured with ERing. With centrality parametrized by the experimentally measured integrated yield, no bias or (Glauber) model dependence is introduced by the choice of centrality variable.
From Fig. 16, it is clear that the difference between the +Au and + spectra depends on both centrality and . If the shape of the two spectra were identical, the relative yield would be constant at unity for all values of and centrality. Instead, the +Au spectra show an enhancement over + that increases with centrality. The strength of this enhancement is observed to increase at higher . It would be interesting to study the relative yield of much higher hadrons, on the order of 10 to 100 GeV, in order to test whether the shape of the + spectra is recovered in hard scattering processes. However, such particles are produced very rarely and too few are present in the PHOBOS data set to allow such a study.
Nevertheless, the data show a smooth extrapolation of the relative yield of +Au collisions to that of + as the +Au collisions become more peripheral. Thus, distortions of the +Au spectra caused by nuclear effects diminish in a smooth way as the amount of nuclear material probed by the deuteron is reduced. The integrated charged particle yield near has been chosen as the centrality measure, since it provides a model-independent variable with which to study the centrality dependence of hadron production in nucleon-nucleus and nucleus-nucleus systems.
VII Charge Transport
The availability of both +Au and +Au collision data presents a unique opportunity to study baryon transport in nucleon-nucleus collisions. Since a +Au collision contains one more charged hadron than an +Au collision, a search for this extra charge near the mid-rapidity region is possible. Previous measurements Alber et al. (1998) of +Au collisions at found that the number of net protons (p - p̄) per unit of rapidity is less than one in the mid-rapidity region. In addition, studies have shown a decrease in the mid-rapidity net proton yield with increasing center of mass energy; see Ref. Back et al. (2007) for a discussion. Further, it has been inferred that hadrons traversing nuclear material do not lose more than about two units of rapidity Busza and Goldhaber (1984). Thus, it is expected that any charge asymmetry between hadrons measured at mid-rapidity in +Au and +Au collisions would be small.
Nevertheless, a comparison of charged hadron production in +Au and +Au allows the transport of charge explicitly from the projectile proton to be studied. Assuming that baryons from the gold nucleus undergo transport to mid-rapidity via the same process in both +Au and +Au collisions, any charge transport to mid-rapidity of protons in the gold nucleus would not lead to an asymmetry.
Simple charge conservation would imply that the total number of positive particles emerging from a +Au collision should be greater (by one) than the number emerging from a +Au collision. Whether or not this charge asymmetry is present near mid-rapidity has been studied using the observable , defined as
| (5) |
where denotes the asymmetry between +Au and +Au in the yield of positively charged hadrons at and denotes the asymmetry of the yield of negatively charged hadrons between the two systems.
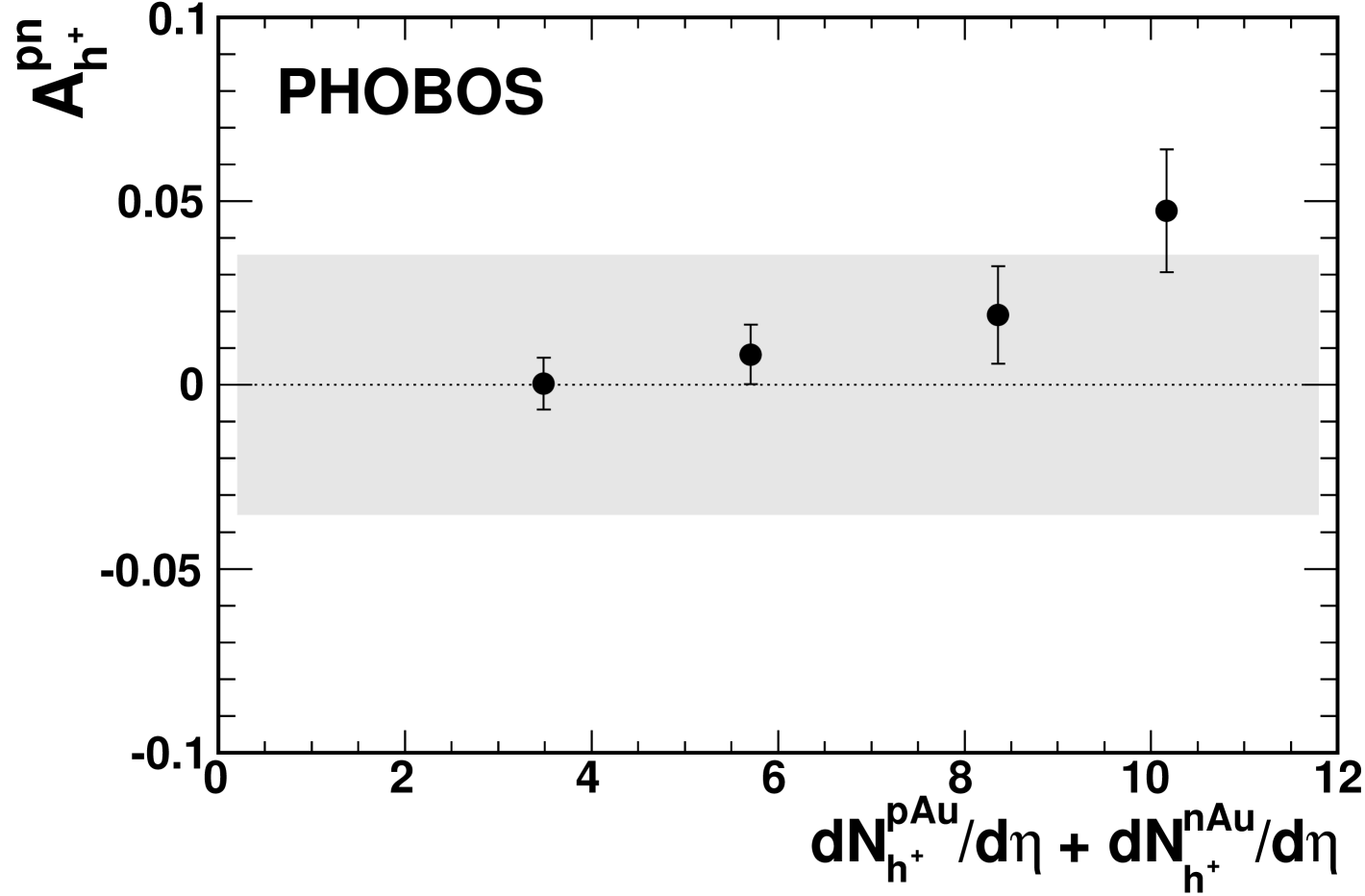
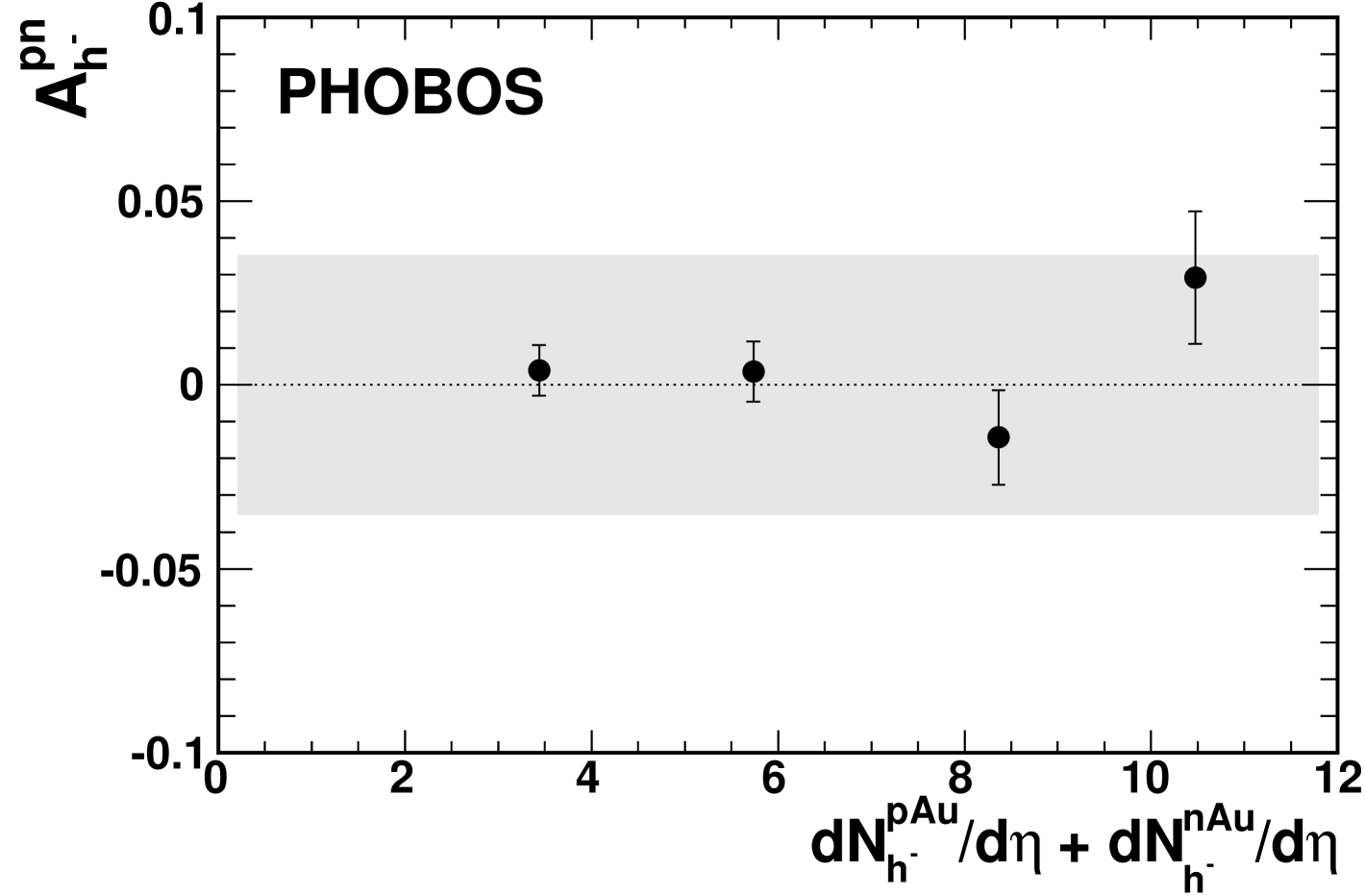
The charge asymmetry defined by Eq. 5 is presented in Fig. 17 for positive hadrons and in Fig. 18 for negative hadrons. The grey band in each figure represents the systematic uncertainty in the asymmetry ratio, propagated from the nucleon tagging component of the systematic uncertainty on the momentum spectra (see Sect. IV). Only uncertainties specific to reconstructing the nucleon-nucleus spectra contribute to this systematic error, as all other effects divide out in the ratio. No evidence for asymmetry between +Au and +Au collisions is observed at , which is slightly forward on the deuteron-going side.
VIII Summary
The addition of two forward proton calorimeters to the PHOBOS detector allows the extraction of +Au and +Au collisions from the +Au data set. Centrality parameters have been determined for each of the collision systems using observables based on the multiplicity at high rapidity and on the number of spectators. The number of particles produced near mid-rapidity is found to scale with across all collision systems. The charged hadron spectra have been measured for +Au, +Au, and +Au collisions and used to construct an ideal nucleon-nucleus reference for Au+Au collisions. The nuclear modification factor of this ideal reference is found to agree with that of +Au. The shape of the nuclear modification factor has been studied in detail and is found to depend on both centrality and transverse momentum. A larger ratio of the +Au over + spectra is found at larger values of and this enhancement is found to extrapolate smoothly as a function of multiplicity at mid-rapidity from + to central +Au collisions. Finally, a comparison of the yield of positively and negatively charged hadrons in +Au and +Au has been conducted in a direct search for evidence of charge transport to mid-rapidity. No significant asymmetry between the charged hadron yields in +Au and +Au is observed at .
This work was partially supported by U.S. DOE grants DE-AC02-98CH10886, DE-FG02-93ER40802, DE-FG02-94ER40818, DE-FG02-94ER40865, DE-FG02-99ER41099, and DE-AC02-06CH11357, by U.S. NSF grants 9603486, 0072204, and 0245011, by Polish MNiSW grant N N202 282234 (2008-2010), by NSC of Taiwan Contract NSC 89-2112-M-008-024, and by Hungarian OTKA grant (F 049823).
References
- Back et al. (2003a) B. Back et al. (PHOBOS Collaboration), Nucl.Instrum.Meth. A499, 603 (2003a).
- Hahn et al. (2003) H. Hahn et al., Nucl.Instrum.Meth. A499, 245 (2003).
- Adamczyk et al. (2003) M. Adamczyk et al. (BRAHMS Collaboration), Nucl.Instrum.Meth. A499, 437 (2003).
- Adcox et al. (2003a) K. Adcox et al. (PHENIX Collaboration), Nucl.Instrum.Meth. A499, 469 (2003a).
- Ackermann et al. (2003) K. Ackermann et al. (STAR Collaboration), Nucl.Instrum.Meth. A499, 624 (2003).
- Back et al. (2003b) B. Back et al. (PHOBOS Collaboration), Phys. Rev. Lett. 91, 072302 (2003b), arXiv:nucl-ex/0306025 .
- Cronin et al. (1975) J. Cronin et al., Phys.Rev. D11, 3105 (1975).
- Adler et al. (2003a) S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 91, 072303 (2003a), arXiv:nucl-ex/0306021 .
- Adams et al. (2003a) J. Adams et al. (STAR Collaboration), Phys. Rev. Lett. 91, 072304 (2003a), arXiv:nucl-ex/0306024 .
- Arsene et al. (2003) I. Arsene et al. (BRAHMS Collaboration), Phys. Rev. Lett. 91, 072305 (2003), arXiv:nucl-ex/0307003 .
- Adams et al. (2006) J. Adams et al. (STAR Collaboration), Phys. Lett. B637, 161 (2006), arXiv:nucl-ex/0601033 .
- Adler et al. (2006) S. Adler et al. (PHENIX Collaboration), Phys.Rev. C74, 024904 (2006), arXiv:nucl-ex/0603010 .
- Adcox et al. (2002) K. Adcox et al. (PHENIX Collaboration), Phys. Rev. Lett. 88, 022301 (2002), arXiv:nucl-ex/0109003 .
- Adcox et al. (2003b) K. Adcox et al. (PHENIX Collaboration), Phys. Lett. B561, 82 (2003b), arXiv:nucl-ex/0207009 .
- Adler et al. (2002) C. Adler et al. (STAR Collaboration), Phys. Rev. Lett. 89, 202301 (2002), arXiv:nucl-ex/0206011 .
- Back et al. (2004a) B. Back et al. (PHOBOS Collaboration), Phys. Lett. B578, 297 (2004a), arXiv:nucl-ex/0302015 .
- Chatrchyan et al. (2013) S. Chatrchyan et al. (CMS Collaboration), Phys. Lett. B 724, 213 (2013).
- Adler et al. (2008) S. S. Adler et al. (PHENIX Collaboration), Phys. Rev. C 77, 014905 (2008).
- Adare et al. (2014) A. Adare et al. (PHENIX Collaboration), Phys. Rev. C 90, 034902 (2014).
- Adler et al. (2003b) C. Adler et al., Nucl.Instrum.Meth. A499, 433 (2003b).
- Armstrong et al. (1998) T. Armstrong et al. (E864 Collaboration), Nucl.Instrum.Meth. A406, 227 (1998).
- Back et al. (2004b) B. Back et al. (PHOBOS Collaboration), Phys. Rev. Lett. 93, 082301 (2004b), arXiv:nucl-ex/0311009 .
- Back et al. (2005a) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C72, 031901 (2005a), arXiv:nucl-ex/0409021 .
- Gyulassy and Wang (1994) M. Gyulassy and X.-N. Wang, Comput.Phys.Commun. 83, 307 (1994), (HIJING v1.383), arXiv:nucl-th/9502021 .
- Zhang et al. (2000) B. Zhang, C. Ko, B.-A. Li, and Z.-w. Lin, Phys.Rev. C61, 067901 (2000), (AMPT v2003-08-18), arXiv:nucl-th/9907017 .
- Brun et al. (1987) R. Brun et al., “Geant3 users guide,” (1987), CERN DD/EE/84-1.
- Back et al. (2002a) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C65, 061901 (2002a), arXiv:nucl-ex/0201005 .
- Hulthén and Sugawara (1957) L. Hulthén and M. Sugawara, “Handbuch der Physik Vol. 30,” (Springer-Verlag, Berlin, 1957) p. 14.
- Back et al. (2002b) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C65, 031901 (2002b), arXiv:nucl-ex/0105011 .
- Back et al. (2005b) B. Back et al. (PHOBOS Collaboration), Nucl. Phys. A757, 28 (2005b), arXiv:nucl-ex/0410022 .
- Back et al. (2011) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C83, 024913 (2011), arXiv:nucl-ex/1011.1940 .
- Adare et al. (2012) A. Adare et al. (PHENIX Collaboration), Phys. Rev. Lett. 109, 152301 (2012), arXiv:1204.1526 .
- Back et al. (2005c) B. Back et al. (PHOBOS Collaboration), Phys. Rev. Lett. 94, 082304 (2005c), arXiv:nucl-ex/0405003 .
- Arsene et al. (2006) I. Arsene et al. (BRAHMS Collaboration), (2006), arXiv:nucl-ex/0602018 .
- Adams et al. (2003b) J. Adams et al. (STAR Collaboration), Phys. Rev. Lett. 91, 172302 (2003b), arXiv:nucl-ex/0305015 .
- Adler et al. (2003c) S. Adler et al. (PHENIX Collaboration), Phys. Rev. Lett. 91, 072301 (2003c), arXiv:nucl-ex/0304022 .
- Adler et al. (2004) S. Adler et al. (PHENIX Collaboration), Phys.Rev. C69, 034910 (2004), arXiv:nucl-ex/0308006 .
- Abelev et al. (2009) B. Abelev et al. (STAR Collaboration), Phys.Rev. C80, 044905 (2009), arXiv:0907.2721 .
- Adare et al. (2008) A. Adare et al. (PHENIX Collaboration), Phys. Rev. Lett. 101, 162301 (2008), arXiv:0801.4555 .
- Alver et al. (2006) B. Alver et al. (PHOBOS Collaboration), Phys. Rev. Lett. 96, 212301 (2006), arXiv:nucl-ex/0512016 .
- Abelev et al. (2010) B. Abelev et al. (STAR Collaboration), Phys.Rev. C81, 054907 (2010), arXiv:0911.3130 .
- Kharzeev et al. (2003a) D. Kharzeev, E. Levin, and L. McLerran, Phys. Lett. B561, 93 (2003a), arXiv:hep-ph/0210332 .
- Baier et al. (1997) R. Baier, Y. L. Dokshitzer, A. H. Mueller, S. Peigne, and D. Schiff, Nucl. Phys. B484, 265 (1997), arXiv:hep-ph/9608322 .
- Arsene et al. (2004) I. Arsene et al. (BRAHMS Collaboration), Phys. Rev. Lett. 93, 242303 (2004), arXiv:nucl-ex/0403005 .
- Fischer (2003) H. Fischer (NA49 Collaboration), Nucl. Phys. A715, 118 (2003), arXiv:hep-ex/0209043 .
- Rybicki (2004) A. Rybicki, J.Phys. G30, S743 (2004).
- Albajar et al. (1990) C. Albajar et al. (UA1 Collaboration), Nucl. Phys. B335, 261 (1990).
- Back et al. (2004c) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C70, 061901 (2004c), arXiv:nucl-ex/0406017 .
- Accardi (2005) A. Accardi, Eur.Phys.J. C43, 121 (2005), arXiv:nucl-th/0502033 .
- Kharzeev et al. (2003b) D. Kharzeev, Y. V. Kovchegov, and K. Tuchin, Phys.Rev. D68, 094013 (2003b), arXiv:hep-ph/0307037 .
- Jalilian-Marian and Kovchegov (2006) J. Jalilian-Marian and Y. V. Kovchegov, Prog.Part.Nucl. Phys. 56, 104 (2006), arXiv:hep-ph/0505052 .
- Shao (2006) M. Shao (STAR Collaboration), AIP Conf.Proc. 828, 49 (2006).
- Hwa and Yang (2004) R. C. Hwa and C. Yang, Phys. Rev. Lett. 93, 082302 (2004), arXiv:nucl-th/0403001 .
- Accardi and Gyulassy (2004) A. Accardi and M. Gyulassy, Phys. Lett. B586, 244 (2004), arXiv:nucl-th/0308029 .
- Adcox et al. (2005) K. Adcox et al. (PHENIX Collaboration), Nucl. Phys. A757, 184 (2005), arXiv:nucl-ex/0410003 .
- Adams et al. (2005) J. Adams et al. (STAR Collaboration), Nucl. Phys. A757, 102 (2005), arXiv:nucl-ex/0501009 .
- Arsene et al. (2005) I. Arsene et al. (BRAHMS Collaboration), Nucl. Phys. A757, 1 (2005), arXiv:nucl-ex/0410020 .
- Alber et al. (1998) T. Alber et al. (NA35 Collaboration), Eur.Phys.J. C2, 643 (1998), arXiv:hep-ex/9711001 .
- Back et al. (2007) B. Back et al. (PHOBOS Collaboration), Phys.Rev. C75, 024910 (2007), arXiv:nucl-ex/0610001 .
- Busza and Goldhaber (1984) W. Busza and A. S. Goldhaber, Phys. Lett. B139, 235 (1984).