Numerical irreducibility criteria for handlebody links
Abstract.
In this paper we define a set of numerical criteria for a handlebody link to be irreducible. It provides an effective, easy-to-implement method to determine the irreducibility of handlebody links; particularly, it recognizes the irreducibility of all handlebody knots in the Ishii-Kishimoto-Moriuchi-Suzuki knot table and most handlebody links in the Bellettini-Paolini-Paolini-Wang link table.
Key words and phrases:
reducibility, handlebody links, knot sum2010 Mathematics Subject Classification:
57M25, 57M271. Introduction
A handlebody link is a union of finitely many handlebodies of positive genus embedded in the -sphere ; two handlebody links are equivalent if they are ambient isotopic [12], [3]. Throughout the paper handlebody links are non-split unless otherwise specified.
A handlebody link is reducible if there exists a cutting -sphere in such that and intersect transversally at an incompressible disk in (Fig. 1.1); otherwise it is irreducible. Note that a cutting sphere
of a reducible handlebody link factorizes it into two handlebody links , where , and , , are the closures of components of the complement (Fig. 1.1); the factorization is denoted by
| (1.1) |
and we call , , a factor of the factorization, where are components of containing , respectively.
Handlebody links are often studied and visualized via diagrams of their spines [3]; it is, however, not an easy task to detect the irreducibility of a handlebody link from its diagram. The complexity lies in the IH-move [3]. In fact, it is not known whether we have an affirmative answer to Conjecture 1.1 or Conjecture 1.2111Conj. 1.1 implies Conj. 1.2 in some special cases [14, Theorem ] and [1, Theorem ]..
Conjecture 1.1.
Every reducible handlebody link admits a minimal diagram whose underlying plane graph is -edge-connected.
Conjecture 1.2.
The crossing number of a reducible handlebody link is the sum of crossing numbers of its factors:
| (1.2) |
If either conjecture is true, it implies the reducible handlebody link table [1, Table ] is complete, and thus, the irreducibility of all handlebody links in [1, Table ] but can be proved by simply comparing their -invariants [6]. The invariant is the number of conjugacy classes of homomorphisms from the knot group , the fundamental group of ’s complement, to a finite group —two homomorphisms are in the same conjugacy class if they are conjugate.
We do not purse these conjectures here but instead introduce some numerical criteria for a handlebody link to be irreducibile. Other irreducibility tests using quandle invariants have been developed by Ishii and Kishmoto [4], and are used in the classification of irreducible handlebody knots of genus [5].
Main Results & Structure. A handlebody link is said to be of type if it consists of handlebodies of genus , , and a handlebody link is -generator if its knot group is of rank . Note that is necessarily larger than or equal to the genus of , which is the sum of genera of components of . Let be alternating groups of degree , respectively.
Theorem 1.3 (Necessary conditions for reducibility–).
Let be a reducible handlebody link of genus . If the trivial knot is a factor of some factorization of , then
| (1.3) |
if a -generator knot is a factor of some factorization of , then
| (1.4) |
if a -generator link is a factor of some factorization of , then
| (1.5) |
Theorem 1.4 (Necessary conditions for reducibility–).
Let be a reducible handlebody link of genus . If the trivial knot is a factor of some factorization of , then
| (1.6) |
From these necessary conditions we derive the irreducibility test for handlebody knots of genus up to and handlebody links of various types.
Corollary 1.5.
The situation with multi-component handlebody links is slightly more complicated as there are more possible combinations; thus we summarize it in a tabular format in Table 1, which is also a corollary of Theorems 1.3 and 1.4. The left two columns in Table 1 list criteria which if a handlebody link fails, it is irreducible. Be aware “ (i.e. and)” and “or” in those two columns.
| no. of components | type | ||
|---|---|---|---|
| is irreducible if it fails criterion/criteria | |||
| (1.3) or (1.6) | (1.3) & (1.4) | ||
| (1.3) or (1.6) | (1.3) & (1.4) | ||
| (1.3) or (1.6) | (1.3), (1.4) & (1.5) | ||
| (1.3) or (1.6) | not applicable | ||
| (1.3) & (1.5) | (1.3), (1.4) & (1.5) | ||
| (1.3) & (1.5) | not applicable | ||
| (1.3) & (1.5) | |||
| 4 | (1.3) & (1.5) | not applicable | |
The set of irreducibility criteria is put to test in Section 4; it detects the irreducibility of all handlebody knots, which are of type , in the Ishii-Kishimoto-Moruichi-Suzuki knot table [5] and the irreducibility of all handlebody links, which are of type or , but two (), in the Bellettini-Paolini-Paolini-Wang link table [1], showing that it is highly sensitive to the irreducibility of a handlebody link.
The major constraint of the irreducibility test is that the rank of the knot group cannot be too large and the difference between the rank and the genus needs to be small; on the other hand, the criteria are easy to implement and can be computed by a code.
The paper is organized as follows: Section 2 recalls basic properties of handlebody links and knot groups. The necessary conditions for reducibility (Theorems 1.3 and 1.4) are proved in Section 3. Section 4 records results of the irreducibility test applying to various families of handlebody links. Lastly, the existence of irreducible handlebody links of any given type is proved by a concrete construction making use of a generalized knot sum for handlebody links.
2. Preliminaries
Throughout the paper we work in the piecewise linear category. We use to refer to general handlebody links (including handlebody knots), and use or when referring specifically for handlebody knots, knots or links, respectively. denotes the knot group of or ; stands for an isomorphism of groups. To begin with, we review some basic properties of reducible handlebody links and the free product of groups.
Definition 2.1.
The rank of a finitely generated group is the smallest cardinality of a generating set of .
Definition 2.2.
A handlebody link is -generator if its knot group is of rank .
The rank respects the free product of groups [2].
Lemma 2.1 (Grushko theorem).
If , then
Lemma 2.2.
A -generator handlebody knot of genus is trivial.
Proof.
The following are corollaries of Lemmas 2.1 and 2.2 and the fact that implies then . The corollaries, together with Theorems 1.3 and 1.4, give Corollary 1.5 and Table 1.
Corollary 2.3.
A -generator handlebody knot of genus is reducible if and only if the trivial knot is a factor of some factorization of .
Corollary 2.4.
A -component, -generator handlebody link of genus is reducible if and only if the trivial knot is a factor of some factorization of .
Corollary 2.5.
A genus , -generator handlebody link of type or is reducible if and only if the trivial knot or a -generator knot is a factor of some factorization of .
Corollary 2.6.
A - or -component, -generator handlebody link of genus is reducible if and only if the trivial knot or a -generator link is a factor of some factorization of .
Corollary 2.7.
A -generator handlebody link of type or is reducible if and only if the trivial knot, -generator knot, or -generator link is a factor of some factorization of .
3. Irreducibility tests
3.1. Homomorphisms to a finite group
Definition 3.1.
Given a handlebody link and a finite group , is the number of conjugacy classes of homomorphissm from to , is the number of conjugacy classes of homomorphisms from to a subgroup of isomorphic to , and is the number of homomorphisms from to .
Lemma 3.1.
Suppose any subgroup of either has trivial centralizer or is abelian, and any two maximal abelian subgroups of have trivial intersection. Let , , be isomorphism types of maximal abelian subgroups of , and be the number of maximum abelian subgroups isomorphic to . Then for any handlebody link , can be expressed in terms of and
| (3.1) |
Proof.
The difference
| (3.2) |
is the number of conjugacy classes of homomorphisms whose images have trivial centralizers. On the other hand, for such a homomorphism , we have
for any non-trivial element , and hence the conjugacy class of contains members. Now, since the intersection of any two maximal abelian subgroups is trivial, the difference
| (3.3) |
is the number of homomorphisms whose images have trivial centralizers. Therefore dividing (3.3) by gives us (3.2), that is,
and this proves the formula (3.1). ∎
It is not difficult to check that satisfy conditions in Lemma 3.1, whence we derive the following formulas.
Corollary 3.2.
Let be the cyclic group of order , and . Then
| (3.4) | ||||
| (3.5) | ||||
Given an injective homomorphism , then the number of conjugacy classes of elements in representable by elements in is independent of if any two subgroups of isomorphic to are conjugate. If furthermore is a maximal abelian subgroup with being the centralizer of every element in , then can be computed explicitly.
Lemma 3.3.
Under the assumptions preceding the lemma, if , then
Proof.
Firstly, since is abelian, any homomorphism from to factors through the abelianization of , which is the free abelian group of rank . Especially, (resp. ) is equal to the numbers (resp. of conjugacy classes) of homomorphisms from to . This implies the first identity.
For the second identity, we let
and be selected representatives of the conjugacy classes of elements in . Note that if , we have .
For , up to conjugation, we may assume the -th copy of is sent to . There are homomorphisms when , and homomorphisms when , because the centralizer of is . As a result, we obtain the recursive formula
and hence
| (3.6) |
This implies the second equality after we substitute into (3.6). ∎
Maximal abelian subgroups of satisfy conditions assumed in Lemma 3.3, and hence we have the formulas:
| (3.7) | ||||
| (3.8) | ||||
| (3.9) |
Corollary 3.4.
For a genus handlebody link , we have
For the sake of convenience, we let denote the set of conjugacy classes of homomorphisms from to ; especially, we have .
Lemma 3.5.
For a -generator knot , or . In each case, contains four conjugacy classes represented by homomorphisms whose images are abelian. If , the two additional conjugacy classes are represented by surjective homomorphisms.
Proof.
Since any non-surjective homomorphism factors throught the abelianization of , is either trivial or isomorphic to or . By (3.8), the number of conjugacy classes of non-surjective homomorphisms are
and hence .
Now, consider a two-generator presentation of
| (3.10) |
and its abelianization:
| (3.11) |
let be the image of under (3.11), respectively. Suppose both and are non-zero, then either or . If , we replace with by ; this implies a new presentation of :
where , and vanishes under the composition
Similarly, if , we replace with by to get a new presentation
where , and vanishes under the composition
Therefore, given a surjective homomorphism , we may assume in (3.10) is in the commutator of and of order and is of order . Up to conjugation, there are only two such homomorphisms: one corresponds to , the other ; note that every two elements of order in are conjugate with respect to or . This shows there are at most two surjective homomorphisms from to , and they always appear in pairs because there exists an automorphism of sending to , namely
| (3.12) |
∎
Lemma 3.6.
If is a -generator link, then is , , , or . In each case, contains elements represented by homomorphisms whose images are abelian. If , then any additional conjugacy class is represented by surjective homomorphisms.
Proof.
Suppose is non-surjective, then it factors through the abelianization of , so by (3.8), the number of conjugacy classes of non-surjective homomorphism can be computed by
and particularly, .
Suppose is onto, and
is a presentation of . Then either both and are of order or one of them is of order and the other order . In the former case, up to conjugation, there are four possibilities:
By (3.12) if and only if since
Therefore, I and IV appear in pair; so do II and IV, for a similar reason. Now, if one of and is of order , we also have four possibilities:
They appear in pairs as in the previous case. Thus, is an even integer between and . ∎
3.2. Necessary conditions for reducibility
Lemma 3.7.
Given a reducible handlebody link of genus , if the trivial knot is a factor of some factorization of , then
Proof.
By the assumption, the knot group is isomorphic to the free product , where is a handlebody link of genus .
Recall that contains four elements by (3.8); let be homomorphism representing these four conjugacy classes with trivial, isomorphic to , and isomorphic to . Then observe that, given a homomorphism ; by conjugating with some elements in , we may assume its restriction is one of
Case 1: . Let be two homomorphisms with
Then they are in the same conjugacy class if and only if their restrictions are conjugate, so there are conjugacy classes in Case 1.
Case 2: . Let be two homomorphisms with
Then they are in the same conjugacy class if and only if
Hence in case 2, the number of conjugacy classes is
Case 3: , or . Let be two homomorphisms with
Then they are in the same conjugacy class if and only if
and therefore for each , there are
conjugacy classes.
Summing the three cases up gives the formula of in terms of the -invariants of :
| (3.13) |
Combining (3.13) with (3.7) and Corollary 3.4, we get the equation
which implies the first assertion.
can be computed in a similar manner. First note that contains five elements by (3.9), and they are represented by homomorphisms
| (3.14) |
with trivial, isomorphic to , isomorphic to , and , isomorphic to . As with the case of , given a homomorphism , by conjugating with some element in , we may assume its restriction on is one of the representing homomorphisms in (3.14). The number of conjugacy classes of homomorphisms that restrict to is and the number of conjugacy classes of homomorphisms that restrict to , or , is
| or |
respectively, and summing them up givues the formula of :
| (3.15) |
The formula (3.15), together with (3.7) and Corollary 3.4, implies the identity:
and thus the second assertion. ∎
Lemma 3.8.
Given a reducible handlebody link of genus , if a -generator knot is a factor of some factorization of , then
where or .
Proof.
By the assumption the knot group is isomorphic to the free product , where is a handlebody link of genus . By Lemma 3.5, might have two more elements than . Let be representing surjective homomorphisms of these two conjugacy classes. Then, since two homomorphisms
| (3.16) |
are conjugate if and only if
there are conjugacy classes of homomorphisms with the property (3.16). Adding this to (3.13), we obtain
| (3.17) |
where or . Plugging (3.7) and Corollary 3.4 into (3.17) implies the identity:
and therefore the assertion. ∎
Lemma 3.9.
Given a reducible handlebody link of genus , if a -generator link is a factor of some factorization of , then
where or .
Proof.
By the assumption, the knot group is isomorphic to the free product , where is a handlebody link of genus . By Lemma 3.6, contains elements, , or , where one conjugacy class for the trivial homomorphism, five for non-trivial homomorphisms whose images are in , eight for homomorphisms whose images isomorphic to , and for surjective homomorphisms. The same argument as in the proof of Lemmas 3.7 and 3.8 gives
| (3.18) |
where , or . Plugging (3.7) and Corollary 3.4 into (3.18), we obtain
and hence the lemma. ∎
4. Examples
4.1. Applications to handlebody knot/link tables
Irreducibility of handlebody knots in [5] and handlebody links in [1] are examined here with the irreducibility criteria (Corollary 1.5 and Table 1). The -and -invariants of handlebody links are computed by the Appcontour [9]; the same software is also used to find an upper bound of the rank of each knot group. In many cases, the upper bound is identical to the rank.
| handlebody knot | rank | -criterion (1.3) | -criterion (1.6) | ||
| 3 | 30 | ✓ | 156 | ✓ | |
| 3 | 22 | ? | 111 | ✓ | |
| 3 | 30 | ✓ | 156 | ✓ | |
| 3 | 30 | ✓ | 105 | ✓ | |
| 3 | 22 | ? | 365 | ✓ | |
| 3 | 30 | ✓ | 143 | ✓ | |
| 3 | 30 | ✓ | 105 | ✓ | |
| 3 | 22 | ? | 83 | ✓ | |
| 3 | 22 | ? | 111 | ✓ | |
| 3 | 22 | ? | 97 | ✓ | |
| 3 | 22 | ? | 97 | ✓ | |
| 3 | 30 | ✓ | 157 | ✓ | |
| 3 | 22 | ? | 105 | ✓ | |
| 3 | 30 | ✓ | 146 | ✓ | |
| 3 | 22 | ? | 195 | ✓ | |
| 3 | 22 | ? | 73 | ✓ | |
| 3 | 30 | ✓ | 135 | ✓ | |
| 3 | 30 | ✓ | 156 | ✓ | |
| 3 | 46 | ? | 353 | ✓ | |
| 3 | 46 | ? | 353 | ✓ | |
| 3 | 22 | ? | 267 | ✓ |
The results of the irreducibility test are recorded in Tables 2 and 3, where the check mark stands for the corresponding condition(s) not satisfied, and hence the handlebody link is irreducibile, and the question mark means the opposite, so its irreducibility is inconclusive. To avoid confusion, is added to the name of each handlebody knot in [5]; so is to the name of each handlebody link in [1].
Since all handlebody knots in [5] are -generator, by Corollary 1.5, if either does not divide , or does not divide , is irreducible. On the contrary, in Table 3 different criteria are required to test each case, depending on the rank and the number of component (the column “comp.”) based on Table 1. For instance, for a -generator handlbody link of type , such as , if it fails either of (1.3) and (1.6), it is irreducible. But, for , which is possibly -generator, we need to have both (1.3) and (1.4) failed in order to draw a conclusion; also, the criterion is not applicable in this case.
| comp. | handlebody link | rank | -criterion | -criterion | ||
|---|---|---|---|---|---|---|
| 2 | 3 | 114 | ✓ | 600 | ✓ | |
| 98 | ✓ | 660 | not applicable | |||
| 3 | 90 | ✓ | 600 | ✓ | ||
| 3 | 106 | ? | 689 | ✓ | ||
| 3 | 90 | ✓ | 469 | ✓ | ||
| 3 | 106 | ? | 689 | ✓ | ||
| 210 | ✓ | 4020 | not applicable | |||
| 3 | 130 | ? | 1380 | ✓ | ||
| 98 | ✓ | 597 | not applicable | |||
| 3 | 114 | ✓ | 1401 | ✓ | ||
| 3 | 4 | 310 | ? | 1841 | not applicable | |
| 4 | 326 | ✓ | 2636 | not applicable | ||
| 4 | 486 | ✓ | 5876 | not applicable | ||
| 4 | 502 | ? | 5883 | not applicable | ||
| 4 | 822 | ✓ | 19308 | not applicable | ||
| 4 | 486 | ✓ | 5876 | not applicable | ||
| 4 | 5 | 1242 | ✓ | 12072 | not applicable |
4.2. Irreducible handlebody links of a given type
Here we present a construction of irreducible handlebody link of any given type. First we introduce the notion of -irreducibility for handlebody-link-disk pairs.
Definition 4.1 (-irreducibility).
A handlebody link is -irreducible if either its complement admits no incompressible disks or it is a trivial knot. A handlebody-link-disk pair is a handlebody link together with an incompressible disk . The pair is -irreducible if there exists no incompressible disk in the complement with . An unknot with a meridian disk is the trivial -irreducible handlebody-link-disk pair.
-irreducibility is equivalent to irreducibility for genus handlebody knots [15] but stronger in general [13, Examples -], [1, Remark ]. Any -irreducible handlebody link with an incompressible disk is a -irreducible pair. On the other hand, the underlying handlebody link of a -irreducible handlebody-link-disk pair could be trivial (left handlebody-knot-disk pair in Fig. 2(a)).
Definition 4.2 (Knot sum).
The knot sum of two handlebody-link-disk pairs is a handlebody link obtained by gluing together as follows: first remove a -ball (resp. ) with a tubular neighborhood of of from , where can be identified with the oriented -manifold using the given orientation on . Then the knot sum is given by gluing resultant -manifolds via an orientation-reversing homeomorphism with , mod .
The knot sum resembles the order- connected sum of spatial graphs [8].
Theorem 4.1.
The knot sum of two non-trivial -irreducible handlebody-link-disk pairs is -irreducible.
Proof.
We prove by contradiction. Suppose the knot sum
is not -irreducible, and is an incompressible disk in .
Let be the -ball such that is the complement of , and denote the intersection annulus by . Isotopy such that the number of components of is minimized.
Claim: . Suppose the intersection is non-empty, then we can choose a component of that is innermost in . must be an arc, for otherwise it would contradict either the -irreducibility of or the minimality. cuts into two disks, one of which, say , has no intersection with . Without loss of generality, we may assume is in .
If is essential in , then is equivalent to the union of a tubular neighborhood of in and in . Since is an arc connecting two sides of in , is not separating and therefore a meridian disk of . In addition, and intersect at only one point, so is either trivial or not -irreducible, contradicting the assumption.
If is inessential in , let be the disk cut off from by . Then is a compressing disk in . If is inessential in , the intersection can be removed—with other intersection arcs intact—by isotopying . On the other hand, the -irreducibility of forces to be inessential in . Thus, we have proved the claim, from which the theorem follows readily. ∎
| incompressible disk |
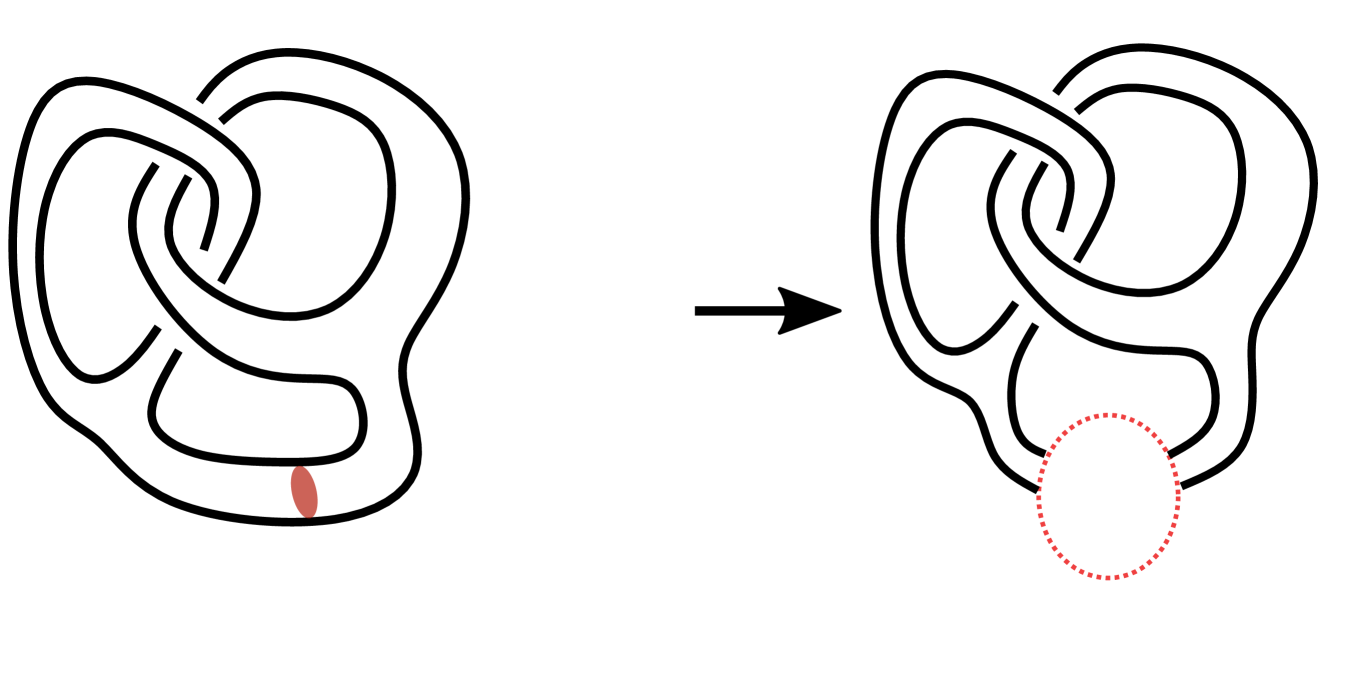
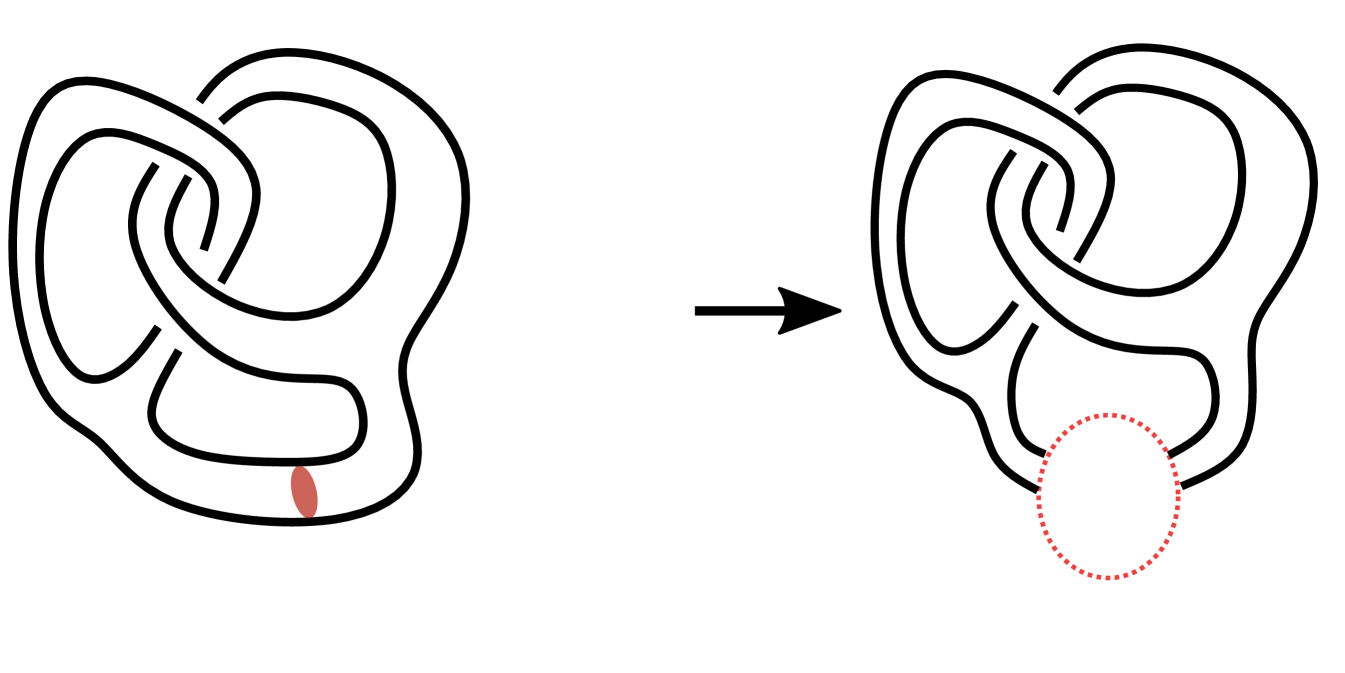
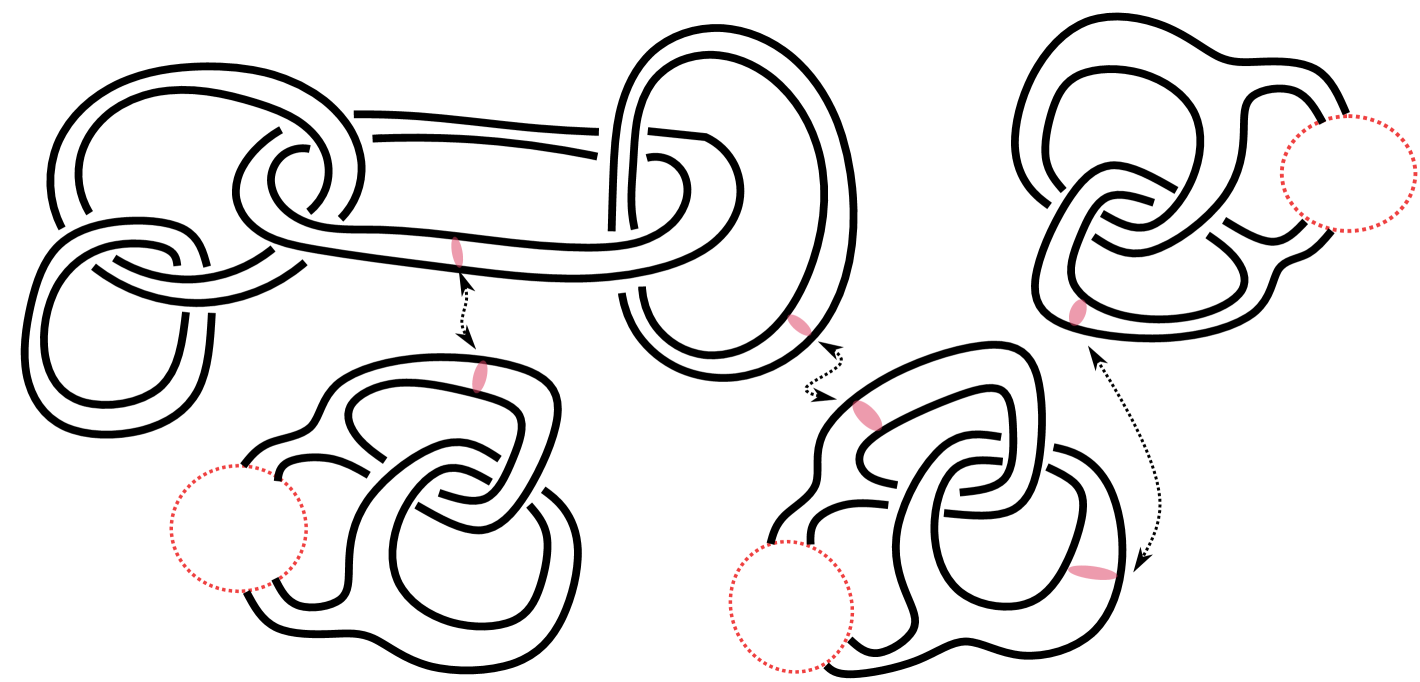
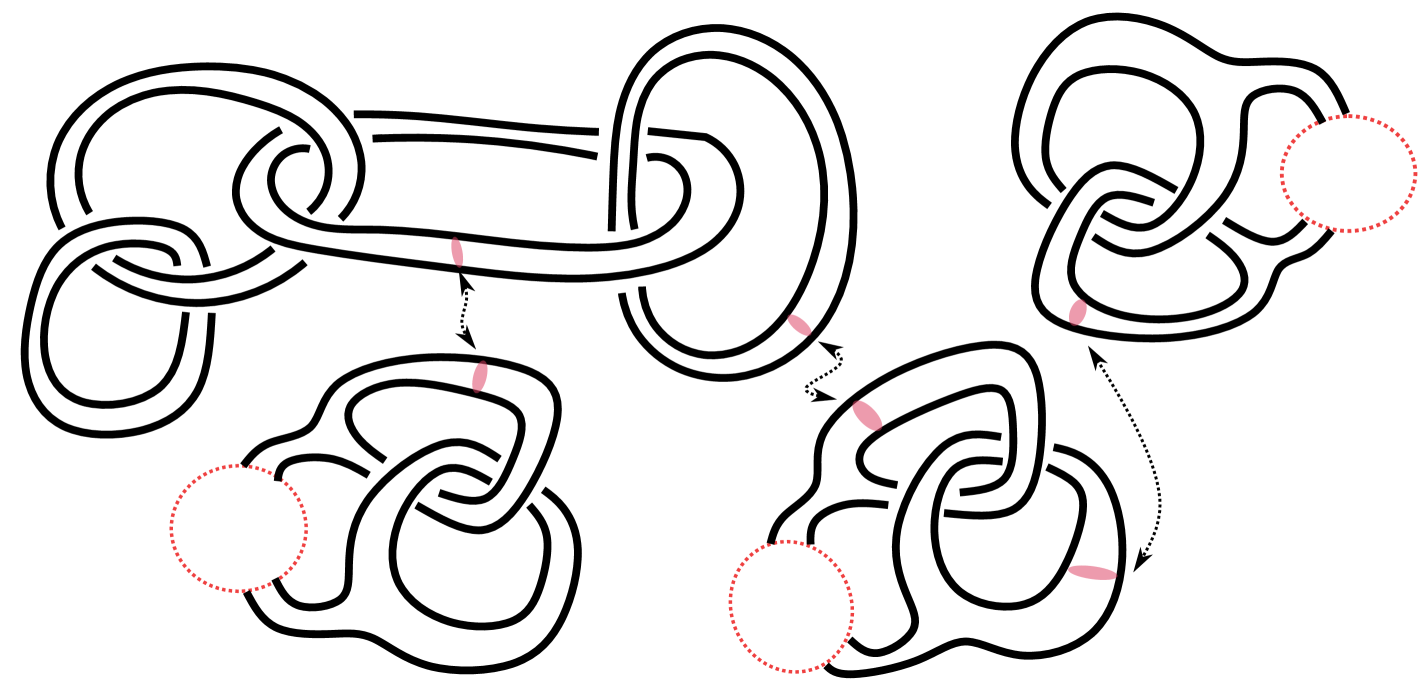
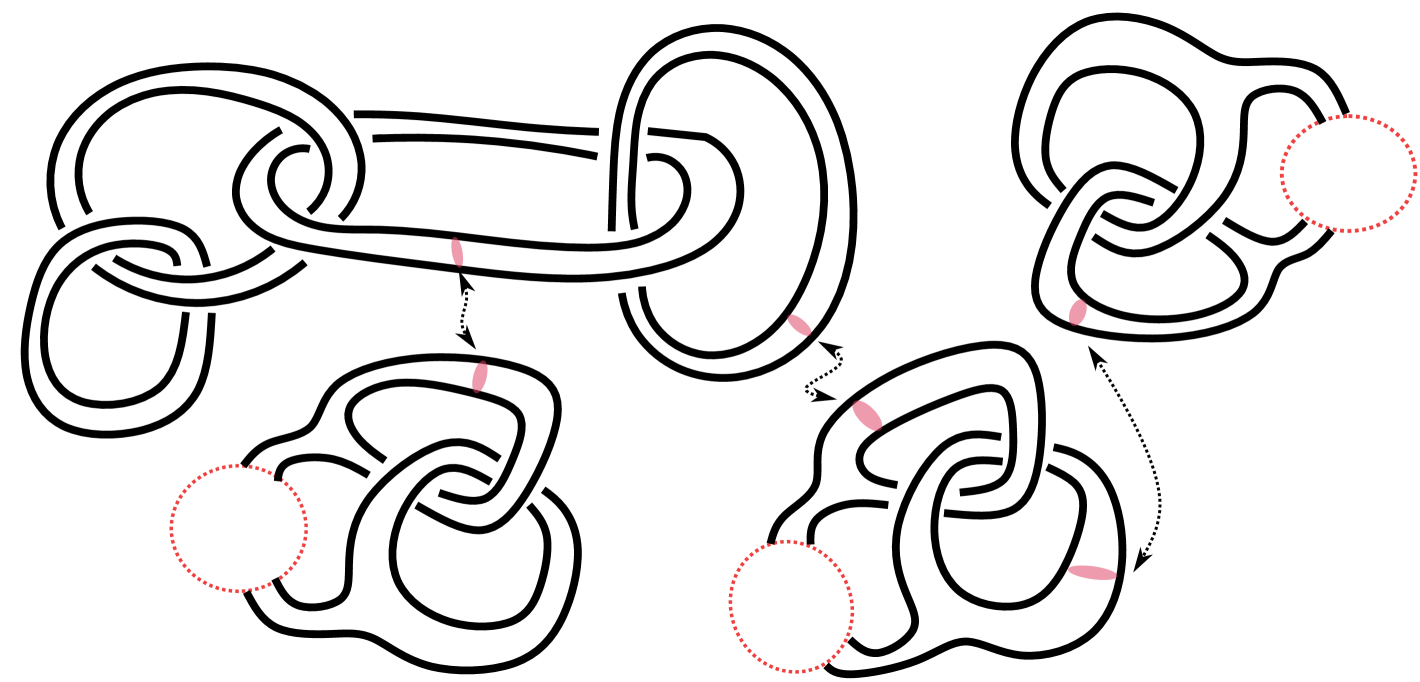
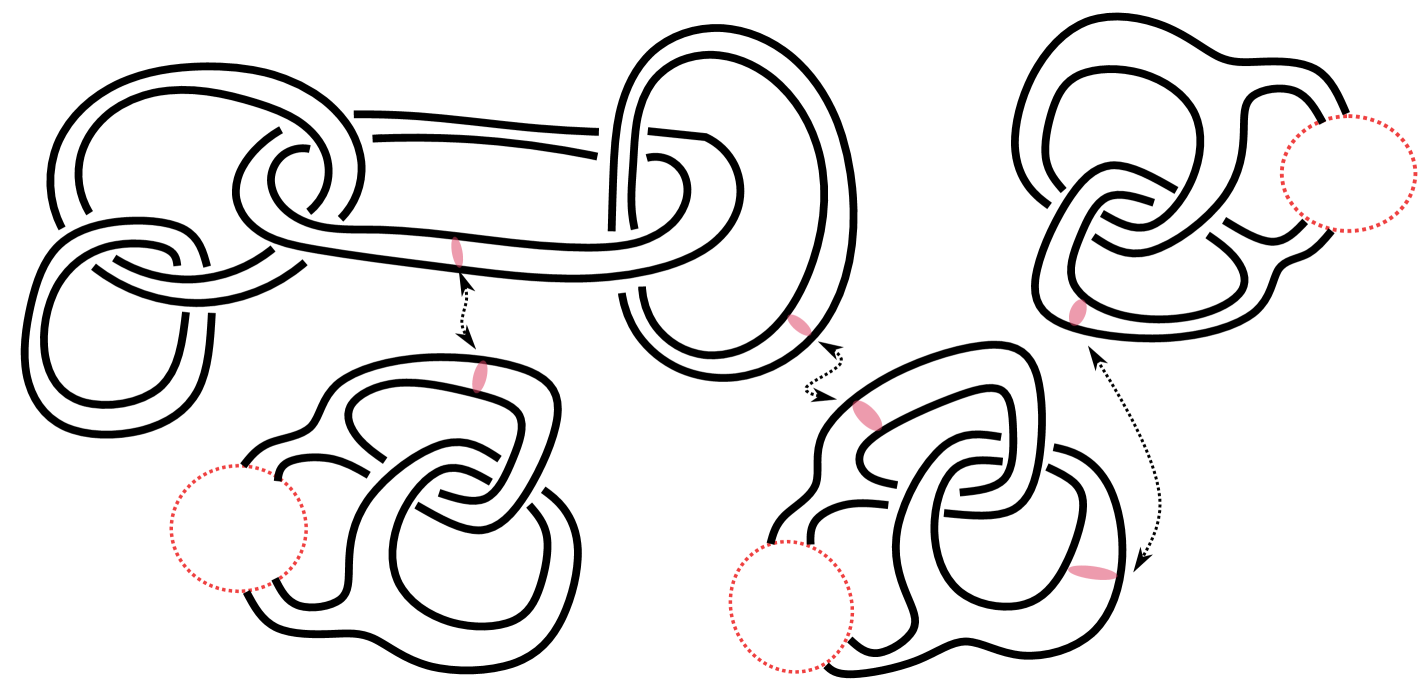
| chain of rings |
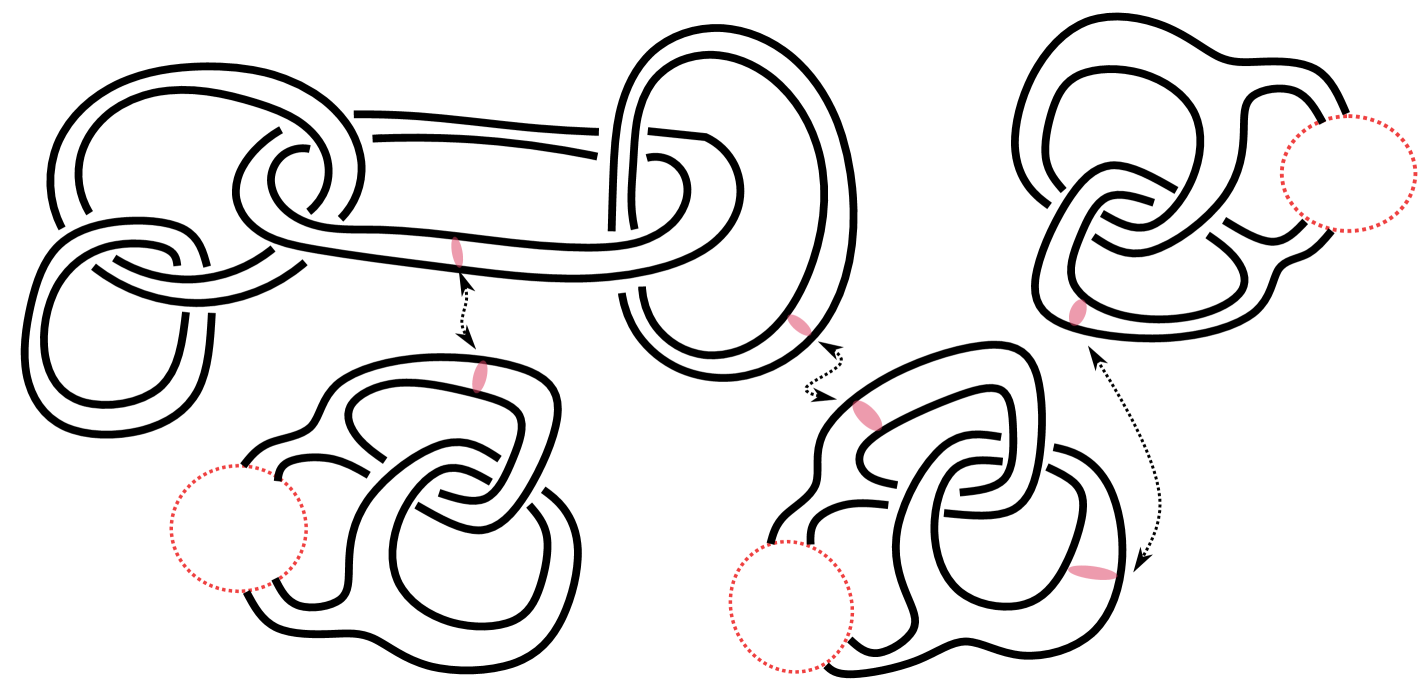
In Fig. 4.2, are knots or links; if in Fig. 2(a) is the composition of two Hopf links, the resulting knot sum is . Hence its irreducibility, which cannot be seen by our irreducibility test, follows from Theorem 4.1. The following corollary generalizes Suzuki’s example [13, Theorem ].
Corollary 4.2.
Given non-negative integers with , there is an irreducible handlebody link of type .
Proof.
Consider a chain of rings with -component—a knot sum of Hopf links (Fig. 2(b)). Label each ring with a number in , and for the ring with label ,
we consider its knot sum with an irreducible handlebody knot of genus , which can be obtained by performing the knot sum operation iteratively on handlebody knots in [5] with meridian disks (Fig. 4.1). The resultant handlebody link is necessarily irreducible by Theorem 4.1 and of the prescribed type. ∎
Acknowledgements
The paper is benefited from the support of National Center for Theoretical Sciences.
References
- [1] G. Bellettini, G. Paolini, M. Paolini, Y.-S. Wang: Complete classification of -handlebody links up to six crossings, to appear.
- [2] I. A. Grushko: On the bases of a free product of groups, Matematicheskii Sbornik, 8 (1940), 169–182.
- [3] A. Ishii: Moves and invariants for knotted handlebodies, Algebr. Geom. Topol. 8, No. 3 (2008), 1403–1418.
- [4] A. Ishii, K. Kishimoto: The quandle coloring invariant of a reducible handlebody-knot, Tsukuba J. Math. 35 (2011), 131–141.
- [5] A. Ishii, K. Kishimoto, H. Moriuchi, M. Suzuki: A table of genus two handlebody-knots up to six crossings, J. Knot Theory Ramifications 21 (2012), 1250035.
- [6] T. Kitano, M. Suzuki: On the number of -representations of knot groups J. Knot Theory Ramifications 21 (2012), 1250035.
- [7] W. Magnus: Über freie Faktorgruppen und freie Untergruppen gegebener Gruppen, Monatsh. Math. 47 (1939), 307–313.
- [8] H. Moriuchi: An enumeration of theta-curves with up to seven crossings J. Knot Theory Ramifications 18 (2) (2009) 67–197.
- [9] M. Paolini: Appcontour. Computer software. Vers. 2.5.3. Apparent contour. (2018) http://appcontour.sourceforge.net/.
- [10] J. Stallings: Homology and central series of groups, J. Algebra 2 (1965), 170–181.
- [11] U. Stammbach: Ein neuer Beweis eines Satzes von Magnus, Proc. Camb. Phil. Soc. 63 (1967), 929–930.
- [12] S. Suzuki: On linear graphs in 3–sphere, Osaka J. Math. 7 (1970), 375–396.
- [13] S. Suzuki: On surfaces in 3-sphere: prime decompositions, Hokkaido Math. J. 4 (1975), 179–195.
- [14] Y. Tsukui: On surfaces in 3-space, Yokohama Math. J. 18 (1970), 93–104.
- [15] Y. Tsukui: On a prime surface of genus and homeomorphic splitting of -sphere, The Yokohama Math. J. 23 (1975), 63–75.